Symmetric Sequential Stability in the Graph Model for Conflict Resolution with Multiple Decision Makers

Abstract

In this work, we generalize a solution concept, called symmetric sequential stability (SSEQ), in the graph model for conflict resolution (GMCR) for conflicts involving n decision makers. We present new relations of this concept with existing stability definitions in the GMCR, namely: Nash stability, general metarational stability, symmetric metarational stability, sequential stability, limited-move stability of horizon 3 and credible metarational stable states of 2 rounds. We also present the SSEQ stability definition for a coalition and its relationship with existing solution concepts in that case. Finally, SSEQ stability is extended for GMCR with uncertain, probabilistic and fuzzy preferences.

1 Introduction

Based on concepts of game theory and on the conflict analysis of Hipel and Fraser (1984), the graph model for conflict resolution (GMCR) is a mathematical tool which can be used to describe and analyze conflicts (Kilgour et al. 1987). This model describes a set of possible states (outcomes) that can arise in a conflict according to actions that can be taken by individuals involved in a conflict, called decision makers (DMs). DMs may change the conflict state by changing some of their actions taking into account their preferences over the set of possible states in the conflict and the countermoves of the other DMs.

Since DMs can behave in different ways, there are several stability definitions (solution concepts) which determine whether or not a DM has incentive to move away from a given state. If some state satisfies a particular stability definition for all DMs, then it is called a possible conflict resolution (equilibrium). In the GMCR, there are a number of stability concepts used in conflict resolution. Some of these concepts are: Nash stability (Nash 1950), general metarationality (${ GMR}$) (Howard 1971), symmetric metarationality (${ SMR}$) (Fraser and Hipel 1979), sequential stability (${ SEQ}$) (Fraser and Hipel 1979), limited-move stability of horizon h ($L_{h}$) (Kilgour 1985) and credible metarational stable states of r rounds (${ CMR}_{r}$) (Zeng et al. 2007). The definition of Nash stability of a state considers only one move beyond the present state, while those of GMR and SEQ take into account one step further to examine countermoves. Finally, the definition of SMR extends it further to two steps ahead. The definitions of $L_{h}$ and $CMR_{r}$ have variable foresight, i.e., the analyst defines the number of foreseeable steps, which is called horizon.

In a preliminary work (Rêgo and Vieira 2015), we proposed the symmetric sequential stability (SSEQ) concept for conflicts with 2 DMs. In this definition, as in the case of SMR, the conflict is analyzed up to three steps ahead from the current state and it is required that the countermove is also beneficial to the opponent, as in the case of SEQ stability notion. Moreover, it is assumed that for stability the focal DM cannot escape to a preferred state once the countermove is taken, as in the SMR stability notion.

In this article, we generalize the SSEQ stability, proposed in Rêgo and Vieira (2015), for n-DM conflicts and we obtain new results relating this new concept to the definitions previously mentioned. We also present the SSEQ stability definition for a coalition and its relations with the classical stability definitions of coalitional analysis. Additionally, we extended the SSEQ concept for n-DM GMCR with uncertain (Li et al. 2004), probabilistic (Rêgo and Santos 2015) and fuzzy preferences (Hipel et al. 2011).

This paper is organized as follows. In Sect. 2, the GMCR and the stability definitions previously mentioned are recalled. In Sect. 3, we present the definition of SSEQ stability for a DM and for a coalition and we present relationships of this definition with the other existing solution concepts. In Sect. 4, we extend the SSEQ concept for other preference structures. In Sect. 5, we present an application to illustrate the proposed solution concept. Finally, in Sect. 6, we give our main conclusions and directions for future work.

2 GMCR and Solution Concepts

In this section, we recall the basic idea of the GMCR and some stability definitions for n-DM conflicts and for coalitional analysis. Recalling such definitions is useful since we establish relationships between them and SSEQ stability.

The GMCR was introduced by Kilgour et al. (1987) and consists of a set of DMs $N=\{1, \ldots , n\}$, a set of possible states or conflict scenarios, $S=\{s_1, \ldots , s_m\}$, and, for each DM $i \in N$, a preference relation over S and a directed graph $D_{i} = \{S, A_{i}\}$, where $A_{i} \subseteq S \times S$ determines to what states DM i can lead the conflict from each state s, called reachable states from s in one step.

As in most game theoretic models, in GMCR it is assumed that preferences of a DM i can be expressed by a binary relation on S, denoted by $\succ _{i}$, where $s\succ _{i}s_1$ indicates that DM i strictly prefers state s to state $s_1$. The weak preference relation, $\succeq _{i}$, is used to model lack of strict preference, where $s\succeq _{i}s_1$ means that DM i does not strictly prefer state $s_1$ to state s.

The study of possible moves and countermoves made by DMs in strategic conflicts is called stability analysis. Several different behaviors can arise in conflict situations, so many concepts of stability have been proposed and are still being obtained. We now recall six stability concepts used in the GMCR, namely: Nash stability, GMR stability, SMR stability, SEQ stability, $L_h$ stability and $CMR_r$ stability.

Let us now introduce some notation. For $i \in N$, define $R_{i}(s) = \{s_1 \in s:(s, s_1) \in A_{i} \}$, the set of reachable states from s by DM i, and $R_{i}^{+}(s) = \{s_1 \in R_{i} (s): s_1 \succ _{i} s \}$, the set of unilateral improvements from s by DM i. As usual in the GMCR literature, we assume that $s\notin R_i(s)$, $\forall s\in S$ and $\forall i\in N$.

Let $H \subseteq N$ be a subset of DMs, called a coalition, and let $R_{H}(s) \subseteq S$ denote the set of states that can be reached from s by any legal sequence of movements by DMs in H, where a legal sequence of movements is one in which no DM moves twice consecutively. Finally, let $R_{H}^{+}(s) \subseteq S$ be the set of states that can be reached from s by any legal sequence of unilateral improvements by DMs in H, where a legal sequence of unilateral improvements is legal sequence of moves in which DMs only make unilateral improvements. The formal definitions of the sets $R_{H}(s)$ and $R_{H}^{+}(s)$ can be found in Inohara and Hipel (2008).

In Table 1, we recall the definitions of Nash, GMR, SMR and SEQ stability of a state s for some DM i for n-DM conflicts.

Table 1 Stability of a state s for some DM i in the GMCR

In what follows, we recall the limited-move stability definition for conflicts with two DMs, which is sufficient to show that in general there is no relationship between SSEQ and this solution concept. Moreover, for this definition, we assume that DMs are not indifferent between any pair of states.

Let $K_i(s)=\#\{s_1\in S:s\succ _i s_1\}$ be the cardinality of the set of states that are worse than s for DM i. For a positive integer number, h, a DM who foresees a sequence of length at most h is said to be a DM with horizon h. Let $G_h(i, s) \in S$, $i \in N$, be the state that DM i believes that will be the final state of a conflict of length h beginning at state s in which DM i moves first. Then $(G_h(i, s), s \in S)$ is the anticipation vector of DM i and, for convenience, $G_{0}(i, s) = s$. The anticipation vector of DM i is constructed, inductively (see, Fang et al. 1993). Thus, a state $s\in S$ is limited-move stable with horizon h ($L_h$ stable) for DM $i \in N$ iff $G_{h}(i, s) = s$.

Finally, we recall a solution concept called i-credible metarationality (Zeng et al. 2007). This concept depends on the total number, h, of moves and counter-moves allowed. This concept is based on the notion of policies for DMs, where $\textit{P}_{j}$ is DM j’s policy, which is a function $\textit{P}_{j}: S \rightarrow S$ such that $\textit{P}_{j}(s) \in R_{j}(s) \cup \{s\}$, i.e., a policy for a DM specifies what his or her action will be at each state if that state arises. The metarational tree consists of a root, controlled by some DM i and vertices which are controlled by some DM. For example, if i takes the initiative and moves from the initial state s to some state $s_1 \in R_i(s)$, then another DM $j \in N-\{i\}$ moves from $s_1$ to $s_2 = \textit{P}_{j}(s_1) \in R_j(s_1)\cup \{s_1\}$. Depending on j’s move, DM $k \in N-\{ j\}$ might move from state $s_2$ to $s_3 = \textit{P}_{k}(s_2) \in R_k(s_2)\cup \{s_2\}$, and so on. It is assumed that no DM may move twice consecutively and that if some DM j stays at a given state, then the conflict ends at that state. Given DM i, a sequence is said to be of r rounds with respect to DM i if there are r states in the sequence at which DM i moves. A sequence of r rounds with respect to DM i is called an i-sequence, if it ends with a final move from DM i.

In Zeng et al. (2007), the authors present a definition of credible metarational stable states of r rounds for the case in which a DM’s policy is deemed to be credible, i.e., if DMs always move to a more preferred state. Hence, a credible policy is defined as $\textit{P}_{i}^{c}(s) \in R_{i}^{+}(s) \cup \{s\}$. By requiring a policy to be credible, one obtains a credible metarational tree, denoted by $CMR_{r}$. Next, we present the definition of an i-credible metarational stable state with r rounds for DM i proposed in Zeng et al. (2007). A state $s \in S$ is i-credible metarational stable with r rounds for DM i, denoted by $CMR_{r}$, if for each $s_1\in R_i^+(s)$, there is a set of credible policies $\textit{P}_{j}^{c}$ for all $j \ne i$, and an i-sequence starting with DM i moving from s to $s_1$ of r rounds or shorter such that DM i does not prefer the result of this sequence to s.

2.1 Coalitional Stability Analysis

A coalition is a set of DMs acting together to achieve results which are desirable for all DMs in the set. Next, we recall the solution concepts in the GMCR which take into account the possibility of coalitions formation. The coalition stability concepts recalled in this subsection are due to Inohara and Hipel (2008) and Kilgour et al. (2001).

Let $\varphi (N)$ be the class of all coalitions of DMs in N and $R_{H}^{++}(s) = \{s_1 \in S : s_1 \in R_{H}(s)$ and $s_1 \succ _{i} s$ for all $i\in H \}$ be the set of coalitional improvement moves from s by coalition H. Let $\textit{C}\subseteq \varphi (N)$ and let $R_{\textit{C}}(s)$ be the set of reachable states by class $\textit{C}$ from s by a legal sequence of movements, where a legal sequence of movements of a class $\textit{C}$ is one in which no coalition moves twice consecutively. Finally, let $R_{\textit{C}}^{++}(s)$ be the set of states that can be reached from s by any legal sequence of coalitional improvement moves by coalitions in $\textit{C}$, where a legal sequence of coalitional improvement moves is a legal sequence of moves in which coalitions only make coalitional improvement moves. The formal definitions of the sets $R_{\textit{C}}(s)$ and $R_{\textit{C}}^{++}(s)$ can be found in Inohara and Hipel (2008) and Kilgour et al. (2001).

In Table 2, we recall the definitions of CNash, CGMR, CSMR and CSEQ stability of a state s for some coalition H for n-DM conflicts

Table 2 Stability of a state s for some coalition H in the GMCR

In this setting, we also have the notions of stability for a DM, where some state is stable for a DM if it is stable for all coalitions including such DM.

3 Symmetric Sequential Stability and its Relations with Other Solution Concepts

In this section we generalize the SSEQ stability definition proposed in Rêgo and Vieira (2015), to conflicts with n-DMs and introduce this definition for a coalition. Additionally, we present results which relate SSEQ and coalitional SSEQ to other stability definitions commonly used in the GMCR.

3.1 Symmetric Sequential Stability

Definition 1

A state $s \in S$ is symmetric sequentially (SSEQ) stable for ${ DM}$ $i \in N$ iff for every $s_1 \in R_{i}^{+}(s)$, there exists $s_2 \in R_{N-\{i\}}^{+}(s_1)$ such that $s\succeq _{i}s_2$ and $s\succeq _{i}s_3$ for every $s_3 \in R_i(s_2)$.

The SSEQ definition, as the name implies, is a type of sequential stability in which a DM, while planning to move, considers not only the reaction of his or her opponents, but also his own counter-reaction. It is important to emphasize that the counter-reaction does not need to be a unilateral improvement for the DM; it is required that the resulting state cannot be better than the current state for every possible reachable counter-reaction. This is specially important in cases where preferences are not negatively transitive.

There are many results that establish relationships between the various notions of stability used in the GMCR. In what follows, we present generalizations of the results established in Rêgo and Vieira (2015) and new ones relating SSEQ stability with $L_3$ and $CMR_2$. Theorem 1 states the relationship between SSEQ, Nash, SMR and SEQ stability.

Theorem 1

The following statements are true in the GMCR:

• (a) If state s is Nash stable for DM i, then s is SSEQ stable for DM i.

• (b) If state s is SSEQ stable for DM i, then s is SEQ stable for DM i.

• (c) If state s is SSEQ stable for DM i, then s is SMR stable for DM i.

Proof

For (a), if s is Nash stable for DM i, then $R_i^{+}(s)=\emptyset$ which implies that s is SSEQ stable for DM i.

For (b), suppose that s is SSEQ stable for DM i. Thus, for all $s_1\in R_{i}^{+}(s)$, there exists $s_2\in R_{N-\{i\}}^{+}(s_1)$ such that $s\succeq _{i}s_2$ and $s\succeq _{i}s_3$ for every $s_3 \in R_i(s_2)$. Therefore, it is true that for all $s_1\in R_{i}^{+}(s)$, there exists $s_2\in R_{N-\{i\}}^{+}(s_1)$ such that $s\succeq _{i}s_2$, which implies that s is SEQ stable for DM i.

For (c) suppose that s is SSEQ stable for DM i. Thus, for all $s_1\in R_{i}^{+}(s)$, there exists $s_2\in R_{N-\{i\}}^{+}(s_1)$ such that $s\succeq _{i}s_2$ and $s\succeq _{i}s_3$ for every $s_3 \in R_i(s_2)$. Since $R_{N-\{i\}}^{+}(s_1) \subseteq R_{N-\{i\}}(s_1)$, it follows that for all $s_1\in R_{i}^{+}(s)$, there exists $s_2 \in R_{N-\{i\}}(s_1)$ such that $s\succeq _{i}s_2$ and $s\succeq _{i}s_3$ for every $s_3 \in R_i(s_2)$, which implies that s is SMR stable for DM i. $\square$

The following hypothetical example illustrates that, in general, SMR and SEQ stability together do not imply SSEQ stability.

Fig. 1

Conflict in the graph form: a DM i; b DM j

Example 1

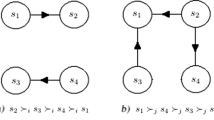
Consider the hypothetical conflict shown in Fig. 1. In this example, state s is SMR and SEQ, but it is not SSEQ for DM j. Indeed, it is SMR since $R_{j}^{+}(s)=\{s_3\}$ and state $s_2$, which is reachable for DM i from $s_3$, is such that $s \succeq _{j} s_2$ and $s \succeq _{j} s_5$, where $s_5$ is the unique reachable state for DM j from $s_2$. Also, we have that s is SEQ for DM j, since $R_{j}^{+}(s)=\{s_3\}$ and $s_1 \in R_{i}^{+}(s_3)$ is such that $s \succeq _{j} s_1$. But state s is not SSEQ for DM j because $s_4 \succeq _{j} s$, where $s_4$ is reachable for DM j from $s_1$.

The next theorem describes a particular case where SSEQ is equivalent to SMR and SEQ together.

Theorem 2

Suppose that a strategic conflict is composed of 2 DMs. If for every $s\in S$ and $i\in N$, the cardinality of $R_i(s)$ is at most equal to one, then a state is SSEQ for DM i if, and only if, it is SMR and SEQ for DM i.

Proof

By Theorem 1, if state s is SSEQ then it is SMR and SEQ. Suppose that s is SMR and SEQ for DM i. Thus, either $R_{i}^{+}(s) = \emptyset$, in which case s is also SSEQ, or $R_{i}^{+}(s) = \{s_1\}$. By hypothesis and since no state is reachable to itself, the fact that s is SEQ implies that there exists a unique state $s_2 \in S$, such that $R_{j}(s_1)=R_{j}^+(s_1)=\{s_2\}$ and $s\succeq _{i}s_2$. Thus, since s is SMR it follows that $s\succeq _{i}s_3$ for all $s_3 \in R_{i}(s_2)$. Therefore, there exists $s_2 \in R_{j}^{+}(s_1)$ such that $s\succeq _{i}s_2$, and $s\succeq _{i}s_3$ for all $s_3 \in R_{i}(s_2)$, which implies that s is SSEQ for DM i. $\square$

The following example illustrates that Theorem 2 is not true if the strategic conflict has more than two DMs.

Example 2

Consider a hypothetical conflict situation in which there are 3 DMs, i, j and k. Suppose that in this conflict there are five states, states s, $s_1$, $s_2$, $s_3$ and $s_4$. Assume that the preferences of DM i, DM j and DM k are, respectively, given by $s_1 \succ _{i}s_4 \succ _{i}s \succ _{i}s_2 \succ _{i}s_3$, $s_1 \succ _{j}s_2 \succ _{j}s \succ _{j}s_3 \succ _{j}s_4$ and $s_3 \succ _{k}s_1 \succ _{k}s \succ _{k}s_4 \succ _{k}s_2$. Consider also that $R_{i}(s) = \{s_1\}$, $R_{j}(s_1) = \{s_2\}$, $R_{i}(s_2)= R_{k}(s_1)=\{s_3\}$, $R_{i}(s_3)=\{s_4\}$ and that $R_{i}(s_1) = R_{i}(s_4) = R_{j}(s) = R_{j}(s_2) = R_{j}(s_3) = R_{j}(s_4)= R_{k}(s) = R_{k}(s_2) = R_{k}(s_3) = R_{k}(s_4)= \emptyset$, as illustrated in Fig. 2.

We now show that state s is SMR and SEQ for DM i, but it is not SSEQ. First, it is SMR since from the unique unilateral improvement for DM i from s, state $s_1$, DM j can lead the conflict to state $s_2$ and from $s_2$ DM i can only move to state $s_3$, but states $s_2$ and $s_3$ are worse than s for DM i. It is SEQ for DM i, since DM k has a unilateral improvement from $s_1$ leading the conflict to state $s_3$, which is worse than s for DM i.

On the other hand, state s is not SSEQ for DM i, since the unique unilateral improvement from state $s_1$ for coalition $\{j,k\}$ is state $s_3$, but from $s_3$ DM i can move to state $s_4$, which is preferred to state s by DM i.

Fig. 2

Conflict in the graph form: a DM i; b DM j and c DM k

Examples 3 and 4 below show that there is no relation between the stability concepts SSEQ and $L_{3}$. More specifically, Example 3 shows that if state s is SSEQ stable, then it may not be $L_{3}$ stable. Conversely, Example 4 illustrates the case of a state that is $L_{3}$ stable but is not SSEQ.

Example 3

Consider the conflict illustrated in Fig. 3, where the state space is given by $S = \{s, s_1, s_2, s_3\}$ and there are two DMs, i and j. Suppose that $R_i(s) = \{s_1 \}$, $R_i(s_1) = \{s \}$ and $R_i(s_2) = R_i(s_3)=\emptyset$. For DM j, suppose that $R_j(s) = R_j(s_2) = R_j(s_3) = \emptyset$ and $R_j(s_1) = \{s_2, s_3 \}$. Consider also that the preference relations of DMs i and j are given by $s_3 \succ _{i} s_1 \succ _{i} s \succ _{i} s_2$ and $s_3 \succ _{j} s_2 \succ _{j} s \succ _{j} s_1$, respectively. We now argue that state s is SSEQ for DM i, because the unique improvement for DM i from s is $s_1$, but, from state $s_1$, DM j can sanction DM i going to state $s_2$ such that $s_2$ is better than $s_1$ to DM j and worse than s to DM i. As DM i can not get out of $s_2$, we have that s is SSEQ for DM i. On the other hand, state s is not $L_3$ stable for DM i because from $s_1$, the anticipated state for DM j is $s_3$ and not $s_2$. Since $s_3$ is better than s to DM i, it follows that he intends to move away from s.

Fig. 3

Conflict in the graph form: a DM i; b DM j

Example 4

An example that illustrates that $L_3$ stability does not imply SSEQ stability is the chicken game described in Rapoport and Guyer (1967). In this game, two DMs, called DM i and DM j, have the choice of either swerving, denoted by S, thereby avoiding a collision, or continuing to drive straight ahead and hence selecting the strategy of not swerving, D. The graph form of the chicken game is shown in Fig. 4. The preference relation of DM i is given by $DS \succ _{i} SS \succ _{i} SD \succ _{i} DD$, and the preference relation of DM j is given by $SD \succ _{j} SS \succ _{j} DS \succ _{j} DD$. Using backward induction, working from the bottom to the top of the diagram in Fig. 5, we have that state SS is $L_3$ stable for DM i. On the other hand, this state is not SSEQ stable for DM i, because from state SS, the unique improvement for DM i is state DS. But from DS, there is no reachable improvement for DM j. Therefore, state SS is not SSEQ stable for DM i.

Fig. 4

Conflict in the graph form: a DM i; b DM j

Fig. 5

$L_3$ stability analysis of state SS for DM i. Source: Fang et al. (1993)

We have the following relationship, established in Theorem 3, between the concepts of SSEQ and $CMR_2$.

Theorem 3

If a state s is SSEQ for DM i, then s is $CMR_{2}$ stable for DM i.

Proof

Suppose that s is SSEQ stable for DM $i\in N$. Let us consider two cases: (a) $R_i^+(s)=\emptyset$ or (b) $R_i^+(s)\ne \emptyset$. If (a) occurs, then the unique credible metarational tree which has DM i moving at the root s has one round and ends once DM i stays at s. Thus, s is ${ CMR}_2$ stable for DM i in that case. If (b) occurs and $s_1\in R_i^+(s)$, then there exists a state $s_2\in R_{N-\{i\}}^+(s_1)$ such that $s \succeq _i s_2$ and $s \succeq _i s_3$, for all $s_3 \in R_i(s_2)$. Thus, there is a sequence of unilateral improvement moves by $N-\{i\}$ from $s_1$ leading the conflict to $s_2$, which is not preferred to s by DM i. If there are more than one of such sequences, choose one of them whose length is minimum, call it x. In x, every DM moves at most once in every state in that sequence. Let us use x to define credible policies for DM $j\in N-\{i\}$, as follows

$$\begin{aligned} P_j^c(s_t)= \left\{ \begin{array}{l@{\quad }l} s_u &{} \text{ if } \text{ there } \text{ is } \text{ a } \text{ move } \text{ by } \text{ DM } j \text{ from } s_t \text{ to } s_u \text{ in } x, \\ s_t &{} \text{ otherwise. } \\ \end{array} \right. \end{aligned}$$

Given that set of credible policies, since from $s_2$ DM i cannot move to a state that is preferred to s, it follows that there exists an i-sequence that starts with DM i moving from s to $s_1$ of 2 rounds and results in a state that is not preferred to s by DM i. Thus, also in this case, s is $CMR_2$ stable for DM i. $\square$

The following example illustrates that the reciprocal of Theorem 3 is not true.

Example 5

Consider a hypothetical conflict with 2 DMs, DM i and DM j, five states, namely, s, $s_1$, $s_2, s_3$ and $s_4$, and suppose that the reachable states are described by $R_{i}(s)=\{s_1\}$ , $R_{i}(s_2)=\{s_3, s_4\}$ and $R_{j}(s_1)=\{s_2\}$, as illustrated in Fig. 6.

Assume that preference relations are given by $s_1 \succ _{i} s_4 \succ _i s\succ _i s_3 \succ _i s_2$, and $s_2 \succ _{j} s_1 \succ _{j} s_3 \succ _{j} s_4 \succ _{j} s$. Suppose that DM i is at state s. State s is not SSEQ for DM i, since from s, DM i can move to a better state $s_1$, and, from $s_1$, the unique reaction of DM j is to lead the conflict to state $s_2$ which is not preferred to s by DM i but it is preferred to $s_1$ by DM j. However, from $s_2$, DM i can move to states $s_3$ and $s_4$, and state $s_4$ is better than s for DM i. On the other hand, s is $CMR_{2}$ stable for DM i, since there is a credible policy of DM j satisfying $P_j(s_1)=s_2$, such that the sequence ($s, i, s_1, j, s_2, i, s_3$) is an i-sequence of round 2 such that DM i does not prefer the result of this sequence to state s.

Fig. 6

A conflict where s is $CMR_2$ stable but not SSEQ stable for DM i

The relationships obtained between the SSEQ stability concept and existing solution concepts in the GMCR, namely: Nash stability, GMCR stability, SMR stability, SEQ stability, $L_3$ stability and $CMR_2$ stability are summarized in Fig. 7. As one can see, the SSEQ stability concept reduces the number of stable states in comparison to SEQ, SMR and $CMR_2$. This is specially useful in conflicts having multiple stable states.

Fig. 7

Relationships between solution concepts

3.2 Coalitional SSEQ

The coalitional stability analysis has been studied in recent works, such as Inohara and Hipel (2008), extending the stability analysis to situations in which DMs can act together forming a coalition. In this context, DMs may achieve improvements that are not possible to achieve if they were acting individually.

Definition 2

(Coalitional SSEQ Stability for a Coalition) Let $H \in \varphi (N)$, a state $s\in S$ is coalitional SSEQ (CSSEQ) stable for coalition H if and only if for every $s_1 \in R_{H}^{++}(s)$, there exists $s_2 \in R_{\varphi (N-H)}^{++}(s_1)$ such that $s \succeq _{i}s_2$ for some $i \in H$ and for every $s_3 \in R_{H}(s_2)$, $s \succeq _{j}s_3$ for some $j \in H$.

Definition 3

(Coalitional SSEQ Stability for a DM) For $i\in N$, a state $s \in S$ is CSSEQ stable for DM i if and only if s is CSSEQ for all coalitions $H \in \varphi (N)$ such that $i \in H$.

Similar results as those of Theorem 1 remain valid for a coalition $H \subseteq N$.

Theorem 4

The following statements are true in the GMCR:

• (a) If state s is coalitional Nash stable for coalition H, then s is CSSEQ stable for this coalition.

• (b) If state s is CSSEQ stable for coalition H, then s is CSEQ stable for this coalition.

• (c) If state s is CSSEQ stable for coalition H, then s is CSMR stable for this coalition.

Proof

The proof of this theorem is similar to proof of Theorem 1. The only necessary changes are to replace $R_i^{+}$ by $R_{H}^{++}$, $R_{N-\{i\}}$ by $R_{\varphi (N-H)}$ and $R_{N-\{i\}}^{+}$ by $R_{\varphi (N-H)}^{++}$ in that proof. $\square$

4 Extension of the SSEQ Stability for GMCR with Other Preference Structures

In this section, we extend the SSEQ stability definition for the GMCR with uncertain (Li et al. 2004), probabilistic (Rêgo and Santos 2015), and fuzzy preference (Hipel et al. 2011) structures. In what follows, we recall, briefly, these models and present the corresponding adapted version of SSEQ to each one of these three preference structures.

4.1 SSEQ Stability in the GMCR with Uncertain Preferences

Li et al. (2004) proposed to use a new preference structure in the GMCR in which DM’s preferences are expressed by a triple of relations $\{\succ _{i}, \sim _{i}, U_{i}\}$, were $s\succ _{i}s_1$ and $s\sim _{i}s_1$ are the strict preference and indifference relations, and $sU_{i}s_1$ means that DM i is uncertain as to whether he or she prefers state s to state $s_1$, prefers $s_1$ to s, or is indifferent between s and $s_1$.

Let $R_{i}^{U}(s) = \{s_1 \in R_i(s): s_1 U_{i}s\}$ be DM i’s reachable list from state s by a unilateral uncertain move. Let $R_{i}^{+, U}(s) = R_{i}^{+}(s)\cup R_{i}^{U}(s) = \{s_1 \in R_i(s):s_1\succ _{i}s \ or \ s_1U_{i}s\}$ be DM i’s reachable list from state s by a unilateral improvement or a unilateral uncertain move. Let $R_{H}^{+, U}(s)$ denote the set of unilateral improvements or unilateral uncertain moves by coalition $H \subseteq N$. If $s_1 \in R_{H}^{+, U}(s)$, then $\varOmega _{H}^{+, U}(s, s_1)$ is the set of all last DMs in unilateral improvements or uncertain moves from s to $s_1$. These sets can be formally defined as the smallest sets (in the sense of inclusion) satisfying: (1) if $i\in H$ and $s_1\in R_{i}^{+,U}(s)$, then $s_1\in R_{H}^{+,U}(s)$ and $i \in \varOmega _{H}^{+,U}(s, s_1)$, and (2) if $s_1\in R_{H}^{+,U}(s)$, $i\in H$, $\varOmega _{H}^{+,U}(s, s_1)\ne \{i\}$ and $s_2 \in R_{i}^{+,U}(s_1)$, then $s_2 \in R_{H}^{+,U}(s)$ and $i \in \varOmega _{H}^{+,U}(s, s_2)$.

Then, based on this extended preference structure we have the following SSEQ definitions. First, if DM i has an incentive to move to states with uncertain preferences relative to the status quo, but, when assessing possible sanctions, he will not consider states with uncertain preferences, then we have the following definition.

Definition 4

A state $s \in S$ is SSEQ stable for DM $i\in N$, denoted by $SSEQ_a$, in a GMCR with uncertain preferences iff for every $s_1 \in R_{i}^{+, U}(s)$, there exists $s_2 \in R_{N-\{i\}}^{+, U}(s_1)$ such that $s\succeq _{i}s_2$ and $s\succeq _{i}s_3$ for every $s_3 \in R_{i}(s_2)$.

Second, if DM i would only move from the status quo to preferred states and would be sanctioned only by less preferred or equally preferred states relative to the status quo, then we have the following definition:

Definition 5

A state $s \in S$ is SSEQ stable for DM $i\in N$, denoted by $SSEQ_b$, in a GMCR with uncertain preferences iff for every $s_1 \in R_{i}^{+}(s)$, there exists $s_2 \in R_{N-\{i\}}^{+, U}(s_1)$ such that $s\succeq _{i}s_2$ and $s\succeq _{i}s_3$ for every $s_3 \in R_{i}(s_2)$.

Third, if preference uncertainty is allowed when DM i considers both incentives to leave a state and sanctions to deter him or her from doing so, then we have the following definition:

Definition 6

A state $s \in S$ is SSEQ stable for DM $i\in N$, denoted by $SSEQ_c$, in a GMCR with uncertain preferences iff for every $s_1 \in R_{i}^{+, U}(s)$, there exists $s_2 \in R_{N-\{i\}}^{+, U}(s_1)$ such that $s\succeq _{i}s_2$ or $sU_{i}s_2$ and $s\succeq _{i}s_3$ or $sU_{i}s_3$ for every $s_3 \in R_{i}(s_2)$.

Finally, if DM i is not willing to move to a state with uncertain preference relative to the status quo, but is deterred by sanctions to states that have uncertain preference relative to the status quo, then we have the following definition:

Definition 7

A state $s \in S$ is SSEQ stable for DM $i\in N$, denoted by $SSEQ_d$, in a GMCR with uncertain preferences iff for every $s_1 \in R_{i}^{+}(s)$, there exists $s_2 \in R_{N-\{i\}}^{+, U}(s_1)$ such that $s\succeq _{i}s_2$ or $sU_{i}s_2$ and $s\succeq _{i}s_3$ or $sU_{i}s_3$ for every $s_3 \in R_{i}(s_2)$.

4.2 SSEQ Stability in the GMCR with Probabilistic Preferences

In Rêgo and Santos (2015), the authors replace the usual preference notion used in GMCR by adopting probabilistic preferences (Luce 1958). According to this model, whenever a DM must state preferences between two particular objects, he or she may do so with a certain probability. Thus, in the GMCR with probabilistic preferences, for any two states s and $s_1$, $P_{i}(s, s_1)$ expresses the chance with which DM i strictly prefers state s to $s_1$. This probability is defined on $S \times S$ and must satisfy:

• (1) $P_{i}(s, s) = 0, \forall s \in S$;

• (2) $P_{i}(s, s_1) \ge 0, \forall s, s_1 \in S$;

• (3) $P_{i}(s, s_1)+P_{i}(s_1, s) \le 1, \forall s, s_1 \in S$.

Consider parameters $\alpha$, $\beta$, $\gamma$ lying in the interval [0, 1]. Let $R_i^{+\gamma }(s)$ be the set of $\gamma$-unilateral improvements from state s for DM i, where a state $s_2$ is a $\gamma$-unilateral improvement from state $s_3$ for DM i, if $s_2 \in R_{i}(s_3)$ and $P_{i}(s_2, s_3)> \gamma$. In order to define the notion of SSEQ stability for the GMCR with probabilistic preferences, we need to present the definition of $\gamma$-unilateral improvement by a coalition, $R_H^{+\gamma }(s)$. Let $\varOmega _{H}^{+\gamma }(s, s_1)$ be the subset of H whose members are the DMs who make the last $\gamma$ improvement move to reach $s_1$ in a legal sequence of $\gamma$ improvement moves from state s. The sets $R_{H}^{+\gamma }(s)$ and $\varOmega _{H}^{+\gamma }(s,\cdot )$ are defined as the smallest sets (in the sense of inclusion) satisfying: (1) if $i\in H$, $s_1 \in R_{i}(s)$ and $P_{i}(s_1, s)>\gamma$, then $s_1\in R_{H}^{+\gamma }(s)$ and $i \in \varOmega _{H}^{+\gamma }(s, s_1)$, and (2) if $s_1\in R_{H}^{+\gamma }(s)$, $i\in H$, $s_2 \in R_{i}(s_1)$, $\varOmega _{H}^{+\gamma }(s, s_1)\ne \{i\}$ and $P_{i}(s_2, s_1)>\gamma$, then $s_2 \in R_{H}^{+\gamma }(s)$ and $i \in \varOmega _{H}^{+\gamma }(s, s_2)$. Additionally, also consider $\varPhi _{i}^{+\gamma }(s) = \{s_1 \in S: P_{i}(s_1, s)>\gamma \}$ as defined in Rêgo and Santos (2015). In this model, we have the following SSEQ definition:

Definition 8

A state $s \in S$ is $(\alpha$, $\beta$, $\gamma )$-SSEQ stable for DM $i\in N$ iff for every $s_1 \in R_{i}^{+(1-\alpha )}(s)$, there exists $s_2 \in R_{N-\{i\}}^{+\gamma }(s_1) \cap (\varPhi _{i}^{+(1-\beta )}(s))^{c}$ such that $R_{i}(s_2) \cap \varPhi _{i}^{+(1-\alpha )}(s) = \emptyset$.

4.3 SSEQ Stability in the GMCR with Fuzzy Preferences

Hipel et al. (2011) proposed the use of fuzzy preferences in the GMCR to indicate the degree of uncertainty that a DM can have when comparing two states. Fuzzy preferences over the set of states, S, is a fuzzy relation in S represented by the matrix $A= (a_{ij})_{m \times m}$, with membership function $\mu _{A}: S \times S \rightarrow [0, 1]$, where $\mu _{A}(s_i, s_j)=a_{ij}$, the degree of preference for $s_i$ over $s_j$, satisfies $a_{ij}+a_{ji}=1$, and $a_{ii}=0.5$, for all $i, j = 1, 2, \ldots , m$.

The authors define DM k’s fuzzy relative certainty of preference for state $s_i$ over $s_j$ as $\alpha ^{k}(s_i, s_j) = a^{k}(s_i, s_j)-a^{k}(s_j, s_i)$, where $a^{k}(s_i, s_j)$ denotes the preference degree of state $s_i$ over $s_j$ for DM k. In this model a state $s_i \in R_k(s)$, where $k \in N$, is called a fuzzy unilateral improvement from s by DM k if and only if $\alpha ^{k}(s_i, s) \ge \gamma _k$, where $\gamma _k$ is the fuzzy satisficing threshold for DM k. Let $\hat{R}_{k, \gamma _k}^{+}(s) = \{ s_i \in R_{k}(s): \alpha ^{k}(s_i, s) \ge \gamma _{k}\}$ be the fuzzy unilateral improvement list for DM k. In order to define the notion of SSEQ stability for the GMCR with fuzzy preferences, we need to present the definition of the fuzzy unilateral improvement list by a coalition. Let $\hat{\varOmega }_{H, \gamma _H}^{+}(s, s_1)$, where $\gamma _H=\times _{i\in H}\gamma _i$, be the set of all last DMs who make the last fuzzy improvement move in a legal sequence from s to $s_1$.

The sets $\hat{R}_{H, \gamma _H}^{+}(s)$ and $\hat{\varOmega }_{H, \gamma _H}^{+}(s,\cdot )$ are defined as the smallest sets (in the sense of inclusion) satisfying: (1) if $i\in H$ and $s_1 \in \hat{R}_{i, \gamma _i}^{+}(s)$, then $s_1\in \hat{R}_{H, \gamma _H}^{+}(s)$ and $i \in \hat{\varOmega }_{H, \gamma _H}^{+}(s, s_1)$, and (2) if $s_1\in \hat{R}_{H, \gamma _H}^{+}(s)$, $i\in H$, $s_2 \in \hat{R}_{i, \gamma _i}^{+}(s_1)$ and $\hat{\varOmega }_{H, \gamma _H}^{+}(s, s_1)\ne \{i\}$, then $s_2 \in \hat{R}_{H, \gamma _H}^{+}(s)$ and $i \in \hat{\varOmega }_{H, \gamma _H}^{+}(s, s_2)$. Then, we have the following SSEQ definition:

Definition 9

A state $s \in S$ is fuzzy-SSEQ stable for DM $i\in N$ iff for every $s_1 \in \hat{R}_{i, \gamma _i}^{+}(s)$, there exists $s_2 \in \hat{R}_{N-\{i\}, \gamma _{N-\{i\}}}^{+}(s_1)$ such that $\alpha ^{i}(s_2, s) <\gamma _i$, and $\alpha ^{i}(s_3, s) <\gamma _i$ for all $s_3 \in R_i(s_2)$.

Fig. 8

Graph form of Rafferty-Alameda dams conflict

5 Application

In this section, the definition of SSEQ stability is applied in the Rafferty-Alameda dams conflict, which is a real-life case involving 4 DMs.

5.1 The Rafferty-Alameda Dams Conflict

We will make now the SSEQ stability analysis for a conflict with four DMs. This conflict, known as Rafferty-Alameda dams conflict, is a problem of dams construction in Canada that occurred in early 1986, and can be found in more details in Roberts (1990), Xu et al. (2009) and Hipel et al. (1993).

The history of that conflict begins when Canadian Province of Saskatchewan, seeking to provide improvements such as the reduction of flooding and water supply to cool a plant that produced energy through coal, decided to build Rafferty and Alameda dams. After the license granted by the Minister of Environment of the Federal Government of Canada, various Environmental Groups were opposed to the construction project and appealed to the Federal Court. The Federal Court suspended the license granted and the Federal Environmental Review Panel was responsible for evaluating the project and making an environmental assessment and review. After starting the project assessments, the panel noted that the project was still being developed and decided to contact the Federal Government to complain, but got no answer and the panel had decided to suspend its review.

In order to model Rafferty-Alameda dams conflict using the GMCR, four DMs are considered as acting in this conflict, namely: Federal Government of Canada (Federal), called DM F, Saskatchewan, called DM S, Environment Groups (Groups), called DM G, and Federal Environmental Review Panel (Panel), called DM P. The graph form of this conflict is illustrated in Fig. 8. The options of DM F are: (1) seek a court order to halt the project (Court order) or (2) to lift the license (Lift). The option of DM S is only to go ahead at full speed (Full speed). The option of DM G is only to threaten court action to halt the project (Court action). The options of DM P is only to resign (Resign).

In this conflict, the number of all states possible is $2^5$. However, the set of states feasible contains only 10 states (s, $s_1$, $s_2$, $\ldots$, $s_9$) and are determined by means of the options shown in Table 3. The notation Y indicates that the DM that controls the corresponding option takes it, while the notation N indicates that the DM that controls the corresponding option does not take it.

Table 3 States in the Rafferty-Alameda dams conflict

Table 4 Set of states reachable and preferences

Table 5 Stable states according to five stability definitions

The sets of reachable states and the usual preferences of DMs in this conflict are summarized in Table 4. The notations $p_F$, $p_S$, $p_G$ and $p_P$ indicate the preference order of DMs F, S, G and P, respectively, where a higher number indicates a more desired state.

Table 5 represents the stable states in Rafferty-Alameda dams conflict, for each DM, according to the notions of Nash, GMR, SMR, SEQ and SSEQ stability. Each cell in the array specifies for which DMs, if any, the line state is stable according to the stability definition of the corresponding column. The results of concepts GMR, SMR, SEQ and SSEQ coincides in this conflict. Thus, even though opponents moves according to SSEQ stability are restricted in comparison to those according to GMR or SMR, or the focal DM gets the opportunity to counter-react, as opposed to what is allowed in SEQ, stability of the states remain the same.

6 Conclusion

This paper extends the notion of SSEQ stability for n-DM conflicts in the GMCR. The SSEQ stability is a kind of sequential stability in which the DM who moves first considers not only the reaction of his or her opponents, but also his own counter-reaction. We also present the relationships of SSEQ with six existing solution concepts in the literature. Additionally, we introduced the SSEQ concept for coalitional analysis and extended SSEQ stability for GMCR with uncertain, probabilistic and fuzzy preferences in n-DM conflicts.

The SSEQ stability can be applied to other preferences structures that have been recently proposed to be used in the GMCR, such as Gray Preference (Kuang et al. 2015) and Upper and Lower Probabilistic Preferences (Santos and Rêgo 2014). The idea to extend this definition to models with other preference structures is that for a state s to be SSEQ stable for DM i, it must be such that for every improvement $s_1$ reachable from s by DM i, there is a series of improvements for the other DMs that leads the conflict from state $s_1$ to a state $s_2$ such that $s_2$ is not preferred to s by DM i and from $s_2$ DM i cannot reach a state $s_3$ which is preferred to s by DM i, where the notion of improvement depends on the preference structure adopted.

The SSEQ concept enriches the SEQ and the SMR concepts providing for both DMs and analysts more information regarding stability of states. It enhances the SEQ concept by allowing DMs to analyze the conflict one further step and the SMR concept by restricting focal DM opponents to use only unilateral improvement moves. Such enhancements may help DMs make better decisions since, in general, they can reduce the number of stable states, which is useful in conflicts having multiple stable states.

In future research, we plan to investigate how to extend the SSEQ stability notion allowing for more rounds of conflict analysis. We also leave for future work, the question of existence of SSEQ equilibrium in finite conflicts. Finally, we are working in the proposal of a more efficient method to obtain SSEQ stable states by means of matrix operations.