The Condorcet Efficiency Advantage that Voter Indifference Gives to Approval Voting Over Some Other Voting Rules

Abstract

Approval Voting is known to possess many good properties when voters have dichotomous preferences. But, when attention was restricted to the limiting case for large electorates with three candidates in an early study, Approval Voting was found to have the same Condorcet Efficiency as both Plurality Rule and Negative Plurality rule when no voter indifference is allowed in voters’ preferences with the assumption of the impartial culture condition (IC). However, a later study by Diss et al. (Handbook on approval voting, 2010) shows that the introduction of any degree of indifference in an extended impartial culture condition leads to a dominance of Approval Voting over both Plurality Rule and Negative Plurality Rule on the basis of Condorcet Efficiency. Scenarios were also found for which Approval Voting had greater Condorcet Efficiency than Borda Rule. The assumptions of that study are analyzed here, and an arguably more reasonable set of assumptions leads to the conclusion that Borda Rule will dominate Approval Voting on the basis of Condorcet Efficiency for all degrees of voter indifference, except for the case of completely dichotomous preferences. The same outcome is found to result in the current study for an extended version of the Impartial Anonymous Culture Condition.

1 Introduction

Studies that pursue the development of formal representations for the probability that various election outcomes might be observed can be traced back to the work of Condorcet (1785), and all such studies must make some assumptions about the likelihood that each of $n$ voters will have each of the possible preference rankings on the available candidates. If we let $A\succ B$ denote the outcome that a given voter prefers Candidate $A$ to $B$ in a three-candidate election on $\left\{ {A,B,C} \right\}$, a voter with a complete preference ranking on candidates would have one of the six possible preference rankings like $A\succ B\succ C$. It is further assumed that $A\succ C$ in this specific case, to prohibit intransitive, or cyclic, individual preferences on candidates. The most elementary of the assumptions about voters’ preference rankings is formalized in Guilbaud (1952) in a study that considered the probability that a Condorcet Winner (CW) would exist in an election on three candidates when voters can only have complete preference rankings. Let A ${{\varvec{M}}}$ B denote the outcome that a majority of voters prefer Candidate $A$ to Candidate $B$ when the voters’ preferences are restricted to considering only the candidates in this pair. That is, where more voters have $A\succ B$ in their complete preference rankings than those who have $B\succ A$. Then, Candidate $A$ is the CW for the three candidates if both $A{{\varvec{M}}}B$ and $A{{\varvec{M}}}C$. The CW is widely viewed as being the best candidate for selection as the winner of an election, but Condorcet showed that such a candidate does not necessarily exist, since there can be majority rule cycles on pairs like $A{{\varvec{M}}}B$, $B{{\varvec{M}}}C$ and $C{{\varvec{M}}}A$. Guilbaud (1952) considered the case of the impartial culture condition (IC), which assumes that all voters independently determine their preference rankings on $m$ candidates, and that each of the $m!$ possible complete preference rankings on candidates is equally likely to represent the preferences of each voter. Let $P_\infty ^{CW} \left( {IC} \right)$ denote the limiting probability as $n\rightarrow \infty$ that a CW exists in a three candidate election with IC, and Guilbaud (1952) showed that

$$\begin{aligned} P_\infty ^{CW} \left( \textit{IC} \right) =\frac{3}{4}+\frac{3}{2\pi }Sin^{-1}\left( {\frac{1}{3}} \right) \approx .91226. \end{aligned}$$

(1)

This result will be obtained as a special case of a much more general model later in this study.

Many generalizations of IC have evolved over time to cover a much broader spectrum of the types of preferences that voters might have on the candidates, and to allow for the derivation of probability representations for other voting outcomes. Much of this further work has been focused on the Condorcet Efficiency of voting rules, which measures the conditional probability that a voting rule will elect the CW, given that such a candidate exists. The most general model of this type to date is the extended impartial culture condition (EIC) from Diss et al. (2010) that integrates the traditional notion of voter preference rankings on three candidates with the concept of the number of candidates that voters consider to be acceptable as a possible winner, following a concept that is presented in Brams and Sanver (2009). The Diss et al. (2010) study reached some unexpected conclusions regarding the Condorcet Efficiency of some voting rules, and the purpose of this study is to evaluate the degree to which the assumptions that are used in that study had an impact on the results that were obtained. We also extend the same type of analysis to consider a different commonly used assumption, known as the impartial anonymous culture condition (IAC), regarding the likelihood that various voters’ preferences will be observed.

2 The EIC Model

The EIC model starts with the six possible complete preference rankings on three candidates from IC and further accounts for the possibility that voters might have dichotomous preferences, with complete indifference between two of the candidates. The possibility that a voter might be completely indifferent between all three candidates is also allowed. To describe the mechanism by which the acceptability of a candidate is introduced into this model, suppose that a given voter has a complete preference ranking on candidates with $A\succ B\succ C$. But, only Candidate $A$ might be viewed as being acceptable, or tolerable, as a winner for this voter, despite the fact that $B\succ C$; or both Candidates $A$ and $B$ might be viewed as being acceptable or tolerable as a winner, despite the fact that $A\succ B$. The notion of strength of preference clearly plays some role in this model. There are five categories of voter preference types that follow from using this model:

$$\begin{aligned} k_1&= \textit{Number of voters with a complete ranking for preference, one acceptable}\\&\qquad \qquad \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} A^{*} \quad &{} A^{*} \quad &{} B^{*} \quad &{} C^{*} \quad &{} B^{*} \quad &{} C^{*}\\ B \quad &{} C \quad &{} A \quad &{} A \quad &{} C \quad &{} B\\ C \quad &{} B \quad &{} C \quad &{} B \quad &{} A \quad &{} A\\ n_1 \quad &{} n_2 \quad &{} n_3 \quad &{} n_4 \quad &{} n_5 \quad &{} n_6 \\ \end{array}\\&\qquad \qquad \begin{array}{l} k_1 =n_1 +n_2 +n_3 +n_4 +n_5 +n_6\\ \end{array}\\ k_2&= \textit{Number of voters with a complete ranking for preference, two acceptable}\\&\qquad \qquad \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} A^{*} \quad &{} A^{*} \quad &{} B^{*} \quad &{} C^{*} \quad &{} B^{*} \quad &{} C^{*}\\ B^{*} \quad &{} C^{*} \quad &{} A^{*} \quad &{} A^{*} \quad &{} C^{*} \quad &{} B^{*}\\ C \quad &{} B \quad &{} C \quad &{} B \quad &{} A \quad &{} A\\ n_7 \quad &{} n_8 \quad &{} n_9 \quad &{} n_{10} \quad &{} n_{11} \quad &{} n_{12}\\ \end{array}\\&\qquad \qquad \begin{array}{l} k_2 =n_7 +n_8 +n_9 +n_{10} +n_{11} +n_{12}\\ \end{array}\\ k_3&= \textit{Number of voters with dichotomous preferences, two acceptable}\\&\qquad \qquad \begin{array}{c@{\quad }c@{\quad }c} \left( {A,B} \right) \quad &{} \left( {A,C} \right) \quad &{} \left( {B,C} \right) \\ C \quad &{} B \quad &{} A\\ n_{13} \quad &{} n_{14} \quad &{} n_{15}\\ \end{array}\\&\qquad \qquad \begin{array}{l} k_3 =n_{13} +n_{14} +n_{15}\\ \end{array}\\ k_4&= \textit{Number of voters with dichotomous preferences, one accptable}\\&\qquad \qquad \begin{array}{c@{\quad }c@{\quad }c} A \quad &{} B \quad &{} C\\ \left( {B,C} \right) \quad &{} \left( {A,C} \right) \quad &{} \left( {A,B} \right) \\ n_{16} \quad &{} n_{17} \quad &{} n_{18}\\ \end{array}\\&\qquad \qquad \begin{array}{l} k_4 =n_{16} +n_{17} +n_{18}\\ \end{array}\\ k_5&= \textit{Number of voters with complete indifference}\\&\qquad \qquad \begin{array}{c} \left( {A,B,C} \right) \\ k_5 =n_{19}\\ \end{array} \end{aligned}$$

Here, $n_i$ denotes the number of voters with the given $i$th preference ranking on candidates for $1\le i\le 19$ in a specific election, and $A^{*}$ denotes that $A$ is considered acceptable in a complete preference ranking for Category 1 and 2 voters. Any specific voter preference profile which associates some preference ranking with each of $n$ voters in an election will have $n=\sum _{i=1}^{19} n_i$. Let $p_i$ denote the probability that a randomly selected voter from the entire population of possible voters will have the associated $i$th preference ranking on candidates for $1\le i\le 19$. We also let $k_j^{\prime }$ denote the probability that a randomly selected voter will have preferences in the $j$th category type for $1\le j\le 5$. The five-dimension vector ${{\varvec{k}}}^{{\prime }}$ is used to denote a specified combination of $k_j^{\prime }$ with $\sum _{j=1}^5 k_j^{\prime } =1$. There is an obvious connection between the definitions of the $p_i$ and $k_j^{\prime }$ terms, such that for example $k_2^{\prime } = \sum _{i=7}^{12} p_i$. The EIC model from Diss et al. (2010) further assumes equal probabilities for rankings within preference categories, such that $p_i =\frac{k_1^{\prime } }{6}$ for $1\le i\le 6$ and $p_j =\frac{k_2^{\prime } }{6}$ for $7\le j\le 12$, $p_a =\frac{k_3^{\prime } }{3}$ for $13\le a\le 15$, $p_c =\frac{k_4^{\prime } }{3}$ for $16\le c\le 18$, with $p_{19} =k_5^{\prime }$.

We start our analysis by developing a representation for the limiting probability $P_\infty ^{CW} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ as $n\rightarrow \infty$ that a randomly selected profile of $n$ voters from the population of possible voters will have a CW with the assumption of EIC for a specified ${{\varvec{k}}}^{\prime }$, following Diss et al. (2010). Voters are assumed to have preferences that are obtained independently of other voters’ preferences, and we define two variables that are used to determine if Candidate $A$ is the CW, when pairs of candidates that are considered to be indifferent in a voter’s preference ranking are ignored in the determination of the CW. Variable $X_1 \, \left( {X_2 } \right)$ will be used to establish that $A{{\varvec{M}}}B$ ($A{{\varvec{M}}}C)$, with:

$$\begin{aligned} X_1&= +1\!\!:p_1 +p_2 +p_4 +p_7 +p_8 +p_{10} +p_{14} +p_{16}\\&-1\!\!:p_3 +p_5 +p_6 +p_9 +p_{11} +p_{12} +p_{15} +p_{17}\\&\quad \!\!0:\hbox {Otherwise}\\ X_2&= +1\!\!:p_1 +p_2 +p_3 +p_7 +p_8 +p_9 +p_{13} +p_{16}\\&-1\!\!:p_4 +p_5 +p_6 +p_{10} +p_{11} +p_{12} +p_{15} +p_{18}\\&\quad \!\!0: \hbox {Otherwise}. \end{aligned}$$

On a random draw of a voter’s preference with EIC, it is obvious from our definitions of the category types that $E\left( {X_1 } \right) =E\left( {X_2 } \right) =0$, so that $E\left( \bar{X}_1\right) =E\left( \bar{X}_2\right) =0$ where $\bar{X}_{i}$ denotes the average of $X_i$ . Then $A$ is the CW over $n$ random draws in a profile if $\bar{X}_1 >0 \left( {A{{\varvec{M}}}B} \right)$ and $\bar{X}_2 >0 \left( {A{{\varvec{M}}}C} \right)$. The probability of this outcome is obviously the same as the joint probability that $\bar{X}_1 \sqrt{n}>E\left( \bar{X}_{1}\sqrt{n} \right)$ and $\bar{X}_2\sqrt{n}>E\left( \bar{X}_2 \sqrt{n} \right)$ since $E\left( \bar{X}_2 \right) =E\left( \bar{X}_2\right) =0$. The Central Limit Theorem applies as $n\rightarrow \infty$, and the joint probability for $\bar{X}_1 \sqrt{n}$ and $\bar{X}_2 \sqrt{n}$ has a bivariate normal distribution with a correlation that is identical to the correlation between the original variables $X_1$ and $X_2$. The limiting probability that $\bar{X}_1 \sqrt{n}>E\left( \bar{X}_1 \sqrt{n} \right)$ and $\bar{X}_2 \sqrt{n}>E\left( \bar{X}_2 \sqrt{n} \right)$ is therefore the same as the joint probability that $\bar{X}_1 \sqrt{n}\ge E\left( \bar{X}_1 \sqrt{n} \right)$ and $\bar{X}_2 \sqrt{n}\ge E\left( \bar{X}_2 \sqrt{n} \right)$, since the probability that any specific value of a variable, including zero, is observed in a continuous distribution is of measure zero. The probability that $A$ is the CW as $n\rightarrow \infty$ is therefore defined by a bivariate-normal positive orthant probability, which is a function of the correlation between these two variables.

To obtain the correlation between the two variables $X_1$ and $X_2$ with EIC:

$$\begin{aligned} E\left( {X_1 ^{2}} \right)&= p_1 +p_2 +p_3 +p_4 +p_5 +p_6 +p_7 +p_8 +p_9 +p_{10} +p_{11} +p_{12}\\&+p_{14} +p_{15} +p_{16} +p_{17}\\ E\left( {X_1 ^{2}} \right)&= \frac{3k^{\prime }_1 +3k^{\prime }_2 +2k^{\prime }_3 +2k^{\prime }_4 }{3}. \end{aligned}$$

By symmetry, $E\left( {X_2 ^{2}} \right) =E\left( {X_1 ^{2}} \right)$, and the covariance between $X_1$ and $X_2$ is denoted $\textit{Cov}\left( {X_1 ,X_2 } \right)$ with:

$$\begin{aligned} \textit{Cov}\left( {X_1 ,X_2 } \right)&= p_1 +p_2 -p_3 -p_4 +p_5 +p_6 +p_7 +p_8 -p_9 -p_{10} +p_{11}\\&+p_{12} +p_{15} +p_{16} =\frac{k^{\prime }_1 +k^{\prime }_2 +k^{\prime }_3 +k^{\prime }_4 }{3}. \end{aligned}$$

The correlation between $X_1$ and $X_2$ is denoted $Cor\left( {X_1 ,X_2 } \right)$ and by definition:

$$\begin{aligned} Cor\left( {X_1 ,X_2 } \right) =\frac{k^{\prime }_1 +k^{\prime }_2 +k^{\prime }_3 +k^{\prime }_4 }{3k^{\prime }_1 +3k^{\prime }_2 +2k^{\prime }_3 +2k^{\prime }_4 }. \end{aligned}$$

(2)

Sheppard’s Theorem of Median Dichotomy [Johnson and Kotz 1972, page 95] can be used to obtain the associated limiting probability that Candidate $A$ is the CW as the bivariate normal positive orthant probability $\varPhi _2 \left( {Cor\left( {X_1 ,X_2 } \right) } \right)$ from the correlation term from (2). Using the symmetry between candidates with the EIC assumption, the same probability is obtained for the likelihood that either $B$ or $C$ is the CW, and it then follows directly from Sheppard’s Theorem that the limiting probability $P_\infty ^{CW} \left( {EIC\left( {k^{\prime }} \right) } \right)$ that CW exists for three candidates with EIC is given by:

$$\begin{aligned} P_\infty ^{CW} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right) =\frac{3}{4}+\frac{3}{2\pi }Sin^{-1}\left( {\frac{k^{\prime }_1 +k^{\prime }_2 +k^{\prime }_3 +k^{\prime }_4 }{3k^{\prime }_1 +3k^{\prime }_2 +2k^{\prime }_3 +2k^{\prime }_4 }} \right) . \end{aligned}$$

(3)

This result is identical to that found in Diss et al. (2010). For the case that $k^{\prime }_2 =1$, EIC reduces to the basic assumption of IC, and Guilbaud’s result in (1) for $P_\infty ^{CW} \left( {IC} \right)$ is obtained from (3).

3 Extended Weighted Scoring Rules

Diss et al. (2010) continue with EIC to develop a limiting representation for the Condorcet efficiency of extended weighted scoring rules (EWSR’s) for three candidate elections with weights $\left( {1,\lambda ,0} \right)$. Following the basic notion of a simple weighted scoring rule (WSR), voters will award points to candidates according to their preference rankings, and the candidate that receives the most total points from voters is determined to be the winner. The $k_2$ voters in preference Category 2 give one point to their most preferred candidate, $\lambda$ points to their second ranked candidate and zero points to the least preferred candidate, just as in the case of a simple WSR. An EWSR then applies variations of these weights to the other categories of voters’ preferences. In the case of dichotomous preferences, with partial indifference, the two top tanked candidates for the $k_3$ voters in Category 3 are given an average weight of $\frac{1+\lambda }{2}$ and the bottom ranked candidate retains the weight of 0. With a tie between the two less preferred candidates for the $k_4$ voters with Category 4 preferences, the top ranked candidate retains a weight of one and the two remaining candidates each receive an average score of $\frac{\lambda }{2}$. Each candidate receives a score of $\frac{1+\lambda }{3}$ for the $k_5$ voters in Category 5 with complete indifference between candidates.

In the special case that $k^{\prime }_1 =0$, the EIC model reduces to the Impartial Weak Order Condition (IWOC) model in Gehrlein and Valognes (2001) if it is further assumed that $k^{\prime }_3 =k^{\prime }_4$, and each voter is given the same total number of points to award to candidates. At this point, Diss et al. (2010) further this extension of WSR’s from IWOC and consider what should be done with the $k_1$ voters with Category 1 preferences. These voters have a complete preference ranking on the three candidates, but only approve of their most preferred candidate. Their argument is that since the second ranked candidate is not considered to be an acceptable option for voters in Category 1, these voters should not give any points to that candidate. So, these voters will therefore give zero points to their second ranked candidate, rather than the $\uplambda$ points that were given to second ranked candidates for voters with Category 2 preferences. The basic logic of their argument is completely understandable, but a further examination of this step uncovers some potentially significant issues that arise from using it.

Suppose that we are considering one of the $n_1$ Category 1 voters with the complete preference ranking $A\succ B\succ C$. This voter actually does have a preference for $B\succ C$. If a voter of this type really has an actual indifference between $B$ and $C$, they would instead have been identified as a Category 4 voter with dichotomous preferences. The existence of an actual voter preference for $B\succ C$ is further reinforced in Diss et al. (2010), because they use the preferences on these two less preferred candidates to determine the CW. This follows from the fact that they use all six $n_i$ terms with $1\le i\le 6$ for Category 1 voters in the definitions of their variables $X_1$ and $X_2$ to determine the CW (page 278 of Appendix C in their paper). The voter’s preference $B\succ C$ is therefore considered strong enough to warrant using it in the determination of the CW. And yet, this voter is assumed to choose the option of not giving more weight to $B$ than $C$, even if it is quite possible that this voter’s most preferred Candidate $A$ might not win the election. While these Category 1 voters might not want to award as many points to their middle-ranked candidate as their counterparts in Category 2 voters, it seems quite plausible that some points would be given to $B$, since $B\succ C$ and $A$ might not win. We therefore start an analysis to determine the weight that should be given to Category 1 voters’ middle ranked candidates.

4 Condorcet Efficiency of EWSR’s

Our first step is to replicate the Diss et al. (2010) study of the Condorcet Efficiency of EWSR’s with the exception of the fact that Category 1 voters will instead award weights according to the schedule $\left( {1,\varepsilon ,0} \right)$. The resulting voting rule is denoted as $Rule\left( {\varepsilon ,\lambda } \right)$. It would make no sense for Category 1 voters to award more points to middle-ranked candidates than Category 2 voters award to their middle-ranked candidates, given the definitions of these voter types. It is therefore assumed that $\varepsilon \le \lambda$, and the Diss et al. (2010) version of this model corresponds to $Rule\left( {0,\lambda } \right)$.

Two new variables are defined in terms of $Rule\left( {\varepsilon ,\lambda } \right)$, with $X_3$ and $X_4$ being used to indicate the advantage that Candidate $A$ gains over $B$ and $C$ respectively in each voters’ preference ranking when $Rule\left( {\varepsilon ,\lambda } \right)$ is employed.

$X_3 =1-\varepsilon \!: p_1$	$X_4 = 1\!: p_1$
$1\!\!: p_2$	$1-\varepsilon \!\!: p_2$
$\varepsilon -1\!\!: p_3$	$\varepsilon \!\!: p_3$
$\varepsilon \!\!: p_4$	$\varepsilon -1\!\!: p_4$
$-1\!\!: p_5$	$-\varepsilon \!\!: p_5$
$-\varepsilon \!\!: p_6$	$-1\!\!: p_6$
1$-\lambda \!\!: p_7$	$1\!\!: p_7$
$1\!\!: p_8$	$1-\lambda \!\!: p_8$
$\lambda -1\!\!: p_9$	$\lambda \!\!: p_9$
$\lambda \!\!: p_{10}$	$\lambda -1\!\!:p_{10}$
$-1\!\!: p_{11}$	$-\lambda \!\!: p_{11}$
$-\lambda \!\!: p_{12}$	$-1\!\!: p_{12}$
$\frac{1+\lambda }{2}\!\!: p_{14}$	$\frac{1+\lambda }{2}\!\!: p_{13}$
$-\frac{1+\lambda }{2}\!\!: p_{15}$	$-\frac{1+\lambda }{2}\!\!: p_{15}$
$\frac{2-\lambda }{2}\!\!: p_{16}$	$\frac{2-\lambda }{2}\!\!: p_{16}$
$\frac{\lambda -2}{2}\!\!: p_{17}$	$\frac{\lambda -2}{2}\!\!: p_{18}$
0: Otherwise	0: Otherwise

Candidate $A$ will be both the CW and the $Rule\left( {\varepsilon ,\lambda } \right)$ winner if $\bar{X}_i >0$ for $1\le i\le 4$, and with the assumptions of EIC, $E\left( {X_3 } \right) =E\left( {X_4 } \right) =0$. The logic of the development of the representation for $P_{CW} \left( {\infty ,EIC} \right)$ above is applied here to the case of four variables and the limiting probability as $n\rightarrow \infty$ that Candidate $A$ will be both the CW and the $Rule\left( {\varepsilon ,\lambda } \right)$ winner is the joint probability that $\bar{X}_i \sqrt{n}\ge E\left( \bar{X}_i \sqrt{n} \right)$ for $1\le i\le 4$. This joint distribution is four-variate normal with correlation terms identical to the correlations between the original variables.

To obtain these correlation terms involving $X_3$ and $X_4$:

$$\begin{aligned} E\left( {X_3 ^{2}} \right)&= \left( {1-\varepsilon } \right) ^{2}p_1 +1p_2 +\left( {\varepsilon -1} \right) ^{2}p_3 +\varepsilon ^{2}p_4 +1p_5 +\varepsilon ^{2}p_6 +\left( {1-\lambda } \right) ^{2}p_7 \\&+1p_8 +\left( {\lambda -1} \right) ^{2}p_9 +\lambda ^{2}p_{10} +1p_{11} +\lambda ^{2}p_{12} +\left( {\frac{1+\lambda }{2}} \right) ^{2}p_{14}\\&+\left( {\frac{1+\lambda }{2}} \right) ^{2}p_{15} +\left( {\frac{2-\lambda }{2}} \right) ^{2}p_{16} +\left( {\frac{2-\lambda }{2}} \right) ^{2}p_{17}\\ E\left( {X_3 ^{2}} \right)&= \frac{2k^{\prime }_1 }{3}\left\{ {1-\varepsilon +\varepsilon ^{2}} \right\} +\frac{2k^{\prime }_2 }{3}\left\{ {1-\lambda +\lambda ^{2}} \right\} +\frac{2k^{\prime }_3 }{3}\left( {\frac{1+\lambda }{2}} \right) ^{2}\nonumber \\&\quad +\,\frac{2k^{\prime }_4 }{3}\left( {\frac{2-\lambda }{2}} \right) ^{2} \end{aligned}$$

By symmetry, $E\left( {X_4 ^{2}} \right) =E\left( {X_3 ^{2}} \right)$.

$$\begin{aligned} \textit{Cov}\left( {X_1 ,X_3 } \right)&= \left( {1-\varepsilon } \right) p_1 +1p_2 -\left( {\varepsilon -1} \right) p_3 +\varepsilon p_4 +1p_5 +\varepsilon p_6 +\left( {1-\lambda } \right) p_7 \\&+1p_8 -\left( {\lambda -1} \right) p_9 +\lambda p_{10} +1p_{11} +\lambda p_{12} +\left( {\frac{1+\lambda }{2}} \right) p_{14} \\&+\left( {\frac{1+\lambda }{2}} \right) p_{15} +\left( {\frac{2-\lambda }{2}} \right) p_{16} -\left( {\frac{\lambda -2}{2}} \right) p_{17}\\ \textit{Cov}\left( {X_1 ,X_3 } \right)&= \frac{2}{3}\left( {k^{\prime }_1 +k^{\prime }_2 } \right) +\left( {\frac{1+\lambda }{3}} \right) k^{\prime }_3 +\left( {\frac{2-\lambda }{3}} \right) k^{\prime }_4.\\ \textit{Cov}\left( {X_1 ,X_4 } \right)&= 1p_1 +\left( {1-\varepsilon } \right) p_2 -\varepsilon p_3 +\left( {\varepsilon -1} \right) p_4 +\varepsilon p_5 +1p_6 +1p_7 \\&+\left( {1-\lambda } \right) p_8 -\lambda p_9 +\left( {\lambda -1} \right) p_{10} +\lambda p_{11} +1p_{12}\\&+\left( {\frac{1+\lambda }{2}} \right) p_{15} +\left( {\frac{2-\lambda }{2}} \right) p_{16}\\ \textit{Cov}\left( {X_1 ,X_4 } \right)&= \frac{1}{3}\left( {k^{\prime }_1 +k^{\prime }_2 } \right) +\left( {\frac{1+\lambda }{6}} \right) k^{\prime }_3 +\left( {\frac{2-\lambda }{6}} \right) k^{\prime }_4 =\frac{1}{2}Cov\left( {X_1 ,X_3^*} \right) . \end{aligned}$$

By symmetry, $Cov\left( {X_1 ,X_4 } \right) =Cov\left( {X_2 ,X_3 } \right)$ and $Cov\left( {X_1 ,X_3 } \right) =Cov\left( {X_2 ,X_4 } \right)$.

$$\begin{aligned} Cov\left( {X_3 ,X_4 } \right)&= \left( {1-\varepsilon } \right) p_1 +\left( {1-\varepsilon } \right) p_2 +\left( {\varepsilon -1} \right) \varepsilon p_3 +\varepsilon \left( {\varepsilon -1} \right) p_4 +\varepsilon p_5 +\varepsilon p_6 \\&+\left( {1-\lambda } \right) p_7 +\left( {1-\lambda } \right) p_8 +\left( {\lambda -1} \right) \lambda p_9 +\lambda \left( {\lambda -1} \right) p_{10} +\lambda p_{11} \\&+\,\lambda p_{12} +\left( {\frac{1+\lambda }{2}} \right) ^{2}p_{15} +\left( {\frac{2-\lambda }{2}} \right) ^{2}p_{16}.\\ Cov\left( {X_3 ,X_4 } \right)&= \left( {1-\varepsilon +\varepsilon ^{2}} \right) \frac{k^{\prime }_1 }{3}+\left( {1-\lambda +\lambda ^{2}} \right) \frac{k^{\prime }_2 }{3} +\left( {\frac{1+\lambda }{2}} \right) ^{2}\frac{k^{\prime }_3 }{3}\\&+\left( {\frac{2-\lambda }{2}} \right) ^{2}\frac{k^{\prime }_4 }{3}. \end{aligned}$$

Correlation Matrix R for variables $X_1 ,X_2 ,X_3 ,X_4$ with EIC is then given by:

$$\begin{aligned}&{{\varvec{R}}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1&{} b&{} \rho &{} {\frac{\rho }{2}} \\ -&{} 1&{} {\frac{\rho }{2}}&{} \rho \\ -&{} -&{} 1&{} {\frac{1}{2}} \\ -&{} -&{} -&{} 1 \end{array} }} \right] \end{aligned}$$

(4)

$$\begin{aligned}&b=\dfrac{k^{\prime }_1 +k^{\prime }_2 +k^{\prime }_3 +k^{\prime }_4 }{3k^{\prime }_1 +3k^{\prime }_2 +2k^{\prime }_3 +2k^{\prime }_4 }\nonumber \\&\rho =\frac{2\left( {k^{\prime }_1 +k^{\prime }_2 } \right) +\left( {1+\lambda } \right) k^{\prime }_3 +\left( {2-\lambda } \right) k^{\prime }_4 }{\sqrt{2\left( {3k^{\prime }_1 +3k^{\prime }_2 +2k^{\prime }_3 +2k^{\prime }_4 } \right) \left( {k^{\prime }_1 \left\{ {1-\varepsilon +\varepsilon ^{2}} \right\} +k^{\prime }_2 \left\{ {1-\lambda +\lambda ^{2}} \right\} +k^{\prime }_3 \left( {\frac{1+\lambda }{2}} \right) ^{2}+k^{\prime }_4 \left( {\frac{2-\lambda }{2}} \right) ^{2} } \right) }}. \end{aligned}$$

(5)

The limiting Condorcet Efficiency, $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$, of $Rule\left( {\varepsilon ,\lambda } \right)$ with EIC is obtained from

$$\begin{aligned} CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) =\frac{3\varPhi _4 \left( {{\varvec{R}}} \right) }{P_\infty ^{CW} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) }. \end{aligned}$$

(6)

Here, $\varPhi _4 \left( {{\varvec{R}}} \right)$ is the positive-orthant probability for the four-variate normal distribution with correlation matrix R. It is interesting to note a symmetry here, since $\rho$ in (5) and therefore $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ does not change under the transition $\lambda \rightarrow 1-\lambda$ if we simultaneously make the interchange $k^{\prime }_3 \leftrightarrow k^{\prime }_4$. We also introduce the notation $k^{\prime }_{ij} =k^{\prime }_i +k^{\prime }_j$.

For the special case $\varepsilon =0$, $\rho$ reduces to $\rho ^{0}$ with:

$$\begin{aligned} \rho ^{0}=\frac{2k^{\prime }_{12} +\left( {1+\lambda } \right) k^{\prime }_3 +\left( {2-\lambda } \right) k^{\prime }_4 }{\sqrt{2\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) \left( {k^{\prime }_1 +k^{\prime }_2 \left\{ {1-\lambda +\lambda ^{2}} \right\} +k^{\prime }_3 \left( {\frac{1+\lambda }{2}} \right) ^{2}+k^{\prime }_4 \left( {\frac{2-\lambda }{2}} \right) ^{2} } \right) }}.\quad \end{aligned}$$

(7)

This representation in (7) corresponds to the same R that is obtained in Diss et al. (2010) in their study (on their page 261 with the representation on their page 280).

For the special case $\varepsilon =\lambda$ let $k^{\prime }_3 =k^{\prime }_4$ so that $k^{\prime }_3 =\frac{k^{\prime }_{34} }{2}$, $\rho$ reduces to $\rho ^{\varepsilon =\lambda }$ with:

$$\begin{aligned} \rho ^{\varepsilon =\lambda }=\frac{4k^{\prime }_{12} +3k^{\prime }_{34} }{\sqrt{\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) \left( {8k^{\prime }_{12} \left\{ {1-\lambda +\lambda ^{2}} \right\} +k^{\prime }_{34} \left( {5-2\lambda +2\lambda ^{2}} \right) } \right) }} \end{aligned}$$

(8)

This corresponds to the same R as obtained in Gehrlein and Valognes (2001) with IWOC.

Diss et al. (2010) were particularly concerned with the relative performance of extensions of some commonly studied WSR’s compared to Approval Voting (AV). With AV, each voter casts a ballot for each candidate that they view as being acceptable. Then, voters would vote for one candidate if their preferences were in Categories 1 or 4, they would vote for two candidates if their preferences were in Categories 2 or 3, and they would vote for all three candidates if their preferences were in Category 5. It should be noted that, with regard to Condorcet Efficiency calculations, voting for all candidates is equivalent to not participating in the election.

5 Condorcet Efficiency of Approval Voting

A limiting representation for the Condorcet Efficiency of AV, $CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$, is obtained in the same fashion that was used above for $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$, with a modification to the definitions for variables $X_3$ and $X_4$ to $X^{\prime }_3$ and $X^{\prime }_4$ respectively, with:

$$\begin{aligned} X^{\prime }_3&= +1\!\!: p_1 +p_2 +p_8 +p_{10} +p_{14} +p_{16}\\&-1\!\!: p_3 +p_5 +p_{11} +p_{12} +p_{15} +p_{17}\\&\quad 0\!\!: \hbox {Otherwise}\\ X^{\prime }_4&= +1\!\!: p_1 +p_2 +p_7 +p_9 +p_{13} +p_{16}\\&-1\!\!: p_4 +p_6 +p_{11} +p_{12} +p_{15} +p_{18}\\&\quad 0\!\!: \hbox {Otherwise} \end{aligned}$$

The associated correlation matrix ${{\varvec{R}}}^{{{\varvec{AV}}}}$ has the same form as R in (4), with $\rho ^{AV}$ replacing $\rho$ in (5) and

$$\begin{aligned}&\displaystyle \rho ^{AV}=\sqrt{\frac{2\left( {k^{\prime }_{12} +k^{\prime }_{34} } \right) }{3k^{\prime }_{12} +2k^{\prime }_{34} }}\end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle \textit{CE}_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right) =\frac{3\varPhi _4 \left( {{{\varvec{R}}}^{{{\varvec{AV}}}}} \right) }{P_\infty ^{CW} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) }. \end{aligned}$$

(10)

Computed values of $CE_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ are obtained from (9) and (10) for each value of $k^{\prime }_5 =0\left( {.2} \right) 1$, with each value of $k^{\prime }_{12} =k^{\prime }_1 +k^{\prime }_2 =0\left( {.1} \right) \left( {1-k^{\prime }_5 } \right)$ by using a procedure that is developed in Gehrlein (1979), and the results are listed in Table 1. The numerical results in Table 1 for $\textit{CE}_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ with $k^{\prime }_5 =0$ are identical to those obtained in Diss et al. (2010) in their Table 11.6.

Whenever $k^{\prime }_{12} =0$, voters’ preferences are either dichotomous or they represent complete indifference between candidates. This case leads to a scenario in which a CW must exist and AV must select it as the winner, except for the specific case with $k^{\prime }_5 =1$, when all voters are completely indifferent and all voting rules, including AV, will effectively become a random chooser of a winner. The results of Table 1 clearly show that $\textit{CE}_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ decreases for any fixed $k^{\prime }_{12}$ as $k^{\prime }_5$ increases, which corresponds to a decrease in $k^{\prime }_{34}$. And, for any fixed $k^{\prime }_5$ we observe that $CE_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ decreases as $k^{\prime }_{12}$ increases, which also corresponds to a decrease in $k^{\prime }_{34}$. So, if either $k^{\prime }_{12}$ or $k^{\prime }_5$ is fixed, then $\textit{CE}_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ will increase as the proportion of voters with dichotomous preferences increases.

Table 1 Computed values of$CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$

When we assume that no voters have dichotomous preferences, with $k^{\prime }_3 +k^{\prime }_4 =0$, $\rho ^{AV}$ in (9) for the Condorcet Efficiency of AV reduces to $\sqrt{\frac{2}{3}}$ for all values of $k^{\prime }_1 +k^{\prime }_2 >0$, which corresponds with a limiting IC representation, $\textit{CE}_\infty ^{AV} \left( {\textit{IC}} \right)$, for the Condorcet Efficiency of AV from Gehrlein and Lepelley (1998).

Another observation regarding $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ follows from assuming that no voters have dichotomous preferences with $k^{\prime }_3 +k^{\prime }_4 =0$ and that $\varepsilon =\lambda =0$ with $k^{\prime }_1 +k^{\prime }_2 >0$. In this case, all voters who have an impact on the outcome of the election, by not having complete indifference, will vote only for their most preferred candidate. This corresponds to the commonly used Plurality Rule (PR) and $\rho$ above in (5) for $Rule\left( {0,0} \right)$ reduces to $\sqrt{\frac{2}{3}}$, just as $\rho ^{AV}$ did for AV in (9), leading to the conclusion from Gehrlein and Lepelley (1998) that $\textit{CE}_\infty ^{AV} \left( {IC} \right) = \textit{CE}_\infty ^{PR} \left( {\textit{IC}} \right)$. Thus, there is nothing to be gained on the basis of Condorcet Efficiency from using AV instead of PR for a three candidate election with IC.

Diss et al. (2010) then point out the well-known result that AV must elect the CW when all voters have dichotomous preferences, so the obvious question concerns how the Condorcet Efficiency of Extended Plurality Rule (EPR) behaves as the proportion of voters with dichotomous preferences increases. When the EIC extension of WSR’s that is described above is applied to PR, the $\rho$ in (5) for the limiting Condorcet Efficiency for $Rule\left( {0,0} \right)$ reduces to $\rho ^{EPR}$, with

$$\begin{aligned} \rho ^{EPR}=\frac{2k^{\prime }_{12} +k^{\prime }_{34} +k^{\prime }_4 }{\sqrt{\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) \left( {\frac{4k^{\prime }_{12} +k^{\prime }_{34} +3k^{\prime }_4 }{2}} \right) }}. \end{aligned}$$

(11)

An interesting observation then follows directly.

Theorem 1

$CE_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \ge CE_\infty ^{EPR} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$, and $CE_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right) = \textit{CE}_\infty ^{EPR} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ in three cases:

• Case 1. $k^{\prime }_5 =1.$

• Case 2. $k^{\prime }_5 <1$ and $k^{\prime }_3 =0$.

• Case 3. $k^{\prime }_5 <1$ and $k^{\prime }_{12} =k^{\prime }_4 =0$

Proof

Using a result from Slepian (1962) with the fact that the correlation matrices that correspond to the Condorcet Efficiencies for AV and PR have the same form, $\textit{CE}_\infty ^{AV} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \ge \textit{CE}_\infty ^{EPR} \left( {\textit{EIC}\left( {{{\varvec{k}}}^{{\prime }}} \right) } \right)$ whenever $\rho ^{AV}\ge \rho ^{\textit{EPR}}$. Since both $\rho ^{AV}\ge 0$ and $\rho ^{\textit{EPR}}\ge 0$, this will be true when $\left( {\rho ^{AV}} \right) ^{2}\ge \left( {\rho ^{EPR}} \right) ^{2}$ and it follows from (9) and (11) that:

$$\begin{aligned} \left( {\rho ^{\textit{AV}}} \right) ^{2}-\left( {\rho ^{\textit{EPR}}} \right) ^{2}=\frac{2\left( {k^{\prime }_{34} -k^{\prime }_4 } \right) \left( {k^{\prime }_{12} +k^{\prime }_4 } \right) }{\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) \left( {4k^{\prime }_{12} +k^{\prime }_{34} +3k^{\prime }_4 } \right) }. \end{aligned}$$

The value of $\left( {\rho ^{\textit{AV}}} \right) ^{2}-\left( {\rho ^{\textit{EPR}}} \right) ^{2}$ must therefore be nonnegative, and the three cases listed above identify the three different scenarios that make it equal to zero. $\square$

The introduction of any degree of dichotomous preferences into voter’s preference rankings will therefore give an advantage to AV over EPR for the case of three candidates, as pointed out in Diss et al. (2010). So, AV looks much better relative to EPR with this addition of this factor allowing for indifference in voters’ preferences than was suggested in the results that are given in Gehrlein and Lepelley (1998) that compared AV to PR with IC.

Diss et al. (2010) then go on to make a comparison between the Condorcet Efficiency of AV and an Extended form of Borda Rule (BR), which is a specific WSR that uses $\lambda =\frac{1}{2}$, and BR has been shown to have many interesting properties (see Young 1974). They perform an evaluation with their extension of BR to EIC by considering $CE_\infty ^{Rule\left( {0,1/2} \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ and they find that $CE_\infty ^{Rule\left( {0,1/2} \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) > CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ over most possible k’, but they also discover that there are regions of possible k’ for which the reverse is true. So, we are left to ask if this result only follows as a consequence of their interpretation of how BR should be extended to EIC. Should we be using $\varepsilon =0$?

Results from Slepian (1962) show that $\varPhi _4 \left( {{\varvec{R}}} \right)$, and therefore $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \!\right) } \!\left( {EIC\left( {{\!{\varvec{k}}}^{\prime }} \right) } \right)$, will not decrease as $\rho$ increases. Therefore, $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ is maximized by the $\varepsilon$ that maximizes $\rho$ from (5) in R. Obviously, that is the value of $\varepsilon$ that minimizes $\left\{ {1-\varepsilon +\varepsilon ^{2}} \right\} =\left\{ {1-\varepsilon \left( {1-\varepsilon } \right) } \right\}$. This function is symmetric about $\varepsilon =\frac{1}{2}$ and it decreases monotonically as $\varepsilon$ increases on the interval $0\le \varepsilon \le \frac{1}{2}$. So, the maximization of $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ occurs with using $\varepsilon =\frac{1}{2}$. However, following earlier discussion, we will require $\varepsilon \le \lambda$ and use $\varepsilon =\lambda$ for $\lambda \le 1/2$. When $\lambda >1/2$, the true maximization of $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ would use $\varepsilon =\frac{1}{2}$.

While the objective in Diss et al. (2010) was to compare voting rules on the basis of their Condorcet Efficiency, this result clearly shows that the use of $\varepsilon =0$ in the EIC model is actually minimizing the value of $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ for any given value of $\lambda >0$, which might explain the results that they observed regarding the relative Condorcet Efficiencies of AV and BR that EIC showed. We note that EPR used $\varepsilon =\lambda =0$ in our earlier discussion, so this observation does not affect the Theorem 1 results.

For the sake of simplicity in our representations, we proceed to analyze $Rule\left( {\lambda ,\lambda } \right)$ for all $0\le \lambda \le 1$, and remember that $Rule\left( {\frac{1}{2},\lambda } \right)$ would have greater Condorcet Efficiency than $Rule\left( {\lambda ,\lambda } \right)$ for $\lambda >1/2$. With $\varepsilon =\lambda$, $\rho$ from (5) can be rewritten as $\rho$* with a corresponding correlation matrix R*:

$$\begin{aligned} \rho ^{*}=\frac{2k^{\prime }_{12} +\left( {1+\lambda } \right) k^{\prime }_3 +\left( {2-\lambda } \right) k^{\prime }_4 }{\sqrt{2\left( {3k^{\prime }_{12} +2k^{\prime }_3 +2k^{\prime }_4 } \right) \left( {k^{\prime }_{12} \left\{ {1-\lambda +\lambda ^{2}} \right\} +k^{\prime }_3 \left( {\frac{1+\lambda }{2}} \right) ^{2}+k^{\prime }_4 \left( {\frac{2-\lambda }{2}} \right) ^{2}} \right) }}.\quad \end{aligned}$$

(12)

Two observations can be made at this point. The first observation involves the use of Negative Plurality Rule (NPR) which is a WSR that uses $\lambda =1$, so that each voters casts a ballot for both of their two more preferred candidates in a three-candidate election. This is equivalent to having each voter cast a vote against their least preferred candidate, with the winner being the candidate who receives the fewest negative votes. A similar observation can be made for Extended NPR (ENPR) with $Rule\left( {1,1} \right)$ as we saw above for EPR with $Rule\left( {0,0} \right)$, and:

Corollary 1

$CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \ge CE_\infty ^{ENPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$, and $CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) = CE_\infty ^{ENPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ in three cases:

• Case 1. $k^{\prime }_5 =1.$

• Case 2. $k^{\prime }_5 <1$ and $k^{\prime }_4 =0$.

• Case 3. $k^{\prime }_5 <1$ and $k^{\prime }_{12} =k^{\prime }_3 =0$.

Proof

This follows from Theorem 1 and the fact that the Condorcet Efficiency of EWSR’s remains unchanged if $\lambda \rightarrow 1-\lambda$ with the simultaneous interchange $k^{\prime }_3 \leftrightarrow k^{\prime }_4$ in (12). $\square$

If we assume that no voters have dichotomous preferences with $k^{\prime }_3 +k^{\prime }_4 =0$ and $k^{\prime }_1 +k^{\prime }_2 >0$, $\rho ^{*}$ in (12) for $Rule\left( {1,1} \right)$ reduces to $\sqrt{\frac{2}{3}}$, just as $\rho ^{AV}$ did for AV in (9), leading to the conclusion from Gehrlein and Lepelley (1998) that $CE_\infty ^{AV} \left( {IC} \right) = CE_\infty ^{NPR} \left( {IC} \right)$. So, there is nothing to be gained on the basis of Condorcet Efficiency from using AV instead of either PR or NPR for a three candidate election with IC and $CE_\infty ^{AV} \left( {IC} \right) = CE_\infty ^{PR} \left( {IC} \right) =CE_\infty ^{NPR} \left( {IC} \right)$. The introduction of a degree of voter indifference between candidates clearly gives an advantage to AV in comparison to both PR and NPR.

The use of EIC also suggests that the Condorcet Efficiencies of EPR and ENPR are not identical, as the early results from IC suggest for PR and NPR, as seen in the following Theorem 2.

Theorem 2

$$\begin{aligned}&CE_\infty ^{EPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) > CE_\infty ^{ENPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \!,\quad \hbox { if }k^{\prime }_4 >k^{\prime }_3 \\&CE_\infty ^{ENPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) > CE_\infty ^{EPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \!,\quad \hbox { if } k^{\prime }_3 >k^{\prime }_4 .\\&CE_\infty ^{EPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) =CE_\infty ^{ENPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \!,\quad \hbox { if }k^{\prime }_4 =k^{\prime }_3 . \end{aligned}$$

Proof

Using the result from Slepian (1962) with the fact that the correlation matrices for the Condorcet Efficiencies of PER and NPER have the same form, $CE_\infty ^{EPR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) > CE_\infty ^{ENPR} \left( {EIC\left( {{{\varvec{k}}}^{{\prime }}} \right) } \right)$ if and only if $\rho ^{EPR}>\rho ^{ENPR}$. Since both $\rho ^{EPR}\ge 0$ and $\rho ^{ENPR}\ge 0$ from (11) and (12), this result will be obtained when $\left( {\rho ^{EPR}} \right) ^{2}\ge \left( {\rho ^{ENPR}} \right) ^{2}$ and it follows from (11) and (12) that:

$$\begin{aligned} \left( {\rho ^{EPR}} \right) ^{2}-\left( {\rho ^{ENPR}} \right) ^{2}=\frac{2\left( {k^{\prime }_4 -k^{\prime }_3 } \right) \left( {4k^{\prime 2}_{12}+3k^{\prime }_3 k^{\prime }_4 +4k^{\prime }_{12} k^{\prime }_{34} } \right) }{\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) \left( {4k^{\prime }_{12} +k^{\prime }_{34} +3k^{\prime }_3 } \right) \left( {4k^{\prime }_{12} +k^{\prime }_{34} +3k^{\prime }_4 } \right) }. \end{aligned}$$

The value of $\left( {\rho ^{EPR}} \right) ^{2}-\left( {\rho ^{ENPR}} \right) ^{2}$ must therefore be positive whenever $k^{\prime }_4 >k^{\prime }_3$, and the remaining observations follow in the same fashion. $\square$

So, EPR and ENPR do not always have the same values of Condorcet Efficiency with EIC, like PR and NPR did with IC. But, both are still dominated by AV with EIC.

The obvious question at this point is: “What value of $\lambda$ will maximize $CE_\infty ^{Rule\left( {\lambda ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$?” The result from Slepian (1962) can be used again to show that $\varPhi _4 \left( {{{\varvec{R}}}^{*}} \right)$, and therefore $CE_\infty ^{Rule\left( {\lambda ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$, is maximized by finding the $\lambda$ that maximizes $\rho ^{*}$ in (12). To facilitate this process, we begin with some substitution of variables. In particular, let $k^{\prime }_3 \rightarrow \frac{k^{\prime }_{34} }{2}-z$ and $k^{\prime }_4 \rightarrow \frac{k^{\prime }_{34} }{2}+z$ with $-\frac{k^{\prime }_{34} }{2}\le z\le \frac{k^{\prime }_{34} }{2}$. Any combination of $k^{\prime }_3$ and $k^{\prime }_4$ can then be obtained by an appropriate selection of $k^{\prime }_{34}$ and $z$. After substitution into (12) and algebraic reduction

$$\begin{aligned} \rho ^{*}=\frac{4k^{\prime }_{12} +3k^{\prime }_{34} +2z\left( {1-2\lambda } \right) }{\sqrt{\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) \left[ {2\left( {4k^{\prime }_{12} +k^{\prime }_{34} } \right) \left( {1-\lambda +\lambda ^{2}} \right) +3k^{\prime }_{34} +6z\left( {1-2\lambda } \right) } \right] }}. \end{aligned}$$

(13)

It is of course still true that $\rho ^{*}$ in (13) does not change under the transition $\lambda \rightarrow 1-\lambda$ if we simultaneously make the interchange $k^{\prime }_3 \leftrightarrow k^{\prime }_4$ by using the transition $z\rightarrow -z$ while $k^{\prime }_{34}$ remains unchanged.

To find the $\lambda$ that maximizes $\rho ^{*}$, we obtain the derivative

$$\begin{aligned} \frac{\partial \rho ^{*}}{\partial \lambda }=\frac{\left( {1-2\lambda } \right) \left[ {16k^{\prime 2}_{12} +16k^{\prime }_{12} k^{\prime }_{34} +3k^{\prime 2}_{34}-12z^{2}} \right] }{\sqrt{\left[ {3k^{\prime }_{12} +2k^{\prime }_{34} } \right] \left\{ {\left( {8k^{\prime }_{12} +2k^{\prime }_{34} } \right) \left( {1-\lambda +\lambda ^{2}} \right) +3k^{\prime }_{34} +6z\left( {1-2\lambda } \right) } \right\} ^{3}}}. \end{aligned}$$

(14)

It is easily shown the value of $3k^{\prime 2}_{34}-12z^{2}$ in the numerator in (14) and the values of both $\left( {1-\lambda +\lambda ^{2}} \right)$ and $3k^{\prime }_{34} +6z\left( {1-2\lambda } \right)$ in the denominator must all be nonnegative if $0\le \lambda \le 1$ and $-\frac{k^{\prime }_{34} }{2}\le z\le \frac{k^{\prime }_{34} }{2}$. The sign of $\frac{\partial \rho ^{*}}{\partial \lambda }$ is therefore completely determined by the sign of $\left( {1-2\lambda } \right)$ since $k^{\prime }_{12} \ge 0$ and $k^{\prime }_{34} \ge 0$. The special case with $k^{\prime }_{12} =0$ and $k^{\prime }_{34} =0$ is the case of all voters being completely indifferent between all candidates, as discussed earlier.

The obvious implication of this observation is that $\rho ^{*}$ increases over the interval $0\le \lambda <\frac{1}{2}$, since $1-2\lambda$ is positive in this range, and it decreases over the interval $\frac{1}{2}<\lambda \le 1$. $CE_\infty ^{Rule\left( {\lambda ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ is therefore maximized by using the EIC extension of BR (EBR) for voters with preferences in both Categories 1 and 2. When we use $\lambda =\frac{1}{2}$, $\rho ^{*}$ from (14) reduces to

$$\begin{aligned} \rho ^{EBR}=\sqrt{\frac{2\left( {4k^{\prime }_{12} +3k^{\prime }_{34} } \right) }{3\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) }}. \end{aligned}$$

(15)

It is interesting to note that $\rho ^{*}$ is not a function of $z$ with EBR.

Theorem 3

$CE_\infty ^{EBR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \ge CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$, and $CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) = CE_\infty ^{EBR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ if $k^{\prime }_{12} =0$.

Proof

Using the result from Slepian (1962) with the fact that the correlation matrices that correspond to the Condorcet Efficiencies for AV and EBR have the same form, $CE_\infty ^{EBR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \ge CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{{\prime }}} \right) } \right)$ whenever $\rho ^{EBR}\ge \rho ^{AV}$. Since both $\rho ^{AV}\ge 0$ and $\rho ^{EBR}\ge 0$, this will be true when $\left( {\rho ^{EBR}} \right) ^{2}\ge \left( {\rho ^{AV}} \right) ^{2}$ and it follows from (9) and (15) that:

$$\begin{aligned} \left( {\rho ^{EBR}} \right) ^{2}-\left( {\rho ^{AV}} \right) ^{2}=\frac{2\left( {4k^{\prime }_{12} +3k^{\prime }_{34} } \right) }{3\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) }-\frac{2\left( {k^{\prime }_{12} +k^{\prime }_{34} } \right) }{3k^{\prime }_{12} +2k^{\prime }_{34} }=\frac{2k^{\prime }_{12} }{3\left( {3k^{\prime }_{12} +2k^{\prime }_{34} } \right) }. \end{aligned}$$

The statement of the theorem follows directly from this result. $\square$

So, EBR dominates AV whenever $k^{{\prime }}_{12} >0$ and the Condorcet Efficiency values of these two rules are identical when $k^{{\prime }}_{12} =0$. Computed values of $CE_\infty ^{EBR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ are obtained from the procedure that is developed in Gehrlein (1979) and they are listed in Table 2 below. The case with $k^{{\prime }}_{12} =1$ is equivalent to IC with a Condorcet Efficiency value for EBR that matches an earlier IC based result from Gehrlein and Fishburn (1978).

Table 2 Computed values of $CE_\infty ^{EBR} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$

The conclusion that AV has greater Condorcet Efficiency than EBR for some regions of k’ in Diss et al. (2010) is therefore completely dependent on their assumption that $\varepsilon =0$, which actually minimizes $CE_\infty ^{Rule\left( {\varepsilon ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ for any given $\uplambda$. If the $\varepsilon$ is used to maximize the Condorcet Efficiency of $Rule\left( {\varepsilon ,\lambda } \right)$, EBR dominates AV. However, their primary observation that the introduction of any level of dichotomous preferences to voter profiles leads to a domination of AV over both EPR and ENPR is completely correct. This observation therefore significantly improves the status of AV compared to PR and NPR on the basis of Condorcet Efficiency from the IC based results in Gehrlein and Lepelley (1998).

It is of interest to consider how widespread the possible Condorcet Efficiency dominance of some EWSR’s over AV might be, and the following result proves that this dominance of AV by voting rules of the form of $Rule\left( {\lambda ,\lambda } \right)$ is restricted to only EBR for $\lambda \le 1/2$.

Theorem 4

$CE_\infty ^{Rule\left( {\lambda ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \le CE_\infty ^{AV} \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right)$ with some ${{\varvec{k}}}^{\prime }$ for every $0\le \lambda <1/2$.

Proof

Following the proof of Theorem 3, $CE_\infty ^{Rule\left( {\lambda ,\lambda } \right) } \left( {EIC\left( {{{\varvec{k}}}^{\prime }} \right) } \right) \le CE_\infty ^{AV} ( EIC( {{{\varvec{k}}}^{{\prime }}})$ whenever $\left( {\rho ^{Rule\left( {\lambda ,\lambda } \right) }} \right) ^{2}-\left( {\rho ^{AV}} \right) ^{2}\le 0$. When we consider the particular case with $k^{\prime }_5 =0$, this result is obtained from (9) and (12) to lead to

$$\begin{aligned}&\left( {\rho ^{Rule\left( {\lambda ,\lambda } \right) }} \right) ^{2}-\left( {\rho ^{AV}} \right) ^{2}\nonumber \\&\qquad = \frac{2\left\{ {k^{\prime }_{12} \left( {\lambda -1} \right) \left( {k^{\prime }_{12} \left( {\lambda -1} \right) +1-5\lambda } \right) +k^{\prime }_4 \left( {2\lambda -1} \right) \left[ {\left( {k^{\prime }_4 -1} \right) \left( {2\lambda -1} \right) +2k^{\prime }_{12} \left( {\lambda -1} \right) } \right] } \right\} }{3\left( {1-2\lambda } \right) \left( {k^{\prime }_4 +k^{\prime }_{12} } \right) +3k^{\prime }_{12} \lambda ^{2}+\left( {1+\lambda } \right) ^{2}}.\nonumber \\ \end{aligned}$$

(16)

If attention is further restricted to the case of completely dichotomous preferences with $k^{\prime }_{12} =0$, then (16) reduces to:

$$\begin{aligned} \left( {\rho ^{Rule\left( {\lambda ,\lambda } \right) }} \right) ^{2}-\left( {\rho ^{AV}} \right) ^{2}= \frac{-2k^{\prime }_4 \left( {1-2\lambda } \right) ^{2}\left( {1-k^{\prime }_4 } \right) }{3k^{\prime }_4 \left( {1-2\lambda } \right) +\left( {1+\lambda } \right) ^{2}}. \end{aligned}$$

It then follows obviously for this case that $\left( {\rho ^{Rule\left( {\lambda ,\lambda } \right) }} \right) ^{2}-\left( {\rho ^{AV}} \right) ^{2}<0$ whenever $0<k^{\prime }_4 <1$ for all $0\le \lambda <1/2$. $\square$

It is clear from Theorem 4 that AV can be dominant over all $Rule\left( {\lambda ,\lambda } \right)$ for $0\le \lambda <1/2$, to make EBR unique among the EWSR’s. We now consider this possible AV dominance over EWSR’s in more detail by using (16) to find the root values of $\lambda$, $R\left( {\lambda |k^{\prime }_{12} ,k^{\prime }_4 } \right)$, for which $\left( {\rho ^{Rule\left( {\lambda ,\lambda } \right) }} \right) ^{2}-\left( {\rho ^{AV}} \right) ^{2}=0$, for given $k^{\prime }_{12}$ and $k^{\prime }_4$ with $k^{\prime }_5 =0$:

$$\begin{aligned} R\left( {\lambda |k^{\prime }_{12} ,k^{\prime }_4 } \right) =\frac{2k^{\prime }_4 \left( {k^{\prime }_4 -1} \right) +k^{\prime }_{12} \left( {k^{\prime }_{12} +3k^{\prime }_4 -3} \right) +\sqrt{k^{\prime }_{12} \left[ {3k^{\prime }_4 \left( {1-k^{\prime }_4 } \right) +k^{\prime }_{12} \left( {4-3k^{\prime }_4 } \right) } \right] }}{\left( {2k^{\prime }_4 +k^{\prime }_{12} } \right) ^{2}-4k^{{\prime }}_4 -5k^{\prime }_{12} }. \end{aligned}$$

(17)

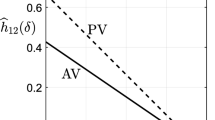
Then, AV dominates $Rule\left( {\lambda ,\lambda } \right)$ for all $0\le \lambda <R\left( {\lambda |k^{\prime }_{12} ,k^{\prime }_4 } \right)$ with specified $k^{\prime }_{12}$ and $k^{\prime }_4$. The representation in (17) is then used for each $k^{\prime }_{12}$ = 0, .1, .3, .5; and $R\left( {\lambda |k^{\prime }_{12} ,k^{\prime }_4 } \right)$ is calculated for each $k^{\prime }_{12}$ for values of $k^{\prime }_4$ in .05 increments from 0 to $1-k^{\prime }_{12}$. The results are shown graphically in Fig. 1.

Fig. 1

Computed values of $R\left( {\lambda |k^{\prime }_{12} ,k^{\prime }_4 } \right)$ with $k^{\prime }_{12} =0, .1, .3, .5$

To interpret the results in Fig. 1, note that the graph of $R\left( {\lambda |0,k^{\prime }_4 } \right)$ represents the case of completely dichotomous preferences, and AV dominates $Rule\left( {\lambda ,\lambda } \right)$ on the basis of Condorcet Efficiency for all $0\le \lambda <.5$, since $R\left( {\lambda |0,k^{\prime }_4 } \right) =.5$ for all $0<k^{\prime }_4 <1$, as observed in the proof of Theorem 4. It is important to note that the area of AV dominance contracts rapidly as $k^{\prime }_{12}$ increases. For the case with $k^{\prime }_{12} =.5$, where half of the voters have dichotomous preferences and half have complete rankings, AV only dominates $Rule\left( {\lambda ,\lambda } \right)$ in the approximate range with $0\le \lambda \le .1$ when $k^{\prime }_4 =0$, and that range of dominance then decreases rapidly as $k^{\prime }_4$ increases to $k^{\prime }_4 =.5$.

Our next step is to determine the impact that the introduction of a degree of dependence among voters’ preferences will have on these results. This is done by considering an extension of the IAC model that was mentioned above.

6 Preliminary Extensions of IAC

The basic IAC model begins just like IC and it assumes that each voter has one of the six possible complete preference rankings on candidates. That is, each voter has one of the preference rankings like those for Category 1 voters, where we temporarily ignore the fact that only one candidate is considered acceptable to these voters. No other preference rankings are allowed with IAC, so $n=\sum _{i=1}^6 n_i$ and we let n denote a six-dimension vector that represents any such combination of $n_i$’s. These n terms are defined as voting situations, to describe an election outcome in which the specific preferences of individual voters are not identified, to make the voters anonymous in terms of their preferences on candidates. Voters are not anonymous in the voter profiles with IC, and there is another important distinction between IC and IAC. IAC assumes that all possible voting situations with $n=\sum _{i=1}^6 n_i$ for a specified $n$ are equally likely to be observed, and it is well known that this implicitly assumes that there is some degree of dependence among the voters’ preferences, unlike the independence of IC (see e.g. Berg 1985). The introduction of some degree of dependence with IAC has been seen to make significant differences in the probability that some election outcomes are observed, relative to IC. We are not aware of any previous work that has been done to evaluate the Condorcet Efficiency of AV under the assumption of IAC or any of its extensions, and we pursue that analysis here, as suggested in Diss et al. (2010).

The first issue is to consider how the basic IAC assumption can be modified to allow for the consideration of voting outcomes with AV, and there are several alternatives that are available. We begin by mirroring the analysis of the Condorcet Efficiency of AV that was performed in Gehrlein and Lepelley (1998). That study used the basic IC model with the assumption that each voter will independently vote for two candidates with AV with probability $p$ in a three-candidate election and found that $CE_\infty ^{PR} \left( {IC} \right) =CE_\infty ^{NPR} \left( {IC} \right) =CE_\infty ^{AV} \left( {IC} \right)$ for all $p$. It is stressed again that this result is only valid for three-candidate elections.

Let $IAC^{{}^{\circ }}$ denote the most elementary adaptation on this model to the IAC format, by restricting the possible EIC voter preference rankings that are shown above to require complete preferences with $k_3 =k_4 =k_5 =0$. Then $k_1 +k_2 =n$, and all possible voting situations with $\sum _{i=1}^{12} n_i =n$ are equally likely to be observed.

Candidate $A$ is the CW in a voting situation whenever:

$$\begin{aligned} n_1&+ n_2 +n_4 +n_7 +n_8 +n_{10} >\frac{n}{2} \, \left( {A{{\varvec{M}}}B} \right) \hbox { and }\\&\quad n_1 +n_2 +n_3 +n_7 +n_8 +n_9 >\frac{n}{2} \, \left( {A{{\varvec{M}}}C} \right) . \end{aligned}$$

A representation for the total number of possible voting situations for which Candidate $A$ is the CW with $IAC^{{}^{\circ }}$can be obtained as a quasi-polynomial as a function of $n$ of degree 11 (see $e.g$. Wilson and Pritchard 2006). Such a representation can be computed by using any of several algorithms; one of the most efficient is due to Barvinok (1993) and is implemented in the software LattE ¹ by De Loera et al. (2004). We use this procedure to obtain the coefficient of the $n^{11}$ component of this representation as

$$\begin{aligned} \frac{79}{10218700800}. \end{aligned}$$

Candidate $A$ is the AV winner in a voting situation whenever:

$$\begin{aligned}&n_1 +n_2 +n_8 +n_{10} >n_3 +n_5 +n_{11} +n_{12} \,\, \left( {A{{\varvec{A}}}B} \right) \hbox { and}\\&n_1 +n_2 +n_7 +n_9 >n_4 +n_6 +n_{11} +n_{12} \,\, \left( {A{{\varvec{A}}}C} \right) . \end{aligned}$$

The number of voting situations for which Candidate $A$ is both the CW and the AV winner with $IAC^{^{\circ }}$ is also a quasi-polynomial as a function of $n$ of degree 11, and the coefficient of the $n^{11}$ component is equal to

$$\begin{aligned} \frac{34409}{5885971660800}. \end{aligned}$$

There are the same number of voting situations in which Candidates $B$ and $C$ will be the CW and in which Candidates $B$ and $C$ will be both the CW and the AV winner. The limiting Condorcet Efficiency, $CE_\infty ^{AV} \left( {IAC^{^{\circ }}} \right)$, of AV will only rely on the quasi-polynomial term of degree 11 when $n\rightarrow \infty$, so it is thus equal to:

$$\begin{aligned} CE_\infty ^{AV} \left( {IAC^{^{\circ }}} \right) =\frac{\frac{34409}{5885971660800}}{\frac{79}{10218700800}}= \frac{34409}{45504}\approx 0.75617. \end{aligned}$$

(18)

In this $IAC^{^{\circ }}$ framework, Candidate $A$ is the PR winner in a voting situation whenever:

$$\begin{aligned}&n_1 +n_2 +n_7 +n_8 >n_3 +n_5 +n_9 +n_{11} \,\, \left( {A{{\varvec{P}}}B} \right) \hbox { and}\\&n_1 +n_2 +n_7 +n_8 >n_4 +n_6 +n_{10} +n_{12} \,\, \left( {A{{\varvec{P}}}C} \right) . \end{aligned}$$

And, following the discussion above we obtain

$$\begin{aligned} CE_\infty ^{PR} \left( {IAC^{^{\circ }}} \right) =\frac{1319347}{1554957}\approx 0.84848. \end{aligned}$$

(19)

Candidate $A$ is the NPR winner for the $IAC^{^{\circ }}$ scenario whenever:

$$\begin{aligned}&n_5 +n_6 +n_{11} +n_{12} <n_2 +n_4 +n_8 +n_{10} \,\, \left( {A{{\varvec{N}}}B} \right) \hbox { and}\\&n_5 +n_6 +n_{11} +n_{12} <n_1 +n_3 +n_7 +n_9 \,\, \left( {A{{\varvec{N}}}C} \right) . \end{aligned}$$

The limiting representation for the Condorcet Efficiency is found to be

$$\begin{aligned} CE_\infty ^{NPR} \left( {IAC^{^{\circ }}} \right) =\frac{132139303}{199034496}\approx 0.66390. \end{aligned}$$

(20)

Finally, it is easily checked that Candidate $A$ is the BR winner under $IAC^{^{\circ }}$ whenever:

$$\begin{aligned}&n_1 +n_2 +2n_3 +2n_4 -n_5 -n_6 -2n_7 -2n_8 +n_9 +n_{10} -n_{11} -n_{12} >0 \,\, \left( {A{{\varvec{B}}}B} \right) \hbox { and}\\&2n_1 +2n_2 +n_3 +n_4 +n_5 +n_6 -n_7 -n_8 -n_9 -n_{10} -2n_{11} -2n_{12} >0 \,\, \left( {A{{\varvec{B}}}C} \right) . \end{aligned}$$

We obtain:

$$\begin{aligned} CE_\infty ^{BR} \left( {IAC^{^{\circ }}} \right) =\frac{17395}{19197}\approx 0.90613. \end{aligned}$$

(21)

The results of (18), (19), (20) and (21) indicate that PR dominates AV under the $IAC^{^{\circ }}$ model, that AV in turn dominates NPR and that BR dominates the three other rules. However, it has been noted that $IAC^{^{\circ }}$ is the most basic possible extension of IAC to consider the Condorcet Efficiency of AV.

We further extend the basic definition of $IAC^{^{\circ }}$ to develop an assumption that is more in alignment with the notions used in Gehrlein and Lepelley (1998), by identifying the number of voters, $q$, in an $IAC^{^{\circ }}$ voting situation that will vote for two candidates with AV, with $q=\sum _{i=7}^{12} n_i$. Then, $IAC^{*}\left( q \right)$ assumes that all voting situations for $n$ voters with a specified value of parameter $q$ are equally likely to be observed. Since Barvinok’s algorithm enables the development of quasi-polynomials as a function of more than one parameter (see Lepelley et al. 2008), it is then theoretically possible to obtain a representation for the Condorcet Efficiency of AV as a function of $n$ and $q$, but this representation would be extremely cumbersome. As a result, we only consider the limiting case as $n\rightarrow \infty$, and use the parameter $\alpha =\frac{q}{n}$ to measure the proportion of voters in a voting situation who will choose to vote for two candidates with AV. The same program that is discussed above is used to obtain the limiting Condorcet Efficiency of AV with $IAC^{*}\left( \alpha \right)$:

$$\begin{aligned}&CE_\infty ^{AV} \left( {IAC^{*}\left( \alpha \right) } \right) =\frac{3050\alpha ^{5}-26040\alpha ^{4}+65430\alpha ^{3}-72360\alpha ^{2}+37485\alpha -7497}{135(42\alpha ^{5}-274\alpha ^{4}+603\alpha ^{3}-624\alpha ^{2}+315\alpha -63)},\nonumber \\&\quad \hbox { for }0 \le \alpha \le 1/2\\&\quad = \frac{\left[ {{\begin{array}{l} {4817408\alpha ^{10}-29821440\alpha ^{9}+80881920\alpha ^{8}-126236160\alpha ^{7}+124750080\alpha ^{6}} \\ {-80172288\alpha ^{5}+32417280\alpha ^{4}-7090560\alpha ^{3}+300600\alpha ^{2}+179370\alpha -26199} \\ \end{array} }} \right] }{34560\left( {\alpha -1} \right) ^{5}(42\alpha ^{5}+64\alpha ^{4}-73\alpha ^{3}+39\alpha ^{2}-10\alpha +1)},\nonumber \\&\qquad \hbox { for }1/2\le \alpha \le 3/4\nonumber \\&\quad = \frac{498\alpha ^{5}+640\alpha ^{4}-1235\alpha ^{3}+975\alpha ^{2}-320\alpha +37}{15(42\alpha ^{5}+64\alpha ^{4}-73\alpha ^{3}+39\alpha ^{2}-10\alpha +1)}\quad \hbox { for }3/4\le \alpha \le 1.\nonumber \end{aligned}$$

(22)

We note that $CE_\infty ^{AV} \left( \mathrm{{IAC}^{*}\left( 0 \right) } \right) =CE_\infty ^{PR} \left( \mathrm{{IAC}} \right) =\frac{119}{135}$ and $CE_\infty ^{AV} \left( \mathrm{{IAC}^{*}\left( 1 \right) } \right) =CE_\infty ^{NPR} \left( \mathrm{{IAC}} \right) =\frac{17}{27}$ in accordance with limiting results from Gehrlein (1982).

Calculated values of $CE_\infty ^{AV} \left( {\mathrm{IAC}^{*}\left( \alpha \right) } \right)$ from (22) are listed in Table 3 for each $\alpha =0\left( {.1} \right) 1$.

Table 3 Computed values of $CE_\infty ^{AV} \left( {IAC^{*}\left( \alpha \right) } \right)$

We observe that $CE_\infty ^{AV} \left( \mathrm{{IAC}^{*}\left( {\frac{1}{2}} \right) } \right)$ is very close to the value of $CE_\infty ^{AV} \left( \mathrm{{IAC}^{^{\circ }}} \right)$ in (18) that was obtained in our first approach to extending IAC. As a result of the values in Table 3, we see that $CE_\infty ^{AV} \left( \mathrm{{IAC}^{*}\left( \alpha \right) } \right)$ is bounded between an upper limit of $CE_\infty ^{AV} \left( \mathrm{{IAC}^{*}\left( 0 \right) } \right) =CE_\infty ^{PR} \left( {IAC} \right)$ and a lower limit of $CE_\infty ^{AV} \left( \mathrm{{IAC}^{*}\left( 1 \right) } \right) =CE_\infty ^{NPR} \left( \mathrm{{IAC}} \right)$. Moreover, $CE_\infty ^{AV} \left( \mathrm{{IAC}^{*}\left( \alpha \right) } \right)$ decreases monotonically as $\alpha$ increases, so increasing the proportion of voters who choose to vote for two candidates with AV results in a decreased value of Condorcet Efficiency for AV.

7 An Extended IAC Model with Indifference Allowed

The analysis that was performed with IC suggested that when voters actually have complete preference rankings on candidates, nothing will be gained by making any distinction between those voters who approve of one or two candidates. As a result, we drop that distinction in our Extended IAC model. We also drop the consideration of voters who are indifferent between all candidates, since they have no impact on the determination of the CW or the winner of the election with the extended voting rules that are being considered. However, voters who do have indifference between two candidates are admitted in this Extended IAC (EIAC) model, with no distinction being made between the voters with dichotomous preferences in Categories 3 and 4 above, making it similar to IWOC.²

There are twelve resulting possible preference rankings on candidates that voters might have with EIAC:

$$\begin{aligned} t_1&= \textit{Number of voters with a complete ranking for preference}\\&\qquad \qquad \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} A \quad &{} A \quad &{} B \quad &{} B \quad &{} C \quad &{} C\\ B \quad &{} C \quad &{} A \quad &{} C \quad &{} A \quad &{} B\\ C \quad &{} B \quad &{} C \quad &{} A \quad &{} B \quad &{} A\\ m_1 \quad &{} m_2 \quad &{} m_3 \quad &{} m_4 \quad &{} m_5 \quad &{} m_6\\ \end{array}\\ t_1&= m_1 +m_2 +m_3 +m_4 +m_5 +m_6\\ t_2&= \textit{Number of voters with dichotomous preferences}\\&\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \left( {A,B} \right) \quad &{} \left( {A,C} \right) \quad &{} \left( {B,C} \right) \quad &{} A \quad &{} B \quad &{} C\\ C \quad &{} B \quad &{} A \quad &{} \left( {B,C} \right) \quad &{} \left( {A,C} \right) \quad &{} \left( {A,B} \right) \\ m_7 \quad &{} m_8 \quad &{} m_9 \quad &{} m_{10} \quad &{} m_{11} \quad &{} m_{12}\\ \end{array}\\ t_2&= m_7 +m_8 +m_9 +m_{10} +m_{11} +m_{12} \end{aligned}$$

Here, $m_i$ terms replace the $n_i$ terms in the reduced set of possible voter preference rankings that were identified for the analysis of EIC, and $t_1 +t_2 =n$. With the assumption of $EIAC\left( {t_2 } \right)$, all voting situations with $n$ voters that have a specified value of parameter $t_2$ are considered equally likely to be observed. It is emphasized here that it does not then follow that all values of $t_2$ are equally likely to be observed for a given value of $n$.

In this EIAC framework, Candidate $A$ is the CW in a voting situation whenever:

$$\begin{aligned}&m_1 +m_2 -m_3 -m_4 +m_5 -m_6 +m_8 -m_9 +m_{10} -m_{11} >0 \,(A{{\varvec{M}}}B)\hbox { and}\\&m_1 +m_2 +m_3 -m_4 -m_5 -m_6 +m_7 -m_9 +m_{10} -m_{12} > 0\, (A{{\varvec{M}}}C). \end{aligned}$$

Candidate $A$ is the AV winner whenever:

$$\begin{aligned}&m_1 +m_2 -m_3 -m_4 +m_8 -m_9 +m_{10} -m_{11} > 0\, (A{{\varvec{A}}}B)\hbox { and}\\&m_1 +m_2 -m_5 -m_6 +m_7 -m_9 +m_{10} -m_{12} > 0 \,(A{{\varvec{A}}}C). \end{aligned}$$

Candidate $A$ is the EPR winner whenever:

$$\begin{aligned}&2m_1 +2m_2 -2m_3 -2m_4 +m_8 -m_9 +2m_{10} -2m_{11} > 0\, (A{{\varvec{P}}}B)\hbox { and}\\&2m_1 +2m_2 -2m_5 -2m_6 +m_7 -m_9 +2m_{10} -2m_{12} > 0\, (A{{\varvec{P}}}C). \end{aligned}$$

Candidate $A$ is the ENPR winner whenever:

$$\begin{aligned}&2m_2 -2m_4 +2m_5 -2m_6 +2m_8 -2m_9 +m_{10} -m_{11} > 0 \,(A{{\varvec{N}}}B)\hbox { and}\\&2m_1 +2m_3 -2m_4 -2m_6 +2m_7 -2m_9 +m_{10} -m_{12} > 0 \,(A{{\varvec{N}}}C). \end{aligned}$$

Candidate $A$ is the EBR winner whenever:

$$\begin{aligned}&2m_1 +4m_2 -2m_3 -4m_4 +2m_5 -2m_6 +3m_8 -3m_9 +3m_{10} -3m_{11} > 0\, (A{{\varvec{B}}}B)\hbox { and}\\&4m_1 +2m_2 +2m_3 -2m_4 -2m_5 -4m_6 +3m_7 -3m_9 +3m_{10} -3m_{12} > 0\, (A{{\varvec{B}}}C). \end{aligned}$$

Limiting representations are obtained as $n\rightarrow \infty$ for the Condorcet Efficiency of AV, EPR, ENPR and EBR as functions of the proportion $\alpha =\frac{t_2 }{n}$ of voters that have indifference in their preference rankings, and hence dichotomous preferences.

Continuing as in the immediately preceding section, we obtain the following representations for $CE_\infty ^{AV} \left( {EIAC\left( \alpha \right) } \right)$, with:

$$\begin{aligned}&CE_\infty ^{AV} \left( {EIAC\left( \alpha \right) } \right) \nonumber \\&\quad = \frac{3(49059\alpha ^{5}-256840\alpha ^{4}+526580\alpha ^{3}-531840\alpha ^{2}+266560\alpha -53312)}{5(33073\alpha ^{5}-176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+181440\alpha -36288)}\\&\qquad \hbox {for }0 \le \alpha \le 1/3\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {16728363\alpha ^{10}-83789640\alpha ^{9}+172560780\alpha ^{8}-194244480\alpha ^{7}+133040880\alpha ^{6}} \\ {-\,59185728\alpha ^{5}+18370800\alpha ^{4}-4147200\alpha ^{3}+605880\alpha ^{2}-51840\alpha +1976} \\ \end{array} }} \right] }{135\alpha ^{5}(33073\alpha ^{5}-176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+181440\alpha -36288)}, \nonumber \\&\qquad \hbox { for } 1/3\le \alpha \le 1/2\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {15069483\alpha ^{10}-90425160\alpha ^{9}+235598220\alpha ^{8}-351008640\alpha ^{7}+331899120\alpha ^{6}} \\ {-\,208692288\alpha ^{5}+88043760\alpha ^{4}-24001920\alpha ^{3}+3787560\alpha ^{2}-272160\alpha +1976} \\ \end{array} }} \right] }{27\left[ {{\begin{array}{l} {890357\alpha ^{10}-5277480\alpha ^{9}+13729500\alpha ^{8}-20707200\alpha ^{7}+20180160\alpha ^{6}} \\ {-13390272\alpha ^{5}+6158880\alpha ^{4}-1929600\alpha ^{3}+388800\alpha ^{2}-45480\alpha +2343} \nonumber \\ \end{array} }} \right] },\nonumber \\&\qquad \hbox { for }1/2\le \alpha \le 2/3\nonumber \\&\quad = \frac{24\left( {1-\alpha } \right) ^{5}(7673\alpha ^{5}+9385\alpha ^{4}-17970\alpha ^{3}+12310\alpha ^{2}-3775\alpha +441)}{\left[ {{\begin{array}{l} {822064\alpha ^{10}-6532320\alpha ^{9}+22880880\alpha ^{8}-46477440\alpha ^{7}+60651360\alpha ^{6}} \\ {-\,53234496\alpha ^{5}+31943520\alpha ^{4}-13000320\alpha ^{3}+3447360\alpha ^{2}-538200\alpha +37593} \\ \end{array} }} \right] },\nonumber \\&\qquad \hbox { for }2/3\le \alpha \le 3/4\nonumber \\&\quad = \frac{7673\alpha ^{5}+9385\alpha ^{4}-17970\alpha ^{3}+12310\alpha ^{2}-3775\alpha +441}{6(1573\alpha ^{5}-1385\alpha ^{4}+2770\alpha ^{3}-2450\alpha ^{2}+985\alpha -149)},\nonumber \\&\qquad \hbox { for }3/4\le \alpha \le 1.\nonumber \end{aligned}$$

(23)

The limiting Condorcet Efficiency representation $CE_\infty ^{ EPR} \left( {{ EIAC}\left( \alpha \right) } \right)$ of EPR obtained as:

$$\begin{aligned}&CE_\infty ^{EPR} \left( {EIAC\left( \alpha \right) } \right) \nonumber \\&\quad = \frac{2(201092\alpha ^{5}-1098775\alpha ^{4}+2319030\alpha ^{3}-2378880\alpha ^{2}+1199520\alpha -239904)}{15(33073\alpha ^{5}-176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+181440\alpha -36288)},\nonumber \\&\qquad \hbox { for }0 \le \alpha \le 1/3\\&\quad = \frac{2\left[ {{\begin{array}{l} {500181480\alpha ^{10}-2445324795\alpha ^{9}+4857370740\alpha ^{8}-5148023040\alpha ^{7}+3186721440\alpha ^{6}} \\ {-1210880664\alpha ^{5}+312201540\alpha ^{4}-62583840\alpha ^{3}+7981740\alpha ^{2}-583020\alpha +18398} \\ \end{array} }} \right] }{10935\alpha ^{5}(33073\alpha ^{5}-176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+181440\alpha -36288)},\nonumber \\&\qquad \hbox { for }1/3\le \alpha \le 1/2\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {7765168032\alpha ^{10}-49109507820\alpha ^{9}+137867605200\alpha ^{8}-226613790720\alpha ^{7}+242043863040\alpha ^{6}} \\ {-175872731328\alpha ^{5}+88076555280\alpha ^{4}-29955394080\alpha ^{3}+6601325040\alpha ^{2}-852079995\alpha } \\ +48972725 \\ \end{array} }} \right] }{4374\left[ {{\begin{array}{l} {890357\alpha ^{10}-5277480\alpha ^{9}+13729500\alpha ^{8}-20707200\alpha ^{7}+20180160\alpha ^{6}} \\ {-13390272\alpha ^{5}+6158880\alpha ^{4}-1929600\alpha ^{3}+388800\alpha ^{2}-45480\alpha +2343} \\ \end{array} }} \right] },\nonumber \\&\qquad \hbox { for }1/2\le \alpha \le 2/3\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {-466599960864\alpha ^{10}+3157812682560\alpha ^{9}-9625336570080\alpha ^{8}+17522753483520\alpha ^{7}}\\ {-21233597696640\alpha ^{6} +17959095185472\alpha ^{5}-10728499980240\alpha ^{4}+4451292105120\alpha ^{3}}\\ {-1222672261680\alpha ^{2}+200674955535\alpha -14922088289} \\ \end{array} }} \right] }{546750\left[ {{\begin{array}{l} {822064\alpha ^{10}-6532320\alpha ^{9}+22880880\alpha ^{8}-46477440\alpha ^{7}+60651360\alpha ^{6}} \\ {-53234496\alpha ^{5}+31943520\alpha ^{4}-13000320\alpha ^{3}+3447360\alpha ^{2}-53820\alpha +37593} \\ \end{array} }} \right] },\nonumber \\&\qquad \hbox { for }2/3\le \alpha \le 3/4\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {770703558912\alpha ^{10}-2569023060480\alpha ^{9}-1200228399360\alpha ^{8}+19448676771840\alpha ^{7}}\\ {-43879150586880\alpha ^{6}+52509746548224\alpha ^{5}-39166923358080\alpha ^{4}+18979282679040\alpha ^{3}}\\ {-5858930536560\alpha ^{2}+1049148150720\alpha -83301605063} \\ \end{array} }} \right] }{629856000\left( {\alpha -1} \right) ^{5}(1573\alpha ^{5}-1385\alpha ^{4}+2770\alpha ^{3}-2450\alpha ^{2}+985\alpha -149)},\nonumber \\&\qquad \hbox { for }3/4\le \alpha \le 5/6\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {1707373824\alpha ^{10}-15575400960\alpha ^{9}+61806401280\alpha ^{8}-141564856320\alpha ^{7}+208503626240\alpha ^{6}} \\ {-207409943552\alpha ^{5}+141770083840\alpha ^{4}-65993041920\alpha ^{3}+20069026880\alpha ^{2}-3603648560\alpha }\\ { +290379249} \\ \end{array} }} \right] }{288000\left( {1-\alpha } \right) ^{5}(1573\alpha ^{5}-1385\alpha ^{4}+2770\alpha ^{3}-2450\alpha ^{2}+985\alpha -149)},\nonumber \\&\qquad \hbox { for }5/6\le \alpha \le 7/8\nonumber \\&\quad = -\frac{19801\alpha ^{5}-94125\alpha ^{4}+106760\alpha ^{3}-53380\alpha ^{2}+10495\alpha -247}{9(1573\alpha ^{5}-1385\alpha ^{4}+2770\alpha ^{3}-2450\alpha ^{2}+985\alpha -149)},\nonumber \\&\quad \quad \hbox { for }7/8\le \alpha \le 1.\nonumber \end{aligned}$$

(24)

The limiting Condorcet Efficiency representation $CE_\infty ^{ENPR} \left( {EIAC\left( \alpha \right) } \right)$ of ENPR obtained as:

$$\begin{aligned}&CE_\infty ^{ENPR} \left( {EIAC\left( \alpha \right) } \right) \nonumber \\&\quad = \frac{6(21003\alpha ^{5}-107760\alpha ^{4}+205020\alpha ^{3}-195200\alpha ^{2}+95200\alpha -19040)}{5(33073\alpha ^{5}-\,176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+\,181440\alpha -36288)},\nonumber \\&\quad \quad \hbox { for }0 \le \alpha \le 1/4\\&\quad \!=\! \frac{3\left[ {{\begin{array}{l} {238152672\alpha ^{10}\!-\!895034880\alpha ^{9}\!+\!1430547840\alpha ^{8}\!-\!1246760960\alpha ^{7}}\\ {\!+\!610462720\alpha ^{6}\!-\!152800256\alpha ^{5}\!+\!17579520\alpha ^{4}\!-\!2741760\alpha ^{3}}\\ {\!+\!278640\alpha ^{2}\!-\!16680\alpha \!+\!447} \\ \end{array} }} \right] }{10000\alpha ^{5}(33073\alpha ^{5}\!-\!\,176904\alpha ^{4}\!+\!361260\alpha ^{3}\!-\!362880\alpha ^{2}\!+\!\,181440\alpha -36288)},\!\!\hbox { for }1/4\le \alpha \le 1/3\nonumber \\&\quad =-\frac{\left[ {{\begin{array}{l} {183441151008 \alpha ^{10}-517565272320 \alpha ^{9}+472996661760 \alpha ^{8}-184489021440 \alpha ^{7}} \\ {+193094254080 \alpha ^{6}-195743568384 \alpha ^{5}+17747009280 \alpha ^{4}+44841807360 \alpha ^{3}}\\ {-13673597040 \alpha ^{2}+1775517480 \alpha -90564767} \\ \end{array} }} \right] }{21870000\alpha ^{5}(33073\alpha ^{5}-176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+181440\alpha -36288)},\nonumber \\&\qquad \hbox { for }1/3\le \alpha \le 1/2\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {1893621760992 \alpha ^{10}-9798698407680 \alpha ^{9}+20744052618240 \alpha ^{8}-22019101378560 \alpha ^{7}}\\ {+10059445105920 \alpha ^{6}+2371336176384 \alpha ^{5}-5782708169280\alpha ^{4}+3448117952640 \alpha ^{3}}\\ {-\,1084583127960 \alpha ^{2}+181583777520 \alpha -\,12810973483} \\ \end{array} }} \right] }{4374000\left[ {{\begin{array}{l} {890357\alpha ^{10}-5277480\alpha ^{9}+13729500\alpha ^{8}-20707200\alpha ^{7}+20180160\alpha ^{6}} \\ {-13390272\alpha ^{5}+6158880\alpha ^{4}-1929600\alpha ^{3}+388800\alpha ^{2}-45480\alpha +2343} \\ \end{array} }} \right] },\nonumber \\&\qquad \hbox { for }1/2\le \alpha \le 2/3\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {27804878424 \alpha ^{10}-245404416960 \alpha ^{9}+937777201920 \alpha ^{8}-2056630072320 \alpha ^{7}} \\ {+2880959477760 \alpha ^{6}-2705698453248 \alpha ^{5}+1733135019840 \alpha ^{4}-750925261440 \alpha ^{3}}\\ {+211357236600 \alpha ^{2}-34960125360 \alpha +2584498375}\\ \end{array} }} \right] }{34992\left[ {{\begin{array}{l} {822064\alpha ^{10}-6532320\alpha ^{9}+22880880\alpha ^{8}-46477440\alpha ^{7}+60651360\alpha ^{6}} \\ {-53234496\alpha ^{5}+31943520\alpha ^{4}-13000320\alpha ^{3}+3447360\alpha ^{2}-53820\alpha +37593} \\ \end{array} }} \right] },\nonumber \\&\qquad \hbox { for }2/3\le \alpha \le 3/4\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {24221999916 \alpha ^{10}-200098913760 \alpha ^{9}+730102481280 \alpha ^{8}-1550742796800 \alpha ^{7}} \\ {+\,2126166174720 \alpha ^{6}-1969967018880 \alpha ^{5}+1252266130080 \alpha ^{4}-540762039360 \alpha ^{3}}\\ {+\,152169076980 \alpha ^{2}-25228472460 \alpha +1873379921}\\ \end{array} }} \right] }{2519424\left( {1-\alpha } \right) ^{5}(1573\alpha ^{5}-1385\alpha ^{4}+2770\alpha ^{3}-2450\alpha ^{2}+985\alpha -149)},\nonumber \\&\qquad \hbox { for }3/4\le \alpha \le 4/5\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {14729812416 \alpha ^{10}-124161413760 \alpha ^{9}+456727481280 \alpha ^{8}-967542796800 \alpha ^{7}} \\ {+\,1309686174720 \alpha ^{6}-1186146218880 \alpha ^{5}+729718930080 \alpha ^{4}-301883319360 \alpha ^{3}}\\ {+\,80505460980 \alpha ^{2}-12488274060 \alpha +854164049}\\ \end{array} }} \right] }{2519424\left( {1-\alpha } \right) ^{5}(1573\alpha ^{5}-1385\alpha ^{4}+2770\alpha ^{3}-2450\alpha ^{2}+985\alpha -149)},\nonumber \\&\qquad \hbox { for }4/5\le \alpha \le 5/6\nonumber \\&\quad = -\frac{25317 \alpha ^{5}-129045 \alpha ^{4}+126390 \alpha ^{3}-51030 \alpha ^{2}+7205 \alpha +107}{18(1573\alpha ^{5}-1385\alpha ^{4}+2770\alpha ^{3}-2450\alpha ^{2}+985\alpha -149)},\hbox { for }5/6\le \alpha \le 1.\nonumber \end{aligned}$$

(25)

The limiting Condorcet efficiency representation $CE_\infty ^{EBR} \left( {EIAC\left( \alpha \right) } \right)$ of EBR obtained as:

$$\begin{aligned}&\!\!\!\!\!CE_\infty ^{EBR} \left( {EIAC\left( \alpha \right) } \right) \nonumber \\&= \frac{\left[ {\begin{array}{l}{3(6178301\alpha ^{5}-30623040\alpha ^{4}+61565280\alpha ^{3}-61716480\alpha ^{2}+30858240\alpha }\\ {-6171648)}\end{array}}\right] }{560(33073\alpha ^{5}-176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+181440\alpha -36288)},\nonumber \\&\quad \hbox {for }0 \le \alpha \le 1/4\\&= \frac{\left[ {{\begin{array}{l} {1149005607\alpha ^{10}-6707395520\alpha ^{9}+14299760160\alpha ^{8}-14666803200\alpha ^{7}} \\ {+\,7402214400\alpha ^{6}-1485259776\alpha ^{5}-430080\alpha ^{3}+80640\alpha ^{2}-6720\alpha +224} \\ \end{array} }} \right] }{45360\alpha ^{5}(33073\alpha ^{5}-176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+181440\alpha -36288)},\nonumber \\&\quad \hbox { for }1/4\le \alpha \le 2/5\nonumber \\&= \frac{\left[ {{\begin{array}{l} {4649005607\alpha ^{10}-19657395520\alpha ^{9}+33829760160\alpha ^{8}-29450803200\alpha ^{7}+12106214400\alpha ^{6}} \\ {-\,356299776\alpha ^{5}-1731072000\alpha ^{4}+756510720\alpha ^{3}-175392000\alpha ^{2}+21784000\alpha -1146656} \\ \end{array} }} \right] }{45360\alpha ^{5}(33073\alpha ^{5}-176904\alpha ^{4}+361260\alpha ^{3}-362880\alpha ^{2}+181440\alpha -36288)},\nonumber \\&\quad \hbox { for }2/5\le \alpha \le 1/2\nonumber \\&=\frac{\left[ {{\begin{array}{l} {28519271107\alpha ^{10}-197466436160\alpha ^{9}+577284291360\alpha ^{8}-955843553280\alpha ^{7}} \\ {+\,1005805893120\alpha ^{6}-709955753472\alpha ^{5}+342199159680\alpha ^{4}-110896961280\alpha ^{3}}\\ {+\,22927922640\alpha ^{2}-2733382960\alpha +142641548} \\ \end{array} }} \right] }{45360\left[ {{\begin{array}{l} {890357\alpha ^{10}-5277480\alpha ^{9}+13729500\alpha ^{8}-20707200\alpha ^{7}+20180160\alpha ^{6}-13390272\alpha ^{5}} \\ {+6158880\alpha ^{4}-1929600\alpha ^{3}+388800\alpha ^{2}-45480\alpha +2343} \\ \end{array} }} \right] },\nonumber \\&\quad \hbox { for }1/2\le \alpha \le 4/7\nonumber \\&= \frac{\left[ {{\begin{array}{l} {389436806993\alpha ^{10}-2245299766640\alpha ^{9}+5652130861440\alpha ^{8}-8159855262720\alpha ^{7}}\\ {+7471050478080\alpha ^{6} -4524686304768\alpha ^{5}+1819993499520\alpha ^{4}-465323953920\alpha ^{3}}\\ {+66179630160\alpha ^{2}-3497854640\alpha -110832148} \\ \end{array} }} \right] }{ 408240\left[ {{\begin{array}{l} {890357\alpha ^{10}-5277480\alpha ^{9}+13729500\alpha ^{8}-20707200\alpha ^{7}+20180160\alpha ^{6}} \\ {-13390272\alpha ^{5}+6158880\alpha ^{4}-1929600\alpha ^{3}+388800\alpha ^{2}-45480\alpha +2343} \\ \end{array} }} \right] },\nonumber \\&\qquad \hbox { for }4/7\le \alpha \le 5/8\nonumber \\&\quad = \frac{\left[ {{\begin{array}{l} {88789096273\alpha ^{10}-366251574640\alpha ^{9}+367307821440\alpha ^{8}+648183137280\alpha ^{7}} \\ {-2162741521920\alpha ^{6}+2700657695232\alpha ^{5}-1943206500480\alpha ^{4}+878676046080\alpha ^{3}}\\ {-248820369840\alpha ^{2}+40252145360\alpha -2845207148} \\ \end{array} }} \right] }{408240\left[ {{\begin{array}{l} {890357\alpha ^{10}-5277480\alpha ^{9}+13729500\alpha ^{8}-20707200\alpha ^{7}+20180160\alpha ^{6}} \\ {-13390272\alpha ^{5}+6158880\alpha ^{4}-1929600\alpha ^{3}+388800\alpha ^{2}-45480\alpha +2343} \\ \end{array} }} \right] },\nonumber \\&\qquad \hbox { for }5/8\le \alpha \le 2/3\nonumber \end{aligned}$$

(26)

$$\begin{aligned}&\quad = -\frac{\left[ {{\begin{array}{l} {88789096273\alpha ^{10}-366251574640\alpha ^{9}+367307821440\alpha ^{8}+648183137280\alpha ^{7}} \\ {-2162741521920\alpha ^{6}+2700657695232\alpha ^{5}-1943206500480\alpha ^{4}+878676046080\alpha ^{3}}\\ {-248820369840\alpha ^{2}+40252145360\alpha -2845207148} \\ \end{array} }} \right] }{408240\left[ {{\begin{array}{l} {822064\alpha ^{10}-6532320\alpha ^{9}+22880880\alpha ^{8}-46477440\alpha ^{7}+60651360\alpha ^{6}} \\ {-53234496\alpha ^{5}+31943520\alpha ^{4}-13000320\alpha ^{3}+3447360\alpha ^{2}-53820\alpha +37593} \\ \end{array} }} \right] },\\&\qquad \hbox { for }2/3\le \alpha \le 7/10\\&\quad = \frac{\left[ {{\begin{array}{l} {15887271961\alpha ^{10}-147678346480\alpha ^{9}+577527454080\alpha ^{8}-1268597591040\alpha ^{7}} \\ {+1749563074560\alpha ^{6}-1595912242176\alpha ^{5}+983494928640\alpha ^{4}-407882749440\alpha ^{3}}\\ {+109664637120\alpha ^{2}-17279908480\alpha +1213530304} \\ \end{array} }} \right] }{58320\left[ {{\begin{array}{l} {822064\alpha ^{10}-6532320\alpha ^{9}+22880880\alpha ^{8}-46477440\alpha ^{7}+60651360\alpha ^{6}} \\ {-53234496\alpha ^{5}+31943520\alpha ^{4}-13000320\alpha ^{3}+3447360\alpha ^{2}-53820\alpha +37593} \\ \end{array} }} \right] },\\&\qquad \hbox { for }7/10\le \alpha \le 8/11\\&\quad = \frac{4\left( {1-\alpha } \right) ^{5}(10468909\alpha ^{5}+9680515\alpha ^{4}-14800970\alpha ^{3}+8155970\alpha ^{2}-1892725\alpha +145613)}{243\left[ {{\begin{array}{l} {822064\alpha ^{10}-6532320\alpha ^{9}+22880880\alpha ^{8}-46477440\alpha ^{7}+60651360\alpha ^{6}} \\ {-53234496\alpha ^{5}+31943520\alpha ^{4}-13000320\alpha ^{3}+3447360\alpha ^{2}-53820\alpha +37593} \\ \end{array} }} \right] }, \\&\qquad \hbox { for }8/11\le \alpha \le 3/4\\&\quad = \frac{10468909\alpha ^{5}+9680515\alpha ^{4}-14800970\alpha ^{3}+8155970\alpha ^{2}-1892725\alpha +145613}{8748(1573\alpha ^{5}-1385\alpha ^{4}+2770\alpha ^{3}-2450\alpha ^{2}+985\alpha -149)},\\&\qquad \hbox { for }3/4\le \alpha \le 1. \end{aligned}$$

Computed values of $CE_\infty ^{AV} \left( {{ EIAC}\left( \alpha \right) } \right)$, $CE_\infty ^{{ EPR}} \left( {{ EIAC}\left( \alpha \right) } \right)$, $CE_\infty ^{{ ENPR}} ({ EIAC} ( \alpha ))$ and $CE_\infty ^{{ EBR}}\left( {{ EIAC}\left( \alpha \right) } \right)$ from (23), (24), (25) and (26) are given in Table 4 for each $\alpha =0\left( {.1} \right) 1$.

Table 4 Computed values of $\textit{CE}_\infty ^{\textit{AV}} \left( { {EIAC}\left( \alpha \right) } \right)$, $\textit{CE}_\infty ^{\textit{EPR}} \left( { {EIAC}\left( \alpha \right) } \right) , \quad \textit{CE}_\infty ^{\textit{ENPR}} \left( {EIAC\left( \alpha \right) } \right)$, and $\textit{CE}_\infty ^{\textit{EBR}} \left( {EIAC\left( \alpha \right) } \right)$

As expected, we obtain the result that $CE_\infty ^{AV} \left( {{ EIAC}\left( 0 \right) } \right) \!=\!CE_\infty ^{{ EPR}} \left( {{ EIAC}\left( 0 \right) } \right) \!=\!CE_\infty ^{PR} \left( {{ IAC}} \right) \!=\!\frac{119}{135}$ when no indifference is allowed. In addition, we observe that $CE_\infty ^{AV} \left( {{ EIAC}\left( 1 \right) } \right) =CE_\infty ^{{ EBR}} \left( {{ EIAC}\left( 1 \right) } \right) =1$, so that AV and EBR always elect the CW when preferences are dichotomous. For AV, EPR and EBR, the Condorcet Efficiency first decreases very slightly as $\alpha$ increases, and it then consistently increases as $\alpha$ increases. By contrast, the Condorcet efficiency of ENPR monotonically increases when $\alpha$ increases but always remains lower than the Condorcet Efficiency of the three other rules.

These EIAC results are completely consistent with our earlier observations regarding Condorcet Efficiency with EIC. In particular, the introduction of any degree of indifference into voters’ preferences leads to a domination of AV over EPR and ENPR on the basis of Condorcet Efficiency. However, while AV and EBR both elect the CW with certainty in the case of completely dichotomous preferences, scenarios with less than completely dichotomous preferences leads to a domination of EBR over AV on the basis of Condorcet Efficiency.

8 Conclusion

Results of the study strongly reinforce the conclusion of Diss et al. (2010) that the introduction of any degree of indifference into voters’ preferences gives a definite advantage to AV over both EPR and ENPR on the basis of Condorcet Efficiency with the EIC model. The same result is now found to be valid when some degree of dependence is inserted into voters’ preferences with the EIAC model. However, EBR is found to dominate AV in all cases of EIC and EIAC, except for the scenario in which all voters have dichotomous preferences, where AV and EBR both elect the CW with certainty.