Gravitational collapse of charged scalar fields

Abstract

In order to study the gravitational collapse of charged matter we analyze the simple model of an self-gravitating massless scalar field coupled to the electromagnetic field in spherical symmetry. The evolution equations for the Maxwell–Klein–Gordon sector are derived in the $3+1$ formalism, and coupled to gravity by means of the stress–energy tensor of these fields. To solve consistently the full system we employ a generalized Baumgarte–Shapiro–Shibata–Nakamura formulation of General Relativity that is adapted to spherical symmetry. We consider two sets of initial data that represent a time symmetric spherical thick shell of charged scalar field, and differ by the fact that one set has zero global electrical charge while the other has non-zero global charge. For compact enough initial shells we find that the configuration doesn’t disperse and approaches a final state corresponding to a sub-extremal Reissner–Nördstrom black hole with $|Q|<M$. By increasing the fundamental charge of the scalar field $q$ we find that the final black hole tends to become more and more neutral. Our results support the cosmic censorship conjecture for the case of charged matter.

1 Introduction

Gravitational collapse is a generic feature of nature and occurs whenever gravitation dominates over the repulsive interactions that take place inside matter. In the context of General Relativity this phenomena is very important since it is the mechanism that drives the formation of singularities in the spacetime itself, and understanding the causal structure of such singularities is of prime importance to ensure the predictability of the theory. It is widely believed that the final fate of gravitational collapse is the formation of a black hole in which the singularities are casually disconnected from distant observers. The fact that no spacetime singularities have been identified has led to establish the cosmic censorship conjecture [1], which states that no naked singularities can develop from generic initial data where the spacetime is regular and the matter satisfies the dominant energy condition. Beyond General Relativity, it is generally expected that a description that accounts for the quantum nature of gravity and/or spacetime should avoid the formation of singularities. Even in that case it is important to understand the dynamics of gravitational collapse since quantum effects should only play a role in those regions where a singularity is expected to form classically, so that for macroscopic black holes the effective dynamics near the horizon should not depart significantly from those predicted by the classical theory.

It is known that the only stationary, asymptotically flat solutions of the Einstein equations that represent a black hole correspond to the Kerr–Newman family which is characterized by the mass, electrical charge and angular momentum. These solutions only represent black holes when the parameters satisfy the relation $M^2>Q^2+a^2$ (with $M$ the mass, $Q$ the total electric charge and $a$ the angular momentum per unit mass), otherwise there is no event horizon present in the spacetime and the singularity is naked. In a realistic scenario of gravitational collapse it is expected that the outer region of the spacetime will correspond asymptotically to this solution, but in principle there is no restriction that ensures the above relation would hold. There have been numerical and analytical studies of collapsing scenarios that lead to naked singularities [2–4], but it has not been asserted that these examples pose a real threat to the cosmic censorship conjecture since these results may come from the symmetries imposed and even from the gauge conditions. It seems that, at least for the uncharged case $q=0$, the generic outcome of gravitational collapse is a black hole and the exceeding angular momentum contained in the initial data is lost due to gravitational radiation.

It is also interesting to consider the collapse of charged matter which could lead to the formation of charged black holes or even naked singularities. It is expected that the collapse of charged matter would not lead to a super-extremal solution ($Q \ge M$) since in this case the electric repulsion is comparable to the gravitational attraction. A simple model for charged matter is that of a complex scalar field coupled to the electromagnetic field, this configuration represents matter made of charged bosonic particles and its antiparticles which have opposite charge. Scalar field matter has been widely used in General Relativity because its evolution is governed by a simple wave equation and does not develop discontinuities as it happens with fluids. Self-Gravitating complex scalar fields may form boson stars, which are regular self-gravitating configurations of scalar field that do not disperse and have properties that resemble those of neutron stars (a recent review can be found in [5]). Boson stars can be made also out of charged scalar field [6], providing an example of an astrophysical system that posses net charge and is susceptible to collapse. The numerical simulation of the collapse of charged scalar fields with spherical symmetry has been previously studied with many different goals: For example, in [7] a standard $3+1$ decomposition is used with polar slicing to analyze critical phenomena, critical behavior similar to the one occurring in the non-charged case [3] is found and the authors show that the charge approaches zero faster than the mass as one approaches the critical solution, resulting in a critical solution that has no charge; in [8] a null formalism is introduced to probe the internal structure of the resulting black hole. In this paper we are interested on the resulting configuration as viewed by outside observers, in particular we want to determine if the outcome of this process can be a naked singularity.

This paper is organized as follows: in Sect. 2 we recast the evolution equations of the matter in spherical symmetry and show the terms of the stress–energy tensor that couple to the evolution equations for the geometric variables. In Sect. 3 we construct initial data that represents collapsing charged matter. Then, in Sect. 4 we discuss some analysis tools and some features of the numerical implementation. In Sect. 5 we present the results of our simulations. We conclude in Sect. 6.

2 Field equations

2.1 Einstein–Maxwell–Klein–Gordon system in spherical symmetry

The study of the collapse of a charged scalar field is addressed by integrating the full Einstein–Maxwell–Klein–Gordon system of evolution equations. We will use the $3+1$ formalism [9–11], and in particular adopt the generalized Baumgarte–Shapiro–Shibata–Nakamura [12, 13] (BSSN) formulation in curvilinear coordinates [14, 15] to recast the Einstein equations as an initial value problem in spherical symmetry. The spacetime metric is then written as

$$\begin{aligned} ds^2 = \left( - \alpha ^2 + \beta _i \beta ^i \right) dt^2 + 2 \beta _i \, dt dx^i + \gamma _{ij} \, dx^i dx^j \, , \end{aligned}$$

(1)

with $\alpha$ the lapse function, $\beta ^i$ the shift vector, and $\gamma _{ij}$ the spatial metric (notice that indexes of spatial quantities are lowered and raised with the spatial metric $\gamma _{ij}$).

The matter, including both the electromagnetic and scalar fields, couples to this system only through contributions from the stress–energy tensor. We require only to analyze the evolution equations of the matter fields in the curved spacetime characterized by the spatial metric $\gamma _{ij}$ and extrinsic curvature $K_{ij}$.

In spherical symmetry the spatial line element can be written without loss of generality as

$$\begin{aligned} dl^2 = \psi (r,t)^4 \left( A(r,t) dr^2 + r^2 B(r,t) d\varOmega ^2 \right) . \end{aligned}$$

(2)

with $\psi$ a conformal factor and $d\varOmega ^2$ the standard solid angle element.

2.2 Electromagnetic field

The evolution equations for the electromagnetic field are naturally formulated in terms of the electric and magnetic fields measured by the Eulerian observers [16]

$$\begin{aligned} E^\mu&:= -n_\nu F^{\nu \mu },\end{aligned}$$

(3)

$$\begin{aligned} B^\mu&:= -n_\nu F^{*\nu \mu }, \end{aligned}$$

(4)

with $n^\mu$ the unit normal future-pointing vector to the spatial hypersurfaces.

When projecting the covariant Maxwell equations onto the normal vector to the spatial hypersurfaces one finds two constraint equations

$$\begin{aligned} D_i E^i&= 4\pi \rho _e, \end{aligned}$$

(5)

$$\begin{aligned} D_i B^i&= 0, \end{aligned}$$

(6)

with $D_i$ the covariant derivative compatible with the spatial metric $\gamma _{ij}$, and where $\rho _e=-n_\mu j^\mu$ is the charge density measured by the Eulerian observers.

On the other hand, when projecting onto the hypersurfaces we obtain the evolution equations for the electric and magnetic fields

$$\begin{aligned} \frac{d}{dt} \, E^i&= (D \times \alpha B)^i - \alpha K E^i - 4 \pi \alpha \, {}^{(3)}\!j_\mathrm{e}^i, \end{aligned}$$

(7)

$$\begin{aligned} \frac{d}{dt} \, B^i&= - (D \times \alpha E)^i + \alpha K B^i, \end{aligned}$$

(8)

where ${}^{(3)}\!j_\mathrm{e}^i := \gamma _{\,\,\,\mu }^{i} j^\mu$ is the current density measured by the Eulerian observers, $d/dt=\partial _t - \pounds _{\varvec{\beta }}{}$ is the derivative in the normal direction to the spatial hypersurfaces, and where the rotational operator acting on a vector $v^i$ is defined as $\left( D \times \, v \right) ^i := \epsilon ^{imn} D_m \,v_n$, with $\epsilon ^{imn}:=n_\mu \epsilon ^{\mu imn}$ the Levi-Civita tensor on the spatial hypersurfaces.

Since the charged scalar field couples directly to the electromagnetic potential $A^\mu$, we also need to specify the evolution equation for the potential. To do this we use the following $3+1$ decomposition of this vector field

$$\begin{aligned} \varPhi&:= -n_\mu A^\mu , \end{aligned}$$

(9)

$$\begin{aligned} a^i&:= {}^{(3)}\!A^i = \gamma ^{i}_\mu A^\mu , \end{aligned}$$

(10)

which defines the scalar and vector electromagnetic potentials respectively as measured by Eulerian observers. Writing the Faraday tensor in terms of the electromagnetic potentials as

$$\begin{aligned} F_{\mu \nu }:=\partial _\mu A_\nu - \partial _\nu A_\mu , \end{aligned}$$

(11)

the definition of the electric field (3) becomes an evolution equation for the vector potential

$$\begin{aligned} \frac{d}{dt} \, a_i = - \alpha E_i - D_i (\alpha \varPhi ), \end{aligned}$$

(12)

while the definition of the magnetic field (4) becomes

$$\begin{aligned} B^i&= \frac{1}{2} \, \epsilon ^{imn} \left( \partial _m a_n - \partial _n a_m \right) \nonumber \\&= \epsilon ^{imn} \partial _m a_n = \left( D \times a \right) ^i. \end{aligned}$$

(13)

In order to find the scalar potential at all times it is now necessary to fix the gauge freedom of the theory. Here and in what follows we choose the Lorentz gauge $\nabla _\mu A^\mu = 0$, which when written in $3+1$ language becomes an evolution equation for the scalar potential

$$\begin{aligned} \frac{d}{dt} \, \varPhi = \alpha K \varPhi - D_i \left( \alpha \, a^{i} \right) . \end{aligned}$$

(14)

When one considers the case of spherical symmetry the above equations simplify considerably since all vector fields can have only a radial component. This then implies, along with Eq. (13), that the magnetic field vanishes, so in practice we only have to consider the equations for the scalar potential and the radial component of both the vector potential and the electric field, which take the form

$$\begin{aligned} \partial _t \varPhi&= \beta ^r \partial _r \varPhi + \alpha K \varPhi \nonumber \\&\quad - \frac{1}{r^2 \psi ^6 \sqrt{A}B} \; \partial _r \left( \frac{ \alpha B r^2 \psi ^2}{\sqrt{A}} \, a_r \right) , \end{aligned}$$

(15)

$$\begin{aligned} \partial _t a_r&= \beta ^r \partial _r a_{r} + a_r \partial _r \beta ^r - \alpha A \psi ^4 E^r - \partial _r \left( \alpha \varPhi \right) , \end{aligned}$$

(16)

$$\begin{aligned} \partial _t E^r&= \beta ^r \partial _r E^r - E^r \partial _r \beta ^r + \alpha K E^r - 4 \pi j_{\,em}^r, \end{aligned}$$

(17)

with $\beta ^r$ the radial component of the shift vector.

2.3 Charged scalar field

For the charged scalar field we can do a similar $3+1$ decomposition. We start from the Lagrangian

$$\begin{aligned} L = -\frac{1}{2}\left[ (\mathcal {D}_\mu \varphi )^*\mathcal {D}^\mu \varphi + 2 V(|\varphi |^2) \right] , \end{aligned}$$

(18)

where $\mathcal {D}_\mu = \nabla _\mu + iq A_\mu$ is the gauge invariant derivative, with $\nabla _\mu$ is the covariant derivative adapted to the spacetime metric, and where $V(|\varphi |^2)$ is a self-interaction potential for the scalar field (in all our numerical simulations below we always take $V=0$, but we consider it here for generality). We say that $\mathcal {D}_\mu$ is gauge invariant in the sense that its application on the scalar field is not altered under a transformation of the form

$$\begin{aligned} \varphi&\rightarrow e^{-iq\vartheta (x^\alpha )} \varphi , \end{aligned}$$

(19)

$$\begin{aligned} A_\mu&\rightarrow A_\mu + \partial _\mu \vartheta (x^\alpha ), \end{aligned}$$

(20)

with $\vartheta (x^\alpha )$ an arbitrary scalar function of spacetime.

The complex scalar field has two degrees of freedom, so we can treat it equivalently as two independent variables corresponding to the real and imaginary parts, or as a complex variable and its complex conjugate. Variation of the action while fixing $\varphi$ gives the following evolution equation

$$\begin{aligned} \left( \mathcal {D}^\mu \mathcal {D}_\mu - 2 V^\prime \right) \varphi = 0, \quad V^\prime := \frac{d}{d(|\varphi |^2)} \, V(|\varphi |^2). \end{aligned}$$

(21)

From the gauge invariance of the scalar field it follows that there is a conserved current which acts as the source of the electromagnetic field

$$\begin{aligned} (j_{\varphi })^\mu = \frac{i}{2} \left( \varphi ^*\mathcal {D}^\mu \varphi - (\mathcal {D}^\mu \varphi )^*\varphi \right) . \end{aligned}$$

(22)

This implies that one has a conserved quantity when integrating the projected component over a spacelike hypersurface. This conserved quantity is the total “boson number” $N$ and is proportional to the total electric charge $Q$ as $Q=qN$, with $q$ the electric charge of the fundamental particles. Thus, for consistency, the electromagnetic current has the form

$$\begin{aligned} (j_{\mathrm{e}})^\mu = \frac{iq}{2} \left( \varphi ^*\mathcal {D}^\mu \varphi - (\mathcal {D}^\mu \varphi )^*\varphi \right) , \end{aligned}$$

(23)

The evolution equation (21) is in fact a wave equation with nonlinear sources on the electromagnetic potentials. Expanding the gauge invariant derivatives we obtain

$$\begin{aligned} \Box \varphi&= 2 V^\prime \varphi - q \left( 2 i A^\mu \nabla _\mu \varphi + i \varphi \nabla ^{\mu } A_\mu - q A_\mu A^\mu \varphi \right) . \end{aligned}$$

(24)

Although in the Lorentz gauge one of the source terms above vanishes, one can see that the two degrees of freedom are coupled by the interaction term $2 iq A^\mu \nabla _\mu \varphi$, while the quadratic term on the electromagnetic potential gives rise to an effective mass for the scalar field. The equation above can be reduced to a first order system by defining the variables

$$\begin{aligned} \varPi&:= n^\mu \nabla _\mu \varphi = \frac{1}{\alpha } \left( \partial _t \varphi - \beta ^i \partial _i \varphi \right) , \end{aligned}$$

(25)

$$\begin{aligned} \chi _i&:= \nabla _i \varphi = \partial _i \varphi . \end{aligned}$$

(26)

In terms of these variables the evolution equation above turns out to be equivalent to the system

$$\begin{aligned} \frac{d}{dt} \, \varphi&= \alpha \varPi , \end{aligned}$$

(27)

$$\begin{aligned} \frac{d}{dt} \, \chi _i&= D_i(\alpha \varPi ) + \beta ^j\left( D_i \chi _j - D_j \chi _i \right) , \end{aligned}$$

(28)

$$\begin{aligned} \frac{d}{dt} \, \varPi&= D_i (\alpha \chi ^i) + \alpha \varPi K \nonumber \\&\quad -\, \alpha \left[ 2 V^\prime + q^2 \left( a_i a^i - \varPhi ^2 \right) - i q \nabla ^{\mu } A_\mu \right] \varphi \nonumber \\&\quad +\, 2i q \alpha \left( a^i \chi _i + \varPhi \varPi \right) . \end{aligned}$$

(29)

When considering the case of spherical symmetry we are left only with the radial derivative $\chi \equiv \chi _r$, and the above equations reduce to

$$\begin{aligned} \partial _t \varphi&= \alpha \varPi + \beta \chi , \end{aligned}$$

(30)

$$\begin{aligned} \partial _t \chi&= \partial _r \left( \alpha \varPi + \beta \chi \right) , \end{aligned}$$

(31)

$$\begin{aligned} \partial _t \varPi&= \beta \partial _r \varPi + \frac{1}{r^2 \psi ^6 \sqrt{A} B }\partial _r \left( \alpha \frac{B r^2 \psi ^2}{\sqrt{A}} \chi \right) \nonumber \\&\quad +\, \alpha \varPi K - \alpha \left[ 2 V^\prime + q^2 \left( \frac{a_{r}^2}{A \psi ^4 } - \varPhi ^2 \right) \right] \varphi \nonumber \\&\quad +\, 2i q \alpha \left[ \frac{a_r \chi }{A \psi ^4} + \varPhi \varPi \right] . \end{aligned}$$

(32)

It turns out that it is also useful to define the gauge invariant versions of the variables $\varPi$ and $\chi _i$ since the source terms appearing in the equations for the gravitational and electromagnetic fields take simpler forms in terms of them:

$$\begin{aligned} \tilde{\varPi }&:= n^\mu \mathcal {D}_\mu \varphi ^*= \varPi -iq\varPhi \varphi , \end{aligned}$$

(33)

$$\begin{aligned} \tilde{\chi }_i&:= \gamma ^\mu _i \mathcal {D}_\mu \varphi = \chi _i + i q a_i \varphi . \end{aligned}$$

(34)

In terms of these variables we can now define the $3+1$ components of the electric current density four-vector (23). The normal projection gives us the charge density measured by Eulerian observers

$$\begin{aligned} \rho _{\mathrm{e}} = - n_\mu j_{\mathrm{e}}^\mu = \frac{iq}{2} \left( \tilde{\varPi }^*\varphi - \varphi ^*\tilde{\varPi }\right) , \end{aligned}$$

(35)

while the spatial projection is the electric current density measured by Eulerian observers

$$\begin{aligned} (j_\mathrm{e})^{i} = \gamma ^{i}_\mu j_{\mathrm{e}}^\mu = \frac{iq}{2} \left( \varphi ^*\tilde{\chi }^i - \tilde{\chi }^{*i}\varphi \right) . \end{aligned}$$

(36)

It is also useful to express these quantities just in terms of the scalar field quantities and the electromagnetic potentials:

$$\begin{aligned} \rho _{\mathrm{e}}&= - q \, \mathbf {Im}(\varPi ^*\varphi ) - q^2 \varPhi \varphi ^*\varphi , \end{aligned}$$

(37)

$$\begin{aligned} (j_{\mathrm{e}})_i&= + q \, \mathbf {Im}(\chi _i^*\varphi ) - q^2 a_i \varphi ^*\varphi . \end{aligned}$$

(38)

2.4 Stress–energy tensor

The sources of the gravitational field are encoded in the stress–energy tensor which is built from the contributions of the electromagnetic and scalar fields

$$\begin{aligned} T^{\mu \nu } = {T_\mathrm{e}}^{\mu \nu } + {T_{\varphi }}^{\mu \nu }. \end{aligned}$$

(39)

This tensor appears in the evolution and constraint equations through the $3+1$ projections which correspond to the energy density $E$, momentum density $J^i$, and stress tensor $S_{ij}$ measured by Eulerian observers:

$$\begin{aligned} {\mathcal E}&= n^\mu n^\nu T_{\mu \nu }, \end{aligned}$$

(40)

$$\begin{aligned} J^i&= -\gamma ^{i \mu } n^\nu T_{\mu \nu }, \end{aligned}$$

(41)

$$\begin{aligned} S_{ij}&= \gamma ^\mu _i \gamma ^\nu _j T_{\mu \nu }. \end{aligned}$$

(42)

The contributions from the electromagnetic field can be written explicitly as [16]

$$\begin{aligned} \mathcal{E}_\mathrm{e}&:= \frac{1}{8\pi } \left( E^2 + B^2 \right) , \end{aligned}$$

(43)

$$\begin{aligned} (J_\mathrm{e})^i&:= \frac{1}{4\pi } \, {\epsilon ^i}_{jk} E^j B^k, \end{aligned}$$

(44)

$$\begin{aligned} (S_\mathrm{e})_{ij}&:= \frac{1}{8\pi } \left[ \gamma _{ij} \left( E^2 + B^2 \right) \right. \nonumber \\&\quad - \left. 2 \left( E_i E_j + B_i B_j \right) \right] . \end{aligned}$$

(45)

In these expressions $E^2=\gamma _{ij}E^i E^j$ and $B^2=\gamma _{ij}B^i B^j$. In spherical symmetry, since there is no magnetic field, the momentum density vanishes and we are left with the simple expressions

$$\begin{aligned} {\mathcal E}_\mathrm{e}&:= \frac{1}{8\pi } \, \psi ^4 A \left( E^r \right) ^2, \end{aligned}$$

(46)

$$\begin{aligned} (S_\mathrm{e})^r_r&:= -\frac{1}{8\pi } \, \psi ^4 A \left( E^r \right) ^2, \end{aligned}$$

(47)

$$\begin{aligned} (S_\mathrm{e})^\theta _\theta&:= \frac{1}{8\pi } \, \psi ^4 A \left( E^r \right) ^2. \end{aligned}$$

(48)

For the scalar field, we start by writing the Lagrangian in terms of the auxiliary variables $\tilde{\varPi }$ and $\tilde{\chi }$ as

$$\begin{aligned} L = - \frac{1}{2} \left( \tilde{\chi }^*_i \tilde{\chi }^i -\tilde{\varPi }^*\tilde{\varPi }+ 2 V(|\varphi |^2) \right) . \end{aligned}$$

(49)

From this we can now calculate the stress–energy tensor and the corresponding $3+1$ projections:

$$\begin{aligned} {\mathcal E}_\varphi&= \frac{1}{2}\left( \tilde{\varPi }^*\tilde{\varPi }+ \tilde{\chi }_{i}^*\chi ^i \right) + V, \end{aligned}$$

(50)

$$\begin{aligned} (J_\varphi )^i&= - \frac{1}{2} \left( \tilde{\varPi }^*\tilde{\chi }^i + {\tilde{\chi }^{*i}} \tilde{\varPi }\right) , \end{aligned}$$

(51)

$$\begin{aligned} (S_\varphi )_{ij}&= \frac{1}{2}\left( \tilde{\chi }^{*}_i \tilde{\chi }_j + \tilde{\chi }^{*}_j \tilde{\chi }_i \right) + \gamma _{ij} L, \end{aligned}$$

(52)

which in spherical symmetry reduces to

$$\begin{aligned} {\mathcal E}_\varphi&= \frac{1}{2} \left( |\tilde{\varPi }|^2 + \frac{|\tilde{\chi }|^2}{A\psi ^4} \right) + V, \end{aligned}$$

(53)

$$\begin{aligned} (J_\varphi )_r&= - \frac{1}{2} \left( \tilde{\varPi }^*\tilde{\chi }+ \tilde{\chi }^*\tilde{\varPi }\right) , \end{aligned}$$

(54)

$$\begin{aligned} (S_\varphi )_r^r&= \frac{1}{2}\left( |\tilde{\varPi }|^2 + \frac{|\tilde{\chi }|^2}{A\psi ^4} \right) - V, \end{aligned}$$

(55)

$$\begin{aligned} (S_\varphi )_\theta ^\theta&= \frac{1}{2}\left( |\tilde{\varPi }|^2 - \frac{|\tilde{\chi }|^2}{A\psi ^4} \right) - V. \end{aligned}$$

(56)

3 Initial data

When looking for suitable initial data that represents a collapsing charged scalar field it is not possible to assign freely all the quantities since the Hamiltonian and momentum constraints

$$\begin{aligned}&{}^{(3)}R - K_{i j}K^{ij} + K^{2} = 16\pi {\mathcal E}, \end{aligned}$$

(57)

$$\begin{aligned}&D_{m} K^{ m }_i - D_i K = 8 \pi J_i, \end{aligned}$$

(58)

along with the electromagnetic constraints (5)–(6) have to be satisfied. Notice that in spherical symmetry the momentum constraint has only one non-trivial component, and the magnetic constraint becomes trivial.

The first strong assumption we will make (apart from the spherical symmetry) is that our initial data is momentarily stationary with zero shift vector, which is equivalent to asking for the extrinsic curvature $K_{ij}$ and the normal derivatives of scalar quantities to vanish. This assumption, although not generic, is quite useful since as long as we can make sure that the momentum density vanishes initially the momentum constraint will be satisfied trivially.

We proceed further to simplify the Hamiltonian constraint by writing the physical metric as $\gamma _{ij}=\psi ^4 \hat{\gamma }_{ij}$, with $\hat{\gamma }_{ij}$ some known conformal metric. In terms of these quantities the Hamiltonian constraint takes the form

$$\begin{aligned} \frac{8}{\psi ^5} \, \hat{D}{}^2\psi - \hat{R}+ 16\pi {\mathcal E} = 0, \end{aligned}$$

(59)

with $\hat{R}$ the Ricci scalar associated with the conformal metric. For a given conformal metric this is an elliptic equation for the conformal factor $\psi$. This has to be solved simultaneously with the Gauss constraint which can also be simplified by a conformal rescaling. Defining the conformal electric field as $\hat{E}{}^i= \psi ^6 E ^i$, the Gauss constraint takes the form

$$\begin{aligned} \hat{D}_i \hat{E}{}^i = 4 \pi \rho _e \psi ^6. \end{aligned}$$

(60)

A further assumption we can make is to take the conformal metric to be flat. By doing this the Laplacian and divergence are the usual ones on flat space and the conformal Ricci scalar $\hat{R}$ vanishes. In spherical symmetry, and with the matter content we are considering, the Hamiltonian constraint takes the final form

$$\begin{aligned}&\frac{1}{r^2} \, \partial _r \left( r^2 \partial _r \psi \right) + 2\pi |\tilde{\chi }|^2 \psi \nonumber \\&\quad +\, \left( \pi q^2 \varPhi ^2 | \varphi |^2 + 2\pi V\right) \psi ^5 + \frac{(\hat{E}^r)^2}{4 \psi ^3} = 0, \end{aligned}$$

(61)

while the Gauss constraint takes the form

$$\begin{aligned} \frac{1}{r^2} \, \partial _r \left( r^2 \hat{E}{}^r \right) - 4 \pi \rho _e \psi ^6 = 0. \end{aligned}$$

(62)

To solve these equations it is also necessary to impose boundary conditions. The equation for the electric field $E^r$ is only first order, so it is enough to specify the value of the field at the origin, which due to the symmetry must be $E^r(r=0)=0$. The equation for the conformal factor $\psi$, on the other hand, is second order so we need to specify two boundary conditions. At the origin we simply ask for $\left. \partial _r \psi \right| _{r=0} = 0$, while far away we ask for $\psi (r \rightarrow \infty )=1+C/r$ for some constant $C$, which in turn implies that at the outer boundary $\partial _r \psi = (1 - \psi )/r$.

Below we will consider two distinct families of initial data, one corresponding to a case with zero global charge, and a second one with a non-zero global charge.

3.1 Zero global charge

The simplest choice for the initial electromagnetic potentials is to just set them equal to zero. With this choice the charge density (37) becomes proportional to $\varPi$, and the current density (38) proportional to $\chi$. We will also assume that $\varPi =0$, so the charge density $\rho _e$ vanishes initially and the spacetime has a vanishing total charge. The current density $(j_e)_r$ does not vanishes as long as the product $\chi ^*\varphi$ has a non-zero imaginary part. This in fact already excludes the naive profile $\varphi = \varphi _0(r) e^{i\theta }$ for constant argument $\theta$, which has as particular cases a purely real or purely imaginary $\varphi$. We will then consider initial data of the form:

$$\begin{aligned} \varphi = f(r) + i g(r), \end{aligned}$$

(63)

with $f(r)$ and $g(r)$ real functions. We then find that $(j_e)_r = i q (g f' - f g')$. So as long as $f$ and $g$ are distinct functions that overlap is some region we will have a non zero current density. In our simulations below we will take $f$ and $g$ as Gaussians centered at slightly different locations.

With these choices it is also easy to verify that the momentum density (54) vanishes, so the momentum constraints are trivially satisfied. That is, initially we have zero charge density and zero momentum density (no energy flux), but non-zero current density. Physically this situation is analogous to a system with identical initial distributions of particles of equal mass and opposite charge, moving in opposite directions.

Since the initial charge density vanishes, the Gauss constraint (60) implies that for regular initial data the electric field must also vanish initially. We therefore need only to solve for the conformal factor from the Hamiltonian constraint, which now takes the simple form

$$\begin{aligned} \frac{1}{r^2} \, \partial _r \left( r^2 \partial _r \psi \right) + \pi |\chi |^2 \psi +2\pi V \psi ^5 = 0. \end{aligned}$$

(64)

In this specific case the Hamiltonian constraint takes exactly the same form it would take if the scalar field was decoupled from the electromagnetic field. It is also remarkable that Eq. (64) does not depend on the value of the fundamental charge of the scalar field $q$, so the initial data sets obtained with this method can be evolved for arbitrary values of $q$.

3.2 Net global charge

We are also interested in constructing initial configurations that have non-zero total charge since we would like to study the case when the initial configuration is such that $Q/M>1$. From Eqs. (37) and (38) we see that this is possible by making a few assumptions. First, since we are considering a momentarily stationary configuration with no shift, we must still have $\varPi =0$. We can obtain configurations with non-vanishing charge density and vanishing current density by setting $a_r=0$, $\varPhi \ne 0$, and $\mathbf {Im}(\varphi )=0$. This choice represents an initially vanishing electric current with non-vanishing charge density given by $\rho _{\mathrm{e}}= -q^2 \varphi ^2 \varPhi$.

With these choices the momentum density still vanishes since $\varPi =0$, and both $\varphi$ and $\chi$ are purely real, so the momentum constraints are again trivially satisfied. Since the charge density is non-zero, we now have to solve simultaneously the Hamiltonian and Gauss constraints once we have chosen both $\varphi$ and $\varPhi$.

Before solving the constraints we can look for some properties of initial data with non-zero charge density by considering a simple model where the charged matter is contained in a thin spherical shell located at $r=r_0$. By Israel’s theorem [17] the exterior region of the spacetime corresponds to the Reissner–Nördstrom (RN) solution [18, 19], which for the initial slice can be written as

$$\begin{aligned} \psi = \left[ \left( 1 + \frac{M}{2r} \right) ^2 - \left( \frac{Q}{2r} \right) ^2 \right] ^{1/2}, \end{aligned}$$

(65)

and

$$\begin{aligned} \hat{E}{}^r = \frac{Q}{r^2}. \end{aligned}$$

(66)

It is straightforward to verify that these functions are solutions to the constraints (61)–(62) when the scalar field vanishes.

The solution in the interior of the thin shell is trivial since we are looking for regular initial data. A flat metric with vanishing electric field is the only solution that is regular at $r=0$, and is characterized only by a constant conformal factor $\psi _0$. These solutions can be matched at $r_0$ to give the spatial metric of the initial slice, and this determines the value of $\psi _0$. The RN geometry in this foliation is known to have a trapped surface at $r=\sqrt{M^2-Q^2}/2$ which only exists if $M>|Q|$. If the initial shell has a radius smaller that this value, then there is an initial black hole in the spacetime and all the matter is enclosed by the horizon. This type of solution is of little interest since distant observers would not distinguish it from a stationary RN black hole. On the other hand, when $|Q|>M$ there exists a pathological behavior in these coordinates, because at the finite radius $r_p = (|Q|-M)/2$ the conformal factor $\psi$ becomes zero. This corresponds to the place where the singularity of the over-extremal RN solution is mapped in these coordinates, and the region $r<r_p$ has no physical relevance.

The analysis of this simplified model shows that we should be cautious when solving the constraint equations for large initial charge densities. In that case, if we ask for the matter to be tightly distributed close to the origin in a region of radius $R$, one could find that $R<r_p$ in which case the initial data will not represent an asymptotically flat spacetime. Numerically, we find that as we construct configurations of localized shells with higher $|Q|/M$ eventually the algorithm fails as a consequence of the conformal factor becoming zero outside the scalar field shell. This was not a problem for the case of vanishing initial charge density presented before, since in that case the solution approaches the Schwarzschild metric outside the matter which does not present such pathologies.

4 Analysis tools and numerical code

For the numerical simulations discussed here we integrate the equations obtained in Sect. 2.1, along with the BSSN equations, using a finite difference scheme. The code uses a method of lines with second or fourth order spatial differences, along with either three-step iterative Crank–Nicholson or fourth order Runge–Kutta time integrators. This code has been previously tested with real scalar fields, and has been used in the context of scalar-tensor theories of gravity with minimal modifications [20, 21].

The evolutions presented below were performed on three different resolutions to rule out discretization effects, namely $\varDelta r = 0.02,0.01,0.005$, with 3,000, 6,000 and 12,000 grid points respectively.

4.1 Gauge choice

For our simulations we choose for simplicity a vanishing shift, whereas for the lapse function we choose the maximal slicing condition $K=\partial _t K=0$, which leads to an elliptic equation for the lapse function $\alpha$ that takes the following form in spherical symmetry

$$\begin{aligned}&\partial ^2_r \alpha + \left( \frac{2}{r} - \frac{\partial _r A}{2A} + \frac{\partial _r B}{B} + 2 \partial _r \ln \psi \right) \partial _r \alpha \nonumber \\&\quad = \alpha A \psi ^4 \left[ K^2 + 4 \pi \left( {\mathcal E} + S \right) \right] , \end{aligned}$$

(67)

with $K^2= K_{ij} K^{ij}$, and $S$ the trace of $S_{ij}$. Since in spherical symmetry this is a linear ordinary differential equation for $\alpha$, it can be solved numerically at each time step by matrix inversion without increasing significantly the computational costs of the whole scheme.

4.2 Regularization

The origin in spherical coordinates is a singular point and its inclusion in the numerical domain may be problematic due to instabilities that arise from numerical errors. The problem comes from the fact that the coordinate transformation induces terms on the evolution equations that go as $1/r$ and seem ill behaved. These divergences cancel analytically, but this may not be the case when we consider the numerical error.

To avoid this problem one needs to take two steps. First, we use a grid that staggers the origin and enforce the parity conditions that must be satisfied by the different functions in order to be regular depending on their tensorial character. Also, special care needs to be taken with the evolution equations for the metric and extrinsic curvature since they contain terms that are not manifestly regular at $r=0$. One then needs to define certain combinations of quantities as new independent variables and evolve them separately (see [15, 22] for details).

One should mention the fact that it has recently been pointed out by Montero and Cordero-Carrion [23] that one can avoid the need of a special regularization algorithm if one uses a partially implicit Runge–Kutta method for the time integration. In fact we have found that with the numerical methods used in our code, which are fully explicit, one can also obtain stable and convergent evolutions without regularization, but at he price of having the numerical errors close to the origin increase considerably. Using the regularization algorithm increases the accuracy significantly at no serious extra computational cost.

4.3 Mass and charge content of the spacetime

A convenient way to determine the mass of a localized distribution that has spherical symmetry is by considering the radial dependence of the metric components. When expressed in terms of the areal radius $R$, in which the area of a sphere is $4\pi R^2$, the radial component of the metric behaves as

$$\begin{aligned} g_{RR}=\left( 1- \frac{2M(R)}{R} \right) ^{-1}. \end{aligned}$$

(68)

After a little algebra we can write the function $M(R)$ in terms of our original radial coordinate $r$ as

$$\begin{aligned} M(r) = \frac{r \psi ^2 B^{1/2}}{2} \left[ 1 - \frac{B}{A} \left( 1 + r \frac{\partial _r B}{2B} + 2 r \frac{\partial _r\psi }{\psi } \right) ^2 \right] . \end{aligned}$$

(69)

This function may be identified with the total mass outside the matter sources, since it attains the value of the ADM mass in the vacuum region. In our case, since the electric field extends to infinity, the value of the mass function is always less than the total ADM mass, but approaches it quickly since the electric field decays as $1/r$.

For the electric charge, all information is contained in Maxwell’s equations. We can define the total charge contained in a region of a constant $t$ hypersurface by integrating the charge density $\rho _e$ over that region. Since we are working on spherically symmetric slices it is convenient to define the charge enclosed inside a sphere of radius $r$ as

$$\begin{aligned} Q(r) = \int _{S(r)}{\rho _e \, dV} . \end{aligned}$$

(70)

Taking the limit when $r\rightarrow \infty$ we get the total charge of the spacetime, which is a conserved quantity as a consequence of the 4-current $j_e^\mu$ satisfying the continuity equation $\nabla _\mu j_e^\mu =0$. By using Gauss law and the divergence theorem, this expression can be converted to a boundary integral as follows

$$\begin{aligned} Q(r)&= \frac{1}{4\pi }\int _{S(r)}{D_a E^a dV} \nonumber \\&= \frac{1}{4\pi }\oint _{\partial S(r)}{{\hat{r}}_a E^a dS}, \end{aligned}$$

(71)

where we have assumed that the interior of the sphere is regular, and where $\hat{r}$ is the outward pointing unit normal vector to the sphere. In spherical symmetry the angular dependency can be integrated immediately yielding

$$\begin{aligned} Q(r) = r^2 \psi ^6 \sqrt{A}B E^r. \end{aligned}$$

(72)

Since in our simulations the numerical domain is finite we can only consider the charge enclosed by spheres of finite radius, which won’t be conserved since there may be scalar field that is scattered to infinity carrying away electric charge with it beyond the computational domain. It is possible, however, to track the rate of change of the enclosed charge by using the continuity equation. After some algebra we find

$$\begin{aligned} \frac{dQ(r)}{dt} = \int _{S(r)}{ D_i \left( \rho _e \beta ^i - \alpha \, {}^{(3)}j_e^i \right) } dV, \end{aligned}$$

(73)

where we have kept the shift vector dependence for generality. Again, this is the integral of a divergence which can be transformed into a boundary integral, and the angular dependence can be immediately integrated yielding

$$\begin{aligned} \frac{dQ(r)}{dt} = 4 \pi r^2 \psi ^6 \sqrt{A}B \left( \rho _e \beta ^r - \alpha \, {}^{(3)}j_e^r \right) . \end{aligned}$$

(74)

The above equation can be integrated in time to find the change of the enclosed charge at fixed coordinate radius $r$ after a time $T$

$$\begin{aligned} \varDelta Q(r,T) = 4 \pi r^2 \int _0^T {\psi ^6 \sqrt{A} B \left( \rho _e \beta ^r - \alpha {}^{(3)}j_e^r \right) dt}. \end{aligned}$$

(75)

4.4 Horizons and irreducible mass

Although the only formal way to identify the presence of a black hole in the spacetime is by identifying its event horizon, one can learn a lot about the dynamics of the collapse from the apparent horizons. Since the strong energy condition holds for charged scalar fields, the singularity theorems [24] imply that the development of trapped surfaces will lead to a singularity in the spacetime. Also, once the final black hole has settled down the apparent horizon will coincide with the event horizon. For a stationary black hole the area $A_\mathrm{H}$ of its event horizon is related to the so-called irreducible mass by

$$\begin{aligned} M_\mathrm{irr}= \sqrt{ \frac{A_\mathrm{H}}{16\pi } }. \end{aligned}$$

(76)

The irreducible mass gets this name because it is the minimum mass value a black hole can attain for a fixed value of the area. The actual mass of a non-rotating charged black hole is related to this quantity by

$$\begin{aligned} M_\mathrm{H} = M_\mathrm{irr} + \frac{Q_\mathrm{H}^2}{4M_\mathrm{irr}}, \end{aligned}$$

(77)

where the horizon charge $Q_\mathrm{H}$ is evaluated at the black hole surface.

4.5 Characteristic adapted boundary conditions

The finiteness of the numerical domain must be dealt with carefully since the boundary conditions imposed may introduce errors that affect the results of the simulations. Usually one imposes outgoing wave boundary conditions to avoid spurious reflections, but it turns out that such conditions are not compatible in general with the evolution equations. In the case of General Relativity the evolution equations preserve the constraints but generic boundary conditions fail to do so. We will deal elsewhere with the problem of applying constraint preserving boundary conditions for the BSSN formulation in spherical symmetry [25], while here we will just discuss the issue of how to apply boundary conditions to the scalar and electromagnetic fields.

We start by looking at the characteristic structure of the evolution equations in order to find the ingoing and outgoing eigenfields. These eigenfields are reconstructed at the boundary after all the dynamical variables have been updated all the way to the boundary (using one-sided differences at the boundary itself). We then apply suitable boundary conditions to the incoming fields while leaving the outgoing fields unchanged. After this we reconstruct the original dynamical fields at the boundary.

In order to find the eigenfields associated with the scalar field, we start from the fact the evolution system up to principal part has the form

$$\begin{aligned}&\partial _t \varphi - \beta \partial _r \varphi \sim 0, \end{aligned}$$

(78)

$$\begin{aligned}&\partial _t \chi - \beta \partial _r \chi - \alpha \partial _r \varPi \sim 0, \end{aligned}$$

(79)

$$\begin{aligned}&\partial _t \varPi - \beta \partial _r \varPi - \frac{\alpha }{A\psi ^4} \, \partial _r \chi \sim 0. \end{aligned}$$

(80)

Diagonalizing this system we find the following eigenfields $\omega$ and corresponding eigenspeeds $\lambda$:

$$\begin{aligned}&\displaystyle \omega ^0_\varphi = \varphi , \quad \lambda ^0_\varphi = - \beta , \end{aligned}$$

(81)

$$\begin{aligned}&\displaystyle \omega ^\pm _\varphi = \varPi \mp \frac{\chi }{\sqrt{A}\psi ^2}, \quad \lambda ^\pm _\varphi = - \beta \pm \frac{\alpha }{\sqrt{A}\psi ^2}. \end{aligned}$$

(82)

Notice that the characteristic speed $\lambda _0$ corresponds to propagation along the normal direction to the hypersurfaces, while the speeds $\lambda ^\pm$ correspond to propagation along the light cone.

We now assume that far from the sources the scalar field behaves as a spherical wave of the form $\varphi =f(r-\lambda ^+ t)/r$. This can be easily shown to imply that the incoming eigenfield must have the form

$$\begin{aligned} \omega ^-_\varphi = - \frac{\varphi }{r \sqrt{A} \psi ^2}. \end{aligned}$$

(83)

Notice that, because of the $1/r$ decay of the spherical wave, the incoming field is not zero as one could naively expect. Setting $\omega ^-_\varphi =0$ at the boundary in fact results in large reflections. In practice, we evolve both $\varPi$ and $\chi$ all the way to the boundary using one-sided derivatives, and use their values to construct the outgoing field $\omega ^+_\varphi$ at the boundary. We then calculate $\omega ^-_\varphi$ from Eq. (83) above, and finally reconstruct $\varPi$ and $\chi$ from the values of $\omega ^+_\varphi$ and $\omega ^-_\varphi$.

The evolution equations for the electric field turn out to be identical to those of the scalar field up to principal part. One only needs to make the identifications $\varPi \rightarrow \varPhi$, $\chi \rightarrow -a_r$, $\varphi \rightarrow E^r$. In this case the eigenfields and corresponding speeds become

$$\begin{aligned}&\displaystyle \omega ^0_E = E^r, \quad \lambda ^0_E = - \beta , \end{aligned}$$

(84)

$$\begin{aligned}&\displaystyle \omega ^\pm _E = \varPhi \pm \frac{a_r}{\sqrt{A}\psi ^2}, \quad \lambda ^\pm _E = - \beta \pm \frac{\alpha }{\sqrt{A}\psi ^2}. \end{aligned}$$

(85)

However, the analogy with the scalar field system ends here since the electromagnetic potentials do not relate to the electric field as its normal and tangential derivatives. Since in absence of a shift vector the electric field evolves trivially up to principal part we just update it using the values of the source terms on the boundary.

For the electromagnetic potentials we are in principle free to specify the incoming eigenfield at the boundary. However, just as it happened with the scalar field, if we want to avoid large reflections at the boundary the incoming field should not be chosen to be equal to zero. But now we face a problem: in the case of the scalar field we could model $\varphi$ as an outgoing spherical wave, and from that deduce the form of $\omega ^-_\varphi$ at the boundary. But for the electric field we can’t do the same since, as we have already mentioned, the electromagnetic potentials are not the time and space derivatives of some other field. Because of this we will simply model the incoming field $\omega ^-_E$ itself as a spherical outgoing wave at the boundary, and consequently we will ask for it to satisfy an advection equation of the form

$$\begin{aligned} \partial _t \omega ^-_E + \lambda \, \partial _r \omega ^-_E + \lambda \frac{\omega ^-_E}{r} = 0. \end{aligned}$$

(86)

This equation is evolved at the boundary to obtain the value of the incoming field on the new time-step, and from this we reconstruct the electromagnetic potentials at the boundary.

5 Results of our numerical simulations

We will now discuss the results of some of our numerical simulations. We will do it first for the configurations with zero global charge, and after that for the configurations with non-zero initial charge.

5.1 Globally uncharged configurations

For the first set of simulations we used the initial data corresponding to scalar field configurations with vanishing global charge. As discussed before, in this case we assume that the electromagnetic potentials $\varPhi$ and $a_r$ vanish initially. We choose a Gaussian profile for the scalar field that represents a shell of matter with non-zero initial current density. Explicitly, at $t=0$ we choose the following gaussian profiles for the real and imaginary parts for the scalar field:

$$\begin{aligned} \mathrm{Re}{(\varphi )}&= \varphi _0 \left[ e^{-(r-r_R)^2/\sigma ^2} + e^{-(r+r_R)^2/\sigma ^2} \right] , \end{aligned}$$

(87)

$$\begin{aligned} \mathrm{Im}{(\varphi )}&= \varphi _0 \left[ e^{-(r-r_I)^2/\sigma ^2} + e^{-(r+r_I)^2/\sigma ^2} \right] , \end{aligned}$$

(88)

where we use the same amplitude $\varphi _0$ and width $\sigma$ for both the real and imaginary part, but with the pulses centered on slightly different places, $r_R \ne r_I$, in order to have a non-vanishing electric current. We also sum the mirror image of the Gaussian to ensure that the scalar field is well behaved at the origin.

For all the simulations shown here we have chosen $r_R=5.0$, $r_I=5.1$ and $\sigma =1.0$, and we solve the Hamiltonian constraint for different values of $\varphi _0$. We performed simulations for a two parametric set of configurations, with the fundamental charge $q$ ranging from 0 to 8, and the initial amplitude of the pulses $\varphi _0$ ranging from 0.03 to 0.1.

The simulations with low values of $\varphi _0$ behave as expected: The scalar field propagates and is eventually dispersed to infinity leaving behind flat spacetime. As an example, we consider the evolution for the case with $\varphi _0=0.03$ and $q=2.0$. Initially the pulse separates into incoming and outgoing parts, and a non-zero charge density quickly develops. This can be seen in Fig. 1, which shows a snapshot of the evolution at $t=4$. The top panel shows the scalar field, while the lower two panels show the integrated mass $M(r)$ and charge $Q(r)$.

Fig. 1

Plot of the early stage of the evolution ($t=4$) of a configuration with zero initial charge density and $\varphi _0=0.03$, $q=2.0$. The top panel shows the scalar field (with the solid and dotted lines corresponding to the real and the imaginary parts), while the lower two panels show the integrated mass $M(r)$ and charge $Q(r)$

Figures 2 and 3 show the evolution of the scalar field and lapse function respectively. We note that at $t \sim 8$ the incoming pulse reaches the origin and the lapse function decreases significantly there. However, in this case the self-gravity of the scalar field is not strong enough to produce a collapse, and the field later disperses away to infinity while the lapse slowly returns to its flat space value. Figures 4 and 5 show the evolution of the integrated mass and charge for this simulation.

Fig. 2

Evolution of the scalar field for a configuration with zero initial charge density and $\varphi _0=0.03$, $q=2.0$. The solid and dotted lines correspond to the real and the imaginary parts respectively

Fig. 3

Evolution of the lapse function $\alpha$ for a configuration with zero initial charge density and $\varphi _0=0.03$, $q=2.0$

Fig. 4

Evolution of the integrated mass $M(r)$ for a configuration with zero initial charge density and $\varphi _0=0.03$, $q=2.0$

Fig. 5

Evolution of the integrated charge $Q(r)$ for a configuration with zero initial charge density and $\varphi _0=0.03$, $q=2.0$

Convergence is verified by analyzing the constraint residuals that arise from the discretization scheme. Figure 6 shows the absolute value of the Hamiltonian constraint at different times for two different resolutions, showing that the error scales with resolution consistently with the expected order of the discretization (fourth order in this case).

Fig. 6

Plot of the absolute value of the Hamiltonian constraint at different times for two different resolutions, for a configuration with zero initial charge density and $\varphi _0=0.03$, $q=2.0$. The higher resolution has been multiplied by 16 showing the expected fourth order convergence

For higher values of the amplitude $\varphi _0$ we find that the outcome is very different from the one described above. To show this we follow the case with $\varphi _0=0.05$ and $q=2.0$ (Figs. 7, 8, 9, 10, 11 and 12). The early stage of the simulation proceeds in the same way as before (Fig. 7), but this time when the incoming pulse arrives at the origin the lapse function collapses dramatically (Fig. 9), and an apparent horizon is eventually found at $t \sim 11$ (Fig. 12), indicating the formation of a black hole.

Fig. 7

Plot of the early stage of the evolution ($t=4$) of a configuration with zero initial charge density and $\varphi _0=0.05$, $q=2.0$. The top panel shows the scalar field (with the solid and dotted lines corresponding to the real and the imaginary parts), while the lower two panels show the integrated mass $M(r)$ and charge $Q(r)$

Fig. 8

Evolution of the scalar field for a configuration with zero initial charge density and $\varphi _0=0.05$, $q=2.0$. The solid and dotted lines correspond to the real and the imaginary parts respectively

Fig. 9

Evolution of the lapse $\alpha$ for a configuration with zero initial charge density and $\varphi _0=0.05$, $q=2.0$

Fig. 10

Evolution of the integrated mass $M(r)$ for a configuration with zero initial charge density and $\varphi _0=0.05$, $q=2.0$

Fig. 11

Evolution of the integrated charge $Q(r)$ for a configuration with zero initial charge density and $\varphi _0=0.05$, $q=2.0$

Fig. 12

Evolution of the apparent horizon for a configuration with zero initial charge density and $\varphi _0=0.05$, $q=2.0$: Coordinate radius (top left), area (top right), enclosed charge (bottom left) and horizon mass (bottom right)

Figures 10 and 11 show the evolution of the integrated mass and charge, and we see that both tend to stabilize quickly outside of the apparent horizon after the dispersed field leaves the central region. Figure 12 shows the evolution of different properties of the apparent horizon. Since this simulation is done with a vanishing shift vector we see that the coordinate radius of the apparent horizon keeps growing as the simulation goes on. This growth of the coordinate radius where the apparent horizon is located is a well known gauge effect coming from the fact that the Eulerian (normal) observers are falling and there is no shift vector to compensate for this. On the other hand, the area, enclosed charge, and mass associated with the horizon rapidly stabilize. These quantities are well defined on the apparent horizon: the charge of the black hole is calculated with Eq. (72) evaluated on the apparent horizon radius, while the total mass is calculated with Eq. (77) which includes the contribution due to the enclosed charge.

Ultimately, the lack of a shift vector leads to slice stretching effects on the metric components that eventually cause our numerical simulations to fail. However, we find that these effects are delayed as the mass of the final black hole increases and the simulations last long enough for us to study the physical properties of the final black hole. Figure 13 is a close up of the area and mass of the apparent horizon that shows how these properties stabilize before the simulation fails (the small oscillations are due to the numerical method and decrease at higher resolutions).

Fig. 13

Close up of the apparent horizon area (top), and mass (bottom) shown in Fig. 12 above. The small oscillations are due to numerical error and decrease at higher resolutions

Once the scalar field outside of the apparent horizon is radiated away we end up with an electro-vacuum region where only the Coulomb field of the trapped scalar field remains. The gauge conditions, and in particular the vanishing shift vector, prevent us from reaching a stationary situation outside of the trapped surface, but as we have seen the relevant physical properties rapidly approach stationary values.

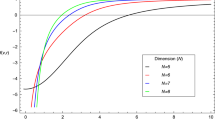
We have also performed simulations for values of the scalar field charge $q$ ranging from 0.0 to 8.0, and initial amplitude $\varphi _0$ from 0.03 to 0.1, focusing on the region of the parameter space that leads to configurations that undergo gravitational collapse. The simulations proceed in a similar way to the one analyzed before, the main difference is that when increasing both parameters the shape of the initial pulses gets much more distorted after they split, showing little resemblance to the initial superposed pulses. In each case, once an apparent horizon is found its physical properties stabilize quickly. Also, after the remaining scalar field is radiated away, the integrated mass and charge stabilize in the electro-vacuum region. It is interesting to note that that in this region of the parameter space the final mass of the black hole is not very sensitive to the value of the fundamental charge $q$ , which is somewhat surprising since this mass includes contributions from the electric field (see Fig. 14). We have also found that the ratio of final mass of the black hole to the initial ADM mass of the configuration, $M_f/M_i$, increases with the amplitude $\varphi _0$ (see Fig. 15), which is easily understood since by increasing the initial amplitude we get a more compact configuration.

Fig. 14

Final mass of the black hole $M_f$ for the configurations with zero initial charge density, as a function of the initial amplitude of the pulse $\varphi _0$ for different values of $q$. Notice that for small values of $\varphi _0$ no black hole forms

Fig. 15

Ratio of the final mass of the black hole $M_f$ to the initial ADM mass $M_i$ for the configurations with zero initial charge density, as a function of the initial amplitude $\varphi _0$

We now turn to the analysis of the charge of the final configurations, which is somewhat less intuitive. For fixed values of the fundamental charge $q$ the final charge of the configuration increases initially with the amplitude of the initial pulse, but it eventually reaches a maximum and decreases again, and might even oscillate around zero (see Fig. 16). We find that as we increase the fundamental charge this maximum is in fact reached for lower initial amplitudes and has lower a value.

Fig. 16

Final charge of the black hole $Q_f$ for the configurations with zero initial charge density, as a function of the initial amplitude $\varphi _0$ for different values of $q$

By combining these results we can calculate the quotient of the final charge and mass of the black hole $Q/M$ (see Fig. 17). We can observe that as we increase the initial amplitude $\varphi _0$ for fixed $q$, this ratio reaches a maximum and then decreases again. The global maximum that we have found for all our different simulations corresponds to the value $Q/M \simeq 0.25$, which shows that the final state of all these configurations is very far from approaching an extreme charged black hole with $Q/M=1$.

Fig. 17

Charge to mass ratio $Q_f/M_f$ of the final black hole for the configurations with zero initial charge density, as a function of the initial amplitude $\varphi _0$ for different values of $q$

5.2 Globally charged configurations

For the configurations with non-vanishing global charge we use the following initial profiles for the scalar field and the scalar potential

$$\begin{aligned} \mathrm{Re}{(\varphi )}&= \varphi _0 \left[ e^{-(r-r_0)^2/\sigma ^2} + e^{-(r+r_0)^2/\sigma ^2} \right] ,\end{aligned}$$

(89)

$$\begin{aligned} \mathrm{Im}{(\varphi )}&= 0, \end{aligned}$$

(90)

$$\begin{aligned} \varPhi&= \varPhi _0 \left[ e^{-(r-r_0)^2/\sigma ^2} + e^{-(r+r_0)^2/\sigma ^2} \right] . \end{aligned}$$

(91)

For all the simulations discussed below the pulses are centered $r_0=5.0$ with a width $\sigma =1.0$. We have also found that by taking the initial amplitude of the electric potential to be $\varPhi _0=1$, it was possible to construct configurations that have initially a charge to mass ratio greater than one.

The evolution of this type of initial data is very similar to the case with vanishing global charge. As an illustrative example we consider the case with $\varphi _0=0.05$ and $q=0.5$, which is a combination of parameters that results in a configuration that undergoes gravitational collapse. As can be seen in Fig. 18, which shows the early stages of the evolution at $t=4$, the initial pulse separates into its incoming and outgoing components, each one retaining approximately half of the original charge. Figures 19, 20, 21 and 22 show snapshots of the scalar field and lapse function, as well as the integrated mass and charge. Again we see that when the incoming pulse arrives at the origin the lapse function collapses. Even though this collapse takes place, some of the scalar field is still dispersed (see Fig. 19) taking away with it part of the mass and the charge of the configuration, as can be seen in Figures 21 and 22. Some of the properties of the apparent horizon for this evolution are shown on Fig. 23.

Fig. 18

Plot of the early stage of the evolution ($t=4.0$) of a configuration with non-vanishing initial charge density and $\varphi _0=0.05$, $q=0.5$. The top panel shows the scalar field (with the solid and dotted lines corresponding to the real and the imaginary parts), while the lower two panels show the integrated mass $M(r)$ and charge $Q(r)$

Fig. 19

Evolution of the real (solid line) and imaginary (dotted line) parts of the scalar field at different times, for of a configuration with non-vanishing initial charge density and $\varphi _0=0.05$, $q=0.5$

Fig. 20

Evolution of the lapse $\alpha$ for of a configuration with non-vanishing initial charge density and $\varphi _0=0.05$, $q=0.5$

Fig. 21

Evolution of the integrated mass $M(r)$ for of a configuration with non-vanishing initial charge density and $\varphi _0=0.05$, $q=0.5$

Fig. 22

Evolution of the integrated charge $Q(r)$ for of a configuration with non-vanishing initial charge density and $\varphi _0=0.05$, $q=0.5$

Fig. 23

Evolution of the apparent horizon for of a configuration with non-vanishing initial charge density and $\varphi _0=0.05$, $q=0.5$: Coordinate radius (top left), area (top right), enclosed charge (bottom left) and horizon mass (bottom right)

We will now concentrate on configurations with amplitude $\varphi _0=0.05$, and with a fundamental charge that varies from $q=0$ to $q=2$. All these configurations are found to undergo gravitational collapse. The initial ADM mass of the configurations turns out to be an increasing function of $q$ as a combined effect of both the presence of a more intense initial electric field and the larger areal radius of the initial shell (see Fig. 24). As one would expect, the mass of the final black hole is also an increasing function of $q$ (see Fig. 25). Figure 26 shows the ratio of the mass of the final black hole to the initial ADM mass, $M_f/M_i$. As expected, this is always lower than 0.5 since half the initial mass is carried away by the outgoing pulse. Notice also that the mass ratio shows a strong dependence on the value of $q$, and in fact decreases for large values of $q$. This can be interpreted as an effect of the electric repulsion of the initial pulse: there is an accumulation of charge of the same sign which repels itself, so that as $q$ increases a larger fraction of the ingoing pulse in fact ends up being dispersed to infinity.

Fig. 24

Initial ADM mass for the configurations with non-vanishing electric charge, as a function of the fundamental charge $q$ for fixed $\varphi _0=0.05$

Fig. 25

Mass of the final black hole for the configurations with non-vanishing electric charge, as a function of the fundamental charge $q$ for fixed $\varphi _0=0.05$

Fig. 26

Ratio of the final mass of the black hole to the initial ADM mass for the configurations with non-vanishing electric charge, as a function of the fundamental charge $q$ for fixed $\varphi _0=0.05$

Considering now the electric charge of these configurations, we find that the initial charge $Q_i$ depends almost quadratically on the fundamental charge $q$, as can be seen in Fig. 27 (notice that the initial charge is negative). On the other hand, the final charge of the black hole $Q_f$ decreases in absolute value for higher values of $q$ and even changes sign, as shown in Fig. 28. The ratio $Q_f/Q_i$ is shown in Fig. 29. This behavior can be understood as follows: when the initial pulse splits the electromagnetic interaction of the ingoing pulse is so strong that it disperses scalar field that carries away the excess charge, while it allows accretion of scalar field that carries electrical charge of the opposite sign, eventually this effect is so strong that the final charge of the black hole changes sign with respect to the initial configuration. This change of sign in the charge of the final black hole is also seen on the initially neutral configurations (Figs. 16 and 17), but in that case there is no initial charge to compare with.

Fig. 27

Initial charge of the configurations, as a function of the fundamental charge $q$

Fig. 28

Final charge of the black hole as a function of the fundamental charge $q$

Fig. 29

Ratio of the final charge to the initial charge $Q_f/Q_i$, as a function of the fundamental charge $q$

Finally, in Fig. 30 we show the behavior of the charge to mass ratio $|Q/M|$, both for the initial data and the final black hole. For the initial data, this ratio grows with the fundamental charge but eventually flattens at around $q \sim 1.5$. One can notice that the ratio in fact becomes greater than one beyond $q \sim 1$. However, for the final black hole this ratio is always lower than its original value, and since the final charge decreases to zero as the fundamental charge $q$ increases we find that the ratio also decreases beyond $q=1$. For this family of configurations the maximum charge to mass ratio for the final black hole is approximately $|Q_f/M_f| \sim 0.62$ and is attained for a value of the fundamental charge $q \sim 1$.

Fig. 30

Charge to mass ratio $|Q/M|$ as a function of the fundamental charge $q$. The solid line corresponds to the initial data, and the dotted line to the final black hole

5.3 Nature of the final black hole

It is a common feature of the configurations that we have analyzed that after the collapse of the scalar field in the central region an apparent horizon forms. We find that even if our gauge conditions prevent us from approaching a completely stationary situation, the physical properties of the apparent horizon, essentially its area and the charge contained within it, settle down quickly. Since we don’t expect the small amount of outgoing scalar field to affect the collapsed object, we may safely assume that once the apparent horizon properties settle down the configuration has turned into a black hole, and that the apparent horizon coincides for all practical purposes with the event horizon. If this is correct the black hole must be of the Reissner–Nördstrom class, in concordance with the uniqueness theorems in the case of spherical-symmetry.

One way to verify this is to compare the asymptotic value of the integrated mass function (69) with the “horizon mass” inferred from the properties of the apparent horizon given by (77), $M_\mathrm{H} = M_\mathrm{irr} + Q_\mathrm{H} / 4 M_\mathrm{irr}$. Since the difference of these quantity between the two greatest resolutions lies within the oscillations shown on Fig. 13 we have chosen to estimate the error using the amplitude of such oscillations. The asymptotic mass, on the other hand, is measured by reading the value of the mass function $M(r)$ at a coordinate radius $r=30$ (the midpoint of our computational domain) at late times, once the final black hole has settled down. The error in this case can be estimated by considering the difference of the mass function evaluated at the two highest resolutions. As we have already mentioned, one should remember the fact that at late times the region outside the horizon is not in fact a vacuum since it contains a non-vanishing electric field, so that the value of the mass function $M(r)$ will always remain smaller that the ADM mass. This effect, however, turns out to be very small. It is worth to note that the quantities associated with the apparent horizon inherit gauge dependence being the later dependent on the foliation, but since we are interested in the values attained when the apparent horizon achieves a stationary state and coincides with the event horizon, those quantities become gauge independent. One should also notice that the reported errors arising from the numerical integration of the evolution equations are consistent with the initial data, since the parameters describing the data are given up to machine precision and the initial error being dominated by that introduced when solving numerically the constraints, which is lower by many magnitude orders.

Table 1 summarizes the results obtained for the family of initial data with zero initial charge density, for different values of $q$ and $\varphi _0$. Notice that, in particular, for the example shown in the text corresponding to $\varphi _0=0.05$, $q=2.0$, we find an estimated asymptotic mass $M_{\infty } = 0.6290\pm 0.0003$, while for the horizon mass we find $M_\mathrm{H} = 0.6294\pm 0.00007$.

Table 1 Properties of the final black hole ($M_\mathrm{irr}, Q_\mathrm{H}, M_\mathrm{H}$), and estimated asymptotic mass $M_\infty$, for the initial data family with zero initial charge density, for different values of $q$ and $\varphi _0$

The results for the family of initial data with non-vanishing charge density are also shown in Table 2, for different values of $q$ and a fixed value of $\varphi _0=0.05$. For the example discussed in the text corresponding to $q=0.5$, we find an estimated asymptotic mass of $M_\infty = 0.3107\pm 0.000576$ and an horizon mass $M_\mathrm{H} = 0.3109\pm 0.000092$.

Table 2 Properties of the final black hole ($M_\mathrm{irr}, Q_\mathrm{H}, M_\mathrm{H}$), and estimated asymptotic mass $M_\infty$, for the initial data family with non-vanishing charge density, for different values of $q$ and $\varphi _0=0.05$

Looking at the tables we see that in all cases there is an excellent a agreement between the asymptotic mass $M_\infty$ and the horizon mass $M_\mathrm{H}$ , with the differences falling within the errors associated with the discretization scheme employed. This result is quite satisfactory since it compares the asymptotic behavior of the metric with local measurements on the horizon (its area) and the integrated charge, and is therefore a strong indicator that the final black hole is indeed of the Reissner–Nördstrom type.

6 Conclusions

We have made a systematic study of the collapse of self-gravitating spherically symmetric configurations of charged scalar field in the $3+1$ formalism. To solve the full Einstein–Maxwell–Klein–Gordon (EMKG) system we coupled the field equations of both the electromagnetic and scalar fields to a generalized version of the BSSN formulation of general relativity [14, 15].

Our main goal in this study was to explore different collapse scenarios in order to test the cosmic censorship hypothesis and analyze the mechanisms that make it hold. We focused on two types of initial data configurations, both of them conformally flat and time-symmetric: the first set possessed zero initial charge density, while the other one possessed zero initial current density. Since the critical collapse of this kind of configurations is well understood [7], we focused on configurations that lead to collapse far from the critical regime. In all such cases, we found that an apparent horizon forms, giving empirical evidence for the validity of cosmic censorship hypothesis.

We also studied the final charge to mass ratio of the collapsing configurations, in order to study how close one can get to an extremal charged black hole with $|Q|/M=1$. For the initially uncharged configurations we performed a series of simulations for different values of the initial amplitude $\varphi _0$ and fundamental charge $q$. The maximum charge to mass ratio found for the final black hole with this type of initial data was of $|Q|/M \sim 0.26$, well below the extremal value of 1. Since these configurations are insensitive initially to the value of the fundamental charge $q$, there are some aspects of the dynamics that are almost unaffected. In particular, the interaction between the ingoing and outgoing components of the field is minimal, so the final mass of the black holes also shows little dependence on the fundamental charge.

The effect of the electromagnetic interaction is better appreciated when considering the charge of the black hole: increasing the values of $\phi _0$ and $q$ leads to a larger electromagnetic repulsion which tends to neutralize the final charge of the collapsed object. For the configurations with non-zero global charge the results are very similar. The maximum charge to mass ratio for the final black hole was found to be $|Q|/M \sim 0.6$. The main difference with the former family of simulations is that in this case the final mass of the black hole depends heavily on the fundamental charge $q$. The presence of an initial electric field produces a considerable electric repulsion of the initial shell that tends to disperse it. However, for intermediate values of $q$ in the region we have explored, this repulsion is not strong enough to have a significant neutralizing effect by the time an apparent horizon forms, leading to black holes with a larger charge to mass ratio than those of the initially uncharged set.

Our results are consistent with the fact that when considering charged matter the cosmic censorship conjecture holds generically. In our case, a strong electromagnetic interaction gives rise to a redistribution of the fields that avoids the concentration of electric charge in small regions. This leads to configurations of collapsed matter that are nearly neutral, and the effect turns out to be greater as we increase the electromagnetic interaction by going to higher values of the fundamental charge $q$. This seem to indicate that overcharged configurations will not be able to collapse while retaining the charge excess.

We also focused on studying the properties of the final stationary black holes. The final configurations observed are consistent with the uniqueness theorems of spherically symmetrical spacetimes in the sense that, once the collapse takes place and the charge excess is radiated away along with the dispersed scalar field, they reduce to the Reissner–Nördstrom geometry outside the horizon. This was verified by comparing the mass function obtained from the metric expressed in Boyer-Lindquist coordinates, and the black hole mass associated to the horizon properties. Of course, the question as to what happens inside the horizon is also very interesting. Eternal Reissner–Nördstrom black holes have a very complex causal structure inside the horizon, with Cauchy horizons, timelike singularities and wormholes connecting an infinite repetition of exterior regions. How exactly this structure changes when instead of an eternal black hole one considers a collapse scenario is something that one would like to address through numerical simulations such as those presented here. However, approaching the singularity in a numerical simulation is far from trivial as dynamical quantities diverge there, and the gauge conditions used for our present study are not adequate for the task (we are using a singularity avoiding slicing condition with no shift).

As a final comment, in this work we only considered the case of a charged massless scalar field, the question of whether the same results will hold in support when considering a massive scalar field (or a more general self-interaction potential) is still open. It is well known that the dynamics of the scalar field changes drastically when considering a non-trivial potential, and that gravitationally bound configurations can be found in that case, which could presumably lead to higher charge to mass ratios for the collapsing scenarios.