1 Introduction

One of the most important open issues in the theory and astrophysical applications of modern day black hole and gravitation physics is that of the Cosmic Censorship Conjecture (CCC) [4]. The CCC postulates that any physically realistic gravitational processes must not lead to the formation of a singularity which is not covered by an horizon, thus hiding it from external observers in the universe. This of course includes the complete gravitational collapse of a massive star which, if the CCC is true, must terminate generically into a black hole final state only. Nevertheless in recent years, a wide variety of gravitational collapse models have been discovered where the dynamical evolution leads to a naked singularity formation rather than a black hole as collapse endstate. The first examples were restricted to some classes of inhomogeneous dust collapse (see e.g. [5–9]), and they were soon to be extended to the case of collapse in the presence of only tangential pressures (see e.g. [10–15]), and perfect fluids (see for example the pioneering work by Ori and Piran on self-similar collapse [16–18] or [19, 20], or see [21–28] for some more recent studies on perfect fluid collapse).

Nevertheless, despite the large number of classes of collapse leading to naked singularities, the OSD collapse model has remained until now the paradigm of stellar collapse. In [3] it was shown that there exist models of collapse in the presence of tangential pressures that are arbitrarily close to the OSD model and that lead to the formation of a naked singularity. In the present work we consider a similar scenario with arbitrarily small perfect fluid perturbations of the OSD model and show that there exist classes of such pressure profiles that lead to the formation of a naked singularity. This is an important and useful indicator in the sense that it relates the counterexamples to the CCC found in the past to the paradigmatic model of OSD, showing that the latter is in some sense ‘unstable’ under small pressure perturbations. This is in the sense that there exist classes of small pressure perturbations as we show here explicitly, such that with the introduction of a smallest pressure, the collapse evolution that was originally going to black hole now develops into a naked singularity. We also note that the treatment here of perfect fluid collapse is more general in that it does not require the restrictive assumption of self-similarity of collapse models used earlier.

The consideration of dynamical evolution of collapse is a crucial element of the CCC in the sense that in the original formulation of the conjecture it is stated that singularities arising from the dynamical collapse from a regular initial data must be covered by an event horizon. Many solutions of Einstein field equations are known which present naked singularities (such as, for example, the super-spinning Kerr solutions), nevertheless almost none of these solutions can be obtained as the dynamically evolved final state of some initially regular matter configuration. For this reason, over the last decades a great deal of work has been done to test the CCC in the few dynamically evolving spacetimes we know. These are typically the scenarios that describe gravitational collapse in spherical symmetry, and some non-spherical collapse models have also been considered (see for example [29] or [30–35] for examples of critical collapse with angular momentum).

In the following, we will consider complete gravitational collapse of a spherical massive matter cloud that leads to the formation of a strong shell focusing naked singularity at the center. In such a case, the super-ultra-dense regions, or the spacetime singularity, that forms at the end of collapse would be visible to faraway observers in the universe, rather than being hidden in a black hole. Therefore, the question crucial now for the CCC is that of how stable and generic are the naked singularities and black holes that form in dynamical gravitational collapse of a massive matter cloud.

The astrophysical significance of the issue, and the importance of considering the gravitational collapse of a matter cloud within the framework of the general relativity theory, with reasonable physical properties for the matter included, stems from the fact that a star more massive than about five to eight times the mass of the Sun, cannot stabilize to a neutron star final state at the end of its life cycle (estimates on the mass limit for a star in order to collapse indefinitely vary depending on different models for the star’s interior and equation of state for matter at very high densities, see e.g. [36–38]). It must collapse continually under the force of its own gravity on exhausting its internal nuclear fuel, and there are no known forces of nature that would halt such a collapse. General relativity predicts that such a star must then terminate into a spacetime singularity where densities and spacetime curvatures blow up and the physical conditions are extreme. The CCC assumption that such a singularity is always covered within an event horizon of gravity, is then crucial and is at the basis of much of the modern theory and astrophysical applications of black holes today. However, despite the past four decades of serious efforts, we do not have as yet available any proof or even any mathematically precise formulation of the cosmic censorship hypothesis.

Actually from the many dynamical gravitational collapse scenarios that have been investigated over the past years, the typical conclusion that has emerged is as follows: Depending on the nature of the initial data for the matter cloud in terms of its initial density, pressure and velocity profiles from which the collapse evolves, there are dynamical evolutions governed by the Einstein equations that take the collapse to either a black hole or naked singularity final state (see e.g. [39] and references therein). Such a naked singularity would be a super-ultra-dense region of extreme gravity that can communicate with faraway observers in spacetime, and this hypothetical astrophysical object, if realized in nature, would have radically different observational signatures from its black hole counterpart.

If, however, the occurrence of naked singularities of collapse were special or ‘non-generic’ in some appropriately well-defined sense, then at least the spirit of CCC would be respected. One can impose various sets of physical reasonability and regularity conditions under which the collapse of a massive star is to be dynamically evolved to examine its final state. What is really needed here is a detailed investigation of the gravitational collapse phenomena within the framework of general relativity, which is the only path that can provide useful and adequate insights into the final fate of collapse in terms of either a black hole or naked singularity. Investigating how the final black hole state is affected, once a small, general, perfect fluid pressure is introduced in the initial data from which the collapse develops would provide a much better understanding of the collapse final states. We show here that the models ending in a naked singularity are in fact not ‘special’, in the sense that they can be generally obtained from perfect fluid collapse, where the initial data is arbitrarily close to models leading to a black hole.

Specifically, we examine here how the evolution of dust collapse models having a black hole final state, is altered when an arbitrarily small perfect fluid pressure perturbation is introduced in the matter source. We show explicitly the existence of classes of small generic pressure perturbations such that an injection of a small positive (or negative) pressure in the OSD model, or in a Tolman-Bondi-Lemaitre (TBL) inhomogeneous dust collapse to a black hole [40–42], leads the collapse to form a naked singularity, rather than a black hole. The classic OSD scenario is the basic paradigm for black hole physics today, and the TBL models describe the most general family of dust, i.e. pressureless, collapse solutions. This result is therefore intriguing, because it shows that arbitrarily close to the dust black hole model, we have collapse evolutions with non-zero pressures that go to a naked singularity final state, thus proving a certain ‘instability’ of the OSD black hole formation picture against the introduction of small pressure perturbations.

Our method consists in ‘injecting’ arbitrarily small but generic pressure perturbations in a dynamical dust collapse which was originally going to a black hole final state. The pressure is chosen in such a way that it remains small as compared to the energy density during the whole collapse and the evolution remains close to the corresponding dust model at all times. We then examine, when the small pressures are considered, whether the collapse would evolve to a black hole or a naked singularity. Our analysis here shows that in the space of initial data from which the gravitational collapse evolves, any arbitrarily small neighborhood of the OSD model would contain collapse evolutions with pressure that go to a naked singularity final fate. While the CCC states that the OSD collapse final fate is necessarily replicated for any realistic stellar collapse in nature, the result here shows that an arbitrarily small pressure perturbation of the OSD model can change the final outcome of collapse to a naked singularity and therefore the OSD black hole may be considered ‘unstable’ in this sense. Since the pressures within a massive star are very important physical forces to take into account, we thus obtain here an important insight into the stability of occurrence of black holes as collapse final states. It is such a clarification of the structure of general relativistic collapse, that may provide us a better understanding of cosmic censorship, and finally resolve the issue of black hole formation in gravitation theory.

2 Small pressure perturbations to dust collapse

The key feature that characterizes black hole formation in gravitational collapse is, as collapse evolves, trapped surfaces and apparent horizon develop at a certain stage within the collapsing cloud, prior to the epoch of formation of the spacetime singularity. Then no timelike or null trajectories can escape from the singularity or its vicinity. An event horizon then must form hiding the singularity, and the collapse ends in a black hole final state. This is the scenario for an homogeneous pressureless collapse model. What we show below is that an arbitrarily small pressure perturbation can radically alter such a scenario. The trapped surface formation is then delayed, and this allows the singularity to be naked where families of non-spacelike curves can escape from the same. We explicitly identify here such a class of pressure perturbations, but it is by no means the only class that can do it. We thus see that the introduction of the slightest pressure in an otherwise pressure free dust model can drastically change the final outcome of collapse.

The most general spherically symmetric metric describing a collapsing matter cloud in comoving coordinates \((t,r,\theta ,\phi )\) is characterized by three free metric functions \(g_{00}=-e^{2\nu (r,t)}, g_{rr}=e^{2\psi (r,t)}\) and the physical radius of the cloud \(g_{\theta \theta }=g_{\phi \phi }/\sin ^2\theta =R^2(r,t)\). These are related via the Einstein equations with the energy-momentum tensor, which for perfect fluid matter sources is given by \(T_t^t\,{=}\,-\rho ; \; T_r^r\,{=}\,T_\theta ^\theta \,{=}\,T_\phi ^\phi \,{=}\,p\), where \(\rho \) is matter energy density and \(p\) is the pressure in the cloud. The Einstein equations are then,

$$\begin{aligned} p&= -\frac{\dot{F}}{R^2\dot{R}}, \end{aligned}$$
(1)
$$\begin{aligned} \rho&= \frac{F^{\prime }}{R^2R^{\prime }},\end{aligned}$$
(2)
$$\begin{aligned} \nu ^{\prime }&= -\frac{p^{\prime }}{\rho +p},\end{aligned}$$
(3)
$$\begin{aligned} 2\dot{R}^{\prime }&= R^{\prime }\frac{\dot{G}}{G}+\dot{R}\frac{H^{\prime }}{H},\end{aligned}$$
(4)
$$\begin{aligned} F&= R(1-G+H), \end{aligned}$$
(5)

where the dot and prime represent derivatives with respect to \(t\) and \(r\) respectively and the functions \(H\) and \(G\) are defined as,

$$\begin{aligned} H =e^{-2\nu (r, t)}\dot{R}^2 , \; G=e^{-2\psi (r, t)}R^{\prime 2} \; . \end{aligned}$$
(6)

Here \(F\) is the Misner-Sharp mass of the system, representing the amount of matter enclosed in a radius \(r\) at the time \(t\).

It is known that since the collapse must evolve from a regular initial data, close to the center the radial and tangential pressures must be equal for any general collapsing matter field. In fact it can be proven that near the center of the cloud, which is the region relevant to our purpose, the pressure gradient must vanish, thus forcing the matter to have a perfect fluid-like behaviour [43]. Therefore we work here with a perfect fluid matter cloud as given by the energy-momentum tensor above.

The model has an additional degree of freedom due to the scale invariance and therefore we can choose the initial time \(t_i\) in such a way that \(R(r, t_i)=r\). We thus introduce the scaling function \(v(r,t)\) defined by \(R=rv\) with \(v(r,t_i)=1\). Collapse is described by the condition \(\dot{v}<0\), and the singularity is reached at \(v=0\), where the density diverges. The energy density \(\rho \) is regular along the central shell \(r=0\) at any time anteceding the singularity, and that requires the Misner-Sharp mass to have a form

$$\begin{aligned} F(r,t)=r^3M(r,v(r,t)), \end{aligned}$$
(7)

with \(M\) being finite at the center. Also, requiring that the energy density has no cusps at the center and is hence a smooth and even function, implies that \(M^{\prime }(0,v)=0\). We then have five equations in six unknowns \(\rho \), \(p\), \(M\), \(\nu \), \(G\) and \(v\) and the system is closed if an equation of state relating pressure and density is assumed. In general, however, it is possible and sometimes even desirable to study physically valid dynamics satisfying various regularity and energy conditions, without assuming a priori any equation of state on which we know little at very high densities of matter.

We therefore choose a suitable physically motivated mass function \(M\) as the free function. The physical validity of this choice suggests to consider a mass profile arbitrarily close to a well-known collapse scenarios such as the OSD or TBL models. We therefore deal with an arbitrarily small pressure perturbation of the TBL model, where by ‘small’ we mean that the pressure remains much smaller than the energy density at all times.

Once \(M\) is fixed, we can evolve the collapse using Einstein equations above and a spacetime singularity develops as collapse final state. Such an evolution from regular initial data in terms of initial density and pressure profiles has been studied in detail and the conditions for the formation of either a black hole or naked singularity have been worked out [43]. The spacetime singularity, corresponding to the epoch \(v=0\), is written as the time curve \(t_s(r)\) which describes the time at which the shell labeled by \(r\) becomes singular and where \(v(t_s(r),r)=0\). In a neighborhood of the center this is given by,

$$\begin{aligned} t_s(r) = t_0 + \chi _2(0)r^2+o(r^3). \end{aligned}$$
(8)

The quantity \(\chi _2(0)\) is the tangent to the singularity curve at the origin, and if it has a positive value then the singularity turns out to be naked, while otherwise it would be hidden in a black hole. When it vanishes, one has to consider the next order in \(r\). Considering collapse of a perfect fluid implies the Misner-Sharp mass \(F\) is in general not conserved, so we have to match the collapsing cloud with an exterior generalized Vaidya spacetime, which is always possible when the pressure of the matter vanishes at the boundary [44, 45].

The overall behaviour of the collapsing cloud is determined by the mass function \(M(r,t)\), the evolution \(v(r,t)\), and the initial velocity profiles \(b(r)\) for the cloud, which are all not independent and are governed by Einstein equations. The special case of homogeneous perfect fluid is obtained when \(M=M(t)\), \(b(r)=k\) and \(v=v(t)\), while the inhomogeneous dust case (TBL) is obtained for \(M=M(r)\) (since \(p_r=p_\theta \), this implies \(p=0\)). Finally the OSD collapse model is obtained when \(M=M_0\), \(b(r)=k\) and \(v=v(t)\).

In the following, for the sake of simplicity, we will consider a constant velocity profile given by \(b(r)=1\), in analogy with the marginally bound collapse in TBL models.

We consider an explicit class of perfect fluid collapse models by introducing a small pressure to the TBL scenario, to solve Einstein equations in a neighborhood of the center. To perturb the TBL model with a small pressure, we must allow in general \(v=v(r,t)\), rather than \(v=v(t)\) only and therefore the simultaneous collapse, which always ends in a black hole, does not happen. We take the mass profile to be

$$\begin{aligned} M=M_0+M_2(v)r^2, \end{aligned}$$
(9)

where \(M_0\) is a constant. The pressure perturbation is small when \(M_0 \gg \mid M_2 \mid \) at all times. We immediately see that setting \(M_2=C\) reduces the model to inhomogeneous dust, and \(M_2=0\) further gives the Oppenheimer-Snyder-Datt homogeneous dust case. To start the collapse from an inhomogeneous dust cloud, triggering the pressure perturbation at a later stage, we take,

$$\begin{aligned} M_2(v)=C+\epsilon (v). \end{aligned}$$
(10)

The initial condition \(M_2(1)=C\) implies \(\epsilon (1)=0\), with \(v\in [0,1]\). For the present choice of the mass profile, the density and pressure, as given by Eqs. (1) and (2) are,

$$\begin{aligned} p=-\frac{\epsilon _{,v}}{v^2}r^2 \; , \; \rho = \rho _{\textit{TBL}}-p+ \frac{5\epsilon -\epsilon _{,v}v}{v^2(v+rv^{\prime })}r^2, \end{aligned}$$
(11)

which are fully determined once the function \(v\) is derived from the Einstein equations.

We now need to determine the behavior of the singularity curve \(t_s(r)\), and hence to evaluate the quantity \(\chi _2(0)\) [43]. To do this, given the choice of \(M\) above, one can integrate (3) in the vicinity of \(r=0\). Once \(\nu \) is obtained as a function of \(M\) and \(v\) we can further integrate (4). The function \(G\) turns out to be dependent on \(M\), \(v\) and the integration function \(b(r)\), which, as said before, is related to the velocity of the collapsing shells. Regularity imposes some constraints that are easily satisfied in this case. Equation (5) then provides the differential equation for \(\dot{v}\) that constitutes the true equation of motion for the system. Integrating it to obtain \(v(r,t)\) thus solves the set of Einstein equations. On the other hand, since \(v\) is monotonically decreasing in time, approaching the singularity \(v=0\), this equation can be inverted to give the solution as \(t(r,v)\), where \(v\) is now treated as a time coordinate. The singularity curve is then given by \(t_s(r)=t(r,0)\), and can be expressed as in Eq. (8).

In the present case, taking \(b(r)=1\), we can evaluate explicitly \(\chi _2(0)\) which turns out to be,

$$\begin{aligned} \chi _2(0)=-\frac{1}{2}I_1-\frac{4}{9M_0^2}I_2, \end{aligned}$$
(12)

with

$$\begin{aligned} I_1&= \int \limits ^1_0(C+Y(v))Z(v)dv, \end{aligned}$$
(13)
$$\begin{aligned} I_2&= \int \limits ^1_0 W(v)Z(v)dv, \end{aligned}$$
(14)

where we have defined the functions \(Y\), \(W\) and \(Z\) as

$$\begin{aligned} Y(v)&= \left(\epsilon +\frac{2}{3}\epsilon _{,v}v\right), \end{aligned}$$
(15)
$$\begin{aligned} W(v)&= \epsilon v (\epsilon +\epsilon _{,v}v), \end{aligned}$$
(16)
$$\begin{aligned} Z(v)&= v\left(M_0+\frac{4}{3}\frac{\epsilon v}{M_0}\right)^{-3/2}. \end{aligned}$$
(17)

We now analyze the condition for the occurrence of naked singularity, namely when \(\chi _2(0)\) is positive, and compare the result with the pressureless case. At first we take \(C=0\), by doing so we are perturbing the OSD model. If we want the sign of the pressure to remain the same during collapse, noting again that \(\epsilon (1)=0\), we see that there are two possibilities for the behaviour of the function \(\epsilon \), namely \(\epsilon >0\), which implies \(\epsilon _{,v}<0\) and positive pressure, and \(\epsilon <0\) giving \(\epsilon _{,v}>0\) and negative pressure. We consider here only the case with positive pressures. Actually, it is easy to see that the negative pressures more easily favor the occurrence of naked singularities, therefore it is more useful and physically interesting to check how positive pressures affect the black hole formation scenario.

To see the sufficient conditions that must be required for \(\chi _2(0)>0\), we analyze the above two integrals separately. Firstly, by evaluating \(Z_{,v}\) we see that if we require,

$$\begin{aligned} \text{ Condition} \text{1a:} \; M_0^2>\max \{2v\left(\frac{1}{3} \epsilon +\epsilon _{,v}v\right), v\in [0,1]\}, \end{aligned}$$
(18)

then \(Z(v)\) will be monotonically increasing. We can therefore apply the mean value theorem to \(I_1\), since \(Y\) is bounded and integrable for \(v\in [0,1]\) and \(Z\) is bounded, integrable, monotonic, increasing and non negative for \(v\in [0,1]\). Therefore

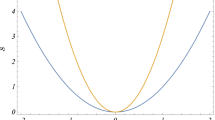
$$\begin{aligned} I_1=Z(1)\int \limits ^1_\eta Y(v)dv \; \text{ for} \text{ some} \; \eta \in [0,1]. \end{aligned}$$

Now we analyze the behaviour of \(Y\), noting that \(Y(0)=\epsilon (0)>0\) while \(Y(1)=\frac{2}{3}\epsilon _{,v}(1)<0\). Therefore, by Weierstrass theorem, we know that there exist \(\bar{v}\in [0,1]\) such that \(Y(\bar{v})=0\) (and \(Y<0\) for \(v>\bar{v}\), see Fig. 1). We shall take \(\epsilon (v)\) in such a way that \(\bar{v}\) is the only zero of \(Y\). Then if \(\eta >\bar{v}\) we have \(I_1<0\) and the first integral in Eq. (12) will be positive. If, on the other hand, \(\eta <\bar{v}\) then we may always choose \(\epsilon \) in such a way that

$$\begin{aligned} \text{ Condition} \text{2:} \; \int \limits _{\eta }^{\bar{v}}Y(v)dv<-\int \limits _{\bar{v}}^1Y(v)dv, \end{aligned}$$
(19)

therefore obtaining again \(I_1<0\) (see Fig. 1).

Fig. 1
figure 1

Illustrative plot of \(\epsilon (v)\) and \(Y(v)\) in the case of naked singularity formation with positive pressures

Full size image

We turn now our attention to the second integral. We see immediately that it is typically negligible with respect to the first one, since it is multiplied by a proportionality factor \(\frac{4}{9M_0^2}\). Nevertheless explicitly requiring it to be small implies that we choose \(M_0\) suitably. We see that to have \(\chi _2>0\) we must have

$$\begin{aligned} I_1+\frac{8}{9M_0^2}I_2<0. \end{aligned}$$

Again applying the mean value theorem we see that

$$\begin{aligned} I_1+\frac{8}{9M_0^2}I_2=Z(1)\int \limits _\eta ^1Y(v)dv+\frac{8}{9M_0^2}W(\omega )Z(1), \end{aligned}$$

for some \(\omega \in [0,1]\). Then \(\chi _2\) will be positive if we choose \(M_0\) such that

$$\begin{aligned} \text{ Condition} \text{1b:} \; M_0^2>-\frac{8}{9} \frac{W(\omega )}{\int _{\eta }^1Y(v)dv} \;. \end{aligned}$$
(20)

If we choose \(\epsilon \) to be at least a cubic function in \(v\) of the type \(\epsilon =av^3+bv^2+cv+d\), it is always possible to choose the four parameters \(a, b, c, d\) in order to fulfill \(\epsilon (1)=0\), \(\epsilon _{,v}\) negative and condition 2 (which implies the values of \(\bar{v}\) and \(\min \{Y(v)\}\)). Then \(M_0\) is chosen in order to satisfy the most stringent between condition 1a and condition 1b.

Note that the ‘steepness’ of \(Y\) close to the singularity is related to the value \(\bar{v}\) for which \(Y=0\). For a cubic function \(\epsilon \) this is related to the value of the parameter \(c\) that determines the behaviour of \(Y\) close to \(v=0\) as well as the value of the pressure close to the singularity. We therefore see that the pressure will be growing much faster close to the singularity in the case where a naked singularity develops as compared to the case where the black hole occurs. While a detailed analysis of the pressure profiles in full generality is beyond the scope of this work and would possibly require some numerical computation tools, we can already gain some useful insights from considerations as above. Again for a cubic profile we see that condition 2 will be satisfied by a suitable choice of the parameter \(c\) (that needs to be negative), and greater the absolute value \(c\) the smaller will be the value of \(\bar{v}\) at which \(Y=0\) and therefore the easier it will be to satisfy condition 2, as said this in turns implies a much faster growth of pressure close to the singularity for the naked singularity case as compared to the case where the black hole occurs.

We therefore see that it is always possible to find a suitable positive pressure perturbation of the OSD collapse model that, however small, will cause the collapse to end in a naked singularity. Furthermore, it can be seen that a perturbation with negative pressure can uncover the OSD black hole in the same manner. We emphasize that the above consideration is only to typically illustrate what is possible in collapse. The above conditions are sufficient for naked singularity formation but not necessary. In fact, the above example and class given indicates that there might well be other classes of perturbations of the OSD model with small perfect fluid pressures, still leading to a naked singularity, and a more detailed discussion will be given elsewhere.

We note that similar considerations also hold for the pressure perturbations of an inhomogeneous dust TBL model. The structure is the same as above, and analogous conclusions hold again, a naked singularity results when we have \(\chi _2>0\). For the sake of clarity we can see that neglecting the second integral in Eq. (12) (which we have shown small compared to the first one), this is certainly the case whenever \(C\) is chosen such that

$$\begin{aligned} \ C<D_1=\min \{Y(v), v\in [0,1]\}<0. \end{aligned}$$
(21)

On the other hand, values of \(C\) such that

$$\begin{aligned} C>D_2=\max \{Y(v), v \in [0,1]\}>0, \end{aligned}$$
(22)

will lead to the formation of a black hole. For \(C\in [D_1,D_2]\) the explicit form of \(\epsilon (v)\) is what determines the sign of \(\chi _2\) (see Fig. 1). Again, by putting \(\epsilon =0\) we recover the TBL inhomogeneous dust model, where positive (negative) \(C\) leads to black hole (naked singularity). It is not difficult to see that a similar reasoning, as given above for the OSD model, applies here. In fact, in this case from Eq. (12) we have

$$\begin{aligned} \chi _2=\chi _{2|C=0}-\frac{1}{2}\int \limits _0^1CZ(v)dv, \end{aligned}$$
(23)

with \(\chi _{2|C=0}\) given by the case \(C=0\) studied above and \(\int ^1_0 CZ(v)dv\) positive whenever \(C>0\), and negative otherwise. Therefore once we evaluate \(\chi _{2|C=0}\) as from the procedure discussed above we easily see that all those values of \(C\) such that \(\frac{1}{2}\int _0^1CZ(v)dv < \chi _{2|C=0}\) will lead to a naked singularity. It is immediate to see that whenever \(\chi _{2|C=0}\) is positive this will include positive values of \(C\) that for the corresponding TBL model were leading to a black hole. For certain choices of \(\epsilon \) we therefore have models where positive values of \(C\) lead to the formation of a naked singularity, even when the TBL collapse went to a black hole. Vice versa, for other choices of \(\epsilon \) we can have models where negative values of \(C\) lead to the formation of a black hole, whereas the corresponding TBL case was leading collapse to a naked singularity.

We thus see that the structure of Einstein equations describing gravitational collapse is indeed very rich and complex. As we see above, both black hole and naked singularity outcomes are possible, in a general and generic manner in the sense described above, evolving from a regular initial data. Of course, in order to be able to check if the black hole that occurs as the endstate of the OSD dust collapse is a generic result, we need an unambiguous definition of genericity, which we do not have today.

In other words, if we call \(\mathcal G \) the set of physically valid initial data for complete collapse of a perfect fluid (thus omitting those configurations that lead to a bounce or to a static regular final configuration), this will be divided into the two possible outcomes of black hole final fate and naked singularity final fate (we denote with \(\mathcal G ^{BH}\) the set of initial data leading to black hole and by \(\mathcal G ^{NS}\) that leading to naked singularity): \(\mathcal G =\mathcal G ^{BH}\bigcup \mathcal G ^{NS}\). Then every point \(I\in \mathcal G \) can be characterized by \(I=\{M(r), p(r), b(r)\}\) (so that the OSD initial configuration is given by \(I_{OSD}=\{M_0, 0, k\}\in \mathcal G ^{BH}\)). We have therefore shown that for every neighborhood \(\mathcal U (I_{OSD})\subset \mathcal G \), however small, there exist (physically valid) pressure profiles with initial data \(I\in \mathcal U \) such that \(I\in \mathcal G ^{NS}\), and similarly for the TBL model. In this sense we say that the dust collapse model leading to a black hole is not ‘stable’ under the introduction of small pressure perturbations. Considering the mass and pressure profiles to be expandable in a neighborhood of the center we can move from the space of functions in which \(M\) and \(p\) are defined to the space of the relevant parameters to determine the outcome of collapse. This can give some further insights in terms of such parameters.

This adds to the known results on the OSD model, namely that the introduction of inhomogeneities or a suitable tangential pressure perturbation can lead to naked singularity formation [3]. In this sense, we have a strong indication that the OSD dust model is ‘unstable’ in that the initial configurations for its endstates lie on the critical surface separating the two possible outcomes of collapse discussed above.

3 Concluding remarks

We have shown that the introduction of a suitable, though general, arbitrarily small, perfect fluid pressure perturbation in the well known OSD collapse model can change the final outcome from a black hole to a naked singularity. The pressure, containing only quadratic terms, is chosen in such a way as to satisfy all usual physical requirements such as energy conditions and regularity of initial data.

We note that our purpose here has not been to examine the effect of a most general pressure perturbation in a pressureless collapse that was terminating into a black hole. Rather, we demonstrated explicitly that there exist classes of small prefect fluid perturbations which when introduced in such a collapse take the same to a naked singularity final state. This is intriguing in that we see that there are collapse evolutions arbitrarily close to the OSD black hole model, which terminate necessarily into a naked singularity. Further, it is clear that every smallest neighborhood of the OSD in the initial data space contains such collapse evolutions.

The model presented above lacks a constitutive relation between the pressure and the energy density. Once such an equation of state is introduced the system becomes closed and we do not have the freedom to chose the matter profile at will. Nevertheless, assuming an equation of state is not likely to change substantially the picture since the above model is arbitrarily close to the well known dust models, and it can be expected to be also arbitrarily close to the solution in the presence an equation of state for a suitable choice of the constitutive relation. Further investigation into perfect fluid collapse with an equation of state is currently in progress. In this case we still expect the initial configurations in the pressureless case to act as a critical surface separating the space of configurations leading to naked singularity from the one leading to black hole.

The important question would be whether naked singularities can actually occur in the observable universe and if so, if they bear signatures in any way different from the black holes. Indeed, if singularities signal a breakdown of classical gravity when very high densities are reached in very small volumes, then these models show that we must consider the possibility that the region of spacetime dominated by quantum gravity can affect outside observers and interact with the rest of the universe.

One should then ask what kind of observational signature these objects bear, if any, and whether such phenomena can possibly be observed. The relevant point is if any measurable amount of energy can come out of such ultra-strong gravity regions and, if so, in what form. We know that non rotating spherically symmetric collapse, settling to a Schwarzschild black hole, cannot emit gravitational waves, still particles and photons can in principle escape the ultra-dense region, thus carrying with them some of the energy [46, 47]. Nevertheless, a more accurate description of the phenomenon must take into account rotation and some constitutive relation for the matter model. At present this is attainable only within the field of numerical relativity and we hope that future research will bring some more light on the nature of the final stages of collapse, since we believe that the next frontier of black hole physics will lie in further investigations on the same.