Shape Effects on Bearing Capacity of Footings on Two-Layered Clay

Abstract

The undrained vertical bearing capacity on a two-layered clay of centrally loaded rigid strip, rectangular and ring footings is studied parametrically with 2D, 3D and axisymmetric finite-element analyses. The shear strength ratio of the two layers and the relative thickness of the uppermost layer with respect to pertinent foundation dimension are the key parameters investigated. In addition, for rectangles and rings the length-to-width (“aspect”) ratio and the ring width to external radius ratio are reported. The results are portrayed in diagrams of bearing capacity and shape modification factors, in the familiar soil mechanics form, along with fitted algebraic expressions to facilitate their numerical use. The failure mechanisms are presented for a number of characteristic cases and are being contrasted with the classical Prandtl failure mechanism, giving additional insight into the mechanics of the problem. The results of the paper can be directly used in practical applications.

1 Introduction

The bearing capacity (B.C.) of a strip foundation resting on the surface of homogeneous soil under undrained conditions is obtained by Prandtl’s classical 2D solution. For the ultimate resistance of square, rectangular and circular footings on homogeneous soil, correction factors are applied to Prandtl’s bearing capacity expression (i.e. Hansen, 1970, Vesic, 1975). A detailed review on the subject has been presented by Poulos et al. (2001). Salgado et al. (2004) presented results of rigorous analyses giving definitive values of shape and depth factors for strip, rectangular and circular footings in homogeneous undrained clay, while Nguyen and Merifield (2012) investigated with finite-elements the shape and depth effects on the undrained bearing capacity in homogeneous soil.

Two-layered soils abound in nature. Bearing capacity of a footing will be affected by the properties of both layers if its dimension is relatively large compared to the thickness of the upper layer. This was also extensively investigated with methods ranging from simplified to rigorous. An early approximate modification of the theoretical B.C. formula for a strip in two-layered clay was presented by Button (1953), who used successfully circular slip surfaces (Puzrin et al. 2010). Empirical modifications were presented by Brown and Meyerhof (1969), who utilised model tests results with circular and strip footings, in which punching failure through the top layer developed. Similar proposals were presented by Meyerhof and Hanna (1978). Numerical solutions for both lower and upper bounds were presented by Chen (1975), Michalowski and Shi (1995), Merifield et al. (1999) and Michalowski (2002) for the undrained bearing capacity for strip footings on a two-layered clay. 2D finite element analyses for strip footings on two-layered soil were presented by Burd and Frydman (1997), Zhu (2004) and Benmebarek et al. (2012).

3D F.E. analyses for rectangular foundations over two-layered clays, were presented by Zhu and Michalowski (2005), Merifield and Nguyen (2006). Salgado et al. (2013) re-examined failure cases of foundations in layered soils by 3D F.E. limit analyses, showing off the practical importance of such problems. According to Salgado (2008), the variation of shear strength with depth affects both the depth and shape of the slip mechanism, so a suitable analysis method is necessary. Moayed et al. (2012) investigated the bearing capacity of ring foundations on two-layered soil (clay and sand), while Lee et al. (2016) presented results for ring foundation on clay layer with linearly increasing undrained shear strength with depth.

In the present paper, a more comprehensive study is reported for rough, rigid footings of various shapes (strip, square, rectangular and ring) on two-layered clays. 2D or 3D F.E. analyses are performed and emphasis is given to evaluation of the results in conjunction with the failure mechanisms. We investigate parametrically two cases depending on the SR = s_u2/s_u1 ratio: SR < 1 and SR > 1, which are separately analyzed. The visual understanding of the unfavourable or favourable effects of second layer is facilitated by modification coefficients of the conventional bearing capacity factors.

2 Problem Definition and F.E. Simulation

For a strip footing on the surface of homogeneous clay, the ultimate bearing pressure can be written in the form:

$${\text{q}}_{\rm {u}} = \frac{{{\text{V}}_{\rm {u}} }}{\text{B}} = {\text{N}}_{\rm {C}} {\text{s}}_{\rm {u}}$$

(1)

where V_u is the ultimate central load, B the width of the strip, s_u the undrained shear strength and N_C = 2 + π, according to Prandtl.

For the case of two-layered undrained clay it is convenient to rewrite Eq. (1), as:

$${\text{q}}_{\rm {u}} = {\text{N}}_{{{\text{C}},1}} {\text{s}}_{{{\text{u}},1}}$$

(2)

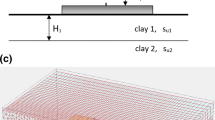
where s_u,1 the undrained shear strength of the upper clay layer and N_C,1 the bearing capacity factor, which depends on the geometry (H₁/B) and the strength ratio SR = s_u,2/s_u,1 (Fig. 1a).

Fig. 1

Geometrical model of rigid foundation on two-layered clays: a strip or rectangular, b ring footing

For footings with different shape (rectangular, square, ring), in case of homogeneous clay, Eq. (1) is modified, as:

$${\text{q}}_{\rm {u}} = \frac{{{\text{V}}_{\rm {u}} }}{\text{A}} = {\text{N}}_{\rm {C}}^{*} {\text{s}}_{\rm {u}}$$

(3)

where A the contact area of the footing and ${\text{N}}_{\rm {C}}^{*}$ the bearing capacity factor, which encompasses the shape effect (shape factor). Accordingly, for two-layered clay, Eq. (2) can be rewritten in the form:

$${\text{q}}_{\rm {u}} = {\text{N}}_{{{\text{C}},1}}^{*} {\text{s}}_{{{\text{u}},1}}$$

(4)

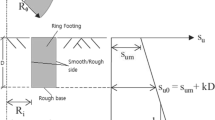
Now, the modified B.C. factor ${\text{N}}_{\rm {C,1}}^{*}$ is a function of H₁/B, SR and the aspect ratio L/B for a rectangular footing or by the ratios H₁/R, SR and b/R₁ for ring foundation, according to Fig. 1b.

The analyses are carried out with the finite element programs Plaxis. The standard boundary conditions for 2D or axisymmetry are applied, where the F.E. program generates in the (x, y) plane (y: vertical direction) full fixity at the base of geometry (u_x = u_y = 0) and roller conditions at the vertical sides (u_x = 0, u_y = free). In the 3D model used, the front and end planes are always fixed in the z-direction (u_z = 0). For the soil modeling in 2D conditions 15-node triangular elements are selected, while in 3D, 15-node wedge elements are used by default. In both cases 12 stress points correspond to each element. The contact surface between foundation and soil is modeled with interface elements, including five pairs of nodes (since the F.E. mesh consists of 15-node elements). The interface elements permit both separation and slip. However, the Mohr–Coulomb criterion is used to distinguish elastic behaviour (where small displacements can occur) and plastic behaviour (where permanent slip may occur), depending on the shear stresses and interface shear strength. Nevertheless, in the present case neither separation nor slip is expected. The overall mesh dimensions in vertical plan view are selected large enough to avoid spurious boundary effects. The thickness of the second layer, H₂, is large enough to have any effect; hence, for stiff over soft clay (SR < 1) the lower boundary is set to depth up to 6B in most cases. On the contrary, for SR > 1 (soft over stiff clay) this depth is selected much smaller, since the failure mechanism is quite shallow. The appropriate refinement of the mesh is provided in the areas of high stress or strain gradient near the vicinity of the footing. A typical 3D mesh is illustrated in Fig. 2 for square footing (case H₁/B = 0.5 and H/B = 3), where the area of the mesh refinement is visible. The soil is modeled as linearly elastic-perfectly plastic material obeying Tresca’s failure law. The geotechnical parameters of clay layers used in the analyses are presented in the Table 1. The strength ratio varied between the values SR = 0.133 − 5, Young’s modulus E = 300 s_u and Poisson’s ratio ν = 0.495. Nevertheless, neither the ratio ν nor the modulus E had any appreciable effect on the resulting ultimate bearing capacity and consequently on the B.C. factors N_C,1 or ${\text{N}}_{\rm {C,1}}^{*}$. The water table was set at the surface. The submerged unit weight of the second layer, γ₂ had no effect on the B.C. factors. Nevertheless, the bearing capacity was slightly influenced by the overburden pressure at the interface of the clay layers, as we found out in several preliminary sensitivity analyses with varying γ₁ values (0 ≤ γ₁ ≤ 20 kN/m³). Indeed, the assumption that the soil can be considered as weightless is accurate only for homogeneous clay under undrained conditions. In this way, Yu et al. (2011) had concluded that in some cases of two-layered clays, the unit weight of the top layer plays a role in the development of the failure mechanism.

Fig. 2

Example of F.E. mesh for square footing (H₁/B = 0.50)

Table 1 Geotechnical parameters of the two clay layers

In order to calculate the equivalent B.C. factors N_C,1 or ${\text{N}}_{\rm {C,1}}^{*}$, the ultimate pressure, according to Eqs. (2) and (4) is resulted by the incremental multipliers procedure: Firstly, the foundation is calculated with initial loading q_o and the gradual increase of the external loading is achieved in only one, next phase, up to failure. From the ultimate loading q_u = (N_C,1 or ${\text{N}}_{\rm {C,1}}^{*}$) s_u1, the corresponding B.C. factors are calculated. At the end of this phase, where the increasing factor reaches the maximum value (corresponding to q_u), the failure mechanism can be observed through the vectors of total displacements in shadings.

3 Shape Factors on a Homogeneous Clay (SR= 1): Comparisons and Verification

The effect of foundation shape is usually expressed through a shape factor s_c = ${\text{N}}_{\rm {C}}^{*}$/N_C, where N_C the B.C. factor for strip and ${\text{N}}_{\rm {C}}^{*}$ for a non-strip footing for homogeneous soil. The theoretical Prandtl’s factor is N_C = 2 + π, while our finite element analysis gave a slightly higher N_C ≈ 5.164. For rectangular footings on undrained clay (φ = 0), the available in the literature s_c relations include:

$${\text{Hansen}}\,(1970 ):\,{\rm {s}}_{\rm {c}} = 1 + 0.2\,\frac{\rm {B}}{\rm {L}}$$

(5a)

$${\text{Vesic}}\,(1975):\,{\rm {s}}_{\rm {c}} = 1 + 0.194\,\frac{\rm {B}}{\rm {L}}$$

(5b)

$${\text{Salgado et al.}}\,(2004):\,{\rm {s}}_{\rm {c}} = 1 + {\rm {C}}_{1}\, \frac{\rm {B}}{\rm {L}}$$

(5c)

where the regression constant (for all cases) is: 0.125 ≤ C₁ ≤ 0.190 for 1 ≥ B/L ≥ 0.2

The values ${\text{N}}_{\rm {C}}^{*}$ from our 3D F.E. analyses for rectangular footings are compared with those from Salgado et al. (2004) and Nguyen and Merifield (2012) in Fig. 3. It is clear that our F.E. results plot in-between the upper and lower bounds of Salgado et al. (2004), while from the comparison with the results after Nguyen and Merifield (2012), the following can be observed:

• 1. In a wide range of B/L, our results are higher. Especially for 1/3 ≤ B/L ≤ 1, the deviation ranges between 1.5 and 3.7%.

• 2. On the contrary, for lower values of the aspect ratio, our results are lower. In the case of strip footing, Nguyen and Merifield (2012) reported N_C = 5.24, while our analyses resulted in N_C = 5.164.

Fig. 3

Comparison of results ${\text{N}}_{\rm {C}}^{*}$ for rectangular footings on homogeneous clay

From the current F.E. analyses, the shape factor can be approximated by the following closely-fitted formula:

$${\text{s}}_{\rm {c}} \approx 1 + 0.2({\text{B/L}})^{0.60}$$

(6)

The deviations of the shape factor according to Eq. (6) from current F.E. results are negligible. However, the deviations from other well-known formulae must be defined:

• 1. The maximum deviation from the linear relationship (5a) is of the order of 3.3%.

• 2. In general, our results indicate shape factors higher than those, according to Nguyen and Merifield (2012). The deviations varied between 2.2 and 5.0%, the higher value corresponding to square.

• 3. Nevertheless, it may be noted that for square footings, our F.E. results gave s_c = 1.195 and Eq. (6) s_c = 1.2, i.e. values almost identical with other well-established formulae.

For ring footings, Fig. 4 presents the F.E. results, where ${\text{N}}_{\rm {C}}^{*}$ increases with increasing the “width” ratio b/R₁, but surprisingly it reaches a peak not at the full circle but at b/R₁ ≈ 0.9, that is for a circle with a small hole in the center. Evidently, the ultimate bearing pressure depends on the failure mechanism, which is strongly affected by the ratio b/R₁. Apart from the main failure surface below the width b₁, a secondary one develops at the region of the ring’s hole. But for very large width (i.e. small hole) 0.9 ≤ b/R₁ ≤ 1, the total ultimate vertical load, V_u = q_u π R²₁ [1 − (1 − b/R₁)²] remains unchanged and thus for increasing the ratio b/R₁ slightly decreases the ultimate pressure q_u along with the B.C. factor ${\text{N}}_{\rm {C}}^{*}$. However, the small difference between the ${\text{N}}_{\rm {C}}^{*}$ factors for b/R₁ = 0.90 and 1 is only 1%, equal to the difference between the corresponding contact areas. For the shape correction factor, the approximate closed formula from regression analysis is derived from:

$${\text{s}}_{\rm {c}} \approx 1 + 0.211({\text{b/R}}_{1} )^{1.25} ,\quad {\text{for}}\;\;0 < {\text{b/R}}_{1 } \le 0.90$$

(7a)

and

$${\text{s}}_{\rm {c}} \approx 1.184,\quad {\text{for}}\;\;0.9 \le {\text{b/R}}_{1} \le 1$$

(7b)

Fig. 4

B.C. factor ${\text{N}}_{\rm {C}}^{*}$ as a function of the normalized width of ring foundation on homogeneous clay

The shape factor for the circular footing (b/R₁ = 1) according to Eq. (7b), is slightly lower than for the square (Fig. 3). In contrast, Nguyen and Merifield (2012) reported slightly higher s_c value for circular footing and correspondingly higher values for bearing capacity factor, ${\text{N}}_{\rm {C}}^{*}$.

4 Stiff Over Soft Clay Layer

4.1 Strip Footing

This profile is of interest in geotechnical practice, where soft or medium clay underlays a stiff clayey “crust”. From extended parametric analyses, when SR = s_u,2/s_u,1 < 1, three failure mechanisms have been observed:

• 1. A failure mechanism approaching Prandtl’s for relatively high values of SR (approaching homogeneous soil) and/or high values of normalized thickness (type I).

• 2. Intermediate type (II): The failure planes of the wedge, according to Prandtl, become gradually curved, approaching the vertical direction. This mechanism can be characterized as partial punching, taking place for various combinations of the normalized values H₁/B and SR.

• 3. A punching failure, according to Meyerhof and Hanna (1978), which is observed for relatively low values of H₁/B and/or low SR values (type III).

Quantitative information regarding the bound values of H₁/B and SR for each mechanism is given in Fig. 7. Figure 5 illustrates these three mechanisms for strip footings in two-clay layers with H₁/B = 0.75. Case (a) refers to a high strength contrast, SR = 0.133, where a punching failure (type III) is clearly developed, despite the rather substantial crust thickness. The failure surface extends to a depth of about 2.5 B, much higher than the theoretical depth of influence for homogeneous clay (≈ 0.7 B). Reducing the strength contrast, i.e. increasing SR, leads to modification of the failure mechanism: in case of SR = 0.40 (b), the mechanism is of type II and in case of SR = 0.80 (c), it is essentially type I. From the analyses, an almost linear relationship between N_C,1 and H₁/B is noted for a wide range of SR values. To better visualize this linear relation and the effect of the lower weaker layer on the bearing capacity, we plot the ratio λ_Ν = N_C,1/N_C as a function of the normalized thickness in Fig. 6. For the linear part of diagrams of Fig. 6, we can express the ultimate pressure and the B.C. factor, as:

$${\text{q}}_{\rm {u}} = 2{\text{s}}_{{{\text{u}},1}} \frac{{{\text{H}}_{1} }}{\text{B}}\uplambda_{\rm {H}} + {\text{N}}_{\rm {C}} {\text{s}}_{{{\text{u}},2 }}\uplambda_{\rm {B}} = {\text{N}}_{{{\text{C}},1}} {\text{s}}_{{{\text{u}},1}}$$

(8a)

and

$${\text{N}}_{{{\text{C}},1}} = 2\frac{{{\text{H}}_{1} }}{\text{B}}\uplambda_{\rm {H}} + {\text{N}}_{\rm {C}} ({\text{SR}})\uplambda_{\rm {B}}$$

(8b)

where N_C = 2 + π for homogeneous clay and λ_Η, λ_Β are (approximately) functions of SR only, independent of the normalized thickness. It is evident that Eq. (8a) reflects the contribution of shear strength of the two clay layers on the bearing capacity, in case of punching failure. The correction coefficients λ_Η and λ_Β are given by the following algebraic expressions, best fitted the analyses results.

$$\uplambda_{\rm {H}} = [0.810 + 1.708({\text{SR}}) - 2.518({\text{SR}})^{2} ]$$

(9a)

and

$$\uplambda_{\rm {B}} = [1 + 0.17 (1{-}{\text{SR)}}^{2} ]$$

(9b)

Fig. 5

Strip footing on two-clay stratum, for H₁/B = 0.75: a SR = 0.133, b SR = 0.40, c SR = 0.80

Fig. 6

Strip footing: Marginal combinations of H₁/B − SR for linear relationship between λ_Ν and Η₁/Β

Note that the correction factor λ_Η is almost equal to 1 for SR ≤ 0.6, but it rapidly drops for higher values of the strength ratio. In contrast, the factor λ_Β is always slightly higher of 1. For the special case of homogeneous soil (s_u,2 = s_u,1), it is obvious that λ_Η = 0 and λ_Β = 1, since the Prandtl’s failure mechanism is developed. The limit curve illustrating the marginal correlation between H₁/B, SR and λ_Ν, for which Eqs. (8b), (9a) and (9b) are valid (punching or even partial failure) is also presented in Fig. 6. This marginal relationship between H₁/B and SR can be calculated by the following expression, valid for SR < 0.8:

$$( {\text{H}}_{1} / {\text{B)}} = 0.537({\text{SR}})^{{{-}0.578}}$$

(10)

The lower bound of H₁/B and SR, for which λ_Ν = 1, is presented in Fig. 7. Just below the curve, the weaker clay marginally influences the bearing capacity. Evidently, for higher values the modification coefficient λ_Ν is equal to 1, while below the curve λ_Ν < 1, generally. In Fig. 7 the combinations of H₁/B and SR are also presented for failure type I (lower bound) and type III (upper bound). The intermediate zone corresponds to failure type II. It can be shown that failure type I is possible for SR > 0.75, independently of normalized thickness. It is also obvious from Fig. 7, that punching failure (III) is possible only for SR < 0.4 and H₁/B < 1.25 in the range of strength ratio investigated (SR ≥ 0.133). Merifield and Nguyen (2006) suggested that full punching shear failure develops for low strength ratios SR < 0.33 and if H₁/B ≤ 0.75, while general shear failure is possible for H₁/B ≥ 1, in all SR cases. These trends seem similar with those of Fig. 7, although in the present paper more detailed results are illustrated. From the comparative presentation of the factor N_C,1 in Fig. 8, it is evident that the current F.E. analyses are in good agreement with most of the previously proposed, slightly higher than Benmebarek’s et al. (2012) and lower than the upper bound of Merifield et al. (1999). The results after Meyerhof and Hanna (1978) deviate somewhat for SR ≥ 0.6.

Fig. 7

Strip footing, failure types depending on the combinations H₁/B, SR

Fig. 8

Comparison of N_C,1 values for centrally loaded strip footing (Case SR < 1)

4.2 Square and Rectangular Footings

The failure mechanisms are similar to those for strips (types I, II, III). However, the comparison of failure surfaces for strips or square footings is only qualitative, since in 3D conditions only the cross-section of these surfaces by the vertical plane of symmetry is conveniently presented and interpreted. Figure 9 illustrates these three mechanisms for a square footing in two clay layers with H₁/B = 0.50. Case (a) refers to low strength ratio SR = 0.133, where a punching failure develops, while a partial punching is shown in case (b) with SR = 0.40. For SR = 0.80, case (c), the mechanism approaches Prandtl’s, type I. For square footings, the results of 3D F.E. analyses are summarized in Fig. 10, in which the bearing capacity factor ${\text{N}}_{\rm {C,1}}^{*}$ is plotted versus the strength ratio for six values of the normalized crust thickness. Note that ${\text{N}}_{\rm {C,1}}^{*}$ values quickly approach the ${\text{N}}_{\rm {C}}^{*}$ values of the homogeneous half space, for H₁/B ≥ 0.50 and SR ≥ 0.50. From the comparative diagrams of Fig. 11, it is shown that our results for square footings approach well those of Merifield and Nguyen (2006), being about 1–5% higher. Note that the influence of the in situ stress field was not taken into account by Merifield and Nguyen (2006). As already mentioned, for SR < 1, of weightless upper layer might result into slightly lower values of bearing capacity.

Fig. 9

Square footing on two-clay layers, for H₁/B = 0.50: a SR = 0.133, b SR = 0.40, c SR = 0.80

Fig. 10

Square footing: Effect of H₁/B and SR on the factor ${\text{N}}_{\rm {C,1}}^{*}$

Fig. 11

Comparison of N_C,1 values for centrally loaded square footing (Case SR < 1)

To further visualize the effect of the lower weaker clay layer, the modification coefficients (λ_N = N_C,1/N_C and $\uplambda_{\rm {N}}^{*}$ = ${\text{N}}_{\rm {C,1}}^{*}$/${\text{N}}_{\rm {C}}^{*}$) are presented in Fig. 12 for strip and square footings respectively. Furthermore, for three cases of H₁/B presented in Fig. 12,it is clear that $\uplambda_{\rm {N}}^{*}$ > λ_N, that is for a square foundation the unfavourable effect of lower clay is smaller than for a strip. It can be also observed that with increasing normalized thickness of the upper layer, the contrast between square and strip, expressed with the ratio $\uplambda_{\rm {N}}^{*}$/λ_N (> 1) also increases, reaching the value of 1.70 for low strength ratios and H₁/B = 0.75. From a practical point of view, for a square footing and normalized thickness H₁/B ≥ 0.50, it is concluded that the lower weaker clay layer may be ignored, if SR ≥ 2/3. On the contrary, for strip footings, the effects of the second layer are more significant, while even in case of H₁/B ≥ 0.75, the weaker lower layer must be taken into consideration, regardless of a relatively high strength ratio. Comparison of the modification coefficient for strip λ_Ν, with $\uplambda_{\rm {N}}^{*}$ for three cases of rectangular footings, is presented in Table 2.

Fig. 12

Comparison of modification coefficients for strip and square rigid footings (SR < 1)

Table 2 Modification coefficients λ_Ν, $\uplambda_{\rm {N}}^{*}$ for rectangular footings

The influence of shape of a rectangular (B, L) footing on the bearing capacity can be also investigated through the shape factor s_c = ${\text{N}}_{\rm {C,1}}^{*}$/N_C,1. The variation of s_c with strength ratio SR is plotted in Fig. 13 for two values of H₁/B and three aspect ratios of rectangular footings (L/B = 1, 1.5, 3.0). Evidently, for L/B = ∞, s_c = 1 in any case. Invariably, the shape factor increases when the ratio SR decreases, with the square factor tending to 1.2 as SR tends to 1 (homogeneous soil). Evidently, for strip foundations, the influence of the lower weaker layer is more important. On the contrary, when the aspect ratio L/B decreases, the strength of the upper layer has the dominant effect on the bearing capacity. Note that for H₁/B = 0.50 the shape factor for square footing and the lowest examined ratio SR = 0.133 (i.e. s_u,1 = 7.5 s_u,2) is s_c ≈ 2.0, while for homogeneous soil s_c ≈ 1.2.

Fig. 13

Shape factor s_c for rectangular footings, as function of the strength ratio

4.3 Ring Footings

For ring foundations, the analyses are carried out under axisymmetric conditions, where the central axis of the ring is set at the left vertical boundary of the mesh. Now, three parameters influence the bearing capacity (Fig. 1b): the strength ratio SR, the normalized thickness of the upper layer, H₁/2R₁ = H₁/B and the geometry of ring, which is defined by the normalized width, b/R₁. The three types of failure mechanism, slightly modified, are developed (depending on the above parameters). An example is given in Fig. 14 for constant H₁/B = 0.25 (or H₁/R₁ = 0.50), SR = 0.25 and varying normalized width of the ring. For the higher value b/R₁ = 0.75 (case a), punching type failure is observed, while for the lower b/R₁ = 0.25 (case c), the failure mode in the radial plane is similar to Prandtl’s (type I), although it is almost imperceptibly asymmetric. Evidently, as b/R₁ tends to 0, the failure mechanism on the radial plane is almost the same with a strip footing (Prandlt’s mechanism). At the other extreme, as b/R₁ increases approaching 1, the footing approaches the circle and the failure mechanism is of scoop type encompassing the whole foundation (similar to Fig. 14a). The B.C. factor ${\text{N}}_{\rm {C,1}}^{*}$ is given in Fig. 15 for two values of H₁/R₁, 0.25 and 0.5 and five values of b/R₁. For low SR values, ${\text{N}}_{\rm {C,1}}^{*}$ increases with decreasing b/R₁. On the contrary, for high strength ratios (i.e. SR ≥ 0.80), the higher values of ${\text{N}}_{\rm {C,1}}^{*}$ correspond to circle. Comparison of the modification coefficients $\uplambda_{\rm {N}}^{*}$ for five values of b/R₁ is presented in Table 3. Obviously, the shape effects of a ring foundation can be considered by two ways: (a) For constant H₁/R₁ (i.e. constant H₁/B, where the diameter B = 2R₁) and varying normalized width b/R₁. (b) For constant H₁/b and varying radius R₁ (or varying H₁/B). The shape factor is calculated, as s_c = ${\text{N}}_{\rm {C,1}}^{*}$/N_C,1, where N_C,1 corresponds to strip (B = 2R₁). It is evident that for decreasing b/R₁, the factor s_c = ${\text{N}}_{\rm {C,1}}^{*}$/N_C,1 increases, as illustrated in Fig. 16, where for low SR = 0.133 reaches values as high as 3. In case of constant H₁/b, both the varying ratios H₁/R and b/R₁ affect the bearing capacity. Now the higher values of s_c correspond to full circle, as indicated in Fig. 17, while for low values b/R₁, the behaviour of the ring approaches this of a strip.

Fig. 14

Deformation pattern at failure for ring footings: H₁/R₁ = 0.50 and SR = 0.25: a b/R₁ = 0.75, b b/R₁ = 0.50, c b/R₁ = 0.25

Fig. 15

Effect of the normalized width and SR on the B.C. factor for ring foundations (SR < 1)

Table 3 Modification coefficient $\uplambda_{\rm {N}}^{*}$ for ring footings

Fig. 16

Shape factors for ring with constant H₁/R₁ = 0.25 and varying width b

Fig. 17

Shape factors for ring with constant H₁/b = 0.50 and varying radius R₁

5 Soft Over Stiff Clay Layer

5.1 Strip Footing

Two basic types of failure are ascertained in our parametric analyses:

• (a) The failure surface is extended into the lower, stiff or very stiff clay layer (type IV). This kind of failure is observed for low values of the normalized thickness H₁/B and/or for strength ratios only slightly higher than the unity.

• (b) The failure surface is restricted into the top layer only (type V) for either high values of H₁/B or high values of SR.

Figure 18 illustrates these two mechanisms for H₁/B = 0.25 and strength ratios (a) SR = 1.25 and (b) SR = 2.5. In case (a), the failure mode is similar to Prandtl’s, but secondary surfaces are observed at the edges of the strip, into the upper weaker clay layer (type IV). In case (b), the failure is clearly restricted to the upper layer (type V). The variation of the bearing capacity factor N_C,1, according to Eq. (2), is presented in Fig. 19, as function of the strength ratio SR for three representative values of the normalized thickness, H₁/B. Therefore, the following conclusions may be drawn:

• 1. The factor N_C,1 rapidly increases with increasing strength ratio, for SR slightly higher than the unity, reaching its maximum value for a critical value (SR_cr), no particularly high. The failure type IV is observed for 1 ≤ SR ≤ SR_cr. Evidently, the B.C. factor is stabilized to its max N_C,1 value for higher values than the critical, since the failure mechanism is restricted into the upper layer (type V).

• 2. For lower values of normalized thickness, higher values of the B.C. factor max N_C,1 are observed. Consequently, the maximum value of modification coefficient λ_Ν = N_C,1/N_C decreases with increasing H₁/B. For example, for H₁/B = 0.4 (Fig. 19) maxλ_Ν ≈ 1.07 (relatively low). It may be concluded from the analyses that the favourable effect of the lower strong clay layer can be ignored for H₁/B ≥ 0.5 independently of the strength ratio. The maximum values of the modification coefficient, maxλ_Ν can be calculated by a closed form equation for strip, best fitting the F.E. results:

  $$\max\uplambda_{\rm {N}} = \hbox{max} {\text{N}}_{{{\text{C}},1}} / {\text{N}}_{\rm {C}} = 0.092\frac{\text{B}}{{{\text{H}}_{1} }} + 0.869$$

  (11)

Fig. 18

Deformation pattern at failure for strip footing on soft over stiff clay, H₁/B = 0.25: Failure mechanisms: a SR = 1.25, Type IV, b SR = 2.5, Type V

Fig. 19

Effect of H₁/B and SR on the B.C. factor for strip footing on soft over stiff clay layer

This equation is valid for H₁/B < 0.7, since for H₁/B ≥ 0.7, max N_C,1 = N_C ≈ 5.164, so the lower clay has no effect on the bearing capacity, regardless of the strength ratio SR. The critical strength ratio, (SR)_cr, for given values of the normalized thickness, H₁/B, is of peculiar interest. From regression analysis of the F.E. analyses the following relationship results, which is also valid for H₁/B < 0.7:

$$({\text{SR}})_{\rm {cr}} = 0.176\frac{\text{B}}{{{\text{H}}_{1} }} + 0.752$$

(12)

5.2 Square Footings

The failure mechanisms in the special case of square footings, are similar to those for strips (types IV and V). For either high values of H₁/B and/or high SR, the failure surfaces are developed in the upper layer, otherwise they extended into the second, stronger one. However, a direct comparison of the failure mechanism either in plane strain (strip) or in 3D conditions (square) is only qualitative. In the latter case, the only one representative cross-section of the failure surface by the central vertical plane is considered.

The bearing capacity factor ${\text{N}}_{\rm {C,1}}^{*}$, according to Eq. (4) from the 3D F.E. analyses, is presented in Fig. 20 versus SR for various values of H₁/B. The trends are similar with those observed in Fig. 19 for strip footings. Interestingly, for H₁/B ≥ 0.50, max ${\text{N}}_{\rm {C,1}}^{*}$ = ${\text{N}}_{\rm {C}}^{*}$ ≈ 6.2, thus the underlying stronger clay layer has no favourable effect on the bearing capacity. In any case, the increase of B.C. due to the second layer, in comparison with the homogeneous clays, is an interesting issue, which is investigated through the corresponding modification coefficient max$\uplambda_{\rm {N}}^{*}$ = max ${\text{N}}_{\rm {C,1}}^{*}$/${\text{N}}_{\rm {C}}^{*}$. Performing the regression analysis, the following formula is resulted:

$$\max\uplambda_{\rm {N}}^{*} = 0.0054\left( {{\text{B/H}}_{1} } \right)^{2} {-}0.0049\left( {{\text{B/H}}_{1} } \right) + 0.9882$$

(13)

Fig. 20

B.C. factor for square footings as a function of H₁/B and SR

The equation is valid for H₁/B ≤ 0.5, since for H₁/B ≥ 0.5, ${\text{N}}_{\rm {C}}^{*}$₁ = ${\text{N}}_{\rm {C}}^{*}$. Figure 21 compares the maximum values of the modification coefficients λ_Ν = N_C,1/N_C (strip) and λ*_Ν = ${\text{N}}_{\rm {C,1}}^{*}$/${\text{N}}_{\rm {C}}^{*}$ (square and circle), which are plotted versus H₁/B. These values are of course independent of SR, as Figs. 19 and 20 show. We note that the strip footing «reaches deeper» than the square and hence more affected by H₁/B; and that for H₁ > 0.5 B, the ultimate capacity of square is not influenced by SR.

Fig. 21

Soft over stiff clay layer: Comparison of maximum modification coefficients for strip, square and circle

5.3 Ring Footings

The B.C. factor ${\text{N}}_{\rm {C,1}}^{*}$ for the special case of a full circular footing (b/R₁ = 1) is presented in Fig. 22 for various values of the strength ratio and the normalized thickness H₁/B (diameter, B = 2R₁,). It seems that for H₁/B ≥ 0.25 the lower clay layer has only a little impact on the bearing capacity, in this case with the circular footing. For example, if H₁/B ≥ 0.40, the factor ${\text{N}}_{\rm {C,1}}^{*}$ is constant, irrespectively of the strength ratio. The maximum values of the modification coefficient, max$\uplambda_{\rm {N}}^{*}$ are already presented in Fig. 21 in comparison with the results for strip and square footings. It is clear that the favourable effects of the second hard layer on the B.C. are lower in the case of circle.

Fig. 22

B.C. factor as function of the ratio SR for circle (B = 2R₁)

In the general case of ring footings, the failure mechanisms depend on both the ratios H₁/R₁ and b₁/R₁, or alternatively on the normalized thickness H₁/b₁ and b/R₁. For relatively low values of H₁/R₁ and high b/R₁, a failure mechanism similar to type IV develops, while for higher values of H₁/R₁ and/or lower b/R₁, the type V takes place. Figure 23 depicts the relationship between ${\text{N}}_{\rm {C,1}}^{*}$ and SR for various values b/R₁, in the case of low value H₁/R₁ = 0.15. The low values of b/R₁ correspond to high values H₁/b, thus the lower, stronger clay layer has no influence on the bearing capacity and consequently it can be ignored. By contrast, for higher values b/R₁, the ratio H₁/b is low enough, and now the second layer has a significant effect on the bearing capacity. For the full circle (b/R₁ = 1), the B.C. factor reaches the max ${\text{N}}_{\rm {C,1}}^{*}$ value for strength ratios SR ≥ 2.40 in this case of low H₁/B, the critical value (SR)_cr is quite lower for lower normalized widths (b/R₁) of a ring footing.

Fig. 23

Effect of b/R₁ and SR on the B.C. factor ${\text{N}}_{\rm {C,1}}^{*}$ for ring foundation

6 Conclusions

• (a) The F.E. results were firstly presented in terms of B.C. factors N_C,1 or ${\text{N}}_{\rm {C,1}}^{*}$ (strip or other footing shape). The visual understanding of the effects of second layer (either weaker or stronger) was facilitated by the modification coefficients λ_Ν or $\uplambda_{\rm {N}}^{*}$.

• (b) In the most interesting case of upper stiff crust (SR < 1) and strip footings, three types of failure are ascertained. Bound values (combinations H₁/B and SR) are presented for each of them (i.e. punching failure, type III seems possible if SR < 0.4 and H₁/B < 1.25). For a wide range of parameters, the B.C. factor N_C,1 is linearly related with H₁/B. For rectangular or ring footings the failure mechanisms are modified accordingly. Modification coefficients λ_N, $\uplambda_{\rm {N}}^{*}$ and shape factors as well, are presented and discussed. In the case of ring footings, $\uplambda_{\rm {N}}^{*}$ and s_c are strongly depended on b/R₁ for given H₁/B.

• (c) For stiffer lower clay (SR > 1) and strip footing, two additional types of failure are noted, while the modification coefficient (λ_N > 1) rapidly increases with increasing SR, reaching the value max λ_N. The bound values H₁/B, for which the favourable effect of the second layer becomes insignificant independently from SR, are estimated (i.e. H₁/B ≥ 0.5) or even lower for ring or square footings.

• (d) Closed form analytical expressions, best fitting the F.E. results, are proposed in several cases of strip and square footings, either for SR < 1 or SR > 1.