1 Introduction

In general, deformation of surrounding rocks of tunnels is caused by the comprehensive effects of excavation disturbance of tunnels and stress release of rock masses. After excavating tunnels, stress of rock masses near a chamber is expected to exceed elastic limit of rock masses, thus entering into plastic deformation state, while elastic deformation occurs to distant rock masses. Therefore, elasto-plastic analysis on surrounding rocks of tunnels, especially soft rocks, is an important basis for judging stability of tunnels and designing supports.

In elasto-plastic analysis of surrounding rocks of tunnels, M–C criterion (Hoek 1990; Carranza 2003; Sofianos and Nomikos 2006) and Hoek–Brown criterion (Hoek et al. 2002; Pan et al. 2011) are generally used and the problems are simplified and solved as plane strain problems. Based on this, research results of influences of intermediate principal stresses on elasto-plasticity are obtained (Peng et al. 2014), and some scholars utilize Drucker–Prager criterion to calculate elasto-plastic solution of circular tunnels (Zhang et al. 2013).

As for tunnels in soft rocks, deformation of surrounding rocks after excavating tunnels constantly increases with time due to the influences of creep effects. However, whether in the design of tunnel structure or in actual construction, the unfavorable influences induced by creep effects of soft rocks are rarely considered (Küpper and Wurm 2015; Briffaut et al. 2016; Shrestha and Panthi 2015). Considering this, it is urgent to analyze creep effects of tunnels in soft rocks and study the influences of creep effects on stress, strain and displacement of surrounding rocks. By using unsteady Nishihara model and combining Lade–Duncan criterion, this research investigated creep timeliness of surrounding rocks of a tunnel.

2 Modified Nishihara Model

2.1 Nishihara Model

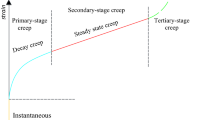
Nishihara model, as a constitutive model for studying creep characteristics of soft rocks, is used to describe the relationships of stress and strain of rocks with time. Similar to most creep models, it is formed by combining the basic models. The basic principle is that the model is a combination of basic elastic, plastic and viscous elements according to specific creep properties of rocks (Liu 1994; Лияцнцoф 1956).

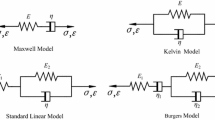
Nishihara model can well reflect the elastic, visco-elastic and plastic characteristics of rocks and is widely applied in studying creep characteristics of surrounding rocks of tunnels. This model is combined by Hookean body and visco-plastic body in basic elements, as shown in Fig. 1.

Fig. 1
figure 1

Nishihara constitutive model

Full size image

The basic equation of Nishihara model is:

When σ ≤ σf,

$$\frac{{\eta_{1} }}{{E_{1} }}\dot{\sigma } + \left( {1 + \frac{{E_{2} }}{{E_{1} }}} \right)\sigma = \eta_{1} \dot{\varepsilon } + E_{2} \varepsilon$$
(1)

While σ > σf,

$$\ddot{\sigma } + \left( {\frac{{E_{1} }}{{\eta_{1} }} + \frac{{E_{2} }}{{\eta_{1} }} + \frac{{E_{1} }}{{\eta_{2} }}} \right)\dot{\sigma } + \frac{{E_{1} E_{2} }}{{\eta_{1} \eta_{2} }}\left( {\sigma - \sigma_{f} } \right) = \frac{{E_{1} E_{2} }}{{\eta_{1} }}\dot{\varepsilon } + E_{1} \ddot{\varepsilon }$$
(2)

where η1 and η2 represent the coefficients of viscosity. E1 and E2 indicate the elastic modulus. \(\sigma\), \(\dot{\sigma }\) and \(\ddot{\sigma }\) denote stress as well as the first-order and second-order derivations of stress on time t, respectively. \(\varepsilon\), \(\dot{\varepsilon }\) and \(\ddot{\varepsilon }\) stand for strain as well as the first-order and second-order differential of strain on time t, respectively. Furthermore, σf stands for the ultimate frictional resistance of St. Venant body.

2.2 Unsteady Viscous Body

In order to study the unsteadiness of the model, the unsteady viscous body is introduced. The power exponential empirical equation can be used to research non-linear visco-elastic problems (Sun 1999).

$$\dot{\varepsilon } = A\sigma^{n} t^{m}$$
(3)

where \(\dot{\varepsilon }\), σ and t indicate the creep strain rate, the equivalent stress and the creep time, respectively. A, n and m represent the fitted creep parameters.

The unsteady viscous body of non-linear visco-elastic creep is characterized and the expression of coefficient of viscosity is (Xiong et al. 2010):

$$\eta (\sigma ,t) = \eta_{0} \left( {\frac{\sigma }{{\sigma_{0} }}} \right)^{n} \left( {\frac{t}{{t_{0} }}} \right)^{m}$$
(4)

where η0 represents the coefficient of viscosity. σ0 indicates the reference value of equivalent stress and values 1. t0 stands for the reference time and is 1.

2.3 Modified Unsteady Nishihara Model

Nishihara model is modified by replacing steady viscous body with unsteady viscous body, as demonstrated in Fig. 2. Owing to this model considers non-linear visco-elastic creep properties, it is known as unsteady Nishihara model.

Fig. 2
figure 2

Unsteady Nishihara constitutive model

Full size image

Therefore, by utilizing the unsteady Nishihara constitutive model, η1 in Formulas (1) and (2) is modified as:

$$\eta_{1} (\sigma ,t) = \eta_{0} \left( {\frac{\sigma }{{\sigma_{0} }}} \right)^{n} \left( {\frac{t}{{t_{0} }}} \right)^{m}.$$
(5)

3 Mechanical Calculation Model of Surrounding Rocks of Tunnels

The circular tunnel model is used to simplify the analysis. The following assumptions including isotropic assumption, continuity assumption and small deformation condition are put forward for analysis based on mechanics of rock masses.

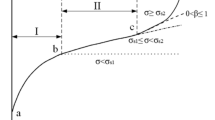
In accordance with elasto-plastic mechanics theory and analysis and calculation theories of surrounding rocks, crack zone, plastic zone and visco-elastic zone are distributed in the analysis model of tunnels from interior to exterior under the condition of creep effects, as displayed in Fig. 3. The radius of excavated tunnels is R1. R1–R2 and R2–R3 are the ranges of crack zone and plastic zone, while elastic deformation zone should be from R2 to infinity in theory. The radial stresses are represented by p1, p2 and p3. In-situ stress is p0 = γh, where γ and h represent the gravity of rock masses and buried-depth of tunnels separately.

Fig. 3
figure 3

Calculation model for surrounding rocks of tunnels

Full size image

4 Visco-Elastic–Plastic Solutions for Surrounding Rocks

4.1 Mechanics Research of Crack Zone

Owing to only micro-cracks can occur to rock masses in this zone, only radial stress can be transferred, while tangent stress does not exist. Therefore, the equilibrium differential equation of this zone is:

$$\frac{{d\sigma_{r} }}{dr} + \frac{{\sigma_{r} }}{r} = 0$$
(6)

According to boundary conditions, when r = R1, then σr = p1; while r = R2, then σr = p2. The integral of Formula (3) is:

$$p_{2} = \frac{{R_{1} }}{{R_{2} }}p_{1}$$
(7)

According to rich blasting experience of tunnel engineering (Tu et al. 2006), the formula of outer diameter R2 in crack zone is obtained using analog method.

$$R_{2} = R_{1} + 1.23.$$
(8)

4.2 Mechanics Researches in Plastic Zone

In mechanics researches of surrounding rocks in plastic zone, the calculation formulas of stress and radius in plastic zone can be obtained by using Lade–Duncan criterion according to literature (Rao et al. 2013).

$$p_{3} = \frac{{2p_{0} - \left( {\eta - 1} \right)c\cot \varphi }}{1 + \eta }$$
(9)
$$R_{3} = R_{2} \left[ {\frac{{2\left( {p_{0} + c\cot \varphi } \right)}}{{\left( {1 + \eta } \right)\left( {p_{2} + c\cot \varphi } \right)}}} \right]^{{\frac{1}{\eta - 1}}}$$
(10)

where \(\eta = \frac{1}{4}\left[ {\sqrt[3]{k} - 1 + \sqrt {(\sqrt[3]{k} - 1)^{2} - 4} } \right]\), \(k = \frac{{(3 - \sin \varphi )^{3} }}{{(1 + \sin \varphi )(1 - \sin \varphi )^{2} }}\).

4.3 Mechanics Researches in Visco-Elastic Zone

The stress on any one micro element is analyzed to obtain static equilibrium equation and geometric equation of visco-elastic zone under axial symmetry.

Equilibrium equation is:

$$\frac{{d\sigma_{r} }}{dr} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = 0$$
(11)

Geometric equation is:

$$\left\{ \begin{aligned} \varepsilon_{r} = \frac{du}{dr} \hfill \\ \varepsilon_{\theta } = \frac{u}{r} \hfill \\ \end{aligned} \right.$$
(12)

Based on elastic mechanics theory, the expression of displacement in visco-elastic zone is shown as:

$$u_{r} = - \frac{1 + \mu }{E}\frac{{R_{3}^{2} }}{r}\left( {p_{3} - p_{0} } \right)$$
(13)

where ur, p0, μ and E represent the displacement in visco-elastic zone (m), the in situ stress (N), the Poisson’s ratio and elastic modulus (N/mm2), respectively. The other parameters are similar to those in the above formulas.

Based on corresponding principles, the displacement solutions under visco-elasticity are obtained by utilizing Laplace transform.

$$\bar{u}_{r} (s) = - \frac{1 + \mu }{G(s)}\frac{{R_{3}^{2} }}{r}\left( {p_{3} - p_{0} } \right)$$
(14)

where G(s) = Q(s)/P(s).

When σ > σf,

$$P(s) = \frac{{E_{1} E_{2} }}{{\eta_{1} (p_{3} ,t) \cdot \eta_{2} }} + s^{2} + \left( {\frac{{E_{1} }}{{\eta_{1} (p_{3} ,t)}} + \frac{{E_{2} }}{{\eta_{1} (p_{3} ,t)}} + \frac{{E_{1} }}{{\eta_{2} }}} \right)s$$
(15)
$$Q(s) = \frac{{E_{1} E_{2} }}{{\eta_{1} (p_{3} ,t)}}s + E_{1} s^{2}$$
(16)

The following formula is obtained by combining with above two formulas.

$$G(s) = \frac{Q(s)}{P(s)} = \frac{{\frac{{E_{1} E_{2} }}{{\eta_{1} (p_{3} ,t)}}s + E_{1} s^{2} }}{{\frac{{E_{1} E_{2} }}{{\eta_{1} (p_{3} ,t) \cdot \eta_{2} }} + s^{2} + \left( {\frac{{E_{1} }}{{\eta_{1} (p_{3} ,t)}} + \frac{{E_{2} }}{{\eta_{1} (p_{3} ,t)}} + \frac{{E_{1} }}{{\eta_{2} }}} \right)s}}$$
(17)

Formula (16) is substituted into Formula (13) to conduct Laplace transform. By looking up the table of Laplace transform and sorting out, the displacement solutions in visco-elastic zone are obtained.

$$u_{r} (t) = - \frac{{\left( {1 + \mu } \right)R_{3}^{2} }}{{E_{1} r}}\left( {p_{3} - p_{0} } \right)F_{1} (t)$$
(18)

where \(F_{1} (t) = \left\{ {1 + \frac{{E_{1} }}{{\eta_{2} }} + \frac{{E_{1} }}{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} t}}{{\eta_{1} (p_{3} ,t)}}} \right)} \right]} \right\}\).

While σ ≤ σf, similarly, the stress of surrounding rocks of tunnels does not reach the ultimate stress, that is, before plastic zone appears, the displacement expression of visco-elastic zone is:

$$u_{r} (t) = - \frac{{\left( {1 + \mu } \right)R_{3}^{2} }}{{E_{1} r}}\left( {p_{3} - p_{0} } \right)F_{2} (t)$$
(19)

where \(F_{2} (t) = 1 + \frac{{E_{1} }}{{\eta_{1} (p_{3} ,t)}}\exp \left( {\frac{{E_{2} t}}{{\eta_{1} (p_{3} ,t)}}} \right)\).

4.4 Visco-Elastic–Plastic Solutions for Surrounding Rocks

The small deformation condition is taken into account in analyzing deformation of surrounding rocks of tunnels. Therefore, the volume of surrounding rocks is unchanged. According to geometric equation and Formula (3), the deformation of surrounding rocks and its integral can be obtained.

$$\Delta u(t) = u_{{R_{1} }} (t) - u_{{R_{2} }} (t) = \int_{{R_{1} }}^{{R_{2} }} {\frac{{p_{1} R_{1} }}{Er}} dr$$
(20)

where uR1 represents the displacement of rocks around the tunnel and other parameters are similar to those in previous formulas.

$$u_{{R_{1} }} (t) = u_{{R_{2} }} (t) + \frac{{p_{1} R_{1} }}{E}\ln \frac{{R_{2} }}{{R_{1} }}$$
(21)

When r = R3 and r = R2, displacement in plastic zone can be obtained according to Formula (17) and the visco-elastic–plastic solutions for surrounding rocks can be obtained in accordance with Formula (21).

$$u_{{R_{1} }} (t) = - \frac{{\left( {1 + \mu } \right)R_{3}^{2} }}{{E_{1} R_{2} }}\left( {p_{3} - p_{0} } \right)F_{1} (t) + \frac{{p_{1} R_{1} }}{E}\ln \frac{{R_{2} }}{{R_{1} }} .$$
(22)

5 Engineering Application

5.1 General Situation of the Project

The tunnel is a typical expressway tunnel in soft rocks and the soft rocks are moderately weathered sandy slate and carbonaceous slate. Moreover, with extremely developed joints and fractures, the rock masses are crushed, showing a crushed breccias-granular structure.

5.2 Selection of Calculation Parameters

The section DK0 + 891 in this tunnel was selected as the research object. The tunnel has a horseshoe section and the equivalent radius of this tunnel is equal to the half of section span (16.6 m), that is R1 = 8.3 m. By combining with investigation reports and uniaxial compression creep tests, the parameter values of unsteady viscous body were obtained through fitting analysis, as shown in Table 1. Physical and mechanical parameters of surrounding rocks of the tunnel are demonstrated in Table 2.

Table 1 Parameters of unsteady viscous body
Full size table
Table 2 Physical and mechanical parameters of surrounding rocks
Full size table

5.3 Calculation of Visco-Elastic Solutions

Considering creep effects, displacement of surrounding rocks of the tunnel increases with time. In order to better study the whole creep process of surrounding rocks, the calculation is carried out under three conditions, namely t = 0, t = c (c is a constant) and t = ∞.

When t = 0,

$$F_{1} (0) = 1 + \frac{{E_{1} }}{{\eta_{2} }} = 1.576$$
$$\begin{aligned} u_{{R_{1} }} & = - \frac{{\left( {1 + \mu } \right)R_{3}^{2} }}{{E_{1} R_{2} }}\left( {p_{3} - p_{0} } \right)F_{1} (0) + \frac{{p_{1} R_{1} }}{E}\ln \frac{{R_{2} }}{{R_{1} }} \\ & = \frac{{28.619^{2} \left( {1 + 0.3} \right)\left( {25 \times 10^{ - 3} \times 80 - 0.161} \right) \times 1.576}}{{18 \times 10^{3} \times 9.53}} + \frac{1.2 \times 8.3}{{15 \times 10^{3} }}\ln \frac{9.53}{8.3} \\ & = 17.860 \times 10^{ - 3} {\text{m}} \\ \end{aligned}$$

When t = c,

$$\begin{aligned} F_{1} (c) & = \left\{ {1 + \frac{{E_{1} }}{{\eta_{2} }} + \frac{{E_{1} }}{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} c}}{{\eta_{1} }}} \right)} \right]} \right\} \\ & = 2.326 - 0.75\exp ( - 0.018c^{0.588} ) \\ \end{aligned}$$
$$\begin{aligned} u_{{R_{1} }} & = - \frac{{\left( {1 + \mu } \right)R_{3}^{2} }}{{E_{1} R_{2} }}\left( {p_{3} - p_{0} } \right)F_{1} (c) + \frac{{p_{1} R_{1} }}{E}\ln \frac{{R_{2} }}{{R_{1} }} \\ & = \frac{{28.619^{2} \left( {1 + 0.3} \right)\left( {25 \times 10^{ - 3} \times 80 - 0.161} \right) \times F_{1} (c)}}{{18 \times 10^{3} \times 9.53}} + \frac{1.2 \times 8.3}{{15 \times 10^{3} }}\ln \frac{9.53}{8.3} \\ & = [26.451 - 8.561 \cdot \exp ( - 0.018c^{0.588} )] \times 10^{ - 3} \;{\text{m}} \\ \end{aligned}$$

While t = ∞,

$$F_{1} (\infty ) = 1 + \frac{{E_{1} }}{{\eta_{2} }} + \frac{{E_{1} }}{{E_{2} }} = 1.732$$
$$\begin{aligned} u_{{R_{1} }} & = - \frac{{\left( {1 + \mu } \right)R_{3}^{2} }}{{E_{1} R_{2} }}\left( {p_{3} - p_{0} } \right)F_{1} (\infty ) + \frac{{p_{1} R_{1} }}{E}\ln \frac{{R_{2} }}{{R_{1} }} \\ & = \frac{{28.619^{2} \left( {1 + 0.3} \right)\left( {25 \times 10^{ - 3} \times 80 - 0.161} \right) \times F_{1} (\infty )}}{{18 \times 10^{3} \times 9.53}} + \frac{1.2 \times 8.3}{{15 \times 10^{3} }}\ln \frac{9.53}{8.3} \\ & = 26.451 \times 10^{ - 3} \;{\text{m}} \\ \end{aligned}$$

According to calculation, creep phenomenon occurs to surrounding rocks of the tunnel as early as t = 0, and the displacement of surrounding rocks is 17.890 mm. When t is a constant, displacement of surrounding rocks gradually rises with time. While t = ∞, surrounding rocks are completely crept and the ultimate displacement of surrounding rocks is 26.451 mm. The results show that displacement gradually increases with time and the increase amplitude reaches 47.85% by taking creep effects of surrounding rocks into account.

5.4 Field Monitoring, Verification and Discussion

In order to verify the correctness and reasonability of long-term creep deformation of surrounding rocks of the tunnel calculated based on the modified Nishihara model and Lade–Duncan criterion, vault settlement was monitored on site. On this basis, the creep deformation of surrounding rocks of the tunnel in 30 days was measured by using the Leica TCA2003 total station instrument. The monitoring scheme was based on the regularly measured vault settlement in Technical Code for Construction of Highway Tunnel (JTG F60-2009) (Ministry of Transport of the People’s Republic of China 2009). Section DK0 + 891 was selected for monitoring and a measured point was arranged in the vault and built-in fitting was buried. By analyzing the data of vault settlement (creep deformation) of section DK0 + 891 monitored in the field, the theoretical calculation results and actual monitoring results on site are compared for analysis and verification.

Figure 4 shows the change curve of vault settlement of section DK0 + 891 monitored in the field with time.

Fig. 4
figure 4

Relational curve of vault settlement monitored in the field with time

Full size image

Based on monitoring results in the field, this section of the tunnel was excavated from June 10, 2016 and then entered into excavation deformation stage. On June 20, vault deformation tended to be stable after 10 days and the accumulative deformation of vault was 19.1 mm. The deformation is not caused by creep of rock masses, but the result of comprehensive effects of excavation disturbance and stress release of rock masses. In 6 days from June 20, deformation was unchanged, so it is considered to entering into stable deformation stage. On June 26, deformation suddenly changed to increase slowly and constantly, indicating that creep effects of surrounding rocks appeared and creep deformation occurred to rock masses. Corresponding to theoretical analysis, this time was set as the time for creep deformation (creep stage began from t = 0). On July 7, creep deformation tended to be stable and the accumulative value of vault settlement was 29.3 mm. By continuing monitoring, deformation did not increase anymore.

By further analyzing monitoring results, creep deformation occurred from June 26, 2016 after this section of the tunnel underwent stable deformation stage and the accumulative deformation of vault was 19.1 mm, showing 6.76% error with displacement (17.89 mm) of surrounding rocks at t = 0 in theoretical calculation. On July 7, creep deformation of surrounding rocks tended to stabilize and then deformation did not increase any more. The accumulative deformation of vault settlement was 29.3 mm, which demonstrated 10.77% error with the calculated ultimate displacement (26.451 mm) of surrounding rocks at t = ∞. According to the results of error analysis, the theoretical calculation results are close to actual monitoring results and the errors are in the tolerance range. This indicates that the method for calculating long-term creep deformation of surrounding rocks in the tunnel based on the modified Nishihara model and Lade–Duncan criterion is reasonable and feasible.

In other words, when creep effects were not taken into account, theoretical calculation showed that vault settlement of this section was only 17.89 mm and the actually monitored vault settlement was 19.1 mm. While considering creep effects, the final vault settlement of this section through theoretical calculation reached 26.451 mm and the actually monitored vault settlement reached 29.3 mm. From theoretical perspective, deformation of surrounding rocks increased by 47.85% after considering creep effects, while it rose by 53.4% in practice. No matter from theoretical or practical perspective, creep effects play a significant role. Therefore, in the design of supports for tunnels in soft rocks, creep effects are bound to be considered, so as to avoid the failure of primary support caused by creep effects of surrounding rock at later stage, thus influencing overall stability of the tunnel.

6 Conclusions

  1. 1.

    By using unsteady viscous body, Nishihara model is modified. Based on Lade–Duncan criterion, this study analyzes the deformation of surrounding rocks in visco-elastic and plastic stages and deduces visco-elastic–plastic solutions for surrounding rocks of the tunnel.

  2. 2.

    Analytic formula of displacement of surrounding rocks of the tunnel is deduced and F1(t) is the parameter formula by taking creep into account. If this item is deleted, the formula can be used to calculate visco-elastic–plastic solutions for hard surrounding rocks, indicating that this formula can suit for tunnels in different lithological properties.

  3. 3.

    By taking the expressway tunnel as the research object, the displacement of surrounding rocks in the creep aging process is calculated and theoretical calculation is verified to be correct by monitoring vault settlement in the field. The results show that 6.76% error is found between theoretical calculation and actual monitoring results of initial creep deformation and the theoretical calculation of final creep deformation shows 10.77% error with actual monitoring results. The small errors between them reveal a high accuracy of theoretical calculation.

  4. 4.

    Theoretically, deformation of surrounding rocks after considering creep effects increases by 47.85%, while that rises by 53.4% in practice, demonstrating the important role played by creep effects. Therefore, when designing supports of tunnels in soft rocks, creep effects have to be taken into account, so as to avoid the failure of primary support caused by creep effects of surrounding rock in the later stage and the impacts on overall stability of the tunnel.