1 Introduction

Rocks, the common and cheap construction materials with high strength, are under complex geological conditions. However, the extensive fissures, cracks and joints, caused by external loads or the internal loads in the diagenetic process, may affect the stability of the rock structures (Park and Bobet 2010; Liu et al. 2014, 2015; Zhao et al. 2016). Extensive fields verified this assertion and further indicated that the propagation of these discontinuities, caused by rock drilling, blasting and manual excavation, may lead to disastrous event (Moradian et al. 2010; Reseride et al. 2010; Lee and Jeon 2011). In the present, the construction design and the stability evaluation are based on the ultimate bearing capacity, the ultimate condition for normal use, and the numerical study (Martin et al. 2013). When the stress or the load exceeds the designed values, rock yields. On the opposite, the rock is stable. However, the widely distributed cracks in rock may result in the variance of the rock strength. Frequently, the strength of the rock, containing cracks, is much less than that of the intact rock. In addition, because the strength of the crack is affected by many factors, it is very hard to quantitatively evaluate the strength and the stability of the rock engineering, and to obtain the precise stress distributions at the crack tips.

The stress intensity factor is frequently used to evaluate the stress field of the cracked rock and the fracture stability of the constructions, as well as to study the initiation condition and the propagation direction of the crack. Stress intensity factor can characterize the intensity level of the stress singular point at crack tips, the stress concentration degree and the stability state of the rock engineering. In addition, the stress intensity factor is affected by the external load, the geometry characteristics of the crack and the structure and the boundary conditions. Simultaneously, the fracture toughness can be obtained by tests. Therefore, the stress intensity factor is widely used in the theoretical and the field investigation on the fissured rock (Baud et al. 1996; Eberhardt et al. 1998; Wang 1998; Cai et al. 2004; Saadaoui et al. 2006; Ghazvinian et al. 2013; Sarfarazi et al. 2014). Until now, the theoretical solutions for the stress intensity factor of the crack are mainly conducted on the single, the coplanar and the parallel cracks, using complex functions, integral transformation, boundary collocation and numerical simulations. For example, Zheng et al. (2013) proposed the theoretical solution of the stress intensity factor for the three symmetric cracks, using the complex function, and further obtained the single peak curve of the lateral stress and the stress intensity factor (Zheng et al. 2013). Wang et al. (2003) equaled multi-cracks pattern into the single crack pattern, and the proposed the theoretical solution of the stress intensity factor for two cracks with curved boundaries, using the boundary collocation method (Wang et al. 2003). Zhao et al. (2016) conducted laboratory and numerical tests on the rock specimens, containing two cracks, to study the stress intensity factors and the fracture criterion for various water contents (Zhao et al. 2012; Lin et al. 2013). Dobroskok et al. (2005) analyzed the radial stress at the most adverse locations and the nonlinear attenuation of the radial stress at crack tips, using the finite analysis method on the axial crack at the large tank (Dobroskok et al. 2005). Xie et al. (2016) studied the crack coalescence pattern, the initiation stress and the propagation direction of the multi-cracks in rock specimens. They proposed the semilog relation between the subcritical propagation velocity and the stress intensity, and established creep model for the fissured rock specimen (Xie et al. 2016). The above studies significantly contribute to understanding the stress intensity factors for various conditions in rock. However, for the coalescence cracks, including of the central symmetric cracks, the edge symmetric cracks and the diagonal symmetric cracks, rare studies were conducted to analyze the stress intensity factor, the stress concentration, and the effect of the crack geometry on the stress intensity factor. In addition, for these cracks, the difference in the stress intensity factor and the relation between crack geometry and the stress intensity factor remains unknown. Therefore, weight function method was applied to study the evolution of the coalescence cracks. The stress intensity factor and the crack propagation direction of the two coalescence cracks were analyzed. Then, numerical tests were further conducted to verify the theoretical results and to revel the relation between the stress intensity factor and the crack geometry.

2 Fracture Characteristics of the Rock Specimen Containing Coalescence Cracks

2.1 Crack Distributions

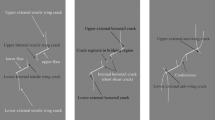
Previous studies show that the natural rock contains extensive disorganized cracks, and the geometry, the occurrence, the strength and the stress condition of these cracks are random (Bobet and Einstein 1998; Zhang and Zeng 2004; Erarslan and Williams 2013). These cracks may propagate because of the disturbances from geological conditions and the manual actions. Therefore, extensive coalescence cracks, including tip–tip coalescence cracks, tip-main coalescence cracks and main–main coalescence cracks (Fig. 1).

Fig. 1
figure 1

Crack distributions

Full size image

2.2 Crack Propagation of Coalescence Cracks

The tensile-shear stress and the compressive-shear stress frequently lead to the initiation and coalescence of the cracks. The wing and the secondary cracks are the main cracks caused by loading. According to the stress conditions and the crack distribution characteristics, the tensile-shear and the compressive-shear cracks are observed. Previous studies showed that the tensile-shear crack instead of the compressive-shear crack is more destructive (Zhao et al. 2012; Lin et al. 2013). Therefore, in the present article, the tip–tip coalescence cracks are investigated under tensile loads. Figures 2 and 3 show the crack distribution and the regional stress distribution, respectively.

Fig. 2
figure 2

Crack distribution

Full size image
Fig. 3
figure 3

Regional stress distribution

Full size image

Previous studies showed that the complex stress conditions frequently lead to the high stress concentrations at crack tips, and these concentrations further lead to the crack propagation and the tip–tip coalescence of the cracks (Hao et al. 2014) (Fig. 1b). When the expansion stress exceeds the critical stress, coalescence between the crack tip and main crack occurs (Fig. 1c). And then, energy releases completely when the plastic zone expands. Finally, failure of the rock results from the main–main coalescence crack (Fig. 1d).

3 Theoretical Solution for the Stress Intensity Factor and Propagation Direction

3.1 The Weighted Function Solution for the Coalescence Cracks

Previous studies on the fracture characteristics and the stability mainly focused on the theoretical solution of the stress intensity factor and the stress concentrations to determine the initiation criterion and the propagation direction. The stress intensity factor is the premise of the stability analysis of rock buildings containing cracks. It is very complicated to compute the accurate stress intensity factor, and to evaluate the effect of the structural distribution, the geometrical parameters of cracks and the boundary conditions on the computation results. The load symmetrical and the geometry symmetrical cracks are the main symmetrical cracks. The stress intensity factors of the collinear cracks and the parallel cracks can be obtained by the combination method and by refereeing to the stress intensity manual. Usually, the stress intensity factor is obtained based on the factored normal and tangential loads (Sih 1973). However, coalescence cracks certainly form in the crack propagation process. The coalescence cracks (mode I-II cracks) are characterized by more complicated singularity. With the limits of the application of the compounded fracture theory, therefore, it is difficult to obtain the stress intensity factor and the propagation direction at the coalescence point. Until now, the complex function method, the integral transform method, the boundary collation method, the weighted function method, the numerical method, the energy difference method and the superposition method have been applied to calculate the stress intensity factor (Sih 1973; Williams and Ewing 1984; Resende et al. 2010). In the weighted function, the load and the geometrical factors are split. Therefore, in the calculation process, the stress intensity factor is determined by boundary conditions, simultaneously, the load on crack is simplified in the form of the load without considering the crack. Thus, in the present article, we tried to investigate the influence of the symmetric characteristics on the stress intensity factor. In addition, the calculation using this method can meet the error requirements. Therefore, the weighted function method has been widely used to calculate the stress intensity factor. The complex stress conditions at crack tips frequently lead to the formation of the Mode I crack, the Mode II crack, the Mode III crack and the mixed cracks. Considering the fracture characteristics under the tensile-shear loads, the Mode I-II cracks, including the central symmetric cracks, the edge symmetric cracks and the diagonal symmetric cracks, were investigated in the present article. Figure 4 shows the corresponding crack distribution and boundary conditions.

Fig. 4
figure 4

Crack distribution

Full size image

According to the crack distribution and the boundary conditions in Fig. 4 and the weighted function method, the stress intensity factor is (Sih 1973):

$$K = \delta \sigma \sqrt {\pi a} \sin^{2} \beta$$
(1)

where

$$\delta = \int_{0}^{a\sin \beta } {\frac{\sigma (x)}{{\sigma \sin^{2} \beta }} \cdot \frac{m(\gamma ,X)}{{\sqrt {\pi a\sin \beta /W} }}} dx,\quad \gamma = \frac{a}{W}\sin \beta ,\quad X = \frac{x}{W}$$

where x is the coordinate along the crack; σ(x) is the stress at the corresponding location when the crack does not exist; σ is the reference load resulting in stress intensity factor instead of displacment, a is the half length of the crack, β is the angle determined by external loads and the crack, W is the width of the crack (a very small value compared to a), m (γ, X) is the weighted function, γ and X are dimensionless factors.

According to the compounded fracture theory of the inclined crack, the stress intensity factor at the crack tip of the Mode I-II mixed crack is (Sih 1973; Lin et al. 2013):

$$K_{I} = \delta \sigma \sqrt {\pi a} \sin^{2} \beta$$
(2)
$$K_{II} = \delta \sigma \sqrt {\pi a} \sin \beta \cos \beta$$
(3)

With Eq. 1, the weighted function can be obtained:

$$m(\gamma ,X) = \frac{4G}{{(\kappa + 1)\sigma \sqrt {\pi a} \sin^{2} \beta }} \cdot \frac{{\partial u(\gamma ,{\text{x)}}}}{\partial a}$$
(4)

where

$$\kappa = \left\{ {\begin{array}{*{20}l} {3 - 4v} \hfill & {planestrain} \hfill \\ {\frac{3 - v}{1 + v}} \hfill & {planestress} \hfill \\ \end{array} } \right.$$

where u(γ, X) is the open displacement of the crack surfaces; G is the shear elastic modulus.

According to Fig. 4, the open displacement can be written as:

$$u(\gamma ,X) = \frac{{\sigma \gamma \sin^{2} \beta }}{{\sqrt {2E^{*} } }}\left[ {4\delta (\gamma ) + \frac{{\sqrt 2 \pi \Phi (\gamma ) - \frac{8}{3}\gamma \delta (\gamma )}}{2/5}} \right]\left( {1 - \frac{x}{a\sin \beta }} \right)^{3/2}$$
(5)

where

$$\Phi (\gamma ) = \frac{1}{{\gamma^{2} }}\int_{0}^{\gamma } {\varepsilon \delta^{2} (\varepsilon )d\varepsilon }$$
$$E^{*} = \left\{ {\begin{array}{*{20}l} E \hfill & {planestrain} \hfill \\ {E/(1 - v^{2} )} \hfill & {planestress} \hfill \\ \end{array} } \right.$$

where \(\varepsilon\) is the integral variable; E and v are the elastic constants.

Furthermore, with the displacement function in Eq. 5, the stress intensity factor, K, can be obtained by introducing the weighted function into Eq. 1. Clearly, when the reference load is fixed, the stress intensity factor is affected by β, and the ratio of W to a. Then, with the propagation criterion for coalescence cracks, the propagation direction can be obtained by processing Eqs. 1, 4 and 5:

$$\frac{\partial K}{\partial \beta } = \sigma \sqrt {\pi a} \left( {\frac{\partial \delta }{\partial \beta }\sin^{2} \beta + \delta \sin 2\beta } \right)$$
(6)
$$\frac{\partial \varPhi }{\partial r} = \frac{{\delta^{2} }}{r}\left[ {6\delta^{{\prime }} + 15\sqrt 2 \frac{{\delta^{2} }}{r} - 40\delta - 40r\delta^{{\prime }} } \right]$$
(7)
$$\frac{\partial u}{\partial \beta } = \frac{\partial u}{\partial r}\frac{\partial r}{\partial \beta } = \frac{{\partial \left\{ {\ln (\sigma \gamma \sin^{2} \beta ) - \ln \sqrt {2E^{*} } + \ln \left[ {4\delta (\gamma ) + \frac{{\sqrt 2 \pi \varPhi (\gamma ) - \frac{8}{3}\gamma \delta (\gamma )}}{2/5}} \right] + \frac{3}{2}\ln \left( {1 - \frac{x}{a\sin \beta }} \right)} \right\}}}{\partial r}\frac{a}{W}\cos \beta$$
(8)

where

$$\delta^{2} = \left( {\int_{0}^{a\sin \beta } {\frac{\sigma (x)}{{\sigma \sin^{2} \beta }} \cdot \frac{m(\gamma ,X)}{{\sqrt {\pi a\sin \beta /W} }}} dx} \right)^{2}$$
$$\delta^{{\prime }} = \frac{\partial \delta }{\partial r}$$

According to Eqs. 6, 7 and 8, the propagation direction in the form of β is:

$$a\sigma (\beta )m(\gamma ,X) + \sigma \delta \tan \beta \sqrt {\pi a\sin (\beta /W)} = 0$$
(9)
$$\frac{\partial \delta }{\partial \beta }\sin^{2} \beta + \delta \sin 2\beta = 0$$
(10)
$$\sin \beta \left( {\frac{\partial \delta }{\partial \beta }\sin \beta + 2\delta \cos \beta } \right) = 0$$
(11)

In Eq. 11, because δ and \(\frac{\partial \delta }{\partial \beta }\) are higher than 0, therefore, when β is equal to 0, the requirement of Eq. 11 is met. Therefore, it can be concluded that cracks will propagation in the symmetric direction for the tip–tip coalescence cracks. Therefore, the crack propagations for these three coalesced cracks are similar.

3.2 The Effect of the Crack Size on the Stress Intensity Factor

The computation result from the weighted function show that the stress intensity factor is affected by the external load, the crack geometry and the boundary conditions, especially the crack sizes. Therefore, to analyze the effect of the crack size on the stress intensity factor, tensile loads were applied on the rock specimens, containing the central symmetric cracks, the edge symmetric cracks and the diagonal symmetric cracks. The stress intensity factors at the coalescence points, KIA and KIIA, were studied, considering the advantages of the separation of the load and the geometry factors, as well as the effect of crack size on the stress intensity factor. Simultaneously, it is critical to obtain the weight function \(m(\gamma ,X)\) and the stress intensity factor. Thus, according to Eqs. 1–3, to eliminate the influence of the load boundary on the stress intensity factor when using the weight function, the effect of the α and the geometry size on the stress intensity factor can be studied by adopting the dimensionless stress intensity factor.

According to the crack length, a, and the crack width, W, the inclination angle, α, satisfies:

(1) Central symmetric crack: \(W = ia\begin{array}{*{20}c} {} & {(i = 4,6,8,10)} \\ \end{array}\)

(2) Edge symmetric crack: \(W = ia\begin{array}{*{20}c} {} & {(i = 1.5,2,3,4)} \\ \end{array}\)

(3) Diagonal symmetric crack: \(W = ia\begin{array}{*{20}c} {} & {(i = 4,6,8,10)} \\ \end{array}\)

The dimensionless stress intensity factor is defined as:

$$K_{I,II} = K/[\sigma (\pi a)^{1/2} ]$$
(12)

The specific results are shown in Figs. 5, 6 and 7.

Fig. 5
figure 5

Dimensionless stress intensity factor of the central symmetric crack

Full size image
Fig. 6
figure 6

Dimensionless stress intensity factor of the edge symmetric crack

Full size image
Fig. 7
figure 7

Dimensionless stress intensity factor of the diagonal symmetric crack

Full size image

The results show that, for the Mode-I distribution, the stress intensity factors of these three types of cracks decrease with the increase in α. When α increases to 60°, the stress intensity factors approximately reach the asymptotic values for the central and edge symmetric cracks, whereas the critical angle is 70° for the diagonal symmetric crack. When α is relatively small, the stress intensity factor decreases in the order of the central symmetric crack, the edge symmetric crack and the diagonal symmetric angle, and the dimensionless factor, decreasing with the increase in W, ranges from 1 to 2.1. Whereas, when α is relatively high, the stable dimensionless stress intensity factor ranges from 0.1 to 0.6, simultaneously, this dimensionless stress intensity factor decreases in the order of the diagonal, the edge and the central symmetric cracks.

For the Mode-II distribution, similar decreases in the dimensionless stress intensity factors and the critical α were observed for the three types of cracks. When α is relatively low, the dimensionless stress intensity factor, range from 1.2 to 1.5, is observed in the diagonal symmetric crack, whereas, the minimum value, ranging from 0.4 to 0.45 is observed for the edge symmetric crack. With the increase in α, the dimensionless factors distribute in a narrow scope, and are hardly affected by the geometric size of the crack. These factors decrease in the order of the diagonal symmetric, the central symmetric and the edge symmetric cracks.

Discreteness occurs in the calculation of the dimensionless factors, influenced by the crack width. For the mode I and Mode II cracks, the increase in crack width will decrease the stress intensity factor. The increase in the angle will impair the influence of the crack width on the factor.

In the calculation process in 3 dimensions, we can discretize a 3D symmetric crack into two groups of 2D strips. Then, change the restraints on the intact 3D crack into the elastic boundary. Subsequently, construct the weight function of the 3D strips, and calculate the stress intensity factors. According to the relation between the 2D and 3D stress intensity factors, we can determine the stress intensity factor at the crack tip.

4 Numerical Tests on the Fracture Characteristics

To verify the correctness of the theoretical study, FLAC 3D was applied to simulate the fracture process of the above symmetric cracks. In numerical studies, the stress concentration conditions, the stress intensity factors and the effect of the crack geometry on the stress intensity factor can be evaluated (Fig. 8). Tetrahedron elements were adopted, and the cracks were simulated by the joint element. In the numerical model, a tensile load on the model top was applied, the bottom boundary was fixed, and the left and right boundaries are free. In addition, the Mohr–Coulomb criterion was adopted. Table 1 lists the parameters of the rock specimen and the crack. Figures 9, 10 and 11 show the numerical results.

Fig. 8
figure 8

Stress distributions (W = 4a)

Full size image
Table 1 Numerical parameters
Full size table
Fig. 9
figure 9

Dimensionless stress intensity factors for central symmetric cracks

Full size image
Fig. 10
figure 10

Dimensionless stress intensity factors for edge symmetric cracks

Full size image
Fig. 11
figure 11

Dimensionless stress intensity factors for diagonal symmetric cracks

Full size image

The stress intensity factor and the stress distribution, obtained from numerical tests, show that stress mainly concentrates at crack tips and more obvious stress concentration and more plastic zones are observed for the diagonal crack. In addition, for the Mode-I cracks, stress concentrations decrease in the order of the diagonal, the central and then edge symmetric cracks. For the Mode-II cracks, stress concentrations decrease in the same order.

Figures 9, 10 and 11 show similar results to the theoretical study. It can be concluded that the crack geometry significantly affect the stress intensity factor. The increases in α, and the ratio of W to a decrease the stress intensity factor. In addition, when the α increases to 60° for the central and the diagonal symmetric cracks, the stress intensity factors reaches the asymptotic values, whereas for the edge symmetric cracks, the critical angle is 70°. Nevertheless, the numerical result is about 3% lower than the theoretical result. This difference may mainly result from that the displacement of the rock and the gravity distribution are neglected in theoretical study, whereas numerical study was conducted in a limited scope with fixed boundary conditions. Furthermore, FLAC 3D can be used to simulate the laboratory tests under many conditions. In the calculation process of the safety factor, the restraints of the surrounding media were considered. The crack was represented by grid elements with certain strength. Because large deformation and far field analysis can be conducted in FLAC 3D, more concentrated stress was observed at cracks tips. Then, the calculated values are slightly smaller than those from the weight function. Furthermore, energy dissipation was also considered in numerical tests.

5 Conclusion

Cracks, fissures and joints are typical discontinuities affecting the engineering stability. To investigate the propagation characteristics of the coalescence cracks, the dimensionless stress intensity factor was adopted based on the weighted function method and the FLAC 3D. The theoretical solution, the propagation direction and the stress concentrations for the Mode I-II crack were obtained. In addition, the theoretical and the numerical studies show that, for the Mode-I and Mode-II cracks, stress concentrations decrease in the order of the diagonal, the central and then edge symmetric cracks. Moreover, cracks propagates along the symmetric axis.