1 Introduction

As compared with circular footings, the ring footing can be economically adopted for footing of structures such as silos, storage tanks, chimneys, and cooling towers. The theoretical prediction of ultimate bearing capacity of ring footings is a requirement to design such structures. Bearing capacity of foundations depends on the shape of the footing, soil parameters and loading conditions. Nγ, N q and N c are bearing capacity factors which are dimensionless, and are only dependent on angle of shear resistance (φ). In the literature, bearing capacity factors are calculated in different conditions and are compared with previous studies if possible. Studies on ring footings are rare and a small number studies has been performed to compute the bearing capacity of ring footings.

In previous studies, there are no exact methods to compute the bearing capacity of ring footings. Kumar and Ghosh (2005) estimate the value of bearing capacity factor Nγ by employing the method of characteristics for both smooth and rough ring footing bases. Zhao and Wang (2008) employ the finite difference method to compute the Nγ for low friction soils for smooth and perfectly rough footing bases.

In the present study, the bearing capacity factors Nγ, N q and N c for ring footings are determined by a written code based on the method of characteristics. These factors are calculated for two types of soil/footing interfaces; smooth and rough. Comprehensive series of bearing capacity factors are presented for different ratio of internal radius to external radius of the ring footings and a wide range of internal friction angle. Also bearing capacity is calculated with simultaneous effects of unit weight (γ), surcharge (q), and the soil cohesion (c) and the results are compared with the superposition method.

2 Problem Definition

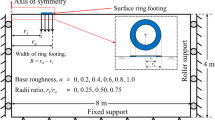
This study problem is shown in Fig. 1, where a rigid ring footing with internal and external radii r i and r o respectively, is illustrated. The footing rests on a frictional–cohesive medium including a horizontal ground surface. In the present study, different radii ratios (n = r i /r o ) are examined. The footing supports vertical and central load.

Fig. 1
figure 1

The plan of ring footing

Full size image

The uniform normal surcharge pressure is loaded on the ground surface besides the footing and there is not any shear stress. Along the footing base, (δ) is the angle of interface friction. The value of the angle (δ) depends on the roughness of the footing-soil. For a smooth base (δ) is zero but footings are usually rough in reality. Shear stress (τ) for a rough footing is according to the frictional–cohesive Coulomb relationship as Eq. (1). (\(c_{\text{int}}\)) stands for the interface cohesion of the footing base (Eq. 2):

$$\tau = c_{\text{int}} + \sigma_{z} \tan \delta$$
(1)
$$c_{\text{int}} = \frac{\tan \delta }{\tan \phi }c$$
(2)

As a result, the stress points (σ z , τ rz ) just beneath the footing base should satisfy both the interface and soil failure criteria. If the friction angle (δ) between soil and base is fully mobilized, the angle between the direction of the major principal stress and the normal to the footing is computed as:

$$\psi = - \frac{1}{2}\left[ {\delta + \sin^{ - 1} \left( {\frac{\sin \delta }{\sin \phi }} \right)} \right]$$
(3)

The smooth footing condition is an ideal case. In reality, footings are usually constructed by pouring concrete directly on a firm surface of soil or lean concrete, and the footing-soil interface is rough enough to restrain the tendency for slip. The lowest value of the interface friction angle occurs for a parabolic concave variation (Eq. 4). In the present study, it is supposed that the interface friction angle (δ) varies along the centerline to edge of footing with a parabolic concave form as a function of soil friction angle (ϕ):

$$\delta = \left( {\frac{r}{{r_{o} }}} \right)^{2} \phi \quad ({\text{ r}}_{\text{i}} < r < r_{o} )$$
(4)

3 Methodology

The method of characteristics transforms a set of hyperbolic differential equations into a system of ordinary differential equations. These equations are then solved by the finite difference method. This method is used to determine the stresses in the soil mass by plastic behavior. Under loading, soil beneath the foundation reaches limit yield and plastic flow occurs in the soil mass. In most problems of soil mechanics, soil plastic behavior is defined by Mohr–Coulomb yield criterion. Differential equation system called the plastic equilibrium equation is established by combining this criteria with equilibrium equations. If these equations are solved by considering the boundary conditions, the stress to the soil mass will be calculated.

The pioneering method of characteristics is employed by Kötter (1903) for plane rotation. Prandtl (1921) offers analytical solution for the foundation of the weightless soil. Reissner (1924) adopts the method of Prandtl (1921) for measuring the bearing capacity of soil in different situations. The issue becomes complicated by extending this method to weighted soil. The main solutions are proposed by Sokolovski (1965).

Solving the problem of ring footings takes place in an axial symmetric condition. According to Fig. 2, the stress components (σ z , σ r , σ θ , τ rz ) of an element in cylindrical coordinates system (r–θ–z) are considered. The equations of equilibrium under axisymmetric conditions can be written in the following form:

Fig. 2
figure 2

Stress components in the cylindrical coordinates system

Full size image
$$\begin{aligned} &\frac{{\partial \sigma_{r} }}{\partial r} + \frac{{\partial \tau_{rz} }}{\partial z} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = 0 \\ &\frac{{\partial \tau_{rz} }}{\partial r} + \frac{{\partial \sigma_{z} }}{\partial z} + \frac{{\tau_{rz} }}{r} = \gamma \\ \end{aligned}$$
(5)

In the present study, it is assumed that the soil obeys the Mohr–Coulomb yield criterion as a frictional–cohesive material. The inclination angle (ψ) is between the major principal surface and the vertical direction. The three stress components (σ z , σ r , τ rz ) can be expressed as follows:

$$s = \frac{{\sigma_{r} + \sigma_{z} }}{2}$$
(6)
$$\begin{aligned} \sigma_{r} = & s \, (1 + \sin \phi \cos 2\psi ) + c\cos \phi \cos 2\psi \\ \sigma_{z} \, = & \, s \, (1 - \sin \phi \cos 2\psi ) - c \, \cos \phi \cos 2\psi \\ \tau_{rz} = & \sin 2\psi \, (c\cos \phi + s\sin \phi ) \\ \end{aligned}$$
(7)

In axisymmetric problems, the hoop stress (σ θ ) is generally supposed to be either the major or minor principal stress in the axial plane (Haar and von Karman 1909). This assumption has also been accepted by Cox et al. (1961) and Lau (1988). Accordingly, (σ θ ) is considered equal to the smallest principal stress:

$$\begin{aligned} \sigma_{\theta } &= \sigma_{3} < \sigma_{1} \hfill \\ \sigma_{\theta } &= s(1 - \sin \phi ) \hfill \\ \end{aligned}$$
(8)

By considering Eqs. (5), (6), (7) and (8), hyperbolic partial differential equations are formed. During the problem solving, two groups of characteristic lines are obtained (Davis and Selvadurai 2002):

$$\frac{dr}{dz} = \tan (\psi \pm \mu )$$
(9)

where μ = π/4 − φ/2 and the upper and lower signs correspond to characteristic lines. Along each of these two lines, the equilibrium is satisfied for stress components. By substituting Eq. (7) in the set of partial differential equations, two ordinary differential equations are expressed:

$$\cos \phi d\sigma \pm \left( {c\cos \phi + s\sin \phi } \right)\left( {2d\psi + \frac{\cos \phi dr \pm (\sin \phi - 1)dz}{r}} \right) + \left( { \pm \cos \phi dz - \sin \phi dr} \right)\gamma = 0$$
(10)

The general scheme of the characteristic lines under the footing zone (drawn by authors’s code) is shown in Fig. 3. This scheme consists of three zones: The active zone (under the footing), the passive zone (vicinity of the footing) and the fan zone (Booker and Davis 1977).

Fig. 3
figure 3

The global scheme of the characteristics lines generated under the ring footing zone, (figure is from authors’s code)

Full size image

The program code is written based on the Eqs. (9) and (10). Values of pressure are calculated along the base of the ring footing. Pressure distribution under the foundation is not uniform. The average pressure is obtained by the following Eq. (11). In this equation, there is pressure on the foundation (σ z ), foundation radius (r), inner radius (r i ), outer radius (r o ). By the following equations, the mean vertical bearing capacity (q u ) of the ring foundation is calculated.

$$\begin{aligned} Q_{u} = \sum\limits_{{r_{i} }}^{{r_{o} }} {2 \, \pi \, r \, } \sigma {}_{z} \hfill \\ q_{u} = \frac{{Q_{u} }}{{\pi \left( {r_{o}^{2} - r_{i}^{2} } \right)}} \hfill \\ \end{aligned}$$
(11)

Soil is considered as cohesive–frictional-weighted with applied surcharge pressure. Bearing capacity (qu) of a ring footing is expressed by the classical bearing capacity equation. The ultimate bearing capacity of the soil under a shallow footing is expressed by the Terzaghi’s classical Eq. (12).

$$q_{u} = cN_{c} + qN_{q} + \gamma (r_{o} - r_{i} )N_{\gamma }$$
(12)

The first term in this equation relates to the shear strength component represented by parameter (c), the second term is attributed to the surcharge pressure (q) and the third term is associated with the weight of the soil below foundation level. The superposition of components of bearing capacity is theoretically incorrect for a plastic material but the resulting error is considered to be on the safe side. Bearing capacity factors of ring footing are obtained for different ratios of inner radius to the outer radius.

Due to non-linear behavior of ground material, using traditional superposition methods of calculating bearing capacity causes error. The main cause of superposition error is decomposition of the total bearing capacity into components. Based on the method of characteristics, the error introduced by superposition method is investigated. Solving several problems showed that bearing capacity calculated by superposition method is conservative (Bolton and Lau 1993; Davis and Booker 1971).

In the present study, each of the bearing capacity factors has been determined in conditions where two terms of the Eq. (12) must become zero and only one of them has to remain in the calculation. In order to determine the factor Nγ, the problem is solved for weighted cohesionless soil (c = 0) without any surcharge on the ground surface. At present, Eq. (13) is used for calculating the factor Nγ, Noting that to avoid floating error, surcharge (q) must be considered near the zero. In order to compute the factor N q , the soil is supposed to be weightless and cohesionless. Instead; there is a uniform surcharge over the ground surface. To continue, by using Eq. (14) the N q is calculated. Factor N c can be assessed by taking the cohesive weightless soil and without any surcharge on the ground surface. The Eq. (15) is used to obtain the N c .

$$N_{\gamma } = \frac{{q_{u} }}{{\gamma (r_{o} - r_{i} )}}$$
(13)
$$N_{q} = \frac{{q_{u} }}{q}$$
(14)
$$N_{c} = \frac{{q_{u} }}{c}$$
(15)

4 Results

The values of the bearing capacity factors Nγ, N q and N c are computed based on the quantities of \({{r_{i} } \mathord{\left/ {\vphantom {{r_{i} } {r_{0} }}} \right. \kern-0pt} {r_{0} }} = 0, \, 0.25, \, 0.5, \, 0.7, \, 0.9\) and a wide range of internal friction angles (ϕ = 5°–50°) with intervals of 5°. These factors are derived for smooth and rough footings as shown in Tables 1, 2 and 3. The magnitudes of the bearing capacity factors for a rough footing are more than a smooth footing base.

Table 1 Values of N γ for smooth and rough ring footing
Full size table
Table 2 Values of N q for smooth and rough ring footing
Full size table
Table 3 Values of N c for smooth and rough ring footing
Full size table

In plane strain footing problem, the footing roughness has no effect on the value of N q and N c (Chen 1975). In the present study, different results are obtained for the axisymmetric ring footing problem. This can be explained by paying attention to the shear stress beneath the rough footing base, which diverts the directions of characteristic lines to be more extended than the smooth footing base.

When the soil is weightless (i.e., γ = 0), the extension of characteristic lines does not influence the stress values [see Eq. (10)], but the existence of unit weight as a body force inside the soil leads to the change the stress Mohr circles.

Figures 4 and 5 shows global scheme of the characteristic lines generated under the footing zone separately to calculate Nγ and Nq (or Nc).

Fig. 4
figure 4

The scheme of the characteristics lines generated under the footing zone, N γ (n = 0.5, figure is from authors’s code)

Full size image
Fig. 5
figure 5

The scheme of the characteristics lines generated under the footing zone, \(N_{q} {\text{ or N}}_{\text{c}}\) (n = 0.5, figure is from authors’s code)

Full size image

5 Comparison

5.1 Nγ

In order to verify the accuracy of the written code to calculate the Nγ of ring footing, the values of Nγ for the circular footing (ri = 0) with smooth and rough base are compared with Bolton and Lau (1993), Cassidy and Houlsby (2002), Kumar and Ghosh (2005), and Zhao and Wang (2008) in Table 4. The results of the present study indicate that the values for smooth base are very close to those of the previous studies. About the circular footing with rough base, the results of the present study are close to Cassidy and Houlsby (2002) and Kumar and Ghosh (2005) but there is considerable difference with Bolton and Lau (1993), and Zhao and Wang (2008) in the assumed rough conditions. Bolton and Lau (1993), and Zhao and Wang (2008) considered a full rough base but others a linear or nonlinear variation of angle of interface friction considered from the centerline to edge of footing. The interface friction angle increases from zero at the axis of symmetry to the outer edge of the footing.

Table 4 Comparison of N γ values for circular footing with smooth and rough base
Full size table

The computed values of Nγ for smooth and rough ring footing with various range of (ϕ) and (r i /r o ) are compared with Kumar and Ghosh (2005) and Zhao and Wang (2008). A comparison of all these results is shown in Figs. 6 and 7. As mentioned earlier for smooth condition, results are close to each other. But due to different conditions for interface angle, the results are different for rough condition.

Fig. 6
figure 6

Comparison of smooth N γ values from this study with the previous studies

Full size image
Fig. 7
figure 7

Comparison of rough N γ values from this study with the previous studies

Full size image

5.2 N q

In order to verify the accuracy of the written code to calculate the Nq of ring footing, the computed values of Nq for the circular footing (ri = 0) with smooth and rough base, are compared with Bolton and Lau (1993) in Table 5. The results of smooth base are very close in these studies. It is worth noting that, there was no similar study to compare N q values for ring footing with the present study.

Table 5 Comparison of \(N_{q}\) values for circular footing with smooth and rough base
Full size table

5.3 N c

The N c values for the circular footing (ri = 0) with a smooth and rough base over cohesive soil are compared with Houlsby and Wroth (1982), Tani and Craig (1995), Houlsby and Martin (2003), Chakraborty and Kumar (2015) in Table 6. The rough values are greater than smooth values. Also there is no similar study (like N q ) to compare values of ring footing with the present study.

Table 6 Comparison of \(N_{c}\) values for the smooth and rough circular footing
Full size table

6 Derived Equations

By analyzing the computed results of bearing capacity factors for ring footing, two equations are suggested.

$$N_{q} \approx \exp \left( {\left( {6.25 - n^{2} } \right) \tan 0.96\phi } \right)$$
(16)
$$N_{\gamma } \approx 0.35\left( {1 - n} \right)\left( {n + 1.5} \right)N_{q} \tan 0.9\phi$$
(17)

Also the relation between N q and N c is checked. The computed values of N c from relation (18) is completely equal to values from the written code in the present study.

$$N_{c} = (N_{q} - 1){ \cot }\phi$$
(18)

7 Principle of Superposition

By considering the frictional–cohesive-weighted soil, bearing capacity is calculated by the written code. Two problems are defined for each of smooth and rough bases of ring footings. The parameters for these problems are shown in Table 7.

Table 7 The parameters for problem 1 and 2
Full size table

Terzaghi (1943) proposes Eq. (12) to calculate the bearing capacity of foundations by considering the principle of superposition. Note that principle of superposition is a conservative method to obtain bearing capacity. In order to verify the accuracy of the written code to calculate the bearing capacity, a comparison between the Superposition method (by using the bearing capacity factors) and the direct results of written code, for ri = 0 (circular footing) is shown in Table 8. The average differences of bearing capacity in these methods are 10%. In the present study, by superposing the calculated bearing capacity factors (and the parameters from Table 7) in Eq. (12), the bearing capacity of ring footing is measured. In Fig. 8a, b, c, d, the results of bearing capacity by using the superposition method (Eq. 12), comparison with the direct result of the written code (without using the bearing capacity factors). So by using the calculated bearing capacity factors in superposition method, the bearing capacity of ring footings can be calculated as a conservative method.

Table 8 Comparison of bearing capacity of problem 1 and 2 for circular foundation
Full size table
Fig. 8
figure 8

Comparison of the written code with superposition principle for a problem 1 (smooth base), b problem 2 (smooth base), c problem 1 (rough base), d problem 2 (rough base)

Full size image

8 Conclusion

The method of characteristics is employed to transform a hyperbolic differential equations into a system of ordinary differential equations. These equations form the coding basis for calculating the bearing capacity of ring footings with smooth and rough bases. In this study, the soil obeys the Mohr–Coulomb yield creation and this soil is cohesive–frictional including unit weight and surcharge. Nγ, N q and N c are bearing capacity factors which are determined for different conditions of soil. In the present study, comprehensive series of bearing capacity factors are presented for different ratio of internal radius to external radius of the ring footings and a wide range of internal friction angle.

By analysis of these values, some equations are suggested for these factors. The findings demonstrate that by using the calculated bearing capacity factors in superposition equation, the bearing capacity of ring foundation can be determined. The average differences of bearing capacity in these methods are 10%.

This study compares Nγ values of ring footing with those of previous studies but there were no similar studies about N q and N c of ring footing to compare. Hence, the calculated bearing capacity factors N q and N c by written code for circular footings (ri = 0) are compared with others studies.

Moreover, Bolton and Lau (1993) point out that the Nq is same for smooth and rough circular foundation, unlike the present study. Hence, Nq and Nc are calculated for a wide range of internal friction angles and different geometric conditions of ring foundation.

Finally, using values of the bearing capacity factors of ring foundation leads to the exact calculation of the bearing capacity and optimal economic design.