Dynamic Response of Pile Reinforced Soils and Piled Foundations

Abstract

The rigid-pile soil-improvement technique aims to increase the bearing capacity of the soil and decrease the settlement of the surface structure. The most remarkable difference of this technique from the deep-foundation system is the soil layer between the pile heads and the structure. This soil layer, called the mattress, is made of compacted granular materials and participates in the load transfer through arching and shear mechanisms. In order to understand the dynamic behavior of rigid-pile reinforced soils, tri-dimensional finite-element analyses of a soil-pile-slab system, a soil-pile-mattress-slab system, and a soil-pile-mattress-embankment system are presented in this paper. Different geometric configurations are studied in terms of dynamic impedances. The soil, piles, mattress, and embankment are represented as continuum solids, and the slab is represented by structural plate-type elements. The horizontal and vertical impedances of pile foundations are presented and the results are compared with studies in the literature. This study shows the influence of the mattress stiffness, the geometrical configuration, and head/tip fixity conditions on the dynamic response of the foundation system. A comparison between rigid piles and pile foundations is then presented.

1 Introduction

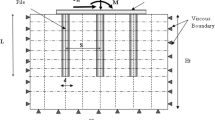
The technique of soil reinforcement by rigid piles, which has been widely used in the construction of industrial structures, slab foundations, and embankments, has experienced tremendous growth in recent years. The design of rigid-pile reinforced soils comprises two main elements: the piles, and the granular mattress (earth-platform). The load transfer is accomplished by a combination of rigid piles through the soft soil and a granular mattress placed between the network of rigid piles and the structure. This mattress distributes the load to the heads of the rigid piles (Fig. 1b, c). The dynamic behavior of rigid piles involves many parameters, including: the mechanical properties of materials; the loading conditions; the interaction between the piles, the soil, and the mattress; and finally, the interactions among all of the soil, piles, mattress, and the structure. It should also be noted that the dynamic behavior of the structure depends on the input frequency.

Fig. 1

Systems studied. a Slab system, b mattress-slab system, c mattress-embankment-slab system

The frequency-domain dynamic analysis of piles and pile groups (Fig. 1a) embedded in a half space has been treated numerically by many authors using either the frequency-domain boundary-element method (BEM) in conjunction with different half-space Green’s function formulations for the soil, or by the finite-element method (FEM) for the piles, considered as mono-dimensional beam elements (Kaynia 1982; Kaynia and Kausel 1991; Mamoon et al. 1990). The coupling of framed structures using 3-D FEM approaches in the time domain has been presented (Coda et al. 1999; Coda and Venturini 1999) where piles are represented by special cylindrical boundary elements. A review of presented techniques concerning the dynamic analysis of piles and pile groups can be found in Beskos (1997). Using BEM for both soil and piles, more versatile and rigorous numerical models have been developed. Vibration isolation by a row of piles has been analysed in Kattis et al. (1999a, b), and dynamic impedances of pile groups have been studied by Vinciprova et al. (2003) and Maeso et al. (2005). The BEM is used to determine the Green’s function, and FEM is used to model the piles, which are considered as one-dimensional beam elements. Piles are modeled using FEM as beam-type elements according to the Bernoulli hypothesis (Padron et al. 2007). The whole system is sub-structured into bounded near field and an unbounded far field systems. The piles-soil system of the near field is modeled using solid finite elements and the unbounded elastic soil system of the far field is modeled using the consistent, infinitesimal, finite-element cell method (CIFECM) in the frequency domain (Emani and Maheshwari 2009).

In order to determine the dynamic response of a structure, it is important to study the dynamic behavior of foundations (Fig. 1a). This research is devoted to the analysis of soil-pile-mattress-structure systems under dynamic loading. Hatem (2009) studied the behavior of the soil-pile-mattress-structure interaction under seismic loads using finite-difference elements. Okyay (2010) studied the influence of the rigid-pile end-fixity conditions on the dynamic behavior of the soil-pile-mattress-structure system under dynamic loading. In this context, Okyay et al. (2012) used a series of dynamic tests conducted on an experimental site and developed numerical models to interpret dynamic response of rigid pile-reinforced soils.

In this article, 3-D finite element analyses of several systems have been performed for the calculation of the dynamic impedances and the amplitude of displacement. The finite-element software CODE-ASTER 10.2 (CODE-ASTER) is used for the numerical analysis. The soil, piles, mattress, and embankment are represented by continuum solids and the slab is represented by structural plate type elements. To simulate a semi-infinite elastic space, quiet boundaries are placed at the borders of the model to avoid wave reflection. The horizontal and vertical impedances of pile foundations are calculated and the results are compared with previous studies.

A selection of numerical results is presented to show the influence of the mattress stiffness, the presence of a slab or an embankment, and the pile-soil contact conditions on vertical and horizontal amplitudes of displacements.

2 The Substructure Theorem

The formulation of the superposition theorem can be obtained using the substructure technique. This approach leads to a set of equations for the forces applied at the foundation of the structure (Kausel et al. 1978; Aubry and Clouteau 1992; Pecker 1984). Assuming a rigid foundation, it makes sense to split the overall problem into sub-problems.

Considering a finite-element discretization of the soil-structure systems as shown in Fig. 2a, the soil and structure have been separated, and the equilibrium between these two zones is preserved by application of the inertial forces P_b and P_f. The model is subjected to an arbitrary excitation (using specified displacements) along the common boundary (Fig. 2b).

Fig. 2

Sub-structure method. a Soil-structure interaction problem, b free-field problem

For a solution in the frequency domain, the matrix equations relating the forces and displacements are $\left( { - \omega^{2} M + i\omega C + K} \right) \cdot U = P,$ where M is the mass matrix, C is the damping matrix, and K is the stiffness matrix. P and U are the force and displacement vectors, respectively, where ω is the circular frequency.

For the sake of simplicity, the frequency-dependent complex sub matrices of the dynamic stiffness matrix will be denoted by $K_{d} = K + i\omega C - \omega^{2} M.$ The force–displacement relationships for the various sub-structures are then:

for the structure,

$$\left[ \begin{aligned} K_{ss} \,\,\,\,\,\,\,\,K_{sb} \hfill \\ K_{bs} \,\,\,\,\,\,K_{bb} \hfill \\ \end{aligned} \right]\,\left\{ \begin{aligned} U_{s} \hfill \\ U_{b} \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} 0 \hfill \\ P_{b} \hfill \\ \end{aligned} \right\};$$

(1)

for the sub-grade, including soil-structure interaction,

$$\left[ {\begin{array}{*{20}c} {K_{ff} } & {K_{fg} } & {K_{fr} } \\ {K_{gf} } & {K_{gg} } & {K_{gr} } \\ {K_{rf} } & {K_{rg} } & {K_{rr} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {U_{f} } \\ {U_{g} } \\ {U_{r}^{*} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {P_{f} } \\ 0 \\ {P_{r} } \\ \end{array} } \right\};$$

(2)

for the sub grade, free-field solution,

$$\left[ {\begin{array}{*{20}c} {K_{ff} } & {K_{fg} } & {K_{fr} } \\ {K_{gf} } & {K_{gg} } & {K_{gr} } \\ {K_{rf} } & {K_{rg} } & {K_{rr} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {U_{f}^{*} } \\ {U_{g}^{*} } \\ {U_{r}^{*} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {P_{f}^{*} } \\ 0 \\ {P_{r}^{*} } \\ \end{array} } \right\};$$

(3)

The sub-indices above refer to the following: s, for the nodes of the structure, excluding the soil-structure interface; b, for the nodes of the structure along the interface; f, for the nodes of the soil along the same interface; g, for nodes of the soil, excluding the interface and boundaries; and r, for the nodes along the boundary. The asterisk refers to the free-field solution.

Notice that both the free-field problem and the soil-structure-interaction problem are subjected to the same excitation $U_{r}^{*} .$ In general, $P_{r} \ne P_{r}^{*}$ unless the boundary is far away from the structure.

Subtracting (3) from (2) leads to

$$\left[ {\begin{array}{*{20}c} {K_{ff} } & {K_{fg} } & {K_{fr} } \\ {K_{gf} } & {K_{gg} } & {K_{gr} } \\ {K_{rf} } & {K_{rg} } & {K_{rr} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {U_{f} - U_{f}^{*} } \\ {U_{g} - U_{g}^{*} } \\ 0 \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {P_{f} - P_{f}^{*} } \\ 0 \\ {P_{r} - P_{r}^{*} } \\ \end{array} } \right\};$$

(4)

Condensing the matrix equation above then gives

$$K(U_{f} - U_{f}^{*} ) = P_{f} - P_{f}^{*}$$

(5)

where K = K(ω) is the sub grade impedance matrix. On the other hand, equilibrium and compatibility require that

$$P_{f} = - P_{b} ,P_{f}^{*} = - P_{b}^{*} ,U_{f} = U_{b} ,U_{f}^{*} = U_{b}^{*} ,\quad{\text{ so that}}\,K\left( {U_{b} - U_{b}^{*} } \right) = - P_{b} - P_{f}^{*} = P_{b}^{*} - P_{b} ,$$

(6)

where P _f vector forces(moments) derived from the inertial effect of the superstructure, the vector of forces (moments); $P_{f}^{*}$ vector forces are derived from kinematic effect of the soil; U _f , is the answer to the soil-foundation interface; and $U_{f}^{*}$ is the response of movement in the free field at the soil-foundation interface.

Taking the system of Eq. (4), only the soil-foundation interface is loaded by the force vector, which is applied to the center of the slab. The impedance matrix is calculated according to the ratio between the applied force and the displacement obtained at the center of the slab:

$$K_{ij} (\omega ) = \frac{{\left( {P_{f} - P_{f}^{*} } \right)\,e^{i\omega t} }}{{(U_{f} - U_{f}^{*} )(\omega )}}$$

(7)

When the rigid foundation is massive, one simply has to replace [K] by [K] − ω ²[M]in the above equations, where [M] is the mass matrix of the slab (foundation).

Substitution of (6) into (1) then yields

$$\left[ \begin{aligned} K_{ss} & \,\,\,\,\,\, K_{sb}\hfill \\ K_{bs} & \,\,\,\,\,\, K_{bb} + K \hfill \\ \end{aligned} \right]\,\left\{ \begin{aligned} U_{s} \hfill \\ U_{b} \hfill \\ \end{aligned} \right\} = \left\{ \begin{array}{*{20}l} 0 \\ KU_{b}^{*} + P_{b}^{*} \\ \end{array} \right\}$$

(8)

and states that the solution to the soil-structure interaction problem can be obtained (for the structure) by application of fictitious forces $P_{b} = P_{b}^{*} + KU_{b}^{*}$ at the foundation-soil interface. $P_{b}^{*} \,{\text{and}}\,U_{b}^{*}$ are once again the free field forces and displacements along this interface. However, the sub-grade impedance matrix K is not easily obtainable, except for the particular case of zero embedment. For ideally rigid embedded foundations, the components of the displacement vector U _b can be expressed in terms of the rigid body displacements and rotations of the foundation, defined at some point (for instance, the center of the foundation)

$$U_{b} = F \cdot U_{0}$$

(9)

where F is the rigid body transformation matrix and U₀ contains the rigid body displacements and rotations.

The solutions presented in the following sections have been obtained by using a 3-D FEM formulation. A fundamental feature of the calculation code is the accurate representation of the model boundary (Fig. 1), which separates the finite-element region from the semi-infinite continuum (the free field). The implementation of the paraxial elements comes primarily from the need to decompose the displacement component along the normal to the element, corresponding to a P wave, and a component in the plane of the element, corresponding to an S wave. This corresponds to viscous dampers distributed along the boundaries of the models. The construction of a viscous damping pseudo-matrix permits us to subsequently represent the presence of an infinite domain.

3 Validation of the Numerical Model

In order to validate the numerical model, several results of impedances of pile groups have been computed and compared with other reference values present in the literature. The dynamic stiffness (impedances) matrix K_ij of a pile relates the vector of forces (and moments) applied at the slab to the resulting vector of displacements (and rotations) at the same point. For a group of piles (Fig. 3), it is assumed that the heads are connected by a rigid slab and that the foundation stiffness is the sum of the contributions of each pile, where L and d are used to denote the length and diameter of the piles, respectively, and S refers to the distance between adjacent piles.

Fig. 3

Numerical model for the validation case (slab system)

The mechanical properties of the soil layer and of the foundations are presented in Table 1. The choice of these properties was based on a literature survey (Emani and Maheshwari 2009; Padron et al. 2007).

Table 1 Geotechnical and mechanical properties of soft soil and slab/piles

The dynamic stiffness is a function of dimensionless frequency a_o and written as

$$K_{ij} = k_{ij} + i\,a_{o} \,c_{ij} ,$$

(10)

where k_ij and c_ij are the dynamic stiffness and damping coefficients, respectively and a_o is the dimensionless frequency.

The dynamic stiffness matrix K_ij of a pile group subjected to a vector of forces applied at the center of the slab is calculated as a function of displacement vectors resulting in the same point of application of vector forces. The piles are connected to the slab which is infinitely rigid.

3.1 Dynamic Impedance Calculation

In this study, a vertical load is used to determine the vertical impedance, and a horizontal load is used to determine the horizontal impedance. The displacement response is obtained by taking the product of the function of the excitation force by the transfer function amplitude of the displacement. The vertical and horizontal impedance functions have been normalized with regard to the respective single-pile static-stiffness (K_s) multiplied by the number (n) of piles in the group. All results are plotted versus the frequency parameter.

Figure 4 shows a comparison between the results obtained by numerical modeling and the results of the literature. Figure 4a shows the variation of the vertical impedance of 3 × 3 pile groups, in which the dimensionless distance S/d between the piles is taken to be equal to 2, 5, and 10 and the dimensionless length L/d is equal to 15. The results of the present study are in good agreement with the results obtained by Padron et al. (2007). Figure 4b shows the variation of the dynamic impedance function K_xx versus the dimensionless frequency with a comparison between the results obtained by the present numerical simulation and the results obtained by Padron et al. (2007). The results obtained by the present study are also in good agreement with the results obtained by Padron et al. (2007). Padron et al. (2007) use a BEM–FEM coupling model for the time harmonic dynamic analysis of piles and pile groups embedded in an elastic half-space. Piles are modelled using FEM as a beam according to the Bernoulli hypothesis, while the soil is modelled by BEM as a continuum, semi-infinite, homogeneous and viscoelastic medium. In the present study the FEM with absorbing boundaries is used.

Fig. 4

Validation case: vertical and horizontal impedance of a 3 × 3 pile groups L/d = 15, S/d = 2, S/d = 5 and S/d = 10. a Vertical (n is the piles number and Ks_zz is the vertical static impedance), b horizontal (Ks_xx is the horizontal static impedance)

4 Numerical Study

4.1 Objectives

In this study, the dynamic response of pile reinforced soils and piled foundations is analysed by means of the impedance approach and evaluated according the elasticity theory. The impedance solutions do not consider soil inelasticity and can only be calculated using an elastic constitutive model. In most of the seismic event cases, the shear strains reached during the event are very low and inferior to 10⁻⁵. Some authors (Hejazi et al. 2008) have shown that for this shear strain levels, the Young modulus can be considered as a constant.

If the strength failure will be reached, the mattress will act as a fuse for the superstructure and will dissipate energy by shearing mechanisms. Our study cannot take into account of these mechanisms and is only valid for the low shear strains.

A new academic case is introduced with four main objectives in terms of dynamic impedances:

• Influence of the pile toe fixity conditions for the Mattress-Slab system. Several cases are tested (floating, placed on bedrock, or anchored);

• Influence of the mechanical properties of the Mattress for the Mattress-Slab system;

• Influence of an embankment (mattress-embankment-slab system); and

• Influence of the thickness of soft soil layer.

A reference case has been defined corresponding to the one presented in Fig. 1b. It represents the Mattress-Slab system with piles placed on the bedrock. Based on this case, several numerical analyses have been performed.

4.2 Numerical Models

4.2.1 Definition of the Reference Case (Mattress-Slab System With Piles Places on the Bedrock)

The geometrical dimensions of the model (Fig. 5) are 40 m × 40 m × 15 m. The numerical analyses were performed with 30 piles. The length of the piles is 10 m. Their diameter is equal to 0.30 m and leads to a length/diameter ratio equal to 33.34. A rectangular grid of 2 m × 2 m was chosen and corresponds to an area ratio of 1.7 %.

Fig. 5

Numerical half model for the validation case (mattress-slab system). a Half numerical model, b zoom on the rigid piles, c geometry of the rigid piles. 1 Slab of 0.5 m thickness, 2 mattress of 0.6 m thickness, 3 soft soil, 4 hard soil, 5 piles. S is the distance between the axis of the pile (axis to axis distance)

A load-transfer mattress of 0.60 m thickness is placed on the top of the piles and then a concrete rigid slab is setup on the top of this model. The slab is represented by 2-D structural elements with a thickness of 0.5 m.

The soil layers are assumed to be horizontal in a semi-infinite medium. The homogeneous medium is considered as a viscoelastic and isotropic half-space. Table 2 shows the used elastic material properties. The characteristics are deduced from the study of Okyay (2010) and Okyay et al. (2012). The choice of the model and the size of the finite elements are in agreement with the wavelength to minimize the effect of distortion waves. The maximum frequency which can be applied depends on the maximum size of the element. Kuhlemeyer and Lysmer (1973) show that the size mesh element must be less than one tenth of the wavelength λ,

Table 2 Geotechnical and mechanical properties of soil and piles for dynamic analysis

$$f = \frac{{C_{s} }}{10.\Delta l} = \frac{\omega }{2\pi }$$

(11)

with C_s the shear-wave velocity, ∆l the size of the mesh element and ω the circular frequency of excitation.

Free-field boundaries are attributed to the vertical faces and to the bottom face of the numerical model. Paraxial elements are assigned to the free boundaries to answer soil-structure interaction problems and to satisfy the Sommerfield conditions. The scattered fields are only outgoing waves at infinity to address the Frequency Domain Problem. Thus, one eliminates the diffracted elastic plane waves and the incoming non-physical waves from infinity.

For the calculation of vertical dynamic impedances, a quarter model of the global system is used (Fig. 5). For the horizontal ones, the half model has been considered (Fig. 5). For all the other systems, only the geometry differs.

4.2.1.1 Slab System

The load-transfer mattress is not present and the same slab as in the reference case (Fig. 6) is placed over the mattress. This slab is perfectly connected to the piles sharing same nodes.

Fig. 6

Numerical half model for the slab system. 1 Quarter slab of 0.5 m thickness; 2 piles; 3 soft soil; 4 hard soil

4.2.1.2 Mattress-Embankment-Slab System

In this case, the mattress of 0.6 m thick is covered by 7 m height embankment and placed over the piles (Fig. 7). It has the shape of a truncated pyramid. The slope of the embankment is 37°. The characteristics of the embankment are presented in Table 2. The embankment has been placed on the transfer mattress in seven steps, each 1 m high. The same slab as in the reference case (Fig. 5a) is placed over the mattress for the dynamic impedance calculation.

Fig. 7

Numerical half model of the mattress-embankment-slab system (5 m embankment height case). 1 Slab, 2 mattress, 3 soft soil, 4 bedrock, 5 piles, 6 embankment layers

4.2.2 Displacements Calculation

To calculate the dynamic displacements, harmonic forces are applied at the centre of the slab. Calculations are performed for each excitation frequency between 0 and 20 Hz. The dynamic response (Pradhan et al. 2004) of the massless foundation is expressed by

$$\left| {u_{0} } \right| = \left| {\frac{F}{{K_{s} \left[ {k(a_{0} ) + ia_{0} \,c\,(a_{0} )} \right]}}} \right|,$$

(12)

where $\left| {u_{0} } \right|$ is the dynamic displacement amplitude, F is the force amplitude, K_s is the static stiffness, k(a₀) is the stiffness coefficient, and c (a₀) the damping coefficient with a₀ the dimensionless frequency.

To simplify the analysis and the comparison between the results of the numerical calculations and the experimental data, the ratio $\left| {{\text{U}}/{\text{F}}} \right|$ is used, i.e., the amplitude of displacement is

$$\left| {\,\frac{1}{{K\,\left( {a_{0} } \right)}}\,} \right| = \left| {\,\frac{{U_{0} \,\left( {\,t\,} \right)}}{{F_{0} \,\left( {\,t\,} \right)}}\,} \right| = \frac{1}{{K_{S} \sqrt {\,\left[ {k\,\left( {a_{0} } \right)} \right]\,^{2} + \left[ {\,a_{0\,} c\,\,\left( {a_{0} } \right)} \right]\,^{2} } }} = \frac{U}{F} ,$$

(13)

where $\left| . \right|$ corresponds to the modulus operator.

4.3 Influence of the Pile Toe Position Versus the Bedrock for the Mattress-Slab System (Reference Case)

Considering the reference case and a soft soil height of 10 m, the pile length is studied in the range [5, 15] m. The cases from 5 to 10 m pile length correspond to floating piles. When the length is equal to 10 m, it represents the case of the piles lying on the hard soil and higher piles lengths correspond to anchored cases.

The variations of the vertical response $\left| {{\text{\bf{U}}}/{\text{\bf{F}}}} \right|$ depending on the frequency are shown on Figs. 8 and 9. They respectively show the influence of the pile toe position on the variation of the vertical dynamic impedance for the Mattress-Slab and the Slab systems. These figures show that the evolution of the dynamic impedances of the two systems is the same, although the amplitudes are different, and also show the influence of the support layer on the dynamic impedance. The peak values of dynamic impedances are given by the floating system.

Fig. 8

Vertical dynamic response—influence of the pile toe position for the mattress-slab system with a modulus of elasticity of the mattress of 50 MPa

Fig. 9

Vertical dynamic response—influence of the pile toe position for the Slab system

The displacements are significantly reduced when the support layer is near the pile toe, especially for low frequencies. The anchored piles provide more rigidity to the system than the other systems.

The horizontal dynamic impedances are calculated by applying a horizontal load on a half-model. The horizontal responses are not affected by the pile toe position (Fig. 11). Only the horizontal responses for the piles lying on the hard soil are then presented in Fig. 10. The comparison between the Mattress-slab and the Slab systems shows that the dynamic responses are strongly attenuated at high frequencies. The Mattress-slab system has a high efficiency in cases of dynamic loading in comparison with the Slab one. It reduces the horizontal dynamic response of 50 %.

Fig. 10

Horizontal dynamic response—comparison between the mattress-slab and the Slab systems with a modulus of elasticity of the mattress of 50 MPa

Figure 11 presents the maximum values of the ratio $\left| {{\text{U}}/{\text{F}}} \right|$ versus piles length obtained at a frequency of 2.5 Hz for the vertical direction and 1.5 Hz for the horizontal one.

Fig. 11

Vertical and horizontal responses for the maximum $\left| {{\text{U}}/{\text{F}}} \right|$—comparison between the slab and the mattress-slab systems

In terms of vertical response, the behaviors of mattress-slab and of slab systems are similar for pile lengths which are superior to 8 m. When the pile toe position is more than 2 m from the substratum, the movement amplification is higher for the Slab system. For a pile length of 5 m, the difference is 30 %. The mattress between the piles and the slab enables absorption of part of the vertical movement.

For the horizontal response, the mattress-slab system is more efficient than the slab system for all piles lengths.

4.4 Influence of the Mattress

An extensive study based on the reference case has been done. The studied range for the elasticity modulus of the mattress is comprised between 10 and 1000 MPa.

Figure 12 shows that the Mattress modulus has a low impact on the vertical response for the Slab and the Mattress-slab system. For this last case, the higher amplifications are observed for the lower modulus.

Fig. 12

Vertical dynamic response—influence of the Young modulus of the mattress

Figure 13 illustrates the horizontal response. A modulus of 25 MPa of the Mattress in the Mattress-slab system is equivalent to the amplification given by the Slab case. The elasticity modulus is an important parameter for values lower than 300 MPa. A modulus of 10 MPa gives an amplification 10 times higher than for a modulus of 300 MPa (Fig. 14). All the moduli of elasticity presented here are dynamic modules. In practice, the Young static modulus of a granular soil is in the range 50–300 MPa. Considering a ratio between the dynamic and static modulus of 6, the value of 300 MPa for a dynamic modulus is in the lower part of the given range and corresponds to a static modulus of 50 MPa. This tends to prove that in practice lower values than 300 MPa will not be realistic and that the high amplification seen in Fig. 14 will not appear in reality.

Fig. 13

Horizontal dynamic response—influence of the Young modulus of the mattress

Fig. 14

Vertical and horizontal responses for the maximum $\left| {{\text{\bf{U}}}/{\text{\bf{F}}}} \right|$—influence of the Young modulus of the mattress

4.5 Influence of an Embankment (Mattress-Embankment-Slab System)

Figure 16 shows the influence of the embankment height on the horizontal response. For low height embankments, the dynamic response is similar as the one of the Mattress-Slab system. The amplification increases with the mattress height and can reach a value of 2.85 for an embankment height of 7 m. In this case, the variation of the embankment height does not change the resonant frequency of the system response.

Figure 15 shows the influence of the embankment height on the vertical response. The amplitude of the amplification increases with the increase of the embankment height. The resonant frequency is reduced with the embankment height. For an embankment height of 0.5 m, the resonant frequency is equal to 3.3 Hz and for a 7 m height embankment this frequency is equal to 2.7 Hz. This is can be due to the increase of the mass of the embankment (increase the height of the embankment) that causes a shift of the resonant frequency to lower frequencies but with increasing amplitudes (well known phenomenon in dynamic) Fig 16.

Fig. 15

Horizontal dynamic response—influence of the embankment height

Fig. 16

Vertical dynamic response—influence of the embankment height

Figure 17 shows the influence of the embankment height on the horizontal dynamic response. The amplification is proportional to the embankment height. A linear relation between $\left| {{\text{U}}/{\text{F}}} \right|$ and the embankment height (H_rs) can be assumed. The unit $\left| {{\text{\bf{U}}}/{\text{\bf{F}}}} \right|$ is in mm/MN. The given relations are equal to:

Fig. 17

Vertical and horizontal responses for the maximum $\left| {{\text{U}}/{\text{F}}} \right|$—influence of the embankment height

for the vertical response

$$\left| {{\text{\bf{U}}}/{\text{\bf{F}}}} \right| = \, 0.11{\text{ H}}_{\text{rs}} + \, 2.62;$$

(14)

for the horizontal response

$$\left| {{\text{\bf{U}}}/{\text{\bf{F}}}} \right| = \, 0.08{\text{ H}}_{\text{rs}} + \, 2.27$$

(15)

The height of embankment induces an increase of respectively 22 and 23 % of the vertical and of the horizontal amplification in the considered range. This parameter does not modify the behavior of the system but modifies the resonant frequency of the system causing a shifting to the low frequency.

4.6 Influence of the Compressible Soil Height

The reference case is used and a parametric study on the soft soil height has been done (see Fig. 18). The Slab and the mattress-slab systems give more less the same vertical dynamic response. It can be considered a linear equation to define the relation between $\left| {{\text{U}}/{\text{F}}} \right|$ and the soft soil heigth (H_ss) (see Fig. 19).

Fig. 18

Vertical and horizontal responses for the maximum $\left| {U/F} \right|$—influence of the soft soil height (reference case)

Fig. 19

Vertical response for the maximum $\left| {{\text{U}}/{\text{F}}} \right|$—influence of the soft soil height (reference case) comparison between the FEM and linear relation

The given relation is equal to:

for the Slab system

$$\left| {{\text{\bf{U}}}/{\text{\bf{F}}}} \right| = \, 0.12{\text{ H}}_{\text{ss}} + 1;$$

(16)

for mattress-slab system

$$\left| {{\text{\bf{U}}}/{\text{\bf{F}}}} \right| = \, 0.11{\text{ H}}_{\text{ss}} + 1.29.$$

(17)

For the horizontal dynamic response, the systems give a different response (Fig. 18). For the Mattress-Slab one, a constant value of 2.6 approximately for $\left| {{\text{U}}/{\text{F}}} \right|$ is obtained. This result shows that the response seems to be independent of the height of the soft soil in the case of piles lying on the hard soil. For the Slab system, an important amplification of the response is observed for soft soil heights inferior to 10 m. When the slab connected to the piles is placed near the surface, important inertial effects appear and can lead to the failure of the surface structure. The recommendation for low soft soil height in seismic zones is to use Mattress-Slab systems.

5 Conclusions

In this study, a tri-dimensional FEM dynamic analysis of several systems (slab, mattress-slab and mattress-embankment-slab), improved by piles, was presented. The calculations took into account the interaction between the several elements: hard soil, soft soil, piles, slab, mattress, and embankment. The developed numerical models permitted the calculation of the dynamic impedance functions, and the vertical and the horizontal dynamic response in terms of $\left| {{\text{U}}/{\text{F}}} \right|$ has been analysed.

A validation of the numerical model has been done by comparison of the numerical results with those of the literature. Then, the influence of the following parameters has been studied:

• Influence of the pile toe position. For floating piles, the amplification for Slab systems is higher than for Mattress-Slab ones. For the horizontal dynamic response, the Mattress-slab systems are recommended. The mattress between the piles and the slab absorbs the inertial effects.

• Influence of the mechanical properties of the mattress. This parameter is very important and the recommandation is that the Young dynamic modulus value must be superior to 300 MPa to avoid important disorders in terms of horizontal dynamic response. This value is however low for a granular material which usually exhibits higher dynamic modulus values.

• Influence of an embankment. The behavior of this type of overload is the same as the Mattress-Slab system. The vertical and horizontal responses of the system increase when the height of embankment increases. An influence of 23 % maximum shows that this parameter is fundamental because it causes a shift of resonant frequency of the system essentially for horizontal case.

• Influence of the soft soil height. In the case of dynamic horizontal responses for Slab system, this parameter has an important influence on amplitudes of vibrations, for attenuating these amplitudes using the Mattress-Slab system.

This study has shed light on the complex phenomenon of the dynamic response of a reinforced system under harmonic loading in the linear domain. This study can be extended to the dynamic response of reinforced system under seismic loading (real earthquake) and under impulsive loading (for road traffic). It is,therefore, necessary to use the laws of non-linear behavior like the elasto-plastic model to the soil surrounding the rigid piles.