Effect of Surcharge on the Stability of Anchored Rock Slope with Water Filled Tension Crack under Seismic Loading Condition

Abstract

In this paper, an analytical expression is derived for the factor of safety of the rock slope incorporating most of the practically occurring destabilizing forces as well as the external stabilizing force through an anchoring system. The slope stability is analyzed as a two-dimensional problem, considering a slice of unit thickness through the slope and assuming negligible resistance to sliding at the lateral boundaries of the sliding block. A detailed parametric study is presented to investigate the effect of surcharge on the stability of the rock slope for practical ranges of governing parameters such as inclination of the slope face, inclination of the failure plane, depth of tension crack, depth of water in tension crack, shear strength parameters of the material at the failure plane, unit weight of rock, stabilizing force and its inclination, and seismic load. For the range of parameters considered in the present study, it is found that the factor of safety of the rock slope decreases with increase in surcharge; the rate of decrease being relatively higher for lower values of surcharge. It is also observed that for a specific surcharge, the factor of safety depends significantly on all other parameters, except for unit weight of rock and higher values of inclination of stabilizing force to the normal at the failure plane. For any combination of these variables, the surcharge plays a vital role in the stability. A perfectly stable slope at relatively low surcharge can become unsafe with the increase in surcharge. The deterioration in the stability can be quite rapid, depending on the combination of the factors under consideration. The analysis and the general expression proposed herein can be used to carry out a quantitative assessment of the stability of the rock slopes.

1 Introduction

Predicting the stability of the rock slopes has always been a challenging problem for civil and mining engineers while dealing with dams, roads, tunnels, opencast mines, etc. Many researchers have focused on problems of the stability of rock slopes even in the recent past (Nawari et al. 1997; Yang et al. 2004; Jimenez-Rodriguez et al. 2006; Yang and Zou 2006; Low 2007; Li et al. 2008). The problems of rock slope stability analysis have also been discussed in many books related to rock engineering (Hoek and Bray 1981; Goodman 1989; Wyllie and Mah 2004; Hoek 2007). There are several ways in which a rock slope can fail such as plane failure, wedge failure or circular failure. In all the plane failure analyzes of rock slopes presented so far in the literature, efforts have been made to consider several destabilizing forces such as weight of the rock mass, uplift force due to water pressure on the failure plane, forces due to water in the tension crack, force applied by anchor system if any, and seismic forces. In spite of the fact that surcharge loading caused by structures, machines, etc., is a common destabilizing force in most mining and civil engineering applications, slope stability analysis considering surcharge, particularly its effect on the factor of safety against the slope failure, has not received proper attention in the past. Therefore, the objective of this paper is to investigate the effect of surcharge load on the stability of a rock slope by developing an expression for the factor of safety incorporating most of the practically occurring destabilizing forces as well as an external stabilizing force through the anchoring system. The expression is used for carrying out a parametric study where the effects of several variables, particularly the magnitude of surcharge, are analyzed.

2 Analytical Formulation

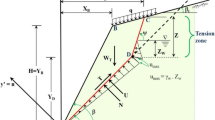
Figure 1 shows a rock slope of height H and inclination ψ _f to the horizontal. PQRS is the sliding block of the rock mass separated by the joint plane QR as the sliding failure plane and a vertical tension crack RS of depth z at a distance B behind the crest P of the slope. The angle of inclination of the joint plane QR to the horizontal is ψ _p. The tension crack is filled with water to a depth z _w. To simulate the effect of rock anchoring system such as rock bolts or cables, an external force T, inclined at an angle θ to the normal at the failure plane QR, is applied on the slope face PQ. The weight of the sliding block is W. The horizontal seismic force k _h W is also considered, where k _h is the horizontal seismic coefficient. It is assumed that water enters the failure plane through the bottom of the tension crack and seeps along the sliding plane, escaping at atmospheric pressure where the failure plane daylights in the slope face. The horizontal force due to water pressure in the tension crack is V, and the uplift force due to water pressure on the failure plane is U. The surcharge acting at the top of the slope is q. The slope stability is studied as a two-dimensional problem, considering a slice of unit thickness through the slope, as suggested by Hoek (2007). It is also important to recognize that this analysis considers only force equilibrium without considering any resistance to sliding at the lateral boundaries of the sliding block.

Fig. 1

Geometry of the anchored rock slope with tension crack and forces acting on the slope

The factor of safety FS of the slope is defined as (Hoek and Bray 1981; Wyllie and Mah 2004; Hoek 2007):

$$ {FS} = \frac{{F_{\text{r}} }}{{F_{\text{i}} }} $$

(1)

where F _r is the total force available to resist sliding, and F _i is the total force tending to induce sliding.

The shear strength of the sliding failure plane can be defined in terms of the Mohr–Coulomb failure criterion as:

$$ \tau = c + \sigma_{\text{n}} \tan \,\phi $$

(2)

where σ _n is the normal stress acting on the failure plane, c is the cohesion, and $\phi$ is the angle of shearing resistance of the material at the failure plane.

From Fig. 1, the total force F _r available to resist sliding is calculated as:

$$ \begin{aligned} F_{\text{r}} = & \tau \times A \\ = & (c + \sigma_{\text{n}} \tan \,\phi )A \\ = & cA + \{ W(\cos \,\psi_{\text{p}} - k_{\text{h}} \sin \,\psi_{\text{p}} ) - U - V\,\sin \,\psi_{\text{p}} + T\,\cos \,\theta + qB\,\cos \,\psi_{\text{p}} \} \tan \,\phi \\ \end{aligned} $$

(3)

where A is the base area of the sliding block.

From Fig. 1, the total force tending to induce sliding is calculated as:

$$ F_{\text{i}} = W(\sin \,\psi_{\text{p}} + k_{\text{h}} \cos \,\psi_{\text{p}} ) + V\,\cos \,\psi_{\text{p}} - T\,\sin \,\theta + qB\,\sin \,\psi_{\text{p}} $$

(4)

Substituting the values from Eqs. 3 and 4 into Eq. 1, the expression for the factor of safety FS is obtained as:

$$ {FS} = \frac{{cA + \{ W(\cos \,\psi_{\text{p}} - k_{\text{h}} \sin \,\psi_{\text{p}} ) - U - V\,\sin \,\psi_{\text{p}} + T\,\cos \,\theta + qB\,\cos \,\psi_{\text{p}} \} \tan \,\phi }}{{W(\sin \,\psi_{\text{p}} + k_{\text{h}} \cos \,\psi_{\text{p}} ) + V\,\cos \,\psi_{\text{p}} - T\,\sin \,\theta + qB\,\sin \,\psi_{\text{p}} }} $$

(5)

From Fig. 1, the expressions for B, A, W, V and U are obtained as follows:

$$ B = (H - z)\cot \,\psi_{\text{p}} - H\,\cot \,\psi_{\text{f}} $$

(6a)

$$ A = (H - z){\text{cosec}}\,\psi_{\text{p}} $$

(6b)

$$ \begin{aligned} W = & \left[ {\frac{1}{2}\{ B + (H - z)\cot \,\psi_{\text{p}} \} H - \frac{1}{2}(H - z)(H - z)\cot \,\psi_{\text{p}} } \right]\gamma \\ = & \frac{1}{2}\gamma \{ BH + z(H - z)\cot \,\psi_{\text{p}} \} \\ = & \frac{1}{2}\gamma H^{2} \left[ {\left\{ {1 - \left( {\frac{z}{H}} \right)^{2} } \right\}\cot \,\psi_{\text{p}} - \cot \,\psi_{\text{f}} } \right] \\ \end{aligned} $$

(6c)

where γ is the unit weight of the rock.

$$ V = \frac{1}{2}\gamma_{\text{w}} z_{\text{w}}^{2} $$

(6d)

where γ _w is the unit weight of water.

$$ \begin{aligned} U = & \frac{1}{2}\{ (H - z){\text{cosec}}\,\psi_{\text{p}} \} (\gamma_{\text{w}} z_{\text{w}} ) \\ = & \frac{1}{2}\gamma_{\text{w}} z_{\text{w}} (H - z){\text{cosec}}\,\psi_{\text{p}} \\ \end{aligned} $$

(6e)

Combining Eqs. 5 and 6a–e gives:

$$ {FS} = \frac{{c(H - z){\text{cosec}}\,\psi_{\text{p}} + \left[ {\begin{array}{*{20}c} {\frac{1}{2}\gamma H^{2} \left[ {\left\{ {1 - \left( {\frac{z}{H}} \right)^{2} } \right\}\cot \,\psi_{\text{p}} - \cot \,\psi_{\text{f}} } \right](\cos \,\psi_{\text{p}} - k_{\text{h}} \sin \,\psi_{\text{p}} )} \hfill \\ { - \frac{1}{2}\gamma_{\text{w}} z_{\text{w}} (H - z){\text{cosec}}\,\psi_{\text{p}} - \frac{1}{2}\gamma_{\text{w}} z_{\text{w}}^{2} \sin \,\psi_{\text{p}} + T\,\cos \,\theta } \hfill \\ { + q\{ (H - z)\cot \,\psi_{\text{p}} - H\,\cot \,\psi_{\text{f}} \} \cos \,\psi_{\text{p}} } \hfill \\ \end{array} } \right]\tan \,\phi }}{{\begin{array}{*{20}c} {\frac{1}{2}\gamma H^{2} \left[ {\left\{ {1 - \left( {\frac{z}{H}} \right)^{2} } \right\}\cot \,\psi_{\text{p}} - \cot \,\psi_{\text{f}} } \right](\sin \,\psi_{\text{p}} + k_{\text{h}} \cos \,\psi_{\text{p}} ) + \frac{1}{2}\gamma_{\text{w}} z_{\text{w}}^{2} \cos \,\psi_{\text{p}} - T\,\sin \,\theta } \hfill \\ { + q\{ (H - z)\cot \,\psi_{\text{p}} - H\,\cot \,\psi_{\text{f}} \} \sin \,\psi_{\text{p}} } \hfill \\ \end{array} }} $$

(7)

Equation 7 provides the general expression for the factor of safety of the rock slope involving all the relevant factors considered in the present study. For convenience in parametric study, this expression can be represented in terms of nondimensional parameters by dividing the numerator and denominator of the above expression by γH ² as follows:

$$ {FS} = \frac{{c^{ *} (1 - z^{ *} ){\text{cosec}}\,\psi_{\text{p}} + \left[ {\begin{array}{*{20}c} {\frac{1}{2}\{ (1 - z^{ *2} )\cot \,\psi_{\text{p}} - \cot \,\psi_{\text{f}} \} (\cos \,\psi_{\text{p}} - k_{\text{h}} \sin \,\psi_{\text{p}} )} \hfill \\ { - \frac{1}{2}\frac{{z_{\text{w}}^{ *} }}{{\gamma^{ * } }}(1 - z^{ *} ){\text{cosec}}\,\psi_{\text{p}} - \frac{1}{2}\frac{{z_{\text{w}}^{ *2} }}{{\gamma^{ * } }}\sin \,\psi_{\text{p}} + T^{ *} \cos \,\theta } \hfill \\ { + q^{ *} \{ (1 - z^{ *} )\cot \,\psi_{\text{p}} - \cot \,\psi_{\text{f}} \} \cos \,\psi_{\text{p}} } \hfill \\ \end{array} } \right]\tan \,\phi }}{{\begin{array}{*{20}c} {\frac{1}{2}\{ (1 - z^{ *2} )\cot \,\psi_{\text{p}} - \cot \,\psi_{\text{f}} \} (\sin \,\psi_{\text{p}} + k_{\text{h}} \cos \,\psi_{\text{p}} ) + \frac{1}{2}\frac{{z_{\text{w}}^{ *2} }}{{\gamma^{ *} }}\cos \,\psi_{\text{p}} - T^{ *} \sin \,\theta } \hfill \\ { + q^{ *} \{ (1 - z^{ *} )\cot \,\psi_{\text{p}} - \cot \,\psi_{\text{f}} \} \sin \,\psi_{\text{p}} } \hfill \\ \end{array} }} $$

(8)

where $z^{ *} = \frac{{z}}{H},$ $z_{\text{w}}^{ *} = \frac{{z_{\text{w}} }}{H},$ $c^{ *} = \frac{{c }}{{\gamma}{\text H}},$ ${\gamma}^{ *} = \frac{{\gamma}}{{\gamma}_{\text w}},$ $T^{ *} = \frac{T}{{\gamma}{\text H^2}},$ and $q^{ *} = \frac{q}{{\gamma}{\text H}}$ are nondimensional forms of z, z _w, c, γ, T, and q respectively.

Equation 8 provides a general expression for the factor of safety in terms of eleven nondimensional parameters, which are relevant in practical situations. Consideration of specific values of all these parameters can result in several special cases that represent real life situations. The analysis can also be applied to man-made slopes, especially slopes resulting from the disposal of mining overburden consisting of soils and rocks, as a special case of Eq. 8. In opencast mines, operations are carried out by placing the heavy earth moving machines like draglines on the top of rock slopes. These machineries can apply a substantial surcharge pressure on the slopes. In hilly areas, many a times a rail line needs to be passed over rock slopes. The pressure applied on the top of such slopes is uniform as assumed in our analysis. In all such cases the surcharge will play an important role in determining the stability of the slope and Eq. 8 can give a fair idea about the stability the slope for plane failure mode under seismic loading condition. It is important to note that the degree of stability improvement through a rock anchoring system can also be analyzed using Eq. 8.

3 Parametric Study

A parametric study is carried out to investigate the effect of surcharge on the stability of rock slope in terms of the factor of safety, considering practical ranges of parameters in their nondimensional form as given below:

 

Angle of inclination of the slope face to the horizontal	ψ f: 40°–60°
Angle of inclination of the failure plane to the horizontal	ψ p: 30°–40°
Depth of tension crack	z*: 0–0.2
Depth of water in tension crack	$z_{\text{w}}^{ *}$: 0–0.1
Cohesion	c*: 0–0.16
Angle of shearing resistance	$\phi$: 20°–40°
Unit weight of rock	γ*: 2–3.3
Surcharge load	q*: 0–2
Stabilizing force	T*: 0–0.04
Angle of inclination of stabilizing force to the normal at the failure plane	θ: 0°–80°
Horizontal seismic coefficient	k h: 0.0–0.2

Figure 2 shows the variation of the factor of safety FS with surcharge q* for three different nondimensional values of cohesion, c* = 0, 0.08 and 0.16, considering a particular set of governing parameters in their nondimensional form as: ψ _f = 50°, ψ _p = 35°, z* = 0.1, $z_{\text{w}}^{ *} = 0.05$, $\phi$ = 25°, γ* = 2.5, T* = 0.02, θ = 10° and k _h = 0.08. It is observed that the factor of safety is greater than unity for c* = 0.08 and 0.16 at lower values of the surcharge, but it decreases with increase in surcharge, the rate of decrease being relatively higher for lower values of surcharge; whereas a slight increase in factor of safety takes place in case of zero cohesion, which is due to the increase in normal stress acting on the failure plane, resulting in increase in frictional resistance. For example, for c* = 0.08, as q* increases from 0 to 0.5, FS decreases by 0.25, whereas decrease in FS is 0.1 for increase of q* from 0.5 to 1. Such difference is further magnified by larger values of c*. As expected, greater the cohesion, greater is the safety factor. It can be seen from the figure that there is significant increase in the safety factor with increase in cohesion. For any surcharge, the difference in the ordinates of the curves corresponding to any non-zero value of c* and c* = 0 will give the contribution to the factor of safety by cohesion only. The horizontal line at FS = 1 divides the figure into safe and unsafe regions. The case with c* = 0 lies in the unsafe region with FS < 1.

Fig. 2

Variation of factor of safety (FS) with surcharge (q*) for different values of c*

Figure 3 shows the variation of the factor of safety FS with surcharge q* for different values of angle of shearing resistance, $\phi$ = 20°, 30° and 40°, considering specific values of governing parameters in their nondimensional form as: ψ _f = 50°, ψ _p = 35°, z* = 0.1, $z_{\text{w}}^{ *} = 0.05$, c* = 0.08, γ* = 2.5, T* = 0.02, θ = 10° and k _h = 0.08. It is noted that the factor of safety is greater than unity for any value of $\phi$ at lower values of the surcharge, but it decreases with increase in surcharge and as before, the rate of decrease is relatively higher for lower values of surcharge. For example, for $\phi$ = 30°, decrease in FS is 0.33 as q* increases from 0 to 0.5, whereas FS decreases by 0.14 for increase of q* from 0.5 to 1. The shapes of the curves are the same, implying that the gradient is independent of $\phi$. In other words, the reduction in safety factor due to increase in surcharge is independent of $\phi$. It is also observed that for any value of surcharge, the factor of safety is relatively higher for large values of angle of shearing resistance.

Fig. 3

Variation of factor of safety (FS) with surcharge (q*) for different values of angle of shearing resistance ($\phi$)

Figure 4 shows the variation of factor of safety FS with surcharge q* for different nondimensional values of unit weight of rock, γ* = 2, 2.5 and 3.3, where the unit weight is 2–3.3 times the unit weight of water, considering a particular set of governing parameters in their nondimensional form as: ψ _f = 50°, ψ _p = 35°, z* = 0.1, $z_{\text{w}}^{ *} = 0.05$, c* = 0.08, $\phi$ = 25°, T* = 0.02, θ = 10° and k _h = 0.08. It is noticed that that the factor of safety decreases with increase in surcharge and the rate of decrease is relatively higher for lower values of surcharge. For example, for γ* = 2.5, FS decreases by 0.25 for an increase in q* from 0 to 0.5, whereas FS decreases by 0.1 as q* increases from 0.5 to 1. It is also observed that for any surcharge, the factor of safety is not much affected by variation in unit weight of rock, mainly because of almost similar effects on resisting and driving forces. In fact, an increase in the self weight of the sliding body has two opposing effects: increasing the driving force causing the instability, and increasing the sliding resistance due to increase in the normal force. The net effect is that they cancel each other such that the magnitude of unit weight has little effect.

Fig. 4

Variation of factor of safety (FS) with surcharge (q*) for different values of unit weight of rock (γ*)

Figure 5 shows the variation of the factor of safety FS with surcharge q* for different values of angle of inclination of slope face to the horizontal, ψ _f = 40°, 50° and 60°, considering specific values of governing parameters in their nondimensional form as: ψ _p = 35°, z* = 0.1, $z_{\text{w}}^{ *} = 0.05$, c* = 0.08, $\phi$ = 25°, γ* = 2.5, T* = 0.02, θ = 10° and k _h = 0.08. It is observed that the factor of safety decreases with increase in surcharge, and at lower surcharge, it is very high, even greater than 2 for ψ _f = 40°, whereas for ψ _f = 50° and 60°, it is less than 1.5. The slope is unstable, with FS < 1 for larger slope angles at higher surcharge. However, the reduction in safety factor with increasing surcharge is less pronounced for larger slope angles.

Fig. 5

Variation of factor of safety (FS) with surcharge (q*) for different values of angle of inclination of the slope face to the horizontal (ψ _f)

Figure 6 shows the variation of the factor of safety FS with surcharge q* for different values of angle of inclination of failure plane to the horizontal, ψ _p = 30°, 35° and 40°, considering a particular set of governing parameters in their nondimensional form as: ψ _f = 50°, z* = 0.1, $z_{\text{w}}^{ *} = 0.05$, c* = 0.08, $\phi$ = 25°, γ* = 2.5, T* = 0.02, θ = 10° and k _h = 0.08. It is observed that the factor of safety is greater than unity for ψ _p = 30°, 35° and 40° at lower values of the surcharge, but it decreases with increase in surcharge, and the rate of decrease is relatively higher for lower values of surcharge. For example, for ψ _p = 35°, decrease in FS is 0.35 as q* increases from 0 to 0.5, whereas FS decreases by 0.15 for increase in q* from 0.5 to 1. It is also noted that at no surcharge, the factor of safety is lowest for ψ _p = 30°, whereas for very high surcharge, the lowest value of factor of safety occurs for ψ _p = 40°. For intermediate surcharge, the factor of safety is lowest for ψ _p = 35°. This is happening mainly because of decrease in the weight of the sliding block with increase in ψ _p. This observation indicates that if several joint planes are present in the rock slope, the actual failure plane is highly dependant on the value of surcharge. The slopes that are quite stable at low values of surcharge can become unsafe, with FS < 1, when the surcharge exceeds a threshold value. This can be seen for all values of ψ _p. In other words, limiting the surcharge can improve the safety of the slope significantly.

Fig. 6

Variation of factor of safety (FS) with surcharge (q*) for different values of angle of inclination of the failure plane to the horizontal (ψ _p)

Figure 7 shows the variation of factor of safety FS with surcharge q* for different nondimensional values of depth of tension crack, z* = 0, 0.1 and 0.2, considering specific values of governing parameters in their nondimensional form as: ψ _f = 50°, ψ _p = 35°, $z_{\text{w}}^{ *} = 0$, c* = 0.08, $\phi$ = 25°, γ* = 2.5, T* = 0.02, θ = 10° and k _h = 0.08. It is observed that the factor of safety is greater than unity for z* = 0, 0.1 and 0.2 at lower values of the surcharge, but it decreases with increase in surcharge, the rate of decrease being relatively higher for lower values of surcharge. For example, for z* = 0.1, as q* increases from 0 to 0.5, FS decreases by 0.27, whereas for increase in q* from 0.5 to 1, decrease in FS is 0.11. It is also noted that for lower values of surcharge, the factor of safety is higher for smaller value of depth of tension crack, whereas for higher surcharge values, the factor of safety becomes higher for greater value of depth of tension crack. This is simply a geometry effect, where the other dimensions are altered which affects the safety factor.

Fig. 7

Variation of factor of safety (FS) with surcharge (q*) for different values of depth of tension crack (z*)

Figure 8 shows the variation of factor of safety FS with surcharge q* for different nondimensional values of depth of water in tension crack, $z_{\text{w}}^{ *} = 0$, 0.05 and 0.1, considering a particular set of governing parameters in their nondimensional form as: ψ _f = 50°, ψ _p = 35°, z* = 0.1, c* = 0.08, $\phi$ = 25°, γ* = 2.5, T* = 0.02, θ = 10° and k _h = 0.08. It is noted that the factor of safety decreases with increase in surcharge and the rate of decrease is relatively higher for lower values of surcharge. For example, for $z_{\text{w}}^{ *} = 0.05$, FS decreases by 0.24 for an increase in q* from 0 to 0.5, whereas decrease in FS is 0.1 as q* increases from 0.5 to 1. It is also noticed that for any surcharge, the factor of safety decreases with increase in depth of water in tension crack. As before, a perfectly stable slope becomes unsafe by increasing the surcharge, and the deterioration in the safety factor is rather rapid for all three cases.

Fig. 8

Variation of factor of safety (FS) with surcharge (q*) for different values of depth of water in the tension crack ($z_{\text{w}}^{ *}$)

Figure 9 shows the variation of factor of safety FS with surcharge q* for different nondimensional values of stabilizing force, T* = 0, 0.02 and 0.04, considering specific values of governing parameters in their nondimensional form as: ψ _f = 50°, ψ _p = 35°, z* = 0.1, $z_{\text{w}}^{ *} = 0.05$, c* = 0.08, $\phi$ = 25°, γ* = 2.5, θ = 10° and k _h = 0.08. It is observed that the factor of safety is greater than unity for T* = 0, 0.02 and 0.04 at lower values of the surcharge, but it decreases with increase in surcharge, and the rate of decrease is relatively higher for lower values of surcharge. For example, for T* = 0.02, FS decreases by 0.25 for an increase in q* from 0 to 0.5, whereas decrease in FS is 0.1 as q* increases from 0.5 to 1. It is also noted that at any surcharge, the factor of safety increases with increase in stabilizing force, and the increase in the safety factor is approximately proportional to the stabilizing force.

Fig. 9

Variation of factor of safety (FS) with surcharge (q*) for different values of stabilizing force T*

Figure 10 shows the variation of factor of safety FS with surcharge q* for different values of inclination of stabilizing force to the normal at the failure plane, θ = 0°, 40° and 80°, considering a particular set of governing parameters in their nondimensional form as: ψ _f = 50°, ψ _p = 35°, z* = 0.1, $z_{\text{w}}^{ *} = 0.05$, c* = 0.08, $\phi$ = 25°, γ* = 2.5, T* = 0.02 and k _h = 0.08. It is observed that factor of safety decreases with increase in surcharge; the rate of decrease being relatively higher for lower values of surcharge. For example, for θ = 40°, FS decreases by 0.28 for an increase in q* from 0 to 0.5, whereas decrease in FS is 0.11 as q* increases from 0.5 to 1. It is also noted that at any particular surcharge, the factor of safety increases significantly when θ increases from 0° to 40°, whereas the increase in factor of safety is insignificant for further increase in θ.

Fig. 10

Variation of factor of safety (FS) with surcharge (q*) for different values of angle of inclination of the stabilizing force to the normal at the failure plane (θ)

Figure 11 shows the variation of factor of safety FS with surcharge q* for different values of horizontal seismic force, k _h = 0, 0.1 and 0.2, considering a particular set of governing parameters in their nondimensional form as: ψ _f = 50°, ψ _p = 35°, z* = 0.1, $z_{\text{w}}^{ *} = 0.05$, c* = 0.08, $\phi$ = 25°, γ* = 2.5, T* = 0.02 and θ = 10°. It is observed that the factor of safety is greater than unity for any value of k _h at lower surcharge, but it decreases with increase in surcharge; the rate of decrease being higher for lower values of surcharge. For example, for k _h = 0.1, FS decreases by 0.23 for an increase in q* from 0 to 0.5, whereas decrease in FS is 0.1 as q* increases from 0.5 to 1. It is also noted that for any value of surcharge, the factor of safety is higher for lower value of horizontal seismic coefficient. The reduction in safety factor appears to be proportional to the increase in the horizontal seismic coefficient.

Fig. 11

Variation of factor of safety (FS) with surcharge (q*) for different values of horizontal seismic coefficient (k _h)

4 Conclusions

On the basis of the results and discussion presented in the previous section, the following general conclusions can be drawn.

• 1. The present study provides an analytical expression for the factor of safety of a rock slope incorporating most of the practically occurring destabilizing forces as well as the external stabilizing force through anchoring system. A detailed parametric study has been carried out to investigate the effect of surcharge on the stability of the rock slope for practical ranges of parameters governing the stability of the slope.

• 2. For the range of parameters considered in the present study, the factor of safety of the rock slope decreases with increase in surcharge; the rate of decrease being relatively higher for lower values of surcharge.

• 3. At any surcharge, the factor of safety of the rock slope is relatively higher for greater value of cohesion, as well as for greater value of angle of shearing resistance of the material at the failure plane. The rate of deterioration in safety factor with increase in surcharge is quite rapid for larger values of cohesion; the rate remains the same for all friction angles.

• 4. The factor of safety of the rock slope is not much affected by variation in unit weight of rock for any value of surcharge.

• 5. The reduction in safety factor with increasing surcharge is less pronounced for larger slope angles.

• 6. If several joint planes are present in the rock slope, the actual failure plane is highly dependant on the magnitude of surcharge. The slopes that are quite stable at low values of surcharge can become unsafe, with FS < 1, when the surcharge exceeds a threshold value. In other words, limiting the surcharge can improve the safety of the slope significantly.

• 7. For lower values of surcharge, the factor of safety is higher for lower value of depth of tension crack, whereas for higher surcharge values, the factor of safety becomes higher for greater value of depth of tension crack.

• 8. At any surcharge, the factor of safety of rock slope decreases with increase in depth of water in tension crack as well as with increase in horizontal seismic coefficient. The reduction in safety factor appears to be proportional to the increase in the horizontal seismic coefficient.

• 9. The factor of safety of the rock slope increases with increase in stabilizing force for any value of surcharge. The increase in safety factor appears to be proportional to the magnitude of the stabilizing force. It also increases with increase in angle of inclination of the stabilizing force to the normal at the failure plane; but very high increase in inclination may not result in significant increase in factor of safety.