Collapse response of two-dimensional cellular solids by plasticity and cracking: application to wood

Abstract

The competition between fracture and plasticity in periodic hexagonal honeycomb structures subjected to (i) intercell cracking, (ii) intrawall cracking and (iii) transwall cracking is examined, and their effect upon the macroscopic collapse response is explored using dedicated FEM analyses of unit cell configurations. These three cracking mechanisms are regularly observed in wood microstructures, and insight into their influence on the macroscopic collapse behavior is necessary for adequately designing timber structures against failure. The numerical results are presented by means of collapse contours in the hydrostatic-deviatoric stress space, illustrating the effects of wall slenderness, relative fracture (versus yield) strength, and the relative size of the plastic zone at the crack tip. Both the hydrostatic and deviatoric collapse strengths of the honeycomb strongly increase in the transition from brittle cell walls with low relative fracture strength to ductile cell walls with high relative fracture strength. This strength increase typically changes the shape of the collapse contour, and is the largest for transwall cracking, followed by intercell cracking and finally intrawall cracking. The ultimate collapse strength of the honeycomb is significantly more sensitive to the fracture strength than to the fracture toughness of the cell walls, and correctly approaches the plastic yield surface under increasing relative fracture strength. The numerical results may serve as a useful guideline in the experimental calibration of the local fracture and yield strengths of cell walls in wood.

1 Introduction

Cellular solids are abundantly present in nature; examples are plant tissues, such as wood, bamboo, plant parenchyma (carrot, potato), cork, and animal tissues, such as sponge, coral and cancellous bone. Natural cellular solids facilitate the concurrent optimization of strength and stiffness at low weight, which has inspired the design of man-made cellular solids, with advanced two-dimensional honeycomb and three-dimensional (open and closed) foam architectures made out of polymers, ceramics, glasses, metals and composites. The unique properties of these materials have led to useful applications of relatively low weight (structural sandwich panels, buoyance devices), excellent energy absorption (helmets) and sound absorption (noise and vibration control), low thermal conductivity (insulation), large heat dissipation (high power electronics), and large surface area (catalytic converters), see Gibson and Ashby (1997), Evans et al. (1999), Fleck et al. (2010).

Detailed understanding of the mechanical failure behavior of natural and man-made cellular solids is of great significance for engineering applications. This has stimulated various analytical and numerical studies on the effective strength and deformation behavior of these materials. In Klintworth and Stronge (1988) failure envelopes were derived for regular honeycomb structures subjected to a combination of elastic buckling and plastic collapse, which subsequently were applied to predict the in-plane indentation of honeycomb structures by plane punch (Klintworth and Stronge 1989). In Gibson et al. (1989) failure contours were developed for regular two-dimensional and three-dimensional cellular solids collapsing by plasticity, elastic buckling and brittle fracture under a large initial flaw. It was demonstrated that the failure contour for plastic collapse may be curtailed by brittle fracture in tension and by elastic buckling in compression. Wang and McDowell (2005) established yield surfaces for various periodic honeycombs, whereby they demonstrated the importance of the cell geometry in determining the yield contour shape at a given relative density. In addition, several studies considered the effect of morphological imperfections on the uniaxial yield strength of cellular solids, such as the influence of non-uniform wall thickness (Simone and Gibson 1998a), the curvatures and wiggles in cell walls (Simone and Gibson 1998b), missing cell walls (Silva and Gibson 1997; Guo and Gibson 1999) and random microstructures (Silva and Gibson 1997). In Chen et al. (1999) the effect of six different types of imperfections on the yield contour of two-dimensional cellular solids was comprehensively studied, showing that fractured cell edges produce the largest knock-down effect on the high hydrostatic strength of ideal honeycombs, followed by missing cells, wavy cell edges, cell edge misalignments, ${\Gamma }$ Voronoi cells, $\delta$ Voronoi cells and non-uniform wall thickness. This result is in agreement with the study of Triantafyllidis and Schraad (1998), who reported that the yield surface of a perfect honeycomb results in an upper bound for the yield surfaces of honeycombs with morphological irregularities. In Lukacevic et al. (2015), multisurface failure criteria were derived for honeycomb-like structures composed of earlywood and latewood unit cells, whereby crack nucleation and propagation mechanisms were simulated with the extended finite element method; the numerical results showed to be in good agreement with the failure response found experimentally.

Inspired by the studies of Silva and Gibson (1997) and Chen et al. (1999) that indicated a significant sensitivity of the effective yield strength of idealized honeycomb microstructures on fractured cell walls, in the present study the interaction between plasticity and cracking is analyzed for various fracture scenarios typical of wood. A unit cell approach is adopted, which is valid for the assumption that under increased loading small micro-cracks may nucleate at numerous locations inside the honeycomb microstructure, such that the overall cracking pattern can be characterized as distributed and (to some extent) periodic. After the loading has reached its maximum value and starts to decrease with increasing deformation (i.e., a softening response), the micro-cracks gradually evolve into an apparent, localized failure crack. This physical picture is supported by detailed experimental observations on Japanese red pine wood, showing a prolonged formation of micro-cracks at bordered pits inside the cell wall before localized fracture took place (Ando et al. 2006). The specific features of the transition from micro-crack nucleation into localized fracture determine the effective (maximal) collapse strength of the honeycomb structure, and are expected to depend upon characteristics such as the relative fracture (versus yield) strength and the fracture toughness of the cell wall. These and other effects will be systematically explored in this paper by considering three types of cracking scenarios commonly observed in wood cell walls, see Fig. 1, namely intercell (IC), intrawall (IW) and transwall (TW) cracking (Koran 1967; Jeronimidis 1976; Boatright and Garrett 1983; Zink et al. 1994; Smith et al. 2003). Cell walls in wood consist of layers composed of (specifically or randomly) oriented cellulose microfibrils embedded within an amorphous lignin matrix. The four main layers are commonly referred to as the inner $(\hbox {S}_{3})$, middle $(\hbox {S}_{2})$ and outer $(\hbox {S}_{1})$ secondary cell walls and the primary wall (P), which are followed by the middle lamella that forms the connection with an adjacent cell with a similar lay-up, see Fig. 2. Accordingly, intercell cracking characterizes cell separation from the middle lamella of the cell wall, intrawall cracking refers to delamination cracking between the middle $(\hbox {S}_{2})$ and outer $(\hbox {S}_{1})$ or (occasionally) inner $(\hbox {S}_{3})$ secondary layers of the cell wall, and transwall cracking is characterized by crack formation in the thickness direction of the cell wall.

Fig. 1

(taken from Smith et al. (2003))

Three typical cracking scenarios observed in wood honeycombs: intercell (IC), intrawall (IW) and transwall (TW) cracking

Fig. 2

(taken from Nikitin (1966))

Wall lay-up in a wood cell

The study starts in Sect. 2 with a review of the analytical yield contour for an infinitely large, regular honeycomb structure subjected to uniform, in-plane stresses. Permanent deformations by plastic yielding at the cell wall level of wood can be associated with a recovery mechanism that under tensile loading reforms the amorphous lignin matrix between the cellulose microfibrils within the cell wall (Keckles et al. 2003). The yield contour of the honeycomb is constructed by using the elementary beam theory, following the approach presented in Chen et al. (1999). The analytical yield contour is compared against the results of a finite element method (FEM) model composed of two-dimensional continuum elements. The effect of the wall slenderness on the yield contour is analyzed, indicating the appearance of an additional size effect on the deviatoric strength for relatively short cell walls (which commonly are present in wood microstructures). It is demonstrated that this size effect can be accurately described by means of a basic geometrical term. Subsequently, Sect. 3 presents the FEM models used for the analysis of the wall cracking scenarios described above, whereby discrete cracking is simulated by interface elements equipped with an interface damage model. In Sect. 4 the numerical results are presented by means of collapse contours in the hydrostatic-deviatoric stress space, illustrating the effects of wall slenderness, relative fracture (versus yield) strength, and the relative size of the plastic zone at the crack tip. The convergence of the collapse contour towards the analytical yield contour under increased relative fracture strength is demonstrated. The section ends with a general comparison of the collapse responses for the three cracking mechanisms under plane-stress and plane-strain conditions, showing the constraining effect in the out-of-plane direction typical of the relatively long honeycomb grains present in various types of wood. Section 5 summarizes the main results of the numerical study.

Fig. 3

a Regular honeycomb micro-structure subjected to uniform macroscopic stresses $\sigma _{11}$, $\sigma _{12}$ and $\sigma _{22}$, and b the corresponding unit cell model subjected to microscopic normal forces $P_{i}$ and shear forces $Q_{i}$, with $i =1,2,3$, taken from Chen et al. (1999)

2 Yield contour for honeycomb micro-structures

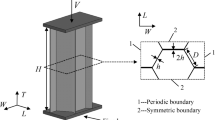
The in-plane yielding behavior of honeycomb micro-structures is analyzed by means of FEM models composed of two-dimensional continuum elements, whereby the yield contours computed numerically are validated against the yield contour obtained from a basic analytical beam model. The honeycomb micro-structure considered is taken to be infinitely large, ideally hexagonal, and subjected to uniform, macroscopic stress conditions, see Fig. 3a, Correspondingly, the mechanical problem may be schematized by means of a planar unit cell composed of three identical cell walls of length l / 2, thickness t and out-of-plane width b, see Fig. 3b. This micro-structural model has been considered in previous studies on the in-plane yielding of cellular materials (Gibson and Ashby 1997; Chen et al. 1999), and the analytical approach presented in these studies is reviewed in Sect. 2.1. Due to symmetry, the bending moments vanish at the midpoints of the three edges of the unit cell. The three cell walls are indicated in Fig. 3b as cell wall 1, cell wall 2 and cell wall 3, and are rigidly connected at the central point O. In the analytical model the material behavior of the cells is considered as rigid-perfectly plastic, with the yield strength given by $\sigma _{y}$. As concluded by Keckles et al. (2003) from tensile tests on individual wood cells and on wood foils combined with X-ray diffraction analysis, permanent deformations by plastic yielding at the cell wall level are related to a recovery mechanism that reforms the amorphous lignin matrix between the cellulose microfibrils within the cell wall, without causing significant mechanical damage to the matrix. Essentially, this stick-slip mechanism induces a plastic response analogous to that originating from dislocation gliding in metals.

The beam theory used for modeling the cell walls typically gives accurate results for relatively slender beams with length-to-thickness ratios of $l/t>10$. The lack of accuracy of this theory for shorter beams becomes evident in the comparison with the yield contours calculated by the FEM continuum model presented in Sect. 2.2. In Sect. 2.3 it is demonstrated that this size effect can be adequately accounted for by means of a simple correction term on the deviatoric strength of the honeycomb structure.

2.1 Analytical yield contour

For the unit cell depicted in Fig. 3b, the normal forces $P_i$ and shear forces $Q_i$, with $i=1,2,3$ indicating the corresponding cell wall, define the three equilibrium conditions as

$$\begin{aligned} P_1 -\frac{1}{2}\left( {P_2 +P_3 } \right) +\frac{\sqrt{3}}{2}\left( {Q_3 -Q_2 } \right)= & {} 0, \nonumber \\ \quad -Q_1 +\frac{1}{2}\left( {Q_2 +Q_3 } \right) +\frac{\sqrt{3}}{2}\left( {P_3 -P_2 } \right)= & {} 0, \nonumber \\ Q_1 +Q_2 +Q_3= & {} 0. \end{aligned}$$

(1)

These forces are related to the macroscopic normal stresses $\sigma _{11}$, $\sigma _{22}$ and shear stress $\sigma _{12}$ via

$$\begin{aligned} P_i= & {} bl\sqrt{3}( {\sigma _{11} \cos ^{2}\theta _i +2\sigma _{12} \cos \theta _i \sin \theta _i +\sigma _{22} \sin ^{2}\theta _i} ),\nonumber \\ Q_i= & {} bl\sqrt{3}(-\sigma _{11} \cos \theta _i \sin \theta _i +\sigma _{12} ( {\cos ^{2}\theta _i -\sin ^{2}\theta _i } )\nonumber \\&+\sigma _{22} \cos \theta _i \sin \theta _i ), \end{aligned}$$

(2)

where $\theta _{i}$ is the angle between the (horizontal) x-axis and the longitudinal axis of cell wall $i=1,2,3.$ For the hexagonal honeycomb sketched in Fig. 3, the angles of the three cell walls are given by

$$\begin{aligned} \theta _1 =\frac{1}{2}\pi , \quad \theta _2 =\frac{7}{6}\pi ,\quad \theta _3 =\frac{11}{6}\pi . \end{aligned}$$

(3)

Under increasing load amplitude, plastic collapse of (one of) the cell walls may take place. The effect on the collapse strength by cracking will be studied in Sect. 4 through advanced finite element modeling; the current analytical model is expected to serve as a reference solution to which the numerical results in Sect. 4 should converge when the amount of plasticity relative to cracking increases.

The present study focuses on the collapse behaviour in the tensile regime, and the effect of cell buckling under compressive loading is left out of consideration; more details on this failure mechanism can be found in the works of Klintworth and Stronge (1988) and Gibson et al. (1989). The combination of axial and bending loading at which plastic collapse occurs can be described by a yield contour Y (Hodge 1959)

$$\begin{aligned} Y=n^{2}+m=1 \quad \hbox {with} \quad n=\frac{N}{N_y } \quad \hbox {and}\quad m=\frac{M}{M_y },\nonumber \\ \end{aligned}$$

(4)

where the normal force and the bending moment for an individual cell wall are given by

$$\begin{aligned} N=P, \quad M=\frac{1}{2}\left| Q \right| l, \end{aligned}$$

(5)

and the ultimate normal force and bending moment at plastic collapse follow as

$$\begin{aligned} N_y =\sigma _y bt, \quad M_y =\frac{1}{4}\sigma _y bt^{2}. \end{aligned}$$

(6)

Inserting Eqs.(5) and (6) into Eq.(4), thereby taking into account that overall plastic collapse occurs when one or more plastic hinges emerge in the unit cell, leads to

$$\begin{aligned} \frac{P_i ^{2}}{4\sigma _y b}+\frac{1}{2}\left| {Q_i } \right| l-\frac{1}{4}\sigma _y bt^{2}=0. \end{aligned}$$

(7)

with $P_{i}$ and $Q_{i}$ presented by Eq.(2). The yield contour for the honeycomb structure is determined by the inner envelope of the set of yield contours defined by Eq.(7), with $i=1,2,3$. For the special case of the macroscopic shear stress vanishing, $\sigma _{12} =0$, the yield contour follows from Eq.(7) as

$$\begin{aligned} \left| {\sigma _{11} -\sigma _{22} } \right| =\frac{2}{3}\sigma _y \frac{t^{2}}{l^{2}}\left( {1-\frac{3}{16}\frac{\left( {3\sigma _{11} +\sigma _{22} } \right) ^{2}}{\sigma _y ^{2}}\frac{l^{2}}{t^{2}}} \right) ,\nonumber \\ \end{aligned}$$

(8)

while under the application of a shear stress only, Eq. (7) results in

$$\begin{aligned} \left| {\sigma _{12} } \right| =\frac{\sigma _y }{2\sqrt{3}}\frac{t^{2}}{l^{2}}. \end{aligned}$$

(9)

Equations (8) and (9) are identical to those presented in Gibson and Ashby (1997) and Chen et al. (1999).

It has been demonstrated by Chen et al. (1999) that the degree of plastic anisotropy for an ideal hexagonal honeycomb appears to be relatively small, with a maximal difference of 15% in effective macroscopic yield strength under a change in principal stress directions. Accordingly, Chen et al. (1999) suggested that the loading conditions may be reasonably simplified by considering the normal stresses $\sigma _{11}$ and $\sigma _{22}$ to act as principal stresses, with their directions being aligned with the symmetry directions of the honeycomb. Hence, this approach will be adopted in the present work. This simplification has also been adopted in the presentation of the numerical results on the three cracking mechanisms in Sect. 4, since the effective tensile strength of a honeycomb structure has a low degree of anisotropy as well (Gibson and Ashby 1997).

2.2 Comparison between analytical and numerical yield contours

The analytical yield contour given by Eq.(8) will be compared to yield contours computed numerically with the finite element method (FEM) software package ABAQUS Standard¹. The honeycomb structures simulated are composed of cell walls of slenderness ratios $l/t= 3.33$, 6.67, 20 and 40. The FEM models use 8-node iso-parametric plane-stress elements equipped with a $2\times 2$ Gauss quadrature, for which the small-strain assumption is adopted. The elastic behavior is taken as isotropic and the perfectly plastic behavior of the continuum elements is described by using $J_{2}$-flow theory with the effective yield stress given by $\sigma _y$. The number of elements varies between approximately 4600 (for honeycomb structures made of relatively slender cell walls $l/t=40)$ and 30,000 (for honeycomb structures made of stocky cell walls $l/t=3.33$). Additional simulations not presented here confirmed that with this number of elements the numerical results converge towards the exact solution. Rigid body motions are prevented by placing fixed and roller supports, see Sect. 3.2 for more details. For a given loading path, the normal force P presented by Eq. (2) is incrementally applied at the centre node at each wall end, whereby the corresponding axial displacement $u_n$ is imposed on the other nodes at the wall end by means of a geometrical tying. This warrants that the wall ends remain straight, as required from the periodicity of the unit cell. The shear force Q is incrementally applied at the wall end through a uniform tangential traction $t_t$, whereby the work-conjugated tangential displacements naturally satisfy the periodicity requirement. Once the microscopic forces P and Q have reached their ultimate values at which cell wall cross-sections have become fully plastic, these values are used to calculate the corresponding macroscopic normal stresses $\sigma _{11}$ and $\sigma _{22}$ by means of the inverse of Eq. (2). Hence, the values of these normal stresses determine a specific point of the yield contour. The total yield contour is constructed by performing the above analysis for a set of five different loading paths, ranging from pure hydrostatic loading to pure deviatoric loading.

Fig. 4

Yield contour constructed for various slenderness ratios l / t, using FEM modeling with continuum elements (solid lines). The FEM results are compared to the analytical yield contour (dashed line), Eq. (8), which has been derived using elementary beam theory

In Fig. 4 the yield contours following from the FEM analyses (solid lines) are compared to the analytical yield contour (dashed line) constructed with Eq.(8). Along the horizontal and vertical axes the biaxial hydrostatic stress, $p=( {\sigma _{11} +\sigma _{22} } )/2$, and deviatoric stress, $q=\left| {\sigma _{11} -\sigma _{22} } \right| /2$, are depicted, normalized by yield stress $\sigma _y$ and multiplied by the slenderness ratios l / t and $l^{2}/t^{2}$, respectively. It can be observed that the hydrostatic yield strength, which relates to cell wall stretching, indeed scales with t / l, and that the deviatoric yield strength, which is dominated by cell wall bending, scales with $t^{2}/l^{2}$ for slender cell walls, $l/t=20$ and $l/t=40$. Since the relative density of the honeycomb can be expressed as ${{\bar{\rho }}} =2t/\left( {\sqrt{3}l} \right)$, the above scaling is equivalent to the hydrostatic yield strength being proportional to the relative density ${\bar{\rho }}$ of the ideal honeycomb structure, and the deviatoric yield strength for slender cell walls being proportional to ${\bar{\rho }}^{2}$, see also Gibson and Ashby (1997), Chen et al. (1999), Tankasala et al. (2017). For stocky cell walls, $l/t=6.67$ and $l/t=3.33$, the scaling of the deviatoric yield strength with respect to t / l appears to be superquadratic. In the section below a simple phenomenological correction term is proposed for the deviatoric yield strength in order to capture this size effect.

Fig. 5

Yield contour constructed for various slenderness ratios $l/t=3.33, 6.67, 20$ and 40, using FEM modeling with continuum elements. The normalized representation accounts for an additional increase in the deviatoric strength typical of stocky cell walls. The factor $\alpha$ quantifying this scaling effect is included in the dimensionless deviatoric strength plotted along the vertical axis, and equals $\alpha =0.85$

2.3 Size effect in the deviatoric strength for stocky cell walls

An improvement in the normalization of the deviatoric yield strength for honeycomb structures composed of stocky cell walls requires accounting for an additional scaling effect primarily caused by cell wall bending. This is done by extending the geometrical scaling term $t^{2}/l^{2}$ for the deviatoric strength to $( {1+\alpha t/l})t^{2}/l^{2}$, where $\alpha$ is a calibration coefficient. For the hexagonal honeycomb structures analyzed in the present study, the plastic collapse behavior can be described accurately by adopting $\alpha =0.85$. This is illustrated in Fig. 5, which depicts the numerical results from Fig. 4 by incorporating the extended geometrical scaling term in the normalized deviatoric strength depicted along the vertical axis. With this simple extension, the difference between the numerical yield contours is always less than 3.5%, which is found acceptable. Furthermore, it can be easily confirmed that the scaling of the deviatoric strength by a factor $( {1+\alpha t/l})t^{2}/l^{2}$ (with $\alpha =0.85$) only starts to give noticeable differences with a scaling by $t^{2}/l^{2}$ when the cell wall becomes stocky, i.e., for $l/t<10$.

3 Numerical modeling of combined fracture and plasticity

The FEM model will now be extended in order to successively account for (i) intercell cracking, (ii) intrawall cracking and (iii) transwall cracking of the honeycomb structure. The discrete fracture behavior of the honeycomb structures is modeled with interface elements endowed with the mixed-mode damage model presented in Cid Alfaro et al. (2009), which has been implemented in ABAQUS as a user-supplied subroutine (i.e., a “UMAT”). In Cid Alfaro et al. (2009) the interface damage model was successfully applied for a three-dimensional analysis of laminate failure mechanisms characterized in Suiker and Fleck (2004, 2006). The model has been further employed for the numerical simulation of complex fracture patterns in thin fiber-epoxy layers, modeling both decohesion at the fiber-epoxy interfaces and matrix cracking in the epoxy in a robust and accurate fashion (Cid Alfaro et al. 2010a, b). Moreover, it has been recently applied for an accurate description of the delamination response of brittle and ductile film-substrate systems subjected to a combination of bending and residual stresses (Forschelen et al. 2016), and for the modeling of discrete fracture in oak wood specimens subjected to three-point bending (Luimes et al. 2018).

3.1 Characteristics of the interface damage model

In the interface damage model of Cid Alfaro et al. (2009), the fracture process in a material point subjected to monotonic loading starts as soon as the effective interfacial traction reaches the fracture strength$t^{u}$, which happens at the relative crack face separation $v^{0}$, see Fig. 6. The fracture process is characterized by a linear softening branch, along which the fracture strength progressively decreases as a result of the development of damage d, whereby the elastic interfacial stiffness K degrades by a factor $(1-d).$ The evolution of the degradation process is monitored by the damage history variable $\kappa _d$. The damage process is completed when the relative ultimate crack face separation$v^{u}$ is reached and the interfacial material point looses its strength. The area under the traction-separation law corresponds to the fracture toughness, $G_c =t^{u}v^{u}/2.$ The loading and unloading conditions during fracture are governed by a damage loading function, and the evolution of the fracture process is described by a rate-dependent kinetic law. The mode-mixity of the fracture process is defined as a combination of the crack face separations in the normal and tangential directions of the crack, which allows for explicitly distinguishing between mode I (tension) and mode II (shear) contributions. For simplicity, in the present work the strength and toughness properties in mode I and mode II are taken equal, unless stated otherwise. The incremental update procedure of the interface damage model is carried out by means of an implicit backward Euler scheme, and a consistent tangent operator is formulated to construct the overall stiffness matrix. The update algorithm is relatively straightforward, stable and fast, since it does not require numerical iterations at material point level, aspects that can be ascribed to the specific form of the damage loading function adopted. For more details on the model formulation and the numerical implementation procedure, the reader is referred to Cid Alfaro et al. (2009).

In all simulations the elastic stiffness K of the interface damage model was set relatively high, as a result of which the overall elastic response of the cell wall is not much affected by this parameter and is determined almost completely by the elastic properties of the continuum elements. In addition, the material parameters related to the rate-dependency of the kinetic law were chosen such that the fracture response closely approximates the rate-independent limit case. More details on these aspects can be found in previous numerical studies performed with the interface damage model (Cid Alfaro et al. 2009, 2010a, b; Forschelen et al. 2016; Luimes et al. 2018).

Fig. 6

Traction-separation law in the interface damage model of Cid Alfaro et al. (2009)

3.2 Geometry, boundary conditions and finite element discretization

The paths along which cracking may occur were modeled with 4-node interface elements equipped with a 2-point Gauss quadrature. In the studies of Cid Alfaro et al. (2009), Forschelen et al. (2016), Luimes et al. (2018) convergence of the finite element results upon mesh refinement was found if the local element size $\Delta$ was taken smaller than about 4 times the ultimate separation $v^{u}$ in the traction-separation law. In the present study the element size near a crack tip therefore is chosen as $\Delta \approx 2v^{u}$.

The cell walls of the honeycomb microstructure were modeled with an elastic-perfectly plastic material model. In the analysis of the results, the plastic zone developing at a crack tip was estimated by means of a material-based length scale parameter $R_0$, which is calculated as (Tvergaard and Hutchinson 1992; Wei and Hutchinson 1997; Forschelen et al. 2016)

$$\begin{aligned} R_0 =\frac{1}{3\pi }\frac{EG_c }{\sigma _y ^{2}}, \end{aligned}$$

(10)

where E and $\sigma _{y}$ are the Young’s modulus and the yield stress of the cell wall material, respectively, and $G_{c}$ is the fracture toughness. Eq. (10) is representative of the size of the plastic zone for a crack subjected to pure mode I loading conditions; as demonstrated in previous studies (Tvergaard and Hutchinson 1992; Wei and Hutchinson 1997; Forschelen et al. 2016), it is insightful to use $R_0$ as an essential variable in parametric analyses on elasto-plastic crack formation. In the present analyses the size of the plastic zone $R_0$ mostly is larger than the ultimate separation $v^{u}$; hence, this parameter is not decisive in the determination of the minimal FEM mesh size required for obtaining converged numerical results.

3.2.1 Intercell cracking

An example of a finite element discretization used for simulating intercell cracking is shown in Fig. 7. The failure crack characterizing this mechanism runs along the centerline of a cell wall. This trajectory is captured by interface elements equipped with the interfacial damage model outlined in Sect. 3.1. Rigid body motions are prevented by placing fixed and roller supports at the edge of cell wall 1. These supports only allow for transferring a normal load P, since the shear force Q along the edge of cell wall 1 is zero when assuming the normal stresses $\sigma _{11}$ and $\sigma _{22}$ to act as principal stresses, see Eq.(2)$_{2}$ . For cell walls 2 and 3, the cell edges at which the loading is applied are assumed to remain straight in the axial direction, which, as explained in Sect. 2.2, has been accounted for by means of geometrical tyings with respect to the axial displacement $u_n$ of the central master node at the cell edge. Since in the transversal direction the periodicity is warranted by prescribing a uniform traction $t_t$ at the cell edges, the crack faces at the edges only displace in the normal (mode I) direction, thereby accounting for the coalescence with the (periodic) crack entering from an adjacent unit cell. For a given loading path, the above periodic boundary conditions essentially prescribe how the loads $P_i$ and $Q_i$ given by Eq.(2) are distributed over the element nodes at the cell edges. The loading given by Eq. (2) is applied incrementally in a quasi-static fashion, and the stress state reached under the ultimate loading corresponds to a point on the collapse contour. This stress state is calculated by inverting Eq.(2), whereby, as indicated previously, the normal stresses $\sigma _{11}$ and $\sigma _{22}$ are assumed to act as principal stresses (i.e., $\sigma _{12} =0$).

Fig. 7

Finite element mesh for intercell cracking, with interface elements located halfway the cell wall thickness t. For illustrative purposes, supports at the boundary of cell wall 1 are only indicated at three locations, but are applied at all boundary nodes. The periodic boundary conditions at cell walls 2 and 3 are prescribed by uniform normal displacements $u_n$ and uniform tangential tractions $t_t$

Due to the unstable character of the fracture process, after having reached the ultimate value, the effective load applied at the cell edges generally decreases with increasing edge displacement. This softening behaviour, which may be occasionally accompanied by a snap-back behaviour in which both the load and displacement decrease (see, e.g., Fig. 11), was treated in a numerically robust fashion by adopting the arc-length method (Riks 1979). The FEM model for a honeycomb structure composed of slender cell walls with $l/t=40$ consist of approximately 32,000 elements, while for honeycombs with stocky cell walls, $l/t=3.33$, the number of elements is about 52,000; this turned out to be sufficient for obtaining converged numerical results.

3.2.2 Intrawall cracking

As discussed in the introduction, intrawall cracking in wood cell walls generally refers to a delaminating crack between the $\hbox {S}_{2}$ and $\hbox {S}_{1}$ layers, and occasionally between the $\hbox {S}_{2}$ and $\hbox {S}_{3}$ layers, see Figs. 1 and 2. The finite element model for the simulation of intrawall cracking is built in a similar way as the model for intercell cracking discussed above. The interface between the $\hbox {S}_{1}$ and $\hbox {S}_{2}$ layers and between the $\hbox {S}_{2}$ and $\hbox {S}_{3}$ layers is assumed to be located at a distance of t / 4, from the cell wall edges, in correspondence with the thickness of the $\hbox {S}_{2}$ layer being equal to t / 2, see Fig. 8. The choice of the locations of the two interfaces for intrawall cracking is representative of real woods, as can be approximately confirmed from the microscopic fracture pattern illustrated in Fig. 1. Nevertheless, small deviations in these locations may occur, depending on the specific wood material considered. The sensitivity of the fracture response to variations in the layer interface locations and to imperfections at these interfaces is not analysed here; these are considered to be topics for future study. The total number of elements used in the FEM model approximately varies between 49,000 and 60,000, and depends on the slenderness ratio l / t of the cell walls.

Fig. 8

Finite element mesh for intrawall cracking, with interface elements located at a distance t / 4 from the cell wall edges. For illustrative purposes, supports at the boundary of cell wall 1 are only indicated at three locations, but are applied at all boundary nodes. The periodic boundary conditions at cell walls 2 and 3 are prescribed by uniform normal displacements $u_n$ and uniform tangential tractions $t_t$

Fig. 9

Finite element mesh for transwall cracking. The interface elements are located between all triangular continuum elements, which naturally allows the location and direction of crack development to be determined by the actual geometry and boundary conditions. For illustrative purposes, supports at the boundary of cell wall 1 are only indicated at three locations, but are applied at all boundary nodes. The periodic boundary conditions at cell walls 2 and 3 are prescribed by uniform normal displacements $u_n$ and uniform tangential tractions $t_t$

3.2.3 Transwall cracking

The third failure mechanism studied is transwall cracking, whereby a tensile crack traverses the cell wall. In contrast to the mechanisms of intercell and intrawall cracking, for transwall cracking the exact location of the crack is a-priori unknown. An example of a finite element mesh used for the simulations of transwall cracking is shown in Fig. 9. In accordance with the approach originally proposed in Xu and Needleman (1994), interface elements are placed between all triangular continuum elements, which naturally allows crack initiation and crack propagation to be determined by the actual geometry of the unit cell and the boundary conditions. The loads are applied at the free edges, in the same fashion as described in Sect. 3.2.1 for the case of intercell cracking. The number of elements in the model varies between 95,000 (for the honeycomb structure with slender cell walls $l/t=40$) and 110,000 (for the honeycomb structure with stocky cell walls $l/t=3.33$). With these discretizations the effect of the finite element mesh on the generated crack pattern turns out to be negligible.

4 Collapse contours for honeycomb micro-structures

The collapse contours for (i) intercell cracking, (ii) intrawall cracking and (iii) transwall cracking of the honeycomb structure are constructed from the results of the FEM simulations, and the effect of geometrical and material properties on the collapse response is analyzed using a minimal number of independent, dimensionless parameters. A dimensional analysis indicates that the (dimensionless) macroscopic normal stresses at failure can be expressed as a function of 5 dimensionless parameters:

$$\begin{aligned} \frac{\sigma _{ii} }{\sigma _y }=f\left( {\frac{l}{t}, \frac{t^{u}}{\sigma _y }, \frac{t}{R_0 },\frac{E}{\sigma _y },\nu } \right) \quad \hbox { with }\quad i\in \left\{ {1,2} \right\} .\nonumber \\ \end{aligned}$$

(11)

The length of the crack does not appear in Eq.(11), since it is irrelevant at which crack length the maximum stress required for cell collapse is reached. In the simulations the ratio between the Young’s modulus and the yield stress, $E/\sigma _y$, was kept fixed and set equal to 300, and the Poisson’s ratio was taken as $\nu =0.3$. Additional simulations not presented here indicated that the influence of these two dimensionless parameters on the simulation results is relatively small. Note that the effect of the fracture toughness $G_c$ on the failure response is accounted for in Eq.(11) via the parameter $R_0$ given by Eq.(10).

The diagrams showing the collapse contours use the normalized hydrostatic and deviatoric strengths along the horizontal and vertical axes, respectively, similar as is done in Fig. 4 for the yield contour.

4.1 Intercell cracking

4.1.1 Crack nucleation and propagation

Intercell cracking may appear in various ways, depending on the specific combination of the normal load P and shear load Q applied on the cell walls. If cell wall 1 is loaded by a normal load and cell walls 2 and 3 by a combination of normal and shear loads [whereby the normalized normal load n presented in Eq.(4) equals 0.75], the intercell crack develops as indicated in Fig. 10 by the four failure states a–d. For clarity reasons, these failure states are marked in the corresponding $F-u$ diagram that qualitatively illustrates the overall failure response, whereby $F=\sqrt{P^{2}+Q^{2}}$ is the effective load applied on cell wall 3, and u is the effective displacement, as determined from the axial displacement $u_n$ and the transversal displacements $u_t$ at the centre node of the end of cell wall 3 as $u=\sqrt{u_n^2 +u_t^2 }$. It can be observed from Fig. 10 that the crack nucleates at the centre of the unit cell, and gradually develops towards the outer edges of cell walls 2 and 3. In cell wall 1 cracking remains absent when the cell wall material has a high tensile strength, while under a low tensile strength a small crack may be initiated, which will unload and close when the main crack in cell walls 2 and 3 starts to develop. The mode-mixity of the main crack is set by the relative magnitudes of the applied normal load P and shear load Q, with the normal load affecting the mode I contribution and the shear load influencing both the mode I and mode II contributions. Due to stress concentrations, plastic zones develop at the crack tip and near the three $120^{o}$corners of the walls of the unit cell. In order to arrive at the final fracture profile represented by failure state “d”, the wall structure needs to undergo substantial softening, as characterized in the $F-u$ diagram by the decrease in the load F under an increasing displacement u. The stress response generated at the maximum load F, which in the $F-u$ diagram corresponds to the crack nucleation state “a”, is used for constructing the collapse contour.

Fig. 10

Nucleation (a) and propagation (b–d) of an intercell crack under a loading path characterized by a normal load P applied at cell walls (c.w.) 1–3 and a shear load Q applied at cell walls 2 and 3 (whereby $Q/P=0.09$) with the displacements magnified 5 times for clarity. The relative interfacial strength is $t^{u}/\sigma _y =0.75$ and the slenderness ratio equals $l/t= 3.33$. The four failure states a–d are indicated in the $F-u$ diagram that reflects the overall failure response. The stress response related to failure state “a”, at which the applied load F is maximal, is used for constructing the collapse contour

Fig. 11

Nucleation (a) and propagation (b–d) of an intercell crack under a loading path characterized by pure normal loading P applied at cell walls (c.w.) 1–3, with the displacements magnified 5 times for clarity. The relative interfacial strength $t^{u}/\sigma _y =0.50$ and the slenderness ratio equals $l/t= 3.33$. The four failure states a–d are indicated in the $F-u$ diagram that reflects the overall failure response. The stress response related to failure state “a”, at which the applied load F is maximal, is used for constructing the collapse contour

Fig. 12

Collapse contours for intercell cracking at various slenderness ratios l / t. The size of the plastic zone is taken relatively small, in correspondence with $t/R_0 =22$. a Low relative fracture strength $t^{u}/\sigma _y = 0.05$ (brittle fracture) and b high relative fracture strength $t^{u}/\sigma _y = 0.65$ (ductile fracture)

A second case of intercell cracking is depicted in Fig. 11, whereby the three cell walls are subjected to a normal force P only [i.e., the normalized normal load n presented in Eq.(4) equals 1.0]. Since this loading configuration is threefold symmetric, the crack develops under pure mode I conditions from the centre of the unit cell simultaneously into the three cell walls.

4.1.2 Effect of slenderness ratio

Figure 12 shows the collapse contours for four different slenderness ratios, $l/t = 3.33$, 6.67, 20 and 40, considering two relative fracture strengths: $t^{u}/\sigma _y =0.05$ (Fig. 12a), and $t^{u}/\sigma _y =0.65$ (Fig. 12b). The collapse contour plotted in Fig. 12a is representative of brittle intercell cracking (i.e., fracture accompanied by limited yielding) while the collapse contour shown in Fig. 12b reflects ductile intercell cracking (i.e., fracture accompanied by substantial yielding). The size of the plastic zone at the crack tip is kept fixed at a relatively small value corresponding to $t/R_0 =22$. The stress concentrations at the three $120^{o}$ corners of the walls induce some additional plasticity at these locations. Similar as for the plastic yield contour plotted in Fig. 4, for both relative fracture strengths the hydrostatic strength scales linearly with t / l for arbitrary wall slenderness ratios, and the deviatoric strength scales quadratically with t / l for slender cell walls ($l/t=20$ and 40). The superquadratic scaling with t / l observed for the deviatoric collapse strength of stocky cell walls ($l/t=6.67$ and 3.33) for brittle intercell cracking clearly is stronger than for ductile intercell cracking. When using a phenomenological scaling law for the deviatoric strength that is similar to that applied for plastic yielding, see Fig. 5, the scaling factor $\alpha$ required for closely matching the size effect for brittle intercell cracking of stocky cell walls equals $\alpha =2.70$, see also Fig. 13. Note that this value is considerably higher than that found in Sect. 2.3 for plastic yielding ($\alpha =0.85)$, which illustrates that the size effect on the deviatoric strength under brittle intercell cracking is stronger than under plastic yielding. Finally, a comparison of Figs. 12a, b shows that for an increasing relative fracture strength $t^{u}/\sigma _y$ the effective collapse strength of the honeycomb structure increases, with the strongest rise of almost a factor of 4 occurring under hydrostatic loading.

Fig. 13

Collapse contour for intercell cracking at various slenderness ratiosl / t. The size of the plastic zone is taken relatively small, in correspondence with $t/R_0 =22$, and the relative fracture strength is low, $t^{u}/\sigma _y = 0.05$ (brittle fracture). The normalized representation accounts for an additional increase in the deviatoric strength typical of stocky cell walls. The factor $\alpha$ quantifying this scaling effect is included in the dimensionless deviatoric strength plotted along the vertical axis, and equals $\alpha =2.70$

Fig. 14

Collapse contours for intercell cracking (solid lines) at various relative fracture strength values$t^{u}/\sigma _y$. The size of the plastic zone is taken relatively small, $t/R_0 =22$. The yield contour (dashed line) taken from Fig. 4 is plotted for comparison. a Slender cell walls $l/t=40$, and b stocky cell walls $l/t= 3.33$

For simplicity, in the above analyses the mode I and mode II fracture toughnesses were taken equal, $G_{Ic} =G_{IIc} =G_c$. However, in practice the mode II toughness may be somewhat larger than the mode I toughness. Additional simulations not presented here nevertheless demonstrated that the collapse contours are not very sensitive to the toughness ratio $G_{IIc} /G_{Ic}$; increasing this ratio towards 4 resulted in a maximal relative difference with the collapse contours in Fig. 12 of only 3% This is the result of intercell cracking being dominated by mode I.

Fig. 15

Collapse contours for intercell cracking (solid line) at various relative sizes of the plastic zone, $t/R_0$. The honeycomb structures are composed of stocky cell walls, $l/t=3.33$. a Low relative fracture strength $t^{u}/\sigma _y = 0.05$ (brittle delamination failure), and b high relative fracture strength $t^{u}/\sigma _y = 0.65$ (ductile delamination failure). The yield contour (dashed line) taken from Fig. 4 is plotted for comparison

4.1.3 Effect of relative fracture strength

The effect of the relative fracture strength $t^{u}/\sigma _y$ on the characteristics of the collapse response is shown in detail in Fig. 14, by plotting the collapse contour for a broad range of relative fracture strength values for honeycomb structures with slender cell walls, $l/t=40$ (Fig. 14a), and stocky cell walls, $l/t=3.33$ (Fig. 14b). The yield contour designated by the dashed line is taken from Fig. 4 and plotted for comparison. A comparison of Figs. 14a, b illustrates that under increased relative fracture strength, $t^{u}/\sigma _y$, the transition from the most brittle collapse contour (related to $t^{u}/\sigma _y =0.05$) to the yield contour (indicated by the dashed line) for slender and stocky cell walls occurs in an analogous fashion, whereby the growth in collapse strength under hydrostatic loading is considerably larger than under deviatoric loading. Notice that for the honeycomb structure composed of slender cell walls the collapse contour virtually coincides with the yield contour at a relative fracture strength of $t^{u}/\sigma _y =0.75$, while for the honeycomb with stocky cell walls this happens at a somewhat larger value of $t^{u}/\sigma _y =0.95$. Obviously, for relative fracture strengths above these limit values intercell cracking will no longer be activated; the honeycomb structure then fails by plastic yielding.

4.1.4 Effect of relative size of the plastic zone

The effect of the relative size of the plastic zone at the crack tip on the collapse contour is considered by examining values ranging from $t/R_0 =22$, via $t/R_0 =10$ and 5, to $t/R_0 =1$, using the honeycomb structure composed of stocky cell walls, $l/t=3.33$. Two relative fracture strengths are analyzed: $t^{u}/\sigma _y =0.05$ (Fig. 15a), and $t^{u}/\sigma _y =0.65$ (Fig. 15b). For brittle fracture with $t^{u}/\sigma _y =0.05$ the effect of the plastic zone on the collapse contour is small, which clearly is due to the fact that the overall plastic deformation generated in the wall structure remains limited. For ductile fracture with $t^{u}/\sigma _y =0.65$ the effect of the plastic zone appears to be more significant. For an increasing size of the plastic zone the collapse contour gradually approaches the analytical yield contour, whereby for $t/R_0 =1$ the amount of intercell cracking becomes negligible, and the collapse response becomes nearly fully determined by plastic yielding. Since the plastic zone $R_0$ scales proportionally with the fracture toughness $G_c$, see Eq.(10), it may be additionally concluded from Fig. 15 that the sensitivity of the collapse response to the fracture toughness is moderate to low. This results from the fact that the collapse contours were determined at a maximum load on the cell walls (i.e., point “a” in Figs. 10 and 11), whereby the effective fracture response is mainly governed by crack initiation (which depends on the fracture tensile strength) and not yet that much by crack propagation (which depends on the fracture toughness). Furthermore, simulation results not presented here have confirmed that honeycomb structures composed of slender cell walls show a qualitatively comparable collapse behavior as depicted in Fig. 15 for the stocky cell walls.

4.2 Intrawall cracking

4.2.1 Crack nucleation and propagation

Similar to intercell cracking, the mechanism of intrawall cracking may develop in various ways, depending on the loading path applied. If cell wall 1 is loaded by a normal load P and cell walls 2 and 3 are loaded by a specific combination of a normal load P and a shear load Q, cracking may develop as depicted in Fig. 16. The crack nucleates under mixed-mode conditions at the centre of the unit cell (a), and propagates into cell walls 2 and 3 (b-d), leaving cell wall 1 intact. Note that the crack develops along the interface between the $\hbox {S}_{1}$ and $\hbox {S}_{2}$ layers, which is in agreement with most experimental observations in wood microstructures. The corresponding $F-u$ diagram indicates that this process is accompanied by a substantially milder softening behaviour than observed for intercell cracking, see Fig. 10.

Fig. 16

Nucleation (a) and propagation (b–d) of an intrawall crack under a loading path characterized by a normal load P applied at cell walls (c.w.) 1–3 and a shear load Q applied at cell walls 2 and 3 (whereby $Q/P=0.09$), with the displacements magnified 5 times for clarity. The relative interfacial strength is $t^{u}/\sigma _y =0.20$ and the slenderness ratio equals $l/t= 3.33$. The four failure states a–d are indicated in the $F-u$ diagram that reflects the overall failure response. The stress response related to failure state “a”, at which the applied load F is maximal, is used for constructing the collapse contour

Fig. 17

Nucleation (a) and propagation (b–d) of an intrawall crack under a loading path characterized by pure normal loading P applied at cell walls (c.w.) 1–3, with the displacements magnified 5 times for clarity. The relative interfacial strength is $t^{u}/\sigma _y =0.20$ and the slenderness ratio equals $l/t= 3.33$. The four failure states a–d are indicated in the $F-u$ diagram that reflects the overall failure response. The stress response related to failure state “a”, at which the applied load F is maximal, is used for constructing the collapse contour

Fig. 18

Collapse contours for intrawall cracking at various slenderness ratios l / t. a Low relative fracture strength $t^{u}/\sigma _y = 0.05$ (brittle delamination failure) and b high relative fracture strength $t^{u}/\sigma _y = 0.65$ (ductile delamination failure). The size of the plastic zone is taken to be relatively small, in correspondence with $t/R_0 =22$

Alternatively, the three cell walls may be subjected to a normal load P only (i.e., a hydrostatic stress path), see Fig. 17. Due to a threefold symmetry in the loading conditions and geometry, intrawall cracking is simultaneously initiated near all three $120^{o}$ corners between the walls of the unit cell. However, due to minor irregularities in the FEM model (i.e., numerical round-off errors, heterogeneities in the finite element discretization), the cracking subsequently develops slightly asymmetrically into three cell walls. The mechanism of crack nucleation in Fig. 17 is different than in Fig. 16, thus leading to a different peak load in the $F-u$ diagram.

4.2.2 Effect of slenderness ratio

Figure 18 illustrates the collapse contours for intrawall cracking for various slenderness ratios l / t, considering the cases of low relative fracture strength, $t^{u}/\sigma _y = 0.05$ (Fig. 18a), and high relative fracture strength $t^{u}/\sigma _y = 0.65$ (Fig. 18b).

As for the case of intercell cracking, for slender cell walls the hydrostatic collapse strength scales linearly with t / l and the deviatoric collapse strength scales quadratically with t / l for slender cell walls. For stocky cell walls the superquadratic scaling of the deviatoric strength with t / l appears to be weaker than for intercell cracking, see Fig. 12, from which it may be concluded that the size effect by wall bending for intercell cracking is stronger.

4.2.3 Effect of relative fracture strength

Figure 19 depicts the collapse contours for various relative fracture strengths $t^{u}/\sigma _y$, thereby distinguishing between honeycomb structures with slender cell walls $l/t=40$ (Fig. 19a) and stocky cell walls $l/t=3.33$ (Fig. 19b). From a comparison of Figs. 14 and 19 it may be concluded that the collapse strength for intrawall cracking generally is larger than for intercell cracking when the relative fracture strength of the delaminating crack is low, i.e., $t^{u}/\sigma _y \le 0.20$, especially under hydrostatic loading. For larger relative strength values the effect by plastic yielding starts to dominate the failure response, as a result of which the differences in the collapse contours of the two cracking mechanisms vanish.

Fig. 19

Collapse contours (solid line) for intrawall cracking at various relative fracture strengths$t^{u}/\sigma _y$. The yield contour (dashed line) taken from Fig. 4 is plotted for comparison. a Slender cell walls $l/t=40$, and b stocky cell walls $l/t= 3.33$. The size of the plastic zone is taken relatively small, in correspondence with $t/R_0 =22$

4.2.4 Effect of relative size of the plastic zone

The effect of the relative size of the plastic zone, $t/R_0$, on the collapse contour is illustrated in Fig. 20a for cell walls of low relative fracture strength, $t^{u}/\sigma _y =0.05$, and in Fig. 20b for cell walls of high relative fracture strength, $t^{u}/\sigma _y =0.65$. The effect of the size of the plastic zone on the collapse contour for intrawall cracking is comparable to that for intercell cracking, see Fig. 15, indicating that the precise location of the delaminating crack is of minor importance here.

Fig. 20

Collapse contours for intrawall cracking (solid line) at various relative sizes of the plastic zone, $t/R_0$. The honeycomb structures are composed of stocky cell walls, $l/t=3.33$. a Low relative fracture strength $t^{u}/\sigma _y = 0.05$ (brittle fracture), and b high relative fracture strength $t^{u}/\sigma _y = 0.65$ (ductile fracture). The yield contour (dashed line) taken from Fig. 4 is plotted for comparison.

The collapse contours for intrawall cracking were determined by taking identical stiffness moduli E for the inner secondary wall, $\hbox {S}_{2}$, and the outer secondary walls, $\hbox {S}_{1 }$and $\hbox {S}_{3}$. In wood, however, the stiffnesses of the three secondary walls may differ. Additional simulations not presented here have shown that for stiffness mismatches ranging from $E_1 /E_2 =E_3 /E_2 = 0.1$ to 10 the relative difference in collapse strength maximally is 11%, which leads to the conclusion that stiffness mismatches between the secondary layers do not have a strong influence on the effective strength for intrawall cracking.

Fig. 21

Nucleation (a) and propagation (b–d) of a transwall crack under a loading path characterized by a normal load P applied at cell walls 1–3 and a shear load Q applied at cell walls 2 and 3 (whereby $Q/P=0.56$), with the displacements magnified 5 times for clarity. The relative interfacial strength is $t^{u}/\sigma _y =0.05$ and the slenderness ratio equals $l/t= 3.33$. The four failure states a–d are indicated in the $F-u$ diagram that reflects the overall failure response. The stress response related to failure state “a”, at which the applied load F is maximal, is used for constructing the collapse contour

4.3 Transwall cracking

4.3.1 Crack nucleation and propagation

In contrast to the mechanisms of intercell cracking and intrawall cracking, for transwall cracking the exact location of a failure crack is a-priori unknown. Figure 21 illustrates the nucleation and propagation characteristics of transwall cracking under combined tensile and shear loading [i.e., the normalized normal loading n presented in Eq.(4) equals 0.25]. It can be observed that a dominant crack initiates at the corner of cell walls 2 and 3, and subsequently propagates vertically upward, whereby at about half of the wall thickness it deflects towards the corner of cell walls 1 and 2. Note that the smaller, secondary cracks characterizing the diffusive fracture process zone (states “b” and “c”) gradually unload through the cell wall material bridging the crack faces, and finally close under the progressive localization into a single, catastrophic failure crack (state “d”). The bridging of crack faces by cell wall material has also been noticed from microscopic observations on real wood samples, see for example the fracture study on historic and new oak wood presented in Luimes et al. (2018). Crack bridging is typically associated to a diffusive fracture pattern, such as a fracture process zone. However, as illustrated in Luimes et al. (2018), once the cell wall material across crack faces is broken or pulled-out, a localized failure crack may develop. The F-u diagram in Fig. 21 illustrates that the softening behaviour experienced during crack propagation is significantly stronger than for intercell and intrawall cracking, see Figs. 10 and 16: the applied load F eventually reaches a value close to zero when the failure crack has almost fully developed across the thickness of the cell wall (state “d”).

When the three cell walls are subjected to a normal force P only [i.e., the normalized normal loading n presented in Eq.(4) equals 1.0], the crack nucleates at one of the three $120^{\circ }$ corners of the cell walls, and subsequently develops straightly towards half of the wall thickness, at which it deflects towards one of the other corners of the unit cell, see Fig. 22.

Fig. 22

Nucleation (a) and propagation (b–d) of a transwall crack under a loading path characterized by pure normal loading P applied at cell walls 1–3, with the displacements magnified 5 times for clarity. The relative interfacial strength is $t^{u}/\sigma _y =0.05$ and the slenderness ratio equals $l/t= 3.33$. The four failure states a–d are indicated in the $F-u$ diagram that reflects the overall failure response. The stress response related to failure state “a”, at which the applied load F is maximal, is used for constructing the collapse contour

Fig. 23

Collapse contours for transwall cracking at various slenderness ratiosl / t. The size of the plastic zone is taken to be relatively small, in correspondence with $t/R_0 =22$. a Low relative fracture strength $t^{u}/\sigma _y = 0.65$ (brittle fracture) and b high relative fracture strength $t^{u}/\sigma _y = 1.20$ (ductile fracture)

The specific corner at which the main crack nucleates is determined by the heterogeneity of the finite element mesh, which essentially breaks the symmetry of the discretized unit cell. Note that the F-u diagram is qualitatively similar to that computed for combined tensile and shear loading, see Fig. 21.

Fig. 24

Collapse contours for transwall cracking (solid line) at various relative fracture strengths$t^{u}/\sigma _y$. The yield contour (dashed line), taken from Fig. 4, is plotted for comparison. a Slender cell walls $l/t=40$, and b stocky cell walls $l/t= 3.33$. The size of the plastic zone is taken to be relatively small, in correspondence with $t/R_0 =22$

4.3.2 Effect of slenderness ratio

In Fig. 23 the collapse contours are plotted for different slenderness ratios l / t, considering the cases of low relative fracture strength, $t^{u}/\sigma _y = 0.65$ (Fig. 23a), and high relative fracture strength, $t^{u}/\sigma _y = 1.20$ (Fig. 23b). Note that the distinctive notions “low” and “high” here are related to larger relative strength values than for the mechanisms of intercell cracking and transwall cracking, see Figs. 12 and 18; this is done because a transverse failure crack characterizing transwall cracking typically induces less plastic yielding than a longitudinal failure crack defining intercell or intrawall cracking. The relative size of the plastic zone is kept fixed in correspondence with the value $t/R_0 =22$. Fig. 23a, b show that for slender cell walls the hydrostatic and deviatoric strengths respectively scale approximately linearly and quadratically with t / l. For stocky cell walls these orders of scaling appear to be slightly larger. Note further that the shape of the collapse contour becomes more convex (i.e., more curved) at the high relative strength $t^{u}/\sigma _y =1.20$, which is due to the generation of plasticity. Essentially, the brittle failure contours computed at low relative strength $t^{u}/\sigma _y =0.65$ are characterized by (almost) straight lines; the minor concavity occasionally observed is likely to be caused by small irregularities in the mesh (and thus in the trajectories of the cracks generated).

4.3.3 Effect of relative fracture strength

Figure 24a, b illustrate the dependency of the collapse contour on the relative fracture strength $t^{u}/\sigma _y$ for slender $(l/t=40)$ and stocky $(l/t=3.33)$ cell walls, respectively. The yield contour taken from Fig. 4 is plotted for comparison (dashed line). For both slenderness ratios it is observed that under arbitrary loading paths the collapse strength for small relative strength values is considerably lower than for large strength values. Furthermore, for relative fracture strengths $t^{u}/\sigma _y <1$ the collapse response is dominated by cracking; only for strength values above unity plastic yielding starts to contribute noticeably to the effective collapse response. The collapse contour virtually coincides with the yield contour at relative strengths of $t^{u}/\sigma _y =1.30$ for slender cell walls, and slightly above 1.40 for stocky cell walls, whereby the amount of transwall cracking has become negligible.

4.3.4 Effect of relative size of the plastic zone

The effect of the relative size of the plastic zone, $t/R_0$, on the collapse contour is illustrated in Fig. 25a for cell walls of low relative fracture strength, $t^{u}/\sigma _y =0.65$, and in Fig. 25b for cell walls of high relative fracture strength, $t^{u}/\sigma _y =1.20$. In both cases a larger plastic zone increases the collapse strength, where for the high relative fracture strength the collapse contour approaches the yield contour indicated by the dashed line.

Fig. 25

Collapse contours for transwall cracking (solid line) at various relative sizes of the plastic zone, $t/R_0$. The honeycomb structures are composed of stocky cell walls, $l/t=3.33$. a Low relative fracture strength $t^{u}/\sigma _y = 0.05$ (brittle fracture), and b high relative fracture strength $t^{u}/\sigma _y$ = 0.65 (ductile fracture). The yield contour (dashed line) taken from Fig. 4 is plotted for comparison

4.4 Summary of the three failure mechanisms

In Fig. 26 the collapse contours following from the above plane-stress analyses on the three failure mechanisms are summarized for the case of slender cell walls, $l/t=40$, whereby Fig. 26a relates to $t^{u}/\sigma _y =0.05$ and Fig. 26b corresponds to $t^{u}/\sigma _y =0.65$. Further, in Fig. 27a and b the results calculated from plane-strain analyses on the same three collapse mechanisms are plotted for comparison, which are representative of the failure behaviour of relatively long honeycomb grains present in various types of wood. The plane-strain yield contour indicated by the dashed line and determined from FEM simulations is plotted for comparison.

Fig. 26

Collapse contours under plane-stress conditions for intercell cracking, intrawall cracking, and transwall cracking for the case of slender cell walls $l/t=40$. The size of the plastic zone is relatively small, in correspondence with $t/R_0 =22$. a Low relative fracture strength $t^{u}/\sigma _y = 0.05$ and b high relative fracture strength $t^{u}/\sigma _y = 0.65$. The yield contour (dashed line) taken from Fig. 4 is plotted for comparison

Fig. 27

Collapse contours under plane-strain conditions for intercell cracking, intrawall cracking, and transwall cracking for the case of slender cell walls $l/t=40$. The size of the plastic zone is taken to be relatively small, in correspondence with $t/R_0 =22$. a Low relative fracture strength $t^{u}/\sigma _y = 0.05$ and b high relative fracture strength $t^{u}/\sigma _y = 0.65$. The yield contour (dashed line, computed with FEM) for a honeycomb subjected to plane-strain loading conditions is plotted for comparison

Observe that for $t^{u}/\sigma _y =0.05$ the differences between the collapse contours computed for plane-stress and plane-strain conditions are negligible; this is, since the collapse response here is dominated by cracking, solely prescribed by the in-plane stress components. Conversely, for $t^{u}/\sigma _y =0.65$ the collapse response significantly depends on plastic yielding, which, via the $J_{2}$-flow criterion, is prescribed by both the in-plane and out-of-plane stress components. Accordingly, the deviatoric collapse strength under plane-strain conditions is somewhat larger than under plane-stress conditions, while the hydrostatic collapse strength is somewhat smaller. Note further that the mechanism of transwall cracking is generally characterized by the lowest collapse strength. However, experimental observations on wood microstructures indicate that all three failure mechanisms may appear in situ, see Fig. 1. It is therefore anticipated that the values of the fracture strength $t^{u}$ for intercell cracking and intrawall cracking (measured perpendicular to the transverse direction of the cell wall) may be considerably lower than that for transwall cracking (measured perpendicular to the longitudinal direction of the cell wall), i.e., the fracture strength of wood cell wall material is anisotropic. Alternatively, the sensitivity of intercell and intrawall cracking to specific geometrical imperfections of the cell wall may generate a knock-down effect on the corresponding collapse strengths, as a result of which these strengths end up lower than the collapse strength for transwall cracking.

5 Concluding remarks

The competition between fracture and plasticity in periodic hexagonal honeycomb structures subjected to (i) intercell cracking, (ii) intrawall cracking and (iii) transwall cracking is studied, and the effect upon the macroscopic collapse response is explored, using dedicated FEM analyses of unit cell configurations. These three cracking mechanisms are regularly observed in wood honeycomb microstructures, and insight into their effect on the macroscopic collapse behavior is useful for adequately designing timber structures against failure. Specifically, the present study provides a direct link between the microstructural geometrical and material properties of wood and their macroscale failure behaviour, which supports a careful selection of wood species based on the material structure needed for reaching a specific failure resistance in a structural application. For intercell and intrawall cracking the hydrostatic strength scales linearly with the thickness-to-length (t / l) ratio of the cell walls. For transwall cracking this order of scaling tends to become slightly larger when the cell walls become stocky, i.e., when $l/t<10$. Further, for all three cracking mechanisms the deviatoric strength of the honeycombs scales quadratically with t / l in the case of slender cell walls, and superquadratically in the case of stocky cell walls. Both the hydrostatic and deviatoric collapse strengths of the honeycomb strongly increase in the transition from brittle cell walls with low relative fracture strength to ductile cell walls with high relative fracture strength. This strength increase typically changes the shape of the collapse contour, and is the largest for the transwall cracking mechanism, followed by intercell cracking and finally intrawall cracking. For the intercell and intrawall cracking mechanisms the collapse contour of the honeycomb approaches its plastic yield surface when the relative fracture strength is close to unity. For transwall cracking this occurs at higher relative fracture strength up to a value of about 1.4. In addition, the mechanism of transwall cracking is generally characterized by the lowest collapse strength; since experimental observations on wood microstructures show the in-situ appearance of all three failure mechanisms, it is anticipated that the values of the relative fracture strength associated with intercell cracking and intrawall cracking (measured perpendicular to the transverse direction of the cell wall) may be substantially lower than that for transwall cracking (measured perpendicular to the longitudinal direction of the cell wall), i.e., the fracture strength of wood cell wall material is anisotropic. Alternatively, the sensitivity of intercell and intrawall cracking to specific geometrical imperfections of the cell wall may generate a knock-down effect on the corresponding collapse strengths, as a result of which these strengths end up lower than the collapse strength for transwall cracking. Finally, the effect on the collapse response by the size of the plastic zone at the crack tip is small at low relative fracture strength (whereby plastic yielding remains limited), and moderate at high relative fracture strength (whereby plastic yielding becomes substantial). This observation also leads to the conclusion that the ultimate collapse strength of the honeycomb is significantly more sensitive to the fracture strength than to the fracture toughness.

In order to further investigate the phenomena discussed above, more systematic experimental studies on wood are necessary, whereby loading experiments performed along a variety of stress paths need to be complemented with detailed micro-structural observations of the corresponding failure mechanisms. With the aid of the results of the present numerical study, such experiments would allow for accurately identifying the competition between fracture and plasticity in wood honeycomb microstructures, thereby supporting an adequate calibration of the fracture strength and yield strength at the cell wall level. The sensitivity of the collapse strength to geometrical imperfections of the cell wall geometry, which, as demonstrated by Chen et al. (1999), may induce a significant knock-down effect on the hydrostatic yield strength of honeycomb structures, is also a topic for future study.