Finite element simulations of notch tip fields in magnesium single crystals

Abstract

Recent experiments using three point bend specimens of Mg single crystals have revealed that tensile twins of $\{10\bar{1}2\}$-type form profusely near a notch tip and enhance the fracture toughness through large plastic dissipation. In this work, 3D finite element simulations of these experiments are carried out using a crystal plasticity framework which includes slip and twinning to gain insights on the mechanics of fracture. The predicted load–displacement curves, slip and tensile twinning activities from finite element analysis corroborate well with the experimental observations. The numerical results are used to explore the 3D nature of the crack tip stress, plastic slip and twin volume fraction distributions near the notch root. The occurrence of tensile twinning is rationalized from the variation of normal stress ahead of the notch tip. Further, deflection of the crack path at twin–twin intersections observed in the experiments is examined from an energy standpoint by modeling discrete twins close to the notch root.

1 Introduction

Magnesium alloys have some attractive mechanical properties such as low density, high specific strength and good damping characteristics. Hence, it is envisaged to employ them for applications in automotive components. However, their poor room temperature formability and corrosion resistance along with low fracture toughness as compared to aluminum alloys have inhibited their usage. Experimental investigations have shown that the fracture toughness $J_{\text{ c }}$ of Mg alloys varies from 1 to 8 N/mm (Yan et al. 2004; Somekawa and Mukai 2006). Somekawa et al. (2009) noted from fracture experiments on coarse grained AZ31 Mg alloy that tensile twins (TTs) of $\{10\bar{1}2\}\langle 10\bar{1}1\rangle$-type form near the crack tip and crack growth occurs along a twin–matrix interface. By contrast, Yu et al. (2012) observed that nanotwins shield the crack tip in Mg single crystals leading to crack deflection, blunting and toughening. This corroborates with an earlier study by Govila (1970) on crack blunting due to occurrence of twins in Be single crystals. Thus, the precise role of twinning on fracture resistance of Mg needs to be clearly understood.

To this end, Kaushik et al. (2014) carried out fracture experiments using notched three point bend specimens of Mg single crystals having three different crystallographic orientations. In the first and second orientations, referred to as A and B, the normal to the flat surfaces of the notch was aligned along c-axis. Orientation C mimicked the basal-textured Mg alloys with the c-axis along the notch front. Several important observations were made from this study based on EBSD, optical metallography and surface profilometry. First, profuse tensile twinning was noticed around the notch root in all three orientations. In orientations A and B, the TTs nucleate at the notch root and spread to regions farther away as load increases. This is accompanied by basal slip activity adjacent to notch flanks and farther ahead of the notch tip. By contrast, in orientation C, the reverse trend was seen with the TTs extending from the loading edge towards the notch root leaving a region close to it free of twins. Further, in this case surface profile scans indicated that out-of-plane bulging of the specimen occurs. This is counter to common perception that out-of-plane dimpling should take place near a notch tip. Secondly, crack initiation occurs before the peak load and the crack grows stably along twin–matrix interface before deflecting at twin–twin intersections resulting in a zigzag crack path. Thirdly, the evolution of average TT volume fraction over a region close to the notch root with load correlates with the energy release rate history implying that tensile twinning is an important energy dissipation mechanism.

The values of notched fracture toughness $J_c$ for orientations A, B and C were 12.2, 4.5 and 9.9 N/mm, respectively. The low $J_c$ value for orientation B as compared to A despite their similarity was attributed to the presence of $\{10\bar{1}2\}$ twins induced during specimen polishing which impeded the nucleation and growth of twins during the deformation of the specimen (Kaushik et al. 2014). Thus, plastic dissipation was restricted to fewer twins and crack growth occurred at a low $J_c$ value due to plastic slip accumulation at the interface between the matrix and the prominent twin near the notch root. Finally, for orientation C, strong 3D influence of twinning development was noticed based on comparison of twin traces at different planes through the specimen thickness. In order to understand the mechanics of fracture in Mg and to explain some of the experimental observations numerical simulations need to be performed. Specifically the following questions are raised by the experiments:

• What is the 3D nature of stress, plastic slip, and twin volume fraction distributions for the three orientations?

• What causes the difference in distribution of TTs in the uncracked ligament for orientation C as compared to the other two orientations?

• Can the observed out-of-plane bulging of the specimen for orientation C be rationalized from the stress distribution prevailing in the uncracked ligament?

• Can numerical simulations accurately predict the evolution histories of twin volume fraction in the ligament, thereby substantiating the claim made in the experiments about the role of TTs in energy dissipation and toughening?

• Can the observed crack deflections at twin–twin intersections be explained through computations of energy release rate and plastic slip concentrations?

Kalidindi (1998) extended the crystal plasticity theory formulated by Asaro (1983b) and Asaro and Rice (1977) to incorporate deformation twinning by considering it as a quasi-slip process, with the twin volume fraction as the important variable that evolves due to nucleation and growth of twins. This modified crystal plasticity theory, implemented in finite element solution procedures, has been widely used to analyze the deformation behavior, stress distributions, texture evolution and formability in HCP metals (Salem et al. 2005; Brown et al. 2005; Graff et al. 2007; Knezevic et al. 2010; Izadbakhsh et al. 2011; Fernandez et al. 2011; Choi et al. 2011). Several hardening models have been proposed to represent slip and twin interactions in Mg for incorporation in the above crystal plasticity formulation (Graff et al. 2007; Homayonifar et al. 2009; Zhang and Joshi 2012). Among these models, the one suggested by Zhang and Joshi (2012) accounts for both compression and tensile twinning. Also their hardening laws are motivated from underlying physical processes. Indeed, their predictions of the microscopic (slip/twin) activities compare well with experimental evidence on Mg (Wonsiewicz 1966; Kelley and Hosford 1968; Barnett 2007).

In order to address the questions posed by the experiments of Kaushik et al. (2014), crystal plasticity based simulations which have been shown to predict mechanical response, formability and failure in the presence of slip and twinning (Graff et al. 2007; Knezevic et al. 2010; Izadbakhsh et al. 2011; Fernandez et al. 2011; Zhang and Joshi 2012) are adequate. It must be mentioned that to model individual twins and their interactions, atomistic or phase-field simulations (Kucherov and Tadmor 2007; Kim et al. 2010; Tang et al. 2011a; Hu et al. 2010; Clayton and Knap 2011, 2013) are required. But such simulations have their limitations from the standpoint of spatial and temporal scales, choice of interatomic potential (in case of atomistic modeling), representation of plastic slip through dislocation motion, modeling of all twin variants and application of boundary and load conditions (in case of phase field method). Further none of these techniques have been quantitatively benchmarked with experimental data unlike crystal plasticity simulations (Salem et al. 2005; Homayonifar et al. 2009; Zhang and Joshi 2012). Also, as noted below, a recent atomistic simulation of fracture in Mg single crystals predicts the occurrence of a TT variant that is not observed in experiments (Tang et al. 2011a).

In the context of FCC single crystals, several investigators have studied the mechanics of fracture using analytical, numerical and experimental techniques (see, for example, Rice 1987; Patil et al. 2008a, b, 2009; Crone et al. 2004; Sabnis et al. 2012; Biswas et al. 2013). Crystal plasticity framework was employed by Patil et al. (2008a) and Biswas et al. (2013) along with finite element analysis to accurately predict the load–displacement response and pattern of slip bands near a notch tip in aluminum single crystals.

By contrast, little effort has been devoted to understand plastic deformation due to combination of slip and twinning near a notch tip in HCP metals. Kucherov and Tadmor (2007) carried out molecular dynamics (MD) simulations of mode I loading on basal crack orientation in zirconium single crystals (which has c/a ratio similar to Mg) and reported the absence of twinning. It must be however noted that, the active slip and twin modes in zirconium are different from those of Mg. In particular, while basal slip occurs easily in Mg, prismatic slip is most active in zirconium. A similar MD simulation on a basal crack orientation (which coincides with orientation B studied in Kaushik et al. (2014)) in Mg single crystals by Tang et al. (2011a) predicted the occurrence of deformation twinning of $\{11\bar{2}1\}\langle \bar{1}\bar{1}26\rangle$-type at the crack tip. However, the experimental observations of Kaushik et al. (2014) indicate the formation of tensile twins of $\{10\bar{1}2\}$-type. Indeed, $\{11\bar{2}1\}$ tensile twins are rarely noticed in experiments on Mg (Yoo 1981). By contrast, atomistic simulations show both $\{11\bar{2}1\}$ as well as $\{10\bar{1}2\}$ twinning (Kim et al. 2010; Tang et al. 2011a, b).

In this work, finite element simulations of the fracture experiments reported by Kaushik et al. (2014) are conducted. The modified crystal plasticity framework given by Kalidindi (1998) is employed along with the hardening laws proposed by Zhang and Joshi (2012). The objectives are to understand the mechanics of fracture in Mg single crystals and to address the issues raised by the experiments of Kaushik et al. (2014). The load–displacement curves, plastic slip and twin activities in the region around the notch root are found to agree well with the experimental observations of Kaushik et al. (2014). The numerical results are also used to study the notch tip fields (for example, the through-thickness variations of hydrostatic stress and plastic slips). Finally, some simulations are conducted by modeling discrete twin bands at the notch tip. The energy release rate associated with continued crack extension along a twin boundary is compared with that pertaining to deflection of the crack at a twin–twin intersection. These simulations show that zigzagging of the crack is favored from an energy standpoint.

2 Constitutive framework

The finite deformation crystal plasticity framework (Asaro 1983a) which was extended to accommodate deformation twinning by Kalidindi (1998) is employed in this work. In this modified theory, twinning is viewed as a quasi-slip process which is represented in a homogenized sense through the twin volume fraction $f^\beta$ corresponding to each twin system ($\beta = 1, 2,\ldots , \hbox {N}_t$, where $\hbox {N}_t$ is the total number of twin systems). The slip rate $\dot{\gamma }_{s}^{\delta }$ (corresponding to each slip system $\delta =1, 2, \ldots , \hbox {N}_s$, where $\hbox {N}_s$ is the total number of slip systems) and twin volume fraction rate $\dot{f}^{\beta }$ (for each twin system $\beta$) are evaluated using viscous power law equations of the form (Zhang and Joshi 2012):

$$\begin{aligned} \dot{\gamma }_{s}^{\delta }&= \dot{\gamma }_{o}\bigg \arrowvert \frac{\tau _{s}^{\delta }}{g_{s}^{\delta }}\bigg \arrowvert ^{\frac{1}{{m}_{s}}}\mathrm {sign}({\tau }_{s}^{\delta }), \nonumber \\ \dot{f}^{\beta }&= \frac{\dot{\gamma }^{\beta }}{\gamma _{tw}} = \dot{f}_{o}{\bigg \langle \frac{\tau _{t}^{\beta }}{s_{t}^{\beta }}\bigg \rangle }^{\frac{1}{{m}_{t}}}. \end{aligned}$$

(1)

Here, $\dot{\gamma }_{o}$ and $\dot{f}_{o}$ are the reference slip and twin rates, $\gamma _{tw}$ is the twinning shear and $m_s,\, m_t$ are rate exponents. The values of both $m_s$ and $m_t$ are chosen as 0.02 in the present simulations in order to represent nearly rate-independent response. Further, $\tau _{s}^{\delta }$ and $g_{s}^{\delta }$ represent the resolved shear stress and slip resistance for the $\delta$th slip system, respectively. Similarly, $\tau _{t}^{\beta }$ and $s_{t}^{\beta }$ denote the resolved shear stress and current strength of twin system $\beta$, respectively.

Zhang and Joshi (2012) proposed phenomenological hardening laws for Mg which were motivated by underlying physical processes involving slip–slip, twin–twin and twin–slip interactions. Here, it must be noted that at room temperature, the total number of slip and twin systems in Mg are $\hbox {N}_s = 18$ and $\hbox {N}_t = 12$. The slip systems involve basal, prismatic, pyramidal $\langle a\rangle$ and pyramidal $\langle c+a\rangle$ (i.e, $\{11\bar{2}2\}\langle \bar{1}\bar{1}23\rangle$) slip systems (Kelley and Hosford 1968). The twin systems comprise of six $\{10\bar{1}2\}\langle 10\bar{1}1\rangle$ systems (referred to as tensile twins or TTs) and six $\{10\bar{1}1\}\langle 10\bar{1}2\rangle$ systems (called as contraction twins or CTs). The former can cause extension along the c-axis (0001), whereas the latter can give rise to contraction along the c-axis. Among the slip systems, only pyramidal $\langle c+a\rangle$ system can cause deformation along c-axis.

Since $g_{s}^{\delta }$ represents the resistance of the $\delta$th slip system, its evolution governs the hardening of the crystal. This is postulated as (Zhang and Joshi 2012):

$$\begin{aligned} {g_{s}^{\delta }}={\tau }_0^{\delta } + \int _{t_0}^{t}\dot{g}_{sl-sl}^{\delta }dt + \int _{t_0}^{t}\dot{g}_{tw-sl}^{\delta }dt, \end{aligned}$$

(2)

where ${\tau }_0^{\delta }$ represents the initial value of slip resistance for $\delta$th slip system. Also, $\dot{g}_{sl-sl}^{\delta }$ and $\dot{g}_{tw-sl}^{\delta }$ represent the hardening rate of the slip system due to slip–slip interaction and twin–slip interaction, respectively. However, in contrast to the above, the twin systems are assumed to harden only due to twin–twin interactions (Zhang and Joshi 2012). The interaction between slip systems is represented by the saturation hardening model (Peirce et al. 1983). The barrier to slip by boundaries of CTs is assumed to result in a Hall–Petch type hardening, whereas TTs are taken to harden the slip systems by the saturation-type law. The latter is also employed for representing interaction between TTs, while a power law form is used for simulating hardening of CT systems.

These constitutive equations and the associated constants have been benchmarked by Zhang and Joshi (2012) against channel-die compression test results on Mg single crystals reported by Kelley and Hosford (1968). These results pertain to seven different crystal orientations with respect to the loading and constraint directions which were chosen by Kelley and Hosford (1968) so that different slip and twin systems are triggered in each test. By systematically tuning the hardening parameters and other constants, Zhang and Joshi (2012) calibrated them so as to obtain close match with all the experimental stress–strain curves given by Kelley and Hosford (1968). These constants are employed in the present simulations.

The modified crystal plasticity formulation of Kalidindi (1998) along with the above hardening laws has been implemented in the general purpose finite element code FEAP (Zienkiewicz and Taylor 1989) using the rate tangent modulus method (Peirce et al. 1983). The B-bar procedure is used to treat nearly incompressible deformation in the fully plastic range (Hughes 1980; Moran et al. 1990).

Twinning induces lattice reorientation which is taken to occur based on the criterion given by Zhang and Joshi (2012):

$$\begin{aligned} \dot{f}^{\beta } > 0, \quad \sum _{\beta =1}^{N_{t}}f^{\beta } \le 0.9. \end{aligned}$$

(3)

When the net twin volume fraction at an element integration station attains a value of 0.9, the crystal lattice at this station is reoriented to that pertaining to the $\beta$th twin with the highest $f^\beta$.

3 Finite element simulations of the fracture experiments

3.1 Modeling aspects

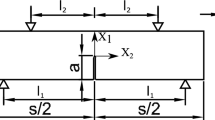
In this work, 3D finite element analyses of the fracture experiments conducted by Kaushik et al. (2014) using three point bend specimens of Mg single crystals are performed.The three crystal orientations considered in the experimental study are shown in the Fig. 1a–c. In orientations A and B, the normal to the flat surface of the notch is aligned along the c-axis (0001). The notch front is aligned with $[1\bar{2}10]$ and the crack growth direction is along $[10\bar{1}0]$ in orientation A. In orientation B, the notch front and crack growth directions are interchanged as compared to orientation A. The c-axis is along the notch front while $[1\bar{2}10]$ and $[10\bar{1}0]$ are aligned with the normal to the flat surface of the notch and crack growth direction, respectively in orientation C.

Fig. 1

Schematic of orientations considered in this work: a orientation-A, b orientation-B and c orientation-C

The in-plane mesh employed to model half the specimen owing to mode I and crystallographic symmetry corresponding to orientation A is shown in Fig. 2a. Here, the $X_1$ axis is along the crack growth direction, $X_2$ along the normal to the flat surfaces of the notch and $X_3$ parallel to the notch front. Also, $L,\, W$ and $h$ are the half-length, width and thickness of the specimen, respectively, and $a,\, r_o$ are the notch length and radius. Figure 2b is a magnified view of the in-plane mesh near the notch root. The 3D mesh is generated by extruding this mesh in the thickness direction and contains 5,334 eight-noded hexahedral elements based on the B-bar formulation (Moran et al. 1990) along with 6,600 nodes. A mesh refinement study was conducted by repeating some of the simulations using a mesh in which the elements near the notch root were refined by a factor of 1.5. It was found that there was negligible change in the load–displacement response, evolution of energy release rate J and the plastic slip and twin volume fraction distributions. Table 1 summarizes the dimensions of the specimens modeled for various orientations (which are same as the corresponding values in the experiments of Kaushik et al. (2014)).

Fig. 2

In-plane finite element mesh for simulating half the three point bend specimen corresponding to orientation A showing a full view and b magnified view of the region near the notch tip. The average tensile twin volume fraction is quantified in the region EFGHI

It is noted that in view of symmetry (both crystallographic and geometric) about the mid-plane ($X_3 = h/2$) of the specimen, only half the specimen through the thickness is considered in addition to half the length. Thus, symmetry conditions are imposed on the mid-plane $X_3 = h/2 (u_3 = 0,\, \tau _{13} = 0,\, \tau _{23} = 0)$ and on the plane $X_2 = 0 (u_{2} = 0, \tau _{12} = 0, \tau _{23} = 0)$. In order to simulate three point bend conditions on the specimen, displacement restraint $u_{1} = 0$ is imposed on the nodes at $X_2 = L$ and $X_1 = -a$. Displacement $(u_1 = -{\varDelta })$ is prescribed on the boundary nodes located in between $X_2 = 0$ and $X_2 = 0.02L$ with $X_1 = W-a$. The contact load is distributed over a region in order to suppress large mesh distortions that would otherwise occur if it is applied at just one node. Further, the finite element mesh close to this boundary region is refined in order to capture large strain gradients.

Seven layers of elements are used to model half the specimen through the thickness. The layers of nodes are located at $X_{3}/h = 0.0$, 0.038, 0.084, 0.14, 0.20, 0.28, 0.38, 0.5. Thus, the layers become gradually thinner as the free surface ($X_3 = 0$) is approached in order to capture the strong through-thickness variation of the field quantities close to the notch root (Narasimhan and Rosakis 1990; Subramanya et al. 2007).

3.2 Results and discussion

In this section, results obtained from the finite element simulations are discussed. They are compared with the experimental observations of Kaushik et al. (2014). The contours of plastic slip, stresses, twin volume fraction are presented to understand the in-plane and thickness distribution of these quantities.

3.2.1 Load versus displacement curves

Figure 3a–c shows the comparison between the load (P) versus displacement ($\varDelta$) curves obtained from experiments and simulations for orientations A, B and C, respectively. It can be seen that there is a good agreement between the two curves for all three orientations. In particular, the simulations represent the bilinear nature of the load–displacement curves well. As in the experiments, the simulations also show that the single crystal fracture specimens display high hardening (as characterized by the slope of the P–$\varDelta$ curve) in all three orientations. This is primarily attributed to profuse formation of TTs that lead to twin–slip and twin–twin interactions (McCabe et al. 2009; Oppedal et al. 2012). In this connection, it must be noted that the experimental results show numerous intersections between different TT variants near the notch tip. As mentioned in Sect. 2, the phenomenological constitutive equations of Zhang and Joshi (2012) incorporate such twin–twin as well as twin–slip interactions. The good agreement between the load–displacement curves predicted by the simulations and experiments lends confidence to use of these equations. The serrations observed in the experimental curves arise due to nucleation of twins (Kaushik et al. 2014) which cannot be reproduced by the present finite element analysis as it does not account for discrete twinning. Instead, a homogenized representation of twinning is employed with the twin volume fraction as the characterizing parameter (see Sect. 2).

Table 1 Dimensions of the notched TBP specimens for the three orientations modeled in the finite element simulations

Fig. 3

Load versus displacement curves obtained from experiments (Kaushik et al. 2014) and 3D finite element simulations for a orientation $A$, b orientation $B$ and c orientation $C$

3.2.2 Variation of local energy release rate through the thickness

The energy release rate $J$ is an important parameter that characterizes the crack tip fields in elastic–plastic materials. In order to evaluate $J$ from the finite element analysis, the domain integral method proposed by Nakamura et al. (1986) is employed with suitable modification for 3D and finite deformation.

The objectives for computing $J$ are twofold. First the thickness variation of local $J$-integral is investigated in this subsection which would shed light on how the crack driving force varies along the notch front. Secondly, the accuracy of evaluating the energy release rate from load–displacement records is examined in the next subsection. The local $J$-integral is calculated as a function of distance $s$ along the notch front $(0\le s \le h/2)$ using each layer of nodes through the specimen thickness. For each node layer, the local $J$ value is computed over a few rectangular domains and is found to vary by less than $5\%$ during the entire loading history for all three orientations. This ensures that the local $J$ values are domain independent. The through-thickness variation of $J$ is employed to determine the average energy release rate value at different stages of loading as:

$$\begin{aligned} J_{ave}=\frac{2}{h}\int _0^{h/2}J(s)ds. \end{aligned}$$

(4)

Figure 4a displays the variations of local $J$ normalized by $J_{ave}$ with normalized distance $s/h$ along the notch front for orientation A at different load levels. At low load levels, the through-thickness variation of $J$ is small indicating that the response of the specimen is still elastic (see Fig. 3). However, at higher load levels, the local $J$ is highest at the mid-plane $(s/h = 0.5)$ and drops appreciably as the free surface $(s/h = 0)$ is approached. Thus, the value of local $J$ at the mid-plane is more than twice that at the free surface for $\hbox {P} > 3.5\,\hbox {N}$.

Fig. 4

a Variations of local $J$-integral value normalized by average $J$ through the specimen thickness plotted with normalized distance $s$/h along the notch front at different load levels for orientation $A$. b Comparison of energy release rate computed from load–displacement curve with that obtained from domain integral method for orientation A

3.2.3 Evaluation of energy release rate from load–displacement curve

Since the experimentally tested specimens do not conform to ASTM standards specifications and are anisotropic single crystals, the expression for obtaining $J$ from the P–$\varDelta$ curve (Rice et al. 1973; ASTM 1981) needs to be modified by determining a suitable shape factor. To this end, $J$ is evaluated as:

$$\begin{aligned}&J = J_{e} + J_{p},\nonumber \\&J_{e} = CP^2, \nonumber \\&J_{p} = \frac{{\eta }A_p}{hb}, \end{aligned}$$

(5)

where $J_{e}$ and $J_{p}$ are the elastic and plastic parts of the $J$-integral, $\eta$ is the shape factor, P is the load and $A_{p}$ is the area enclosed between the P–$\varDelta$ curve, the unloading line which is taken to have the same slope as the initial elastic part of the P–$\varDelta$ curve and the abscissa. Further, $b = W-a$ is the uncracked ligament length of the specimen and C is a constant which is determined by calibrating with finite element computations for purely elastic material response.

The shape factor $\eta$ is determined by fitting Eq. (5) to the $J_{ave}$ computed by the domain integral method from elastic–plastic finite element analysis of the single crystal specimen as a function of load P. The shape factor $\eta$ thus estimated is found to be about 1.65 for all the three orientations as opposed to a value of 2 which is assumed in the ASTM $J_c$ test procedure (ASTM 1981) based on the analysis of Rice et al. (1973) for a deeply cracked bend specimen. In Fig. 4b, $J$ computed from Eq. (5) using the numerically obtained load–displacement curve with above $\eta$ value is plotted as a function of load for orientation A. Also shown in the figure is the $J_{ave}$ variation with load determined directly from the domain integral method. It may be seen that the two curves compare well which lends confidence to applying Eq. (5) for the single crystal bend specimens. Hence, this procedure was used to evaluate the energy release rate and the notched fracture toughness from the experimental load–displacement records by Kaushik et al. (2014).

3.2.4 Contours of equivalent plastic slip

The contours of equivalent plastic slip $\bar{\gamma }_{s} \!= \sum _{\alpha =1}^{N_s}|\gamma ^\alpha |$, are presented in the Fig. 5 at $\hbox {P} = 5.3$ N ($\varDelta = 0.4$ mm) for orientation A. Figure 5a pertains to the free surface of the specimen and Fig. 5b to the specimen mid-plane. It is observed that the plastic zone due to activity on various slip systems spreads over the entire uncracked ligament. The spatial distribution of the plastic slip bands can be divided into a forward sector P and sector R behind the notch tip. The sector Q separating P and R is free of any plastic slip activity. The main contribution to plastic slip $\bar{\gamma }_{s}$ in both the sectors P and R arises from basal slip system which has a very low CRSS value of 0.5 MPa (Zhang and Joshi 2012). This corroborates with the basal slip traces observed in the optical metallographs taken on the specimen free surface in the experimental study (Kaushik et al. 2014). However, prismatic slip traces were also observed adjacent to the extended segments of the crack in the experiments. These traces arise during the crack extension phase which is not simulated here and hence, this activity is not captured in the numerical results. On comparing Fig. 5a, b, it may be seen that equivalent plastic slip contours at mid-plane and free surface are similar. In order to ascertain the through-thickness plastic slip variation, a section parallel to $X_2-X_3$ located at $X_1 = -0.088$ mm (i.e., slightly behind the notch tip) is chosen and the equivalent plastic slip contours are plotted on this plane in Fig. 5c. It can be seen that the magnitude of plastic slip increases marginally from the free surface to the mid-plane very close to the notch surface (see the red color contours in the lower portion) but remains almost constant at larger distances above the notch surface. The equivalent plastic slip contours for orientation B are qualitatively similar to that of orientation A, and hence, are not presented.

Fig. 5

Contours of equivalent plastic slip $\bar{\gamma }_s$ for orientation $A$ corresponding to $\hbox {P} = 5.3$ N ($\varDelta = 0.4$ mm) at a free surface and b mid-plane. c Through-thickness contours of $\bar{\gamma }_s$ at a distance of $\mathrm {X}_1 = -0.088$ mm with respect to the notch tip, where KK corresponds to mid-plane and LL to the free surface of the specimen

Figure 6a, b shows the equivalent plastic slip contours for orientation C at the free surface and mid-plane, respectively, at $\hbox {P} = 8.9$ N ($\varDelta = 0.4$ mm). The contours predict predominant slip activity in the region ahead of the notch tip. However, unlike orientation A, the plastic slip activity is less above the notch surface and the magnitude of $\bar{\gamma }_s$ is also significantly smaller at the mid-plane of the specimen as compared to the free surface. The contribution to $\bar{\gamma }_{s}$ in this case is from basal and prismatic slip. The latter’s activity is localized at the notch root (see location E in Fig. 6a, b) while the magnitude of the plastic slip due to the former is higher farther ahead of the notch (see location F in Fig. 6a). It can also be noted from Fig. 6b that slip activity at the mid-plane occurs only due to prismatic slip systems close to the notch tip. However, no slip traces were observed for orientation C in the experiments because in this case basal slip does not leave any traces on the specimen free surface. Also prismatic slip appears to be confined to a small region close to the notch tip in Fig. 6a which could not be clearly resolved in the optical metallographs. The equivalent plastic slip contours through the specimen thickness are shown in Fig. 6c on a plane parallel to $X_2-X_3$ located at $X_1 = 0.172$ mm. It can be seen from this figure that there is an increase in the magnitude of $\bar{\gamma }_s$ up to a distance of 0.2 mm from the free surface before gradually dropping towards the mid-plane.

Fig. 6

Contours of equivalent plastic slip $\bar{\gamma }_s$ for orientation $C$ corresponding to $\hbox {P} = 8.9$ N ($\varDelta = 0.4$ mm) at a specimen free surface and b mid-plane. c Through-thickness contours of $\bar{\gamma }_s$ at a distance of $\mathrm {X}_1 = 0.172$ mm with respect to the notch tip, where KK corresponds to mid-plane and LL to free surface of the specimen

3.2.5 Contours of net tensile twin volume fraction

The contours of net TT volume fraction defined as $\bar{f}_{tt} = \sum _{\chi =1}^{N_{tt}} f^{\chi }$, where $f^{\chi }$ is the volume fraction of the $\chi$th TT variant and $N_{tt}$ is the number of such TT variants, are shown in the Fig. 7a, b corresponding to the specimen free surface and mid-plane, respectively, for orientation A at $\hbox {P} = 5.3$ N. The twin volume fraction has evolved predominantly in front of the notch root, and within a rectangular region PQRS extending orthogonal to the flat surface of the notch which corroborates well with the EBSD observations made by Kaushik et al. (2014). It can be seen from Fig. 7a, b that the region close to the notch root experiences high levels of $\bar{f}_{tt}$. The net TT volume fraction decreases with increasing radial distance from the notch root. On comparing the above two figures, it can be noticed that the distribution of twin volume fraction in the rectangular region PQRS ahead of the notch tip is similar in both the specimen mid-plane and free surface although the levels of $\bar{f}_{tt}$ are slightly higher immediately close to the notch tip at the mid-plane.

Fig. 7

Contours of net tensile twin volume fraction ${\bar{f}}_{tt}$ for orientation $A$ corresponding to $\hbox {P} = 5.3$ N ($\varDelta = 0.4$ mm) at a free surface and b mid-plane. c Through-thickness contours of ${\bar{f}}_{tt}$ at a distance of $\mathrm {X}_1 = 0.016$ mm with respect to the notch tip, where KK corresponds to mid-plane and LL to free surface of the specimen

The near-uniform distribution of net TT volume fraction along the notch front can be understood clearly from Fig. 7c which shows the thickness variation of $\bar{f}_{tt}$ on a plane parallel to $X_2-X_3$ located at $X_1 = 0.016$ mm. This behavior predicted by the numerical simulation agrees well with the observations made by Kaushik et al. (2014) based on EBSD maps that the average TT volume fraction at the specimen free surface, quarter-plane and mid-plane are almost equal for orientation A. It is found that the net TT volume fraction is distributed in a similar manner for orientation B as well.

The contours of $\bar{f}_{tt}$ for orientation C on the specimen free surface, mid-plane and through the thickness at load $\hbox {P} = 8.9$ N are shown in Fig. 8a–c, respectively. On comparing Fig. 8a, b with Fig. 7a, b, it can be seen that unlike orientation A, contours of TT volume fraction in orientation C spread almost over the entire uncracked ligament (up to the edge of the specimen) except for a small region close to the notch tip. Thus, in contrast to orientation A (and B), $\bar{f}_{tt}$ decreases in magnitude as the notch tip is approached and vanishes near it. Thus, there is a zone close to the notch tip which is free of TT activity. By contrast, high levels of TT volume fraction may be perceived at the edge of the specimen close to the line of application of the load. This corroborates well with the EBSD observations made by Kaushik et al. (2014), which show similar spread of TT bands in the ligament except for a small region surrounding the notch tip.

Fig. 8

Contours of net tensile twin volume fraction ${\bar{f}}_{tt}$ for orientation $C$ corresponding to $\hbox {P} = 8.9$ N ($\varDelta = 0.4$ mm) at a free surface and b mid-plane. c Through-thickness contours of ${\bar{f}}_{tt}$ at a distance of $\mathrm {X}_1 = 1.78$ mm with respect to the notch tip, where KK corresponds to mid-plane and LL to free surface of the specimen

On comparing Fig. 8a, b, it can be noticed that the levels of $\bar{f}_{tt}$ are higher (especially close to the load application zone) in the specimen mid-plane as compared to the free surface. The 3D nature of the twin volume fraction development for this orientation can be understood well from Fig. 8c which shows the thickness variation of $\bar{f}_{tt}$ on a plane parallel to $X_2-X_3$ located at $X_1 = 1.78$ mm ahead of the notch tip. This contour plot (taken close to the load application zone) demonstrates that much higher TT volume fraction has accumulated on the specimen mid-plane and it decreases as the free surface is approached which again corroborates well with the EBSD observations of Kaushik et al. (2014). This behavior is in strong contrast to orientation A (and B) where a near-uniform distribution of $\bar{f}_{tt}$ through the specimen thickness was noted (see Fig. 7c).

3.2.6 Variation of out-of-plane displacement ahead of the notch tip and contours of out-of-plane strain

The observation of TT formation in the uncracked ligament for orientation C suggests that out-of-plane bulging should occur since the c-axis is parallel to the specimen thickness for this case which was confirmed from surface profile maps by Kaushik et al. (2014). However, this is in contrast to the common perception that significant out-of-plane dimpling of the fracture specimen would occur in ductile solids which is indeed the basis of optical experimental techniques such as the method of caustics and Twyman–Green interferometry (Narasimhan and Rosakis 1990; Zehnder and Rosakis 1990). This issue is examined from the numerical results by plotting the out-of-plane displacement $u_3$ as a function of distance ahead of the notch tip on the specimen free surface at different loads in Fig. 9a. Further, contours of out-of-plane strain $\epsilon _{33} = \partial {u_3}/\partial {X_3}$ on the specimen free surface and mid-plane at $\hbox {P} = 8.9$ N are presented in Fig. 9b, c, respectively.

Fig. 9

a Out-of-plane displacement ($u_3$) on the free surface plotted with distance ahead of the notch tip at different load levels corresponding to orientation C. Out-of-plane strain ($\epsilon _{33}$) contours for orientation C corresponding to $\hbox {P} = 8.9$ N ($\varDelta = 0.4$ mm) at b free surface and c mid-plane

From Fig. 9a, it can be seen that $u_3$ is negligibly small over a distance of about 0.2 mm ahead of the notch tip and then becomes positive (i.e., the specimen bulges) increasing montonically towards the edge of the specimen. This corroborates well with the experimental observations from surface profile maps (Kaushik et al. 2014), except that these maps showed some dimpling of the specimen surface very close to the notch tip. This probably occurs due to activation of pyramidal ${\mathrm {\langle c+a\rangle }}$ dislocations since no compression twinning (CT) was noticed from EBSD maps. However, the present numerical simulations showed neither CT nor pyramidal ${\mathrm {\langle c+a\rangle }}$ activity close to the notch tip resulting in absence of dimpling (see Fig. 9a).

On examining contours of $\epsilon _{33}$ presented in Fig. 9b, c it can be seen that they are qualitatively similar to the $\bar{f}_{tt}$ contours shown in Fig. 8a, b. Thus, it may be observed from Fig. 9b, c that $\epsilon _{33} > 0$ over the entire region ahead of the notch tip (except very close to the tip where it is negligibly small). Further, $\epsilon _{33}$ increases towards the specimen edge and is maximum close to the zone of load application. On comparing Fig. 9b with c, it can be noticed that $\epsilon _{33}$ is higher in the specimen mid-plane especially close to the specimen edge which corroborates with the distribution of $\bar{f}_{tt}$ in Fig. 8. It is interesting note that recent experiments and simulations with compact tension specimens of a polycrystalline AZ31 Mg alloy which has a predominantly basal texture (with most grains having c-axis close to the specimen free surface normal) have shown profuse TT activity ahead of the notch tip (Prasad et al. 2014). However, in this case, as shown by Koike et al. (2008) tensile twins are also triggered owing to stress concentrations created by pile up of basal dislocations at grain boundaries.

3.2.7 Evolution of average net tensile twin volume fraction

The average net TT volume fraction ${\bar{f}}^{a}_{tt} = \frac{1}{V} \int _{V}{\bar{f}}_{tt}dV$ is computed over the region EFGHI marked in Fig. 2b (and extruded through the specimen thickness) using Gauss quadratures. This is plotted as a function of load P for orientations A, B and C in Fig. 10a–c, respectively. Also shown in these figures are the evolution histories of average TT volume fraction over a similar rectangular region determined from the EBSD maps on the specimen free surface (Kaushik et al. 2014).

Fig. 10

Comparison of average twin volume fraction computed over the domain EFGHI indicated in Fig. 1, $\bar{f}_{tt}^a$, versus load variations obtained from experiments and 3D finite element simulations for a orientation $A$, b orientation $B$ and c orientation $C$

It can be seen from Fig. 10a, c that the evolution of average TT volume fraction predicted by the numerical simulations is in reasonable agreement (although slightly higher) when compared with the experimental data for orientations A and C. In the case of orientation B, while the numerical results show that ${\bar{f}}^{a}_{tt}$ starts increasing with load from an initial value of zero, the experimental data commences with a non-zero initial value owing to existence of polishing twins (Kaushik et al. 2014). The presence of these twins impedes the subsequent nucleation and growth of deformation twins in the upper-half of the specimen (Kaushik et al. 2014). Hence, the average twin volume fraction measured from the experimental data falls below that predicted by the numerical simulations as the load increases. On comparing Fig. 10a–c, it may be seen that the evolution of ${\bar{f}}^{a}_{tt}$ with respect to load is slowest for orientation C. Kaushik et al. (2014) noted that there is a qualitative similarity between the evolution histories of ${\bar{f}}_{tt}^a$ shown in Fig. 10 and energy release rate J. Thus, they concluded that profuse tensile twinning contributes to energy dissipation and toughening.

3.2.8 Contours of normal and hydrostatic stress

The contours of the normal Kirchhoff stress component $\tau _{22}$ for orientation A are shown in Fig. 11a, b at the specimen free surface and mid-plane, respectively, corresponding to $\hbox {P} = 5.3$ N. The normal stress is high at the notch tip (especially in the specimen mid-plane) owing to intense stress concentration and drops with increasing distance ahead of it. It becomes compressive beyond the vertical line MN. Thus, point M which corresponds to the plastic hinge point is located far ahead of the notch tip (close to the specimen edge) for this orientation. Since in this orientation the c-axis is aligned along the $X_2$ axis, the tensile $\tau _{22}$ stress in the region ahead of the notch tip drives the formation of TTs to accommodate extension of the c-axis. On comparing Fig. 11a, b, it can be seen that stress values at the notch root are higher at the mid-plane as compared to the free surface. This trend is also reflected in the thickness variation of the hydrostatic stress $\tau _h = \tau _{kk}/3$ shown in Fig. 11c on a plane parallel to $X_2-X_3$ located at $\mathrm {X}_1 = 0.016$ mm. This figure confirms that stress levels drop appreciably as free surface of the specimen is approached. The above behavior is similar to that reported for isotropic plastic solids where high hydrostatic stress levels are found to prevail close to the crack tip at the mid-plane and reduce as the free surface is approached (Narasimhan and Rosakis 1990; Subramanya et al. 2007).

Fig. 11

Contours of Kirchhoff stress component $\tau _{22}$ for orientation $A$ corresponding to $\hbox {P} = 5.3$ N ($\varDelta = 0.4$ mm) at a specimen free surface and b mid-plane. c Through-thickness contours of hydrostatic stress ($\tau _h$) at a distance of $\mathrm {X}_1 = 0.016$ mm in front of the notch tip, where KK corresponds to mid-plane and LL to free surface of the specimen

In Fig. 12a, b, contours of $\tau _{22}$ on the free surface and mid-plane for orientation C at $\hbox {P} = 8.9$ N are presented. The contours of $\tau _h$ through the specimen thickness corresponding to the same load at $X_1 = 0.016$ mm are displayed in Fig. 12c. In this case, although large $\tau _{22}$ prevails close to the notch tip both in the mid-plane and free surface, it drops very rapidly with increasing distance from the tip and changes sign (see Fig. 12a, b). Thus, the plastic hinge point M for orientation C at both free surface and mid-plane is located close to the notch tip as can be seen from Fig. 12a, b which is in contrast to orientation A. The compressive stress zone bounded by MNOP also corresponds to the region wherein TT activity occurs (refer Fig. 8a, b). This suggests that the negative $\tau _{22}$ stress prevailing over a large region ahead of the notch tip drives out-of-plane bulging of the specimen and the occurrence of tensile twinning to accommodate it. The through-thickness variation of hydrostatic stress shown in Fig. 12c indicates that there is only marginal change in stress levels from mid-plane to free surface for this orientation.

Fig. 12

Contours of Kirchhoff stress component $\tau _{22}$ for orientation $C$ corresponding to applied load of 8.9 N ($\varDelta = 0.4$ mm) at a specimen free surface and b mid-plane. c Through-thickness contours of hydrostatic stress ($\tau _h$) at a distance of $\mathrm {X}_1 = 0.016$ mm in front of the notch tip, where KK corresponds to mid-plane and LL to free surface of the specimen

In a very recent work, Kondori and Benzerga (2014) have investigated the effect of stress triaxiality on fracture mechanisms in polycrystalline AZ31B Mg alloy. They have shown from detailed fractographic investigations that for low to moderate levels of stress triaxiality (similar to those seen close to the notch front in Figs. 11c, 12c) the dominant failure mechanism is micro-void coalescence which results in high strain to failure. Indeed, high notched $J_c$ values have been obtained in a rolled AZ31 alloy by Prasad et al. (2014). On the other hand, when stress triaxiality increases (for example if notches with radii smaller than those employed in this work are used), the fracture mechanism in polycrystalline Mg alloys may be governed by a combination of shallow dimples and twin-size microcracks (Kondori and Benzerga 2014). This would result in lower strains to failure. In terms of fracture behavior, one would therefore expect a reduction in fracture toughness with decrease in notch root radius.

4 Finite element modeling of discrete intersecting twins near the notch root

In order to gain insights about the zigzag path followed by the extended crack due to deflections at twin–twin intersections (Kaushik et al. 2014), finite element simulations are performed incorporating two discrete intersecting twins near the notch root. Attention is focused only on orientation B since the behavior in other orientations would also be similar. Here, the two possibilities involving continued crack growth along the twin boundary and deflection of the crack path at the twin–twin intersection are analyzed. For this purpose, two discrete twins labeled as 1 and 2, corresponding to variants $[\bar{1}101](1\bar{1}02)$ and $[1\bar{1}01](\bar{1}102)$, respectively, are modeled as shown in Fig. 13 (with the boundaries of the twins indicated by thick black lines). These variants were chosen since they are observed to occur near the notch root for orientation B in the experiments of Kaushik et al. (2014). Figure 13a corresponds to the situation wherein the crack has extended from the notch root along the boundary OA between twin $\#$1 and the matrix so that the tip is located at point A. Figure 13b, c correspond to two possible scenarios of further crack growth beyond the initial position A of the crack tip. In case-1, the crack is assumed to have extended along OAB with the current crack tip located at point B (see Fig. 13b). In case-2, the crack is taken to have deflected at point A and grown along the boundary of twin $\#$2 such that the current crack tip is located at C.

Fig. 13

Finite element model of two discrete intersecting twins, labeled as twin $\#$1 and $\#$2 with a crack lying along OA, b crack lying along OAB, referred to as case-1 and c crack lying along OAC, referred to as case-2

It must be mentioned that in order to rationalize the observed crack deflection at twin–twin intersections from an energy release rate standpoint, the above model involving just two intersecting twins is adequate. The full specimen is simulated without assuming symmetry about the plane ahead of the notch front using one layer of eight-noded hexahederal elements through the specimen thickness. The mesh employed in the simulations comprises of 4850 elements and 9968 nodes. The $u_3$ displacement (i.e., along the specimen thickness) is restrained at all nodes to enforce plane strain conditions. Further, plastic slip is permitted in both the matrix and within the pre-existing discrete twins, whereas deformation twinning is allowed only in the matrix.

The contours of equivalent plastic slip and net TT volume fraction pertaining to case-1 at $\varDelta = 0.24$ mm are shown in Fig. 14a, b, respectively. It can be seen from these figures that there is intense concentration of both ${\bar{\gamma }}_s$ and ${\bar{f}}_{tt}$ at the point of intersection A between the two discrete twins. Here, the main contribution to ${\bar{\gamma }}_s$ is from basal slip activity. The large concentration of plastic slip spreading along the boundary of twin $\#$2 near point A corroborates with the observations of dislocation accumulation at the twin boundaries near a crack tip in AZ31 Mg alloy by Somekawa et al. (2009). The present simulations also show large values of ${\bar{f}}_{tt}$ along the twin–matrix boundaries suggesting intersection of twins nucleated in the matrix with these boundaries (as seen in the experiments of Kaushik et al. (2014)). Interestingly, the levels of ${\bar{\gamma }}_s$ and ${\bar{f}}_{tt}$ near the crack tip (point B) are lower than near the twin intersection point A. The above results imply that the boundary of twin $\#$2 is more prone to extension of the crack than continued growth along the boundary of twin $\#$1. This will be confirmed below from computation of energy release rate $J$ for the two cases. Further, plastic slip contours may be noticed within the twinned regions in Fig. 14a (see in particular, twin $\#$1) suggesting the presence of secondary slip. Indeed, this has been reported from observations of basal slip traces within twinned regions by Kaushik et al. (2014). They noted that deflection of the slip traces occurs from the matrix to the twinned region.

Fig. 14

Contours of a equivalent plastic slip $\bar{\gamma }_s$ and b net tensile twin volume fraction $\bar{f}_{tt}$ corresponding to case-1 at $\varDelta = 0.24$ mm

The differences in the strain energy (i.e., the area under the P–$\varDelta$ curves) for cases-1 and 2 with respect to the initial cracked geometry (Fig. 13a) at the same $\varDelta$ are determined. The energy release rate values for both cases are then evaluated by dividing these changes in strain energy by the increment in crack area (Anderson 2005). The energy release rate $J$ thus determined is plotted against $\varDelta$ for the two cases in Fig. 15. From this figure it can be seen that $J$ for continued crack extension along twin $\#$1 (case-1) is much lower than that for crack deflection at the point of intersection of the two twins (case-2). The value of $J$ corresponding to case-2 is almost twice as much as that for case-1 at $\varDelta = 0.24$ mm. This indicates that deflection of the crack path at twin–twin intersections is more favorable from an energy standpoint and provides an explanation for the zigzag crack path seen in the experiments of Kaushik et al. (2014).

Fig. 15

Comparison of energy release rate $J$ versus $\varDelta$ variations between case-1 and case-2

5 Summary and conclusions

In this work, finite element simulations have been carried out of the fracture experiments on notched three point bend Mg single crystal specimens reported by Kaushik et al. (2014). The main observations/conclusions are listed below.

• Basal slip activity is preponderant on the notch surface and ahead of the notch root in orientations A & B whereas in orientation C both basal and prismatic slip are observed ahead of the notch root. The former is in agreement with experimental observations while it was not possible to perceive the latter in the experiments.

• Simulations show spatial distribution of twin volume fraction in corroboration with experiments. The thickness distribution of twin volume fraction is relatively weak for orientations A & B whereas it is quite strong in case of orientation C with significantly higher values noticed in the specimen mid-plane. The evolution histories of average twin volume fraction with load ahead of the notch for orientations A & C obtained from simulations are in good agreement with experiments. However, owing to the presence of polishing twins in case of orientation B the predicted evolution of average twin volume fraction differs from the experiments.

• The occurrence of TTs in all three orientations has been rationalized from distribution of normal stress ahead of the notch tip. Specifically, in orientation C, the plastic hinge forms quite close to the notch root in the uncracked ligament. Thus, there is a large region beyond the hinge point which experiences compressive normal stress that is responsible for causing out-of-plane bulging and occurrence of TTs.

• It has been shown that the energy release rate $J$ associated with deflection of the crack at twin–twin intersection is higher than that pertaining to continued crack extension along a twin boundary. Thus, crack deflection will be favored as seen in the experiments. There is intense concentration of plastic slip at the twin–twin intersection suggesting accumulation of dislocations.

• Both experiments and simulations show that there is not much difference in development of plastic slip and twinning as well as stress distributions for the two basal crack orientations A and B. By contrast, plastic anisotropy manifests strongly when the results of orientations A or B are compared against orientation C in all the above aspects. Also a vast difference in load–displacement curve for orientation C with respect to the other two orientations can be perceived.

In closing, it must be mentioned that these simulations complement the earlier experimental work and substantiate the argument that profuse tensile twinning imparts toughening through plastic dissipation. On the other hand, the present simulations and the experiments show that crack propagation may ultimately happen along twin boundaries. Thus, if there is impediment to profuse nucleation of tensile twins (as in case of orientation B) then it may lead to brittle behavior with low fracture toughness.