Abstract
This is an essay about general covariance, and what it says (or doesn’t say) about spacetime structure. After outlining a version of the dynamical approach to spacetime theories, and how it struggles to deal with generally covariant theories, I argue that we should think about the symmetry structure of spacetime rather differently in generally-covariant theories compared to non-generally-covariant theories: namely, as a form of internal rather than external symmetry structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This essay is about the feature of General Relativity from which the hole argument springs: namely, general covariance. Famously, Einstein took the general covariance of the theory to express its commitment to a notion of “general relativity”, i.e., of the equivalence of all states of motion (just as the special covariance of special relativity expressed the equivalence of all inertial motion). In general, philosophers have been unpersuaded by Einstein’s claim, pointing to two problems in particular: the fact that general-relativistic spacetimes have a covariant derivative operator, and hence the resources to distinguish between inertial and non-inertial motion; and the fact that other theories (e.g. special relativity) can also be given a generally covariant formulation, which suggests that general covariance per se cannot be a physically significant feature of a theory.
In this paper, I want to do two things. First, I want to retrace why one might think that general covariance signals something like a commitment to the general relativity of motion, by drawing on the so-called “dynamical approach” to spacetime structure. Second, I argue that in trying to resolve the problems posed by this way of approaching general covariance, we are naturally led to a somewhat different way of analysing the symmetry structure of spacetimes: namely, an analysis of it as a form of “internal” symmetry structure.
To this end, the paper proceeds as follows. Section 2 introduces the notion of an external symmetry. Section 3 lays out (one approach to) the dynamical approach to spacetime theories. Section 4 applies these ideas to General Relativity, thereby illustrating the problem with trying to apply these ideas to generally covariant theories. Section 5 concerns how spacetime symmetries can be thought of as internal symmetries. Section 6 concludes, by considering the question of how to distinguish spatiotemporal from non-spatiotemporal structure.
2 External Symmetries
Let us start with an example: the theory of Maxwell electromagnetism on Minkowski spacetime. Models of this theory consist of a two-form \(F_{ab}\) and a vector field \(J^a\) on Minkowski spacetime M (i.e. a flat affine space equipped with a Minkowski metric \(\eta _{ab}\)), satisfying the equations
where \(\nabla \) is the flat affine connection on Minkowski spacetime, \(\eta ^{ab}\) is the inverse Minkowski metric, and square brackets indicate antisymmetrisation on indices. Note that here (and throughout this paper) I use Latin letters as abstract indices: so, for instance, \(J^a\) is a vector field, not the components of that field in some coordinate system.
An external transformation of this theory is just a diffeomorphism from spacetime points to spacetime points. Note that any such diffeomorphism naturally induces a transformation from one model to another, since tensor fields may be pushed forward under diffeomorphisms.Footnote 1 We can now define an external symmetry of this theory as a diffeomorphism \(f: M \rightarrow M\) which maps models of the theory to other models: denoting the pushforward under f of a tensor field T by \(f_*T\), f is an external symmetry if \((F_{ab}, J^a)\) satisfies (1) just in case \((f_*F_{ab}, f_*J^a)\) does. For example, an arbitrary spatiotemporal translation is a symmetry of this theory; a time-dependent rotation is not.Footnote 2
Thus, our definitions are as follows: an external transformation is a diffeomorphism on spacetime, and an external symmetry is an external transformation which preserves the solutions of the theory. Note, however, that these definitions work because of a rather special feature of the theory above: that any diffeomorphism of Minkowski spacetime naturally induces a transformation of the fields (i.e., from \((F_{ab}, J^a)\) to \((f_*F_{ab}, f_*J^a)\)). In general, there are theories for which this is not the case.
Consider, for example, U(1) gauge theory. A model of this theory consists of a section \(\psi \) of a U(1) fibre bundle E (with, say, base space B), and a connection D on that same bundle. For readers not familiar with the fibre-bundle formalism,Footnote 3 a U(1) fibre bundle is a structure consisting of a collection of “fibres”, each of which is a one-dimensional complex vector space equipped with a unitary inner product; one such fibre is associated to each point of B. Consequently, given two fibres associated to distinct points of B, there is no privileged way of identifying the points of one fibre with those of the other.Footnote 4 Let \(\pi : E \rightarrow B\) be the projection map; i.e., the map which takes any point in any fibre to the base-space point to which that fibre is associated.
A section of the bundle maps each point of B to a point in the fibre associated to it, and a connection identifies the points in a given fibre with the points in infinitesimally nearby fibres.Footnote 5 If we now suppose that we are given a diffeomorphism \(f: B \rightarrow B\) of the bundle’s base space, then that does not tell us how to transform a section or connection into another section or connection. For instance, given a section \(\psi \), we want to say that its pushforward under f is the section \(f_*\psi \) such that for all \(x \in B\), \(f_*\psi (f(x)) = \psi (x)\); but since \(f_*\psi (f(x))\) and \(\psi (x)\) live in different fibres (respectively, the fibres associated with f(x) and x), this equality does not make sense.
In this context, therefore, we cannot define an external transformation as (just) a diffeomorphism on the base space: we must define it instead as a bundle automorphism. A bundle automorphism is a pair of maps \(\alpha : E \rightarrow E\) and \(\beta : B \rightarrow B\) such that \(\beta \circ \pi = \pi \circ \alpha \), i.e., such that the following diagram commutes:

In a context such as this, one usually defines the internal transformations to be the vertical bundle automorphisms: i.e., those bundle automorphisms such that \(\beta = \text {Id}_B\). That makes it tempting to define the external transformations to be the non-vertical bundle automorphisms. Note, however, that doing so would mean that the external transformations do not form a group; for this reason, it strikes me as better to identify the external transformations with the bundle automorphisms, whether vertical or non-vertical (which, admittedly, has the consequence that internal transformations become a subspecies of external transformations).
I raise this issue only to warn the reader that care is needed in speaking of external transformations in the context of a general gauge theory. For the purposes of this essay, however, we can put this issue aside, by limiting our attention to those fibre bundles in which any diffeomorphism on the base space is uniquely associated with a bundle automorphism. The paradigm examples are tensor bundles (i.e., fibre bundles whose fibre at each point is the set of tensors of a given rank). In a tensor bundle, any diffeomorphism on the base space is naturally associated with a bundle automorphism of the tensor bundle: namely, the pushforward. Thus, it is because the data for our Maxwell theory consisted of sections of tensor bundles (i.e., a section \(J^a\) of the tangent bundle and a section \(F_{ab}\) of the rank-(0, 2)-tensor bundle) that we could identify external transformations with diffeomorphisms on the base space. More generally, we can make this identification provided that we are working with so-called natural bundles: a natural bundle is a fibre bundle which is associated to the rth-order frame bundle, for some finite r.Footnote 6 Crucially, in a natural bundle \(E \overset{\pi }{\rightarrow } B\) every diffeomorphism \(f: B \rightarrow B\) of the base space is associated with a bundle automorphism \(f^\#: E \rightarrow E\).Footnote 7
The above constitutes what I’ll call the coordinate-free approach to thinking about external symmetries: given some theory set on a natural bundle, an external transformation is a diffeomorphism of the base space, and an external symmetry is an external transformation which maps models of the theory to other models. In the example of Maxwell electromagnetism, the external symmetries are precisely the automorphisms of Minkowski spacetime (i.e., the external symmetries are the Poincaré transformations). In general, though, the external symmetry group may be larger than the automorphism group of the base space.
For example, consider the theory of Newtonian electromagnetism.Footnote 8 In this theory, the base space is Newtonian spacetime: the space \(T \times X\), where T is a one-dimensional Euclidean space and X is a three-dimensional Euclidean space (recall that a Euclidean space is an affine space whose associated vector space carries a Euclidean inner product).Footnote 9 The kinematically possible models are also given by a two-form \(F_{ab}\) and vector field \(J^a\), albeit on Newtonian rather than Minkowski spacetime; and the dynamically possible models are those which satisfy the same equations (1) (where \(\eta ^{ab}\) is the inverse of the Minkowski metric definable from Newtonian spacetime).Footnote 10 For this theory, the external symmetries are still the Poincaré transformations (on Newtonian spacetime this time), but the automorphisms of the base space are the Newton transformations (a strict subgroup of the Poincaré transformations).Footnote 11
It is widely held that in cases such as this, the fact that the external symmetry group outstrips the automorphism group of the base space shows there to be something deficient about the theory: that is, that this shows the theory to contain “surplus structure”. Exactly how this “symmetry-to-reality” argument goes, and what kind of response is appropriate, are matters of controversy. Since the details of that controversy are not relevant to our purposes, I pass over them here.Footnote 12
3 The Dynamical Approach
In a slogan, the dynamical approach to spacetime structure holds that (external) dynamical symmetries are prior to spacetime structure.Footnote 13 This slogan raises two immediate questions. The first is what this slogan means. The second is what this slogan could possibly mean, given the story laid out above. If the symmetries of the dynamics are prior to the structure of spacetime, then that suggests that we must specify the dynamics before specifying the spacetime. But that looks straightforwardly impossible. Without first specifying a spacetime, how are we supposed to write down the dynamical equations of the theory? For instance, the equations (1) contain terms such as \(\nabla \) or \(\eta _{ab}\). Without commitment to a spacetime adequate to define those terms, what are they supposed to refer to?Footnote 14
The way out, however, is to recognise that there is an alternative way to specify what spacetime structure one is committed to. On the approach outlined in Sect. 2, one specifies spacetime structure by starting with a manifold, and building it up from there. On the dynamical approach, we will specify spacetime structure by starting with a coordinate system, and cutting down from there. This will presuppose that the spacetime structure is some substructure of \(\mathbb {R}^4\), but not which substructure. (Note that these two strategies correspond, respectively, to Riemannian and Kleinian ways of characterising geometrical structure.)Footnote 15 Wallace [49] provides an extended defence of the use of coordinate-based methods in the context of spacetime theories; the below is closely modelled on Wallace’s treatment.
For a spacetime theory given in coordinates, we take as given 4 independent variables (t, x, y, z) and some number q of dependent variables.Footnote 16 In addition, we specify transformation rules for the dependent variables, associating every diffeomorphism \(f: \mathbb {R}^4 \rightarrow \mathbb {R}^4\) with a smooth map \(f^\#: \mathbb {R}^4 \times \mathbb {R}^q \rightarrow \mathbb {R}^q\). For example, one might specify that four dependent variables \(v^0\), \(v^1\), \(v^2\) and \(v^3\) are to transform “as a (four-)vector”: that means that a transformation \(x^\mu \mapsto \widetilde{x}^\mu \) of \(\mathbb {R}^4\) is to be accompanied by the (\(\mathbb {R}^4\)-dependent) transformation
Note that I use Greek letters (\(\mu \), \(\nu \), \(\alpha \), \(\beta \), etc.) as non-abstract indices.
The transformation rules are there to encode the nature of the changes to the independent variables under coordinate changes, and hence to determine the geometric character of the objects being described.Footnote 17 This corresponds to thinking of such transformations as “passive” transformations. But we also use the transformation rules to do “active” transformations, by telling us how to move such objects around on the manifold. Thus, given a transformation \(f: \mathbb {R}^4 \rightarrow \mathbb {R}^4\), any function \(\phi : \mathbb {R}^4 \rightarrow \mathbb {R}^q\) can be transformed into the pushforward \(f_*\phi \), defined (for any \(x \in \mathbb {R}^4\)) by
It is straightforward to show that, if the variables \(v^\mu \) transform as a vector (i.e. have (2) as their transformation rule), then (3) is the standard definition for the pushforward of a vector field.
We take the dynamics of the theory to be given by some set of differential equations over the dependent variables (with respect to the independent variables); a model of the theory is a solution to these equations. As before, an external transformation f is an external symmetry if it preserves the dynamics: i.e., if for any function \(\phi : \mathbb {R}^4 \rightarrow \mathbb {R}^q\), \(\phi \) is a model (solution) if and only if \(f_*\phi \) is a dynamically possible model.
For example, consider the coordinate-based version of Maxwell electromagnetism. This theory has ten independent variables: the six independent components of the antisymmetric matrix \(F_{\mu \nu }\), and the four components \(J^\mu \) (where Greek lower-case indices such as \(\mu , \nu , \alpha , \beta \) range from 0 to 3). The transformation rules are the following: a transformation \(x^\mu \mapsto \widetilde{x}^\mu \) transforms \(F_{\mu \nu }\) to \(\widetilde{F}_{\mu \nu }\) and \(J^\mu \) to \(\widetilde{J}^\mu \) according toFootnote 18
The dynamical equations for this theory are
where \(\eta ^{\mu \nu }\) is the inverse of the matrix of coefficients
As with the coordinate-free version (1) of this theory, the (external) dynamical symmetries are the Poincaré transformations: in this context, we characterise the Poincaré transformations as those transformations \(x^\mu \mapsto \widetilde{x}^\mu \) such that \(\partial \widetilde{x}^\mu /\partial x^\alpha \) is constant and SO(3, 1)-valued, i.e. such that
To be clear, the fact that this is the symmetry group of the theory is not supposed to be obvious from the mere statement of the theory’s equations: in general, working out the symmetry group of some dynamical equations is a difficult and strenuous task.Footnote 19
Now, note that we have identified the symmetries of this theory without explicitly committing to a specific structure for spacetime. Thus, we can take the dynamical approach to be a prescription for extracting spacetime content from a theory: namely, that the spatiotemporal commitments of a theory are exactly those aspects of \(\mathbb {R}^4\) which are invariant under the dynamical symmetry group. Note that this is, in a certain sense, more radical than the symmetry-to-reality inference. The proposal here is not merely that there is something virtuous about theories in which the spacetime symmetries and external symmetries are in tune (and something vicious about theories in which they are not); rather, the proposal is that what it is for something to be a spacetime symmetry is, in effect, for it to be an external symmetry—because what it is for something to be spacetime structure is for it to be an invariant of \(\mathbb {R}^4\) under external symmetries.Footnote 20
Thus, for example, the theory of Maxwell electromagnetism (i.e. the differential equations (5), supplemented by the appropriate transformation rules), is committed to Minkowski spacetime: for Minkowski spacetime is exactly the structure of \(\mathbb {R}^4\) invariant under Poincaré transformations.Footnote 21 However, it can seem a little as though we have obtained a reductio of the dynamical approach: surely it doesn’t follow just from Maxwell’s equations that spacetime has a Minkowskian structure, rather than a Newtonian (or Galilean) one? After all, the view that spacetime had a non-Minkowskian structure certainly persisted after the acceptance of Maxwell’s equations—that is what made Einstein’s postulation of special relativity such a profound scientific achievement! Furthermore, this view led to concrete empirical predictions: predictions which were refuted by (inter alia) the Michelson-Morley experiment, but need not have been. Surely if Michelson and Morley had not got a null result, we would have learnt that spacetime was not Minkowskian, the validity of Maxwell’s equations notwithstanding?
The answer is that, as per usual, what was empirically tested were not the bare theories themselves, but the conjunctions of those theories with certain auxiliary hypotheses. In this example, the auxiliary hypotheses concerned the behaviour of rigid mechanical objects. In particular, pre-relativistic physics assumed that if a rigid rod’s equilibrium state when at rest with respect to the ether is such as to occupy a region of length L, then its equilibrium state when in motion with respect to the ether is still to occupy a region of length L. In other words, what was refuted by the Michelson-Morley experiment was not merely electrodynamics set upon Newtonian spacetime,Footnote 22 but that theory plus a number of assumptions about how Newtonian spacetime bore on the mechanics of rigid bodies. In the terms of the dynamical approach, this amounts to assuming that the dynamics of rigid bodies are governed by dynamics exhibiting Galilean symmetry, not Lorentz symmetry. As a consequence, the combined theory, including electromechanical coupling, exhibited Newtonian symmetry (since the Newton group is the common subgroup of the Lorentz and Galilei groups).Footnote 23 This illustrates the sense in which, on the dynamical approach, spacetime structure is associated with universality: the nature of spacetime depends upon the totality of all dynamical interactions.
Finally, note that this approach to determining spacetime structure also puts the covariance of the dynamics in contact with relativity of motion. If we apply the dynamical approach, then we will be led to a spacetime in which physically significant facts must be invariant under the covariance group of the dynamics. Where that covariance group includes time-dependent spatial transformations, then it follows that the only physically significant aspects of the motion of a body are those which are invariant under such transformations. Thus, in the case of special-relativistic theories, we find that the velocity of a body cannot be of absolute physical significance, since it is not invariant under the Poincaré symmetries of the theory: in other words, we determine that the theory obeys a principle of special relativity.Footnote 24
4 General Covariance
Let us now try applying this story to the case of General Relativity. One immediate complication is that General Relativity allows for much more exotic possibilities for the global structure of spacetime than do others—in particular, it allows that spacetime may not be homeomorphic to \(\mathbb {R}^4\). To sidestep this, let’s just do local General Relativity: i.e. the theory concerned with general-relativistic spacetime structure on subregions of spacetime, where those subregions are homeomorphic to \(\mathbb {R}^4\). So, as per usual on the dynamical approach, we take \(\mathbb {R}^4\) itself as our base space. We then take General Relativity as a theory with 20 dynamical variables, expressed as the (independent) components of the symmetric matrices \(g_{\mu \nu }\) and \(T_{\mu \nu }\), where \(g_{\mu \nu }\) is non-degenerate and of signature (1, 3); their transformation rules are
The dynamical equations are just the Einstein field equations,
where
with \(g^{\mu \nu }\) being the inverse matrix to \(g_{\mu \nu }\).
We now note that the theory (9) is covariant under arbitrary smooth coordinate transformations: that is, it is generally covariant (in at least one sense of that phrase). So, applying the reasoning above, we conclude that the spacetime structure for general relativity is the structure invariant under the group of all smooth coordinate transformations—to wit, the manifold structure.Footnote 25 It also follows that the relativity principle associated to the theory is seemingly one of general relativity, insofar as no aspects of motion (save for continuity and differentiability) are invariant under the theory’s covariance group: so no such aspect of motion can be of absolute physical significance.
Correspondingly, no differences between solutions related by such a transformation are of physical significance. In particular, this means that if \((g_{\mu \nu }, T_{\mu \nu })\) and \((\tilde{g}_{\mu \nu }, \widetilde{T}_{\mu \nu })\) are a pair of solutions to (9) related by such a transformation that goes to the identity on the boundary of \(\mathbb {R}^4\),Footnote 26 then they should be interpreted as representing the same state of affairs—even if we stipulate that the same coordinate system is being used to interpret both solutions. And this is, of course, precisely the solution to the hole argument as that problem was faced by Einstein (to wit, in terms of coordinates rather than differential geometry).Footnote 27
But, the happy resolution of the hole argument notwithstanding, this is still a problematic case for the story told in Sect. 3.Footnote 28 This is so for two (interrelated) reasons. First, there is very good reason to think that the spacetime structure of General Relativity is not captured merely by the manifold structure, but rather by the metric \(g_{ab}\): it is this structure, after all, that has chronometric significance (i.e., which is associated most directly with the behaviour of rods and clocks). Putting the point in terms of motion rather than spacetime structure, the problem is that (as many commentators since Einstein have pointed out) General Relativity does not enact any kind of principle of general relativity of motion, given that the theory distinguishes between inertial and non-inertial trajectories.Footnote 29
Second, a wide variety of theories can be stated in a generally covariant form: in fact, for almost all the spacetime theories we know of, there is an equivalent theory which is generally covariant.Footnote 30 For example, the electromagnetic theory considered earlier can be expressed in generally covariant form as follows:

But this threatens to undermine the possibility of Sect. 3’s ontological reduction (of spacetime to dynamics): how can the dynamical symmetry group of a theory be a guide to spacetime structure, if that group can be made arbitrarily large? And we most naturally regard a generally covariant formulation of a theory as being just that—a different formulation of the same theory. But that suggests that the spatiotemporal commitments of a theory are not invariant under reformulation, i.e., that the theory itself (as opposed to its various formulations) has no spatiotemporal commitments per se.Footnote 31
5 Internal Lorentz Transformations
The resolution of this problem, I suggest, lies in the following straightforward observation: that making a theory generally covariant involves treating spacetime structures as dynamical fields. All I mean by this is that in the generally covariant version, we introduce extra dependent variables to codify (what we would previously have identified as) spacetime structure, and add new dynamical equations to ensure that this structure behaves in the appropriate fashion. (So, for instance, I don’t mean that the spacetime structure is “dynamical” in the Anderson-Friedman sense of varying from one model to the next.) In the generally covariant electromagnetic theory (11), for example, our new dynamical variables are the components \(g_{\mu \nu }\), and the new dynamical equation is the condition (11c).
But this means that it would be extraordinary to expect information about the spacetime structure to be encoded in the external symmetries of the theory. If spacetime is now being represented as a dynamical field, then we should expect the relevant symmetries to be internal symmetries. So first, let us briefly review what an internal symmetry is. As mentioned in Sect. 2, in the context of the fibre-bundle formalism an internal transformation is a vertical bundle automorphism. In the context of coordinate-based theories of the kind discussed in Sect. 3, an internal transformation is a map \(\chi : \mathbb {R}^4 \rightarrow (\mathbb {R}^q \rightarrow \mathbb {R}^q\)): specifically, we associate a diffeomorphism \(\mathbb {R}^q \rightarrow \mathbb {R}^q\) to every point of \(\mathbb {R}^4\). Either kind of transformation induces a transformation on dynamical data (i.e. on sections and connections, or on functions from \(\mathbb {R}^4\) to \(\mathbb {R}^q\)); and as before, an internal transformation is a symmetry just in case it maps dynamically possible models to dynamically possible models.
This suggests a way in which we might be able to maintain the dynamical approach even for generally covariant theories: rather than (analytically) identifying the spacetime symmetries with the external symmetries, we identify them instead with (some appropriate subset of) the internal symmetries.Footnote 32 As a first pass at implementing this idea, suppose that we consider linear transformations of \(g_{\alpha \beta }\): specifically, those of the form

where  is a matrix whose components are functions of \(\mathbb {R}^4\). Now, \(g_{\alpha \beta }\) (at any point in the base space) is a real, nondegenerate symmetric matrix (equivalently, a nondegenerate symmetric bilinear form on \(\mathbb {R}^4\)). Thus, there exists a group of matrices of the form
is a matrix whose components are functions of \(\mathbb {R}^4\). Now, \(g_{\alpha \beta }\) (at any point in the base space) is a real, nondegenerate symmetric matrix (equivalently, a nondegenerate symmetric bilinear form on \(\mathbb {R}^4\)). Thus, there exists a group of matrices of the form  , such that for any matrix in the group,
, such that for any matrix in the group,  :Footnote 33 this group will, as a group, be the Lorentz group O(1, 3).Footnote 34 So we could consider transformations whose action at each point is given by such a matrix, which evidently will preserve solutions to equations in which \(g_{\alpha \beta }\) features (assuming we don’t change anything else).
:Footnote 33 this group will, as a group, be the Lorentz group O(1, 3).Footnote 34 So we could consider transformations whose action at each point is given by such a matrix, which evidently will preserve solutions to equations in which \(g_{\alpha \beta }\) features (assuming we don’t change anything else).
However, this is a little delicate. For one thing, we might be perturbed by the fact that “applying” such a transformation is, in some sense, a misnomer: all that we have in fact done is left every solution well alone. More seriously, though, we need to spell out the sense in which a transformation like this “preserves the dynamics”. The problem is that that means reassuring ourselves that we are applying the same transformation to every solution, and seeing if that transformation maps solutions to solutions. Now, the latter part is fine, since every solution (and non-solution) is invariant under this transformation. However, the above transformation is not solution-independent: the prescription was to find, for each solution \((g_{\alpha \beta }, \dots )\) a specific transformation  such that \(g_{\alpha \beta }\) is preserved. But that kind of fine-tuning is against the spirit of a dynamical symmetry; to assess whether a certain transformation preserves the dynamics, we need to be able to apply one and the same transformation to different models of the dynamics.Footnote 35 Moreover, note that this second problem isn’t that we somehow under-specified things: in general, a transformation which preserves \(g_{\alpha \beta }\) on one solution will not preserve it on another.
such that \(g_{\alpha \beta }\) is preserved. But that kind of fine-tuning is against the spirit of a dynamical symmetry; to assess whether a certain transformation preserves the dynamics, we need to be able to apply one and the same transformation to different models of the dynamics.Footnote 35 Moreover, note that this second problem isn’t that we somehow under-specified things: in general, a transformation which preserves \(g_{\alpha \beta }\) on one solution will not preserve it on another.
However, we can do things slightly differently, by reformulating our theory somewhat. Consider again a specific \(g_{\alpha \beta }\). At any given point \(x^\mu \in \mathbb {R}^4\), Sylvester’s law of inertia tells us that we can find a matrix \(e_\alpha ^\Theta \), where \(0 \le \Theta \le 3\), such that
where \(\eta _{\Theta \Omega }\) is the diagonal Minkowski matrix we previously labelled as \(\eta _{\mu \nu }\) (in (6)). The reason to use uppercase Greek letters (e.g. \(\Theta , \Omega \)) as indices arises from the transformation law for \(e_\alpha ^\Theta \). Clearly, we want a transformation law that will preserve the transformation law (8a) for the metric \(g_{\alpha \beta }\). Since \(\eta _{\Theta \Omega }\) is a fixed matrix,Footnote 36 and so invariant under coordinate transformations, the transformation rule for \(e_\alpha ^\Theta \) under the coordinate transformation \(x^\mu \mapsto \widetilde{x}^\mu \) must be
The use of an uppercase Greek index also enables us to stipulate—without risk of ambiguity—that the inverse matrix to \(e_\alpha ^\Theta \) is \(e_\Theta ^\alpha \) (so \(e_\alpha ^\Theta e^\alpha _\Omega = \delta ^\Theta _\Omega \), and \(e^\alpha _\Theta e_\beta ^\Theta = \delta ^\alpha _\beta \)).
We can now interpret the generally covariant electromagnetic theory (11) as equations for the dynamical variables \(e_\alpha ^\Theta \), \(F_{\mu \nu }\) and \(J^\alpha \). This theory has the following (internal) dynamical symmetry:

where  is an SO(3, 1)-valued function of \(\mathbb {R}^4\): that is, it is a map \(\mathbb {R}^4 \rightarrow \mathbb {R}^{16}\) such that at any point \(p \in \mathbb {R}^4\),
is an SO(3, 1)-valued function of \(\mathbb {R}^4\): that is, it is a map \(\mathbb {R}^4 \rightarrow \mathbb {R}^{16}\) such that at any point \(p \in \mathbb {R}^4\),

The reason that (15) is a symmetry of (11) is straightforward: the metric \(g_{\alpha \beta }\) is invariant under the transformation (15) (and as a result, so are the structures derived from it such as \(\nabla \)). Of course, it also follows that the other theories we have formulated in terms of a Lorentzian metric (and associated connection), such as (9), will admit the transformation (15) as a symmetry.
Let us now ask what kind of surplus structure the symmetries of these theories reveal. First, we should take a moment to analyse the implications of the general covariance of these theories: what does that imply about the geometric structures being employed here? As is well-known, \(g_{\alpha \beta }\) can be interpreted as the components of a metric tensor, and \(T_{\alpha \beta }\) as the components of a tensor. But it is worth saying something about the fields \(e_\alpha ^\Theta \). Given the coordinate transformation (14), we should interpret each \(e_\alpha ^\Theta \) (for each value of \(\Theta \), i.e. for \(\Theta = 0\), 1, 2, or 3) as representing a covector field \(e_a^\Theta \); and we should interpret each \(e^\alpha _\Theta \) as representing a vector field \(e_\Theta ^a\).
We then turn to the internal symmetry. The internal symmetry maps a quadruple of covector fields \((e_a^0, e_a^1, e_a^2, e_a^3)\) into a quadruple of covector fields \((\widetilde{e}_a^0, \widetilde{e}_a^1, \widetilde{e}_a^2, \widetilde{e}_a^3)\). To give a geometrical interpretation that incorporates this symmetry, it’s easiest to think about the effect of the transformation when we imagine “feeding” the covector fields an arbitrary vector field \(X^a\): the effect of the transformation is then a map

At each point p, this is exactly the action of a linear transformation in a vector space which we can call \(V_p\): that is, we are motivated to interpret \(e^\Xi _a X^a|_p\) as the components of a vector \(e^I_a X^a|_p \in V_p\) (switching from non-abstract uppercase Greek indices to abstract uppercase Roman indices).Footnote 37 Moreover, since the symmetries are all Lorentz transformations, \(V_p\) is equipped with a Minkowski inner product \(\eta _{IJ}\)—i.e., it is a Minkowski vector space. In turn, this implies interpreting the set of covectors \(e^\Xi _a|_p\) as the components of a map from \(T_p M\) to \(V_p\). And finally, we interpret the set of fields \(e^\Xi _a\) as the components of a bundle section \(e^I_a\): namely, a section of the bundle \(T^*M \otimes E\), where E is the (Minkowski) vector bundle with standard fibre V. By analogous reasoning, we interpret \(e^a_\Theta \) as the components of a section \(e^a_I\) of \(TM \otimes E^*\).
From this perspective, then, General Relativity or generally covariant Maxwell electromagnetism are theories whose spacetime structure is given by a section of \(T^*M \otimes E\): using such a section \(e^I_a\), one can define a metric on the base space \(g_{ab} := \eta _{IJ} e_a^I e_b^J\), define the Levi-Civita connection from that, and then proceed as normal. Thus, what we have effectively done here is to recover a (well-known) motivation for the so-called “tetrad” formulation of a relativistic theory: it lets us capture the Lorentz symmetry of generally-covariant relativistic theories.Footnote 38 Although I don’t have the space to discuss this here, it is straightforward to extend this kind of analysis to pre-relativistic theories, so as to capture their Galilei symmetry in an analogous tetrad formalism.Footnote 39
However, there’s a worry that this is just giving with the one hand and taking away with the other. We’ve picked up this symmetry because of our decision to express the metric field \(g_{\alpha \beta }\) in terms of \(e_\alpha ^\Theta \): there is an underdetermination in which \(e^\Theta _\alpha \) expresses \(g_{\alpha \beta }\), an underdetermination which is exactly tracked by (15). Haven’t we just manufactured a gauge symmetry?
In particular, consider an arbitrary fibre bundle—say, the U(1) bundle discussed in Sect. 2. We could, of course, introduce a copy of this bundle, with a “monad field” linking the two (i.e., playing the same role that the tetrad field plays in linking the tangent bundle with E). If we then take the unitary inner product to reside on the fibres of the new bundle, with such an inner product being induced on the fibres of the old bundle via the monad field, then there will (of course) be an underdetermination of the latter inner product by the former: if I apply a U(1) transformation to the monad field, then the induced inner product stays numerically identical. But it is hard to believe that we have really gained any new insight through this rigmarole; what is different about the analysis above?
The difference, put simply, is that the tetrad field is not merely linking one fibre bundle with another: it is linking a fibre bundle with the tangent bundle.Footnote 40 This means that it is a necessary step in analysing spacetime symmetries as internal symmetries (unlike the case of the U(1) gauge theory, where the original bundle was perfectly apt for internal transformations). To explain this fully, we need to say a little more about why the tangent bundle is not just any old bundle. There are two perspectives from which we can make the point: the intrinsic geometric perspective utilised in Sect. 2, and the coordinate-based perspective used in Sect. 3.
From the geometric perspective, the difference is that the tangent space (and the tensor bundle more generally) enters into special relationships with material on the manifold, and those relationships will not be preserved by “internal” transformations of the tangent bundle. For example, if we apply such a transformation to a vector field, then the integral curves of the new vector field (if they exist) will not be the same as the old. Similarly, if a one-form field is the exterior derivative of a function f, its transform will (in general) not be the exterior derivative of f: indeed, its transformed version may well not be the exterior derivative of any function whatsoever. For example, on the punctured plane \(\mathbb {R}^2\setminus \{0\}\), we could transform the one-form \(d_a r\) into the one-form \(d_a \theta \); and the latter, its formal name notwithstanding, is not an exact one-form.
From the coordinate-based perspective, the difference is that our freedom to choose internal coordinates is independent of our freedom to choose external coordinates. Sure, we could (in principle) choose internal coordinates such that the inner product on our U(1) gauge bundle has to be represented by a set of coefficients, rather than being encoded by the natural inner product on \(\mathbb {C}\)—but why would we bother? (Note that there is an advantage to being coordinate-free, but essentially no advantage to being coordinate-general, in the context of internal structure.)
By contrast, our choice of tangent coordinates is uniquely fixed by our choice of external coordinates. That means that we are far more constrained in whether we can find tangent coordinates with nice properties, or rather, in whether we can find tangent coordinates with nice properties over any finite region. Riemann normal coordinates are important because they yield tangent coordinates with nice properties at a point—but in general, that’s the best we can do. By contrast, internal coordinates can be chosen so as to be nice over neighbourhoods. (Note that even internal coordinates can’t be chosen so as to be nice globally, in general: e.g. one can’t give global coordinates for the Möbius strip. But they can be chosen so as to be nice locally: this is essentially what is expressed by the condition of local triviality on fibre bundles.)
Either of these perspectives draws out the difference between our tetrad field and the monad field. The monad field sets up a pointwise isomorphism between two internal vector bundles; this means that it doesn’t give us any new or helpful resources for analysing the structure of that bundle, since we were already able to apply vertical bundle automorphisms to the U(1) bundle. The tetrad field, by contrast, sets up a pointwise isomorphism between the tangent bundle and an internal vector bundle (the bundle we called E earlier). One cannot apply (nontrivial) vertical bundle automorphisms directly to the tangent bundle, on pain of disrupting the relationships between vector fields (sections of the tangent bundle) and their integral curves; one cannot change tangent coordinates without changes to the external coordinates. However, we can apply vertical bundle automorphisms to the auxiliary bundle E (provided we make appropriate compensating changes to \(e^I_a\), so that those changes do not “feed through” into the tangent bundle); and we can always use internal coordinates for E in which its Lorentzian inner product is expressed by the fixed matrix \(\eta _{\Theta \Omega }\), even as we change the external coordinates (provided we make appropriate compensating changes to \(e^\Theta _\mu \), so that the external coordinate changes do not “feed through” to the coordinates on the auxiliary bundle).
The challenge with which we began this section ran as follows: according to the dynamical approach, the symmetries of the dynamics should reveal the structure of spacetime; yet this idea seemed to trivialise in generally covariant theories, since their external symmetry group is the full diffeomorphism group. We have now seen that if we turn our attention to internal symmetries, we can “rediscover” a nontrivial symmetry structure which is naturally taken as expressing the spacetime structure. In the non-generally-covariant electromagnetic theory of Sect. 2, it was the symmetries captured by (7) which picked out the spacetime commitments of the theory; in the generally-covariant electromagnetic theory (11), it is the symmetries captured by (15) which do so. Hence, there is good reason for advocates of the dynamical approach to broaden their gaze so that it includes internal symmetries as much as external symmetries—and, in the context of generally covariant theories, to think that spacetime structure is expressed by the former rather than the latter.
6 Identifying Spacetime Structure
However, there is still one issue that needs addressing. Suppose that we carry through the above analysis. At the end, we are left with some fields, residing on a four-dimensional manifold. Some of these fields (such as \(g_{ab}\)) are spatiotemporal in character; some of them (such as \(F_{ab}\)) are not. What makes it the case that \(g_{ab}\) is a part of the “structure of spacetime”, in a way that \(F_{ab}\) is not? Previously, we could have said: because the spacetime structure is whatever substructure of \(\mathbb {R}^4\) is invariant under external symmetries; but now that we are taking spacetime structure to be a species of internal structure, this answer will no longer do. Having severed the link between external symmetries and spacetime structure, we must find some other way to determine how spacetime structure is distinguished from other forms of physical structure: equivalently, given the story we have told, we must determine how the spacetime symmetries are to be identified within the broader class of internal symmetries to which they now belong.
I don’t have a definitive answer to this question; it is too large a topic to be settled here. All I’ll do here is sketch a potential answer, based on Knox’s “spacetime functionalism”—just to show that the advocate of the dynamical approach does have resources to draw upon in answering it. The spacetime functionalist holds that a certain kind of physical structure is spacetime in virtue of playing the role of spacetime. The best-known candidate for spacetime’s functional role is Knox’s view, that “the spacetime role is played by whatever defines a structure of local inertial frames”.Footnote 41 The idea here is that the characteristic spatiotemporality of the metric arises via the role of the Strong Equivalence Principle, formulated by Brown as follows:
There exist in the neighbourhood of each event preferred coordinates, called locally inertial at that event. For each fundamental non-gravitational interaction, to the extent that tidal gravitational effects can be ignored, the laws governing the interaction find their simplest form in these coordinates. This is their special relativistic form, independent of spacetime location.Footnote 42
By way of reminder, locally inertial coordinates (also referred to as Riemann normal coordinates) at p are coordinates such that in those coordinates, (i) \(g_{\mu \nu } = \eta _{\mu \nu }\) and (ii) \(\Gamma ^\rho _{\mu \nu } = 0\).Footnote 43 Note that the caveat “insofar as tidal forces can be ignored” is important: as Read et al. [40] discuss, laws containing curvature terms will not reduce to the special-relativistic laws in locally inertial coordinates (since derivatives of the metric tensor of order higher than one will, in general, not vanish in such coordinates).
However, this proposal deserves unpacking a little more. What is it about these coordinates that makes the nomenclature “locally inertial” appropriate? It cannot merely be the fact that they are Riemann normal coordinates, since that will not generalise to other spacetime contexts (in a pre-relativistic spacetime, for instance, where spacetime structure is not encoded in a metric tensor). More subtly, it cannot just be that these are coordinates in which the connection coefficients vanish and the spacetime tensors take a diagonal form; although this would cover pre-relativistic spacetimes, it presupposes that we can identify which terms in our field equations are to be interpreted as “connection coefficients”, which is just the question of how to distinguish spatiotemporal from non-spatiotemporal structure.Footnote 44
Fortunately, Knox has provided an analysis or definition of what inertial frames are:Footnote 45
- 1.
Inertial frames are frames with respect to which force free bodies move with constant velocities.
- 2.
The laws of physics take the same form (a particularly simple one) in all inertial frames.
- 3.
All bodies and physical laws pick out the same equivalence class of inertial frames (universality).
As Knox discusses, the application of this definition to General Relativity is a delicate matter (the above is intended, in the first instance, as a definition of inertial frames in Newtonian and special-relativistic theories). But it fits well with the analysis given above, since it helps us answer the question: why is the tetrad field necessary? The tetrad field serves (among other things) to establish a pointwise isomorphism between the Minkowski vector bundle and the tangent bundle. (When it is being thought of in this form, one often refers to the tetrad field as a “solder form”, as it “solders” the Minkowski vector bundle to the tangent bundle.) But why is this needed? What would be insufficient about a theory of a connection on a Minkowski vector bundle? I claim that a part of the answer (at least) lies in the fact that such a theory would be unable to draw any distinction between natural and unnatural motion: as with any other theory of a connection on a fibre bundle, a connection on a Minkowski vector bundle does not pick out certain curves as privileged geodesics.
Ironically, this means that in most of the theories above, we do not immediately have the resources to identify spacetime structure—since most of these are merely field theories, having only field equations rather than equations of motion. On this account, it is only when they are supplemented by equations of motion (Newton’s Second Law, the geodesic equation, force laws, etc.) that we get an understanding of how the theory constrains the motion of bodies, and hence of what structures are playing the spacetime role.Footnote 46
This is not the only approach one could take to identifying spacetime structure, of course. For example, Read et al. [40] focus on the metric’s chronogeometric role, and argue that this is grounded in the local coincidence of the dynamical and metrical symmetries (although see Appendix 1 for some concerns about their analysis). Or, one could look to historical approaches to the question “what is space?” for inspiration: for instance, the work of Helmholtz or Weyl on the so-called Problem of Space (Raumproblem).Footnote 47 Even within spacetime functionalism, one need not subscribe to Knox’s specific claim that the functional role of spacetime is the fact that it characterises inertial frames.Footnote 48 All I have sought to show here is that there exists at least one way of determining what represents spacetime that is compatible with the argument of Sect. 5.
7 Conclusion
To summarise, the dialectic of this paper runs as follows:
On a standard way of thinking about external symmetries—as automorphisms of bundles—the dynamical approach’s central slogan (that dynamical symmetries are prior to spacetime symmetries) appears not so much false as incoherent.
We can resolve this by (following Wallace [49]) working with a coordinate-based theory in the first instance, and thinking of the dynamical approach as telling us which bits of the mathematics are merely artefacts of the coordinates.
But even this understanding of the dynamical approach turns out to founder on generally covariant theories: it appears to recommend that any such theory is committed merely to spacetime having the structure of a manifold.
This problem can be resolved by treating Lorentz symmetry—and spacetime symmetry more generally—as a species of internal symmetry, associated to an auxiliary vector bundle (soldered to the tangent bundle by the tetrad field).
Finally, the question of how spacetime structure is to be distinguished from other forms of internal structure is (or at least, could be) answered by Knoxian spacetime functionalism.
None of this is to claim that there might not be other ways of understanding the dynamical approach, or of carrying out elements of what I’ve canvassed here. In particular, my treatment of the last point has been very programmatic; I hope to discuss this issue more fully in future work.
Notes
For details of the pushforward operation on tensor fields, see e.g. [28, §1.5].
Note that \(\eta _{ab}\) is not acted upon by the diffeomorphism, since it is considered part of the Minkowski spacetime rather than as a field (we will soon see what happens if it is instead treated as a field). Compare [39]’s “final version” of diffeomorphism invariance.
Cf. Maudlin [29].
That is, with the points whose associated base-space points are infinitesimally close to the original fibre’s base-space point. Note that this doesn’t typically yield an identification of arbitrary points of fibres with one another: unless the connection is “flat”, the identification between finitely separated fibres will be path-dependent.
See Kolář et al. [25], and especially chapter 12, for an exposition of the theory of natural bundles.
Cf. the notion of an induction in Curiel [15].
Note that this simpler definition of Newtonian spacetime (which I learned from David Wallace) still captures the relevant structure: the persistence of points of absolute space is represented by the projection \(\pi _X : T \times X \rightarrow X\) (i.e. two points (t, x) and \((t', x')\) of Newtonian spacetime correspond to the same persisting points of absolute space just in case \(x = x'\)).
Let \(\delta ^T_{ab}\) be the Euclidean metric on T, \(\delta ^X_{ab}\) be the Euclidean metric on X, and any vector \(\xi ^a\) over \(T \times X\) decompose as \((\xi ^a_T, \xi ^a_X)\). Then we may define \(\eta _{ab}\) by \(\eta _{ab}\xi ^a \zeta ^b := \delta ^T_{ab}\xi ^a_T \zeta ^b_T - \delta ^X_{ab}\xi ^a_X \zeta ^b_X\).
See Barrett [4].
Cf. Norton [35].
Norton [34] gives a detailed account of how these strategies feature in the work of Klein and Riemann.
For a broader discussion of symmetries in the context of coordinate-based theories, see Olver [36].
Of course, these are just the expected transformation rules for a rank-(0, 2) tensor and a vector. But the rules are not to be thought of as manifestations of the fact that we are representing (independently defined) geometric objects in coordinates; rather, the rules are constitutive of those objects. This is why I specify the rules explicitly.
See [10, chap. 4] for some of the history of how the symmetry group of Maxwell’s equations was determined.
See also Myrvold [30] and Acuña [1] for further discussion and defence of the idea that the claim “spacetime symmetries are dynamical symmetries” is analytic. As Myrvold (§5) discusses, it is not clear to what extent Brown [10] should be interpreted as supporting this way of reading the dynamical approach (although Brown and Read [12] declare themselves sympathetic).
The sense in which Minkowski spacetime is a substructure of \(\mathbb {R}^4\) is just that all the structure of the former can be defined in terms of the structure of the latter: that is, one can define the Minkowski metric in \(\mathbb {R}^4\) by \(\eta _{\mu \nu } \xi ^\mu \zeta ^\nu := \xi ^0 \zeta ^0 - \xi ^1 \zeta ^1 \xi ^2 \zeta ^2 - \xi ^3 \zeta ^3\).
Barrett [4]
For more discussion of the relationship between symmetries and relativity principles, see Brown and Sypel [13].
By “manifold structure”, I mean the structure of a differentiable manifold (i.e., a set equipped with an atlas of compatible charts).
The stipulation that the coordinate system go to the identity as we approach the boundary is necessary because we are, after all, only treating some subregion of spacetime. For more discussion of the subtleties here, see Belot [6].
See Norton [33] for further discussion.
This need not be a criticism of the dynamical approach per se, insofar as the dynamical approach could perhaps be adapted to generally covariant theories (by, for instance, dropping the claim of ontological reduction): see [10, chap. 5] and [24, §3]. (I thank an anonymous referee and James Read for pressing this point.)
Cf. Norton [34].
This observation, of course, goes back to Kretschmann [26].
Alternatively, one could argue that the theory’s spatiotemporal commitments should be the intersection of the commitments of its various formulations. But it’s not clear to me what the motivation for this move would be, beyond a vague appeal to supervaluationist semantics; and in any event, the effect of such a prescription will be to claim that any theory with a generally covariant formulation is—at most—committed to spacetime being a manifold.
How to pick out the appropriate subset will be addressed in Sect. 6.
Trivially, of course, whatever \(g_{\alpha \beta }\) were this claim would be true for the group \(\{\delta ^\alpha _\beta \}\). But the existence of a nontrivial group of transformation matrices, under which \(g_{\alpha \beta }\) is invariant, reflects important facts about \(g_{\alpha \beta }\).
I say “as a group” because the matrices themselves will not be the “Lorentz matrices”
 one sometimes meets in introductions to special relativity: those are the real-valued matrices which preserve the coefficients \(\eta _{\mu \nu }\), i.e., which preserve the diagonalised form of the metric. But as discussed below, there are transformations which transform between \(\eta _{\mu \nu }\) and \(g_{\mu \nu }\); these same transformations will transform between
one sometimes meets in introductions to special relativity: those are the real-valued matrices which preserve the coefficients \(\eta _{\mu \nu }\), i.e., which preserve the diagonalised form of the metric. But as discussed below, there are transformations which transform between \(\eta _{\mu \nu }\) and \(g_{\mu \nu }\); these same transformations will transform between  and
and 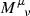 , constituting a group isomorphism between the two sets of matrices.
, constituting a group isomorphism between the two sets of matrices.Without a proviso of this sort, we would end up counting arbitrary permutations of the space of models as dynamical symmetries (cf. Belot [5]’s “Fruitless Definition” of symmetry).
It is a “confined object” in the sense of Pitts [37].
My use of uppercase indices for internal vector spaces follows Weatherall [51].
For more on the tetrad formalism, see Rovelli [43] and Wallace [48]. Read et al. [40] offer an alternative analysis of how to get at the Lorentz symmetry of a generally-covariant theory, by seeking to show that minimally coupled dynamical equations will be invariant under (only) Poincaré transformations. However, they are using a somewhat different sense of “invariant”: see Appendix 1.
For discussion of and references on the tetrad formalism applied to Newton-Cartan theory, see Read and Teh [41].
Cf. Weatherall [51].
Knox [24]. Note that as Robertson [42] observes, almost any theoretical quantity could be taken to be functionally defined by its total role in that specific theory; the hard (and interesting) project is finding smaller functional roles that are present in distinct theories, and so let us identify physical quantities across theories.
[10, p. 169]
The existence of such coordinates is related to the considerations raised in Sect. 5: if \(\xi ^\mu \) are Riemann normal coordinates for p, and \(x^\mu \) are our original coordinates, then the matrix given by the value at p of \(\partial \xi ^\mu /\partial x^\alpha \) will diagonalise the metric in the manner of equation (13). But the presence of inertial coordinates is stronger than the possibility of such a diagonalisation, for two reasons: (a) diagonalising amounts to a choice of basis at each point, with no requirement that it be a coordinate (or “holonomic”) basis; (b) inertial coordinates have the further property that the connection coefficients vanish.
In the context of Newtonian gravitation, for instance, Knox [23] argues that the local inertial frames are the free-fall frames, and hence that the spacetime structure is encoded in the curved Newton-Cartan connection rather than the flat Galilean connection: in other words, that the connection coefficients are not the Galilean coefficients \(\Gamma ^\rho _{\mu \nu }\), but rather the Newton-Cartan coefficients \(\Gamma ^\rho _{\mu \nu } + t_{\mu \nu } h^{\rho \sigma } \nabla _\sigma \phi \) (where \(\phi \) is the gravitational field).
[22, p. 348]
That said, there are ways in which one can see the role of spacetime structure in the field equations as being what gives rise to such equations of motion [52]: one can use a variational analysis to ground a certain kind of conservation condition, and then employ that condition to prove an appropriate equation of motion. The best-known example of this kind of construction is the geodesic theorem in GR, but one can similarly prove a geodesic theorem in Newtonian theories [50], and the Lorentz force law in electromagnetism [20].
Assuming that this is how the left-hand equality is meant to be justified.
The remarks below draw heavily on correspondence with James Read.
This paraphrases an argument put to me by Read (in correspondence).
References
Acuña, P.: Minkowski spacetime and Lorentz invariance: the cart and the horse or two sides of a single coin? Stud. Hist. Philos. Sci. Part B 55, 1–12 (2016)
Anderson, J.L.: Principles of Relativity Physics. Academic Press, New York (1967)
Baker, D.J. On spacetime functionalism [preprint]. (2019). Retrieved 24 April 2019, from http://philsci-archive.pitt.edu/15860/
Barrett, T.W.: Spacetime Structure. Stud. Hist. Philos. Sci. Part B 51, 37–43 (2015)
Belot, G.: Symmetry and equivalence. In: Batterman, R.W. (ed.) The Oxford Handbook of Philosophy of Physics. Oxford University Press, New York (2013)
Belot, G.: Fifty million elvis fans can’t be wrong. Noûs 52(4), 946–981 (2018). https://doi.org/10.1111/nous.12200
Bernard, J.: Riemann’s and Helmholtz-Lie’s problems of space from Weyl’s relativistic perspective. Stud. Hist. Philos. Sci. Part B 61, 41–56 (2018)
Brading, K., Castellani, E. (eds.): Symmetries in Physics: Philosophical Reflections. Cambridge University Press, Cambridge (2003)
Brown, H.R.: The origins of length contraction: I. The FitzGerald–Lorentz deformation hypothesis. Am. J. Phys. 69(10), 1044–1054 (2001)
Brown, H.R.: Physical Relativity: Space-Time Structure from a Dynamical Perspective. Oxford University Press, Oxford (2005)
Brown, H.R., Pooley, O.: Minkowski Space-Time: A Glorious Non-Entity. In: Dieks, D. (ed.) The Ontology of Spacetime, vol. 1, pp. 67–89. Elsevier, Amsterdam (2006)
Brown, H.R., Read, J.: The dynamical approach to spacetime theories. In: Knox, E., Wilson, A. (eds) The Routledge Companion to Philosophy of Physics, page 25. Routledge, London. Forthcoming (philsci-archive: 14592) (2018)
Brown, H.R., Sypel, R.: On the meaning of the relativity principle and other symmetries. Int. Stud. Philos. Sci. 9(3), 235–253 (1995)
Caulton, A.: The role of symmetry in the interpretation of physical theories. Stud. Hist. Philos. Sci. Part B 52, 153–162 (2015)
Curiel, E.: On Geometric Objects, the Non-Existence of a Gravitational Stress-Energy Tensor, and the Uniqueness of the Einstein Field Equation. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. Forthcoming. References are to draft of February 2nd, 2017 (2017)
Dewar, N.: Sophistication about symmetries. Br. J. Philos. Sci. Forthcoming (2017)
Earman, J.: World Enough and Space-Time: Absolute versus Relational Theories of Space and Time. MIT Press, Cambridge, MA (1989)
Dewar, N., Eisenthal J.: A raum with a view: Hermann Weyl and the problem of space. In: Beisbart, C., Sauer, T., Wüthrich, C. (eds.) Thinking About Space and Time. Springer. Forthcoming
Friedman, M.: Foundations of Space-Time Theories: Relativistic Physics and Philosophy of Science. Princeton University Press, Princeton, NJ (1983)
Geroch, R., Weatherall, J.O.: The motion of small bodies in space-time. Commun. Math. Phys. 364(2), 607–634 (2018). https://doi.org/10.1007/s00220-018-3268-8
Healey, R.: Gauging What’s Real. Oxford University Press, Oxford, UK (2007)
Knox, E.: Effective spacetime geometry. Stud. Hist. Philos. Sci. Part B 44(3), 346–356 (2013)
Knox, E.: Newtonian spacetime structure in light of the equivalence principle. Br. J. Philos. Sci. 65(4), 863–880 (2014)
Knox, E.: Physical relativity from a functionalist perspective. Stud. Hist. Philos. Sci. Part B (2017)
Kolář, I., Michor, P.W., Slovák, J.: Natural Operations in Differential Geometry, Electronic edn. Springer-Verlag, Berlin, Heidelberg (1993)
Kretschmann, E.: über den physikalischen Sinn der Relativitätspostulate, A. Einsteins neue und seine ursprüngliche Relativitätstheorie. Ann. Phys. 53(16), 575–614 (1917)
Lam, V., Wüthrich, C.: Spacetime is as spacetime does. Stud. Hist. Philos. Sci. Part B 64, 39–51 (2018). https://doi.org/10.1016/j.shpsb.2018.04.003
Malament, D.B.: Topics in the Foundations of General Relativity and Newtonian Gravitation Theory. University of Chicago Press, Chicago, IL (2012)
Maudlin, T.: Suggestions from Physics for Deep Metaphysics. In: Maudlin, T. (ed.) The Metaphysics Within Physics, pp. 78–103. Oxford University Press, Oxford (2007)
Myrvold, W.C.: How could relativity be anything other than physical? Stud. Hist. Philos. Sci. Part B (2017). https://doi.org/10.1016/j.shpsb.2017.05.007
Nijenhuis, A.: Theory of the Geometric Object. PhD thesis, Universiteit van Amsterdam (1952)
Nijenhuis, A.: Natural bundles and their general properties. Differ. Geom. Honor of K. Yano, Kinokuniya, Tokyo 317, 334 (1972)
Norton, J.D.: Coordinates and covariance: Einstein’s view of space-time and the modern view. Found. Phys. 19(10), 1215–1263 (1989)
Norton, J.D.: Geometries in Collision: Einstein, Klein and Riemann. In: Gray, J.J. (ed.) The Symbolic Universe: Geometry and Physics 1890–1930, pp. 128–144. Oxford University Press, Oxford; New York (1999)
Norton, J.D.: Why constructive relativity fails. Br. J. Philos. Sci. 59(4), 821–834 (2008)
Olver, P.J.: Applications of Lie Groups to Differential Equations. Springer-Verlag, New York (1986)
Pitts, J.B.: Absolute objects and counterexamples: Jones-Geroch dust, Torretti constant curvature, tetrad-spinor, and scalar density. Stud. Hist. Philos. Sci. Part B 37(2), 347–371 (2006)
Pitts, J.B.: The nontriviality of trivial general covariance: How electrons restrict ‘time’ coordinates, spinors (almost) fit into tensor calculus, and 716 of a tetrad is surplus structure. Stud. Hist. Philos. Sci. Part B 43(1), 1–24 (2012)
Pooley, O.: Background independence, diffeomorphism invariance, and the meaning of coordinates. In: Lehmkuhl, D., Schiemann, G., Scholz, E. (eds.) Towards a Theory of Spaceme Theories, number 13 in Einstein Studies. Birkhäuser, Basel (2017)
Read, J., Brown, H.R., Lehmkuhl, D.: Two miracles of general relativity. Stud. Hist. Philos. Sci. Part B 64, 14–25 (2018). https://doi.org/10.1016/j.shpsb.2018.03.001
Read, J., Teh, N.J.: The teleparallel equivalent of Newton–Cartan gravity. Class. Quantum Gravity 35(18), 18LT01 (2018)
Robertson, K.: Functionalism fit for physics. Unpublished (2018)
Rovelli, C.: Quantum Gravity. Cambridge University Press, Cambridge, New York (2004)
Saunders, S.: To what physics corresponds. In: French, S., Kamminga, H. (eds.) Correspondence, Invariance and Heuristics, number 148 in Boston Studies in the Philosophy of Science, pp. 295–325. Kluwer, Dordrecht (1993)
Scholz, E.: The problem of space in the light of relativity: The views of Hermann Weyl and Elie Cartan. In: Bioesmat-Martagon, L. (ed.) Eléments d’une Biographie de l’espace Géométrique, pp. 255–312. Presses Universitaires de Nancy, Nancy (2016)
Schouten, J.A., Haantjes, J.: On the theory of the geometric object. Proc. Lond. Math. Soc. s2–42(1), 356–376 (1937)
von Helmholtz, H.: über den Ursprung und die Bedeutung der geometrischen Axiome. In: Vorträge Und Reden, volume 2, pp. 1–31. Vieweg, Braunschweig, 4th edition (1896)
Wallace, D.: Fields as Bodies: A unified presentation of spacetime and internal gauge symmetry. (2015). arXiv:1502.06539
Wallace, D.: Who’s afraid of coordinate systems? An essay on representation of spacetime structure. Stud. Hist. Philos. Sci. Part B. Forthcoming (2017)
Weatherall, J.O.: The motion of a body in Newtonian theories. J. Math. Phys. 52(3), 032502 (2011)
Weatherall, J.O.: Fiber bundles, Yang-Mills theory, and general relativity. Synthese 193(8), 2389–2425 (2016)
Weatherall, J.O.: Conservation, inertia, and spacetime geometry. Stud. Hist. Philos. Sci. Part B. Forthcoming (2017)
Weyl, H.: Mathematische Analyse des Raumproblems. Verlag von Julius Springer, Berlin (1923)
Acknowledgements
I’m very grateful to the participants in the conference “Thinking About Space and Time” (University of Bern) for their comments and questions, and to James Read and two anonymous referees for comments on earlier drafts.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Covariance, Unvariance, and Transformations
Covariance, Unvariance, and Transformations
[40, Appendix A] seek to show that “minimally coupled dynamical equations in GR manifest local Poincaré symmetry, when written in normal coordinates at any \(p \in M\).” Here, I critically review their proof.
Read et al. begin by assuming that any minimally coupled dynamical equation in GR is of the form
where each \(O_i\) is either:
a tensor;
a partial derivative of a tensor; or
a partial derivative of a connection coefficient.
The reason to exclude (undifferentiated) connection coefficients—according to Read et al.—is that we are assuming the equation (18) is written in normal coordinates, in which (at the point p under consideration) connection coefficients vanish. However, this already risks introducing confusion. There is, I claim, a significant difference between an equation involving a partial derivative, and an equation involving a covariant derivative whose connection coefficients happen to be zero, even though the formal expression of these two equations will be the same. Specifically, two such equations will involve different transformation rules, and hence will have different invariance properties.
To see this, consider the two equations
and
and suppose that we are in a flat space to which our coordinates are adapted, such that \(\nabla _\mu J^\nu = \partial _\mu J^\nu \) (since \(\Gamma ^\rho _{\mu \nu } = 0\)). It follows that the two equations pick out exactly the same class of solutions. However, if we apply a coordinate transformation
then we transform \(\nabla _\mu J^\nu \) as a rank-(1, 1) tensor, but transform \(\partial _\mu J^\nu \) as the partial derivative of a components of a vector. This means that our two equations are transformed into
and
respectively. The first of these is equivalent to \(\widetilde{\nabla }_\alpha \widetilde{J}^\beta = 0\) (in the sense of having the same solutions), and so equation (19) is invariant under the coordinate transformation; but the second is not equivalent to \(\widetilde{\partial }_\alpha \widetilde{J}^\beta = 0\), and so equation (20) is not invariant under the coordinate transformation. Another way of seeing what’s going on here is to observe that equation (19) is more fully expressed as
and although \(\Gamma ^\nu _{\mu \rho }\) takes the value zero, its transformation rule means that the coordinate transformation (21) will (in general) transform it away from zero—in just such a way, of course, as to cancel out the extra terms arising from the transformation of \(\partial _\mu J^\nu \). Equation (20), on the other hand, has no connection coefficients figuring at all (whether zero-valued or not); so such coefficients cannot step out from the shadows to guarantee invariance, in the way they do for equation (19).
What this means is that we should include connection coefficients on the list of possible ingredients for our equation: although such coefficients might be zero in the coordinate system we start with, if we are assessing which coordinate transformations preserve the form of the equations, we need to check that they will preserve the vanishing of those connection coefficients! Fortunately, adding them to the list of ingredients doesn’t make a significant difference to Read et al.’s next observation: that for affine coordinate transformations, all the ingredients transform tensorially. Recall that an affine coordinate transformation is a transformation of the form

where  and \(a^\mu \) are constant. Note that
and \(a^\mu \) are constant. Note that

and

where  is the inverse to
is the inverse to  (i.e. is the matrix such that
(i.e. is the matrix such that  ). As is well-known, connection coefficients transform tensorially under affine coordinate transformations (since the non-tensorial part of the transformation rule features a second partial derivative). In the interests of space, I do not reproduce Read et al.’s proof that partial derivatives of tensors or partial derivatives of connection coefficients transform tensorially under affine transformations.
). As is well-known, connection coefficients transform tensorially under affine coordinate transformations (since the non-tensorial part of the transformation rule features a second partial derivative). In the interests of space, I do not reproduce Read et al.’s proof that partial derivatives of tensors or partial derivatives of connection coefficients transform tensorially under affine transformations.
However, they then proceed to say
We have found that each of the \(O_i\) featuring in any minimally coupled dynamical equation in GR, written in normal coordinates at a point \(p \in M\), is covariant—i.e., transforms tensorially—under affine coordinate transformations. However, we have yet to show that all such equations are invariant—i.e. take the same form—under affine coordinate transformations. In fact, this is in general not the case.
Prima facie, this claim is somewhat surprising. For consider again the expression (18). In order for the left-hand-side to be well-formed, each \(O_i\) must have the same index structure: i.e., they must have the same free covariant and contravariant indices (where a “free index” is one that has not been contracted with another index). But if two terms have the same index structure, then when they are transformed tensorially, they will pick up the same partial derivative terms; owing to the linearity of tensor calculus these terms can then be uniformly multiplied away, as we did in observing that equation (22) is equivalent to \(\widetilde{\nabla }_\alpha \widetilde{J}^\beta = 0\). And note that the presence of bound indices (those which have been contracted) doesn’t make any difference: if we have an expression of the form

then applying the tensorial transformation rule yields

and so such indices “cancel out”.
Read et al. argue that this doesn’t hold, in general, “due to the potential contraction of indices in some terms with respect to the metric” (p. 11). As an example, they give (in my notation)
They argue that the affine transformation (25) transforms this (again, using my notation) into

and that this latter equation is only equivalent to (30) if  ; i.e., if
; i.e., if  is a Lorentz transformation (and hence, (25) a Poincaré transformation).
is a Lorentz transformation (and hence, (25) a Poincaré transformation).
Now, this last assertion is correct in the sense that the right-hand equality in (31) is, indeed, only equivalent to (30) if  is a Lorentz transformation. But the left-hand equality also only holds if
is a Lorentz transformation. But the left-hand equality also only holds if  is a Lorentz transformation: that’s the only way to use \(\eta \) to raise or lower indices and convert
is a Lorentz transformation: that’s the only way to use \(\eta \) to raise or lower indices and convert  into
into  .Footnote 49 And if we look at the leftmost term in equation (31), we observe that—just as our general discussion of contracted indices would lead us to expect—we have a matrix term
.Footnote 49 And if we look at the leftmost term in equation (31), we observe that—just as our general discussion of contracted indices would lead us to expect—we have a matrix term  and its inverse
and its inverse  ; cancelling these out, we see that (30) transforms into
; cancelling these out, we see that (30) transforms into

and (32) is equivalent to (30). Thus, the supposed counterexample is invariant under arbitrary affine transformations (not just Poincaré transformations).
Indeed, it seems to me that we have good grounds to expect equations formed from minimal coupling to be invariant under arbitrary coordinate transformations (not just affine transformations)—i.e. to be generally covariant. The reason why the above proof was limited to affine transformations is that, in general, partial derivatives and connection coefficients will transform non-tensorially, and hence we will get “extra” terms showing up in the transformed equation—terms which will prevent the transformed equation from being equivalent to the original. But if partial derivatives and connection coefficients show up together, then it may be that the extra terms from the one cancel out the extra terms from the other, and we do get invariance under (non-affine) coordinate transformations.
The condition under which such cancellations happen is, of course, that the partial derivatives and connection coefficients in the equation are such as to form a covariant derivative—indeed, the whole point of covariant differentiation is that the result of applying a covariant derivative to a tensor is, itself, another tensor (as reflected in the transformation (22)). But now consider Read et al.’s definition of minimal coupling (pp. 2–3):
Minimally coupled dynamical equations for matter fields in GR are constructed from dynamical equations for matter fields featuring coupling to a fixed Minkowski metric field \(\eta _{ab}\) and no curvature terms, by replacing all instances of \(\eta _{ab}\) with a generic Lorentzian metric field \(g_{ab}\), and replacing all instances of the torsion-free derivative operator compatible with \(\eta _{ab}\) with the torsion-free derivative operator compatible with \(g_{ab}\).
Thus, on the face of it, one would expect a minimally coupled dynamical equation to consist of tensors and covariant derivatives of tensors (with respect to the torsion-free derivative operator compatible with \(g_{ab}\))—that is, tensors and tensors. And clearly, if all the terms \(O_i\) in (18) are tensors (with the same index structure), then (18) will be invariant under arbitrary coordinate transformations.
The above, I claim, is the standard argument for the claim that generally covariant equations—including those obtained through minimal coupling—to be invariant under arbitrary (smooth) coordinate transformations. However, there is a different analysis one can give.Footnote 50 Suppose that our dynamical equation features the metric; very schematically, we give it the form
Now, if we have written this equation in normal coordinates, then \(g_{\mu \nu } = \eta _{\mu \nu }\), where \(\eta _{\mu \nu }\) denotes the matrix of coefficients (6). What is it for this expression to “retain the same form” under a coordinate transformation, from \(x^\mu \) to \(\widetilde{x}^\mu \)? First answer: it is for it to be (or to be equivalent to) an equation with the same syntactic structure, albeit with tildes over everything; schematically, the form is preserved if (33) is transformed into something (equivalent to)
(A non-schematic example is given by the comparison of (30) with (32).) This first answer is the answer that the argument above assumed, and so this is the sense in which its conclusion holds.
Second answer: it is for it to have the same syntactic structure, and for certain simplifying identities to continue to hold. In the case at hand, this will mean that the form is preserved if (33) is transformed into something equivalent to (34), and—in addition—\(\widetilde{g}_{\mu \nu } = \eta _{\mu \nu }\). In defence of this answer, one can argue that part of what makes the normal-coordinate form the “simplest” form is that writing the equation out in components would be considerably simpler if the metric diagonalises than if it does not; and it is in this sense that a transformation away from normal coordinates makes the equation into one with a less simple form, and so ipso facto one with a different form.Footnote 51
Evidently, if we require this second (stronger) sense of invariance, then any equation featuring the metric will be invariant only under coordinate transformations which are Poincaré in form, i.e. where
since it is only these equations which preserve the metric’s being diagonal.
Thus, the question becomes which of these two senses is more appropriate. The problem with the latter sense is that it risks overgenerating, and will lead us to underestimate the size of a theory’s symmetry group. In the context of electromagnetic theory on curved spacetime, for example, there will exist at any point Riemann normal coordinates with respect to which \(J^\mu = (\rho , 0, 0, 0)\). Adopting those coordinates will simplify the dynamical equations, just as the adoption of Riemann normal coordinates does; and such equations will be preserved only under spatial translations and rotations. This suggests that on the stronger sense of invariance just canvassed, the equations of electromagnetism turn out to be invariant only under the Newton group of transformations. This seems to me a reason to prefer the former, weaker, notion of invariance.
Rights and permissions
About this article
Cite this article
Dewar, N. General-Relativistic Covariance. Found Phys 50, 294–318 (2020). https://doi.org/10.1007/s10701-019-00256-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-019-00256-0




 one sometimes meets in introductions to special relativity: those are the real-valued matrices which preserve the coefficients
one sometimes meets in introductions to special relativity: those are the real-valued matrices which preserve the coefficients  and
and 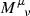 , constituting a group isomorphism between the two sets of matrices.
, constituting a group isomorphism between the two sets of matrices.