1 Introduction

There are a number of paradoxes attributed to quantum mechanics involving the transition to macroscopic physics. As pointed out by Einstein et al. [1] a “collapse” of the wave function seems to violate the local structure of the theory. There are a number of other odd features connected to the measurement process [2,3,4]. They are widely discussed in the extensive literature on the philosophy of quantum mechanics (see e.g. [5,6,7,8,9]).

These discussions neglect an in our opinion more illuminating paradox, which relies on a careful consideration of the Hanbury-Brown Twiss interferometry [10]. The Hanbury-Brown Twiss interferometry—or the time when it was generally accepted—is comparatively young. It also involves quantum statistics.

To resolve the paradox a quantum mechanical world without time ordered causal structure with a fixed initial and fixed or strongly restricted final state is conjectured. Our basic idea is that there is no problem in the backward causation, if there is a way to restore causality in the transition to the usual known part of the macroscopic world.

The aim of this note is to better understand how such a restoration could work. On general terms two obviously needed rules for the transition to macroscopia are formulated. In Sects. 3 and 4 we turn to a general discussion of a quantum mechanics with two boundary state vectors following the work of Aharonov and coauthors [11, 12]. A cosmological consideration similar to an idea of Gell-Mann and Hartle  [13] follows in Sects. 5 and 7. The paper argues how the cosmological expansion allows for something which locally looks like a collapse structure and effectively introduces a time arrow. How in such a scenario a time-ordered causal macroscopia could arise, is outlined with a simple router picture and a small toy program in the central Sect. 6.

2 Argument for Backward Causation

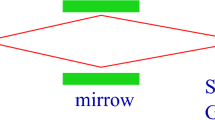
Following Hanbury-Brown Twiss (Fig. 1) we consider a star emitting two photons with equal frequency, polarization and phase in direction of an observatory with two telescope detectors. The star should be light years away and an attribution of the photons to the closely neighboring detectors \((\mathrm {separation}\,\Delta \rightarrow 0)\) should not be possible. If the observatory happens to observe them the interference term leads to a quantum statistical enhancement of the emission probability by a factor two. If it mirrors them back in space—with a mirror large enough to allow for a resolution of the positions of the emitters—no such factor occurs. So the choice affects a probability of an event way past.

Fig. 1
figure 1

Hanbury-Brown Twiss observation

Full size image

Of course there is the opposite phase case where a corresponding equal quantum statistical suppression occurs. In this way summing up both situations the observation choice does not affect the total emission probability. It just affects the wave function in the past by enhancing its same phase component. Such backward causation in wave functions is known from Wheelers delayed-choice gedanken experiment [14,15,16,17].

However the emission process here doesn’t have to be incoherent and phases can be correlated in the emission process. We therefore conclude that there can be special situations where past emission probabilities are changed. The causal direction is broken independent of the ontological role of wave functions [18].

We stress that the observation of the second order Hanbury-Brown Twiss correlation and devices with coherent emission are real and not gedanken constructs. The conclusion is not optional. What follows is not another interpretation of quantum mechanics but anattempt to encounter this observation.

Similar observations exist in other contexts. Consider multi-particle production in nuclei or particle scattering. A quantum statistical enhancement in the production of very closely neighboring identical bosons and a corresponding suppression in that of very closely neighboring identical fermions was observed as peak or dip against a smoother background [19]. The enhancement or suppression of the emission obviously could be eliminated after the initial scattering if a third particle crosses the paths of the pair. The crossing had to be in a region where the different emission regions of both particles would still be distinguished.

In atomic physics it could be shown that the absorption probability of a photon by an atom can be drastically increased by a parabolic mirror  [20, 21]. In the reverse process the emission probability depends on the presence of the parabolic mirror which can be far away and thus manipulated at a later time. Again there is a backward causation effect on a probability (see also [22, 23]). I am aware that the absence of a microscopic causal structure is not widely accepted and this is a point where more real experiments would be persuasive.

The backward causation of emissions contradicts the De-Broglie-Bohm theory [24,25,26]. If one photon is observed in the first telescope Bohms law of motion (\(\psi \) is the usual wave function).

$$\begin{aligned} \left. \left( \psi ^{*}\psi \right) \cdot d\overrightarrow{Q}/dt=\frac{\hbar }{m_{i}}\left( \psi ^{*}\nabla \psi \right) \right| _{\mathrm {for\, all\, points\, on\, path}\, Q(t)} \end{aligned}$$

can non-locally guide the path Q(t) of the second particle to the second telescope with the required enhanced probability for the second order correlation. But in the manifest forward evolution past emission probabilities cannot be affected.

Can the broken causal direction be understood in usual quantum mechanics? Quantum mechanics knows the amplitude that a given initial state evolves to a given final one. The calculation uses a collapse-less theory (Sakurai uses the name “quantum dynamics” [27]) which contains no intrinsic time direction. No contradiction to quantum dynamics arises.

The absence of a time direction in basic laws is intuitively annoying and many authors tried to introduce dynamical time arrows. In field theory it is possible to basically admit only advanced solutions and create in this way an asymmetry [28,29,30]. However this apparent asymmetry gets lost in the path integral formalism of Feynman [31]. The hypothesis adhered to here is that the dynamical equations are time invariant and that there is no quantum dynamical time arrow. It sides with Einstein in its controversy with Ritz [32] and follows many outstanding authors like [14]. For a detailed consideration of the time arrows we refer to Zeh’s book [33].

3 Correspondence Transition Rules

The backward causation has to be restricted to microscopic phenomena. A key point is what has to be taken as microscopic and macroscopic. The example of backward causation discussed in the beginning tells us that the initial state in the “macroscopic” (non quantum) world cannot contain correlated phases. In this way the example with locked-in phases has—albeit the possible extension of the process—to be attributed to the “microscopic” (quantum) world.

Backward causation in the microscopic world involves interference effects. The absence of backward causation in the macroscopic world indicates:

  • Macroscopically prepared initial states contain no correlated phases.

  • Macroscopic measurements obtain an equal contribution from states with quantum statistical enhancement and suppression.

We denote this as “correspondence transition rules” (i.e. rule of the transition to macroscopia described by the correspondence principle). The cause of the rules is macroscopically unavoidable phase averaging in the initial state and a macroscopically unavoidable averaging over enhancing and suppressing contribution in final state measurements.

The second rule claims it is not possible to obtain enhancement or suppression through subsequent interference effects. It is called no post-selection [33] by macroscopic devices. To observe interferences one has to join distinct paths. As a consequence of the quantum Liouville theorem any device cannot reduce the number of available paths. The joining essentially works like a partially reflecting mirror. Ignoring irrelevant aspects there are two incoming paths and two outgoing ones. For given photon-phases \(\phi _{1}\) and \(\phi _{2}\) there can be a suppression like \(\sin ^{2}(\phi _{1}-\phi _{2})\) in one of the directions and a corresponding enhancement like \(\cos ^{2}(\phi _{1}-\phi _{2})\) in the other. Macroscopically both channels have to be included and the overall probability is not affected.

The rules were developed for models of multi-particle production where peaks or dips against a smoother background are observed. The rule postulates that in an average over the neighboring peak or dip region and the not so neighboring region enhancement and suppression effects occur with an equal weight (see [34, 35] for an effective implementation in simulations codes). In this way quantum statistical enhancement or suppression doesn’t destroy the well tested factorization between the initial and the hadronization process. (The percent level determination of the QCD coupling constant from the hadronic structure in \(e^+ e^-\)- annihilation depends on this factorization. No quantum statistical effect enhancing large multiplicity production is allowed.)

The correspondence transition rule plays an important role in the understanding of lasers. The lasing equation [36] is:

$$\begin{aligned} \frac{dn}{dt}=\left[ (N_{2}-N_{1})\cdot W\cdot n\right] +\left[ W\cdot N_{2}\right] -\left[ 2\cdot \kappa \cdot n\right] \end{aligned}$$

where \(N_{2}\,\mathrm {and}\, N_{1}\) are the occupation numbers of the excited and the ground state, where n is the number of photons, where W is the transition probability, and where \(\kappa \) denotes the absorption coefficient. It contains three terms (enclosed by rectangular brackets): the stimulated emission or absorption, the spontaneous emission, and the spontaneous absorption. To obtain the required exponential growth in the photon number (lasing condition) a positive right side is needed.

This argument misses the crucial mechanism working in lasers. The emission of a photon has—depending on the angular momentum of the states—only a slight preference of the forward direction. The coherent, precisely forward emission in the laser is a quantum statistical enhancement not considered in above equation.

Why the lasing condition argument still makes sense is a consequence of the correspondence transition rule. The lasing condition is a purely macroscopic consideration just counting the number of photons for which the quantum statistical enhancement and suppression effects cancel and—in spite of their otherwise pivotal role—can safely be ignored. 

4 Two Boundary Quantum System

The argument above shows that the present can be affected by the past and by the future. It means that two boundaries are needed to describe the present situation and to avoid an artificial time asymmetry. A two boundary quantum mechanics is possible but it will significantly change the picture [11, 13, 37,38,39,40,41]. Except for the matching procedure discussed below it is unitary. It provides a completely consistent theory without paradoxes. No other change to the usual quantum dynamics is needed. The apparent macroscopic time asymmetry will be attributed to our cosmological situation.

Such a symmetric theory can avoid collapsing wave functions. Obviously quantum mechanics with a two directional constraint does not contain locality problems like the EPR paradox [42]. Simply, if a state can change backward in time it can obviously also change faster than light in mixed forward backward processes.

’t Hooft [43] recently advocated that a suitable deterministic local cellular automaton theory could underlay quantum mechanics. Any such underlying deterministic theory involves a fixed predetermined final state and therefore shares our question how a fixed final quantum state can coexist with a causal macroscopic world.

The strategy is to take these initial and final states far away so that there is a region in between which is in principle known by quantum dynamics and which is huge enough so that something like classical aspects of the intermediate evolution appears within the closed system. Without contact to an “outside” there are no collapses. As in Everett’s interpretation [44] different multi-worlds can contribute in between. But the fixed final state severely limits the proliferation of such intermediate “universes”. The hypothesis is that in the present situation coexisting paths essentially only survive as usual “quantum effects” on a microscopic level.

The picture with the fixed final state will obviously in the end also involve a modification of classical physics. As quantum dynamics is tested to a considerably higher precision than classical mechanics, it should be taken as better known [45] and untested parts of classical physics might be modified.

5 Measuring Processes Within a Closed System

Two boundary quantum systems were investigated with great care [13, 39, 46]. We recap parts needed to understand the resulting macroscopic description.

An essential element of a measurement in open systems is to ensure that states observed with different eigenvalues can no longer interfere. It prohibits reconstruction of the premeasured state and introduces a time arrow.

In a closed system the situation is actually quite similar. As in the open system the evolving wave function contains manifest deterministic parts with all kinds of interactions, including branching and merging. The system also contains seemingly non deterministic measuring processes corresponding to the usual measurements in open systems. A measured subsystem is brought in contact with a witnessing subsystem [47] by a suitable interaction

$$\begin{aligned} H_{\mathrm {interaction}}=-g(t)\,\dot{p}\, A+H_{\mathrm {enviroment}}(p,\epsilon _{1},\cdots \,,\epsilon _{n}) \end{aligned}$$

where g(t) is a function (non vanishing during the measurement time), A the measurement operator and p a pointer state which changes during the measurement and anchors down its properties in a “macroscopic” number of tracers in the witnessing subsystem \(\epsilon _{1},\cdots \,,\epsilon _{n}\).

As in open systems the decoherence concept (einselection [48, 49]) plays a central role. It describes how a quite classical description is reached by restricting the consideration to a local subsystem. The trick is to dislocate unavoidable entanglements to unconsidered remote parts.

For a subsystem in a huge surrounding there are obviously a large number of measurement processes as there is usually no shielding from such interactions. Estimates showed [48,49,50] that the bulk of the interactions does not change the state of the considered system but just introduces a phaseFootnote 1 and a localization. The outcome is, that off-diagonal contributions in local density matrices will effectively disappear. Coexisting essentially coarse grained classical paths entangled to remote parts will remain.

Einselection does not help to select the actual classical path, but the selections no longer have to originate in interactions within the local system. Our concept is that in a second step the multi-world structure entangled to remote areas can be eliminated (collapsed) by a projection to a given fixed final state.

In a two boundary system intermediate measurements have to be conditional and yield the so called “weak value” [12]:

$$\begin{aligned}<A>_{\mathrm {weak}}=<\mathrm {initial\, state}\,|A|\,\mathrm {final\, state}>/<\mathrm {initial\, state\,}|\,\mathrm {final\, state}> \end{aligned}$$

For non degenerate eigenvalues \(a_{i}\) the probability that A finds an intermediate state \(a_{k}\,\)is:

$$\begin{aligned} P(a_{k})=|<\mathrm {initial\, state}\,|a_{k}>\,<a_{k}|\,\mathrm {final\, state}>|^{2}\,/\,|<\mathrm {initial\, state\,}|\,\mathrm {final\, state}>|^{2} \end{aligned}$$

The phase averaging eliminates interference contributions and the denominator can be simplified to:

$$\begin{aligned}&\sum _{i,j}<\mathrm {initial\, state\,}|a_{i}>\,<a_{i}|\,\mathrm {final\, state}> <\mathrm {final\, state\,|a_{j}>\,<a_{j}|}\,\mathrm {initial\, state}>=\\&\quad =\sum _{i,}|<\mathrm {initial\, state\,}|a_{i}> <a_{i}|\,\mathrm {final\, state}>|^{2} \end{aligned}$$

yielding the Aharonov–Bergman–Lebowitz equation [11].

Their picture is two symmetric evolutions one from the initial state and one from the final one matching at the measurement times and fixing the measurement outcome. The choice in the matching time

$$\begin{aligned} U(t_{\mathrm {initial}},t_{\mathrm {final}})=U(t_{\mathrm {initial}},t_{\mathrm {match}})U(t_{match},t_{\mathrm {final}})\,\,\,\,\,\,\,\mathrm {with}\,\, t_{match}\in [t_{\mathrm {initial}},t_{\mathrm {final}}] \end{aligned}$$

is, of course a question of convenience. Except chapter 7 we use \(t_{match}=t_{\mathrm {final}}\) so that the so called quantum collapses are encountered by projecting out the fixed final state.

As the matching replaces a huge number of measurement collapses it will naturally yield a tiny value (evaluated as “tiny” in Zeh’s book [33] for a big bang/crunch scenario). In contrast to Schulman’s statistical two boundary concept [37] the fixed final state doesn’t select “special” initial states. The density matrix of the initial state is not taken as origin of the rich structure of the universe. Also the wave functions are physical objects with no hidden properties.

Weak values can be unreasonable. The concept for their values to conform with usual quantum predictions relies on the statistical assumption that (in the Schrödinger picture):

$$\begin{aligned}&|<\mathrm {initial\, state\,|}U(t_{1}-t_{0})|\, a_{i}>/<\mathrm {initial\, state\,}|U(t_{1}-t_{0})|a_{j}>|=\\&\quad =\lim _{(t_{2}-t_{1})\rightarrow \infty }(|<\mathrm {initial\, state\,}|\, U(t_{1}-t_{0})\,|\mathrm {\, projection}(a_{i})\,|\, U(t_{2}-t_{1})\,|\mathrm {\,\mathrm {final\, state}}>| \, / \\&\qquad |<\mathrm {initial\, state\,}|\, U(t_{1}-t_{0})\,|\mathrm {\, projection}(a_{j})\,|\, U(t_{2}-t_{1})\,|\mathrm {\,\mathrm {final\, state}}>|) \end{aligned}$$

The idea is that in a huge system and a long evolution time \(t_{2}-t_{1}\) all intermediate states will find their matches with essentially equal probability.

Let us consider one example. The probability of an emission of a photon \(e \rightarrow e + \gamma \) is according to the numerator of the first line proportional to \(\mathrm {e}^2\). If the photon is not contained in the final state it has to be captured again and its emission probability is therefore proportional to \(\mathrm {e}^4\).Footnote 2 This doesn’t contradict the above equation. The concept is that the situation is rich enough to offer many absorptive channels. In this way the absorption probability \(\sum _\mathrm {channels} \mathrm {e}^2\) can be unity.Footnote 3 There is no intrinsic distinction between emission and absorption in the argument.

Aharanov et al. [51] showed that fixed initial and final states reclaims determinism. To avoid determinism slight variation in the the boundary states have to be admitted.

6 Cosmology and the Time Arrow

As the closed system is not truly random it does not contain a time arrow. Instead one can expect a complicated mesh of phases correlated over large time distances.

However as Gold observed [52] the special boundary conditions of our expanding cosmos are quite consequential. It is counter intuitive as quantum mechanical processes and the cosmos involve quite different scales. It is somewhat reminiscent to the resolution of Olber’s paradox.

In macroscopia the cosmological expansion arrow of time is coupled to the thermodynamic one [53] p.e. by allowing the emission of thermal radiation in the dark sky of the expanding universe. The not returned radiation allows stars to loose energy. It facilitates the formation of cold stars, etc.

The time interval of our two boundary quantum system is taken to be large enough to include this expansion. It is easy to see how the expansion transfers to a quantum mechanical time arrow. All quantum decision are encoded in the environment. In an expanding universe the environmental witnesses predominantly live in the much richer future. A tiny local changes at the time \(t_{A}\) will therefore mainly affect the future environment not involving the past one. Inversely at a time \(t_{A}\) the environment \(\epsilon (t_{A})\) will mainly reflect the past.

How do local measurements inherit the cosmic time arrow? In a measuring process local phase correlations are destroyed as in an open system. The not so local witnessing system will typically spread out fast making a rejoining of different outcomes on a short time scale unlikely. It will involve distinct thermal radiation and eventually it will be in contact with cosmic thermal radiation processes. The central point is that the entangled thermal cosmic radiation is sufficiently separate from its partners so that the disentanglement is done by an projection on the far away final state and not by rejoining interactions.

Rejoining interactions could lead to a large number of macroscopically coexisting classical paths causing a intermediate Everett system with a growing number of multi-worlds. Our hypothesis is that—in spite of many somewhat accidental choices—essentially only one coarse grained “dominant path” survives on a macroscopic scale. The concept of “dominant path” will be clarified below.

The cost of fixed boundary states is an in the end deterministic macroscopic world. Determinism is, of course, common to classical theories. A philosophical complication arises as the system includes us. To be consistent with the felt reality one would need to keep some not predetermined genuine “free will” [54,55,56]. Within the framework of physics an unpredictable piece of reality seems prerequisite for such an influence. However this is not an argument for canonical quantum mechanics with its unpredictable random collapses. In this context there is no distinction between physically unpredictable collapses and unpredicted slight variations in the future boundary state. In both cases outside interventions can’t be excluded as long as they stay on a statistically insignificant level.

7 The Time-Ordered Causal Macroscopia

How can one understand that such a theory with a fixed final quantum state can coexist with a time-ordered seemingly causal interactive world. To avoid the obvious contradiction one has to separate the “far future” macroscopia from the “near future” macroscopia we are usually concerned with. The conjecture is that if the fixed final state is far away enough it cannot control our “near future”.

To illustrate the basic argument we consider a “router” which is a slightly random program which calculates the best way for a car to come from position A to position B . In the “router” program it should be possible to enforce an intermediate position \(A'\) and at such an intermediate positions the velocity and the direction should be taken into account.

We consider the case where the final position B is very far away from a narrow region around A and \(A'\). The route behind \(A'\) will then within this region strongly depend on the position \(A'\) and on the velocity and direction at this point. The location of B will be at first almost irrelevant. In this way the required fixed outcome seems not to concern the nearby region.

We now consider tiny variations of \(A'\). Between the closely neighboring A and \(A'\) there will be a correspondingly tiny change. As the path from \(A'\) and B will have many options at furcation points considerable changes can be caused by tiny variations in \(A'\). In this way the different scales of the distances introduce something like a causal forward direction.

To formulate the idea more precisely we used a toy program. In a two dimensional space-time array we follow a moving object. Usually with a probability of \(1-2\epsilon \) it moves:

Two left

If it moved two left one step before

One left

If it moved one left one step before

Straight

If it moved stright one step before

One right

If it moved one right one step before

Two right

If it moved two right one step before

and each with a probability \(\epsilon \):

As above, but +1 resp -1

The lattice is taken periodic to avoid edge effects. Steps are limited to two units movements in \(\delta x\). The algorithm is time symmetric. We fix the initial position to \(x=0\) and \(\frac{dx}{d\delta t}|_{x=0}=1\) and using rejection the final potion to \(x=0\) and \(\frac{dx}{d\delta t}|_{x=0}=0\). With 1\(0^{9}\) tries and 84663 (for the last time step weighted) counts we obtain the density profile of the reached points shown in Fig. 2. For the random number generator we use the method of [57] implemented by Hahn. A degree of causality and retro causality for the near future or past is clearly seen. The direction of the initial resp. final state is maintained for a few steps. The causal influence vanishes for central times.

Fig. 2
figure 2

Density profile in a symmetric world

Full size image

Can such a situation result from quantum physics?

The randomness in the toy model reflects the influence of unconsidered radiation constrained by the unknown final boundary state. Einselection explains why classical paths (collections of quantum paths) appear. To argue why typically one coarse grained path dominates we consider a bad double-slit experiment shown in Fig. 3.

Fig. 3
figure 3

A bad double-slit experiment

Full size image

The intensity of the contribution of a light source (indexed as “o”) through slits (indexed as “s” or separate as “\(s_{A}\)” and “\(s_{B}\)”) in the detector (indexed as “d”) in a two dimensional configuration with the plain of the slits at \(y_{s}=0\) is:

$$\begin{aligned} I=|A+B|^{2}\propto |\int dx_{o}\, dx_{s}\, dx{}_{d}\,\exp (ik\cdot \mathrm {exponent})\,|^{2} \end{aligned}$$

The light with wave vector k passing through lower slit contributes with a weight A to the amplitude, the light passing through the upper slit with a weight B. Defining \(x_{s}=\tilde{x}_{s}+\Delta \) to first order of \(\Delta \) one obtains:

$$\begin{aligned} \mathrm {exponent}=\mathrm {const}.+\left( \frac{x_{o}-\tilde{x}_{s}}{\sqrt{(x_{o}-\tilde{x}_{s})^{2}+y_{o}^{2}}}+\frac{\tilde{x}_{s}-x_{d}}{\sqrt{(\tilde{x}_{s}-x_{d})^{2}+y_{d}^{2}}}\right) \cdot \Delta \end{aligned}$$

For the slit s(A) the coordinate \(\tilde{x}_{s(A)}\) can be chosen that the round bracket vanishes and in absence of an oscillating phase the contribution A will be proportional to the size of the slit s(A).

Using distance h between the slits we define \(\tilde{x}_{s(B)}=\tilde{x}_{s(A)}+h\) and obtain for the slit s(B):

$$\begin{aligned} \mathrm {exponent}=\mathrm {const}.+\left( \frac{h}{\sqrt{(x_{o}-\tilde{x}_{s(B)})^{2}+y_{o}^{2}}}+\frac{h}{\sqrt{(\tilde{x}_{s}-x_{d(B)})^{2}+y_{d}^{2}}}\right) \cdot \Delta \, . \end{aligned}$$

As all distances are large against 1 / k the integral \(\int _{s(2)}d\Delta \,\exp (ik\cdot bracket\cdot \Delta )\) contains an oscillating phase massively reducing its contribution to the amplitude (i.e. \(|B|\ll |A|\)) .

The decoherence effects and the extent of source e.c.t. eliminates interference contributions between both classical paths. Two coarse grained “classical” contribution a “dominant path” (\(\propto |A|^{2}\)) and a tiny “detour-path” (\(\propto |B|^{2}\)) remain.

The appearance of a “dominant path” and a almost negligible “detour-path” seems typical. The conjecture is that during the evolution such choices will repeat themselves over and over again. Given the required final state an essentially single macroscopic “dominant global path” is postulated.

In principle there are two kind of interactions. “Protected” [12] measurement processes leave the classical path unaffected, furcation processes allow for alternate classical paths. As in the “router” picture tiny changes in the initial condition can change the way these furcation points are met and so eventually lead to a completely different classical path. This resurrects forward causality in the near future macroscopia.

The absence of backward causality might require that our expanding universe is close to its initial state. It somehow fits with the presently non decreasing expansion rate. We do not agree with Zeh (5.3.3) [33] that this means “improbably young”.

To conclude this part we restate our conjecture:

  • The influence of the not-open-ended nature is weak enough not to disturb the seemingly causal near future of macroscopic physics,

  • But strong enough to limit coexisting evolution paths to a microscopic level typical for quantum phenomena.

The initial and final states do not have to be pure states. However, the richness of the choices is taken to originate in the evolution. Even for pure states if the match

$$\begin{aligned} |<\mathrm {initial\, state}\,|S(t_i ,t_f)|\,\mathrm {final\, state}>|^{2} \end{aligned}$$

happens to be really tiny irregular disturbances will play an enhanced role. This should increase the number of furcation points. In this way the system can be externally adjusted to meet the required conditions.

The conjecture offers a way to reconcile quantum mechanics with the known part of classical physics in a completely consistent way without invoking epistemological limitations of our description of quantum collapses. That such a theory might be realized we consider an important point strongly limiting the motivation to search for modified quantum theories.

8 Cosmology and the Matching Final State

The considered evolution from a tiny initial state to a huge arbitrary fixed final one is a simple and straight forward cosmological possibility. It is tempting to consider more complex scenario’s. A persuasive concept could relay on the central role of the forward backward CPT symmetry. Often what is allowed by symmetry is realized. An eventually at least for a while contracting phase of the universe with an inverted time is therefore quite plausible. For simplicity we here discuss a big bang / crunch theory.

Quantum cosmology is clearly not a simple field. Prerequisite for the consideration is a unitary evolution including of non trivial general relativistic structures [58].

The time direction originating in radiating off witnesses into an expanding universe is reversed during the contracting phase. However, after a CPT transformation

$$\begin{aligned}<a(t_1)|U|b(t_2)>\,\,\,\,\mathop {\rightarrow }\limits ^{\mathrm {CPT}}\,\,\,\,<a(T-t_1)|U|b(T-t_2)>^{*} \end{aligned}$$

(where T is the lifetime of the universe) probabilities are identical.Footnote 4 Except for how quantum measurements are recorded the time direction is not relevant.

The physics in the in-between phase is unknown. The lack of expansion might not be important as the density could be very low and if the period is sufficiently short the sky might stay a dark sink for radiations in both directions. It is cold enough so that emitted and absorbed radiation are insignificant.

A big bang / crunch scenario was considered by Gell-Mann and Hartle  [13]. They were particularly interested in a symmetric situation with a single density matrix describing initial and final state. If such a scenario can be excluded from observations is not clear  [13, 59].

In the here considered collapse-less quantum dynamic identical density matrices at both boundaries mean identical evolutions.Footnote 5 At the boundary all evolved multi-versa will match. In such a scenario the role of the fixed final states to eliminate or reduce multi-versa is therefore completely lost.

To keep our central argument it is necessary to have at least very different final and initial density matrices. To consider their evolution of \(\phi (t)\) and \(\phi ^*(T-t)\) one can formally split the two fixed boundary system into two parts of again two boundary ones each with one fixed and one matching intermediate boundary. Following the time arrow one replaces the expanding and contracting evolution by two separate evolutions.

All quantum decisions have to be encoded in the final state. In a big bang / big crunch scenario this might be problematic as both states are limited. Possibly the richness of the intermediate (matching) state helps to sufficiently reduce entanglement between the expanding and contracting world so that not much is changed if one replaced the fixed final states by matching ones. To explain the mechanism we denote entangled connections by underlining

$$\begin{aligned} \underline{ab}=a'b'+a''b'' \end{aligned}$$

and write an exemplaric final state of the expanding universe as

$$\begin{aligned} \underline{ab}cde\underline{fg}hijklm \end{aligned}$$

and that of the contracting one as

$$\begin{aligned} ab\underline{cd}efg\underline{hi}jklm ~. \end{aligned}$$

As matching entanglements vanish in the limit of a huge intermediate state all entanglement will get typically lost. The matching albeit not fixed final state might suffice to avoid multi-verses.

9 Conclusion

To conclude heuristic arguments are given that dropping time ordered causality for quantum states needs not destroy the apparent causality on a macroscopic level. If the conjecture is correct one would obtain a consistent synthesis of microscopic and macroscopic physics. A more formal, less heuristic description would clearly be helpful.