A scheduling problem for a novel container transport system: a case of mobile harbor operation schedule

Abstract

Mobile Harbor (MH) is a movable floating platform with a container handling system on board so that it can load/discharge containers to/from an anchored container ship in the open sea. As with typical quay crane operation, an efficient schedule for its operation is a key to enhancing its operational productivity. A MH operation scheduling problem is to determine a timed sequence of loading/discharging tasks, assignment of MH units to each task, and their docking position, with an objective of minimizing the makespan of a series of incoming container ships. A mixed integer programming model is formulated to formally define the problem. As a practical solution method to the problem, this paper proposes a rule-based algorithm and a random key based genetic algorithm (rkGA). Computational results show that the rkGA method produces a better-quality solution than the rule-based method, while requiring longer computation time.

1 Introduction

1.1 Open sea container loading and discharging operation

In response to the continued increase in the volume of worldwide maritime container transport, container ports face an increasing demand for their service capacity. Many terminal operators respond to this challenge by extending their infrastructure (Meisel 2009). The approaches include building new terminals, expanding the existing terminals, constructing or upgrading to faster equipment and optimizing port operations.

As an alternative to these approaches, various non-traditional offshore container port service concepts have been proposed (Kim and Morrison 2011). One such alternative solution is loading and discharging in the open sea. This type of solution is called mid-stream operation. Mid-stream operation has been in service at Hong Kong container port for many years. It uses barges with its own derrick crane (Fig. 1) to provide offshore container handling services. Mid-stream operation is reported to handle about 10% of the total container volume at Hong Kong port (HKMOA 2009). While mid-stream operation’s utility is acknowledged—especially under severe congestion, this system has been criticized for its looser safety standard and lower quality of container handling than container terminals do. Recently, a group of researchers at Korea Advanced Institute of Science and Technology (KAIST) has developed a new system, called Mobile Harbor (MH) (Suh 2008). MH resolves the weaknesses of existing mid-stream operation by deploying advanced technologies. Similar to the mid-stream operation, MH units go out to a container ship anchoring in the open sea, to (un)load containers on sea and take them to their destination.

Fig. 1

An example of Mid-stream operation (TS & LHT 2011)

A basic MH model has the maximum container carrying capacity of 250 TEU. This model, called MH-250, is shown in Fig. 2, and Table 1 lists its physical dimensions. A MH unit is a specially designed floating platform equipped with a modern container handling system, so it offers more efficient and safer services than the current mid-stream operation. Major technological developments include a crane balance technology (Jung and Kwak 2009; Kwak and Oh 2009), spreader stabilization technology (Han and Lee 2009; Kim et al. 2009), and robot arm docking system (Lee et al. 2009; Shin et al. 2009). Technical feasibility of these new technologies has been successfully demonstrated in a recent open-sea test (MHBT 2011).

Fig. 2

A 250 TEU Mobile Harbor unit (MH-250)

Table 1 Physical dimension of 250 TEU MH unit

An illustrative operational scenario of a MH is as follows:

• A container ship calls at a port, and instead of berthing at a terminal, it anchors at an anchorage, remotely located from the terminal.

• For discharging operation, an empty MH unit travels to anchorage, and docks with the container ship (port or starboard side).

• Once the docking operation is completed, the MH unit starts to unload containers from the container ship on the deck (container storage area) of the unit.

• The MH unit may move to another ship-bay, re-dock with the container ship, and continue to unload containers at the new docking position.

• It continues to unload containers until the maximum container storage capacity is reached or there is no more container to be unloaded from the container ship.

• The MH unit travels back to the terminal, docks at a berth, and unloads containers using its own container crane.

• If there are more containers to be unloaded in the container ship, it travels back to the ship to unload another round of containers.

• For loading operation, containers are loaded on to a MH unit at a berth in a terminal.

• The loaded MH travels to the container ship, establishes a docking position, and loads containers on to the container ship.

• When all loading operations are carried out, the container ship departs the anchorage and the MH unit returns to the terminal.

According to the study by Kim and Morrison (2011)—also published in this special issue—MH-based container handling system can be an economically viable solution in spite of its apparent disadvantage of double-handling. A MH-based system consists of a fleet of MH units and, possibly, some number of small berths dedicated for MH operation. Kim and Morrison (2011) investigate the economic feasibility of a MH-based system across a variety of operational environments, and conclude that a 250 TEU MH system is favorable compared to other options in a few cases. Although the MH only proves competitive for limited applications, they do not include the indirect benefits by MH’s flexibility. For example, a MH system can be used for direct ship-to-ship container transfer. In addition, MH can deliver containers to locations where container handling infrastructure does not exist. It can also offer a solution to respond to a temporary congestion at a busy port. Increasing productivity of MH operation is a key to improving its economic feasibility. As with conventional container terminals, planning and scheduling of the system’s resources is a very important problem for enhancing the system productivity.

While various off-shore container operation concepts have been suggested and may seem promising, there has been little research on scheduling of off-shore operations. Therefore, our work on the MH system operations scheduling goes beyond its direct applications to the MH system, and provides a useful understanding for operations of off-shore container port service concepts.

1.2 Literature reviews

This paper focuses on a detailed work schedule for each MH unit for a MH fleet. In this MH scheduling problem, we determine a sequence of discharging and loading tasks, their start time, and a docking position of each MH unit for the tasks. The objective of this scheduling problem is to minimize total ship staying time for a series of incoming container ships. This problem shares common features with quay crane scheduling problem, which is an important research topic in the field of maritime operations research.

In a quay crane scheduling problem, it is common to define a task as a basic unit for jobs that a quay crane has to conduct. A task is a set of loading or discharging operations for a group of containers, where this group of containers is called a cluster. A task may be simply defined for the collocated containers—that is, containers that are stacked in the same bay always belong to one task (Peterkofsky and Daganzo 1990; Liu et al. 2006). Some researchers define a task in more detail by including such attributes as destination ports, stack locations, and others (Kim and Park 2004; Moccia et al. 2006; Sammarra et al. 2007). In this case, there can be more than one task in a single bay. In this study, we follow the latter type of task definition as it offers flexibility to capture unique characteristics of MH operations. With the definition, individual quay cranes are assigned to the tasks. Various types of constraints are considered depending on the specifics of an individual problem environment. Commonly found constraints from the literature include non-preemptable task, interference between quay cranes, and precedence relationships between tasks.

A quay crane scheduling problem is often formulated based on a more general type of scheduling problems. For example, it has been modeled as a parallel uniform machine scheduling problem with precedence constraints (Kim and Park 2004). Alternatively, it can be viewed as a variant of a vehicle routing problem. Moccia et al. (2006) apply solution techniques for the precedence constrained traveling salesman problem to crane scheduling. Additional constraints such as crane interference condition can be included to modify a basic vehicle routing problem (Sammarra et al. 2007). Problem formulation and constraints expressed in these models provide useful insight for building a MH scheduling model.

One of the operational features of a MH system is that multiple number of MH units travel between the origin of a cluster and its destinations. This feature is found in a pickup-delivery vehicle routing problem with a single depot, finite number of vehicles of a limited capacity, and a number of customers. Each customer must be picked up at his origin and delivered to his destination with the goal of minimizing total travel cost. Solution methods to this problem are available in the literature. Casco et al. (1988) developed a load-based insertion procedure, where they insert pickup customers into the routes initially formed by delivery customers. This method is improved by Salhi and Nagy (1999) by allowing pickup customers to be inserted in clusters. Solutions to a vehicle routing problem can be modified to find a solution to a corresponding pickup/delivery vehicle routing problem (Nagy and Salhi 2005).

While many previous researches share some of the common features with a MH system scheduling problem, those models and solution methods are not directly transferrable to the MH scheduling problem, mainly because of the unique operational features of MH. For example, the MH problem has a concurrent operation constraint, i.e. some operations cannot be carried out simultaneously, and this constraint is coupled with a MH unit’s docking position selection. More of these unique operational features are discussed in detail in Sect. 2.2.

This article is structured as follows. In Sect. 2, we define a MH operation scheduling problem in detail, and examine the characteristics of this problem. Section 3 presents a mathematical formulation as a mixed integer programming problem. As the mathematical model becomes intractable as the size of a problem gets bigger, a rule-based algorithm and a meta-heuristic approach based on genetic algorithm are developed in Sect. 4. Computational results from the proposed methods are compared and discussed in Sect. 5. Summary and conclusions follow in Sect. 6.

2 Problem descriptions

2.1 MH operation scheduling problem

A MH system operates a multiple number of MH units as a MH fleet, to serve a series of incoming container ships. For such a system, a MH operation scheduling problem is to determine an optimal sequence of discharging and loading operations, their start time, and a docking position of each MH unit for the specific task. The objective of this scheduling problem is to minimize total ship staying time, makespan, for a series of incoming container ships.

In this study, we use the MH-250 model’s design information to determine necessary input values for the problem. The MH-250 model is designed to cover the width dimension of a (up to) 5,000 TEU container ship, as shown in Table 1. For this problem, we assume that the container ship to be handled by a MH unit is a 4,000 TEU ship. In a typical 4,000 TEU ship, the number of bays (forty-foot) is 14. Given the relative dimensions and configurations of a container ship and a MH unit, maximum of four MH units can concurrently operate on a container ship with two MH units docked at starboard and the other two at port side. The target maneuvering speed of a MH-250 unit is 8 knot, and we assume that an anchorage point for container ships is located 12 nautical miles away from a container terminal. This gives 90 min for a MH unit to make a one-way trip between a container ship and a berth at a terminal. Docking operation involves a fine maneuver for a MH unit at the proximity of a container ship and steps of mechanical operations (Lee et al. 2009; Shin et al. 2009), and it takes 30 min to complete a docking operation. The target value for on-board crane’s container handling speed is approximately 60 TEU/h.

As a pre-process to solving a MH operational scheduling problem, we first define a cluster. A cluster is a group of containers, and it is represented as a set of container slot positions (bay-row-tier) on a container ship. A cluster is a basis to define a unit task to be executed by a MH unit. There are two types of a cluster: a discharging cluster and a loading cluster. A discharging cluster is a group of inbound containers to be unloaded from a container ship, and a loading cluster is a group of outbound containers to be loaded on a ship. Given a discharging and loading stowage plan, containers are grouped into a set of clusters as follows. For discharging containers:

• A cluster consists of containers from a single ship-bay. That is, containers from two or more ship-bays are not grouped as a single cluster, even when they are adjacent bays.

• The number of containers of a cluster cannot exceed 250 TEU (a MH-250 unit’s maximum capacity).

• If there are more than 250 TEU containers in a single ship-bay, they are evenly divided into two or more clusters (e.g. 300 TEU containers are stacked in a single bay, two clusters are formed, each with 150 TEU containers). In this case, we assume that these clusters are located above and below each other, creating a precedence relationship between the two clusters.

Clusters for loading containers are grouped in the same way.

Actual operation on a cluster, discharging or loading, is referred to as a task. Due to the double-handling feature of MH, each cluster requires two tasks executed during its operational cycle. A discharging cluster is unloaded from a container ship to a MH unit, and later unloaded from the MH unit at a container terminal (MH berth). Thus, there are two tasks for a single discharging cluster: a discharging task on sea and discharging task at berth. Likewise, a loading cluster requires a loading task at berth, where a loading cluster is first loaded on to the deck of a MH, and a loading task on sea to load the cluster on to a container ship. Figure 3 illustrates the four types of tasks for a MH unit operation.

Fig. 3

The four types of tasks in the context of MH unit operation

With a set of tasks as inputs, a MH operation scheduling problem is to assign each task to a set of available MH units, determine its docking position/side and the start time for each task.

There are a few assumptions on the MH operation scheduling problem:

• Arrival time of each container ship is a constant and known beforehand.

• Processing time of a task (loading/discharging time by onboard crane of a MH unit) is proportional to the number of containers in the cluster.

• Docking time is a constant regardless of docking position.

• Travel time between a container terminal and a container ship (moored at a remote location) is a constant.

• Dual cycle operation is allowed; that is, a MH unit carries a loading cluster, loads them on to a container ship, and then works on a discharging cluster to carry them to a terminal.

• MH system’s container terminal has unlimited resources (berths, yard truck, etc.) so that it does not cause any delay.

2.2 Unique operational features of MH operation

As with quay crane operation, a few fundamental constraints exist in the MH operation schedule problem. First and obvious is that there are precedence relationships among on-sea tasks. When more than one discharging clusters exist in a single ship-bay, the task for a cluster located above must be performed before the cluster below. Likewise, for single ship-bay loading tasks, the task for clusters located below must be conducted first. In addition, if one ship-bay hosts both discharging and loading clusters, the discharging task must precede the loading task. While MH operation is in general similar to quay crane operation, there are a few unique features specific to the MH operation scheduling problem. Unlike a quay crane working at a berth, a MH unit has a limit on the number of containers to handle in a single task due to its container carrying capacity limit. The number of containers to be stacked in the deck of a MH unit cannot exceed the maximum carrying capacity for both discharging and loading operation. Another feature that needs to be reflected in the modeling is that a cluster always generates a pair of tasks, and they must be operated by an identical MH unit. These pairs of tasks have a precedence relationship: a loading task at berth must precede its pair task—loading task on sea, and vice versa for discharging tasks.

Physical configurations and dimensions of a MH unit also need to be taken into account in the modeling. MH’s on-board crane can move only within a range of the length dimension of MH unit. For MH-250 model, this length dimension is approximately 70 m, and the crane can travel for about 50 m in the aft to bow direction. This is equivalent to four 40-ft ship-bays length. The implication of this range restriction is that, once a MH unit docks at a certain position alongside a container ship, the crane’s operating range is limited to a four 40-ft bay range with respect to the docking position.¹ Thus, to conduct a task for a cluster in a bay outside of the range, a MH unit has to disengage from its current docking position, maneuver to a new docking position, and conduct another docking at the new position. Additional implication of this restriction is that, in executing an on-sea task for a cluster, there are total of eight possible docking positions, four on each side of container ship.

It is important to properly determine a docking position for a MH unit because it can affect the interference condition. Just as a quay crane requires a minimum safety distance with its neighboring quay crane working on a same container ship, MH units require a safety distance. It is assumed here that the minimum safety distance between the crane working ranges of two MH units is three 40-ft ship-bays. This applies when two MH units dock on the same side of a container ship as shown in Fig. 4a. If two MH units dock on the opposite side (Fig. 4b), the two units can dock much closer to each other—up to the point their working ranges do not overlap. Thus, two tasks located nearby—within the three 40-ft bays—may be operated simultaneously by two MH units if the units can dock at an opposite side to each other. Whether this opposite-side-docking and simultaneous execution of the two tasks indeed improves the overall productivity is determined as part of the optimization problem.

Fig. 4

The minimum safety distance for MH units (Sung et al., accepted). a Docking on the same side of a container ship. b Docking on the opposite side of a container ship

Table 2 shows an example of a MH operation schedule for illustration purpose. It shows the sequence of tasks to be performed by each MH units, the time schedule for performing each task, and the docking position for the on-sea tasks.

Table 2 An example of a MH operation schedule

3 Mathematical formulation

In this section, we present a mixed integer programming model for the MH operation scheduling problem where there are total of n clusters (n _l loading clusters and n _d discharging clusters).

This model builds upon the constraints commonly used in a quay crane scheduling problem (Kim and Park 2004; Moccia et al. 2006; Sammarra et al. 2007) and a pickup-delivery vehicle routing problem (Desrochers et al. 1988). Some of those constraints are modified and additional constraints are added to express the unique features of MH operation schedule.

The notation to be used in a mixed integer programming is followed below: Indices:

i, j :

Tasks Index, where i, j ∈ $\{ 1, \ldots ,2n\} \cup \{ 0,T\}$. Task 0 and T are dummy tasks to indicate an initial task and a final task, respectively

k :

MH unit Index, where k = 1, …, K (K is the total number of MH units in a fleet)

v :

Possible docking positions for a (on-sea) task, v = 1, …, 8

c :

Container ships Index, where c = 1, …, C (C is the number of container ships to be served)

Set of indices:

M :

The set of discharging tasks ($M = M^{ + } \cup M^{ - }$). It also consists of two subsets: a subset of discharging tasks on sea, $M^{ + } = \left\{ {j|j \in \{ 1, \ldots ,n_{d} \} } \right\}$, a subset of discharging tasks at berth, $M^{ - } = \left\{ {j|j \in \{ n + 1, \ldots ,n + n_{d} \} } \right\}$

N :

The set of loading tasks ($N = N^{ + } \cup N^{ - }$). It consists of two subsets: a subset of loading tasks at berth, $N^{ + } = \left\{ {i|i \in \{ n_{d} + 1, \ldots ,n_{d} + n_{l} \} } \right\}$, and a subset of loading tasks on sea, $N^{ - } = \left\{ {i|i \in \{ n + n_{d} + 1, \ldots ,n + n_{d} + n_{l} \} } \right\}$

A :

The set of all tasks $\left( { = N \cup M = \{ 1, \ldots 2n\} } \right)$

$\Upphi$ :

The set of task pairs that cannot be operated concurrently due to closeness of their positions. It has a pair of on-sea tasks and their docking positions as its member: $(i,v_{1} ,j,v_{2} )$

$\Upomega$ :

The set of pairs of tasks between which there is a precedence relationship. When task i must precede task j: (i, j)

$\Uppsi_{c}$ :

The set of on-sea tasks which belong to container ship c

Problem data:

q _i :

Changes in the number of containers on a MH unit after a task i is completed. If a task i is a loading-at-berth or discharging-on-sea task $\left( {i \in N^{ + } \cup M^{ + } } \right)$, q _i is a positive value. If a task j is a loading-on-sea or a discharging-at-berth task $\left( {j \in N^{ - } \cup M^{ - } } \right)$, q _i is a negative value

Q :

Maximum container carrying capacity of a MH unit (=250 TEU)

p _i :

The processing (container loading/discharging) time for task i

t _ij :

The travel time from the location of task i to task j. If task i is an on-sea task and task j is a at-berth task, or vice versa, t _ij is 120 min (90 min for one-way trip plus 30 min for docking). Otherwise, t _ij  = 0

$ts_{{iv_{1} jv_{2} }}$ :

Re-docking time between task i and task j. If a docking position v ₁ for task i is different from a docking position v ₂ for task j, $ts_{{iv_{1} jv_{2} }}$ is 30 min. Otherwise, $ts_{{iv_{1} jv_{2} }} = 0$

r _i :

The earliest possible start-time of task i. When task i is on-sea task, it is determined by arrival time of container ship. When task i is at-berth task, r _i  = 0

U :

A sufficiently large constant

Decision variables:

$X_{ij}^{k}$ :

1, if MH k performs task j immediately after completing task i;

0, otherwise

$D_{i}$ :

The completion time of task i

$Y_{c}$ :

The makespan of container ship c

$Z_{ij}$ :

1, if task j starts later than the completion time of task i; 0, otherwise

$S_{iv}$ :

1, if task i is performed at the docking position v; 0, otherwise

$Mjob_{i}$ :

The number of containers currently stacked in a MH unit immediately before task i is performed by a MH unit

The MH operation scheduling problem can be formulated as follows:

$$ {\text{Minimize}}\sum\limits_{c = 1}^{C} {Y_{c} } $$

(1)

subject to

$$ Y_{c} \ge D_{i} \quad \forall i \in \Uppsi_{c} ,\;\forall c = 1, \ldots ,C $$

(2)

$$ \sum\limits_{{j \in A \cup \left\{ T \right\}}} {X_{0j}^{k} = 1\quad \forall k = 1, \ldots ,K} $$

(3)

$$ \sum\limits_{{i \in A \cup \left\{ 0 \right\}}} {X_{iT}^{k} = 1\quad \forall k = 1, \ldots ,K} $$

(4)

$$ \sum\limits_{k = 1}^{K} {\sum\limits_{{i \in A \cup \left\{ 0 \right\}}} {X_{ij}^{k} = 1\quad \forall j \in A} } $$

(5)

$$ \sum\limits_{{j \in A \cup \{ T\} }} {X_{ij}^{k} } - \sum\limits_{{j \in A \cup \{ 0\} }} {X_{ji}^{k} = 0\quad \, \forall i \in A ,\;\forall k = 1, \ldots ,K} $$

(6)

$$ D_{i} - p_{i} \ge r_{i} \quad \forall i \in A \, $$

(7)

$$ D_{i} \le D_{j} - p_{j} \quad \forall (i,j) \in \Upomega $$

(8)

$$ D_{i} + p_{j} - D_{j} \le U*\left( {1 - Z_{ij} } \right)\quad \forall i,j \in A $$

(9)

$$ D_{j} - p_{j} - D_{i} \le U*Z_{ij} \quad \forall i,j \in A $$

(10)

$$ \sum\limits_{v = 1}^{8} {S_{iv} = 1\quad \forall i \in \left( {N^{ - } \cup M^{ + } } \right)} $$

(11)

$$ Z_{ij} + Z_{ji} - 1 \ge U*\left( {S_{{iv_{1} }} + S_{{jv_{2} }} - 2} \right)\quad \forall (i,v_{1} ,j,v_{2} ) \in \Upphi $$

(12)

$$ \sum\limits_{{j \in A \cup \{ 0\} }} {X_{ji}^{k} } - \sum\limits_{{j \in A \cup \{ T\} }} {X_{i + n,j}^{k} = 0\quad \forall i \in \left( {N^{ + } \cup M^{ + } } \right),\quad \forall k = 1, \ldots ,K} $$

(13)

$$ D_{i} + t_{i,i + n} \le D_{i + n} - p_{i + n} \quad \forall i \in \left( {N^{ + } \cup M^{ + } } \right) $$

(14)

$$ D_{i} + t_{ij} + p_{j} - D_{j} \le U*\left( {1 - X_{ij}^{k} } \right)\quad \forall i \in (A \cup \{ 0\} ),\;\forall j \in (A \cup \{ T\} ),\;\forall k = 1, \ldots ,K $$

(15)

$$ D_{i} + ts_{{iv_{1} jv_{2} }} + p_{j} - D_{j} \le U*\left( {3 - \sum\limits_{k \in K} {X_{ij}^{k} } - S_{{iv_{1} }} - S_{{jv_{2} }} } \right)\quad \forall i,j \in \left( {N^{ - } \cup M^{ + } } \right),\;\forall v_{1} ,v_{2} = 1, \ldots ,8 $$

(16)

$$ Mjob_{i} + q_{i} - Mjob_{j} \le U*\left( {1 - X_{ij}^{k} } \right)\quad \forall i \in (A \cup \{ 0\} ),\;\forall j \in (A \cup \{ T\} ),\;\forall k = 1, \ldots ,K $$

(17)

$$ 0 \le Mjob_{i} \le Q\quad \forall i \in A $$

(18)

$$ X_{ij}^{k} = X_{j - n,i + n}^{k} = X_{j - n,i}^{k} = X_{i,j - n}^{k} = 0\quad \forall i \in M^{ + } ,\;\forall j \in N^{ - } ,\;\forall k = 1, \ldots ,K $$

(19)

$$ X_{ij}^{k} = 0\,{\text{or}}\,1\quad \forall i \in (A \cup \{ 0\} ),\;\forall j \in (A \cup \{ T\} ),\;\forall k = 1, \ldots ,K $$

(20)

$$ Z_{ij} = 0\,{\text{or}}\,1\quad \forall i,j \in A $$

(21)

$$ S_{iv} = 0\,{\text{or}}\,1\quad \forall i,j \in \left( {N^{ - } \cup M^{ + } } \right),\;\forall v = 1, \ldots ,8 $$

(22)

$$ Y_{c} ,D_{i} \ge 0\quad \forall c = 1, \ldots ,C,\;\forall i \in A $$

(23)

The objective function (1) minimizes the sum of the makespans for each container ship. Constraint (2) defines the final completion time to be the completion time of the last on-sea task. Constraints (3) and (4) set the first and last task of each MH. Task 0 and T are dummy tasks which represent the initial state and final state, respectively. Constraint (5) guarantees that each task is performed by exactly one MH unit. Constraint (6) is a flow balance constraint that ensures the continuity of a task sequence assigned to a MH unit. Constraint (7) ensures that each task cannot be started before its earliest available time. Constraint (8) states that task j should not start before the completion of task i if $(i,j) \in \Upomega$. Constraints (9) and (10) define Z _ij such that Z _ij  = 1 when the operation for task j starts after the operation for task i is completed; Z _ij  = 0, otherwise. If Z _ij  + Z _ji  = 0, it means that task i and task j can be performed simultaneously. If Z _ij  + Z _ji  = 1, it means that either task i or task j gets started first and the other waits until the preceding task is completed. Z _ij  + Z _ji cannot be 2 by definition of Z _ij . Constraint (11) ensures that all on-sea tasks are assigned one of the docking positions. Constraint (12) prevents interference between MH units. If task i, performed at docking position v ₁, and task j, at docking position v ₂, cannot be operated simultaneously, it makes Z _ij  + Z _ji  ≥ 1. Constraint (13) ensures that two tasks representing the pickup and delivery request of the same cluster must be assigned to the same MH unit. Constraint (14) represents the precedence relationship between pickup and delivery points. Constraints (15) and (16) determine the completion time for each task and eliminate sub-tours. Constraint (15) determines the task completion time including the docking time and the travel time between a container terminal and container ship. Constraint (16) supplements constraint (15), and calculates the completion time when re-docking occurs. Constraints (17) and (18) guarantee that the number of containers stacked in a MH unit does not exceed MH’s maximum container carrying capacity. Constraint (19) requires that, if a MH deck is holding containers that need to be unloaded at the current position (e.g. loading-on-sea task), these containers must be unloaded from the MH first before other containers can be loaded on to the MH. This is to ensure there is no need for a remarshaling operation on a MH unit.

It is well known that both a parallel uniform machine problem with precedence constraints and a vehicle routing problem with pickups and deliveries are NP-hard problem. It is also known that a quay crane scheduling problem is an NP-hard problem. Since this MH operation scheduling problem possesses their characteristics as well as its own additional complicating features, this problem is also deemed as an NP-hard problem, albeit we do not provide a formal proof in this work.

4 Proposed algorithm

Since solving the mixed integer programming model requires a considerable amount of computation time, it is practically infeasible to solve a problem with a reasonably large number of clusters. Thus, it is necessary to develop a heuristic algorithm to obtain a near-optimal solution within a reasonable amount of computation time. At first, a rule-based algorithm is developed. Then, a meta-heuristic method based on genetic algorithm is developed as an alternative.

4.1 A rule-based algorithm

A rule-based algorithm proposed in this section uses a relatively simple set of rules with a goal of obtaining a reasonable MH operation schedule in a short computation time. This algorithm consists of six steps, from forming a group of on-sea tasks to computing the objective value. Basic idea of each step is briefly discussed below, and the details of this algorithm procedure can be found in “Appendix”.

Step 1. Form task groups out of all on-sea tasks

The first step is to form task groups out of all on-sea tasks. A task group here refers to a set of tasks that will be carried out by a MH unit at a single docking position. On-sea tasks located within a neighboring four 40 ft-bay range can be handled by a MH unit at a single docking position. As such, it may be advantageous to group them as one task group, as it will possibly reduce the number of re-docking operation.

To form task groups, we first generate a randomly ordered sequence of all “on-sea tasks”. Starting from the very first task, say task 1, in the sequence, we examine the second task, task 2, to see if the two tasks can be grouped together. Conditions (a)–(e) are checked in this step. If the conditions are satisfied, move on to task 3 to see if it satisfies the conditions. If task 3 does not satisfy any of the five conditions, the first task group is determined as task 1 and task 2. Then, starting from task 3, the above procedure is repeated. This process continues until all on-sea tasks belong to a task group.

• (a) Only tasks within four 40 ft-bay apart can be included in a same group.

• (b) Number of containers in a task group cannot exceed a MH unit’s maximum capacity.

• (c) Tasks included in a same task group do not violate any precedence relationship between them.

• (d) No remarshaling operation is required (recall the explanation on constraint (19) in Sect. 3).

• (e) A random number generated between (0,1) is greater than 0.3.

Step 2. Determine a docking position for each task group

The second step is to determine a docking position for each task group. Recall that a docking position is defined as a ship-bay number at which the first MH deck-bay will be aligned to when a MH unit docks. For a task group whose target clusters are confined to one bay, say kth bay, there are four docking positions—k-3, k-2, k-1 and k—at which a MH unit can execute the task. Likewise, for a task group with its target clusters spread through two consecutive bays, three docking positions are feasible. If target clusters are distributed over three consecutive bays, two docking positions are possible, and for four consecutive bays, there is only one docking position for the task group. In determining a docking position for each task group, we would want to minimize the number of conflicts—a conflict being an overlap between two MH units’ length range. To achieve this, a docking position for each task group is determined as follows:

• (a) For each of the possible docking positions, count the number of clusters contained in the corresponding four-bay range, and choose a docking position with the least number of such clusters.

• (b) If there is a tie for more than two docking positions, count the additional number of clusters in a six-bay range (extended by one bay in both direction from the four-bay range), and choose the one with a smaller count.

The counting scheme is based on a simple rationale. If there exists a cluster from other task group in the working range by a docking position, it necessarily means there is a conflict between the two task groups. Higher number of such clusters implies a longer duration for the conflict. Thus, we count the number of clusters from other tasks in the range, and select the position that has the minimum number of such clusters. This scheme does not give an optimal set of docking positions (that minimize the number of conflict). But, for the sake of simplicity for the rule-based approach, we use this method as an alternative.

Step 3. Assign task groups to MH units

Now that task groups and their docking positions have been determined, each task group is assigned to a MH unit. As there are typically more task groups to be handled than the number of MH units in a fleet, one MH unit will be assigned multiple task groups. As with the first step, this step starts with randomly ordering task groups to generate an arbitrary sequence. Given a sequence, each group is assigned to a MH unit starting from the first group in the sequence. A basic idea behind determining which MH unit takes on a task group is that a task group is assigned to a MH unit that allows the earliest starting time for the first task in the task group. This starting time depends on quite a few factors, and Table 3 summarizes how the starting time is computed.

Table 3 Table for determining the earliest starting time of task group

In addition to the earliest starting time, precedence conditions between the groups are checked to ensure that the task groups are ordered properly.

Step 4. Insert at-berth tasks into the groups

Up to Step 3, at-berth tasks have not been explicitly considered in constructing an operations sequence for task groups. In this step, these at-berth tasks are inserted to an appropriate on-sea task group. Two conditions are considered in this process: (1) on-sea discharging tasks or at-berth loading tasks—in which MH unit is being loaded—are scheduled consecutively as long as a MH unit has sufficient space to store them all, (2) no remarshaling is allowed on a MH unit.

Step 5. Determine a completion time of each task

In the fifth step, a true completion time for the above-obtained sequence of all tasks is computed. In this process, a docking side for a docking position needs to be determined. As mentioned in Sect. 2.2, whether two tasks can be executed concurrently by two MH units is affected by docking side selection, and this in turn affects the task completion time. In this sense, the completion time estimated by step 4 is a lower bound for a true completion time. Starting from the very first task in the sequence obtained from the fourth step, the earliest possible starting time is assigned to the task. For this first task, docking side is determined arbitrarily as there is no restriction. For the second task and on, the true earliest possible starting time may depend on whether concurrent operations by two MH units are allowed or not. Thus, a docking side is chosen such that a task can begin at the earliest possible time.

Step 6. Calculate the objective value and update the best schedule

With a complete sequence of tasks and MH assignment determined, the objective value, sum of makespans of all container ships, is computed for the schedule. Since this rule-based algorithm has some random factors, we repeat steps 1–6 to generate 10,000 schedules for a given set of tasks. Through the replication, the best schedule is updated as a better schedule is generated.

4.2 A random key based genetic algorithm

As an alternative to the rule-based algorithm, a meta-heuristic method using random key based genetic algorithm (rkGA) is developed. rkGA, first introduced by Bean (1994), uses indirect representation of permutations. A random key representation encodes a solution with random numbers, and these numbers are later used as a sorting key to decode a solution. The advantage of this algorithm is that no infeasible offspring is produced even with the traditional crossover operators. This advantage makes rkGA an attractive meta-heuristic method for various scheduling problems. (Goncalves et al. 2005; Bean 1994; Norman and Bean 1999; Okada et al. 2010; Xu and Bean 2007).

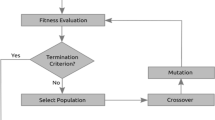
The overall procedure of rkGA for the MH operation scheduling problem is represented in Fig. 5. P(t _gen ) and C(t _gen ) are parents and offspring respectively, at the current generation, t _gen . The procedure starts with constructing initial population by using a random key based encoding routine. A decoding routine, then, evaluates each member in the initial population. In the subsequent steps, elitist reproduction, crossover, post tournament selection and immigration are sequentially carried out until a termination condition is met.

Fig. 5

The overall procedure of random key based genetic algorithm

4.2.1 Random key based encoding process

The genetic representation (s, b) of a solution is composed of two parts of chromosomes, as shown in Fig. 6. The first part of chromosome, s, shows the sequence of each task along with an index number of MH units to take the task. The second part of chromosome, b, represents a docking position for each task. Recall that one cluster requires two tasks, one on sea and the other at berth. Thus, when there are n clusters, both parts of chromosomes have 2n genes, where each gene represents a task. The first n genes represent the information for the on-sea tasks, and the second n genes represent the information for at-berth tasks. Task j and task j + n are the two tasks associated with one cluster—one at berth and the other on sea.

Fig. 6

The genetic representation of an individual solution

Each gene in a task sequence chromosome, s(i), is given a real number. Integer part of this number is interpreted as the index number for a MH unit the task is assigned to. The integer part is randomly generated from {1,…,K}, where K is the total number of MH units. It should be noted that s(j) and s(j + n) must have the same integer value, which indicates that a pair of tasks associated with an identical cluster should be assigned to the same MH unit. Decimal part of s(i) is used as a sorting key when the sequencing and time schedule of each task is determined. It is generated randomly from a uniform distribution, uniform(0, 1).

Recall that in performing an on-sea task, a MH unit can dock at one of the four candidate docking positions (this is not considering its docking side). A docking position chromosome, b(i), contains docking position information. Entries to the chromosome, b(i) is generated randomly from {1, 2, 3, 4} to indicate the four candidate docking position, 1 being the leftmost position. Since at-berth tasks do not need a docking position, this part of the chromosome, b(n + 1) to b(2n), is set to 0.

Later in the experiments, we use the rule-based algorithm to generate a subset of an initial population. The use of the rule-based algorithm for generating initial population aims to improving the quality of an initial population.

4.2.2 Random key based decoding process

To decode a solution from a chromosome, we first extract the integer part from a task sequence chromosome, s(i), to group tasks by each MH unit. Integer part of s(i) represents the index number of MH that will perform task i. A group of tasks that have the same integer value are then assigned to the MH whose index number is the integer value from s(i).

Next, for the tasks in a group, decimal part of s(i) determines a sequence of the tasks. A lower decimal value means the higher priority, and thus earlier position in the sequence. A task may lose its priority to a task with the next-highest priority if:

• (a) A precedence relationship requires other task be executed ahead of it.

• (b) Adding the task results in the number of containers on the MH unit greater than its maximum carrying capacity.

• (c) Adding the task causes remarshaling operation on the MH unit.

If a task loses its priority, then a task with the next highest priority takes the position in the sequence. Figure 7 illustrates a simple example of this procedure.

Fig. 7

An example of random key based decoding routine

Note that a task sequence determined in the above step is within the group of tasks by each MH unit, and we need to determine the complete sequence across all MH task groups. As with the sequencing within a MH task group, a decimal part of s(i) is used to provide a default sequence for all tasks. For this cross-group task sequencing, there is only one condition by which a task loses its default priority: a precedence relationship for the current task requires other task (from other MH task group) be executed ahead of it. Now that a complete sequence for entire set of tasks is determined, the final task completion time can be computed. Here, a key consideration is a possibility for concurrent execution of on-sea tasks by multiple MH units. Whether concurrent execution is allowed or not depends on the choice of a docking side for the tasks in question. Determining a docking side and computing task completion times can be done in the same way as the fifth step of the rule-based algorithm (see Sect. 4.1).

Once all tasks are scheduled, sum of the completion times of the last on-sea task for each container ship. The result is then used as a fitness value for this solution.

4.2.3 Generation of next population

Four strategies are applied to construct a new population for a next generation: elitist reproduction, uniform crossover, post tournament selection and immigration.

First, the top 15% of the current population is passed down to the next generation. This procedure is called elitist reproduction, which is to copy the best individual chromosome from one generation to the next (Goldberg 1989). The advantage of the elitist strategy is that the best solution is monotonically improving from one generation to the next.

Next step is to apply a crossover operator. To do this, two chromosomes are randomly selected from the current population as parents. Then, for a task sequence chromosome, s(i), a parameterized uniform crossover (Spears and DeJong 1991) is applied. For each gene of s(i), we toss a biased coin to select which parent will contribute the allele (mid-left of Fig. 8). Amount of this bias indicates the degree of change for the chromosomes. Preliminary experiments show that bias probability of 0.7 works well for our scheduling problem. Note that, in this crossover operation, we still keep the integer value of s(i + n) to be the same integer value of s(i). For a docking position chromosome, b(i), one point crossover is employed, as shown on the mid-right of Fig. 8.

Fig. 8

Crossover operator (parameterized uniform crossover + one-point crossover)

Once two offspring chromosomes are generated as a result of the crossover operation, a post-tournament selection (Norman and Bean 1999) is applied. The two offspring chromosomes are evaluated, and the one with a better objective value enters the next generation. The other offspring is discarded. This process is repeated until the rest of the population (85%) is filled up.

The final step is to replace some percentage of the chromosomes with a low fitness value with randomly generated chromosomes. This is the concept of immigration (Bean 1994). An immigration operation is better than a traditional mutation operation in terms of preventing premature population convergence due to the elitist reproduction. From preliminary experiments, it is found that replacing the bottom 3% yields good results.

5 Computational results

To evaluate the performance of the proposed methods for the MH operation scheduling problem, we conduct a number of computational experiments using various problem instances. For small sized problems where the exact solution is available from solving MIP problem, we compare results from the rule-based algorithm and rkGA to the exact solution. For larger-sized problems, we develop a heuristic to estimate a lower bound for the problem, and use the results to evaluate the performance of the rule-based algorithm and the rkGA-based method.

The mixed integer programming is coded in CPLEX 11.0. The rule-based algorithm and rkGA are coded in C#. We run on a desktop computer with Core 2 Quad 2.40 GHz CPU and 3.00 GB RAM. The rkGA uses four parameters: the ratio of elitist reproduction, the ratio of immigration, the population size, and the number of generation. The ratio of elitist reproduction and immigration are set to 15 and 3% respectively. Population size is 100, and the number of generations is 1,000. For initial population of the rkGA method, about 10% of the initial population is generated from the solutions by the rule-based algorithm. The other 90% of the initial population are randomly generated.

5.1 Computational results for small sized problem instances

For a relatively small-sized problem instances, we conduct comparison between the solutions from the mixed integer programming, rule-based algorithm, and the rkGA. As test cases, we consider two factors to generate problem instances: the number of clusters and distribution of clusters across ship-bays. The number of clusters determines the size of the scheduling problem, and we use four levels for the cluster size: 4, 5, 6, and 7 clusters. The spread of clusters across ship-bays is also likely to affect the difficulty of obtaining a scheduling solution. For this, we use two levels: clusters are concentrated at certain ship-bays (C), and uniformly distributed across ship-bays (U). In addition, to account for other factors such as variance of the number of containers across clusters, four different stowage plans–a, b, c, d–are used for each {number of clusters–spread type} combination. Finally, the number of MH units is varied from 1 to 4 units. So there are total of 128 problem instances.

As shown in Table 4, the mixed integer programming is solved to provide the optimal solution for 107 tested problem instances, and for the remaining 21 instances, a lower and upper bound at the program termination is reported. With the rkGA, it turns out that the method finds the optimal solution for the 107 instances. For the 21 cases, where a lower and upper bound are given, the objective value found by rkGA lies inside the lower and upper bound. Thus, it seems that rkGA performs very well in terms of its solution quality for small sized problem instances. The rule based algorithm also finds the optimal solution for majority of the problem instances, but it does not find the optimal solution in 19 cases. For the 21 lower- and upper-bound ranges, two cases lie outside the bounds.

Table 4 Comparison between mixed integer programming, rule-based algorithm, and the rkGA for a relatively small-sized problem instances

As expected, the computation time of the mixed integer programming tends to increase as the size of a problem. The computation time of rkGA also increases, but not as significantly as the MIP case. It does not change much for the rule-based algorithm.

5.2 Computational results for large sized problem instances

For the problem instances with more than eight clusters, it turns out that a mixed integer programming problem cannot be solved with the solver and a meaningful lower and upper bound is not obtainable.

In order to evaluate the quality of the solutions of the proposed algorithms for these problems, a heuristic method is developed to estimate a lower bound as a reference for comparison. As developing a tight lower bound for general cases turns out to be difficult, we design 1-container ship problem instances where we can derive a reasonable lower bound by introducing a set of relaxing assumptions:

• There is no interference between any set of on-sea tasks, and thus multiple units of MH can carry out on-sea tasks concurrently.

• Time for re-docking operation is ignored.

With the above assumptions, we decompose a lower bound into two components: container handling time and traveling time. Suppose there are L [TEU] containers to be loaded, and D [TEU] containers to be discharged. The number of MH units is K. For the container handling time component, the best way to utilize K MH units is to evenly distribute the workload across them. So, each MH unit has to load $\left\lceil {L/K} \right\rceil = w_{L}$ containers and discharge $\left\lceil {L/K} \right\rceil = w_{D}$ containers, respectively. $\left\lceil r \right\rceil$ denotes a function to return the minimum integer that is greater or equal to r. Since a container, either loading or discharging, involves two handling steps—one at berth and the other on sea, total container handling time for this MH unit is 2·w _L ·t _C  + 2·w _D ·t _C , where t _C is a container handling time per TEU. Note that a container ship can depart once the last on-sea discharging task is complete. Thus, we need to deduct one at-berth discharging task time from the above container handling time. For this, we assume the last discharging task has 250 TEU containers (maximum carrying capacity, Q), and so this amount of container handling time is subtracted to give the following lower bound for the container handling time component:

$$ 2 \cdot w_{L} \cdot t_{C} + 2 \cdot w_{D} \cdot t_{C} - Q \cdot t_{C} $$

(24)

For the traveling time components, we estimate a lower bound by counting the minimum number, H, of one-way trips required to complete all tasks. When L loading containers and D discharging containers are ideally clustered, we have $\left\lceil {L/Q} \right\rceil = N_{L}$ loading clusters and $\left\lceil {D/Q} \right\rceil = N_{D}$ unloading clusters. Each cluster requires one round trip. Note that by the dual cycle operation assumption, a pair of loading-discharging cluster can be handled in one round trip. There are Min(N _L , N _D ) loading-discharging cluster pairs, and the rest are either loading-only or discharging-only clusters. Total number of round trips to handle all clusters is Max(N _L , N _D ), say R. Number of one-way trips is 2R. Recall that a container ship can depart as soon as the last on-sea task is complete. Thus, some of the 2R one-way trips do not contribute to the container ship staying time, and are irrelevant. We determine the number of such one-way trips by assigning K MH units to R round trips. Let us take an example of R = 5 and K = 2. The two MH units, MH_A and MH_B, will make their first round trip. In the next round, MH_A and MH_B make another round trip. By then, four out of five (R = 5) round trips have been completed. For the last round trip, only MH_A will need to make a trip. In the second round trip, MH_B’s return trip is irrelevant. Likewise, the return trip for MH_A is irrelevant as well. Therefore, the minimum number of one-way trips, H, is 10 − 2 = 8. This procedure can be expressed by the following equation:

$$ H = \left\{ {\begin{array}{*{20}c} {2 \cdot K \cdot \left( {\left\lfloor {R/K} \right\rfloor - 1} \right) + K + 2 \cdot \bmod (R,K) = 2R - K,} \hfill & {K \le R,} \hfill \\ R, \hfill & { \, K > R} \hfill \\ \end{array} } \right. $$

(25)

Thus, total minimum time for traveling component is H·t _tr , where t _tr is a one-way travel time for a MH unit. Then, a lower bound for the traveling time component is obtained by simply dividing this total time by the number of MH units: (H·t _tr )/K.

The overall lower bound value is the sum of the two components, container handling time component and traveling time component, and it is

$$ \{ 2 \cdot w_{L} \cdot t_{C} + 2 \cdot w_{D} \cdot t_{C} - Q \cdot t_{C} \} + \{ (H \cdot t_{tr} )/K\} $$

(26)

54 problem instances in total are tested. We use three levels for the cluster size: 12, 15 and 18 clusters. Also, six different stowage plans are used for each level of cluster size. These stowage plans are randomly generated. Finally, the number of MH units is varied from 1 to 3 units.

Table 5 shows that the average gap between the lower bound and the rkGA solution is 11.3%. Out of 54 tested instances, rkGA produces a solution within 10% of the lower bound value in 26 cases. For the rule-based algorithm, the average gap is 14.1%, and there are 18 within-10% cases. Thus, for this limited set of test cases, we see that the rkGA produces a reasonably good solution compared to the lower bound, and generates better quality solutions than the rule-based algorithm.

Table 5 Comparison between lower bound, rule-based algorithm, and rkGA for a relatively larger sized problem instances

6 Conclusions

Mobile Harbor is a specially designed floating platform equipped with a modern container handling system that can load/discharge containers to/from an anchored container ship in the open sea. With its unique operational features, a MH system introduces novel scheduling issues. A MH unit has a limited capacity, and tasks may have conflicts with each other depending on its docking position.

A mixed integer programming model for this scheduling problem is presented. The mathematical formulation builds upon a quay crane scheduling problem and vehicle routing problem with pickups and deliveries. As this problem is only solvable for very small-sized problem instances and quickly becomes intractable, two alternative solution methods have been proposed: a rule-based algorithm and a random key based genetic algorithm (rkGA). A rule-based algorithm is based on the rational that reducing the number of re-docking operations and possibility for inter-MH interference would result in a reasonably good schedule. rkGA uses a random key concept to represent an order schedule, and it offers a convenience in handling an order-based scheduling problem.

For small-sized problem instances where the exact optimal solution or reasonable bound information is available from the mixed integer problem, rkGA is shown to be able to produce the optimal solution or a solution within the bounds. The rule-based algorithm finds optimal solutions and solutions within the bounds for majority of cases, but there are 21 cases out of 128 test problems that the method does not perform well.

For large-sized problem instances, we calculate an approximate lower bound for a comparison purpose. The method we develop to compute a lower bound cannot be applied for a general case, but in a single container ship case, it provides a reasonable lower bound. Experimental results show that the proposed rkGA works reasonably well, with about 11% gap from the lower bound. The rule-based algorithm’s performance is worse than the rkGA, showing about 14% gap. Overall, quality of the solutions obtained from the rkGA based method is better than the rule-based algorithm.

Computation time for the rkGA based method is in the order of tens of seconds for small-sized problems and hundreds of seconds for large-sized problems (one container ship cases). On the other hand, the computation time for the rule-based algorithm is roughly an order of magnitude smaller than the rkGA method. Though not presented here, we have tested the rkGA method to solve for more than one container ship cases, and the computation time dramatically increases as high as over an hour (~3,900 s for two container ships each with 16 clusters). With the rule-based algorithm, it is in the order of a minute. Whether 10 min to 1 h of extra time to compute a near optimal schedule is acceptable or not depends on a practical operational environment of MH-based system. If a quick response is required, the rule-based algorithm will be appropriate, and if a better solution is desired and 10–15 min response time is tolerable, the rkGA method is recommended.

There are a few areas that future study may further investigate. First, computing more reliable lower bound from the exact algorithm such as branch and bound will be desirable. Also, more realistic and dynamic operational environments, such as dynamic arrival time of container ships and a hatch cover constraint, can be incorporated in the modeling and solution procedure.

Appendix: Detail explanation of rule-based algorithm

1.1 Form task groups out of all on-sea tasks

1.2 Determine a docking position for each task group

1.3 Assign task groups to MH units

1.4 Insert at-berth tasks into the groups

See Fig. 9.

Fig. 9

Explanation of variable pl and pd for STEP 4 in rule-based algorithm

1.5 Determine a completion time of each task