1 Introduction

As the economy has been on the ever-fast moving track, flexibility is more critical for a supply chain to survive in this complex business environment. Thus, more information is required to be on the enterprises’ discretion to tackle the increasing uncertainty and complexity, such as strengthened competition and resource constraints. Information sharing has been proved to be such an effective strategy to enhance the flow of information along the supply chain; however, the research on the strategy considering this complicated setting has been limited. Therefore, this research attempts to fill this gap by studying information sharing in a capacitated supply chain with downstream competition.

Flexible capabilities have been gradually considered to be a source of coping with uncertainties and creating sustainable competitive advantages by bringing enterprises more agility, adaptability, and alignment (Lee 2004). To establish the flexibility, enterprises in a supply chain need to constantly communicate such information as supply and demand with their partners, so that all parties could make prompt collaborative responses to any noteworthy change in the business environment. Therefore, information sharing becomes an essential strategy for enterprises to achieve flexibility. It is widely known that Wal-Mart and Proctor & Gamble (P&G) share information regarding the retail sales of P&G products at Wal-Mart stores to achieve flexible synergy. Furthermore, companies such as Dell and Cisco share information with their suppliers and customers, so that they can adjust their strategies in time to closely match supply with demand and to anticipate variation in the marketplace.

Information sharing can bring more flexibility to the enterprises that suffer from resource constraints such as capacity constraint. When a manufacturer has a limited capacity, it can utilize the shared information to delay production or to produce a larger quantity in a given period (Gavirneni et al. 1999). The benefits of information sharing increase as the capacity shrinks. In the presence of insufficient capacity, the manufacturer has the motivation to acquire the information from the downstream to make such a critical decision as the wholesale price, for it in general depends on the quantity of products actually sold (Gavirneni 2001). Meanwhile, when the downstream consists of multiple competitors, the allocation of products shows its importance in such a situation. Thus the downstream enterprises may be willing to share its owned demand information in exchange for more products.

Although it can offer the downstream enterprises advantages to share information when the capacity constraint exists, those enterprises are also exposed to risks. Information leakage is such an adverse effect. In such a pyramid structure of a supply chain with an upstream monopoly and multiple downstream informative competitors, the information holders have the possibility of deducing the private information of the information disclosers, thus taking the strategies unfavorable for the latter (Li 2002). However, little research has focused on the tradeoff between the information leakage and the supply priority, and the properties of information sharing in such a business environment are still unknown. Therefore, the objective of this research is to investigate the performance of information sharing and its effects on related parties in a competitive supply chain with a capacity constraint.

The rest of the paper is organized as follows. Section 2 reviews the related prior research. Section 3 describes the research model. Section 4 solves the model and analyzes the equilibrium outcomes. Section 5 conducts a welfare analysis. Section 6 shows several numerical examples to illustrate the analytical results. Concluding remarks and directions for future research are made in Section 7.

2 Literature review

It is well-known that the “Bullwhip effect” is an inevitable phenomenon in a supply chain. The information transferred from the downstream of a supply chain to the upstream is distorted so much that it leads to tremendous efficiency loss: sales forecast deviation, excessive inventory, misguided capacity plans, poor customer service, etc. (Lee et al. 1997). In order to reduce those losses, many researchers devote themselves to investigating how to relieve the information distortion. They have found information sharing to be a useful way to achieve this objective. A series of studies prove that the information sharing is a valuable means to coordinate the supply chain with one supplier and one retailer (Bourland et al. 1996; Chen 1998; Hariharan and Zipkin 1995). In addition, prior research also theoretically and empirically proves that information sharing between one supplier and multiple independent retailers is beneficial to the supply chain (Aviv and Federgruen 1998; Cachon and Fisher 2000; Moinzadeh 2002). However, those positive effects of information sharing are obtained in the absence of horizontal competition. Lee and Whang (2000) conduct an extensive investigation into a variety of shared information in industrial examples, and doubt the feasibility of information sharing in a competitive environment.

Li (2002) is the first to explicitly incorporate the horizontal competition into the study of information sharing. By focusing on a two-echelon supply chain in which n retailers engage in a Cournot competition and a monopolistic manufacturer supplies one type of product, he analyzes the incentives for retailers to share demand information vertically. His study concludes that information sharing can only hurt retailers’ interests, and thus the retailers are discouraged from sharing their demand information with the manufacturer. Zhang (2002) extends Li (2002)’s model by considering both Cournot and Bertrand duopolistic retailers who sell substitutable or complementary goods. He also shows that the consequence of demand information sharing is always negative to the retailers. Following this lead, Li and Zhang (2008) consider the confidential information sharing, i.e., the shared demand information is only disclosure to the designated parties. They show that the information sharing can neither be realized on a voluntary basis when the competition among the retailers is low.

However, the aforementioned studies assume that the manufacturer has an infinite capacity, and thus, leave out some important cases in which the limit of the manufacturer’s capacity takes effect. For example, the demand during the Christmas season typically exceeds the available manufacturing capacity (Agrawal et al. 2002). The sale of fashionable goods such as best-selling books or stylish apparel may also experience the temporary lack of the manufacturing capacity (Donohue 2002; Fisher et al. 1994). Some research studies the value of information sharing in a supply chain composed of a capacitated supplier and a retailer. This stream of research shows that the high capacity offers the supplier flexibility in using the shared information to make the production decision, which reduces the supplier’s cost (Gavirneni et al. 1999; Simchi-Levi and Zhao 2003, 2004). All of them study the value of information sharing in a two-stage supply chain with a single manufacturer and a single retailer, however, little research incorporates the production capacity constraint into studying the information sharing between one manufacturer and multiple competitive retailers. In this situation, retailers can only receive an allocated quantity of the product when the manufacturer’s capacity is not sufficient, and the allocation strategy can thus be an incentive for retailers to voluntarily share information with the manufacturer.

Several papers have studied allocation strategies. Aviv and Federgruen (1998) propose an allocation mechanism based on the expected sales of the retailers in a supply chain consisting of a supplier and several independent retailers. In a similar setting, Cachon and Fisher (2000) consider a batch priority policy under which all the retailers’ batches ordered are ranked such that the retailer ordering the largest batches will get the highest priority in obtaining products, when the supplier’s capacity is insufficient. However, they only consider the allocation schemes when no information sharing is conducted, while do not think about the possible role of the allocation strategy in promoting information sharing.

Based on the above consideration, the research on information sharing in a competitive and capacitated supply chain is still lacking. Therefore in this paper, we would like to investigate whether the exchange of demand information can be voluntarily realized between a monopolistic manufacturer that has a capacity constraint and multiple Cournot retailers. The manufacturer sets a discriminated allocation strategy which will be applied if the retailers’ total orders exceed the manufacturer’s capacity. We prove that both the manufacturer and the retailers can be better off from information sharing when the discriminated allocation parameter satisfies a certain condition. And we also show that social welfare and consumer surplus will be locked by the manufacturer’s capacity.

3 The model

We consider a two-echelon supply chain with one upstream firm, a manufacturer (referred to as “she”), and n downstream firms, retailers (a retailer is referred to as “he”). Denote the manufacturer by M and her production capacity by Q 0. Let \( N \equiv \,\left\{ {1,\,2,\, \ldots ,n} \right\} \) be the set of retailers. The retailers are engaged in a Cournot competition by selling an identical product at a constant marginal cost. Without any loss of generality, we assume each retailer’s marginal cost to be zero. Let q i be the order of retailer i, \( i \in \,N, \) and \( D \equiv \,\sum\nolimits_{i \in N} {q_{i} } \) be the total order. The inverse demand function in the downstream market is given by

$$ p = a + \theta - Q, $$

where Q = min (D, Q 0) denotes the total sales, i.e., the demand that the manufacturer actually satisfies, and p is the prevailing price in the downstream market. The potential size of the downstream market is a + θ where a is a constant and θ is a random variable with mean zero and variance σ 2, capturing the demand uncertainty.

Before making the quantity decision, each retailer i observes a signal Y i about θ, which is not observable to the manufacturer. Note that the manufacturer will set a wholesale price as \( w\, = \,\frac{a}{2} \) if none of the retailers decide to disclose their information Y i to the manufacturer (Li 2002). To avoid trivial problems, we assume (A0): \( Q_{0} \, \le \,\frac{a}{2}, \) which guarantees that the retailers’ expected marginal profit is not less than zero (i.e., \( E\left( {(p - w) \ge 0} \right), \) that is, the retailers are profitable in this setting.

Furthermore, to facilitate analysis, we adopt the same assumptions about the information structure as those in Li (2002):

  • (A1) The joint probability distribution of \( \left( {\theta ,Y_{i} , \ldots ,Y_{n} } \right) \) is common knowledge and each Y i is an unbiased estimator of θ, i.e., \( E\left[ {Y_{i} \left| \theta \right.} \right] = \theta , \) for all \( i \in N. \)

  • (A2) \( E\left[ {\theta \left| {Y_{i} , \ldots ,Y_{n} } \right.} \right] = \alpha_{0} + \sum\nolimits_{i \in N} {\alpha_{i} Y_{i} ,} \) where α 0 and α i ’s are constants.

  • (A3) \( Y_{i} , \ldots ,Y_{n} \) are identically distributed and independent, conditional on θ.

By Lemma 1 of Li (1985), the assumptions (A1)–(A3) imply that, for any given set \( K \subseteq N, \) \( \left| K \right| = k, \) and any \( i \in N\backslash K, \)

$$ E\left[ {\left. \theta \right|Y_{j} ,j \in K} \right] = E\left[ {Y_{i} \left| {Y_{j} } \right.,j \in K} \right] = \frac{1}{k + s}\sum\limits_{j \in K} {Y_{j} ,} $$

where \( s \equiv \frac{{E\left[ {{\text{Var}}\left[ {Y_{i} \left| \theta \right.} \right]} \right]}}{{{\text{Var}}\left[ \theta \right]}}. \)

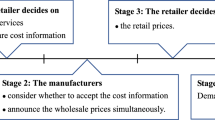
The manufacturer and the retailers play a three-stage Stackelberg game. At the first stage before learning his private signal, each retailer decides whether to disclose his demand information to the manufacturer and the manufacturer decides whether to accept the information simultaneously. Let \( K \equiv \left\{ {1,2, \ldots ,k} \right\}\left( {K \subseteq N} \right) \) be the set of retailers who decide to disclose their information Y j to the manufacturer. If retailer j decides to disclose his demand information Y j to the manufacturer and the manufacturer decides to accept it, then an information sharing agreement (for Y j ) is reached. If either firm decides to do otherwise, the agreement becomes null and void. Similar to Li (2002), we also assume that if both sides decide to share information, then information transmission will be truthful.

At the second stage, if an information sharing agreement is reached, the manufacturer M will make the wholesale price decision based on \( (Y_{j} )_{j \in K} . \) If not, she will set the wholesale price w with her ex ante information about θ. At the third stage, the retailer i decides his order quantity q i based on his private information Y i and the wholesale price w. The manufacturer then produces Q = min (D, Q 0) subsequently.

After that, she uses a simple “discriminated allocation” strategy to distribute the products. Let S i be the product quantity that retailer i receives from the manufacturer, and then the allocation strategy is defined as follows:

$$ S_{i} = \left\{ {\begin{array}{*{20}l} {q_{i} ,} & {D \le Q_{0} } \\ {\alpha Q_{0} ,} & {i \in N\backslash K,D > Q_{0} ,} \\ {\left( {\alpha + \beta } \right)Q_{0},} & {i \in K,D > Q_{0} } \\ \end{array} } \right. $$
(1)

where \( \beta \in (0,\frac{1}{n}] \) is the allocation parameter set by the manufacturer, and α is generated in (1) by \( \alpha = \frac{1 - k\beta }{n}. \)

In terms of the allocation strategy, when the retailers’ total order quantity D is less than the manufacturer’s capacity Q 0, each retailer will receive the quantity of the products equivalent to his placed order; however, when the total order quantity exceeds the manufacturer’s capacity, each information discloser will receive \( (\alpha + \beta )Q_{0} , \) which is not less than \( \frac{{Q_{0} }}{n}, \) while an information hider will only receive \( \alpha Q_{0} , \) which is not more than \( \frac{{Q_{0} }}{n} \). It is possible that retailer i who discloses his information Y i and sets an initial order \( q_{i} \left( {q_{i} < \frac{{Q_{0} }}{n}} \right) \) will actually receive \( (\alpha + \beta )Q_{0} , \) an amount greater than \( \frac{{Q_{0} }}{n}, \) according to the allocation strategy. However, such a situation has no effects on the decision of both the manufacturer and the retailers because the market is always clear out in the Cournot competition. In fact, it is always beneficial for retailers to get more products in such a type of competition.

The following summarizes the sequence of events and decisions:

  1. 1.

    The manufacturer declares the allocation strategy, i.e., announcing the discriminated allocation parameter β.

  2. 2.

    Each retailer decides whether to disclose his private demand information and the manufacturer decides whether to accept the information.

  3. 3.

    Retailer i observes a signal Y i about θ. Then the manufacturer observes the shared signals from the retailers that participate in information sharing.

  4. 4.

    Based on the available information, the manufacturer sets the wholesale price w.

  5. 5.

    Upon knowing the wholesale price, retailer i determines his order q i , \( i = 1,2, \ldots ,n \) .

  6. 6.

    Upon receiving the retailers’ orders, the manufacturer produces Q = min (D, Q 0). If D ≤ Q 0, all orders can be satisfied; otherwise the manufacturer allocates the products among retailers according to the “discriminated allocation” strategy defined in (1).

The whole three-stage Stackelberg game is displayed in Fig. 1.

Fig. 1
figure 1

Sequence of events

Full size image

4 Equilibrium analysis

To analyze the game, we first solve the third-stage sub-game (i.e., ordering decisions made by retailers and the production and allocation decisions made by the manufacturer) and then the second-stage sub-game (i.e., the wholesale price decision made by the manufacturer) for any given information sharing arrangement at the first stage. Next, we present all the possible outcomes at the first stage of the game. Finally, we give the appropriate range that the feasible discriminated allocation parameter belongs to.

4.1 Retailers’ strategies at the third stage

At the third stage, retailer i has the information (Y i , w) when making his ordering decision, where Y i represents his private information and w is the wholesale price set at the second stage. Following Li (2002), the retailers are first assumed to guess that the manufacturer’s wholesale price is a strictly monotone function of the sum of the shared signals, \( \sum\nolimits_{j \in K} {Y_{j} } , \) and then we shall prove that this conjecture is correct in the equilibrium in the subsequent section. With this conjecture, retailers can infer \( \sum\nolimits_{j \in K} {Y_{j} } \) from the announced wholesale price w, and hence (Y i , w) is equivalent to \( \left( {Y_{i} ,\sum\nolimits_{j \in K} {Y_{j} } } \right). \)

Given this information, the retailer i will set his order q i to maximize his expected profit. The expected profit for retailer i, i ∈ N is

$$ E\left[ {\Uppi_{R}^{i} \left| {Y_{i} ,w} \right.} \right] = \left( {a + E\left[ {\theta \left| {Y_{i} ,w} \right.} \right] - q_{i} - \sum\limits_{m \ne i} {E\left[ {q_{m} \left| {Y_{i} ,w} \right.} \right] - w} } \right)q_{i} . $$

By the first order condition, the retailers’ equilibrium strategies are as follows (Li 2002):

For j ∈ K, a retailer who shares Y j with the manufacturer sets his optimal order as

$$ q_{j}^{ * } \left( {Y_{j} ,w} \right) = \frac{1}{n + 1}\left( {a - w + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} } } \right), $$
(2)

where \( A_{1}^{k} \, = \,\frac{1}{k + s}. \)

For l ∈ N \ K, a retailer who does not disclose his information sets his optimal order as

$$ q_{l}^{*} \left( {Y_{l} ,w} \right) = \frac{1}{n + 1}\left( {a - w + B_{1}^{k} \sum\limits_{j \in K} {Y_{j} + B_{2}^{k} Y_{l} } } \right), $$
(3)

where \( B_{1}^{k} \, = \,\frac{K + 2s}{{\left( {k + s} \right)\left( {n + k + 1 + 2s} \right)}},\,B_{2}^{K} \, = \,\frac{n + 1}{n + k + 1 + 2s} \).

When the capacity can satisfy the total order of the retailers, the expected profit of retailer i, i ∈ N is

$$ E\left[ {\Uppi_{R}^{i\;*} \left| {Y_{i} ,w,D \le Q_{0} } \right.} \right] = \left[ {q_{i}^{*} \left( {Y_{i} ,w} \right)} \right]^{2} . $$
(4)

However, when the capacity is less than the total order, the profits of retailers are as follows by applying (1),

$$ E\left[ {\left( {\Uppi_{R}^{l\;\;*} } \right)_{l \in N\backslash K} \left| {Y_{j} ,w,D > Q_{0} } \right.} \right] = \alpha Q_{0} \left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - Q_{0} - w} } \right), $$
(5)
$$ E\left[ {\left( {\Uppi_{R}^{j\;\;*} } \right)_{j \in K} \left| {Y_{j} ,w,D > Q_{0} } \right.} \right] = \left( {\alpha + \beta } \right)Q_{0} \left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - Q_{0} - w} } \right). $$
(6)

4.2 Manufacturer’s equilibrium price at the second stage

At the second stage of the game, the manufacturer sets the wholesale price w in anticipation of retailers’ equilibrium strategies at the third stage, \( \left( {q_{i}^{*} \left( {Y_{i} ,w} \right)} \right)_{i \in N} . \) Without a capacity constraint, given \( \left( {Y_{j} } \right)_{j \in K} , \) Li (2002) gives the expected downstream demand of the manufacturer as follows:

$$ E\left[ {D\left| {\left( {Y_{j} } \right)_{j \in K} } \right.} \right] = \frac{n}{n + 1}\left( {a - w + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} } } \right). $$
(7)

The expected profit of manufacturer M is accordingly:

$$ E\left[ {\Uppi_{M} \left| {\left( {Y_{j} } \right)_{j \in K} } \right.} \right] = w\,E\left( {D\left| {\left( {Y_{j} } \right)_{j \in K} } \right.} \right) = w\frac{n}{n + 1}\left( {a - w + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} } } \right). $$

By the first order condition, the optimal wholesale price can be obtained as follows:

$$ w^{ * } = \frac{1}{2}\left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} } } \right), $$
(8)

and the corresponding expected downstream demand is displayed below by substituting (8) into (7):

$$ E\left[ {D\left| {\left( {Y_{j} } \right)_{j \in K} } \right.} \right] = \frac{n}{{2\left( {n + 1} \right)}}\left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} } } \right). $$
(9)

Given the manufacturer’s capacity Q 0, if \( Q_{0} \, > \,\frac{n}{{2\left( {n + 1} \right)}}\left( {a\, + \,A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right) \), without any further information, the manufacturer, in an average sense, believes that she has enough capacity to satisfy the downstream demand. Thus she will set the wholesale price defined by (8). However, if \( Q_{0} \le \frac{n}{{2\left( {n + 1} \right)}}\left( {a + A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right), \) the manufacturer anticipates that she is not able to fully fulfill the retailers’ orders, and consequently will decide the wholesale price by taking her capacity Q 0 into consideration. In that case, to maximize her expected profit, the manufacturer will supply the retailers as much as possible, that is, she will set such a wholesale price that the expected downstream demand is lowered just to Q 0. By letting (7) equal Q 0, we get the optimal wholesale price in this situation:

$$ w^{ * } = \overline{w} = a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - \frac{n + 1}{n}Q_{0} .} $$
(10)

Summarizing the above argumentation, we get the following proposition about the equilibrium wholesale price of the manufacturer.

Proposition 1

At the second stage of the game, for any given information arrangement K, the manufacturer’s equilibrium wholesale price w* is

$$ w^{*} \left( {(Y_{j} )_{j \in K} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}\left( {a + A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right),} & {Q_{0} > \frac{n}{{2\left( {n + 1} \right)}}\left( {a + A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right)} \\ {a + A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} - \frac{n + 1}{n}Q_{0} ,} } & {Q_{0} \le \frac{n}{{2\left( {n + 1} \right)}}\left( {a + A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right)} \\ \end{array} } \right.. $$
(11)

This proposition shows the monopolistic position of the manufacturer in the upstream market, and also proves the correctness of the retailers’ conjecture about the wholesale price’s property with respect to the sum of the shared signals at the last stage of the game. It also clearly shows the effect of the production capacity on the wholesale price. The smaller the capacity compared with the expected downstream demand, the higher the wholesale price rises. Moreover, the coefficient of the shared signals \( \sum\nolimits_{j \in K} {Y_{j} } \) in the case where the capacity is insufficient is twice the coefficient in the case where the capacity is sufficient. That is, when she anticipates that her capacity is insufficient to satisfy the downstream demand, the manufacturer becomes more sensitive to the shared demand information than she does when she believes her capacity to be sufficient. As a result, the wholesale price can be set with more elasticity in the former case than that in the latter case.

4.3 Equilibrium outcomes at the first stage

At the first stage of the game, for any information sharing arrangement \( K\left( {\left| K \right| = k} \right), \) we can obtain the equilibrium outcomes (expected profits) of the manufacturer and the retailers, on the basis of their equilibrium strategies solved, respectively, at the second and third stage of the game. Since both the actual total order and the manufacturer’s estimated downstream demand may be either greater or less than her capacity, there exist four combinations. Accordingly, we will analyze the equilibrium outcomes of every player in each situation, respectively.

In the following analysis, we denote \( \Uppi_{R}^{S(k)} \) to be the expected profit of one of the k retailers that engage in the vertical information exchange, \( \Uppi_{R}^{N(k)} \) to be the expected profit of each retailer that is not engaged in information sharing, and \( \Uppi_{M}^{k} \) to be the expected profit of the manufacturer.

Case 1

\( Q_{0} \ge D \) and \( Q_{0} \, > \,\frac{n}{{2\left( {n + 1} \right)}}\left( {a\, + \,A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right). \)

Case 1 describes the situation that the manufacturer believes her capacity to be sufficient when making the wholesale price decision according to Eq. 8, and the actual total order is indeed less than her capacity. In this case, the capacity of the manufacturer never affects the retailers’ ordering decisions. Accordingly the equilibrium outcomes are the same as those given by Li (2002):

$$ \Uppi_{R}^{S(k)} ({\text{case}}\;1) \equiv E\left[ {\left( {q_{j}^{*} } \right)^{2} \left| {{\text{case}}\; 1} \right.} \right] = \frac{{a^{2} }}{{4\left( {n + 1} \right)^{2} }} + \frac{{\sigma^{2} }}{{4\left( {n + 1} \right)^{2} }}\left( {A_{1}^{k} } \right)^{2} \left( {k^{2} + ks} \right)\quad {\text{for}}\;j \in K, $$
$$ \begin{aligned} \Uppi_{R}^{N(k)} ({\text{case}}\;1) & \equiv E\left[ {\left( {q_{l}^{*} } \right)^{2} \left| {{\text{case}}\; 1} \right.} \right] \\ & = \frac{{a^{2} }}{{4\left( {n + 1} \right)^{2} }} + \frac{{\sigma^{2} }}{{4\left( {n + 1} \right)^{2} }}\left[ {\left( {B_{1}^{k} - \frac{1}{2}A_{1}^{k} } \right)^{2} \left( {k^{2} + ks} \right) + 2\left( {B_{1}^{k} - \frac{1}{2}A_{1}^{k} } \right)B_{2}^{k} + \left( {B_{2}^{k} } \right)^{2} \left( {1 + s} \right)} \right]\quad {\text{for}}\;l \in N\backslash K, \\ \end{aligned} $$
$$ \Uppi_{R}^{k} ({\text{case}}\;1) \equiv E\left[ {\Uppi_{M}^{*} \left| {{\text{case}}\;1} \right.} \right] = \frac{n}{n + 1}\left[ {\frac{{a^{2} }}{4} + \frac{{\sigma^{2} }}{4}\left( {A_{1}^{k} } \right)^{2} \left( {k^{2} + ks} \right)} \right]. $$
(12)

When exactly k retailers engage in information sharing, the difference of the profit of a retailer who shares his demand information and the one who does not can be calculated in (13). We call this difference the Marginal Profit Increment (MPI), which determines the retailer’s choice of information sharing.

$$ {\text{MPI}}^{k} \left( {{\text{case}}\; 1} \right) = \Uppi_{R}^{S(k)} ({\text{case}}\;1) - \Uppi_{R}^{N(K)} ({\text{case}}\;1) = - \frac{{s\left( {k + s + 1} \right)\sigma^{2} }}{{\left( {k + s} \right)\left( {n + k + 2s + 1} \right)^{2} }} < 0. $$
(13)

In case 1, the manufacturer’s expected profit is increasing in k, indicating that she will get more benefits when more retailers share their information with her. As more retailers share their information, the manufacturer has a better knowledge about the downstream demand than any single retailer, and thereby she can take advantage of this position to acquire the information rent from the retailers. However, the retailer who discloses his private demand information to the manufacturer will be at a disadvantage (MPIk (case 1) < 0).

Case 2

\( Q_{0} \ge D \) but \( Q_{0} < \frac{n}{{2\left( {n + 1} \right)}}\left( {a + A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right). \)

Case 2 implies that the manufacturer underestimates her capacity according to her acquired information, yet the actual total order is less than what she is able to provide. Substituting (10) and (2) into (4), we get the expected profit of the retailer engaged in the information exchange as follows:

$$ \Uppi_{R}^{S(k)} ({\text{case}}\;2) \equiv E\left[ {\left( {q_{j}^{*} } \right)^{2} \left| {{\text{case}}\; 2} \right.} \right] = \frac{{Q_{0}^{2} }}{{n^{2} }},\quad {\text{for}}\;j \in K. $$

Substituting (10) and (3) into (4), we get the expected profit of the retailer who is unwilling to share his information:

$$ \Uppi_{R}^{N(k)} ({\text{case}}\;2) \equiv E\left[ {\left( {q_{l}^{*} } \right)^{2} \left| {\text{case2}} \right.} \right] = \frac{{Q_{0}^{2} }}{{n^{2} }} + \frac{{s\left( {k + s - 1} \right)\sigma^{2} }}{{\left( {k + s} \right)\left( {n + k + 2s + 1} \right)^{2} }},\quad {\text{for}}\;l \in N\backslash K. $$

Subsequently, we can get MPI in this case,

$$ {\text{MPI}}^{k} \left( {{\text{case}}\;2} \right) = \Uppi_{R}^{S(k)} ({\text{case}}\;2) - \Uppi_{R}^{N(k)} ({\text{case}}\;2) = - \frac{{s\left( {k + s - 1} \right)\sigma^{2} }}{{\left( {k + s} \right)\left( {n + k + 2s + 1} \right)^{2} }} < 0. $$
(14)

According to (10) and (7), the expected profit of the manufacturer is

$$ \begin{aligned} \Uppi_{M}^{k} ({\text{case}}\;2) & \equiv E\left[ {\left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - \frac{n + 1}{n}Q_{0} } } \right)\frac{n}{n + 1}\left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - a - A_{1}^{k} \sum\limits_{j \in K} {Y_{j} + \frac{n + 1}{n}Q_{0} } } } \right)} \right] \\ & = aQ_{0} - \frac{n + 1}{n}Q_{0}^{2} . \\ \end{aligned} $$
(15)

Comparing Eqs. 13 and 14, we find that the retailer who discloses his information in case 2 has a little bit better position than he dose in case 1. In spite of this, in both cases information sharing brings negative effects to retailers who share private information and this phenomenon generates some common results about a retailer’s profit, which is summarized in the following proposition.

Proposition 2

At the first stage of the game, for any given information sharing arrangement K, if the realized total order is less than the manufacturer’s capacity, then \( {\text{MPI}}^{k} \left( {D < Q_{0} } \right) < 0 \) for all \( k = 1, \ldots ,n, \) and \( {\text{MPI}}^{k} \left( {D < Q_{0} } \right) \) is increasing in k.

See “Appendix 1” for proof.

This proposition leads to the following conclusion: each retailer is worse off by disclosing his information to the manufacturer if the total order doesn’t exceed the capacity (D ≤ Q 0), no matter what wholesale price decision is made by the manufacturer. Therefore, no information sharing is the unique equilibrium in case 1 and case 2. Since the wholesale price is a monotone function of the shared information, the retailer who hides his information has more knowledge (his private information and the shared information) about the demand than the one who discloses his information. Thus, the information advantage gives the information hiders the information rent which, however, hurts the information disclosers.

Case 3

Q 0 < D and \( Q_{0} < \frac{n}{{2\left( {n + 1} \right)}}\left( {a + A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right). \)

This case indicates that the manufacturer forecasts her lack of capacity according to the acquired information, and indeed the manufacturer’s estimate complies with the reality that she cannot satisfy the actual total order. Accordingly, the capacity constraint takes effect in both the wholesale price decision and the product allocation. We can obtain the expected profits of both types of retailers by substituting (10) into (5) and (6):

$$ \begin{aligned} \Uppi_{R}^{S(k)} ({\text{case}}\;3) & \equiv E\left\{ {\left( {\alpha + \beta } \right)Q_{0} \left[ {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - Q_{0} - \left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - \frac{n + 1}{n}Q_{0} } } \right)} } \right]} \right\} \\ & = \frac{{\left( {\alpha + \beta } \right)Q_{0}^{2} }}{n} = \frac{{1 + \left( {n - k} \right)\beta }}{{n^{2} }}Q_{0}^{2} , \\ \end{aligned} $$
(16)
$$ \begin{aligned} \Uppi_{R}^{N(k)} ({\text{case}}\;3) & \equiv E\left\{ {\alpha Q_{0} \left[ {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - Q_{0} - \left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - \frac{n + 1}{n}Q_{0} } } \right)} } \right]} \right\} \\ & = \frac{{\alpha Q_{0}^{2} }}{n} = \frac{1 - k\beta }{{n^{2} }}Q_{0}^{2} . \\ \end{aligned} $$
(17)
$$ {\text{MPI}}^{k} \left( {{\text{case}}\; 3} \right) \equiv \Uppi_{R}^{S(k)} ({\text{case}}\;3) - \Uppi_{R}^{N(k)} ({\text{case}}\;3) = \frac{\beta }{n}Q_{0}^{2} > 0. $$
(18)

The expected profit of the manufacturer is

$$ \Uppi_{M}^{k} ({\text{case}}\;3) \equiv E\left[ {Q_{0} \left( {a + A_{1}^{k} \sum\limits_{j \in k} {Y_{j} - \frac{n + 1}{n}Q_{0} } } \right)} \right] = aQ_{0} - \frac{n + 1}{n}Q_{0}^{2} . $$
(19)

According to (15) in case 2 and (19), we come to the following proposition:

Proposition 3

At the first stage of the game, for any given information sharing arrangement K, if the manufacturer’s anticipation at the total order is more than her capacity, the expected profit of the manufacturer is constant in terms of the capacity.

This proposition implies that when the manufacturer anticipates that the total order exceeds her capacity, she will not get any more benefits from acquiring the demand information because she can only offer Q 0 products, which lock her cashbox.

Case 4

Q 0 < D but \( Q_{0} \ge \frac{n}{{2\left( {n + 1} \right)}}\left( {a + A_{1}^{k} \sum\nolimits_{j \in K} {Y_{j} } } \right). \)

In case 4, the manufacturer overrates her supply ability, namely, underestimates the demand level. We can obtain the expected profits of both types of retailers by substituting (8) into (5) and (6):

$$ \begin{aligned} \Uppi_{R}^{S(k)} ({\text{case}}\;4) & \equiv E\left[ {\left( {\alpha + \beta } \right)Q_{0} \left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - Q_{0} - \frac{a}{2} - \frac{1}{2}A_{1}^{k} \sum\limits_{j \in k} {Y_{j} } } } \right)} \right] \\ & = \frac{{1 + \left( {n - k} \right)\beta }}{n}Q_{0} \left( {\frac{a}{2} - Q_{0} } \right), \\ \end{aligned} $$
(20)
$$ \begin{aligned} \Uppi_{R}^{N(k)} ({\text{case}}\;4) & \equiv E\left[ {\alpha Q_{0} \left( {a + A_{1}^{k} \sum\limits_{j \in K} {Y_{j} - Q_{0} - \frac{a}{2} - \frac{1}{2}A_{1}^{k} \sum\limits_{j \in k} {Y_{j} } } } \right)} \right] \\ & = \frac{1 - k\beta }{n}Q_{0} \left( {\frac{a}{2} - Q_{0} } \right). \\ \end{aligned} $$
(21)

With assumption (A0), we have

$$ {\text{MPI}}^{k} \left( {{\text{case}}\; 4} \right) \equiv \Uppi_{R}^{S(k)} ({\text{case}}\;4) - \Uppi_{R}^{N(k)} ({\text{case}}\;4) = \beta Q_{0} \left( {\frac{a}{2} - Q_{0} } \right) > 0. $$
(22)

The expected profit of the manufacturer is

$$ \Uppi_{M}^{k} ({\text{case}}\;4) \equiv E\left[ {Q_{0} \left( {\frac{a}{2} + \frac{1}{2}A_{1}^{k} \sum\limits_{j \in k} {Y_{j} } } \right)} \right] = \frac{{aQ_{0} }}{2}. $$
(23)

Similar to that in case 3, MPI in case 4 is also greater than zero. These two consistent results generate the following proposition.

Proposition 4

When the actual total order exceeds the capacity and the manufacturer applies a discriminated allocation strategy, it is a retailer’s dominated strategy to be engaged in information sharing, independent of the manufacturer’s estimation of the total order.

In the Cournot competition, as long as a retailer sells more products, he will gain a higher profit. When his order cannot be fully satisfied, the ability to acquire as many products as possible implies a high profit for a retailer. The discriminated allocation strategy endows the retailer with this ability. Therefore, the retailer is willing to share his private information with the manufacturer in exchange for the priority in the product allocation.

In addition, if we let β = 0 in both case 3 and case 4, then MPIk (D > Q 0) = 0 for all \( k = 1, \ldots ,n. \) This observation implies that it is indifferent for a retailer to disclose or hide his private demand information when the manufacturer applies an average allocation strategy. This result combined with Proposition 2 gives the condition for not sharing the private information, which is summarized in Proposition 5.

Proposition 5

At the first stage of the game, if the retailers are treated without discrimination (i.e. \( \beta \, = \,0 \) ), for any given information sharing arrangement K and any possible capacity Q 0 of the manufacturer, retailers always have no incentive to share their private demand information with the manufacturer. In fact, it is worse off (/indifferent) for retailers to disclose information when the total order is less than (/exceeds) the manufacturer’s capacity.

The argumentation in the above four cases mainly discusses the effects of information sharing on the retailers. The last part of this sub-section will examine the effects of information sharing from the manufacturer’s perspective. As (12) shows, the manufacturer’s expected profit is an increasing function of k, while (15), (19), and (23) displays that the manufacturer’s expected profit is irrelevant of k. Then would the manufacturer like to participate in the information exchange? We compare the manufacturer’s expected profit under information sharing with the ones under no information sharing, and deduce the following proposition.

Proposition 6

For any information arrangement K and any possible capacity, the manufacturer would like to receive the demand information from the retailers.

See “Appendix 2” for proof.

4.4 Allocation strategy

Proposition 4 and Proposition 5 show that the discriminated allocation strategy plays a pivotal role in promoting information sharing. Accordingly, this sub-section is devoted to finding the appropriate allocation parameter β. As a prerequisite, let’s work on the probabilities of the four cases discussed above. To facilitate calculation, we make another assumption here (A4): \( Y_{i} ,i = 1, \ldots ,n, \) follows a normal distribution. Let \( x = \frac{{Y_{i} }}{{\sqrt {1 + s\sigma } }}, \) and then x is a random variable that follows a standard normal distribution (it can be deduced from A1 to A3 in Sect. 2). Denote F(x) as the cumulated distribution function of x and we can get the probabilities of the four cases as follows.

Lemma 1

The probabilities of the four cases are

$$ \begin{aligned} \Pr \left( {{\text{case}}\; 1} \right) & = F\left( {T_{1} } \right)F\left( {T_{2} } \right) \\ \Pr \left( {{\text{case}}\; 2} \right) & = \Pr \left( {{\text{case}}\; 3} \right) = \frac{1}{2} - \frac{1}{2}F\left( {T_{2} } \right), \\ \Pr \left( {{\text{case}}\; 4} \right) & = F\left( {T_{2} } \right)\left[ {1 - F\left( {T_{1} } \right)} \right] \\ \end{aligned} $$
(24)

where \( T_{1} = \frac{{\left[ {2\left( {n + 1} \right)Q_{0} - an} \right]}}{V},\;T_{2} = \frac{{\left( {k + s} \right)\left[ {2\left( {n + 1} \right)Q_{0} - na} \right]}}{{n\sigma \sqrt {k\left( {s + 1} \right)} }} \) and V’s value is demonstrated in the “ Appendix 3 ”.

See “Appendix 3” for proof.

Clearly, T 2 is decreasing in k when \( Q_{0} < \frac{na}{{2\left( {n + 1} \right)}}, \) and increasing in k when \( Q_{0} > \frac{na}{{2\left( {n + 1} \right)}}. \) This property of T 2 implies that the more retailers participate in the information sharing, the more accurate demand information the manufacturer can obtain, and this improved knowledge about the demand actually strengthens the manufacturer’s confidence in her original estimate of the relationship between her capacity and the market demand. When \( Q_{0} < \frac{na}{{2\left( {n + 1} \right)}}, \) as more retailers share their private information, the probability of case 2 or case 3 is increasing, indicating that the manufacturer more strongly believes her capacity to be less than the market demand. Similarly, when \( Q_{0} > \frac{na}{{2\left( {n + 1} \right)}}, \) as more retailers share their private information, the probability of case 1 or case 4 is increasing, implying that the manufacturer more strongly believes her capacity to be larger than the market demand.

Equipped with the occurring probability of the four cases, we can find the appropriate range of β that can motivate the retailers to disclose their private information. Denote \( \underline{\beta } \) to be the lower bound of the discrimination parameter β, and then we can arrive at the following proposition.

Proposition 7

If the manufacturer with a capacity constraint applies the discriminated allocation strategy and chooses \( \beta \in \left( {\underline{\beta } } \right.,\left. \frac{1}{n} \right], \) each retailer will voluntarily share his private demand information with the manufacturer, where

$$ \underline{\beta } = \mathop {\max }\limits_{k} \left\{ {\frac{{ns\sigma^{2} \left[ {2\left( {k + s + 1} \right)F\left( {T_{1} } \right)F\left( {T_{2} } \right) + \left( {k + s - 1} \right)\overline{F} \left( {T_{2} } \right)} \right]}}{{Q_{0} \left( {k + s} \right)\left( {n + k + 1 + 2s} \right)^{2} \left[ {Q_{0} \overline{F} \left( {T_{2} } \right) + 2n\left( {\frac{a}{2} - Q_{0} } \right)F\left( {T_{2} } \right)\overline{F} \left( {T_{1} } \right)} \right]}}} \right\},\quad for\;k = 1, \ldots ,n. $$
(25)

See “Appendix 4” for proof.

Every number of retailers that share their demand information corresponds to a lower bound of the allocation parameter \( \underline{\beta }_{k} . \) In order to encourage all the retailers to share their information, the manufacturer will choose the maximum of the sequence \( \left\{ {\underline{\beta }_{k} ,k = 1,2, \ldots ,n} \right\}. \)

5 Discussions

This section will further discuss the equilibrium and the effects of the manufacturer’s capacity on the profit of the supply chain, the consumer surplus, and the social welfare.

Proposition 6 and Proposition 7 state that information sharing on average has positive effects on the manufacturer and the retailers, respectively. These results further imply that information sharing is the equilibrium of this model, which is stated in the following proposition.

Proposition 8

In a supply chain with one capacitated manufacturer and multiple Cournot retailers, if the manufacturer applies a discriminated allocation strategy and the allocation parameter satisfies (25), then it is the unique equilibrium for the manufacturer and all the retailers to participate in information sharing (full information sharing).

The discriminated allocation strategy applied by the manufacturer actually make the retailers step into the “Prisoner’s Dilemma”. When the allocation parameter satisfies (25), as long as the capacity is insufficient, the retailer who shares his private information will get a higher profit than the one who does not; therefore, no information sharing can not be an equilibrium. On the other hand, when all the retailers take part in information sharing, no one would like to deviate from this state. Although each retailer will get the same expected profit when full information sharing is reached, anyone who deviates will be worse off than the rest of the retailers. Thus, the discriminated allocation strategy makes full information sharing the unique equilibrium under the capacity constraint.

Next, we examine the effect of the capacity on the supply chain. Define the expected total profit of the supply chain as \( \Uppi^{k} \equiv \Uppi_{M}^{k} + k\Uppi_{R}^{S(k)} + (n - k)\Uppi_{R}^{N(k)} . \) By calculating Πk when the manufacturer’s capacity is insufficient, we can generate the following proposition.

Proposition 9

If the realized total order exceeds the manufacturer’s capacity, for any given information sharing arrangement K, the expected total profit of the supply chain will be constant in terms of the manufacturer’s capacity, i.e., \( \Uppi^{k} \left( {D > Q_{0} } \right) = aQ_{0} - Q_{0}^{2} . \)

See “Appendix 5” for proof.

This proposition indicates that the manufacturer’s capacity is a determinant of the profit of the supply chain when it is less than the actual demand. Li (2002) shows that the profit of the supply chain would increase as more retailers share their private information when the capacity is infinite (case 1 in this paper), and therefore it is possible for the manufacturer to motivate the retailer to disclose his information by compensation. However, this method is not effective when the capacity constraint is tight because the manufacturer has no extra money to compensate the retailer. In such a situation, the discriminated allocation strategy which redistributes the fixed profit between information disclosers and hiders represents a possible way to create inequality that functions as a compensation to attract the retailer to share his information.

Finally, we consider the impact of vertical information sharing on the total social welfare when the demand exceeds the manufacturer’s capacity. Define the expected social welfare under the capacity constraint as

$$ W \equiv E\left[ {\int\limits_{0}^{{Q_{0} }} {\left( {a + \theta - q} \right)dq\left| {\sum\limits_{j \in K} {Y_{j} } } \right.} } \right] = aQ_{0} - \frac{1}{2}Q_{0}^{2} , $$

which is the sum of the expected total profit of the supply chain in Proposition 7 and the consumer surplus under the capacity constraint calculated as \( CS \equiv \frac{{Q_{0}^{2} }}{2}. \) From the above equation, we can get the next proposition:

Proposition 10

If the manufacturer’s capacity cannot satisfy all the retailers’ orders, for any given information sharing arrangement K, the expected social welfare and the expected consumer surplus become constants in terms of the manufacturer’s capacity.

In Li (2002)’s model where the manufacturer has an infinitive capacity, the monopolistic manufacturer can exploit the consumer surplus through information sharing. Our model, however, shows that when the capacity constraint is tight, the manufacturer cannot seize the profit from consumers because the capacity confines such capabilities of hers.

6 Numerical examples

The above analytical results show that the equilibrium outcomes are affected by an interaction of parameters, i.e., the number of information disclosers k, the manufacturer’s capacity Q 0, the uncertainty of the market demand σ 2, and the accuracy of the information s. This section will further investigate how these parameters affect the retailers’ profits and the allocation parameter β through a numerical experiment.

The random variable θ is assumed to follow a normal distribution \( N\left( {0,\sigma^{2} } \right). \) Reference to \( \underline{\beta } \) generated in (25), we set \( \beta = \min \left( {2\underline{\beta } ,\frac{1}{n}} \right) \) in the discriminated allocation strategy. This research intends to study information sharing in a competitive environment. The more retailers, the more intensified horizontal competition for a Cournot game. Considering this point, we set the number of retailers to be 10. Because of the assumption A0: \( Q_{0} \le \frac{a}{2} \) and a = 500, Q 0 should be <250. Therefore, we let Q 0 increase from 130 to 220 by a step of 10. The effects of information sharing are impaired under too much fluctuated demand, and thus we confine the fluctuation of the demand within a small to medium range by selecting σ from the set {10, 30, 50, 70, 100}. Since s represents the estimating precision, it is less than 1. Thus, we let s increase from 0.1 to 0.9 by a step of 0.1. These parameter values used in the numerical experiment are listed in Table 1.

Table 1 Parameter values in the numerical experiment
Full size table

6.1 The effect of the number of retailers who share their information

Figure 2 shows the trend of the retailers’ profits with the number of the information disclosers increasing. It displays that the average profits of both retailers who share their information and the ones who do not decline as more retailers take part in information sharing. In addition, the profit of a retailer who shares his demand information with the manufacturer is always greater than that of a retailer who does not, when \( k\left( {k = 1, \ldots ,n - 1} \right) \) retailers have been engaged in information sharing. Thus, this figure clearly confirms that information sharing adopted by all the retailers is the only equilibrium in which each retailer receives the same profit.

Fig. 2
figure 2

Profits of cooperative and non-cooperative retailers when k retailers share information

Full size image

The pattern in this figure reflects two points. First, information sharing hurts the retailers’ interests, as shown in Li (2002). Given the parameter values displayed in Fig. 2, when no retailers participate in information sharing, the manufacturer can charge the wholesale price of 280. When full information sharing is achieved, the manufacturer can increase the wholesale price up to 292.6 averagely according to her acquired information, so that she captures more profit from the retailers. Second, Li (2002) concludes that the profit of the information discloser is worse than that of the information hider, however, our study displays an opposite result when the capacity constraint is considered, i.e., the information discloser is better than the information hider. When the manufacturer’s capacity is tight, to acquire as many products as possible becomes a key point. The priority offered by the discriminated allocation strategy in the product allocation outweighs the loss resulting from the information leakage. Thus, the retailer who discloses his information has a better position.

6.2 The effect of the manufacturer’s capacity

Figure 3 demonstrates Q 0’s impact on the lower bound of the allocation parameter \( \underline{\beta } \) and the marginal profit increment (MPI) of the retailer who discloses his demand information. It shows that as the capacity increases, \( \underline{\beta } \) decreases. When Q 0 is small, the manufacturer has to set a relatively high β (the narrow range of β [0.050, 0.100]). In such a situation, the wholesale price when the capacity is insufficient is higher than the one when the capacity is sufficient (see Eq. 11). Consequently the retailer will lose much more profit by disclosing his information. Because of this, a large allocation quota is necessary to cover the retailer’s loss in order to attract him to share his information. On the contrary, when Q 0 is large, the manufacturer can set a low β (the wide range of β [0.018, 0.100]). At this moment, the wholesale price under the capacity constraint is lowered to be comparable to the one without this constraint. Accordingly, a smaller quota is enough to compensate the retailer’s reduced loss.

Fig. 3
figure 3

Q 0’s impact on \( \underline{\beta } \) and MPI

Full size image

In addition, MPI displays a “concave”-like curve. Two forces result in this trend. On the one hand, the allocation quota is decreasing with the expansion of the capacity due to a decreasing \( \underline{\beta } \). On the other hand, the marginal profit of the retailer is an increasing function of the capacity when the capacity is insufficient because the wholesale price under this condition is decreasing in Q 0 (see Eq. 11). Consequently, there may exist a critical value for capacity at which the MPI reaches its maximum. Before that critical value, the increase of the marginal profit dominates the decrease of the allocation quota, and thereby MPI is augmenting. After that critical value, the latter dominates the former, and hence MPI is falling off.

However, when the capacity continues increasing to be more than the expected downstream demand, the result will return to the original Li (2002)’s conclusion that information discloser is worse than the information hider. Therefore, our model generalizes the previous research [e.g., Li (2002) and Zhang (2002)] in which demand information sharing always hurts the retailer who takes this practice.

6.3 The effect of the demand uncertainty

Figure 4 describes the impact of the demand uncertainty on the lower bound of the allocation parameter and the marginal profit increment. It illustrates that as the standard deviation of θ increases, \( \underline{\beta } \) augments and MPI increases as well. The increasing value of σ implies that the end-market fluctuates more greatly. Consequently, the realized demand can be either less than or greater than the manufacturer’s capacity, even if the capacity is larger than the expected downstream demand. If the realized demand is less than the capacity, then the retailer will be hurt by sharing his information. Therefore, a larger allocation quota (a high β) is needed to compensate the retailer for disclosure of his information, so that on average such a retailer can be better off than the one who hides his information, when the market is more uncertainty. Because of this, MPI grows and the increased MPI reflects the reward paid for the information value.

Fig. 4
figure 4

The impact of the standard deviation on \( \underline{\beta } \) and MPI

Full size image

Furthermore, the incremental standard deviation of θ indicates that the market demand is more difficult for the manufacturer to predict. Under this condition, the manufacturer would like to grasp demand information from as many retailers as possible so that she can refine her estimate of the downstream market demand. By thus, the chance that the unnecessary loss results from a false decision of the wholesale price will be reduced. Drawn on this reason, the manufacturer is willing to incentive retailers to engage in information sharing by setting a high β.

6.4 The effect of the accuracy of retailer’s private information

Figure 5 illustrates the impact of the information accuracy s on the lower bound of the allocation parameter and the marginal profit increment of the retailer who shares his information. Regardless of the values of these parameters, \( \underline{\beta } \) and MPI demonstrate similar patterns as they co-varies with the standard deviation of the random variable (Fig. 4): both \( \underline{\beta } \) and MPI swell with s increasing.

Fig. 5
figure 5

The impact of the information accuracy on \( \underline{\beta } \) and MPI

Full size image

The reason lies in that both s and σ reflects the fact that the market demand is hard to predict. The high standard deviation directly indicates the wide spread of the variant of the market demand and the low accuracy of the information means that the observation of the demand information displays high fluctuation. In spite of this difference, the large values of both parameters reveal that the true market demand is difficult to capture by both retailers and the manufacturer. Therefore, the argumentation in sub-section 6.3 can also be applied here to explain the impact of s on \( \underline{\beta } \) and MPI.

7 Conclusion and future works

In this paper, we mode a supply chain composed of a manufacturer with a finite capacity and many homogenous retailers that engage in a Cournot competition. We consider a discriminated allocation strategy to distribute products when the capacity is insufficient. We show that when the discriminated allocation strategy satisfies a certain condition, participating in information sharing will be a unique equilibrium behavior of all the parties. Thus, this paper displays that the capacity constraint of a monopolistic manufacturer can make information sharing possible in a competitive environment. This conclusion is different from the previous research when the capacity is assumed to be infinitive. This way, this paper makes an early effort towards studying incentives for information sharing in a complicated supply chain.

However, the “discriminated allocation” strategy used in this paper is quite simple and “rude”. Other allocation mechanisms such as “batch priority policy” can be applied by the future research and the result should be reevaluated. In addition, the future research can relax the assumption that the downstream market is clear, and thereby incorporate some cases which may make the capacity more important for optimal strategies of the supply chain members.