A numerical study on the effect of the balance assumption in one-warehouse multi-retailer inventory systems

Abstract

One-warehouse multi-retailer systems under periodic review have been studied extensively in the literature. The optimal policy has not been characterized yet. It would require solving a multi-dimensional dynamic program, which is hard due to the curse of dimensionality. In order to let the dynamic program decompose, researchers often make the so-called balance assumption. All available heuristics for periodic review distribution systems are based on some form of this assumption. For these heuristics, often further approximate steps are applied. We investigate the pure effect of the balance assumption in this paper. The balance assumption is the relaxation of a set of constraints in the original dynamic program and yields a lower bound model, which we solve exactly. This gives us a lower bound for the optimal cost of the original model. An upper bound for the true optimal cost is obtained by simulating the optimal policy for the relaxed problem with a slightly modified allocation rule. This modified policy is referred to as the LB heuristic policy. We use the relative gap between the upper and lower bound as a measure to assess the impact of the balance assumption. Based on extensive testing, we identify when the gap is small, and when not. For those instances with small gaps, both the lower bound is tight and the performance of the LB heuristic policy is close to the optimal. We also identify many practically relevant settings under which the balance assumption yields large gaps. For these instances, either the lower bound is poor or the LB heuristic policy is far from optimal, or both. In any case, it implies that more research is needed to develop better lower bounds and/or better heuristics for these instances.

1 Introduction

This paper considers a two-echelon divergent (distribution, arborescent) inventory system where a central stock point, called the warehouse, supplies N downstream stock points, called retailers. Demands of the customers originate at the retailers. The warehouse orders from an external supplier with ample stock and ships to the retailers as needed. There are fixed lead times between the supplier and the warehouse (l ₀), and in between the warehouse and the retailers. Any unfulfilled demand of a customer is backlogged. The system is controlled centrally under periodic review.

The model considered is also relevant in a manufacturing context. Suppose an intermediate product/subassembly is stocked at a central location, and used in the manufacturing/assembly of multiple different end products. Production/inventory decisions in such a system can be determined using the one-warehouse multi-retailer model. Moreover, the model can be used to study hierarchical production planning (see de Kok (1990)) and delayed product differentiation (see Aviv and Federgruen (2001)).

The seminal work on periodic review multi-echelon inventory systems is by Clark and Scarf (1960). The authors developed a dynamic programming formulation for the inventory control of an N-echelon serial system in a finite horizon. By introducing the concept of echelon stock and induced penalty cost, they were able to decompose the resulting multi-dimensional dynamic program (DP) into a series of single-dimensional programs (referred to as the decomposition property), and characterize the optimal policy, which is an echelon base stock policy. Clark and Scarf (1960) also tried to apply their decomposition technique to divergent structures, but it is not possible to show the decomposition property due to the allocation (rationing) problem. (In a one-warehouse multi-retailer setting, in each period the decision maker decides on the amount of stock to keep at the warehouse and ship to each retailer, which is called the allocation problem.) Thus, the optimization problem requires the solution of a multi-dimensional DP with N + l ₀ + 1 dimensions, which is unrealistic to calculate for a real life application. The structure of the optimal policy for the one-warehouse multi-retailer model is unknown. However, an assumption, known as the balance assumption, leads to the decomposition property and a full characterization of the optimal policy. This key assumption is the relaxation of the physical constraint that the inventory positions of the retailers just after the allocation decision are greater than or equal to the inventory positions prior to this decision. Other interpretations of the balance assumption are (1) allowing negative quantities to be shipped to the retailers, (2) permitting immediate return (with no lead time) of stock at any retailer to the warehouse at no cost, (3) allowing the lateral transhipment (shipments between the retailers) of stock with the lead time of the receiving retailer at no cost. ¹

The balance assumption allows the shipment decisions to be just based on the echelon stock of the warehouse. The individual inventory positions of the retailers become irrelevant since negative shipments are permitted. The inventory positions of the retailers under such a shipment scheme represent an ideal state where the retailer inventories are said to be in balance. However, in a real setting, there may be departures from the ideal state and this contributes to the imbalance of the system.

The balance assumption was introduced by Eppen and Schrage (1981) who coined the phrase allocation assumption for what we refer to as the balance assumption. In the multi-echelon inventory literature, any multi-period model that includes the allocation problem makes the balance assumption in some form. On one hand, the studies by Federgruen and Zipkin (1984b, c), Erkip et al. (1990), Chen and Zheng (1994), Bollapragada et al. (1998), Diks and de Kok (1998), Cachon and Fisher (2000), and Özer (2003) have equal frequency of ordering and shipment (i.e., the system orders and ships every period), so the system is assumed to be in balance at the beginning of each period. On the other hand, if the warehouse orders less frequently than it ships to the retailers, e.g., Jönsson and Silver (1987), Jackson (1988), Jackson and Muckstadt (1989), McGavin et al. (1993), van der Heijden (1999), then the balance of the system is assumed at each epoch an order is received by the warehouse. Kumar et al. (1995) incorporate another form of the balance assumption.

To our knowledge, all heuristics developed for periodic review divergent systems that benefit from risk pooling ² are based on the balance assumption in some form, e.g., Federgruen and Zipkin (1984a), van der Heijden et al. (1997), Diks and de Kok (1999), Kumar and Jacobson (1998), Axsäter et al. (2002), Cao and Silver (2005), Gallego et al. (2007), Kunnumkal and Topaloglu (2008). The majority of these heuristics apply further approximate steps after making the balance assumption. For example, consistent appropriate share and balanced stock heuristic as discussed in van der Heijden et al. (1997) assume linear allocation functions, which ration the on-hand warehouse stock with respect to fixed retailer specific fractions.

There is an established belief in the literature that the balance assumption is a good approximation. In his comprehensive survey study, Axsäter (2003, p. 544) states:

The balance assumption has been used extensively in the inventory literature and has been shown to produce solutions of very good quality in many different situations, ...

The numerical results of the aforementioned references advocate the use of the balance assumption with an exception of Axsäter et al. (2002). We review the literature on the balance assumption in Sect. 2. Although Axsäter et al. (2002) and Gallego et al. (2007) report results that hint the possibility of large errors due to the balance assumption, there is no clear-cut study in the literature that questions the appropriateness of this assumption. Our paper tries to fill this gap by a numerical study conducted over a wide range of parameters.

Our methodology can be explained as follows. The optimization problem under the balance assumption, which we refer to as the relaxed model or the lower bound model, is a relaxation of the original problem. Hence, the corresponding optimal cost is a lower bound (LB) for the true optimal cost. When the optimal base stock levels of the relaxed problem are coupled with a myopic allocation procedure, ³ the resulting policy is a feasible heuristic policy, referred to as the LB heuristic policy. An estimate for the average expected cost of the LB heuristic policy can be determined by simulation, which serves as an upper bound (UB) for the true optimal cost. The relative gap between the bounds $\left(\epsilon\%=100\frac{UB-LB}{LB}\right)$ is used as a measure to assess the impact of the balance assumption. Since the optimal cost is enveloped by LB and UB, a small relative gap implies that the balance assumption leads to a good approximation for that particular input parameter setting: while LB is an accurate proxy for the optimal cost, the LB heuristic policy performs well. Hence, we conclude that a small relative gap justifies the use of balance assumption for that setting. On the other hand, when there is a moderate or a large relative gap, the exact position of the true optimal cost between LB and UB becomes an important issue. When $\epsilon\%$ is considerable, either LB is an inaccurate proxy or the LB heuristic policy is mediocre, or both. If LB is tight, then there is a need for a better heuristic. If the cost of the LB heuristic policy is close to the true optimal cost, then this should be established either by developing a better lower bound or determining the optimal cost. As long as it is not demonstrated, neither the LB heuristic policy, nor the heuristics based on the balance assumption can be trusted for the instances with moderate or large gaps.

The following input parameters are considered in the numerical study: holding and penalty costs, warehouse and retailer lead times, the number of retailers, and the mean and the coefficient of variation of the demand processes. We generated two test beds consisting of 2,000 and 3,888 problem instances for identical (in terms of costs, lead times, and demand distributions) and nonidentical retailers cases, respectively. The number of retailers is restricted to two in the nonidentical retailers case.

The results directed us to a clear and complete overview on when the relative gap is small and when not. In the identical retailers case, the relative gap is small when one of the following conditions holds:

• the coefficient of variation is low or moderate,

• the added value at the warehouse is negligible compared to the ones at the retailers,

• the warehouse lead time is short and the retailer lead times are long.

As long as any one condition is satisfied, independent of the extent of the other input parameters, the relative gap is found to be small. In other problem instances, large relative gaps up to 38.6% are observed. The main drivers of large relative gaps are high coefficients of variation and a long warehouse lead time. In the nonidentical retailers case, the relative gap is small when the warehouse lead time is short and lead time of the big retailer (in terms of mean demand) is long. The main determinants of large gaps (up to 186.9%) are positive added value at one retailer and zero at the other, and long warehouse lead time.

Our main contribution to the literature is as follows. To the best of our knowledge, this is the most comprehensive numerical study specifically targeting to assess the impact of the balance assumption on the expected long-run cost. We explicitly identify the parameter settings under which the relative gaps are small. We show that the balance assumption may lead to large gaps in many settings, which contradicts with the conviction that it leads to an accurate approximation in almost all cases. The settings with considerable gaps indicate that either LB is an inaccurate approximation or the LB heuristic policy performs poorly, or both. Further, the available heuristics in the literature, which are based on the balance assumption, cannot be relied on for these problem instances. Our results point out that the scenarios with moderate or large relative gaps are practically relevant, so there is a good prospect for future research on these settings (e.g., to determine the position of the true optimal cost between the bounds). The analysis of the relations between the relative gap and the input parameters led us to new and interesting insights, e.g., shrinkage in the relative gap when retailer lead times increase, the so-called forwarding-to-the-small-retailer phenomenon, and the combined effect of retailer size and other input parameters on the relative gap.

The rest of the paper is organized as follows. The literature review on the balance assumption is given in Sect. 2. We present the notation, the model and a brief analysis in Sect. 3. Section 4 is dedicated to the presentation and discussion of the numerical results. A detailed summary of the results and the insights learned are given in Sect. 4.3. We close with a brief conclusion and directions for further research in Sect. 5.

2 Literature on the balance assumption

As discussed in Sect. 1, the balance assumption is utilized extensively in the literature, but there are only a few studies that analyze the quality of this assumption. Zipkin (1984) proposed the first analytical approach, which uses dynamic programming. In a relatively simple setting (zero lead times for orders and shipments, warehouse as a cross-docking point), the author developed a DP that accounts for the imbalance in the system. In the spirit of the induced penalty cost approach of Clark and Scarf (1960), the system cost is modelled consisting of two components: cost obtained under the balance assumption, and an additional cost that is a consequence of the imbalance in the system. A numerical study shows the accuracy of the approximation for the limited number of scenarios considered. It is concluded that imbalance can be considerable when demand variances are large. The studies by van Donselaar and Wijngaard (1987), and van Donselaar (1990) investigate the effect of imbalance on P ₁ service level, i.e., probability of stockout. In the former study, the results of a numerical study conclude the little impact of imbalance on the system service level. We believe that the numerical study conducted is rather restricted to come to such a conclusion. The latter paper, incorporates the effect of batch sizes on the imbalance of retailer inventories.

Federgruen and Zipkin (1984a), Kumar and Jacobson (1998), Axsäter et al. (2002), and Gallego et al. (2007) developed heuristics for the control of one-warehouse multi-retailer systems. Since the optimal policy and the associated cost is unknown, instead of comparing the cost of their heuristics to the true optimal cost, they all used the relative gap between the optimal cost of the system under the balance assumption and the cost of the heuristics (found by simulation) as a performance measure. The numerical results of these papers give rough ideas on the effect of the balance assumption on the system-wide cost. The results by Federgruen and Zipkin, and Kumar and Jacobson indicate that the gaps are small in general, with maximum relative gaps of 6.42 and 0.78%, respectively. Axsäter et al. considered a total of 68 scenarios where several of them exhibit high relative gaps with a maximum of 226.5%. Similarly, Gallego et al. report cases with high relative gaps, especially when some of the retailers have negligible added value.

In this study, we follow the same line of thought of Federgruen and Zipkin (FZ), Kumar and Jacobson (KJ), Axsäter et al. (AMS) and Gallego et al. (GOZ), but our study is different in certain aspects. The main dissimilarities are:

• (1) The focal point of these four studies is the performance of their heuristics; we focus particulary on the effect of the balance assumption. Hence, while we consider 5888 scenarios, FZ, KJ, AMS and GOZ have 138, 68, 68 and 409 scenarios, respectively.

• (2) FZ consider a fixed cost for ordering from the external supplier and AMS assume a fixed batch size for warehouse orders; we do not consider these issues.

• (3) FZ and KJ consider a warehouse that cannot hold stock; we relax this restriction.

• (4) FZ, and KJ assume normal demands at the retailers; when the coefficient of variation is higher than 0.5, the normal distribution assumption creates complications due to significant probability of negative demand appearing in the analysis. In real life, the coefficient of variation is higher than 0.5 in many cases, and can even be more than three, see Doğru (2006) for real life examples. GOZ consider Poisson demands. The Poisson distribution has a coefficient of variation that is equal to the inverse of the square root of the mean. Hence, demand streams with high coefficient of variation can only be created with very low arrival rates. We model one-period demands as mixtures of Erlang distributions, which allows us to incorporate instances with coefficients of variation up to three, and change the coefficient of variation while keeping the mean demand constant.

• (5) For nonidentical retailers, FZ require the holding and penalty costs to be proportional, and KJ assume identical cost parameters among the retailers. We relax such restrictions.

• (6) GOZ consider a continuous-review model while the rest, including ours, study a periodic-review setting.

Especially, the points (4) and (5) allow us to consider some extreme scenarios (e.g., coefficient of variation of demand equal to 3, or added value of zero at a retailer) for the purpose of finding out the extent of the impact of the balance assumption.

3 Model and analysis

Consider a one-warehouse multi-retailer inventory system controlled centrally under a periodic review setting. The warehouse (indexed as stock point 0) places orders to an exogenous supplier with ample stock, and the retailers are replenished by shipments from the warehouse. The warehouse is allowed to hold stock. All lead times are assumed to be fixed. The retailers face the stochastic i.i.d. demand of the customers that are stationary and continuous on (0, ∞) with no probability mass at zero. Costs consist of linear inventory holding and penalty costs. Time is divided into periods of equal length and we assume that the following sequence of events takes place during a period:

• inventory levels are observed, the warehouse replenishes its inventory from the exogenous supplier, and any order due to arrive is received (at the beginning of the period);

• the on-hand inventory at the warehouse is allocated and the shipments due to arrive are received by the retailers (at the beginning of the period);

• demand occurs;

• holding and penalty costs are assessed on the period ending inventory and backorder levels (at the end of the period).

The objective is to minimize the expected holding and backordering costs of the system in the long-run. We use the conventional definition of echelon stock of a stock point, which is the stock at that stock point plus in transit to or on-hand at any stock point downstream minus the backorders. Echelon inventory position of a stock point is the echelon stock plus all inventory that is in-transit to this stock point. The notation used is given in Table 1.

Table 1 The notation for the study

3.1 Dynamics of the system

Before discussing the dynamics of the system, we introduce the concept of cost attached to an echelon. The total cost of the system at the end of an arbitrary period t is

$$ h_0\left(\hat{I}_0(t)-\sum\limits_{i\in J}\hat{I}_i(t)\right)+\sum\limits_{i\in J}(h_0+h_i)\hat{I}_i^+(t)+\sum\limits_{i\in J}p_i\hat{I}_i^-(t), $$

where a ⁺ = max{0, a} and a ⁻ =  − min{0, a} for $a\in {\mathbb{R}}$. Substituting $\hat{I}_i(t)=\hat{I}_i^+(t)-\hat{I}_i^-(t)$, rearranging the terms, and then using the identity $\hat{I}_i^+(t)=\hat{I}_i(t)+\hat{I}_i^-(t)$ yields

$$ \begin{aligned} h_0\left(\hat{I}_0(t)-\sum\limits_{i\in J}\hat{I}_i(t)\right)+\sum\limits_{i\in J}(h_0+h_i)\hat{I}_i^+(t)+\sum\limits_{i\in J}p_i\hat{I}_i^-(t) &\quad = h_0\hat{I}_0(t)+\sum\limits_{i\in J}h_i\hat{I}_i^+(t)+\sum\limits_{i\in J}(h_0+p_i)\hat{I}_i^-(t) \\ &\quad = h_0\hat{I}_0(t)+\sum\limits_{i\in J}h_i\hat{I}_i(t)+\sum\limits_{i\in J}(h_0+h_i+p_i)\hat{I}_i^-(t). \end{aligned} $$

We define $C_0(t)=h_0\hat{I}_0(t)$ as the cost attached to the echelon of the warehouse (echelon 0) at the end of period t, and $C_i(t)=h_i\hat{I}_i(t)+(h_0+h_i+p_i)\hat{I}_i^-(t)$ as the cost attached to the echelon of retailer i ∈ J at the end of period t.

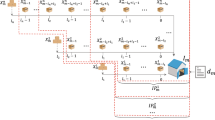
Consider the following two decisions and their effects on the expected costs, which starts with an order given to the supplier in period $t, t\in{\mathbb{Z}}^+_0$. Figure 1 illustrates the arguments.

• Ordering Decision: At the beginning of period t, the warehouse gives an order that raises the inventory position of the system up to y₀, i.e., IP₀(t) = y₀. (Note that y₀ is not bounded from above due to the assumption that the supplier has ample stock). The order materializes at the beginning of period t + l₀ and the available stock in the echelon of the warehouse at that epoch is y₀ − D₀(t,t + l₀ − 1). First, this ordering decision directly affects the cost attached to the echelon of the warehouse at the end of period t + l₀. The expectation of C₀(t + l₀) conditioned on IP₀(t) is

  $$ {\sf {\rm E}}[C_0(t+l_0)|IP_0(t)=y_0]={\sf {\rm E}}[h_0(y_0-D_0(t,t+l_0))]= h_0(y_0-(l_0+1)\mu_0). $$

  Second, it puts an upper bound on the level to which one can increase the aggregate echelon inventory position of the retailers in period t + l₀, i.e., ∑_i∈JIP _i (t + l₀) ≤ y₀ − D₀(t,t + l₀ − 1).

• Allocation Decision: At the beginning of period t + l₀, shipments to the retailers are determined; equivalently, the system-wide stock is allocated among all stock points. That is to say, the decisions of how much to send to each retailer and how much to keep at the warehouse are made. The inventory position of retailer i is increased up to w _i , i.e., IP _i (t + l₀) = w _i . Note that retailer replenishment decisions should be made subject to $\hat{IP}_i(t+l_0-1) {\leq}w_i$ for all i  ∈ J, and ∑_i∈Jw _i ≤ y₀ − D₀(t,t + l₀ − 1). These decisions directly affect the cost attached to echelon i at the end of period t + l₀ + l _i ; let G _i (w _i ) be the expected value of this cost conditioned on IP _i (t + l₀) = w _i :

  $$ \begin{aligned} G_i(w_i) & = {\sf {\rm E}}[C_i(t+l_0+l_i)|IP_i(t+l_0)=w_i] \\ & = {\sf {\rm E}}\left[h_i(w_i-D_i(t+l_0,t+l_0+l_i))+(h_0+h_i+p_i)\left(w_i - D_i(t+l_0,t+l_0+l_i)\right)^-\right] \\ & = h_i(w_i-(l_i+1)\mu_i)+(h_0+h_i+p_i){\sf {\rm E}}\left[(w_i - D_i(t+l_0,t+l_0+l_i))^-\right], \\ \end{aligned} $$

  for all i  ∈ J. Define C _cyc (t) as the sum of the costs that are a consequence of the warehouse’s ordering decision in period t:

  $$ C_{cyc}(t) = C_0(t+l_0)+\sum_{i \in J}C_i(t+l_0+l_i). $$

  (1)

  We refer to C _cyc (t) as the cycle cost of periodt.

Fig. 1

The consequences of an order placed in period t

Let $\Uppi$ denote the set of all ordering/allocation policies. Define g _π(x ₀) as the long-run average expected cost of policy π given an initial state x ₀, which is an N + l ₀ + 1 dimensional vector showing echelon stock of the warehouse, the echelon inventory positions of the retailers, and all the orders in-transit at time zero just before the decisions are made. The expected long-run average cost of any policy $\pi\in\Uppi$ is simply the average of the expected value of the sum of all costs attached to each echelon in an infinite horizon:

$$ g_{\pi}({\bf x}_0) \stackrel{\hbox{def}}{=} \lim_{T\longrightarrow\infty}\frac{1}{T} {\sf {\rm {E}}}\left[\sum\limits_{t=0}^{T-1}\sum\limits_{i=0}^NC_i(t)\right]. $$

Assuming that the limit exists and finite⁴, the expression above can be streamlined as

$$ \begin{aligned} g_{\pi}({\bf x}_0) & = \lim_{T\longrightarrow\infty}\frac{1}{T}{\sf {\rm E}} \left[\sum\limits_{t=0}^{T-1}\sum\limits_{i=0}^NC_i(t)\right] \\ & = \lim_{T\longrightarrow\infty}\frac{1}{T} {\sf {\rm E}} \left[\sum\limits_{t=0}^{l_0-1}C_0(t)+\sum\limits_{i \in J}\sum\limits_{t=0}^{l_0+l_i-1}C_i(t) +\sum\limits_{t=0}^{T-1}C_{cyc}(t)-\sum\limits_{t=T}^{T+l_0-1}C_0(t)-\sum\limits_{i \in J}\sum\limits_{t=T}^{T+l_0+l_i-1}C_i(t) \right] \\ & = \lim_{T\longrightarrow\infty}\frac{1}{T} \sum\limits_{t=0}^{T-1}{\sf {\rm E}}[C_{cyc}(t)], \\ \end{aligned} $$

where substituting (1) yields the second equality, and the third equality follows from all terms except the third term in the second equality being finite.

The optimization problem for a given initial state x ₀ is

$$ \mathop{\hbox{min}}\limits_{ \pi\in\Uppi} \,\, g_{\pi}({\bf x}_0), $$

(2)

and we denote the optimal cost by g*. The minimization problem given above is intricate since the decisions are highly interdependent. In the next subsection, we introduce the myopic allocation problem and discuss the balance assumption.

We close this subsection with a final remark on variable ordering and transportation costs. Let c ₀ be the variable ordering cost per unit at the warehouse and c _i be the unit transportation cost between the warehouse and retailer i. In an infinite horizon, μ₀ is the average quantity ordered in a period and μ _i is the average quantity shipped to retailer i per period. The average variable cost associated to ordering and shipments is c ₀μ₀ + ∑_i∈J c _i μ _i and constant in an infinite horizon average cost model, hence, it does not influence the ordering and allocation decisions. That is why it is common practice in the literature to omit these costs in the analysis.

3.2 Myopic allocation problem

Consider the sequence of decisions and the resulting costs as a result of increasing the inventory position of the system up to y ₀ at the beginning of period $t,\, t \in {\mathbb{Z}}_0^+$. Assume that the stock in the system at the beginning of period t + l ₀ (i.e., y ₀ − D ₀(t, t + l ₀ − 1)) is allocated among all stock points such that the sum of the expected holding and backordering costs of the retailers in the periods during which the allocated quantities reach their destinations (i.e. period t + l ₀ + l _i for retailer i) is minimized. Since the effect of the allocation decision on the subsequent periods is not considered, this way of rationing is called myopic allocation. The mathematical formulation of the myopic allocation problem of period t + l ₀ is as follows:

$$ \mathop{\hbox{min}}\limits_{w_i, \, \forall i \in J} \quad \sum\limits_{i\in J}G_i(w_i) $$

(3)

$$ s.t. \quad \sum\limits_{i\in J}w_i \leq y_0-D_0(t,t+l_0-1) $$

(4)

$$ \hat{IP}_i(t+l_0-1) \leq w_i \quad \forall i \in J, $$

(5)

where both constraints serve for the physical balance of the stocks. While (5) restricts the allocated quantities to be nonnegative, (4) assures that the sum of the allocated quantities cannot exceed the stock in the system. The solution of the myopic allocation problem depends on the amount to allocate, y ₀ − D ₀(t, t + l ₀ − 1), and each retailer’s inventory position, $\hat{IP}_i(t+l_0-1)$.

Although myopic allocation allows the allocation decisions to be made independent of the future allocation and ordering decisions, it still depends on previous periods’ decisions due to (5). Consider a relaxed version of the myopic allocation problem where (5) is omitted. This is equivalent to assuming that the quantities allocated to the retailers may be negative. We refer to this assumption as the balance assumption. This relaxation helps the analysis as follows. In the absence of (5), C _cyc (t) depends only on the ordering and allocation decisions that start with the order placed in period t; not on decisions of other periods. Then, it can be proved that a myopic allocation is optimal for (2), and the decomposition technique of Clark and Scarf (1960) can be applied to characterize the optimal ordering and allocation decisions (see Federgruen and Zipkin (1984b); Federgruen and Zipkin (1984c)). In addition, the myopic allocation problem becomes a convex and separable nonlinear optimization problem subject to a linear constraint, which can be solved by the Lagrangian technique.

Let $z_i:{\mathbb{R}} \rightarrow {\mathbb{R}}, i \in J$ be an allocation function such that z _i (a) is the portion of a allocated to retailer i for $a \in {\mathbb{R}}$. Assume that the system-wide stock at time $t\in{\mathbb{Z}}_0^+$ is $x\in {\mathbb{R}}$, i.e., I ₀(t) = x. The myopic allocation problem of period t under the balance assumption may be rewritten as:

$$ \mathop{\hbox{min}}\limits_{z_i(x), \, \forall i \in J} \left\{\sum_{i\in J}G_i(z_i(x)): \sum_{i\in J} z_i(x) \leq x, \, z_i(x)\in {\mathbb{R}}\, \forall\, i \in J\right\} $$

(6)

where a solution is denoted by {z _i (x)}_{i  ∈ J}. Let $\left\{z^{\ast}_i(x)\right\}_{i \in J}$ be an optimal solution of (6) for a given x. Define

$$ \begin{aligned} {\bf z} & = \hbox{set of allocation functions, i.e., } \{z_i(x),\, x\in {\mathbb{R}}\}_{i \in J}. \\ {\bf z}^{\ast} & = \hbox{set of optimal allocation functions, i.e.,} \left\{z_i^{\ast}(x),\, x\in {\mathbb{R}}\right\}_{i \in J}.\\ \end{aligned} $$

Note that G _i (·) is a newsvendor function, thus, is convex. Let $y_i^{\ast} = \hbox{arg\,min}\,G_i(y_i)$, and verify that $y_i^{\ast}$ satisfies the following well-known newsvendor equation:

$$ F_i^{(l_i+1)}\left(y_i^{\ast}\right)=\frac{h_0+p_i}{h_0+h_i+p_i} \quad {\rm for} \quad i=1,2,\ldots,N. $$

(7)

The interpretation of the expression above is that $y_i^{\ast}$ corresponds to a level at which the probability of being out of stock is $\frac{h_i}{h_0+h_i+p_i}$ for retailer i.

The objective function in (6) is separable and consists of N convex components. The solution $\left\{z_i^{\ast}(x)=y_i^{\ast}\right\}_{i \in J}$ is optimal for (6) when the constraint is not binding, i.e., for $x > \sum_{i\in J}y_i^{\ast}$. For $x < \sum_{i\in J} y_i^{\ast}$, Lagrangian relaxation can be used to find an optimal solution for (6).

3.3 Lower bound model

The balance assumption relaxes a constraint in the original optimization problem. Thus, (6) is used for allocation instead of (3)–(5). Due to this relaxation, the expected average cost obtained by an optimal policy derived under the balance assumption serves as a lower bound for (2).

Denote a base stock policy by a tuple (y ₀, z), where y ₀ is the target echelon inventory position of the warehouse, and z _i (x) for all i  ∈ J are the target levels of the retailers when the system-wide on-hand stock is x. The decisions are made such that, at the beginning of each period $t\in {\mathbb{Z}}^+_0$:

• the echelon inventory position of the warehouse is increased to y ₀, i.e., IP ₀(t) = y ₀,

• the inventory position of retailer i is raised to z _i (I ₀(t)) where {z _i (I ₀(t))}_i∈J is a solution that satisfies the constraints of (6).

Consider the expected cycle cost of period t. As mentioned before, under the balance assumption, ${\sf {\rm E}}[C_{cyc}(t)]$ depends only on the ordering and allocation decisions that start with an order placed in period t. As a result, it can be shown that a base stock policy $\left(y_0^{\ast}, {\bf z}^{\ast}\right)$ is the optimal replenishment policy with $y_0^{\ast}$ satisfying the following newsvendor-type equations:

$$ \int\limits_{0}^{\infty}F_i^{(l_i+1)}\left(z_i^{\ast}\left(y_0^{\ast}-u\right)\right) dF_0^{(l_0)}(u)=\frac{p_i}{h_0+h_i+p_i} \quad \forall i \in J, $$

(8)

(cf. Diks and de Kok (1998)). Equation (8) indicates that $y_0^{\ast}$ is the level at which the probability of being out of stock at retailer i is $\frac{h_0+h_i}{h_0+h_i+p_i}$ assuming that the system never experiences imbalance.

Due to the fact that the warehouse order-up-to level $\left(y_0^{\ast}\right)$ and optimal allocation functions $\left({\bf z}^{\ast}\right)$ are independent of time, policy $\left(y_0^{\ast}, {\bf z}^{\ast}\right)$ can be applied to optimize each period’s cycle cost within the horizon. Thus, the expected average cost obtained by following $\left(y_0^{\ast}, {\bf z}^{\ast}\right)$ is a lower bound (LB) for (2).

3.4 Constructing an upper bound

Consider base stock policy $\left(y_0^{\ast}, {\bf z}^{\ast}\right)$, which is discussed in Sect. 3.3. When policy $\left(y_0^{\ast}, {\bf z}^{\ast}\right)$ is implemented, there might be negative allocations, which make it infeasible to apply the solution of (6). Consider the following feasible policy, which we refer to as LB heuristic policy since it is based on the lower bound model:

• ordering: the inventory position of the warehouse is raised to $y_0^{\ast}$ at the beginning of each period,

• allocation: the myopic allocation problem given in (3)–(5) is solved to determine the shipment quantities.

The expected cost of the LB heuristic policy is an upper bound (UB) for g ^*. Unfortunately, it is not that straightforward to calculate the expected average cost of the LB heuristic policy, so an estimate can be obtained by simulating the system under this policy. (See also Axsäter et al. (2002, p. 79).)

3.5 The gap between LB and UB

For a given problem instance, the optimal inventory control parameters can be calculated for the lower bound model since analytical results are available. An estimate for an upper bound can be determined by simulating the LB heuristic policy. Since g ^* lies between LB and UB, the gap can be used to measure the impact of the balance assumption on the expected system-wide cost. Recall that $\epsilon\%= 100\frac{UB-LB}{LB}$ where $\epsilon\%$ is defined as the relative gap. If $\epsilon\%$ is small for a problem instance, then one can conclude that the balance assumption is not restrictive for that setting. While LB is an accurate proxy for g ^*, the LB heuristic policy is a good heuristic. On the other hand, a moderate or a large $\epsilon\%$ requires further investigation, which is not the purpose of this paper (we have already discussed this issue in Sect. 1; see also Sect. 5).

4 Numerical study and results

Our main objective is to identify the input parameter settings for which the resulting relative gaps are small and for which they are not. In addition, we try to illustrate the effect of lead times, holding and penalty costs, and the demand processes of the retailers on the relative gap. In order to achieve these goals, two test beds are generated; one for the case where retailers are identical, and the other for nonidentical retailers.

We use the words scenario and problem instance interchangeably for each combination of the input parameters N, l ₀, h ₀ and h _i , p _i , μ _i , l _i , cv _i for i = 1, ..., N. For the calculation of UB, each scenario was simulated for at least 200 replications and terminated as soon as the width of a 95% confidence interval was within 1% of the estimated average cost.

We assume that the underlying demand distribution of a retailer in a given period is a mixture of Erlang distributions with the same scale parameter. An Erlang-k distributed random variable (which is a sum of $k\in {\mathbb{Z}}^+$ independent exponentially distributed random variables with the same mean λ⁻¹) is denoted by E _k,λ and the cumulative probability distribution function is $E_{k,\lambda}(x)=1-\sum_{j=0}^{k-1}\frac{(\lambda x)^j} {j!}e^{-\lambda x}$ for x ≥ 0.

When cv _i ≤ 1, a mixture of E _k-1,λ and E _k,λ distributions is fitted for the one-period demand distribution of retailer i; i.e., $F_i^{(1)}(x)=pE_{k-1,\lambda}(x)+(1-p)E_{k,\lambda}(x)$ for x ≥ 0. The parameters k ≥ 2, 0 ≤ p ≤ 1 and λ are chosen such that:

$$ \frac{1}{k} \leq cv_i^2 \leq \frac{1}{k-1}, \quad p= \frac{1}{1+cv_i^2} \left[ kcv_i^2-\sqrt{k\left(1+cv_i^2\right)-k^2cv_i^2} \right], \quad \lambda =\frac{k-p}{\mu_i}. $$

When cv _i  > 1, a mixture of E _1,λ and E _k,λ distributions is fitted; i.e., $F_i^{(1)}(x)=pE_{1,\lambda}(x)+(1-p)E_{k,\lambda}(x)$ for x ≥ 0. The smallest k ≥ 3 that satisfies $cv_i^2 \leq \frac{k^2+4}{4k}$ is chosen. The values of p and λ are determined by:

$$ p= \frac{2kcv_i^2+k-2-\sqrt{k^2+4-4kcv_i^2}}{2(k-1)\left(1+cv_i^2\right)}, \quad \lambda =\frac{p+k(1-p)}{\mu_i}. $$

(See Tijms (2003, pp. 444–446) for details.)

4.1 Identical retailers

The retailers are identical in terms of lead time, holding and penalty costs, and the demand processes, i.e., l _i  = l _i+1, h _i  = h _i+1, p _i  = p _i+1,  μ _i  = μ_i+1, and cv _i  = cv _i+1 for i = 1, ..., N − 1. Without loss of generality, the mean demand (μ _i ) and the holding cost (h ₀ + h _i ) at each retailer i is kept at 1 for all scenarios. The following set of parameters is used (for i = 1, 2, ..., N):

$$ \begin{aligned} h_i & = 0,0.1,0.5,0.9,0.99 \quad \quad \quad \quad p_i = 4,9,19,99 \quad N=2,3,4,5 \\ (l_0,l_i) &= (1,1),(1,3),(3,1),(1,5),(5,1) \quad cv_i = 0.25,0.5,1,2,3. \\ \end{aligned} $$

The penalty costs are chosen to assure no-stockout probabilities of 80, 90, 95, and 99% at each retailer under an optimal policy in the lower bound model. Additional inventory holding cost at a stock point reflects the added value at that point. Notice that as h _i increases from 0 to 0.99, the added value at the warehouse decreases since h ₀ + h _i  = 1. A full factorial design is used to generate a test bed that consists of 2,000 problem instances.

During the simulation runs for computing UB, the probability of imbalance was also estimated. The probability of imbalance is defined as the fraction of periods in which a negative quantity is allocated to a retailer when (6) is solved.

We use the analysis of variance to test the impact of the factors (cv _i , h _i , p _i , N, l ₀, l _i ) and their two-factor interactions on $\epsilon\%$. The results of the analysis showed that there is no statistical evidence suggesting N and its two-factor interactions with the other factors have affect on $\epsilon\%$. Also, the interaction between some other factors were found to be not statistically significant. Table 2 summarizes the results of the analysis of variance with statistically significant factors and interactions. All effects considered in the model are significant at 99% level. The R ² and adjusted R ² for the model are 0.76 and 0.75, respectively. The ANOVA table suggests that most of the variance in the data set can be explained by the main effects of cv _i , h _i and l ₀, and their interactions. For example, the largest partial sum of squares in the model is due to the interaction between cv _i and h _i , which implies that the effect of the coefficient of variation on the relative gap varies as a function of the additional holding cost at the retailers. Thus, we give the statistics related to the data in two-by-two tables, each corresponding to one interaction in the ANOVA model. The results are given in Tables 3 and 4. For example, the first part of the table shows the effect of the coefficient of variation of demand and the additional holding cost at the retailers. The upper left corner of the table gives various statistics for a set of 80 problem instances having cv _i  = 0.25 and h _i  = 0 for i = 1, 2, ..., N. The tabulated statistics are average, standard deviation and maximum relative gap (denoted by $ave. {\,}{\epsilon\%,}std. {\,}\epsilon\%$ and $max.{\,}{\epsilon}\%$, respectively), and average, standard deviation and maximum probability of imbalance (denoted by ave.  π, std. π and max π, respectively).

Table 2 ANOVA table for fixed-effects model for identical retailers case

Table 3 The summary of the results from scenarios with identical retailers for different cv _i levels

Table 4 The summary of the results from scenarios with identical retailers for different h _i levels

The main findings are summarized below.

• 1. There is statistical evidence that all parameters considered in the numerical experiments except the number of retailers (cv _i , h _i , p _i , l ₀, l _i ) have impact on the relative gap. Further, some two-way interactions of these parameters are also found to have an effect on $\epsilon\%$ as shown in Table 2.

• 2. In order to identify the impact of the balance assumption, we looked at $max{\,}\epsilon\%$ and $ave.{\,}\epsilon\%$ values in Tables 3 and 4. An input parameter resulting in $max{\, \epsilon\%\leq}5$ and $ave.{\,}{\epsilon\%\leq}1$ is considered to be a setting with a small relative gap. The results for identical retailers show that the relative gap is small when

  • the coefficient of variation of the retailers is low or moderate (i.e., cv _i  = 0.25, 0.5), or

  • the added value at the retailers is very high compared to the one at the warehouse (i.e., h _i  = 0.99).

  Especially in scenarios with low coefficient of variation, the relative gap is negligible, see $max{\,}\epsilon\%$ and $ave.\, \epsilon\%$ figures for cv _i  = 0.25 and 0.5. There are also some restricted regions where the relative gap is considered to be small, e.g., coefficient of variation of 1 and short warehouse lead time (l ₀ = 1), but we leave the discussions for later.

  Out of the 2,000 problem instances studied, 1,713, 1,487 and 1,275 of them have $\epsilon\%$ less than or equal to 5, 2, and 1, respectively. When the $\epsilon\%$ values (of all instances) are sorted, the scenarios with high relative gap figures have the following common parameter settings:

  • 40 scenarios with ${\epsilon\%}>25$; all having cv _i  = 3, l _i  = 1, l ₀ = 3 or 5, and h _i  = 0, 0.1 or 0.5,

  • 12 scenarios with $25 {\geq}{\epsilon\%}>20$; all having cv _i  = 3, l _i  = 1, and h _i  = 0, 0.1 or 0.5,

  • 36 scenarios with $20 {\geq}{\epsilon\%}>15$; all having cv _i  = 2 or 3, l _i  = 1, and h _i  = 0, 0.1 or 0.5,

  • 70 scenarios with $15 {\geq}{\epsilon\%}>10$; all having cv _i  = 2 or 3, and l _i  = 1.

  The common factor in settings above is high coefficient of variation and short retailer lead times. These observations and the figures in Tables 3 and 4 suggest that when a high coefficient of variation is coupled with moderate or low added value at the retailers, a long warehouse lead time and short retailer lead times, the gaps tend to be high.

• 3. We also analyzed the relationship between the relative gap and the imbalance probability. The Pearson correlation coefficient is estimated as 0.659, which indicates a positive correlation. Further, the imbalance probabilities are plotted against the corresponding $\epsilon\%$ values in Fig. 2, where a different symbol is used for each coefficient of variation value. First, the results show that a high probability of imbalance does not necessarily yield a high $\epsilon\%$, but a high π is a necessity for a large relative gap. Among all the instances, 273 and 85 of them have $\epsilon\%< 2$ and π > 0.15, and ${\epsilon\%<}1$ and π > 0.20, respectively. Second, when the points with very high $\epsilon\%$ and π values are analyzed, it turns out that they have long warehouse lead time, short retailer lead time and high coefficient of variation in common. There are 44 points in the region ${\epsilon\%\geq}24.03$ and π ≥ 0.37, all coming from scenarios with cv _i  = 2 or 3, and (l ₀, l _i ) = (3, 1) or (5,1).

• 4. The probability of having imbalanced retailer inventories tend to increase as the added value at the warehouse increases For any level of another factor (e.g., l ₀ = 1), observe that ave. π and max  π increases as h _i decreases in Tables 3 and 4.

Fig. 2

π (in percentage) vs. ${\epsilon\%}$ for scenarios with identical retailers

Having highlighted the main points, next, we further discuss the effect of the coefficient of variation, lead times, and cost parameters on the performance measures.

4.1.1 Coefficient of variation

There is a clear relationship between the coefficient of variation and the imbalance of inventories. For any level of another factor, observe in Table 3 that $max{\,}\epsilon\%$ and $ave.{\,}\epsilon\%$ both grow as the coefficient of variation increases. This phenomenon is intuitive suggesting that as the variance in the demand process gets larger, the retailer inventories become more imbalanced. max  π and ave. π figures seem to support this argument. In Table 3, for max π and ave. π, a steady rise is observed as the coefficient of variation increases from 0.25 to 2, but the figures drop for 3. In order to explain this decline, we compared the order-up-to level of each of the 400 scenarios with cv _i  = 2 against the corresponding one with cv _i  = 3. It turns out that more stock is kept at the warehouse in the scenarios with cv _i  = 3, which results in lower imbalance probability. Even though the imbalance probability figures decrease for cv _i  = 3, it does not seem to effect the trend for gap measures.

4.1.2 Holding costs

In order to see the effect of the holding costs better, we extended the study for more h _i values between 0.1 and 0.8, see Table 5. The cost figures in Table 5 are chosen in a way that at one extreme there is no added value at the retailers (h _i  = 0); at the other extreme, 99% of an item’s value is attained at the retailers (h _i  = 0.99). Although Table 5 is organized such that the results are summarized with respect to h _i level, the trends observed are also valid when the level of cv _i , p _i , l ₀ or l _i is fixed like in Table 4. Our observations are as follows:

• Compare max π figures for different h _i values in Table 5. Between 0 and 0.7, max π is level at 0.64, and max  π decreases as h _i grows starting from h _i  = 0.8. For ave.  π, there is a steady decline as h _i increases. The trend in imbalance probability measures is due to keeping more stock at the warehouse than at the retailers as h ₀ decreases (compared to h _i ) since it is less costly. As a result, the chance of imbalance decreases.

• Compare $max{\,}\epsilon\%$ figures in Table 5. There is an increasing trend starting from h _i  = 0 until h _i  = 0.5. Then a sharp decline occurs at h _i  = 0.6 ($max{\,}\epsilon\%=38.55$ for h _i  = 0.5 and $max{\,}\epsilon\%=20.15$ for h _i  = 0.6). From this point on, $max{\,}\epsilon\%$ values decrease with another sharp decline at h _i  = 0.99. For $ave.{\,}\epsilon\%$, there is a steady decreasing trend as h _i increases starting from h _i  = 0.1 with sharp declines at h _i  = 0.6 and h _i  = 0.99.

Table 5 The summary of the results for various values of h _i (= 1 − h ₀) with identical retailers

These observations point out a general tendency that the relative gap decreases as the added value at the upper echelon decreases relative to the one at the lower echelon. This pattern is more apparent when the added value at the warehouse is less than the one at the retailers (i.e., for h _i  > 0.5).

4.1.3 Lead times

Recall from the analysis of variance that the main effect of l ₀ as well as its interactions with the coefficient of variation or the holding cost are found to be significant. The overall trend observed in Tables 3 and 4 is that all statistics tend to increase as l ₀ grows. For example, average (standard deviation) of relative gap is 1.42 (2.70), 4.13 (7.78) and 4.38 (8.43) for l ₀ equal to 1, 3 and 5, respectively. The logic behind this behavior is that it takes a longer time to recover from an imbalance situation when the warehouse lead time is long. If the system stays in imbalance for more periods in a row, the effect on the expected cost amplifies. However, this behavior seem not to hold for high h _i or low cv _i . As an example, consider h _i  = 0.9 in Table 4. All statistics increase when the warehouse lead time is extended from 1 to 3, but the same statistics decrease when l ₀ is further increased to 5.

Similar to the warehouse lead time, the main effect of the retailer lead time as well as its interactions with the coefficient of variation or the holding cost are found to be significant in the analysis of variance. Table 3 (4) show that for any level of cv _i (h _i ) all relative gap statistics decrease as l _i increases.

In the light of the trends observed for lead times, we extend the numerical study for more retailer lead time values while fixing the warehouse lead time at 1. The results are tabulated in Table 6. The first observation is that the relative gap is small when the warehouse lead time is short, and retailer lead time is long (i.e., (l ₀, l _i ) = (1, 7), (1,9), (1,11) or (1,13)). This observation is valid even if cv _i or h _i is fixed at any level considered in the numerical study. The steady decline in $ave. {\,}\epsilon\%$ and $std. {\,}\epsilon\%$ and a decreasing trend in $max{\,}\epsilon\%$ in Table 6 indicate that the relative gap shrinks as retailer lead time grows. This observation might seem counterintuitive at first sight because the variance faced by the system grows and the warehouse is forced to ration far in advance as retailer lead time increases. This is expected to have a negative effect on the balance of retailers and reflected by flat imbalance probability statistics for l _i ≥ 3. However, the impact of retailer lead time on the mean and the standard deviation of demand is different resulting in a lower coefficient of variation. As l _i increases, the mean and standard deviation of demand over the retailer lead time increases at the respective rate of l _i and $\sqrt{l_i}$, which yields a coefficient of variation decreasing at a rate $\sqrt{l_i}$. As we have demonstrated clearly, low coefficient of variation leads to smaller relative gaps.

Table 6 The summary of the results for l _i with identical retailers

4.1.4 Penalty costs

Even though the effect of the penalty cost is found to be statistically significant in the analysis of variance, the results do not show a clear trend between p _i and the measures considered. Consider the overall $\epsilon\%$ statistics in Table 3 in row titled “Total”. The measures first increase, then decrease and finally increase again as p _i increases. Although $ave. {\epsilon\%,} \,std. \epsilon\%$ and $max \,\epsilon\%$ show an increasing trend for cv _i  = 0.25,0.5,1, the results are mixed for cv _i  = 2,3. Moreover, we do not observe a common trend for each level of h _i in Table 4. Thus, we conclude that the results do not reveal any clear trend for the relative gap as p _i is perturbed.

4.2 Nonidentical retailers

We restricted the number of retailers to two (N = 2) so that the effect of asymmetry in each parameter can be captured easily. The following parameter settings are used:

$$ \begin{aligned} (h_0,h_1,h_2) & = (0.5,0,0.5),(0.5,0.5,0),(0.5,0.5,0.5),(0.9,0,0.1),(0.9,0.1,0), (0.9,0.1,0.1) \\ (cv_1,cv_2) & = (0.5,0.5),(0.5,1),(0.5,2),(1,0.5),(1,1),(1,2),(2,0.5),(2,1),(2,2)\\ (l_0,l_1,l_2) & = (1,1,1),(1,1,5),(1,5,1),(1,5,5),(5,1,1),(5,5,5) \\ (\mu_1,\mu_2) & = (0.05,0.95),(0.2,0.8),(0.5,0.5) \\ (p_1,p_2) & = (9,9),(9,19),(19,9),(19,19) \\ \end{aligned} $$

All combinations of the parameters generate a test bed of 3888 problem instances. All through the paper, we interpret the mean demand as a representative of the size of a retailer. The values for mean demands are chosen to see the effect of big/small retailer and without loss of generality, the sum is kept at 1. Note that in all the problem instances considered, the first retailer is equal or smaller in size compared to the second. Three values are selected for the coefficient of variation: 0.5 (low), 1 (moderate), 2 (high). This leads to nine distinct combinations. We picked lead time values to reflect the effect of short warehouse and retailer lead times [(1,1,1)], long warehouse and retailer lead times [(5,5,5)], long warehouse-short retailer lead times [(5,1,1)] and vice versa [(1,5,5)], and short warehouse lead time and asymmetric retailer lead times [(1,1,5) and (1,5,1)]. From two values selected for penalty costs, high (19) and moderate (9), four combinations are generated to see the effect of equal and asymmetric penalty costs. We interpret the holding costs as a way of reflecting the added value. While (0.5,0.5,0.5) combination corresponds to an equal added value at all stock points, (0.9,0.1,0.1) represents high added value at the warehouse. The other combinations are chosen to see the effect of having zero added value at one of the retailers. This situation is relevant to production and distribution environments. Consider a finished product or a semi-finished assembly that is stored centrally to supply two downstream stock points: at one, negligible value is added, e.g., just transportation or packaging, and at the other there is a positive added value, e.g., a module is added or further assembly operations are carried out. In a distribution environment, the added value at the retailers may consist of transportation costs and the cost of the storage space, which might be almost zero for one and considerable for another.

Recall that except the number of retailers, all other parameters in the stochastic model are found to have a significant impact on the relative gap. Even though we restrict the number of retailers to two, the number of factors and their interactions to be considered in an analysis of variance is high in the nonidentical retailers case. Hence, we decided not to conduct an analysis of variance, but to discuss the trends and patterns in the results. A summary of the results can be found in Table 7, which is similar to Tables 3 and 4 in terms of organization. The main findings are given below.

• 1. Recall that we consider the conditions $max{\,}{\epsilon\%\leq}5$ and $ave.{\,}{\epsilon\%\leq}1$ as criteria for a relative gap to be small. The results in Table 7 show that for nonidentical retailers, the relative gap is small when the warehouse lead time is short, and the lead time of the second retailer (equal or larger in size) is long (i.e., (l ₀, l ₁, l ₂) = (1, 5, 5) or (1,1,5)).

  There are 1,888, 2,652 and 3,390 problem instances having $\epsilon\%$ less than or equal to 1, 2, and 5, respectively. The instances with high $\epsilon\%$ figures have the following common parameter settings:

  • 27 scenarios with ${\epsilon\%}{\geq}69.76$; all having (l ₀, l ₁, l ₂) = (5, 1, 1), (h ₀, h ₁, h ₂) = (0.5, 0, 0.5), and (μ₁, μ₂) = (0.05, 0.95),

  • 36 scenarios with $69.76>{\epsilon\%}{\geq}43.65$; all having h ₁ = 0 and (l ₀, l ₁, l ₂) = (5, 1, 1),

  • 55 scenarios with $43.65>{\epsilon\%}>25$; all having h ₁ = 0 and l ₀ = 5,

  • 23 scenarios with $25 {\geq}{\epsilon\%}>17.85$; all having h ₁ = 0 or h ₂ = 0, and l ₀ = 5,

  • 35 scenarios with $17.85 {\geq}{\epsilon\%}>15.3$; all having h ₁ = 0 or h ₂ = 0.

  The figures above reveal the fact that long warehouse lead time and having zero added value at one of the retailers may yield high gaps (especially zero added value at the small retailer). A through explanation of this issue is presented later where holding costs are discussed.

  It is interesting to notice that although the coefficient of variation turned out to be the main determinant of gaps in the identical retailers case, even (cv ₁, cv ₂) = (0.5, 0.5) may lead to $\epsilon\%$ as high as 178.17 in the nonidentical retailers case. Unlike in the identical retailers case, the relative gap is small only in a few parameter settings. In many practically relevant parameter combinations, we observe large gaps. Especially, when there is asymmetry in the size of the retailers, long warehouse lead time, or negligible added value at one of the retailers, large gaps may occur.

• 2. The Pearson correlation coefficient between $\epsilon\%$ and π is 0.542, which indicates a positive correlation. However, while a high relative gap requires a high imbalance probability, a high imbalance probability does not necessarily correspond to a high gap. The imbalance probabilities are plotted against the corresponding $\epsilon\%$ values in Fig. 3. Observe that no point is in the region low π and high $\epsilon\%$. In the region with high $\epsilon\%$ and π, there are 118 problem instances with ${\epsilon\%\geq}25.94$ and π% ≥ 62.51. All these instances have l ₀ = 5 and zero added value at the small retailer (μ₁ = 0.05 or 0.2).

Table 7 The summary of the results from scenarios with nonidentical retailers, N = 2

Fig. 3

π (in percentage) vs. ${\epsilon\%}$ for scenarios with nonidentical retailers

In the rest of this subsection, we discuss the relationships between the input parameters and the measures on the basis of trends. For example, we analyze how relative gap and imbalance probability measures are affected when μ₁ is decreased with respect to μ₂, and identify whether a clear trend exists.

4.2.1 Retailer size

The results show that as the size of the retailers become disproportionate, the relative gap grows. When μ₁ is decreased with respect to μ₂, we observe that all gap and probability measures increase. The impact of retailer size will be more evident as we discuss the other parameters like holding costs and coefficient of variation.

4.2.2 Holding costs

• Similar to the identical retailers case, we observe that as the added value at the warehouse increases, the retailer inventories tend to become more imbalanced. Compare $max\, \epsilon\%$ and $ave.{\,}\epsilon\%$ values in columns (0.5,0.5,0.5) and (0.9,0.1,0.1) of Table 7. When h ₀ gets larger, the system prefers to keep less stock at the warehouse, which in return increases the chance of imbalance. Larger max π and ave.  π in column (0.9,0.1,0.1) support the claim.

• We can also discuss the combined effect of size and holding costs. Recall that the first retailer is equal to or smaller than the second one with respect to size. In Table 7, compare the following columns: (0.5,0,0.5) to (0.5,0.5,0.5), and (0.9,0,0.1) to (0.9,0.1,0.1). The results indicate that when the added value at the first retailer becomes zero, imbalance emerges as an important issue. Note that low added value at a retailer increases its order-up-to level, see Eq. (7), so instead of retaining stock, the warehouse ships to this retailer. Since little or no inventory is kept at the warehouse, the chance of imbalance increases. There are two observations that verify this argument. First, all measures show a considerable increase when the holding cost at the first retailer becomes zero. Second, in terms of all measures the trend is stronger when h ₀ = 0.5 because all the stock kept at the warehouse is routed to the small retailer. Since not much stock is kept at the warehouse when h ₀ = 0.9 (due to high holding cost), the impact is weaker compared to h ₀ = 0.5 case. We do not observe such a strong trend when the added value at the second retailer decreases; compare the following columns in Table 7: (0.5,0.5,0) to (0.5,0.5,0.5), and (0.9,0.1,0) to (0.9,0.1,0.1).

  Table 8 shows all scenarios with (h ₀, h ₁, h ₂) equal to (0.5,0,0.5) and (0.5,0.5,0), grouped with respect to the mean demands. When the added value at the first retailer is zero, all statistics show a sharp increase when the first retailer’s mean demand decreases. In contrast, the aforementioned measures except max π and std. π decrease as the second retailer’s mean demand increases in case (0.5,0.5,0). In the light of these observations, we conclude that when the added value at one retailer is zero, both the probability and the extent of imbalance grows considerably as this retailer’s mean demand decreases with respect to the other. Under the balance assumption, the amount of stock to keep at the warehouse is underestimated. Since the optimal order-up-to level for the retailer with zero added value is infinity, anything that might have been kept at the warehouse is sent to this retailer. As the mean demand of this retailer decreases it creates more and larger imbalance in the system. We call this phenomenon of the system getting severely imbalanced due to no added value at the small retailer as forwarding-to-the-small-retailer.

Table 8 Forwarding-to-the-small-retailer effect

4.2.3 Penalty costs

Unlike the identical retailers case, interesting relationships are identified:

• The results confirm that as the penalty costs get larger, the relative gap grows. When (9,9) is compared against (19,19) in Table 7, all relative gap statistics increase.

• For the effect of size, compare: i. (9,9) against (9,19), ii. (9,9) against (19,9). In case (i), while probability measures do not show a trend, $max{\,}{\epsilon\%,}ave.{\,}\epsilon\%$ and $std.\, \epsilon\%$ all increase when the penalty cost of the second retailer is increased. However, in case (ii), there is hardly any change in any of the measures. We can conclude that as the penalty cost of the second retailer increases, the relative gap widens. When the penalty cost of the big retailer is high, the negative effect of overstocking at the small retailer gets stronger, resulting in a larger gap.

4.2.4 Coefficient of variation

In line with the identical retailers case, the impact of the coefficient of variation on the imbalance of inventories is well established. Compare the statistics for (0.5,0.5), (1,1) and (2,2) in Table 7. We observe that $ave.{\,}\epsilon\%$ grows while $std.\, \epsilon\%$ shrinks. Interestingly, $max{\,}\epsilon\%$ shows a considerable decrease as the demand variance grows. All these indicate an increasing trend in the relative gap as the coefficient of variation increases. Growing ave. π figures also support this tendency.

The joint effect of the retailer size and the coefficient of variation is more complicated. Recall that the first retailer is smaller or equal to the second retailer in terms of size (mean demand). In Table 7, when the second retailer’s coefficient of variation is kept constant and the first retailer’s is varied (compare columns i. (0.5,0.5), (1,0.5), (2,0.5) ii. (0.5,1), (1,1), (2,1) iii. (0.5,2), (1,2), (2,2)), or the coefficient of variation of the first retailer is fixed and the second retailer’s is varied (compare columns iv. (0.5,0.5), (0.5,1), (0.5,2) v. (1,0.5), (1,1), (1,2) vi. (2,0.5), (2,1), (2,2)), we observe different trends in the measures. In cases (i)–(iii), all measures show a positive trend as the coefficient of variation of the first retailer increases. For example, in case (i), $ave.{\,}\epsilon\%$ is 3.15, 3.92 and 5.48 for (0.5,0.5), (1,0.5) and (2,0.5), respectively. This behavior is intuitive since the demand variability faced by the system grows. However, the results are mixed for cases (iv)–(vi). On one hand, $max.{\,}\epsilon\%$ figures decrease considerably as cv ₂ is increased. On the other hand, $ave.{\,}\epsilon\%$ first increases (as cv ₂ increases to 1), and then decreases when cv ₂ becomes 2. For example, in case (iv), $ave.{\,}\epsilon\%$ is 3.15, 3.24 and 1.95 for (0.5,0.5), (0.5,1) and (0.5,2), respectively. These results hint that size asymmetry and coefficient of variation have a more complicated joint effect on the balance of inventories. Hence, we conducted further analysis, see Doğru et al. (2005), but the results had not revealed any clear trend or findings.

4.2.5 Lead times

• Warehouse lead time: The impact of warehouse lead time is in line with the observations from the identical retailers case. When the columns (1,1,1) and (5,1,1) of Table 7 are compared, one sees the drastic effect of warehouse lead time: $max{\, \epsilon\%,}\,ave.{\,}\epsilon\%$ and $std.{\,}\epsilon\%$ obtain very high values for l₀ = 5. When the warehouse lead time extends, the probability of having imbalanced inventories increases and an imbalance situation takes a longer time to fix, both of which widen the gaps.

• Retailer lead times: In Table 7, compare column (1,1,1) to (1,5,5). Although imbalance probability measures do not show a clear difference, $max{\,}{\epsilon\%,}\,ave.{\,}\epsilon\%$ and $std.{\,}\epsilon\%$ figures point out a considerable decrease as both retailer lead times increase. This observation is in line with the results of the identical retailers case. Next, we consider the impact of asymmetry in retailer lead times. The relative gap statistics are lower for (1,1,5) and (1,5,1) in comparison to (1,1,1). The extent of the decrease seems to depend on the size of the retailer whose lead time grows. If the big retailer’s lead time is increased (compare (1,1,5) against (1,1,1)), then the decrease in the relative gap tend to be more in comparison to the decrease observed when the small retailer’s lead time is increased (compare (1,5,1) against (1,1,1)). This observation can be explained by the phenomenon discussed for the identical retailers case that the lower coefficient of variation over the retailer lead time results in the gap shrinking. The decrease in the coefficient of variation of demand over the lead time of the retailer with the lower mean demand has limited impact.

4.3 Summary and insights

In this subsection, we summarize the results and insights obtained. Recall that a setting is considered to lead to a small relative gap when $max{\,}{\epsilon\%}{\leq}5$ and $ave.{\,}{\epsilon\%}\leq1$.

The results from the test bed of 2000 scenarios for the identical retailers show that the relative gap is small (irrespective of the values of the other input parameters) when one of the following conditions is satisfied:

• the coefficient of variation is low or moderate (cv _i  = 0.25 or 0.5),

• the added value at the warehouse is insignificant with respect to the retailers (h ₀ = 0.01 and h _i  = 0.99),

• short warehouse lead time and long retailer lead times ((l ₀, l _i ) = (1, 7),(1,9),(1,11) or (1,13)).

Under these settings, the use of the balance assumption is justified. Especially when the coefficient of variation is low (i.e., cv _i  = 0.25 or 0.5), $max.{\,}{\epsilon\%}\leq0.36$ and $ave.\, \epsilon\%$ is negligible. If none of these conditions hold then high relative gaps may occur; we have observed $\epsilon\%=38.6$. A high coefficient of variation, a long warehouse lead time, and a low or moderate added value at the retailers (relative to the warehouse) are the main determinants of large relative gaps.

The results from the test bed of 3,888 problem instances with nonidentical retailers indicate that the relative gap is small when the warehouse lead time is short and the lead time of the big retailer is long ((l ₀, l ₁, l ₂) = (1, 1, 5) or (1,5,5)). Note that the relative gap is small over a limited set of input parameters when the retailers are not identical. Large gaps (as high as 186.9%) are observed in scenarios with long warehouse lead time and/or positive added value at one retailer and zero at the other. The last point regarding negligible added values has also been reported by Gallego et al. (2007).

In the test bed for identical retailers, it is observed that the relative gap increases as (1) the added value at the warehouse (h ₀) increases relative to the one at the retailers (h _i ), (2) the coefficient of variation (cv _i ) increases, (3) the warehouse lead time (l ₀) increases, (4) the retailer lead times (l _i ) decreases. The last point is an interesting observation because as the retailer lead times extend, the demand variance faced by the system increases and the warehouse rations the on-hand stock far in advance, which may seem to cause the relative gap to grow. However, as the retailer lead times get larger, the coefficient of variation of demand over the lead time decreases, which leads to smaller relative gaps. The aforementioned four points are also observed in the test bed for nonidentical retailers. In addition, it is observed that the relative gap increases as (5) the asymmetry in the size of the retailers grows (i.e., as μ₁ and μ₂ become more disproportionate), (6) the added value at the small retailer becomes zero, (7) the size (i.e., the mean demand) of the retailer with zero added value decreases, (8) the penalty cost of the big retailer (p ₂) increases. The phenomenon in (6) is referred to as as forwarding-to-the-small-retailer, which is a result of overstocking at the small retailer due to negligible added value at this retailer. Forwarding-to-the-small-retailer leads to a severely imbalanced system, which results in big gaps. In such a case, one may consider putting an upper bound on the order-up-to level of the small retailer.

Scenarios with a high relative gap also exhibits a high imbalance probability, but a high imbalance probability does not necessarily imply a large relative gap. There are 85 and 601 scenarios with ${\epsilon\%<}1$ and π > 20 in identical and nonidentical retailers cases, respectively. These results may be important for developing heuristics that are based on or use imbalance probability (e.g., Verrijdt and de Kok (1995) and van der Heijden (1997)). Eppen and Schrage (1981) derived an approximate term for the probability of having a balanced allocation, and the findings reveal the fact that probability of imbalance grows as the number of retailers increases; our results for the imbalance probabilities are in line with this fact. In addition, our results show that the imbalance probability increases as the warehouse lead time extends, the added value at the warehouse increases (with respect to the one at the retailers), and the retailers become more disproportionate in terms of size.

5 Conclusion and further research

In this paper, we studied the effect of the balance assumption on the average expected cost in divergent inventory systems. The balance assumption is widely used in the analysis of periodic review divergent inventory systems and accepted to lead to a good approximation in many different settings. A relaxation of the original problem is obtained under the balance assumption, and the corresponding average expected cost is a lower bound. When the optimal policy of the relaxed model is modified (LB heuristic policy) and simulated, an upper bound is obtained. The relative gap between these bounds is used as a measure for the effect of the balance assumption. We explicitly determined the scenarios that lead to small relative gaps (i.e., the settings under which the use of the balance assumption is justified). In many practically relevant scenarios, which are identified expressly, the relative gaps are found to be moderate or large. This implies either the lower bound or the LB heuristic policy, or both are mediocre for such settings. For future research, the original optimization problem can be solved optimally by dynamic programming. Due to the curse of dimensionality, it is not possible to solve the problem instances of this paper (even for the simple one-warehouse two-retailers system) as they are. Thus, simple discrete demand structures and limited input parameters can only be considered. The results may help to assess the precise impact of the balance assumption and shed light on the optimal policy behavior, which can be important for developing better heuristics. We are actively working on this follow-up study.