1 Introduction

The invasion by exotic species has become one of the most serious threats to biodiversity and ecosystem functioning [35, 19, 39, 29]. Exotic species can ruin the ecological health and economic value of ecosystems [38, 34]. Native species can be negatively affected by exotic species or ecosystem changes caused by exotic invaders. Many species listed as threatened or endangered under the Endangered Species Act are at risk because of competition with, predation by, and pressures of nonnative species [27]. In parallel, some nonnative tree species used in commercial forestry cause major problems as invaders of natural ecosystems [10, 36]. For illustration purposes, we can quote American black cherry (Prunus serotina), which is an aggressive invader of forests with understories dominated by Scots pine (Pinus sylvestris) and spreads throughout European temperate forests (Starfinger 1997, [33, 16]).

Despite a number of empirical and theoretical studies [19, 40, 9, 23, 29], there is still no general model about why or when settlement becomes an invasion. Both the attributes that make a species an invader [17] and the characteristics that predispose an ecosystem to invasion [29] are still weakly understood.

What we know is that three factors promote the settlement of new species on an area: the availability of resources,Footnote 1 the absence of natural enemies or competitors, and the physical environment [30, 3]. Elton [12] addressed the subject of ecosystems’ biotic resistance and asserted that strong interactions between native and exotic species prevent the latter from spreading. For instance, competition theory postulates that competition arises when the niches of native and exotic species overlap [37]. However, strong interactions can also facilitate the settlement of invading species, which increases the survival rate of exotic species and decreases the survival rate of native species [32].

So as to limit the environmental and economic impacts of invasion [27], the invasive species management aims at reducing the invasion pace. Such as pointed out by Ramula et al. [28], the literature on this subject is substantial [2, 22], but the lack of general guidelines generates a multitude of population models for each invader. These population models work according to the demographic processes based on survival, growth, and fecundity. Given the absence of clear demographic profile of a successful invader, Crawley (1986) [6] asserted that simple demographic models are not useful. Nevertheless, models based on the logistic population growth, where the rate of reproduction is proportional to the existing population and the amount of available resources, have emerged (see [5, 14]). Our approach concurs with the latter.

Invasive species establish and spread stochastically (Davis et al. 2006, [9, 30]); fluctuations of the activities of invaders and residents are stochastic [30]. Indeed, provided that the ecological knowledge is not very strong and must be used cautiously, a degree of uncertainty over dynamics ought to be considered [2]. Therefore, a deterministic model is reductive, since it does not capture the environmental stochasticity. Although uncertainty is a central characteristic of the invasion process [39], the survey on biological invasion done by Born et al. [2] indicates that uncertainty arising in the ecological context of the invasive process is not handled. For example, the uncertainty about the impacts of an invasion on an ecosystem depends on the stage in the invasion process, which is the abundance of invading individuals; between emergence and full invasion, uncertainty is overriding. Marten and Moore [22] emphasize that the absence of biological uncertainty in deterministic bioeconomic models leads to significant bias in management solutions. Likewise, Olson and Roy [24] show that stochastic shocks to the population growth affect the choice of management strategy.

This paper answers the calls by Born et al. [2] and Saphores and Shogren [31] to study exotic pests respectively in uncertainty and Bayesian framework. Such as stated by Williamson [39], the quantitative prediction of invasion potential is equivalent to identifying hazards and risk probability. Along the lines of Ramula et al. [28], who explore general patterns based on survival and following the work by Bischi et al. [1], we aim at modeling population dynamics based on best responses and conditional probabilities that could guide resource managers and bioeconomists.

Our static game unveils pure and mixed Nash-equilibrium strategies. While not invading and not resisting are always the pure-strategy equilibria, there is a breaking-level probability in mixed strategies where, given the species survival rate, the best response for exotic species is to invade and the best response for native species is to resist. In a dynamic setting, we introduce a stochastic version of the semi-discrete balance equation in which we insert the probabilistic best responses. When the species survival probability is high and the availability of resources in the ecosystem is low, the Bayesian population dynamics shows that the rebalancing of populations operates in rapid dynamics, which is full density or extinction rapidly occurs.

After this opening section, we begin with the static game and present the pure- and mixed-strategy Nash equilibria in Section 2. Section 3 introduces the Bayesian population dynamics and discusses the properties of equilibria. Conclusive remarks are given in Section 4.

2 Static Model

Let e and n be an exotic and a native species that simultaneously interact. Let w > 0 represent the value of resources in the ecosystem, notably that of the biotope community resources, in which the two species evolve. Let α ∈ [0, 1] be the rate of availability of resources in the ecosystem. The availability factor reflects the hypothesis that the spreadFootnote 2 of nonnative species depends on the resource availability in the ecosystem [19].

Exotic species e’s behavior is defined by a set of two actions: it either settles or spreads in native species n’s environment. When e spreads, it does it at a cost or effort of c e  ≥ 0. Following the results in Ortega and Pearson [25], we consider c e  → 0 to stand for strong invaders, while c e  ≫ 0 describes weak invaders. Native species n holds a set of two actions as well. It can either endorse the invasion or resist it at a cost or effort of c n  ≥ 0. As hereinbefore, c n  → 0 portrays highly resistant residents, while c n  ≫ 0 stands for weak invasion resistance (see [21]). In sum, low cost reveals the ability to effortlessly invade or resist, and vice versa. In what follows, the cost for both species is assumed proportional, i.e., c e  ∝ c n  ≡ c.

Finally, let μ ∈ [0, 1] be the species survival probability. Even though a species is endowed with some resilience in the habitat, the confrontation with the other species reduces its payoff by the mortality rateFootnote 3 1 − μ. We assume that α and μ are exogenous, which is the nature decides ex ante on the rate of availability of resources and the likelihood of survival.

The symmetric game payoff matrix,Footnote 4 inspired by the tragedy of the commons, is as follows.

 

Species n

 

Resists

Endorses

Species e

Spreads

\( \left(1-\mu \right){\scriptscriptstyle \frac{\left(1-\alpha \right) w- c}{2}};\left(1-\mu \right){\scriptscriptstyle \frac{\left(1-\alpha \right) w- c}{2}} \)

μ(αw − c); 0

Settles

0; μ(αw − c)

\( \mu {\scriptscriptstyle \frac{\alpha w}{2}} \); \( \mu {\scriptscriptstyle \frac{\alpha w}{2}} \)

2.1 Pure Strategies

We consider the death probability of an invader (resister) and the survival probability of a settler (endorser). When a species spreads or resists, its expected payoff amounts to

$$ E\left({\pi}_{s, r}\right)=\left(1-\mu \right)\frac{\left(1-\alpha \right) w- c}{2}+\mu \left(\alpha w- c\right) $$
(1)

When a species settles or endorses, its expected payoff amounts to

$$ E\left({\pi}_{\overline{s},\overline{r}}\right)=0+\mu \frac{\alpha w}{2} $$
(2)

In pure strategy, a species will spread or resist only if \( {\pi}_{s, r}>{\pi}_{\overline{s},\overline{r}} \). It means that

$$ \mu <\frac{\left(1-\alpha \right) w- c}{\left(1-2\alpha \right) w+ c} $$
(3)

When the survival probability is low enough, native (exotic) species will resist (spread). Yet, if native (exotic) species resists (spreads), exotic (native) species should not invade (resist) because of the cost. Exotic (native) species best response is then to settle (endorse). Thereby, when the survival probability is high enough, the species best response is to endorse (settle), which in pure strategy is the Nash equilibrium.

Proposition 1

For any survival probability such that \( \mu >{\scriptscriptstyle \frac{\left(1-\alpha \right) w- c}{\left(1-2\alpha \right) w+ c}} \), the Nash equilibrium corresponds to the pair of pure strategies {species e settles; species n endorses}.

2.2 Mixed Strategies

  1. a.

    Equilibrium strategy of species e given the expected payoff of species n

    Let p be the probability that exotic species e spreads and 1 − p that it settles. The expected payoff of native species n that resists resumes to

    $$ E\left({\pi}_n^r|\mu \right)= p\left[\left(1-\mu \right)\frac{\left(1-\alpha \right) w- c}{2}\right]+\left(1- p\right)\left[\mu \left(\alpha w- c\right)\right] $$
    (4)

    The expected payoff of native species n that endorses resumes to

    $$ E\left({\pi}_n^{\overline{r}}\Big|\mu \right)= p\left[0\right]+\left(1- p\right)\left[\mu \frac{\alpha w}{2}\right] $$
    (5)

    Equalizing \( E\left({\pi}_n^r\Big|\mu \right)= E\left({\pi}_n^{\overline{r}}\Big|\mu \right) \) yields

    $$ {p}^{\ast }=\frac{ w\alpha \mu -2 c\mu}{w\left(\alpha +\mu -1\right)- c\left(3\mu -1\right)} $$
    (6)

Lemma 1

In mixed strategies, the best response for exotic species e is to spread with probability p ∗.

  1. b.

    Equilibrium strategy of species n given the expected payoff of species e

    Let q be the probability that native species n resists and 1 − q that it endorses. Setting up \( E\left({\pi}_e^s\Big|\mu \right)= E\left({\pi}_e^{\overline{s}}\Big|\mu \right) \) yields

    $$ {q}^{\ast }=\frac{ w\alpha \mu -2 c\mu}{w\left(\alpha +\mu -1\right)- c\left(3\mu -1\right)} $$
    (7)

Lemma 2

In mixed strategies, the best response for native species n is to resist with probability q*.

We can now write the following statement.

Proposition 2

Given the survival probability of species, the mixed-strategy Nash equilibrium corresponds to {species e spreads with p*, species n resists with q ∗|α, μ, w, c}.

3 Dynamic Model

Understanding population attributes of invasive species is a prerequisite to manage invasions efficiently [29]. For that reason, let us carry out an evolutionary analysis over the species spreading. Species can invade and resist at any time. Since they do not have knowledge of the underlying structure of the game, we assume that the switching mechanism takes place according to a social learning mechanism [11, 13, 1]. It is now admitted that social learning generates imitation and protoculture. As well, we know that ecological selection favors successful strategies which will replicate and spread in the population in time [13].Footnote 5

Following a work by Bischi et al. [1], we assume that a species samples a species that has chosen the opposite strategy in the past. At each time period, if the payoffFootnote 6 of the sampled species is greater than its own, the latter switches to this strategy. The sampling follows the uniform probability law so the probability of comparing payoffs with species of a given strategy is proportional to the fraction of species using that strategy.

Let the population of exotic species be divided in fractions of spreaders s t and settlers \( {\overline{s}}_t \) operating in period t, such that \( {s}_t+{\overline{s}}_t=1 \). In parallel, let the population of native species be divided in fractions of resisters r t and endorsers \( {\overline{r}}_t \) operating at t, with \( {r}_t+{\overline{r}}_t=1 \). The sum denotes a normalized subpopulation proportion where 0 corresponds to extinction and 1 to the maximal subpopulation proportion.

3.1 Spreading Dynamics of Exotic Species

The probability to switch from spreading to settlement is \( {\rho}_{s\overline{s}} \). This probability is obtained as follows

$$ {\rho}_{s\overline{s}}=\overline{s} \Pr \left({\pi}_e^{\overline{s}}>{\pi}_e^s\right)=\left(1- s\right) \Pr \left({\pi}_e^{\overline{s}}>{\pi}_e^s\right) $$
(8)

Given that the native species equilibrium strategy equates the exotic species expected payoffs at q ∗, we have \( \Pr \left({\pi}_e^{\overline{s}}>{\pi}_e^s\right)=\tilde{q} \), with \( \tilde{q}\ge {q}^{\ast } \). It implies that \( {\rho}_{s\overline{s}}=\left(1- s\right)\tilde{q} \).

Symmetrically, we have \( {\rho}_{\overline{s} s} \) such that

$$ {\rho}_{\overline{s} s}= s \Pr \left({\pi}_e^s>{\pi}_e^{\overline{s}}\right) $$
(9)

This time, we have \( \Pr \left({\pi}_e^s>{\pi}_e^{\overline{s}}\right)=1-\tilde{q} \), with \( 1-\tilde{q}<{q}^{\ast } \), and \( {\rho}_{\overline{s} s}= s\left(1-\tilde{q}\right) \).

The semi-discrete dynamic equation describing the expected fraction of spreaders among exotic species is given by

$$ {s}_{t+1}=1-\left[{s}_t+{\overline{s}}_t \Pr \left[{\rho}_{\overline{s} s}\Big|{s}_t\right]-{s}_t \Pr \left[{\rho}_{s\overline{s}}\Big|{\overline{s}}_t\right]\right] $$
(10)

Since resistance deters invasion, s t + 1 decreases with \( \tilde{q} \). Equation (10) can be interpreted as a variant of the balance equation, where species change strategies in light of conditional probabilities but cannot appear nor disappear from nowhere.

We follow the rationale of population growth models, but the novelty of our dynamic balancing lies in the probability of switching strategy conditional on the density of species which strategy is being benchmarked. We term it Bayesian population dynamics. Indeed, an entity is likely to be prone to the mass effect, which is its likelihood to switch strategy is proportional to the size of the population already using that strategy. Rewritten, the precedent equation yields

$$ {s}_{t+1}={s}_t\left(2\tilde{q}-2{\tilde{q}}^2\right)+{\left(\tilde{q}-1\right)}^2 $$
(11)

3.2 Resistance Dynamics of Native Species

The probability of switching from resistance to endorsement is \( {\rho}_{r\overline{r}} \). We thus have

$$ {\rho}_{r\overline{r}}=\overline{r} \Pr \left({\pi}_n^{\overline{r}}>{\pi}_n^r\right)=\left(1- r\right) \Pr \left({\pi}_n^{\overline{r}}>{\pi}_n^r\right) $$
(12)

The precedent involves that \( \Pr \left({\pi}_n^{\overline{r}}>{\pi}_n^r\right)=\tilde{p} \), with \( \tilde{p}\le {p}^{\ast } \), and \( {\rho}_{r\overline{r}}=\left(1- r\right)\tilde{p} \).

In parallel, we have \( {\rho}_{\overline{r} r} \) such that

$$ {\rho}_{\overline{r} r}= r \Pr \left({\pi}_n^r>{\pi}_n^{\overline{r}}\right) $$
(13)

Again, \( \Pr \left({\pi}_n^r>{\pi}_n^{\overline{r}}\right)=1-\tilde{p} \), with \( 1-\tilde{p}>{p}^{*} \), and \( {\rho}_{\overline{r} r}= r\left(1-\tilde{p}\right) \).

The equation describing the expected fraction of resisters among native species is given by

$$ {r}_{t+1}={r}_t+{\overline{r}}_t \Pr \left[{\rho}_{\overline{r} r}\Big|{r}_t\right]-{r}_t \Pr \left[{\rho}_{r\overline{r}}\Big|{\overline{r}}_t\right] $$
(14)

This time, r t + 1 increases with \( \tilde{p} \), which is a higher probability of spread is an incentive to resist. Rewritten, the Bayesian population dynamics yields

$$ {r}_{t+1}={r}_t\left(2{\tilde{p}}^2-2\tilde{p}\right)+2\tilde{p}-{\tilde{p}}^2 $$
(15)

3.3 Dynamical System

We assume that the fractions of spreading and resisting species are subject to a nonlinear system. The dynamic system D t + 1 can be described by the following map in ℝ2 in the variables s and r

$$ {D}_{t+1}:\left\{\begin{array}{l}{s}_{t+1}={s}_t\left(2\tilde{q}-2{\tilde{q}}^2\right)+{\left(\tilde{q}-1\right)}^2\\ {}{r}_{t+1}={r}_t\left(2{\tilde{p}}^2-2\tilde{p}\right)+2\tilde{p}-{\tilde{p}}^2\end{array}\right. $$
(16)

Any population configuration is represented by the pair of subpopulation densities of exotic and native species. The system has four corner equilibria, which is S = (0, 0), S = (0, 1), S = (1, 0), S = (1, 1), and an inner equilibrium S = (s*, r*). All corner equilibria represent null or full equilibria and can be easily interpreted. For example, S = (1, 0) means that the density of spreading individuals is 1 and the density of resisting individuals is 0. The inner equilibrium signifies that some of the individuals in the respective populations spread or resist.

The next stage consists in proving that the dynamic system yields inner solutions. It can be interpreted as a system of recurrence relations yielding unique solutions of

$$ \left\{\begin{array}{l}{s}_t^{*}=\frac{{\left(\tilde{q}-1\right)}^2{\left(2\tilde{q}-2{\tilde{q}}^2\right)}^t}{\left[1-{\left(2\tilde{q}-2{\tilde{q}}^2\right)}^{t-1}\right]\left[\kern0.5em {\left(2\tilde{q}-2{\tilde{q}}^2\right)}^t-{\left(2\tilde{q}-2{\tilde{q}}^2\right)}^{t-1}\right]}\\ {}{r}_t^{*}=\frac{\left(2\tilde{p}-{\tilde{p}}^2\right){\left(2{\tilde{p}}^2-2\tilde{p}\right)}^t}{\left[1-{\left(2{\tilde{p}}^2-2\tilde{p}\right)}^{t-1}\right]\kern0.5em \left[{\left(2{\tilde{p}}^2-2\tilde{p}\right)}^t-{\left(2{\tilde{p}}^2-2\tilde{p}\right)}^{t-1}\right]}\end{array}\right. $$
(17)

where for s ′ t  > 0 for \( \tilde{q}\ge 0.5 \) and r ′ t  > 0 for \( \tilde{p}\le 0.5 \).

In Williamson and Fitter [38]), we learn that invasions can be divided in stages of casual, established, and pest. Through biotic resistance, we similarly consider that plants progressively develop the ability to limit invasion (see [4]). By means of the bifurcation diagrams, let us now conduct numerical simulations to give an insight on the possible long-term population values, while the proportions of spreading and resisting individuals stand at one of the stages listed hereinabove.

As we now launch simulations, which start from different stages of s 0 and r 0, the dynamic mapping yields the following results.

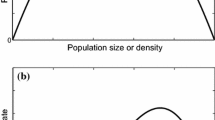
Figure 1 show the corner and inner equilibria trajectories of spreading species in view of the native species best response.

Fig. 1
figure 1

Bifurcation diagrams of \( \left( s\Big|\tilde{q}\right) \) for s 0 = {0, 1, s*}

Full size image

The corner equilibrium s 0 = 0 exhibits two types of patterns. The first pattern is a fixed point of s = 0 independent from \( \tilde{q} \) and corresponds to the continuance of the initial proportion of spreading individuals. The second pattern corresponds to a series of periodic orbits which all begin at 1 when \( \tilde{q}=0 \) and bifurcate toward 0 in different shapes as \( \tilde{q}\to 1 \) or μ → 1. Thereby, for any level of availability of resources, the higher the native species survival rate, the lower the density of spreading species. The orbits we perceive are either convex or s-shaped suggesting singular velocities of trajectories. Most of the simulated trajectories are s-shaped with an inflection point of coordinates {0.5, 0.5}. At these coordinates, decelerations are slow for \( \tilde{q}\in \left[0,0.25\right]\cup \left[0.75,1\right] \) or μ ∈ [0, 0.10] ∪ [0.60, 1] and fast for \( \tilde{q}\in \left[0.25,0.75\right] \) or μ ∈ [0.20, 0.50]. As a result, the strongest impact of resistance on the fall of spreaders is at the expected average value.

Similar behavior is observed with s 0 = 1. We have an independent fixed point of s = 1. Periodic orbits start at 1 when \( \tilde{q}=0 \) and bifurcate toward 0 as \( \tilde{q}\to 1 \). The orbits are either concave or s-shaped. When simulated trajectories are s-shaped, we observe that the highest increase of resisters occurs for \( \tilde{p}\in \left[0,0.25\right]\cup \left[0.75,1\right] \). This means that resisters greatly respond to the risk of invasion when the probability is either low or high.

At last, the inner equilibrium exhibits periodic orbits attracted by s = 0. In equilibrium, there is either a full best response or some germinal response condemned to fade.

The spreaders inner equilibrium comes off when the native species survival rate is low. It increases in α, confirming the result by Kolb et al. [18] which states that increases in resource availability increase the invasibility of communities.

Given the evenness of s t + 1 and r t + 1, similar patters can be observed with the resisting population, except that r increases with \( \tilde{p} \) (Fig. 2).

Fig. 2
figure 2

Bifurcation diagrams of \( \left({r}_t\Big|\tilde{p}\right) \) for r 0 = {0, 1, r*}

Full size image

As for the inner equilibrium which occurs when resources become depleted and the spreaders survival rate increases, periodic orbits end either at 1 or 0. When the orbit ends at full density, its shape is concave, suggesting a deceleration of resisters starting from \( \tilde{p}=0.5 \).

We now analyze the stability of equilibria by means of the linearization analysis (see the Appendix). We assume that w = 10 and c = 5, meaning that the value the native species places on the biotope resources equals 10, for a cost or effort of resistance equal to 5. The probabilistic best response for exotic species is then to spread with probability

$$ {p}^{*}=\frac{2\mu \left(\alpha -1\right)}{2\alpha -\mu -1} $$

The same reasoning can be applied to native species. The eigenvaluesFootnote 7 we obtain indicate that the inner and corner equilibria display both stable and unstable configurations, depending on the values of α and μ.

Proposition 3

The stability of equilibria is parameter dependent.

In addition to the nature of steady–states, the eigenvalues also inform on the pace of rebalancing or convergence toward the steady–states. The numerical simulations reveal that, regardless of the stationarity, all five configurations display similar distributions of convergence pace. Roughly 95 % of cases reveal low rates of convergence (λ = ± 0.00). This is verified for nearly all levels of availability of resources and all rates of survival.

The only zone where the convergence pace suddenly becomes high and steady–states rapidly occur is when the survival probability tends to certainty, i.e., lim(μ) = 1, and resources become scarce, i.e., lim(α) = 0. This particularity is verified for both corner and inner equilibria and can be easily justified. When species are highly likely to survive in an environment where resources are in short supply, they are drawn into a race for resources. This, in turn, provokes a rapid population rebalancing, be it toward the steady–states.

Proposition 4

When the species survival rate and availability of resources in the ecosystem are respectively high and low, the rebalancing of subpopulations operates at a high pace.

4 Conclusion

As explained in the “Introduction,” there is still no global model about why or when an invasion occurs. We try to give an answer to this shortage by means of game theory and Bayesian population dynamics, using probabilistic best responses that we infuse in balance equations dependent on conditional probabilities.Footnote 8 Following this methodological novelty, our model yields a couple of intuitive results, such as invasion and resistance as best-response strategies or species fierce struggle for scarce resources.

Patten [26] states that the useful steady-state question is not whether steady–states are achieved in ecosystems, but rather whether there is a directing tendency that organizes the succession process. Our results give the intuition that a directing tendency could lie in the availability of resources in the ecosystem and the survival probability of species that compete for those resources.

To its detriment, our framework does not take into account other traits of exotic species than their resistance potential—life cycle or behavioral aspects of reproduction—or the abiotic components of the environment—light, temperature, water, gases, or soil properties—which clearly complexify the interactions between native and exotic species [38]. Nevertheless, its minimalism and Bayesian approach enable to emphasize the population dynamics when the subpopulation model species are endowed with the best-response strategies.

Following the literature on field experiments, case studies should be undertaken so as to confirm or infirm our theoretical results. For example, forest ecologists could initiate experiments by investigating the competition between the exotic and the native tree species or understory plants. In that way, they could test the population dynamics under different degrees of resource availability at various stages of the invasion process.