The importance of being thin

Abstract

This article outlines a family of approximations for solutions to the incompressible Navier–Stokes equations valid for flow domains that have one small dimension. The approach is applicable to two- or three-dimensional systems, steady or unsteady flows, viscous or inviscid fluids, high or low Reynolds numbers, and internal or external domains. Among the methods in this class are lubrication theories, slender-body theories, shallow-water theories, Hele–Shaw flows, and boundary layers. By displaying the commonalities in these, one sees a systematic approach to many fluid- flow problems as well as those in other fields.

1 Introduction

Arguably, the most important approximation in engineering and science is the Continuum Hypothesis in which the interactions of constituent entities are replaced by quantities averaged over a large-enough scale. The entities may be atoms, molecules, sand grains, automobiles, planets, or stars, depending on the system of interest. The mathematical systems that emerge are usually expressed in terms of partial-differential equations such as the Navier–Stokes equations of fluid mechanics, the Navier equations of solid mechanics, Maxwell’s equations in electromagnetics, or the equations of traffic flow. To be sure, these equations are great simplifications compared to the ‘molecular’ ones, but they are generally strongly nonlinear, and to learn the physics contained in them, one must ‘solve’ them. Exact solutions of these exist but only in the simplest of circumstances. Normally, one must find approximate solutions that capture the physics and give insight. Such approximations may depend on finding limiting cases that lead to analytic methods or they may be numerical simulations that often depend on the solutions being ‘well-behaved.’

One can imagine many techniques of approach to approximations, say, using asymptotic/perturbation methods, variational approaches, and a host of numerical simulations. The object of the present paper is to give an overview of a widely used family of approximations, all members of which utilize essentially the same observation: the domain of interest is thin in at least one direction. Different areas of application give rise to lubrication theory, slender-body theory, shallow-water theory, Hele–Shaw theory, and boundary-layer theory, among others. All of these are thin-domain theories though each has its own peculiarities. Sometimes the thinness is geometric in that it is known a priori and sometimes it is dynamically determined. It will be seen that the commonalities of the methods allow one to understand how to proceed on new problems that arise in practice.

In what follows, the methods will be discussed in fluid mechanical contexts, but it is quite clear that they have broad applications elsewhere.

Fig. 1

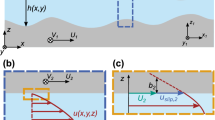
Two-dimensional domains containing liquid in D: a a rectangle, b a gentle-sloped region, and c a region with vertically-sloped ends [1]

Fig. 2

A horizontal rectangular domain containing liquid subject to a temperature gradient that drives a steady buoyancy-driven 2D steady flow [2]

2 Geometric thinness

2.1 A toy problem

In order to help define the means of approximation, it is convenient to consider a very simple problem discussed by Young and Davis [1]. The domains D for solutions are shown in Fig. 1; in (a) the thin slot is rectangular, in (c) it has vertical sides of various strengths and in (b) the top smoothly approaches zero height at the ends. These are two-dimensional regions in which the x-axis is horizontal and the z-axis points upward, as shown.

The problem is to find $\phi (x,z)$ in D such that

$$\begin{aligned} \phi _{xx}+\phi _{zz}=-k\quad \text {in}\;D \end{aligned}$$

(1)

with

$$\begin{aligned} \phi =0\quad \text {on}\;\partial D. \end{aligned}$$

(2)

Subscripts denote partial differentiation and constant $k>0$.

In particular, we seek solutions $\phi$ such that variations in x and z scale on width l and height $h_\mathrm{M}$, respectively. Introduce scaled variables

$$\begin{aligned} X=\frac{x}{l},\quad Z=\frac{z}{h_\mathrm{M}},\quad \text {and}\quad \Phi =\frac{\phi }{h_\mathrm{M}^2k} \end{aligned}$$

(3)

with $H=h=O(1)\;\text {as}\;\epsilon \rightarrow 0$, in which $h_\mathrm{M}$ is the maximum height of h and

$$\begin{aligned} \epsilon =\frac{h_\mathrm{M}}{l}. \end{aligned}$$

(4)

The domain is deemed thin if

$$\begin{aligned} \epsilon \ll 1. \end{aligned}$$

(5)

The scaled system now has the form

$$\begin{aligned} \epsilon ^2\Phi _{XX}+\Phi _{ZZ}=-1\quad \text {in}\;D \end{aligned}$$

(6)

and

$$\begin{aligned} \Phi =0\quad \text {on}\;\partial D. \end{aligned}$$

(7)

One can take advantage of the thinness of the domain by writing the formal perturbation series:

$$\begin{aligned} \Phi (X,Z)=\Phi _{0}+\epsilon ^2\Phi _{1}+O(\epsilon ^4), \end{aligned}$$

(8)

substituting into system (6, 7), and equating to zero coefficients of like powers of $\epsilon ^2$. At O(1)

$$\begin{aligned} \Phi _{0_{ZZ}}=-1\quad \text {in}\;D \end{aligned}$$

(9)

with

$$\begin{aligned} \Phi _{0}=0\quad \text {on}\;\partial D, \end{aligned}$$

(10)

so that

$$\begin{aligned} \Phi _{0} = \frac{1}{2}Z(H-Z). \end{aligned}$$

(11)

At $O(\epsilon ^2)$

$$\begin{aligned}&\Phi _{1_{ZZ}}=-\Phi _{0_{XX}}\quad \text {in}\;D \end{aligned}$$

(12)

$$\begin{aligned}&\Phi _{1}=0\quad \text {on}\;\partial D, \end{aligned}$$

(13)

giving

$$\begin{aligned} \Phi _{1}=\frac{1}{12}Z(H^2-Z^2)H'', \end{aligned}$$

(14)

where primes denote differentiation and thus

$$\begin{aligned} \Phi \sim \frac{1}{2}(H-Z)Z\left\{ 1+\frac{1}{6}\epsilon ^2(Z+H)H''\right\} . \end{aligned}$$

(15)

This approximation is well controlled if the sidewalls of D were absent. As well, if the slopes of H are moderate, e.g. if $H(X)=1-X^2$, form (15) holds in the whole domain. Otherwise, the dropping of the term $\epsilon ^2\Phi _{XX}$ as $\epsilon \rightarrow 0$ in the first approximation represents a singular perturbation, given that the highest X-derivative is lost. The most severe case is seen in Fig. 1a in which the sidewalls are vertical, and representation (15) loses validity near the ends.

In this singular case, there are boundary layers at $X=\pm 1$ that require reinstating the X-derivatives. Near $X=1$, write

$$\begin{aligned} \xi =\frac{1-X}{\epsilon } \end{aligned}$$

(16)

leading to

$$\begin{aligned} \Phi _{\xi \xi }+\Phi _{ZZ}=-1, \end{aligned}$$

(17)

returning the original equation, but now the domain is $\xi$ in the range $0\le \xi \le \infty$ on which one must solve Eq. (17) with $\Phi =0$ on the boundaries. That solution will automatically match the core solution (15) at leading order [1].

Consider now case (c) of Fig. 1 with

$$\begin{aligned} H = (1-X^2)^\alpha , \end{aligned}$$

(18)

where $\alpha \ge 0$ determines the severity of the vertical slopes at $X=\pm 1$. Near $X=1$, write

$$\begin{aligned} \eta =\frac{1-X}{g(\epsilon )}, \end{aligned}$$

(19)

where g is determined by the order of the non-uniformity in $\epsilon ^2HH''$ in Eq. (15), and further write

$$\begin{aligned} H(X)\sim f(\epsilon )H_{0}(\eta ), \end{aligned}$$

(20)

and because H vanishes at $X=1$, stretch Z as well

$$\begin{aligned} \zeta =\frac{Z}{f(\epsilon )} \end{aligned}$$

(21)

resulting in

$$\begin{aligned} \Psi _{\zeta \zeta }+\frac{\epsilon ^2f(\epsilon )}{g(\epsilon )} \Psi _{\eta \eta }=-f^2(\epsilon ), \end{aligned}$$

(22)

where $\Psi$ represents $\Phi$ in the new variables. To retain both derivative terms, take

$$\begin{aligned} \epsilon ^2 f(\epsilon )=g(\epsilon ). \end{aligned}$$

(23)

Now write

$$\begin{aligned} \Psi \sim f^2(\epsilon )\Psi _{0} \end{aligned}$$

(24)

so that

$$\begin{aligned}&\Psi _{0_{\zeta \zeta }}+\Psi _{0_{\eta \eta }}=-1, \end{aligned}$$

(25)

$$\begin{aligned}&\Psi _{0}=0\quad \text {on}\;\zeta =0, \end{aligned}$$

(26)

$$\begin{aligned}&\Psi _{0}=0\quad \text {on}\;\zeta =H_{0}(\zeta ). \end{aligned}$$

(27)

Here $f^2(\epsilon )\Psi _{0}$ must match $\Phi _{0}$,

$$\begin{aligned} \Phi _{0}=\frac{1}{2}(H-Z)\sim \frac{1}{2}f^2(\epsilon ) \left[ \zeta H_{0}-\zeta ^2\right] \end{aligned}$$

(28)

so that

$$\begin{aligned} \Psi _{0}\sim \frac{1}{2} \left[ \eta H_{0}-\eta ^2\right] \quad \text {as}\;\xi \rightarrow \infty . \end{aligned}$$

(29)

Now, if $\alpha =0$, this reduces to case (a) of Fig. 1, $H_{0}\equiv 1$, and there are $O(\epsilon )$ boundary layers at the ends. If $0<\alpha <1$, all derivatives are unbounded at the ends so that near $X=1$, the boundary-layer thickness is $1-X=O(\epsilon ^{\frac{1}{1-\alpha }})$. As $\alpha \rightarrow 0$, case (a) again emerges. As $\alpha$ increases from zero, the boundary layer shrinks and vanishes as $\alpha \rightarrow 1$ and the core solution becomes uniformly valid.

These examples show that thin domains spawn asymptotic solutions in which the details of the domain shapes determine the solution structures. In the sections to follow, mainly two-dimensional problems in fluid mechanics will be discussed.

Lubrication scaling In these 2D fluids problems, the coordinates will be (x, z) with corresponding velocity components (u, w), pressure p, and possibly a temperature T. Define the lubrication scalings and scaled variables as follows:

$$\begin{aligned} X= & {} \frac{x}{l},\quad Z=\frac{z}{h_\mathrm{M}}, \end{aligned}$$

(30)

$$\begin{aligned} U= & {} \frac{u}{u_{*}},\quad W=\frac{wl}{u_{*}h_\mathrm{M}}, \end{aligned}$$

(31)

and

$$\begin{aligned} P=\frac{p}{p_{*}}. \end{aligned}$$

(32)

The x-velocity scale $u_{*}$ is chosen by the dominant physical force balance, and the pressure scale $p_{*}$ is chosen so that $p_{x}$ balances either the viscous forces or the inertial terms in the x-component of the Navier–Stokes equation. For $\text {Re} \ll 1$,

$$\begin{aligned} p_{*}=\frac{\mu u_{*}l}{h_\mathrm{M}} \end{aligned}$$

(33)

and $\text {Re} \gg 1$,

$$\begin{aligned} p_{*}=\rho \mu _{*}^{2}, \end{aligned}$$

(34)

where $\mu$ is the viscosity, and $\rho$ is the density. The temperature scale needs no present explanation. The vertical height scale can be $h_\mathrm{M}$, the maximum as in Fig. 1b, the height h as in Fig. 1a, or the mean height $h_{0}$ in cases in which there is surface deformation.

2.2 Steady buoyancy-driven convection in a slot

Consider the slot shown in Fig. 2 in which the endwall temperature difference $\Delta T=T_\mathrm{H}-T_\mathrm{C}>0$ produces a horizontal density difference that drives a convective flow, as studied by Cormack et al. [2]. The flow and heat transfer are governed by the Navier–Stokes, continuity, and energy equations subject to the Boussinesq approximation [3] in which the density is constant everywhere except when multiplied by gravity g in the buoyancy. Introduce lubrication scalings, (30–32), in which $u_{*}=\kappa /h$ and define $p_{*}$, by (33), along with a scaled temperature $\theta$

$$\begin{aligned} \theta =\frac{2(T-T_\mathrm{C})}{\Delta T}-1 \end{aligned}$$

(35)

so that

$$\begin{aligned} -1\le \theta \le 1\quad \text {on}\;-1\le X\le 1. \end{aligned}$$

(36)

Here $\kappa$ is the thermal diffusivity.

The scaled governing system is then

$$\begin{aligned}&\epsilon \textit{Pr}^{-1}(UU_{X}+WU_{Z})=-P_{X}+U_{ZZ}+\epsilon ^2U_{XX}, \end{aligned}$$

(37)

$$\begin{aligned}&\epsilon ^3\textit{Pr}^{-1} (UW_{X}+WW_{Z})=-P_{Z} +\epsilon ^2 [W_{ZZ}+\epsilon ^2W_{XX}]+\textit{Ra}\;\theta , \end{aligned}$$

(38)

$$\begin{aligned}&U_{X}+W_{Z}=0, \end{aligned}$$

(39)

$$\begin{aligned}&\epsilon (U\theta _{X}+W\theta _{Z}) =\theta _{ZZ}+\epsilon ^2\theta _{XX} \end{aligned}$$

(40)

with zero flux conditions, say, on top and bottom,

$$\begin{aligned} \theta _{Z}=0\quad \text {on}\;Z=0,1 \end{aligned}$$

(41)

and no slip on all boundaries,

$$\begin{aligned} U,W= & {} 0\quad \text {on}\;Z=0,1, \end{aligned}$$

(42)

$$\begin{aligned} U,W= & {} 0\quad \text {on}\;X = \pm 1, \end{aligned}$$

(43)

as well as

$$\begin{aligned} \theta =\mp 1\quad \text {on}\;X=\pm 1, \end{aligned}$$

(44)

where $\textit{Pr}=\nu /\kappa$ is the Prandtl number, $\nu$ is the kinematic viscosity. $\textit{Ra}$ is the Rayleigh number, $\textit{Ra}=\alpha g \Delta T h^4/(2 L \kappa \nu )$, and $\alpha$ is the volume-expansion coefficient in a linear equation of state for density $\rho$. The core solutions (valid away from $X=\pm 1$) can be represented as

$$\begin{aligned}&(U,W)=(U_{0},W_{0})+\epsilon (U_{1},W_{1})+\cdots \end{aligned}$$

(45)

$$\begin{aligned}&P=P_{0}+\epsilon P_{1}+\cdots \end{aligned}$$

(46)

$$\begin{aligned}&\theta =\theta _{0}+\epsilon \theta _{1}+\cdots \end{aligned}$$

(47)

for fixed $\textit{Pr}$ and $\textit{Ra}$. At leading order in $\epsilon$

$$\begin{aligned}&-P_{0_{X}}+U_{0_{ZZ}}=0, \end{aligned}$$

(48)

$$\begin{aligned}&-P_{0_{Z}}+\textit{Ra}\;\theta _{0}=0, \end{aligned}$$

(49)

$$\begin{aligned}&U_{0_{X}}+W_{0_{Z}}=0, \end{aligned}$$

(50)

$$\begin{aligned}&\theta _{0_{ZZ}}=0. \end{aligned}$$

(51)

Equation (51) allows a standing gradient in temperature end-to-end,

$$\begin{aligned} \theta _{0}=-X, \end{aligned}$$

(52)

which satisfies the end conditions without the need to introduce a thermal boundary layer. Equation (49) can be integrated to yield

$$\begin{aligned} P_{0}=-\textit{Ra}\;XZ+\Pi (X), \end{aligned}$$

(53)

where the excess pressure $\Pi$ is the ‘integration constant.’ This is substituted into (48) yielding

$$\begin{aligned} U_{0_{ZZ}}=-\textit{Ra}\;Z+\Pi '(X) \end{aligned}$$

(54)

so that

$$\begin{aligned} U_{0}=-\frac{1}{6}{} \textit{Ra}\;(Z^3-Z)+\frac{1}{2}\Pi ' (Z^2-Z), \end{aligned}$$

(55)

which satisfies the boundary conditions (42) for $U_{0}$. Here $\Pi$ is, as yet, undetermined. A consequence of the presence of the solid endwalls and the equation of continuity is that across any vertical cross-section, the flow rate Q must be zero. At leading order

$$\begin{aligned} Q_{0}&=\int _{0}^{1}U_{0}\text {d}Z =\frac{1}{24}{} \textit{Ra}\;-\frac{1}{12}\Pi '=0 \end{aligned}$$

so that

$$\begin{aligned} \Pi '(X)=\frac{1}{2}{} \textit{Ra}. \end{aligned}$$

(56)

It is this pressure gradient, generated by the presence of the endwalls, that is responsible of the turning of the flows. Before examining the end layers, consider the $O(\epsilon )$ thermal field, generated by Eq. (40),

$$\begin{aligned} \theta _{1_{ZZ}}&=U_{0}\theta _{0_{X}} = \textit{Ra}\;\left[ \frac{1}{6} (Z^3-Z) -\frac{1}{4} (Z^2-Z)\right] , \end{aligned}$$

which integrates to

$$\begin{aligned} \theta _{1}=\frac{1}{12}{} \textit{Ra}\;\left[ \frac{1}{10}Z^5 -\frac{1}{4}Z^4+\frac{1}{6}Z^3\right] \end{aligned}$$

(57)

and satisfies ${\partial \theta _1}/{\partial Z}=0\;\text {at}\;Z = 0,1$. Form (57) shows that the horizontal temperature distribution, $\theta _{0}=-X$, interacts with the leading-order shear to generate a vertical temperature distribution. The core velocity field $(U_{0},W_{0})$ must be corrected at $X=\pm 1$ by boundary layers having thicknesses $O(\epsilon )$ [2]. This gives rise to turning flows like those sketched schematically in Fig. 3.

Cormack et al. [2] generate higher-order core and turning flows and discuss in detail the fluid mechanics of the convection in a slot. The ‘thinness’ approximation has given rise to a quasi-parallel core flow plus boundary-layer corrections as shown.

Fig. 3

A sketch of the recirculation of the buoyancy-driven convection near the right-hand end of the domain of Fig. 2 [2]

Fig. 4

An open rectangular box containing liquid with upper free surface. A horizontal temperature gradient induces a steady flow driven by the variation of surface tension with temperature [4]

2.3 Steady thermocapillary convection in a slot

Consider the slot shown in Fig. 4 as considered by Sen and Davis [4] a flow similar to that in Sect. 2.2 except that now gravity is absent and the upper boundary is a deformable interface between the liquid and a passive gas. On the interface there is surface tension $\sigma$ that depends linearly on temperature T,

$$\begin{aligned} \sigma (T)=\sigma _{0}-\gamma (T-T_{0}), \end{aligned}$$

(58)

where $T_{0}$ is a constant and typically $\gamma >0$ so a liquid flow is generated on the surface as shown, and due to viscous drag generates a bulk flow. Again, the bulk equations are as in Sect. 2.2 but with $g=0$. The boundary conditions on the sides and bottom are identical to the previous but now on the interface S, $z=h(x)$, there is the kinematic condition

$$\begin{aligned} w=uh_{x}, \end{aligned}$$

(59)

the Laplace relation

$$\begin{aligned} S_{ij}n_{i}n_{j}=\sigma \kappa \end{aligned}$$

(60)

and the Marangoni balance tangent to $S$

$$\begin{aligned} S_{ij}n_{j}t_{i}=\frac{\partial \sigma }{\partial s}=-\gamma \frac{\partial T}{\partial s} \end{aligned}$$

(61)

and, say, the zero thermal flux condition,

$$\begin{aligned} \frac{\partial T}{\partial n}=0. \end{aligned}$$

(62)

Here the curvature K is

$$\begin{aligned} K=\frac{h_{xx}}{(1+h_{x}^2)^{3/2}}, \end{aligned}$$

(63)

s measures of arc length on S, n and t are unit normal; and tangential vectors on S; and $S_{ij}$ is the stress tensor for a Newtonian liquid. Introduce lubrication scales (30–32) with $u_{*}$ chosen by the Marangoni balance (61) and $p_{*}$ by (33).

$$\begin{aligned} u_{*}=\frac{\epsilon (\gamma \Delta T)}{\mu } \end{aligned}$$

(64)

and define the Marangoni number M,

$$\begin{aligned} M=\frac{u_{*}h_{0}}{\kappa }=\frac{\epsilon (\gamma \Delta T)h_{0}}{\kappa \mu }, \end{aligned}$$

(65)

and the Prandtl number $\textit{Pr}$,

$$\begin{aligned} \textit{Pr}=\frac{\nu }{\kappa }. \end{aligned}$$

(66)

In addition, $\theta$ is defined by

$$\begin{aligned} \theta =\frac{2(T-T_\mathrm{c})}{\Delta T}-1. \end{aligned}$$

(67)

The scaled governing system is then

$$\begin{aligned}&\epsilon M\textit{Pr}^{-1} (UU_{X}+WU_{Z})=-P_{X}+U_{ZZ}+\epsilon ^2U_{XX}, \end{aligned}$$

(68)

$$\begin{aligned}&\epsilon ^3M\textit{Pr}^{-1} (UW_{X}+WW_{Z})=-P_{Z}+\epsilon ^2 (W_{ZZ}+\epsilon ^2 W_{XX}), \end{aligned}$$

(69)

$$\begin{aligned}&U_{X}+W_{Z}=0, \end{aligned}$$

(70)

$$\begin{aligned}&\epsilon M (U\theta _{X}+W\theta _{Z})=\theta _{ZZ}+\epsilon ^2\theta _{XX} \end{aligned}$$

(71)

with conditions on solid boundaries

$$\begin{aligned}&U=W=0,\quad \theta =\mp 1\quad \text {on}\;X=\pm 1, \end{aligned}$$

(72)

$$\begin{aligned}&U=W=0,\quad \theta _{Z}=0\quad \text {on}\;Z=0. \end{aligned}$$

(73)

The governing interfacial conditions have the form

$$\begin{aligned}&-P+2\epsilon ^2 (1+\epsilon ^2H_{X}^2)^{-1} \left[ (W_{Z}-H_{X}U_{Z})+\epsilon ^2H_{X} (-W_{X} +H_{X}U_{X})\right] = \epsilon ^3C^{-1}H_{XX} (1+\epsilon ^2H_{X}^2)^{-1} [1+\epsilon ^{-1}C\theta ], \nonumber \\\end{aligned}$$

(74)

$$\begin{aligned}&(1-\epsilon ^2H_{X}^2) (U_{Z}+\epsilon ^2W_{X})+2\epsilon ^2H_{X} (W_{Z}-U_{X}) = -(1+\epsilon ^2H_{X}^2)^{1/2} (\theta _{X}+H_{X}\theta _{Z}), \end{aligned}$$

(75)

$$\begin{aligned}&(1+\epsilon ^2H_{X}^2)^{-1/2}(\theta _{Z}-\epsilon ^2H_{X}\theta _{X})=0, \end{aligned}$$

(76)

where C is the capillary number, and $C=\mu u_{*}/\sigma _{0}$.

In addition, one needs to specify conditions at the contact line where the interface intersects the solid boundary. For simplicity, here, take the meniscus to attach to the sharp corners of the slot

$$\begin{aligned} h(\pm l)=h_{0}. \end{aligned}$$

See [4] for more general cases. The dependent variables can now by expressed in power series of $\epsilon$ with one observation necessary. Letting $\epsilon \rightarrow 0$ in Eq. (74) with $C=O(1)$ formally eliminates surface tension from the problem. In order to retain surface tension it must be made large, viz.,

$$\begin{aligned} C=\epsilon ^{-4}\bar{C},\quad \bar{C}=O(1)\;\quad \text {as}\;\epsilon \rightarrow 0. \end{aligned}$$

(77)

Given this assumption, write

$$\begin{aligned}&(U,W)= (U_{0},W_{0})+\epsilon (U_{1},W_{1})+\cdots , \end{aligned}$$

(78)

$$\begin{aligned}&\theta =\theta _{0}+\epsilon \theta _{1}+\cdots , \end{aligned}$$

(79)

$$\begin{aligned}&H=1+\epsilon H_{1}+\cdots . \end{aligned}$$

(80)

The governing system at O(1) is then

$$\begin{aligned}&U_{0_{ZZ}}-P_{0_{X}}=0, \end{aligned}$$

(81)

$$\begin{aligned}&P_{0_{Z}}=0, \end{aligned}$$

(82)

$$\begin{aligned}&U_{0_{X}}+W_{0_{Z}}=0, \end{aligned}$$

(83)

$$\begin{aligned}&\theta _{0_{ZZ}}=0 \end{aligned}$$

(84)

with the same homogenous conditions on $Z=0$ as above but now with

$$\begin{aligned} \left. \begin{array}{l} -P_{0} = \bar{C}^{-1}H_{1_{XX}} \\ U_{0_{Z}}=-\theta _{0_{X}} \\ \theta _{0_{Z}}=0 \end{array}\right\} \ \text {on}\;Z=1. \end{aligned}$$

(85)

As in Sect. 2.2, the leading-order thermal field from (84) is

$$\begin{aligned} \theta _{0}=-X, \end{aligned}$$

(86)

which satisfies the end conditions without the need of introducing thermal boundary layers. At $O(\epsilon )$ there is again an induced temperature field that has a vertical profile. From Eq. (82), $P_{0}=P_{0}(X)$ only, and then Eq. (81) gives $U_{0}$

$$\begin{aligned} U_{0}(Z)=P_{0_{X}}\left( \frac{1}{2}Z^2-Z\right) +Z, \end{aligned}$$

(87)

which satisfies $U_{0}(0)=0$ and $U_{0_{Z}}(1)=1$. The pressure is determined by setting the horizontal flow rate to zero,

$$\begin{aligned} Q_{0}=-\frac{1}{3}P_{0_{X}}+\frac{1}{2}=0 \end{aligned}$$

(88)

so that

$$\begin{aligned} P_{0_{X}}=\frac{3}{2}, \end{aligned}$$

(89)

which induces deformation of the interfaces as shown in Fig. 4; there is a depression near $X=-1$ and an elevation near $X=1$. To see this explicitly, consider the leading-order normal-stress balance from Eq. (74), viz

$$\begin{aligned} \bar{C}^{-1}H_{1_{XX}}=-P_{0}=-\frac{3}{2}X \end{aligned}$$

(90)

with

$$\begin{aligned} H_{1}(\pm 1)=0 \end{aligned}$$

(91)

yielding

$$\begin{aligned} H_{1}=\frac{1}{4}\bar{C} [X-X^3]; \end{aligned}$$

(92)

the deformation is shown in Fig. 4.

The $O(\epsilon )$ end layers must then be computed and matched to the core giving the turning flows at each end [4], reminiscent of that in Fig. 3.

Again, it is seen that by taking advantage of the thinness of the domain, analytical expressions can be obtained leading to a quasi-parallel core and interface deformation. The boundary-layer corrections are similar in spirit to those in Fig. 3.

2.4 Hele–Shaw approximations

Consider now the three-dimensional flow between two closely-spaced parallel planes as shown in Fig. 5. There is an obstacle in the gap in the form of a circular cylinder normal to the planes and having a radius large compared to the gap width.

These flows in three dimensions have coordinates (x, y, z) with corresponding velocity components (u, v, w).

The first step is to integrate the equation of continuity across the gap

$$\begin{aligned} \int _{0}^{h} (u_{x}+v_{y}+w_{z})\text {d}z=0 \end{aligned}$$

yielding

$$\begin{aligned} \frac{\partial }{\partial x}\int _{0}^{h}u\text {d}z+\frac{\partial }{\partial y}\int _{0}^{h}v\text {d}z+w (h)-w(0)=0. \end{aligned}$$

(93)

Because of the zero-penetration conditions on the walls, the result has the form

$$\begin{aligned} \nabla _\mathrm{H}\cdot \mathbf {v}_\mathrm{H}=0, \end{aligned}$$

(94)

where $\nabla _\mathrm{H}$ is the x–y gradient and the average horizontal velocity is

$$\begin{aligned} \mathbf {v}_\mathrm{H}=(u_\mathrm{H},v_\mathrm{H})=\left( \frac{1}{h}\int _{0}^{h}u\;\text {d}z,\quad \frac{1}{h}\int _{0}^{h}v\;\text {d}z\right) , \end{aligned}$$

(95)

seemingly two dimensional. This is called Hele–Shaw [5] flow. Consider (inertialess) Stokes flow in the gap giving

$$\begin{aligned} (u_\mathrm{H},v_\mathrm{H})=\frac{1}{\mu h} (h-z)z\nabla _\mathrm{H}P_{z}. \end{aligned}$$

(96)

Now note that the vorticity component, $\omega _\mathrm{H}={\partial u_\mathrm{H}}/{\partial y}-{\partial v_\mathrm{H}}/{\partial x}$, of the flow field is zero, viz.

$$\begin{aligned} \nabla _\mathrm{H}\times \mathbf {v}_H=\mathbf {0}, \end{aligned}$$

(97)

so that there exists a (average) velocity potential $\bar{\phi }$ such that

$$\begin{aligned} \nabla _\mathrm{H}^2\bar{\phi }=0 \end{aligned}$$

(98)

with

$$\begin{aligned} u_\mathrm{H}=\bar{\phi }_{x},\quad v_\mathrm{H}=\bar{\phi }_{y} \end{aligned}$$

(99)

and either at any fixed z, or for the vertically averaged version of Eq. (96), the streamlines about the obstacles generated by this viscously-dominated flow describe those of (high Reynolds number) potential flow; see Fig. 5b [6]. Of course, the approximation fails in an $O(\epsilon )$ neighborhood of the obstacle, but the usefulness of the approximation should not be underestimated. Again, thinness defines a good approximation.

Fig. 5

Flow past a circular obstacle in a Hele–Shaw cell: a side view, and b top view, [6]

Fig. 6

Uniform flow past an axisymmetric obstacle: a where the ends are tapered, and b where the ends are bluff

There is a related set of approximate equations valid for flow through porous materials. It again relates average velocities with pressure gradients. Here, one considers velocities averaged over many pore lengths and yields Darcy’s law [7]

$$\begin{aligned} \frac{\mu }{k}\nabla \bar{p}=\mathbf {v}, \end{aligned}$$

(100)

where k is a proportionality constant called the permeability of the medium. The spirit of Darcy’s law is the same as that of Hele–Shaw flow but in contrast it is applicable in three-dimensions and is not limited to thin domains.

2.5 Slender-body theory

Flow past a slender body is a situation present for a wide range of Reynolds numbers applying to flow over spermatozoa, micro-organisms, long-chain polymers, torpedoes, submarines, and rockets. In all these cases, a slender body induces a ‘thin’ flow near-by, but the far-field flow is not thin, and matched-asymptotic expansions is required to link the two. This is analogous to the slot flows in Sects. 2.2 and 2.3 where the ‘thin’ core flows must be linked with boundary layers at the ends which are not thin.

Consider first uniform potential flow past a slender body aligned with it as shown in Fig. 6. This exposition largely follows Hinch [8] and in greater detail in Cole [9]. For simplicity, take the body to be axis-symmetric of length l and radius $r=F(z)$. The body is slender if

$$\begin{aligned} \epsilon =F_\mathrm{M}/l\ll 1, \end{aligned}$$

(101)

where $F_\mathrm{M}=\text {max}\;F(z)\;\text {on}\;-\frac{l}{2}\le z\le \frac{l}{2}$. Note that this is an external-flow problem. The flow is expressible in terms of a velocity potential $\varphi$ such that

$$\begin{aligned} u=\varphi _{r},\quad w=\varphi _{z}, \end{aligned}$$

(102)

which satisfies

$$\begin{aligned} \nabla ^2\varphi =\frac{1}{r} (r\varphi _{r})_{r}+\varphi _{zz}=0 \end{aligned}$$

(103)

with uniform flow at $z\rightarrow -\infty$,

$$\begin{aligned} \varphi \rightarrow U_{0}z \end{aligned}$$

(104)

and zero penetration of the flow into the body

$$\begin{aligned} \varphi _{n}\propto \varphi _{r}-F'\varphi _{z}=0\;\quad \text {on}\;r = F(z). \end{aligned}$$

(105)

Introduce lubrication scalings in cylindrical coordinates appropriate to the near field as follows:

$$\begin{aligned} R= & {} \frac{r}{F_\mathrm{M}},\quad Z=\frac{z}{l}, \end{aligned}$$

(106)

$$\begin{aligned} \mathbf {V}= & {} \frac{\mathbf {v}}{U_{0}},\ \Phi =\frac{\phi }{U_{0}F_\mathrm{M}},\quad \text {and}\quad P=\frac{p}{\rho U_{0}^2}. \end{aligned}$$

(107)

The governing system is then

$$\begin{aligned}&\frac{1}{R} (R\Phi _{R})_{R}+\epsilon ^2\Phi _{ZZ}=0, \end{aligned}$$

(108)

$$\begin{aligned}&\Phi _{R}-\epsilon ^2F'\Phi _{Z}=0\quad \text {on}\;R=F(Z) \end{aligned}$$

(109)

and

$$\begin{aligned} \Phi \sim Z\quad \text {as}\;Z\rightarrow -\infty . \end{aligned}$$

(110)

Represent $\Phi$ as a formal expansion in $\epsilon ^2$,

$$\begin{aligned} \Phi =\Phi _{0}+\epsilon ^2\Phi _{1}+\cdots . \end{aligned}$$

(111)

At O(1), the system (108–110) yields

$$\begin{aligned} \Phi _{0}=A_{0}(Z)+B_{0}Z\ln R \end{aligned}$$

(112)

with

$$\begin{aligned} \Phi _{0_{R}}=0\quad \text {on}\;R=F(Z), \end{aligned}$$

(113)

which gives $B_{0}\equiv 0$, and hence

$$\begin{aligned} \Phi _{0}(Z)=A_{0}(Z). \end{aligned}$$

(114)

At $O(\epsilon ^2)$, system (108–110) yields

$$\begin{aligned} \Phi _{1}=-\frac{1}{4}A_{0}''R^2+C_{0}\ln R+D_{0} \end{aligned}$$

(115)

with

$$\begin{aligned} \Phi _{1_{R}}=A_{0}'F\quad \text {on}\;R=F(Z), \end{aligned}$$

(116)

which gives

$$\begin{aligned} \Phi _{1}=-\frac{1}{4}A_{0}''R^2+A_{2}(Z)+B_{2}\ln R, \end{aligned}$$

(117)

where

$$\begin{aligned} B_{2}(Z)=FF'A_{0}'+\frac{1}{2}FA_{0}'. \end{aligned}$$

(118)

In the outer region, R must be rescaled as

$$\begin{aligned} \rho =\epsilon R,\quad z=Z, \end{aligned}$$

(119)

so that

$$\begin{aligned}&\frac{1}{\rho } (\rho \phi _{\rho })_{\rho } +\phi _{zz}=0\quad \text {on}\;\rho =\epsilon F(z), \end{aligned}$$

(120)

$$\begin{aligned}&\phi _{\rho }-\rho '\phi _{z}=0\quad \text {on}\;\rho =\epsilon F(z). \end{aligned}$$

(121)

Write an expansion in powers of $\epsilon ^2$,

$$\begin{aligned} \phi \sim \phi _{0}+\epsilon ^2\phi _{1}+\cdots . \end{aligned}$$

(122)

Clearly, $\phi _{0}=z$ and in the outer region the body shrinks to a line on $\rho =0$.

A source at the origin is by definition

$$\begin{aligned} \phi =\frac{1}{4\pi }\int \frac{\text {d}z}{\sqrt{r^2+z^2}}, \end{aligned}$$

(123)

which is a solution of Laplace’s equation. In the outer region, the slender body is now a line on $-\frac{1}{2}<z<\frac{1}{2}$, and the solution can be represented as a superposition of forms (123) as follows:

$$\begin{aligned} \phi (\rho ,z)\sim z-\frac{1}{2}\epsilon ^2\int _{-1/2}^{1/2}\frac{f(\xi )\text {d}\xi }{\sqrt{\rho ^2+ (z-\xi )^2}}. \end{aligned}$$

(124)

In order to match with the near-field solution, one needs the small-$\rho$ asymptotics (for $\rho \rightarrow 0$). A bit of subtlety [8, 9] is required to give

$$\begin{aligned} \phi \sim z-\epsilon ^2f(z)\left[ \ln \frac{1}{\rho }+O(1)\right] \quad \text {as}\;\rho \rightarrow 0, \end{aligned}$$

(125)

which must be matched to Eqs. (114, 117). Not surprisingly, at leading order

$$\begin{aligned} A_{0}(z)=z \end{aligned}$$

(126)

and

$$\begin{aligned} f(z)=B_{2}(z)=FF'. \end{aligned}$$

(127)

It turns out that the formal expansion (111) is insufficient and needs to be augmented [8, 9] by a logarithm term to give

$$\begin{aligned} A_{2}=B_{2}\ln (\epsilon ^{-1}) \end{aligned}$$

(128)

and now a uniform approximation may be obtained which allows one to calculate the forces exerted on the body by the fluid.

The solution would be valid for the whole length of the body shown in Fig. 6a because the ends are ‘thin,’ but fail near the ends of Fig. 6b where the body has blunt ends. A special local expansion would then be required in the latter case to find valid representations near the ends.

In the opposite extreme $\text {Re} \rightarrow 0$, one has (inertialess) Stokes flow. Now for this axisymmetric problem, one has the biharmonic equation of the Stokes stream function $\psi$, $\nabla ^4\psi =0$ with conditions of no penetration on the body as well as no slip; there is uniform flow as $z\rightarrow -\infty$. The same procedure as above is followed (see Cox [10] and Batchelor [11]). The far field sees a line, and the solution is now represented by a superposition of Stokeslets (rather than sources) and gives rise to a representation for the velocity as

$$\begin{aligned} \mathbf {v}(\mathbf {x})=\frac{1}{8\pi \mu }\int _{0}^{l}\mathbf {f}(s) \left\{ \frac{I}{\left| x-X\right| }+\frac{(x-X)(x-X)}{\left| x-X\right| ^3}\right\} \text {d}s \end{aligned}$$

(129)

in terms of the Oseen tensor, and s is the arc length. The slenderness can be used to argue that $\mathbf {f}(s)\approx \mathbf {f}(s_{0})$, a constant, which can be removed from the integral allowing direct integration. Again, one can obtain the forces [11] on the body. In particular, the drag $D_{\parallel }$ on a rod oriented along the flow compared to that $D_{\perp }$ perpendicular to the flow is

$$\begin{aligned} D_{\perp }=2D_{\parallel } \end{aligned}$$

(130)

and

$$\begin{aligned} D_{\parallel }\sim \frac{2\pi \mu l}{\ln (l/F_\mathrm{M})}U_{0}. \end{aligned}$$

(131)

Fig. 7

A sketch of a fiber-forming device in which liquid emerges from an orifice and is wound by a wheel l units away

Fig. 8

A liquid film on a solid substrate having a wavy disturbance of the upper free surface

2.6 Fiber forming

Glass and polymer fibers are manufactured by placing molten material in a chamber, see Fig. 7, and forcing it through an orifice, pulling the strand to a distant wheel, and winding the fiber at a given speed.

Like the flow described in Sect. 2.5, the geometry is slender but in contrast to that case, fibers forming is an interior flow confined within a free surface.

In actual manufacturing, the molten liquid is at high temperature, and as it emerges through the orifice is subjected by cooling jets of air that reduces the temperature to the laboratory ambient in a matter of one or two centimeters. This rapid cooling causes the material properties to undergo massive changes in, for example, the viscosity which can change by factors of $10^{20}$.

In the present discussion, the method of approximation is described on the simplest case of an isothermal, Newtonian-viscous fluid with constant viscosity, initially with gravity g, surface tension $\sigma$, and inertia being ignored. Here the liquid emerges from the orifice of radius $r_\mathrm{I}$ located at $z=0$ and is wound at axial speed $W_\mathrm{W}$ at $z=l$. In axisymmetric cylindrical coordinates (r, z), the velocity components are (u, w). The lubrication scalings are introduced but now with the radial pressure gradient balancing the viscous forces. The scaled system has the form (see Schultz and Davis [12]):

$$\begin{aligned}&\frac{1}{R}(RU)_{R}+W_{Z}=0, \end{aligned}$$

(132)

$$\begin{aligned}&\epsilon \text {Re}(UU_{R}+WU_{Z})=-P_{R} +\left[ \frac{1}{R}(RU)_{R}\right] _{R}+\epsilon ^2U_{ZZ}, \end{aligned}$$

(133)

$$\begin{aligned}&0=-\epsilon ^2P_{Z}+\frac{1}{R}(RW_{R})_{R}+\epsilon ^2W_{ZZ}. \end{aligned}$$

(134)

On the interface $R=F(Z)$

$$\begin{aligned} U=WF_{Z} \end{aligned}$$

(135)

and

$$\begin{aligned} \epsilon \left\{ P (1+\epsilon ^2F_{Z}^2) -2\left[ U_{R}+\epsilon ^2F_{Z}^2W_{Z}-F_{Z} (\epsilon ^2U_{Z}+W_{R})\right] \right\} =0 \end{aligned}$$

(136)

and

$$\begin{aligned} 2\epsilon ^2F_{Z}(U_{R}-W_{Z}) +(1-\epsilon ^2F_{Z}^2) (\epsilon ^2U_{Z}+W_{R})=0. \end{aligned}$$

(137)

Further, all physical quantities are bounded on the axis,

$$\begin{aligned} |U|, |W|, |P|<\infty \quad \text {on}\;R=0. \end{aligned}$$

(138)

At the orifice, the liquid attaches to the inner corner and

$$\begin{aligned} U=\hat{U}(R),\quad W=\hat{W}(R),\quad R=1\quad \text {on}\;Z=0. \end{aligned}$$

(139)

Finally, the fiber is wound up at $Z=1$

$$\begin{aligned} U=\hat{U}_\mathrm{W}(R),\quad W=\hat{W}_\mathrm{W}(R). \end{aligned}$$

(140)

The slenderness approximation breaks down near a boundary layer at $Z=0$ requiring a numerical solution of the full equations with $\epsilon =1$. This boundary layer will be not be pursued here. Instead, replace condition (139) by the cross-sectional average of $\hat{W}(R)$, called $W_\mathrm{I}$. Similarly, replace conditions (140) at the winder by an average value of $\hat{W}_\mathrm{W}$ called $W_\mathrm{W}$.

Define

$$\begin{aligned} \alpha =\ln ({W_\mathrm{W}}/{W_\mathrm{I}}). \end{aligned}$$

(141)

and

$$\begin{aligned} \epsilon =\frac{r_{_\mathrm{I}}}{l}. \end{aligned}$$

(142)

Express all dependent variables in powers of $\epsilon ^2$. At leading order,

$$\begin{aligned}&\frac{1}{R}(RU_{0})_{R}+W_{0_{Z}}=0, \end{aligned}$$

(143)

$$\begin{aligned}&\left[ \frac{1}{R}(RU_{0})_{R}\right] _{R}-P_{0_{R}}=0, \end{aligned}$$

(144)

$$\begin{aligned}&\frac{1}{R}(RW_{0_{R}})_{R}=0 \end{aligned}$$

(145)

with

$$\begin{aligned}&U_{0}=W_{0}F_{0Z}\quad \text {on}\;R=F_{0}, \end{aligned}$$

(146)

$$\begin{aligned}&W_{0_{R}}=0\quad \text {on}\;R=F_{0}, \end{aligned}$$

(147)

$$\begin{aligned}&P_{0}-2(U_{0_{R}}-F_{0_{Z}}W_{0_{R}})=0\quad \text {on}\;R=F_{0}, \end{aligned}$$

(148)

$$\begin{aligned}&|U_{0}|,\quad |W_{0}|,\quad |P_{0}|<\infty \quad \text {on}\;R=0, \end{aligned}$$

(149)

$$\begin{aligned}&2\int _{0}^1RW_{0}\;\text {d}R=1\quad \text {on}\;Z=0 \end{aligned}$$

(150)

and

$$\begin{aligned} \frac{2}{F_{0}^2}\int _{0}^{F_{0}}RW_{0}\;\text {d}R=\text {e}^\alpha \quad \text {on}\;Z=1. \end{aligned}$$

(151)

This leading-order system has simple solutions, viz.

$$\begin{aligned} W_{0}=\mathcal {W}_{0}(Z), \end{aligned}$$

(152)

where $\mathcal {W}_{0}$ is undetermined at this stage. Equation (143) then yields

$$\begin{aligned} U_{0}=-\frac{1}{2}R\mathcal {W}_{0}'(Z) \end{aligned}$$

and the normal-stress condition (148) gives

$$\begin{aligned} P_{0}=-\mathcal {W}_{0}'(Z). \end{aligned}$$

(153)

The end condition then gives

$$\begin{aligned} F_{0}^2\mathcal {W}_{0}=1. \end{aligned}$$

(154)

To determine $\mathcal {W}_{0}$, one must examine the $O(\epsilon ^2)$ equations. From Schultz and Davis [11],

$$\begin{aligned} W_{2}=-\frac{1}{2}R^2\mathcal {W}_{0}''+\mathcal {W}_{2}(Z), \end{aligned}$$

where $\mathcal {W}_{2}$ is arbitrary. If this is substituted into the $O(\epsilon ^2)$ shear-stress condition $W_{2_{R}}=2F_{0_{Z}}(W_{0_{Z}}-U_{0_{R}})-U_{0_{Z}}$, one finds that

$$\begin{aligned} F_{0}\mathcal {W}_{0}''+2F_{0}'\mathcal {W}_{0}'=0. \end{aligned}$$

(155)

Equations (154, 155) give the leading-order fiber equations. Eliminating $F_{0}$ between the two gives

$$\begin{aligned} \mathcal {W}_{0}''\mathcal {W}_{0}=\mathcal {W}_{0}'^2, \end{aligned}$$

(156)

subject to

$$\begin{aligned} \mathcal {W}_{0}(0)=1 \end{aligned}$$

(157)

and

$$\begin{aligned} \mathcal {W}_{0}(1)=\text {e}^\alpha . \end{aligned}$$

(158)

The solution for the speed is then

$$\begin{aligned} \mathcal {W}_{0}(Z)=\text {e}^{\alpha Z} \end{aligned}$$

(159)

and the radius is

$$\begin{aligned} F_{0}(Z)=\text {e}^{-\alpha Z/2}. \end{aligned}$$

(160)

Schultz and Davis [12] then derive the equations including the physical factors earlier ignored to obtain

$$\begin{aligned} 3(\mathcal {W}_{0}'^2\mathcal {W}_{0}^{-1} -\mathcal {W}_{0}'')+\frac{1}{2}\bar{C}^{-1} \mathcal {W}_{0}'\mathcal {W}_{0}^{-\frac{1}{2}} +\bar{R}e\mathcal {W}_{0}\mathcal {W}_{0}'-G=0 \end{aligned}$$

(161)

with

$$\begin{aligned}&\mathcal {W}_{0}=1, \end{aligned}$$

(162)

$$\begin{aligned}&\mathcal {W}(1)=\text {e}^\alpha . \end{aligned}$$

(163)

Here the scaled capillary number $\bar{C}$ is

$$\begin{aligned} \bar{C}=\frac{\epsilon W_\mathrm{I}\mu }{\sigma }=O(1) \end{aligned}$$

(164)

the scaled Reynolds number $\bar{R}e$ is

$$\begin{aligned} \bar{R}e=\frac{\epsilon ^{-1}W_\mathrm{I}r_{I}}{\nu }=O(1) \end{aligned}$$

(165)

and the gravitation parameter G is

$$\begin{aligned} G=\frac{\epsilon ^{-2}gr_\mathrm{I}^2}{\nu W_\mathrm{I}}=O(1). \end{aligned}$$

(166)

System (161–163) is identical to that of Matovich and Pearson [13] who assume one-dimensional flow at the outset and use physical reasoning to obtain this result.

Notice the similarities and differences between the slender-body theories for external and interior flows. Both theories use lubrication scalings, and the solutions in the thin domains are relatively simple. However, in the interior case, one must go to higher order to close the system (in this case because of the zero-shear conditions on the interface). Both theories require boundary-layer corrections. In the external case, there is one for large radius (but also one at the ends if the body is not tapered), whereas for the internal case, there are only boundary layers at the ends. In the external case, the radial boundary layers are required in order to obtain any usable result. In the internal case, the quasi-one-dimensional solutions are valuable even when the boundary layers are not found.

2.7 Shallow-water theory

Traditionally, when studying gravity-driven water waves, one assumes that the fluid is inviscid because typical Reynolds numbers are very large and the viscous boundary layers on the free surface and bottom of the channel are relatively passive. Further, if at time zero, the flow is irrotational, then vorticity remains zero forever. As shown in Fig. 8, if $h_{0}$ is the mean depth of the water and l is a typical wave length of a wave, then the channel is considered shallow if

$$\begin{aligned} \epsilon =\frac{h_{0}}{l}\ll 1. \end{aligned}$$

For two-dimensional waves, introduce the lubrication scalings into the potential flow equations with $u_{*}=\sqrt{gh_{0}}$ and pressure $p_{*}=\rho u_{*}^2=\rho gh_{0}$ into the Euler equations yielding

$$\begin{aligned}&U_{T}+UU_{X}+WU_{Z}=-P_{X}, \end{aligned}$$

(167)

$$\begin{aligned}&\epsilon (W_{T}+UW_{X}+WW_{Z})=-P_{Z}-1, \end{aligned}$$

(168)

$$\begin{aligned}&U_{X}+W_{Z}=0 \end{aligned}$$

(169)

with the zero vorticity condition

$$\begin{aligned} U_{Z}-\epsilon ^2W_{X}=0 \end{aligned}$$

(170)

and the boundary conditions are

$$\begin{aligned}&H_{T}+UH_{X}=W\quad \text {on}\;Z=H, \end{aligned}$$

(171)

$$\begin{aligned}&P=0\quad \text {on}\;Z=H \end{aligned}$$

(172)

and

$$\begin{aligned} W=0\quad \text {on}\;Z=0. \end{aligned}$$

(173)

Fig. 9

A period cartoon of solitary wave. http://cdn.grindtv.com/uploads/2014/09/Calcutta-tidal-bore_1880.jpg

Here, the term $-1$ in Eq. (168) represents gravity in non-dimensional form. If one integrates the continuity equation (169) over Z,

$$\begin{aligned} \int _{0}^{H} (U_{X}+W_{Z})\;\text {d}Z=\frac{\partial }{\partial X}\int _{0}^{H}U\text {d}Z-U(H)H_{X}+W(H)-W(0)=0 \end{aligned}$$

uses $W(0)=0$, and the kinematic equation (171), one obtains a global mass conservation equation

$$\begin{aligned} H_{T}+\frac{\partial }{\partial X}\int _{0}^{H}U\text {d}Z=0. \end{aligned}$$

(174)

One can now obtain leading-order approximate solutions. From (170), $U_{0_{Z}}=0$, so that $U_{0}=U_{0}(X,T)$. From (174) then

$$\begin{aligned} H_{0_{T}}+ (U_{0}H_{0})_{X}=0. \end{aligned}$$

(175)

Now, from Eq. (168) with condition (172), the pressure, which vanishes on the free surface, is purely hydrostatic,

$$\begin{aligned} P_{0}=H_{0}-Z \end{aligned}$$

(176)

and because U is independent of Z, Eq. (167) becomes

$$\begin{aligned} U_{0_{T}}+U_{0}U_{0_{X}}=-H_{0_{X}}. \end{aligned}$$

(177)

Equations (175–177) are the classical shallow-water equations.

This system is strongly nonlinear and can be used to describe solitary waves and its generalizations can be used to monitor the dynamics of the Earth’s atmosphere, which itself is a thin shell enclosing the Earth. See Fig. 9 for a period cartoon of a solitary wave.

Many of the uses of shallow-water theory are in oceanographic or meteorological applications in which case one may have to augment Eqs. (175–177) by the Earth’s rotation [14, 15].

2.8 Thin viscous films

Consider now a viscous film of mean thickness $h_{0}$ on a substrate as shown in Fig. 8. Here the upper free surface at $z=h(x,t)$ is susceptible to various force fields. Gravity could be directed upward or downward, a heated substrate could induce thermocapillary (Marangoni) stresses and the liquid could evaporate. If the film has thickness smaller than 0.1 $\upmu$m, van der Waals attractions can generate an instability that leads to the rupture of the film in a finite time. All of the possibilities are discussed in great detail in Oron et al. [16]. Here the single case of van der Waals (vdW) instability is discussed as first treated by Williams and Davis [17].

The vdW force can be represented as the gradient of an excess potential $\phi$ that induces a body force across the layer, say

$$\begin{aligned} \phi =\phi _{B}+\frac{A}{6\pi h^3}, \end{aligned}$$

(178)

where A is the Hamaker constant and $\phi _{B}$ is a constant. The forces are attractive, $A>0$, if the liquid poorly wets the substrate.

Typically, A is numerically very small so that $\phi$ is appreciable only for h very small. Introduce lubrication scales appropriate to instabilities where unstable wave lengths $\lambda$ are much larger than the film thickness so define

$$\begin{aligned} \epsilon =\frac{2\pi h_{0}}{\lambda }. \end{aligned}$$

(179)

The lubrication scalings give $X={2\pi x}/{\lambda }, Z = {z}/{h}, U={u}/{u_{*}},\ W= ({w}/{u_{*}})\epsilon$, and $u_{*}={\nu }/{h}$. The pressure scale is given by $\mu u_{*}/\epsilon h$. Define the scaled generalized Navier–Stokes equations augmented by the van der Waals potential

$$\begin{aligned}&\epsilon \text {Re}(U_{T}+UU_{X}+WU_{Z}) =-(P+\Phi )_{X}+U_{ZZ}+\epsilon ^2U_{XX}, \end{aligned}$$

(180)

$$\begin{aligned}&\epsilon ^3\text {Re}(W_{T}+UW_{X}+WW_{Z}) =-P_{Z}+\epsilon (W_{ZZ}+\epsilon ^2W_{XX}), \end{aligned}$$

(181)

$$\begin{aligned}&U_{X}+W_{Z}=0, \end{aligned}$$

(182)

with

$$\begin{aligned} U=W=0\quad \text {on}\;Z=0 \end{aligned}$$

(183)

and

$$\begin{aligned} W=H_{T}+UH_{X}\quad \text {on}\;Z=H. \end{aligned}$$

(184)

At leading order in $\epsilon$,

$$\begin{aligned} P_{0}=P_{0}(X,T) \end{aligned}$$

and from $U_{0_{ZZ}}= (P_{0}+\Phi )_{X}$,

$$\begin{aligned} U_{0}= (P_{0}+\Phi )_{X}\left( \frac{1}{2}Z^2-HZ\right) , \end{aligned}$$

which satisfies $U_{0_{Z}}=0$ on $Z=H$ and $U_{0}=0$ on $Z=0$. If $U_{0}$ is substituted into the global conservation of mass, Eq. (174), one obtains a nonlinear evolution equation for H, viz.

$$\begin{aligned} H_{T}+(H^3H_{XXX}+H^{-1}H_{X})_{X}=0. \end{aligned}$$

(185)

This equation from Williams and Davis [16] contains surface tension effects via forward, higher-order diffusion and vdW instability via backward diffusion, the ‘diffusivity’ $H^{-1}$ increasing in depressions, accelerating as $H\rightarrow 0$ locally. Figure 10 shows a sequence of interfacial shapes leading to rupture. In physical times, the rupture occurs in milliseconds.

In all the thin-viscous-film applications, the advection/convection effects are absent in the leading order, and hence strongly nonlinear evolution equations can be derived in 2D or 3D. These descriptions result from asymptotics that regard slopes as small but amplitudes as arbitrary. The same approach allows one to include buoyancy, thermocapillarity, phase transformation, etc. and to monitor their interactions [16].

Fig. 10

Successive interfacial shapes of a van der Waals instability in a liquid layer and leading to rupture in a finite time

Fig. 11

2D spreading of a liquid drop: a the drop at time $t=0$, and b the drop at a later time

2.9 Viscous spreading of drops

Consider placing a liquid drop on a smooth substrate, shown in Fig. 11a. The drops will spread, Fig. 11b, due to two mechanisms [18]. Firstly, if the meniscus h(X, 0) is not an equilibrium shape, viz an arc of a circle, capillary pressure gradients will form that drives the drop toward equilibrium. Secondly, if the contact angle $\theta$ is not an admissible static angle, the edge of the drop will ‘pull’ outward until $\theta \rightarrow \theta _{A}$, the equilibrium angle. If $\theta _{A}>0$, the drops stop at some stage, but if $\theta _{A}=0$, complete spreading drives the drop forever (really, until there is a mono-molecular film). There is a conceptual complication at the contact line. Dussan and Davis [19] have shown that if the no-slip condition is applied everywhere on the wetted area, it requires an infinite force for a Newtonian viscous liquid to spread. Thus, slip must be allowed on the substrate near the contact line. The formulation for spreading drops is identical to that of viscous films are discussed in Sect. 2.7 in that the Navier–Stokes and continuity hold in the bulk. On the interface, the kinematic condition holds as well as zero shear stress and normal stress balancing surface tension times curvature. On the wetted substrate, there is zero penetration, $w=0$, but now the slip must be allowed, say, on $z=0$, $-a<x<a$,

$$\begin{aligned} u=\beta u_{z}, \end{aligned}$$

(186)

where $\beta \ne 0$ relieves the non-integrable singularity in the stress. The slip coefficient $\beta$ is numerically small but $\beta \rightarrow 0$ is a singular perturbation. Finally, one must apply conditions on the contact lines. Say at $x=a(t)$, the height of the drop is zero,

$$\begin{aligned} h(x,a(t))=0 \end{aligned}$$

(187)

and the contact angle is given,

$$\begin{aligned} h_{x}(x,\pm a(t))=\mp \tan \theta , \end{aligned}$$

where $\theta$ may be the constant $\theta _{A}$ or $\theta =\theta (U_\mathrm{CL})$ where $U_\mathrm{CL}$ is the speed of the contact line.

The concept of thinness here applies when $\tan \theta \approx \theta \equiv \epsilon \ll 1$. The first use of lubrication theory to the spreading of a thin drop is due to Greenspan [20]. Using his ideas, but slightly changing his model, leads to the following leading-order non-dimensional system:

$$\begin{aligned} c_{m}H_{T}+\left\{ (H^3+\widetilde{\beta }H^2)h_{XXX}\right\} _{X}=0 \end{aligned}$$

(188)

here $\tilde{\beta }$ is the scaled slip coefficient. With

$$\begin{aligned} h(X,\pm A(t))=0 \end{aligned}$$

(189)

with either

$$\begin{aligned} H_{X}(X,\pm A(t))=\mp 1 \end{aligned}$$

(190)

or using the microscopic angle $\theta$ in

$$\begin{aligned} {A}_T=h_{X}^3(X,\pm A(t))-\theta _{A}^3. \end{aligned}$$

(191)

When $\theta =\theta (U)$, one finds asymptotically the form (191) for the microscopic angle (see Cox [21]). Here $c_{m}$ is a non-dimensional version of ${\text {d}\theta }/{\text {d}U_\mathrm{CL}}$ at $U_\mathrm{CL}=0$.

One can analyze system (188–191) to find that

$$\begin{aligned} A(T)\sim T^{\alpha }\quad \text {as}\;T\rightarrow \infty \end{aligned}$$

for $\theta _{A}=0$ or $A(T)\rightarrow A^{\infty }$ as $T\rightarrow \infty$ for $\theta _{A}>0$. A table of exponents $\alpha$ for theorw, and experiment is given in Ehrhard and Davis [22].

3 Dynamic thinness

3.1 Steady boundary layer over a flat plate

In all previous cases, the thinness of the domain is known a priori. Consider now the case of uniform flow $U_{0}$ over the leading edge of a plate aligned with the flow. The steady flow is measured by Reynolds number $\text {Re}$,

$$\begin{aligned} \text {Re}=U_{0}l/\nu , \end{aligned}$$

(192)

where l measures a ‘long’ length from the leading edge as shown in Fig. 12; the leading edge may be blunt as in (13a) or tapered as in (13b).

Prandtl [23] recognized for $\text {Re} \gg 1$ that the no-slip condition on the plate induces a thin viscous region near the plate, whereas at a distance the flow is inviscid. See O’Malley [24] for a detailed history of the early years of boundary-layer theory.

One introduces lubrication scales, (30–31), using pressure scale (34) where $z\sim h$, a length normal to the plate giving $\epsilon =h/l$, the special form taken here is

$$\begin{aligned} \epsilon =\text {Re}^{-1/2}\quad \text {as}\;\text {Re}\rightarrow \infty , \end{aligned}$$

(193)

giving rise to at leading-order the boundary-layer equations

$$\begin{aligned}&UU_{X}+WU_{Z}=-P_{X}+U_{ZZ}, \end{aligned}$$

(194)

$$\begin{aligned}&0=-P_{Z}, \end{aligned}$$

(195)

$$\begin{aligned}&U_{X}+W_{Z}=0 \end{aligned}$$

(196)

with the boundary conditions

$$\begin{aligned} U,W=0\quad \text {on}\;Z=0,\quad X>0 \end{aligned}$$

and the matching condition

$$\begin{aligned} U\rightarrow 1\quad \text {as}\;Z\rightarrow \infty ,\;X>0. \end{aligned}$$

(197)

Clearly, the loss of the term $U_{XX}$ in Eq. (194) is formally a singular perturbation but in this case a fortunate one in the sense that a boundary condition for $X\rightarrow \infty$ required for solving the Navier–Stokes equation, impossible to pose systematically, is now not required. The system (194–196) is parabolic in X so only a profile at fixed X is required for solutions valid for larger X to be obtained. Clearly, a neighborhood of $X=0$, the blunt-nose leading edge of Fig. 12a must be excluded as not having lubrication-like scaling. On the other hand, the tapered nose of Fig. 12b requires no such excision.

The solution of system (194–196) leads to U-profiles sketched in Fig. 12 that are used to calculate the skin friction of the plate.

Fig. 12

A boundary layer on a flat plate with sketched velocity profiles: a for a plate with a bluff leading edge, and b for a plate with a tapered leading edge

Fig. 13

Oscillatory flow in a circular tube with a Stokes layer on the wall and oscillatory plug flow in the core

3.2 Unsteady viscous flow in a channel

Consider now a channel of width 2h shown in Fig. 13 in which a zero-mean oscillatory pressure gradient

$$\begin{aligned} P_{X}=A_{0}\cos \omega t \end{aligned}$$

(198)

is applied. When the angular frequency $\omega$ is large in the sense that boundary-layer thickness $\delta$,

$$\begin{aligned} \delta =(2\nu /\omega )^{1/2} \end{aligned}$$

(199)

satisfies

$$\begin{aligned} \delta \ll h. \end{aligned}$$

(200)

In this sense, the boundary layers are thin. Outside the boundary layers, there is a potential flow that satisfies

$$\begin{aligned} u_{t}=-A_{0}\cos \omega t \end{aligned}$$

(201)

or

$$\begin{aligned} u=-\frac{A_{0}}{\omega }\sin \omega t \end{aligned}$$

(202)

representing an oscillating plug flow. This cannot satisfy the no-slip conditions on $z=\pm h$, so lubrication scales are introduced near the walls. For z near h, write

$$\begin{aligned} Z=(1-z)/\delta \end{aligned}$$

(203)

giving rise to the boundary-layer equations:

$$\begin{aligned} 2U_{T}=U_{ZZ}-A_{1}\cos T \end{aligned}$$

(204)

with

$$\begin{aligned} W,\ U=0\quad \text {on}\;Z=0. \end{aligned}$$

(205)

Near $Z=h/\delta$,

$$\begin{aligned} U=A\text {e}^{-Z}\cos T \end{aligned}$$

(206)

known as the Stokes layer [25]. Figure 13 shows how the approximate solution has an inviscid core, a plug flow that oscillates with the pressure field, and boundary-layer corrections that bring the core flow to satisfy the no-slip condition.

This example is simple in that the full Navier–Stokes problem is linear and can easily be solved without invoking ‘thinness.’ However, if the boundaries were curved, the full problem would be nonlinear. For small amplitude A, one would again have Stokes layers on the walls, but now at $O(A^2)$, there would be steady drift in a thin layer of thickness $O(\delta /A_{1})$, a second, thicker layer containing the Stokes layer [26].

4 Discussion

This article outlines a family of approximate solutions to the Navier–Stokes equations appropriate to thin domains and applicable to a variety of situations that include two- and three-dimensional geometries, steadw, and unsteady flows, viscous and inviscid fluids, high and low Reynolds numbers, and internal and external domains. In nearly all cases the thin-domain flows must be matched to those in regions that are not thin, such as endwall boundary layers or inviscid far fields. The thin-domain solutions supply simplified expressions faithful to the physics and hence give scaling information even for flows in which the domain is not so thin.

Those cases in which there is ‘geometric thinness,’ the large aspect ratio $\epsilon ^{-1}$ follows directly from the given dimensions of the domain. When there is ‘dynamic thinness,’ $\epsilon ^{-1}$ emerges from scale analysis giving, say, boundary-layer thicknesses. Two such cases are described, one steady and one time periodic in which the boundary-layer thicknesses $\delta$ scale with the kinematic viscosity $\nu$ as $\delta \sim \nu ^{1/2}$. There are several thermal or compositional boundary layers that scale like $\delta \sim \kappa ^{1/2},D^{1/2}$, where D is the species diffusivity. Another ‘standard’ layer is established in differentially rotating systems, [27] in which the Ekman layer has $\delta \sim \nu ^{1/2}$ and also Stewartson layers on the sidewalls of the container having $\delta \sim \nu ^{1/4},\nu ^{1/3}$.

In addition, there are physical systems in which there are thin layers interior to the domains. An inviscid model of the ocean, rotating at angular speed $\Omega$ contains one such with $\delta \sim \Omega ^{-1/2}$ giving rise to the Gulf Stream in the North Atlantic [28]. In a premixed flame, the unburnt gas is separated from the burnt by a double-layer structure in which a hydrodynamic layer with $\delta \sim \kappa ,D$ contains a thinner one with $\delta \sim E^{-1}$ for large activation energy E [29]. Finally, shock waves in a compressible fluid give structures with $\delta$ depending on a power of the Mach number [30].

The family of thin-layer dynamics is huge, and the approaches outlined here aid in understanding quantitatively the mechanisms at work.