Modeling flow of nematic liquid crystal down an incline

Abstract

The flow of nematic liquid crystals down an inclined substrate is studied. Under the usual long wave approximation, a fourth-order nonlinear parabolic partial differential equation of the diffusion type is derived for the free surface height. The model accounts for elastic distortions of the director field due to different anchoring conditions at the substrate and the free surface. The partial differential equation we derive admits 2D traveling-wave solutions, which may translate stably or exhibit instabilities in the flat film behind the traveling front. These instabilities, which are distinct from the usual transverse instability of downslope flow, may be analyzed and explained by linear stability analysis of a flat translating film. Intriguing parallels are found with the instabilities exhibited by Newtonian fluid flowing on an inverted substrate and Newtonian fluid flow outside a vertical cylinder.

1 Introduction

There is great interest in understanding the dynamics of thin films due to their many applications. For Newtonian isotropic fluids a vast literature already exists on both experimental data and theoretical models for thin films. For complex fluids, such as liquid crystals (LCs), however, the theoretical and analytical literature is far more limited.

Thin films of LCs, and particularly of nematic liquid crystals (NLCs), find wide industrial application in display devices due to their optical properties (birefringence) and electric field response. The reader is referred to the books by Castellano [1] and Johnstone [2] for a history of liquid crystal display (LCD) development. The dielectric tensor for NLCs is anisotropic, which may lead to very large refractive indices, a property used in the design of superlenses that are capable of overcoming the resolution limits of conventional imaging techniques (diffraction limit) [3]. The dielectric property may also be used to accurately control electromagnetic waves, a desired feature in the design of devices for the purposes of optical imaging, space communication, and object detection by lasers [4]. The reader is referred to the review paper by Palffy-Muhoray [4] for more information on these and many other applications.

LCs are a state of matter intermediate between fluid and solid that have some short-range order to their molecular structure. In the nematic phase, the molecules have no positional order. Typically, LC molecules are rodlike rigid structures with a dipole moment associated with the anisotropic axis (the axis parallel to the length of the rodlike molecule). The interactions of the dipole moments cause molecules to align locally, giving rise to an elastic response; however, in general, fluid flow and external forces may distort the local alignment. At a surface or interface, NLC molecules have a preferred orientation, a phenomenon known as anchoring. Therefore, to model NLCs it is important to consider the velocity field, the local average orientation of molecules (director field), and the anchoring condition at interfaces.

One approach to modeling the spreading of NLC droplets is within the framework of the long wave approximation. Within this context, different anchoring conditions have been considered, including various combinations of weak anchoring and strong anchoring (a Dirichlet condition on the director field) at the free surface and underlying substrate [5–10]. In an alternative approach, energetic arguments were used to derive an equation governing free surface evolution [11]. This approach leads to predictions that differ from those of [5–7]. The differences between the approaches were recently reconciled [8, 12], leading to consistent predictions.

In experiments [13–15], spreading droplets of NLCs exhibit a diverse range of instabilities. Moreover, these instabilities exist in regimes where a Newtonian droplet would be stable. In this paper we consider a paradigm problem that highlights some key features of NLC coating flows and the differences with Newtonian cases [16, 17]: the flow of a thin film of NLC down an inclined substrate. Our work builds upon an earlier model [10] and modifies the free surface conditions to be thermodynamically consistent [18]. The resulting long wave model is a modified version of the model presented in [8], which contains an additional term related to the component of gravity in the downslope direction.

2 Model derivation

As was noted by Rey and Denn [19], the Leslie–Ericksen equations [20] are applicable for NLCs composed of rigid rod-like molecules with no spatiotemporal variations in the scalar-order parameter (a measure of how well a unit vector represents the local average orientation of LC molecules). Moreover, it was noted that the Leslie–Ericksen equations had been very successful in modeling NLCs with low molar mass. For other materials, such as NLC polymers (flexible rods), there may exist spatiotemporal dependencies in the order parameter, and other theories may be more appropriate to describe such flows: for example, the Landau-de Gennes tensor model (a generalization of the Leslie–Ericksen theory) or the Doi theory (a probabilistic description). In this paper, variations in the scalar-order parameter are not considered, and we work with the Leslie–Ericksen theory throughout. The reader is referred to the review paper by Rey and Denn [19] for further information on the strengths and weaknesses of the various models.

The main dependent variables within the Leslie–Ericksen formulation are the velocity field, $\mathbf {v}=(v_1,v_2,v_3)$, and the director field,

$$\begin{aligned} \mathbf {n}=(n_1,n_2,n_3)=( \sin \theta \cos \phi , \sin \theta \sin \phi , \cos \theta ). \end{aligned}$$

The Leslie–Ericksen equations describe the conservation of energy, momentum, and mass for a NLC in terms of $\mathbf {v}$ and $\mathbf {n}$. The governing equations are

$$\begin{aligned} \frac{\partial W}{\partial n_i} + \left( \frac{\partial W}{\partial n_{i,j}}\right) _{,j}-G_i&= 0, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \Pi }{\partial x_i} + G_k\, \frac{\partial n_{k}}{\partial x_i} + \frac{\partial \tau _{ij}}{\partial x_j}&= 0, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial v_i}{\partial x_i}&= 0, \end{aligned}$$

(3)

where we use subscript notation such that

$$\begin{aligned} {W}_{,j} = \frac{\partial W}{\partial x_j} \quad {\text {and}} \quad n_{i,j} = \frac{\partial n_i}{\partial x_j} \; . \end{aligned}$$

Here the important quantities are the total potential energy, $\Pi$; the bulk elastic distortion (Frank) energy, $W$; the kinetic rotational energy associated with viscous forces in each direction, $G_i$; and the viscous non-Newtonian stress tensor, $\tau$. The bulk elastic energy $W$ for NLC is given by

$$\begin{aligned} 2W=K_1\!\left( \nabla \cdot { \mathbf {n} } \right) ^2 + K_2 \left( \mathbf {n} \cdot \nabla \times { \mathbf {n} } \right) ^2 + K_3 \left| \mathbf {n} \times \nabla \times { \mathbf {n} } \right| ^2, \end{aligned}$$

where $K_i$, $i=1,2,3$, are elastic constants related to pure splay, pure twist, and pure bend distortions. Note that $W$ is zero if and only if the director field, $\mathbf {n}$, is constant.

The elastic constants are of the same order of magnitude, and it is common to make the so-called one constant approximation [7, 8, 10, 14, 21–23], $K=K_1=K_2=K_3$, reducing $W$ to

$$\begin{aligned} 2W=K\left( \left( \nabla \cdot \mathbf {n}\right) ^2+\left| \nabla \times \mathbf {n}\right| ^2\right) . \end{aligned}$$

(4)

The remaining quantities are given by

$$\begin{aligned} G_i&= \gamma _1\,N_i+\gamma _2\,e_{ik}n_k, \quad \Pi =p+W+\psi _g, \\ N_i&= -\dot{n_i}-\omega _{ik}\,n_k, \quad e_{ij}=\frac{1}{2}\left( \frac{\partial v_i}{\partial x_j} +\frac{\partial v_j}{\partial x_i}\right) , \quad \omega _{ij}=\frac{1}{2}\left( \frac{\partial v_i}{\partial x_j} -\frac{\partial v_j}{\partial x_i}\right) , \\ \tau _{ij}&=\alpha _1n_kn_p e_{kp}n_in_j + \alpha _2N_in_j+\alpha _3 N_jn_i +\alpha _4 e_{ij}+\alpha _5 e_{ik}n_kn_j +\alpha _6 e_{jk}n_kn_i, \end{aligned}$$

where $p$ is the pressure and $\psi _g$ the gravitational potential. The constants $\gamma _i$ and $\alpha _i$ are viscosities satisfying $\gamma _1 = \alpha _3 - \alpha _2$ and $\gamma _2 = \alpha _6 - \alpha _5$. Furthermore, the $\alpha _i$ satisfy the Onsager relation, $\alpha _2 + \alpha _3 = \alpha _6-\alpha _5$.

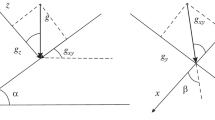
We consider the flow of a thin film of NLC down an inclined substrate, as indicated in Fig. 1. We define our coordinates $(x,y,z)$ such that the in-plane coordinates $(x,y)$ point down and across the incline, respectively, and $z$ is perpendicular to the plane of the substrate; $\chi$ is the inclination angle. In our formulation, we follow [8] but include a new gravitational potential, $\psi _g = -g \rho z \cos \chi + g \rho x \sin \chi$, where $g$ is the gravitational acceleration and $\rho$ the density of the NLC.

Fig. 1

Diagram showing coordinate system used relative to substrate

As noted in the introduction, NLC molecules have a preferred orientation with respect to a surface, a phenomenon known as anchoring [19, 24]. At a free surface, the director often prefers to align normal to the surface (so-called homeotropic anchoring). At a solid substrate, the anchoring is determined by the chemical interactions between the NLC and the substrate. It is common in applications to treat substrates chemically to impose planar anchoring with respect to the surface. In our analysis we assume strong planar anchoring at the substrate $z=0$ (the director field is always at the preferred orientation, which here is parallel to the substrate) and weak homeotropic anchoring at the free surface $z=h$ [21], as discussed subsequently in Sect. 2.1.1. Variations on these anchoring conditions are easily addressed within the current framework.

2.1 Long wave approximation

Let $h_0$ be a representative film height, $L$ the lengthscale of variations in the $x$ direction, $U$ the characteristic flow velocity down the plane, and $\mu$ a representative viscosity scale. Defining the aspect ratio, $\delta = h_0/L \ll 1$, we scale the variables as follows:

$$\begin{aligned} (x,y,z)=( L \hat{x} , L \hat{y} , L \delta \hat{z} ), \; \; \, (u,v,w)=( U \hat{x} , U \hat{y} , U \delta \hat{z} ), \;\; \, t = \frac{L}{U} \hat{t}, \end{aligned}$$

(5)

where hatted variables are dimensionless. Inspection of the energy (4) and momentum balance (2) then suggests the following scalings:

$$\begin{aligned} W = \frac{K}{L^2\delta ^2} \hat{W} \quad {\text {and}} \quad p = \frac{\mu U}{\delta ^2 L}\hat{p}. \end{aligned}$$

(6)

Using (5) and (6), two dimensionless parameters may be defined:

$$\begin{aligned} \mathcal{{B}}=\frac{\delta ^3\rho g L^{2}}{\mu U} \quad \hbox {and} \quad \tilde{\mathcal{{N}}} = \frac{K}{ \mu U L}, \end{aligned}$$

(7)

the Bond and inverse Ericksen numbers, respectively.

2.1.1 Energetics of the director field

In this section, we follow the novel approach to the energetics of the director field presented in [8]. In terms of the dimensionless variables, and dropping the hats, to leading order the bulk energy (4) is

$$\begin{aligned} 2W = \theta ^2_z + \phi _z^2\sin \theta , \end{aligned}$$

(8)

and energy conservation (1) becomes

$$\begin{aligned} \frac{\partial W}{\partial n_i} + \left( \frac{ \partial W }{\partial n_{i,j}}\right) _{,j} + \delta \tilde{\mathcal {N}} {\bar{G}}_i= 0, \quad {\bar{\mathbf G}} = \big ( u_z n_3 , v_z n_3 , u_z n_1 + v_z n_2 \big )^\mathrm{{T}}, \end{aligned}$$

(9)

where the terms in $\bar{{\mathbf G}}=(\bar{G}_1,\bar{G}_2,\bar{G}_3)^\mathrm{{T}}$ are the leading-order terms of ${\mathbf {G}}=(G_1,G_2,G_3)^\mathrm{{T}}$ in (1).

If $\tilde{\mathcal{{N}}}= O($1$)$, then the coupling term, ${\bar{\mathbf G}}$, in (9) is of lower order. This implies that the time scale on which elastic reorientation occurs is faster than the time scale of fluid flow. In this limit, (9) reduces to the Euler–Lagrange equations. The energy of the system consists only of the bulk energy, $W$, and the surface energy $\mathcal{{G}}$ associated with the weak (conical) homeotropic anchoring at the free surface. Therefore,

$$\begin{aligned} J = \int _0^h \int _\Omega \tilde{\mathcal{{N}}} W \, \mathrm{{d}}S\,\mathrm{{d}}z + \int _\Omega {\mathcal {G}} \, \mathrm{{d}}S, \end{aligned}$$

(10)

where $\Omega$ is the fluid domain in the $(x,y)$ plane.

To find the energy minimum, we use a variational approach and consider small variations in the director angles, $\phi$ and $\theta$. Using integration by parts for the volume integral in (10), the vanishing of the bulk terms in the first variation of $J$ leads to

$$\begin{aligned}&\theta _{zz} = \frac{\phi _z}{2} \sin 2 \theta \quad {\text {in}} \,\Omega \cup \{0 < z < h\},\end{aligned}$$

(11)

$$\begin{aligned}&\left[ \phi _z \sin ^2 \theta \right] _z = 0 \quad {\text {in}} \,\Omega \cup \{0 < z < h\}. \end{aligned}$$

(12)

The surface contribution, $\mathcal{{G}}$, is assumed to be independent of the angle $\phi$ (conical anchoring); therefore, the vanishing of the surface contributions leads to

$$\begin{aligned}&\phi _z \sin ^2 \theta = 0 \quad {\text {in}} \, \Omega \cap \{z=h\},\end{aligned}$$

(13)

$$\begin{aligned}&{\mathcal {G}}_{\bar{\theta }} + \tilde{\mathcal{{N}}} \theta _z = 0 \quad {\text {in}} \, \Omega \cap \{z=h\}, \end{aligned}$$

(14)

where $\bar{\theta }$ is the director angle on the free surface, i.e., $\bar{\theta }(x,y,t)=\theta (x,y,z=h,t)$. Equations (12) and (13) show that the angle $\phi$ must be independent of $z$, which reduces (11) to $\theta _{zz}=0$. Satisfying the strong anchoring condition on the substrate, $\mathcal {S}$ ($z=0$ here), gives

$$\begin{aligned} \phi (x,y,t)=\phi _\mathcal {S}(x,y), \quad \theta \ = a(x,y,t)z + \frac{\pi }{2}. \end{aligned}$$

(15)

If strong anchoring is imposed on both surfaces, then in a very thin film, adjusting between two antagonistic angles leads to unrealistically large energy penalties in the bulk. To resolve this issue, we impose weak homeotropic anchoring, with energy $\mathcal{{G}}(\bar{\theta })$, at the free surface. This means that the director angle $\theta$ is approximately zero at the free surface only for thick films ($h\gg 1$), but it can depart from zero significantly for very thin films ($h\ll 1$). More precisely, we write [consistent with (15)]

$$\begin{aligned} \theta = \frac{\pi }{2} \left( 1-\frac{m(h)}{h} z \right) , \end{aligned}$$

(16)

where $m(h)$ is a monotonically increasing function such that $m(0)=0$ and $m(\infty )=1$. This function $m(h)$ is directly related to the surface anchoring energy $\mathcal{{G}}$ via Eq. (14). Using the chain rule, we find

$$\begin{aligned} \frac{\mathrm{{d}}\mathcal {G}}{\mathrm{{d}}h} =\mathcal {G}_{\bar{\theta }} \frac{\mathrm{{d}}\bar{\theta }}{\mathrm{{d}}h} = - \tilde{\mathcal{{N}}}a \frac{\mathrm{{d}}\bar{\theta }}{\mathrm{{d}}h} = -\mathcal{{N}}\frac{m(h)m'(h)}{h}, \end{aligned}$$

where $\mathcal{{N}}= \pi ^2 \tilde{\mathcal{{N}}}/4$ is the scaled inverse Ericksen number. We choose the same form for $m(h)$ as was used in [8],

$$\begin{aligned} m(h) = f(h;b) \frac{h^\alpha }{h^\alpha +\beta ^\alpha }, \quad f(h;b) = \frac{1}{2}\left[ \tanh \left( \frac{h-2b}{w} \right) + 1 \right] . \end{aligned}$$

(17)

Here, $b\ll 1$ is the thickness of a preexisting precursor film that is assumed to be present in all our numerical simulations and $\alpha$ and $\beta > 0$ are constants that tune the relaxation of the anchoring at the free surface. The functional form of $m(h)$ corresponds to choosing a specific form of the free surface anchoring energy $\mathcal{{G}}(\bar{\theta })$ [it is easily verified that the corresponding $\mathcal{{G}}(\bar{\theta })$ has a unique minimum at $\bar{\theta }=0$]. The function $f(h;b)$ provides a continuous “cutoff” behavior, i.e., it imposes planar anchoring at the free surface to match that at the substrate when the film height goes below the precursor thickness, $b$. The constant $w$ provides control over the range of $h$ for which such planar anchoring is imposed.

2.1.2 Flow equations

Under the long wave scalings, coupled with the assumed form of the director field given by (15) and (16), to leading order momentum conservation (2) becomes

$$\begin{aligned}&\!\!\!\!\nabla \left( p + \mathcal{{N}}m^2 \right) + \mathcal{{U}}{\hat{\mathbf{i}}} = \frac{ \partial }{\partial z} \left[ \left( \begin{array}{cc} B_1 &{} B_3 \\ B_3 &{} B_2 \end{array} \right) \left( \begin{array}{c} u_z \\ v_z \end{array} \right) \right] , \end{aligned}$$

(18)

$$\begin{aligned}&\!\!\!\!\frac{ \partial p }{\partial z} = - \mathcal {D} , \end{aligned}$$

(19)

where $\nabla = (\partial _x , \partial _y)^\mathrm{{T}}$, ${\hat{\mathbf{i}}}=(1,0)^\mathrm{{T}}$,

$$\begin{aligned} \mathcal{{U}}= \mathcal{{B}}\sin \chi , \quad \mathcal{{D}}= \mathcal{{B}}\cos \chi \end{aligned}$$

(20)

and $B_i$ are given by

$$\begin{aligned} B_{1}&= A_1 + A_2 \cos 2 \phi , \quad B_{2} = A_1 - A_2 \cos 2 \phi , \quad B_{3} = A_2 \sin 2 \phi ,\\ A_1&= 1 + ( \alpha _5 - \alpha _2 ) \cos ^2 \theta + \alpha _1 \sin ^2 \theta \cos ^2 \theta + \frac{\alpha _3 + \alpha _6}{2} \sin ^2 \theta ,\\ A_2&= \alpha _1 \sin ^2 \theta \cos ^2 \theta + \frac{\alpha _3 + \alpha _6 }{2} \sin ^2 \theta . \end{aligned}$$

To proceed, we first integrate (19). To fix the constant of integration, we assume that in the direction normal to the surface, fluid stresses (elastic and viscous) are balanced by surface tension,

$$\begin{aligned} p + \mathcal{{N}}m^2 = - \mathcal{{C}}\nabla ^2 h \quad {\text {on}} \, z=h(x,y,t), \end{aligned}$$

(21)

where

$$\begin{aligned} \mathcal{{C}}=\frac{\delta ^3\gamma }{\mu U} \end{aligned}$$

(22)

is the inverse capillary number and $\gamma$ is surface tension. The left-hand side of (18) is now known explicitly and furthermore is independent of $z$; therefore, (18) may be integrated. To find the constant of integration, note that in the directions tangential to the surface, fluid stresses are balanced by surface energy gradients,

$$\begin{aligned} -\tilde{\mathcal{{N}}}\left[ \theta _z \nabla \theta + \theta _z^2 \nabla h \right] + \left( \begin{array}{cc} B_1 &{} B_3 \\ B_3 &{} B_2 \end{array} \right) \left( \begin{array}{c} u_z \\ v_z \end{array} \right) = \tilde{\mathcal{{N}}}\nabla \mathcal {G}= -\mathcal{{N}}\frac{mm'}{h} \nabla h, \end{aligned}$$

on $z=h(x,y,t)$. Substituting (16) in the preceding equation yields

$$\begin{aligned} \left( \begin{array}{cc} B_1 &{} B_3 \\ B_3 &{} B_2 \end{array} \right) \left( \begin{array}{c} u_z \\ v_z \end{array} \right) = 0 \quad \hbox {on}\, z=h(x,y,t). \end{aligned}$$

(23)

Integrating (18) over the film height and imposing (23) at the free surface, we find a matrix equation for $u_z$ and $v_z$,

$$\begin{aligned} \left[ \mathbf F(h) + \mathcal {U} { \hat{\mathbf i}} \right] (h-z) = \left( \begin{array}{c c} B_1 &{} B_3 \\ B_3 &{} B_2 \end{array} \right) \left( \begin{array}{c } u_z \\ v_z \end{array} \right) , \end{aligned}$$

(24)

where

$$\begin{aligned} \mathbf {F}(h)&= \nabla \left( p + \tilde{\mathcal {N}} W \right) = \mathcal {D} \nabla h - \mathcal {C} \nabla \nabla ^2 h + \mathcal {N} \frac{m^2-hmm'}{h^3} \nabla h . \end{aligned}$$

We assume there is no penetration and no slip at the substrate, $w=u=v=0$ on $z=0$, and we enforce the kinematic condition (to leading order) at the free surface, $h_t(x,y,t)= w(x,y,z=h,t)$. The conservation of mass (3) may then be integrated over the film height to obtain

$$\begin{aligned} h_t + \int _0^h \nabla \cdot ( u , v )^\mathrm{{T}} \; \mathrm{{d}}z = 0. \end{aligned}$$

(25)

The determinant of the $B_i$ matrix on the right-hand side of (24) is $D=A_1^2-A_2^2$. Assuming $|A_1|\ne |A_2|$, this matrix is nonsingular and may be inverted to obtain $u_z$ and $u_v$. We also have the following identities:

$$\begin{aligned} \int _0^h u_z (h-z) \;\mathrm{{d}}z = \int _0^h u\; \mathrm{{d}}z , \quad \int _0^h v_z (h-z) \;\mathrm{{d}}z = \int _0^h v\; \mathrm{{d}}z, \end{aligned}$$

which we use to combine expressions (24) and (25) to yield

$$\begin{aligned} h_t + \int _0^h \nabla \cdot \left( E(h) \left[ \mathbf {F}(h) - \mathcal {U} { \hat{\mathbf i}} \right] \right) \;\!\!\!\mathrm{{d}}z = 0, \end{aligned}$$

(26)

where the matrix $E(h)$ is defined by

$$\begin{aligned} E(h) = \int _0^h \frac{1}{D} \left( \begin{array}{c c} B_2 &{} -B_3 \\ -B_3 &{} B_1 \end{array} \right) (h-z')^2 \; \mathrm{{d}}z'. \end{aligned}$$

(27)

The integral in (27) is difficult to evaluate directly; therefore, we follow [8] in using a two-point trapezoidal rule for its estimate. This reduces (26) to the following fourth-order nonlinear parabolic partial differential equation for the film thickness, $h$,

$$\begin{aligned} h_t + \nabla \cdot \ \left( \mathcal {C} h^3 \tilde{\nabla } \nabla ^2 h - \mathcal {D} h^3 \tilde{\nabla } h - \mathcal {N} M(h) \tilde{ \nabla } h \right) + \mathcal {U} \mathcal {L}h^3 = 0, \end{aligned}$$

(28)

where

$$\begin{aligned} M(h)&= m^2-hmm' , \end{aligned}$$

(29)

$$\begin{aligned} \tilde{\nabla }&= \left[ \lambda I + \nu \left( \begin{array}{c@{\quad }c } \cos 2 \phi &{} \sin 2 \phi \\ \sin 2 \phi &{} - \cos 2 \phi \end{array} \right) \right] \left( \begin{array}{c} \partial _x \\ \partial _y \end{array} \right) , \\ \mathcal {L}&= \left[ \lambda + \nu \cos 2\phi \right] \partial _x + \nu \sin 2 \phi \partial _y + 2 \nu \left[ \phi _y \cos 2\phi - \phi _x \sin 2\phi \right] , \end{aligned}$$

$$\begin{aligned} \lambda = \frac{2+\alpha _3 + \alpha _6}{4\left( 1 + \alpha _3 + \alpha _6 \right) }, \quad \nu = -\frac{\alpha _3 + \alpha _6}{4\left( 1 + \alpha _3 + \alpha _6 \right) } , \end{aligned}$$

and $m(h)$ is defined by Eq. (17). Note that for the majority of NLCs, $-1<\alpha _3+\alpha _6<0$; therefore, $\lambda >\nu >0$ and $\tilde{\nabla }$ has positive coefficients.

3 Analysis: two-dimensional flow

To simplify the analysis and gain better insight into the phenomena captured by the model, only two-dimensional flow will be considered for the remainder of this paper, with a full investigation of the characteristics of the three-dimensional model deferred to a future publication. Under this restriction, $\phi =0,\,\pi$ are the only consistent values for the substrate anchoring. In either case, this leads to a factor of $\lambda + \nu$ in front of all spatial derivatives, which may be removed by rescaling time. Under this rescaling, Eq. (28), in two space dimensions with a free surface $z=h(x,t)$, becomes

$$\begin{aligned} h_t + \left[ \mathcal {C} h^3 h_{xxx} - \mathcal {D} h^3 h_{x} - \mathcal {N} M(h) h_{x} +\mathcal {U} h^3 \right] _x=0, \end{aligned}$$

(30)

with $M(h)$ as defined in (29) and dimensionless parameters as defined in (7), (20), and (22). It should be noted that if $\mathcal{{N}}=0$, then (30) describes the flow of a Newtonian thin film down an inclined plane [25]. In two dimensions and in the absence of a contact line, a Newtonian film described within the long wave approximation with inertial effects ignored flows stably down an inclined surface with only a hump (capillary ridge) forming near the front of the fluid. Therefore, any qualitatively different instability mechanism may only be a result of the $\mathcal{{N}}$ term.

3.1 Traveling-front solution

Motivated by known results for Newtonian films [16, 26], we first seek traveling-wave solutions, $h(x,t)=H(x-Vt)=H(s)$, where $V$ is the wave speed. Inserting this ansatz into (30) and integrating once with respect to the new variable $s=x-Vt$, we obtain

$$\begin{aligned} -VH + \mathcal {C} H^3 H''' - \mathcal {D} H^3 H' - \mathcal {N} M(H) H' + \mathcal {U} H^3 = c, \end{aligned}$$

(31)

where $c$ is a constant of integration. Applying the far-field boundary conditions, $H(s \rightarrow \infty )=b$ and $H(s \rightarrow -\infty )=h_0$ (corresponding to constant undisturbed flow), where $h_0$ is the free surface height behind the front and $b$ is the precursor thickness, the front velocity satisfies

$$\begin{aligned} V = \mathcal {U} \left( h_0^2 + h_0b + b^2 \right) . \end{aligned}$$

(32)

The preceding expression is the usual traveling-front speed for a Newtonian film; however, recall that a factor of $\lambda +\nu$ has been scaled out of the two-dimensional governing Eq. (30).

3.2 Linear stability of a flat film

We start by carrying out linear stability analysis (LSA) of a uniform film, which describes the situation far behind the traveling front. Consider a flat film with a small perturbation, $h(x,t) = h_0 + \epsilon h_1(x,t)$, where $\epsilon \ll 1$. If we substitute this form of the solution into (30), then the $O$($\epsilon$) equation is

$$\begin{aligned} \frac{ \partial h_1 }{\partial t} + \mathcal {C} h_0^3 \frac{ \partial ^4 h_1 }{\partial x^4} - \mathcal {D} h_0^3 \frac{ \partial ^2 h_1 }{\partial x^2} - \mathcal {N} M{\left( h_0\right) } \frac{ \partial ^2 h_1 }{\partial x^2} + 3 \mathcal {U} h_0^2 \frac{ \partial h_1 }{\partial x} =0. \end{aligned}$$

(33)

Assuming the plane wave form $h_1 = \mathrm{{e}}^{\omega t + \mathrm{{i}} k x}$ leads to the dispersion relation

$$\begin{aligned} \omega = -\left( \mathcal {C} h_0^3 k^ 2 + \left[ \mathcal {D} h_0^3 + \mathcal {N} M{\left( h_0\right) } \right] \right) k^2 - 3 \mathcal {U} h_0^2 k \mathrm {i}. \end{aligned}$$

(34)

The wavenumber $k$ is real, and for instability we require ${\text {Re}}(\omega ) > 0$ for some range of $k$. Hence, the sign of the term $h_0^3 \mathcal {D} + \mathcal {N} M(h_0)$ determines the stability of the film: if it is negative, then there is a range of unstable wavenumbers. By assumption, $\mathcal {D},\,\mathcal {N}>0$; thus, $M(h)$, given by Eq. (29), must be negative for some range of film heights for instability. Figure 2 shows $M(h)/h^3$ and Fig. 3 the dispersion relation in the unstable regime. In this case, the modes $|k| \in ( 0 , k_\mathrm{{c}})$ are unstable, where

$$\begin{aligned} k_\mathrm{{c}} = \sqrt{- \frac{1}{\mathcal {C}} \left[ \mathcal {D} + \frac{ \mathcal {N}M(h_0)}{h_0^3} \right] }. \end{aligned}$$

(35)

Furthermore, the fastest growing mode is given by

$$\begin{aligned} k_\mathrm{{m}} = \sqrt{- \frac{1}{2\mathcal {C}} \left[ \mathcal {D} + \frac{ \mathcal {N}M(h_0)}{h_0^3} \right] } \end{aligned}$$

(36)

and its growth rate is

$$\begin{aligned} \omega _\mathrm{{m}} = \frac{ 1 }{4\mathcal {C}} \left[ \mathcal {D} + \frac{ \mathcal {N}M(h_0)}{h_0^3} \right] ^2. \end{aligned}$$

(37)

Fig. 2

Plot of $M(h)/h^3$, where $M(h)$ is given by (29) and $m(h)$ is as defined in (17), with $\alpha =2$, $\beta =0.5$, and $w=0.05$. For a thin film of height $h$ such that $M(h)/h^3<0$, elastic effects are destabilizing

Fig. 3

Example of dispersion relationship (34) in unstable regime ($\mathcal{{D}}h_0^3 + \mathcal{{N}}M(h_0)<0$). Plane wave disturbances with wavenumber $k \in [ 0 , k_\mathrm{{c}} ]$ are unstable

We will assume throughout that the precursor film ahead of the traveling front lies in the stable regime of film thicknesses.

3.3 Absolute and convective instability

It is known from earlier work [25] that if $\mathcal{{N}}=0$ and $\mathcal{{D}}>0$, then there exist stable traveling fronts that are solutions to Eq. (31). Furthermore, based on other results [16], for $\mathcal{{N}}=0$ and $\mathcal{{D}}<0$, it is known that a traveling front may exhibit several types of instabilities. It is of interest to analyze the analogous instabilities that arise within the context of the present model specified by Eq. (30).

Within the unstable regime, it is instructive to discuss the evolution of surface perturbations. We may exploit existing results by noting that (33) may be transformed into the linearized symmetric Kuramoto–Sivashinsky (KS) equation. Following [16], we consider a moving reference frame, rescaling variables as

$$\begin{aligned} \eta = \sqrt{\frac{-\kappa }{\gamma }} \left( x -\zeta t \right) ,\quad \tau = \frac{\left( -\kappa \right) ^2}{ \gamma } t, \end{aligned}$$

(38)

where

$$\begin{aligned} \kappa = \mathcal {D} h_0^3 + \mathcal {N} M (h_0), \quad \zeta = 3 \mathcal {U} h_0^2, \quad {\text {and}} \quad \gamma = \mathcal {C} h_0^3. \end{aligned}$$

Under this transformation, (33) reduces to

$$\begin{aligned} h_\tau + h_{ \eta \eta \eta \eta } + h_{\eta \eta } = 0. \end{aligned}$$

We now consider the velocity of the left- and right-hand boundaries (denoted by $-$ and $+$, respectively) of an expanding so-called wave packet of perturbations to a flat film of height $h_0$. Following the techniques in [27], the velocities of the expanding wave packet boundaries are found numerically as $(\eta /\tau )_{\pm }=\pm 1.622$. Reverting to $x$ and $t$ variables yields, for the boundaries of the wave packet,

$$\begin{aligned} \left( \frac{x}{t} \right) _\pm = 3 \mathcal {U} h_0^2 \pm 1.622 \sqrt{ -\frac{ \left[ \mathcal {D} h_0^3 + \mathcal {N} M (h_0) \right] ^{3}}{{\mathcal {C} h_0^3} }}. \end{aligned}$$

(39)

The square root term is real since we are (by assumption) in the unstable regime. Comparing the wave packet velocity (39) to the traveling-front velocity (32), we see that the rightward moving wave packet boundary is always faster than the traveling front for $b<h_0$. This boundary may therefore always be ignored since it will move to the (stable) precursor side of the traveling front. There are three different cases to be considered for the left wave packet boundary, which we now discuss.

3.3.1 Type 1 (stable)

The left wave packet boundary also travels faster than the front:

$$\begin{aligned} V < \left( {x}/{t}\right) _{-}. \end{aligned}$$

For this case, perturbations propagate ahead of the traveling front (into the physical region occupied by the stable precursor) and are thus never observed.

3.3.2 Type 2 (convectively unstable)

The left wave packet boundary velocity is slower than the front velocity but still positive:

$$\begin{aligned} 0 < \left( {x}/{t}\right) _{-} < V. \end{aligned}$$

In this case, perturbations grow, and propagate more slowly than the front itself. Since the wave-packet velocity is positive, it travels to the right, thus does not propagate beyond the initial front position. The film remains flat behind the initial front.

3.3.3 Type 3 (absolutely unstable)

The left wave packet boundary velocity is negative,

$$\begin{aligned} \left( {x}/{t}\right) _{-} < 0, \end{aligned}$$

and hence travels to the left. As with Type 2, perturbations grow, but since the wave packet travels to the left, the disturbance is not confined, and the entire film is ultimately destabilized.

4 Computational results and discussion

In this section the results obtained from numerical simulations of Eq. (30) are compared to the analytical and LSA predictions derived in Sect. 3. To simplify the parameter study, unless stated otherwise, we vary $\mathcal{{N}}$, and for the other parameters we use the values specified in Table 1. The numerical simulations are based on a Crank–Nicolson (implicit) discretization scheme coupled with a Newton–Raphson iterative method to evaluate the nonlinear terms and an adaptive time stepping scheme. The reader is referred to [16] for more information on the numerical method. To study the dynamics of a traveling front, the domain and boundary conditions are given by

$$\begin{aligned} h(x_0,t) = h_0 , \quad h(x_\mathrm{{L}},t) = b , \quad h_x(x_0,t)=h_x(x_\mathrm{{L}},t)=0, \end{aligned}$$

(40)

where we set $x_0=0$ and $x_\mathrm{{L}}=400$. We use the initial condition (IC)

$$\begin{aligned} h(x,0)&= \frac{(h_0-b)}{2} \tanh \left[ -5\left( x-x_\mathrm{{f}}\right) \right] + \frac{h_0+b}{2}, \end{aligned}$$

(41)

which transitions from some height, $h_0$, behind the front at $x=x_\mathrm{{f}}$ to the precursor thickness, $b$. We set the initial front position $x_\mathrm{{f}}$ to be far from the boundaries; more precisely, for $x \in [x_0,x_\mathrm{{L}}]$, $x_\mathrm{{f}} = 2 \left( x_\mathrm{{L}}+x_0 \right) /3$. For simulations of a perturbed flat film, the initial condition

$$\begin{aligned} h(x,0)&= h_0 \left\{ 1+0.1 \exp \left[ - \frac{k}{10} \left( x-x_\mathrm{{c}} \right) ^2 \right] \cos \Big [ k\left( x-x_\mathrm{{c}} \right) \Big ] \right\} \end{aligned}$$

(42)

is used, where $x_\mathrm{{c}}$ is the center of the interval, and $k$ is given by (36). In the unstable regime ($\mathcal{{D}}+ \mathcal{{N}}M(h)/h^3 < 0$), the maximum of the growth rate (37) with respect to $h$ corresponds to the minimum of $M(h)/h^3$,

$$\begin{aligned} h_0=\max _{ h } \omega _\mathrm{{m}}=\min _h \frac{M(h)}{h^3}; \end{aligned}$$

therefore, for any $\mathcal{{N}}$, $\mathcal{{C}}$, $\mathcal{{U}}$, and $\mathcal{{D}}$ considered, the same $h_0$ maximizes (37). Hence, with fixed $\alpha$ $\beta$, and $w$, we may fix $h_0$ and analyze instability in the $\mathcal{{C}}$–$\mathcal{{D}}$–$\mathcal{{N}}$–$\mathcal{{U}}$ or $\mathcal{{B}}$–$\chi$–$\mathcal{{C}}$–$\mathcal{{N}}$ parameter spaces.

Table 1 Values of parameters chosen for simulations (except where specified otherwise). Here, $n$ is the number of discretization points

4.1 Traveling wave

To analyze the validity of our predictions for traveling-wave speed (32), we carried out simulations using (41) as the initial condition. Table 2 shows that for Type 1 (stable) cases, the relative difference between the front speed $V$ predicted by (32) and the average speed of the front calculated from numerical simulations is less than 1 % (the average speed was computed by averaging over the period of time sufficiently long that the results do not depend on the length of the averaging period). For the unstable Types 2 and 3, instabilities may interact with the front, causing oscillations in the height of the capillary ridge (the hump that forms behind the traveling front, seen in the Type 1 simulations in Fig. 4) as well in the front speed.

Table 2 Comparison of LSA predictions given by (32) with average front speed calculated from numerical simulations. Unless specified otherwise, in the Parameters column, $\mathcal{{N}}=1.25$, with other parameters as given in Table 1

Figure 4 compares the height profiles for various $\mathcal {N}$ at $t \sim 400$. A larger $\mathcal{{N}}$ leads to stronger instability, as expected based on (37). In this expression, $M(h)<0$; thus, increasing $\mathcal {N}$ results in larger growth rates, $\omega _\mathrm{{m}}$. To compare with the LSA results, Fig. 5 gives the LSA predictions based on (36). We note that, although the agreement between the LSA and numerical results is not perfect, the LSA captures the monotonic increasing dependence of $k_\mathrm{{m}}$ on $\mathcal{{N}}$ when $M(h)<0$.

Fig. 4

Comparison of height profiles at $t \sim 400$ for various values of $\mathcal {N}$. Dashed line: initial front position

Fig. 5

Comparison of LSA prediction given by (36) with average wave number $k$ calculated from direct numerical simulations of (30). Here $\mathcal{{N}}$ is increasing, with other parameters as specified in Table 1

4.2 Stable, convectively unstable, and absolutely unstable traveling waves

As mentioned in Sect. 3.3, there are three cases to consider for the left wave packet boundary. The threshold between the Type 1 and Type 2 regimes is found by equating the front speed (32) to the wave packet speed given by (39). The transition from Type 2 to Type 3 is given by the parameter set such that the speed of the left-hand boundary of the wave packet is zero. We also consider the stability threshold of a perturbed flat film, specified by the requirement that the $O(k^2)$ coefficient in the dispersion relation (34) vanishes. In terms of $\mathcal {N}$, with parameters as specified in the caption of Table 1, these regimes are as follows:

$$\begin{aligned} \begin{array}{l@{\quad }r@{\quad }l@{\quad }l@{\quad }l@{\quad }l} \mathrm{Stable \ Perturbed \ Flat \ Film:} &{} 0 \; \; < &{} {\mathcal {N}} &{} < \; \; 0.2810 \\ \mathrm{Type \ 1 \ (Stable \ Traveling \ Front):} &{} 0.2810 \; \; < &{} \mathcal {N}&{} < \; \; 0.9351\\ \mathrm{Type \ 2 \ (Convectively \ Unstable):} &{} 0.9351 \; \; < &{} \mathcal {N} &{} < \; \; 1.3480 \\ \mathrm{Type \ 3 \ (Absolutely \ Unst able):} &{} 1.3480 \; \; < &{}\mathcal {N} \end{array} \end{aligned}$$

In what follows we concentrate on the unstable regimes and consider the evolution of a traveling front and that of a perturbed flat film for $\mathcal{{N}}=0.7,1.2,1.7$ (Types 1–3, respectively).

Figure 6 shows a perturbed flat film in the Type 1 regime, $\mathcal{{N}}=0.7$. We see that the perturbation does not decay but rather slowly spreads over the film. On the other hand, Fig. 7 shows that the analogous traveling front is stable once the capillary ridge has formed at the front. This is as expected since here the left wave packet boundary is predicted to move faster than the front itself; this can also be seen by direct comparison of the speed of perturbation in Fig. 6 and of the front in Fig. 7. Figure 8 shows a perturbed flat film in the Type 2 regime, $\mathcal{{N}}=1.2$. We observe stronger instability (initial perturbation grows noticeably in amplitude) compared to the Type 1 case and the initial formation of solitary-like waves, similar to those observed for hanging films [16]. The waves do not propagate beyond the center, $x_\mathrm{{c}}$, of the initial perturbation (42), suggesting convective instability. Figure 9 shows the corresponding results for a traveling front. We confirm that the left boundary of the perturbation is traveling to the right (velocity is positive) and the front remains flat behind the initial front position, showing consistently the convective nature of the instability.

Fig. 6

Height profiles for perturbed flat film (42) in Type 1 regime for $\mathcal {N}=0.7$. Top to bottom: $t = 0,~100,~200,~300,~400$

Fig. 7

Height profiles for traveling front (41) in Type 1 regime for $\mathcal {N}=0.7$. Top to bottom: $t = 0,~100,~200,~300,~400$

Fig. 8

Height profiles for perturbed flat film (42) in Type 2 regime for $\mathcal {N}=1.2$. Top to bottom: $t = 0,~100,~200,~300,~400$

Fig. 9

Height profiles for traveling front (41) in Type 2 regime for $\mathcal {N}=1.2$. Top to bottom: $t = 0,~100,~200,~300,~400$

In the Type 3 regime ($\mathcal{{N}}=1.7$), absolute instability is observed for both a perturbed flat film and a traveling front, as shown in Figs. 10 and 11, respectively. The left wave packet boundary propagates to the left and therefore would eventually destabilize the entire film behind the front.

Fig. 10

Height profiles for perturbed flat film (42) in Type 3 regime for $\mathcal {N}=1.7$. Top to bottom: $t = 0,~100,~200,~300,~400$

Fig. 11

Height profiles for traveling front (41) in Type 3 regime for $\mathcal {N}=1.7$. Top to bottom: $t = 0,~100,~200,~300,~400$

4.3 Parametric dependence

To study the effect of the inclination angle, first recall the relationship between the $\mathcal{{D}}$–$\mathcal{{U}}$ domain and the $\mathcal{{B}}$–$\chi$ domain (20). We may then fix $\mathcal{{B}}=\sqrt{2}$ and study the effect of $\chi$ on the stability regimes. Figure 12 shows the stability zones in the $\chi$–$\mathcal{{N}}$ plane with other parameters defined in Table 1. Clearly, when $\mathcal{{N}}$ is large enough, for any small angle of inclination, $\chi$, the film is absolutely unstable. The dependence on $\chi$ may be surprising: this figure shows that increasing $\chi$ may lead to a transition from absolutely unstable (Type 3) to convectively unstable (Type 2), and even to Type 1, where a traveling front is stable. An example of where all three (in)stability regimes are possible by varying the inclination angle is shown by the dashed–dotted line $\mathcal{{N}}=0.6$ in Fig. 12. We note that the effect of $\mathcal{{C}}$ and $\mathcal{{B}}$ on the results is as expected, with larger values of both $\mathcal{{C}}$ and $\mathcal{{B}}$ stabilizing the flow.

Fig. 12

Plot of stability zones for traveling front in $\chi$–$\mathcal {N}$ plane. The dashed-dotted line gives an example of where, when the inclination angle $\chi$ is varied, all three stability regimes are possible. Note the entire region below the dashed curve is a stable regime for a traveling front. In this and the following figures, $S$ denotes the region (below the solid curve) in which a perturbed flat film is stable. Note that $V$ is defined by Eq. (32) and the transformation between the $\mathcal{{D}}$–$\mathcal{{U}}$ plane and $\mathcal{{B}}$–$\chi$ plane is defined by Eq. (20)

It is of interest to discuss the stability zones in terms of the intrinsic parameters: $h_0$ and $\chi$. In Figs. 13–15 we plot the stability zones for three values of $\mathcal{{N}}$, with fixed values for all other parameters, given in Table 1. We observe a rich structure involving transitions between stability and instability within the considered parameter space, with the general trend that the surface becomes increasingly unstable for larger values of $\mathcal{{N}}$, as expected.

Fig. 13

Plot of stability zones for traveling front in $\chi$–$h_0$ plane for $\mathcal{{N}}=0.25$. $S$ denotes stable region

Fig. 14

Plot of stability zones for traveling front in $\chi$–$h_0$ plane for $\mathcal{{N}}=0.8$. $S$ denotes stable regions

Fig. 15

Plot of stability zones for traveling front in $\chi$–$h_0$ plane for $\mathcal{{N}}=2.0$. $S$ denotes stable regions

5 Conclusions

To summarize, we find that, in contrast to Newtonian films, two-dimensional flows of nematic liquid films down an incline may be unstable with respect to surface perturbations. Furthermore, the analysis and simulations suggest that, depending on the physical parameters of the system, a traveling front can be stable, convectively unstable, or absolutely unstable. Consideration of perturbed flat films leads to consistent results. Relating the parameters in our dispersion relation back to the angle of inclination $\chi$, we find an interesting interplay between the destabilizing effects of gravity and the liquid crystalline nature of the film, such that for a given $\mathcal{{N}}$ (inverse Ericksen number) an increase of $\chi$ may bring the film from the absolute to the convective instability regime and even stabilize a traveling front.

There are striking parallels between the results obtained in this work and those obtained for the flow of a Newtonian fluid on an inverted substrate [16] or for the flow of a Newtonian fluid on the outer surface of a vertical cylinder [17]. For Newtonian films, surface instability is caused by destabilizing gravity; for NLC films it is due to the interplay between elastic properties and the anchoring conditions. In the present work we have focused on the two-dimensional geometry only and have not considered an interplay between free surface instability and the transverse instability of the contact line leading to so-called fingering. We leave a detailed study of this problem for future work.