1 Introduction

In a recent paper by Vitral [1], the author described interesting new results on the Poynting effect in simple shear and pure torsion that can be derived from stretch formulations for incompressible isotropic hyperelastic materials. The particular example of a strain-energy given in terms of the Bell strains is used in [1] to illustrate the results. The Bell strain is a linear function of the stretch tensor and the quadratic model used in [1] is called the quadratic-Biot material and is composed of both even and odd powers of stretches. This strain-energy appears in the work of Lurie [2] and was later revisited by Vitral and Hanna [3]. In the present paper, we use an alternative strain-energy that is a linear function of the stretch invariants to obtain results similar to those obtained in [1]. For both problems, some qualitative results are found that differ from those obtained in [1]. The material model used here is called the generalized Varga model and is a well-known strain-energy that has been previously used in several application of nonlinear elasticity. While numerous results for the problems of simple shear and pure torsion are well-known, it turns out that stretch formulations provide useful alternative outcomes for these problems that are different from the classical formulations that use invariants of the Cauchy-Green tensors. In particular, it is found that for both problems, a transition in the Poynting effect from the classical to a reverse Poynting effect can occur depending on the ratio of the two material constants appearing in the strain-energy.

In the next Section, we briefly discuss some relevant preliminaries from the stretch formulation of nonlinear hyperelasticity for isotropic incompressible materials. In Sect. 3, we consider the problem of simple shear and describe some results for the generalized Varga model defined in (2.2) below, adopting both plane stress and zero normal traction formulations. Similar results for the problem of pure torsion of a solid circular cylinder are obtained in Sect. 4. Some concluding remarks are made in Sect. 5.

2 Preliminaries

Here we briefly summarize some relevant equations pertaining to the stretch formulation of the response of incompressible isotropic hyperelastic materials. On using the standard notation

$$ i_{1} = \lambda _{1} + \lambda _{2} + \lambda _{3}, \qquad i_{2} = \lambda _{1}\lambda _{2} + \lambda _{2}\lambda _{3} + \lambda _{3}\lambda _{1},\qquad i_{3} = \lambda _{1}\lambda _{2}\lambda _{3} $$
(2.1)

for the three invariants of the stretch tensor in terms of the principal stretches \(\lambda _{i}\), the incompressibility condition \(i_{3} = 1\) yields \(\lambda _{1}\lambda _{2}\lambda _{3} = 1\) so that only two independent stretches arise. The strain energy density per unit undeformed volume is given by \(w(i_{1},i_{2})\). In this paper, we confine attention to the particular model

$$ w = c_{1}(i_{1} - 3) + c_{2}(i_{2} - 3), $$
(2.2)

where the constants \(c_{i}\) are such that

$$ c_{1} + c_{2} = 2\mu , $$
(2.3)

where \(\mu \) is the shear modulus for infinitesimal deformations. The model (2.2) is known as the modified (or generalized) Varga model as it generalizes a one-term model (\(c_{2} = 0\)) originally proposed by Varga [4] for natural rubber vulcanizates and later by Dickie and Smith [5] for styrene-butadiene rubber. See Hill [6] for a comprehensive review of the model (2.2) and its various applications. This model has also been used in [7] to investigate in a very transparent way the effect of slight compressibility of elastomers on the mechanical response in a variety of deformations.

On using (2.1) and the incompressibility condition on the principal stretches, the model (2.2) can be written as

$$ w = c_{1}(\lambda _{1} + \lambda _{2} + \lambda _{3} - 3) + c_{2}(\frac{1}{\lambda _{1}} + \frac{1}{\lambda _{2}} + \frac{1}{\lambda _{3}} - 3), $$
(2.4)

which can be viewed as a two-term incompressible power model of Ogden type [8] with powers of 1 and −1 respectively. Note that (2.2) differs from the quadratic-Biot material in both terms, since the latter is quadratic in \(\left ( i_{1} -3 \right )\) and its second term is function of the second invariant of the Bell strain – which is not the same as \(\left ( i_{2} -3 \right )\).

It is of interest to examine the response of the model (2.2) in uniaxial extension. We begin with the principal Cauchy stresses in terms of the principal stretches as

$$ t_{i} = - p + \lambda _{i}\frac{\partial w}{\partial \lambda _{i}}, \quad (\mbox{no sum}), $$
(2.5)

where \(p\) is the hydrostatic pressure arising due to the incompressible constraint. For uniaxial extension in the 1-direction with \(\lambda _{1} = \lambda\), \(\lambda _{2} = \lambda _{3} = \lambda ^{ - 1/2}\) so that \(t_{1} \equiv T\), \(t_{2} = t_{3} = 0\), we obtain

$$ T = \lambda _{1}\frac{\partial w}{\partial \lambda _{1}} - \lambda _{2}\frac{\partial w}{\partial \lambda _{2}} $$
(2.6)

which for the model (2.2) reads

$$ T = c_{1}(\lambda - \lambda ^{ - 1/2}) + c_{2}(\lambda ^{1/2} - \lambda ^{ - 1}). $$
(2.7)

It is convenient to nondimensionalize this result as

$$ \bar{T} \equiv \frac{T}{\mu} = (2 - \gamma )(\lambda - \lambda ^{ - 1/2}) + \gamma (\lambda ^{1/2} - \lambda ^{ - 1}), $$
(2.8)

where we have used (2.3) and introduced the dimensionless material parameter ratio

$$ \gamma = \frac{c_{2}}{\mu}. $$
(2.9)

The stress response (2.7), with positive constants \(c_{1},c_{2}\), is shown in Fig. 1 of [6] to agree with experimental data for maximum stretch up to \(\lambda = 3\). The figure in [6] corresponds to taking \(\gamma = 0.124\) in (2.8). A plot of (2.8) for a range of \(\gamma \) both positive and negative is given in Fig. 1 below. As can be seen from the figure, both ranges for \(\gamma \) are physically reasonable.

Fig. 1
figure 1

Dimensionless axial stress \(\overline{T}\) as a function of the stretch \(\lambda \) for the generalized Varga material under uniaxial extension. A range of \(\gamma \) are considered, and the original one-term Varga model is recovered for \(\gamma =0\)

Full size image

We record here some further preliminaries from the standard stretch formulation for incompressible isotropic materials (see, e.g., [9–11] for details). We use standard notation for the deformation gradient tensor \(\boldsymbol{F}\), left Cauchy-Green strain tensor \(\boldsymbol{B} = \boldsymbol{FF}^{T}\) and the left stretch tensor \(\boldsymbol{V}\) so that \(\boldsymbol{V}^{2} = \boldsymbol{B}\). The constitutive law for the Cauchy-stress can then be written as (see, e.g., Rivlin [11])

$$ \boldsymbol{T} = - p\boldsymbol{I} + (w_{1} + i_{1}w_{2})\boldsymbol{V} - w_{2}\boldsymbol{V}^{2}, $$
(2.10)

where \(w_{\alpha} \equiv \frac{\partial w}{\partial i_{\alpha}} \ (\alpha = 1,2)\) and \(\boldsymbol{I}\) denotes the unit tensor.

3 Simple Shear

The simple shear deformation is described by

$$ x_{1} = X_{1} + \kappa X_{2},\qquad x_{2} = X_{2},\qquad x_{3} = X_{3}, $$
(3.1)

where \(\left ( X_{1},X_{2},X_{3} \right )\) and \(\left ( x_{1},x_{2},x_{3} \right )\) denote the Cartesian coordinates of a typical particle before and after deformation respectively and \(\kappa > 0\) is an arbitrary dimensionless constant called the amount of shear. The angle of shear is \(\tan ^{ - 1}\kappa \). For the deformation (3.1), the formulation in terms of the principal stretches of the stretch tensor may be found, for example, in Ogden [9], Horgan and Murphy [10] and Vitral [1]. The deformation gradient tensor \(\boldsymbol{F}\) and the left Cauchy-Green strain tensor \(\boldsymbol{B} = \boldsymbol{FF}^{T}\) for the deformation (3.1) are

$$ \boldsymbol{F} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & \kappa & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ], \qquad \boldsymbol{B} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 + \kappa ^{2} & \kappa & 0 \\ \kappa & 1 & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ]. $$
(3.2)

The in-plane principal stretches \(\lambda _{1}\) and \(\lambda _{2}\) are given by (see, e.g., [10])

$$ \lambda _{1} = \frac{\kappa + \sqrt{4 + \kappa ^{2}}}{2}\quad ( > 1), \qquad \lambda _{2} = \frac{1}{\lambda _{1}}, $$
(3.3)

while the out-of-plane stretch is \(\lambda _{3} = 1\). Thus the principal stretch invariants (2.1) are

$$ i_{1} = i_{2} = 1 + \eta , \qquad \eta \equiv \sqrt{4 + \kappa ^{2}}. $$
(3.4)

These kinematic quantities are all constants and so the deformation is homogeneous.

As described in [10], the Cauchy stress distribution \(\boldsymbol{T}\) for this deformation in an incompressible material may be obtained using two different approaches to determine the hydrostatic pressure:

(A) Plane Stress: The most common approach is to assume plane stress conditions so that \(T_{33} = 0\). We confine attention here to the two stress components \(T_{12}\) and \(T_{22}\) which may be written as (see equations (20), (21) of [1])

$$ T_{12} = \left ( w_{1} + w_{2} \right )\frac{\kappa}{\eta}, $$
(3.5)

and

$$ T_{22} = - \left [ w_{1} + (1 + \eta )w_{2} \right ]\frac{\kappa ^{2}}{\eta ^{2} + 2\eta}, $$
(3.6)

respectively, where we recall the notation

$$ w_{\alpha} \equiv \frac{\partial w}{\partial i_{\alpha}} \quad (\alpha = 1,2), $$
(3.7)

and these derivatives are evaluated at the values of the invariants given in (3.4).

Remark 1

Although our primary focus here is on the model (2.2), it is of interest to examine the lateral normal stress (3.6) for general \(w(i_{1},i_{2})\) as this is the stress component that determines the Poynting effect. In particular, there is no Poynting effect if \(T_{22} = 0\), i.e., if \(w_{1} + (1 + \eta )w_{2} = 0\). It is easily verified that this condition holds if \(w(i_{1},i_{2}) = w(i_{1}^{2} - 2i_{2})\) where \(w\) is an arbitrary function of its indicated argument. Since \(i_{1}^{2} - 2i_{2} = I_{1}\) where \(I_{1}\) is the first invariant of the Cauchy-Green tensor, we thus recover the well-known result that there is no Poynting effect in simple shear for the class of generalized neo-Hookean materials defined by \(W = W(I_{1})\).

For the generalized Varga model (2.2), the stresses (3.5) and (3.6) reduce to

$$ T_{12} = \kappa \frac{(c_{1} + c_{2})}{\eta} = \frac{2\mu \kappa}{\sqrt{4 + \kappa ^{2}}}, $$
(3.8)

and

$$ T_{22} = - \left ( 2\mu + \eta c_{2} \right )\frac{\kappa ^{2}}{\eta ^{2} + 2\eta}, $$
(3.9)

respectively, where (2.3) and (3.4) have been used to obtain the final expressions.

It is of interest to also obtain an expression for the normal traction \(N\) on the slanted face of the sheared specimen. As shown in [10], one has

$$ N = T_{22} - \frac{\kappa T_{12}}{1 + \kappa ^{2}} $$
(3.10)

so that, on using (3.5) and (3.6) we find that

$$ \frac{N}{\kappa ^{2}} = - \frac{(w_{1} + w_{2})}{\eta} \left [ \frac{1}{\eta + 2} + \frac{1}{1 + \kappa ^{2}} \right ] - \frac{w_{2}}{\eta + 2}. $$
(3.11)

For the generalized Varga model (2.2), this may be written in dimensionless form as

$$ \bar{N} = \frac{N}{\mu} = - \frac{2\kappa ^{2}}{\eta} \left [ \frac{\kappa ^{2} + \eta + 3}{\left ( \eta + 2 \right )\left ( 1 + \kappa ^{2} \right )} \right ] - \frac{\gamma \kappa ^{2}}{\eta + 2}. $$
(3.12)

(B) Zero Normal Traction formulation:

As described in detail in [10], an alternative approach to obtaining the hydrostatic pressure is to assume that \(N = 0\) at the outset rather than the plane stress assumption. This is motivated by the fact that such normal tractions on the slanted faces are not normally applied in experiments involving simple shear. One now finds that

$$ T_{22} = \frac{\kappa ^{2}}{1 + \kappa ^{2}}\frac{\left ( w_{1} + w_{2} \right )}{\eta}. $$
(3.13)

For the generalized Varga model (2.2), this may be written as

$$ T_{22} = \frac{2\mu \kappa ^{2}}{(1 + \kappa ^{2})\eta}. $$
(3.14)

The expressions (3.5) and (3.8) for the shear stress remain unchanged.

Discussion:

Our primary focus here is on investigation of the Poynting effect in simple shear so we begin with the plane stress formulation (A). The non-dimensional normal stress \(\bar{T}_{22} \equiv T_{22}/\mu \) is given by (3.9) as

$$ \bar{T}_{22} = - \left ( 2 + \eta \gamma \right )\frac{\kappa ^{2}}{\eta ^{2} + 2\eta} $$
(3.15)

where we have used the notation \(\gamma = c_{2}/\mu \) already introduced in (2.9) and we recall from (3.4) that \(\eta \equiv \sqrt{4 + \kappa ^{2}}\).

There are two cases to consider:

  1. 1.

    \(c_{2} \ge 0\) and thus \(\gamma \ge 0\): It is seen from (3.15) that \(\bar{T}_{22} < 0\) so that the lateral normal stress is compressive and we have the usual Poynting effect.

  2. 2.

    \(c_{2} < 0\) and thus \(\gamma < 0\): If \(2 - \eta |\gamma |\ > 0\) so that \(\eta < 2/|\gamma |\), we still have a compressive normal stress and the usual Poynting effect holds. However if \(2 - \eta |\gamma |\ < 0\), i.e., \(\eta > 2/|\gamma |\), then the normal stress is tensile and we have a reverse Poynting effect. In the special case when \(\eta = - 2/\gamma \), then \(\bar{T}_{22} = 0\) and there is no Poynting effect in this case. On recalling from (3.4) that \(\eta \equiv \sqrt{4 + \kappa ^{2}}\), we conclude that if

    $$ \sqrt{4 + \kappa ^{2}} < 2/|\gamma | \mbox{ or equivalently } |\gamma | < 2/\sqrt{4 + \kappa ^{2}} $$
    (3.16)

    then the usual Poynting effect occurs while if the inequalities in (3.16) are reversed, one has the reverse Poynting effect. If the strict inequality signs in (3.16) were replaced by equality, then there is no Poynting effect.

The result (3.16) may be interpreted in two ways: For a given material constant ratio in the range \(- 1 < \gamma < 0\), the first inequality in (3.16) holds (so that the usual Poynting effect occurs) for a sufficiently small amount of shear. Alternatively, for a given amount of shear \(\kappa \), the second inequality in (3.16) holds for a sufficiently small negative \(\gamma \). Conversely, the reverse inequalities in (3.16) hold (so that we get a reverse Poynting effect) for a sufficiently large amount of shear or for a sufficiently large negative material constant ratio. These results are similar to, but differ qualitatively from those found in [1] for the quadratic-Biot material. This type of transition in the Poynting effect was observed experimentally in shearing of bio-gels [12]. See also the discussion in Destrade et al. [13].

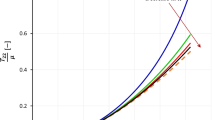
The critical amount of shear at which the transition in the Poynting effect occurs is given by (3.16) as \(\kappa _{c} = 2\sqrt{\gamma ^{ - 2} - 1}\) so that the relevant range of \(\gamma \) is \(- 1 < \gamma < 0\). Figure 2 shows a plot of curves for \(\bar{T}_{22}\) as a function of \(\kappa \) for various values of \(\gamma \) in this range.

Fig. 2
figure 2

Dimensionless normal stress \(\overline{T}_{22}\) as a function of the amount of shear \(\kappa \) for the generalized Varga material (2.2) in the negative range of \(\gamma \). At each fixed sufficiently large \(\kappa \), note the transition from the classic Poynting effect (\(\bar{T}_{22} < 0\)) to the reverse Poynting effect (\(\bar{T}_{22} > 0\)) as \(\gamma = c_{2}/\mu \) decreases from 0 to −1

Full size image

We turn now to an analysis of the normal traction on the slanted sides given in (3.12). The dimensionless normal traction \(\bar{N} \equiv N/\mu \) is given in (3.12) as

$$ \bar{N} = \frac{N}{\mu} = - \frac{2\kappa ^{2}}{\eta} \left [ \frac{\kappa ^{2} + \eta + 3}{\left ( \eta + 2 \right )\left ( 1 + \kappa ^{2} \right )} \right ] - \frac{\gamma \kappa ^{2}}{\eta + 2}. $$
(3.17)

Again, there are two cases to consider:

  1. 1.

    \(c_{2} \ge 0\) and thus \(\gamma \ge 0\): We see from (3.17) that \(\bar{N} < 0\) and so is compressive.

  2. 2.

    \(c_{2} < 0\) and thus \(\gamma < 0\): From (3.17) we see that \(\bar{N}\) is still compressive if

    $$ \frac{2}{\eta} \frac{(\kappa ^{2} + \eta + 3)}{1 + \kappa ^{2}} > - \gamma \mbox{ or equivalently } \gamma > - \frac{2}{\eta} \frac{(\kappa ^{2} + \eta + 3)}{1 + \kappa ^{2}}. $$
    (3.18)

    Thus, we conclude that \(\bar{N} < 0\) when (3.18) hold while if the inequalities in (3.18) are reversed, then \(\bar{N} > 0\). In the special case when equality holds in (3.18) rather than the strict inequality, then \(\bar{N} = 0\) so that there is no normal traction on the slanted faces in this case. The inequalities (3.18) are the analogs of (3.16) and may be interpreted in similar ways to those outlined after (3.16). Figure 3 shows a plot of curves for \(\bar{N}\) as a function of \(\kappa \) for various values of \(\gamma \) in the range \(- 1 < \gamma < 0\). Note that the values of \(\kappa \) at which the transition in \(\bar{N}\) occur are much larger than their counterparts in Fig. 2.

    Fig. 3
    figure 3

    Dimensionless normal traction \(\bar{N}\) on the slanted sides as a function of the amount of shear \(\kappa \) for the generalized Varga material (2.2) in the negative range of \(\gamma \). At each fixed sufficiently large \(\kappa \), note the transition from the Poynting effect (\(\bar{N} < 0\)) to the reverse Poynting effect (\(\bar{N} > 0\)) as \(\gamma = c_{2}/\mu \) decreases from 0 to −1

    Full size image

It is of interest to consider also the shear stress given in (3.8) which we write in dimensionless form as

$$ \bar{T}_{12} = \frac{T_{12}}{\mu} = \frac{2\kappa}{\sqrt{4 + \kappa ^{2}}}. $$
(3.19)

Note that this is independent of the material constant ratio \(\gamma \) and is shear hardening, i.e., a monotonic increasing function of \(\kappa \). We note that the shear stress obtained in [1] for the quadratic-Biot material was also shear hardening but did depend on a material constant ratio.

Finally, here we consider the zero normal traction formulation (B). In this case the non-dimensional normal stress on the lateral surface is given by (3.14) as

$$ \bar{T}_{22} = \frac{2\kappa ^{2}}{(1 + \kappa ^{2})\sqrt{4 + \kappa ^{2}}}. $$
(3.20)

In contrast with (3.15) this is independent of the material constant ratio \(\gamma \) and is seen to be always positive, i.e., tensile. Thus, one always has a reverse Poynting effect in this case. The dimensionless shear stress is still given by (3.19). This result that a reverse Poynting effect always occurs when the zero normal traction on the slanted faces is assumed was shown in [10] to hold for a general isotropic material on using the usual formulation in terms of the classical invariants of the Cauchy-Green strain tensor.

4 Pure Torsion

The stretch formulation of pure torsion of a solid circular cylinder of radius \(A\) has been described in [11], [14] and [1]. On using cylindrical coordinates (\(R,\Theta ,Z\)) in the undeformed configuration and (\(r,\theta ,z\)) in the current configuration, this inhomogeneous deformation is characterized by

$$ r = R, \qquad \theta = \Theta + \tau Z, \qquad \mathrm{z} = \mathrm{Z}, $$
(4.1)

where \(\tau \) denotes the twist per unit length. In this case, the principal stretch invariants are

$$ i_{1} = i_{2} = 1 + d, \qquad d = d(R) \equiv \sqrt{4 + \tau ^{2}R^{2}}, $$
(4.2)

which are functions of the radial coordinate \(R\).

To assess the Poynting effect, it is sufficient to simply analyze the resultant axial force \(N\) required to maintain pure torsion. This can be obtained from equation (41) in [11] or directly in equation (48) of [14] as

$$ N = - \pi \tau ^{2}\int _{0}^{A} \frac{R^{3}}{i_{1}^{2} - 1}\left [ (i_{1} + 2)w_{1} + (2i_{1} + 1)w_{2} \right ]dR, $$
(4.3)

where we recall that \(A\) is the radius of the cylinder.

For the generalized Varga model (2.2), one finds that

$$ N = - \frac{\pi}{6\tau ^{2}}\left [ c_{1}\left [ 2d(A) + 11 \right ] + c_{2}\left [ 4d(A) + 13 \right ] \right ](d(A) - 2)^{2}, $$
(4.4)

where \(d(A) = \sqrt{4 + \tau ^{2}A^{2}}\). This can be written as

$$ \frac{N}{\mu} = - \frac{\pi}{3\tau ^{2}}\left [ \left [ 2d(A) + 11 \right ] + \gamma \left [ d(A) + 1 \right ] \right ](d(A) - 2)^{2}, $$
(4.5)

on using (2.3) and (2.9). For \(\gamma = 0\), we recover from (4.5) the result of Horgan and Murphy [14] for the classic one-term Varga model (see also Vitral [1]). If \(\gamma \ge 0\), then \(N < 0\) and we get the usual Poynting effect. If \(\gamma < 0\), then we see from (4.5) that \(N \le 0\) still holds if

$$ \left [ 2d(A) + 11 \right ] + \gamma \left [ d(A) + 1 \right ] \ge 0 $$
(4.6)

which we write as

$$ \frac{\left [ 2d(A) + 11 \right ]}{\left [ d(A) + 1 \right ]} \ge - \gamma \mbox{ or equivalently } \gamma \ge - \frac{\left [ 2d(A) + 11 \right ]}{\left [ d(A) + 1 \right ]}. $$
(4.7)

These are the analogs of (3.16) obtained for simple shear. When equality holds in (4.7) we have \(N = 0\) so that there is no Poynting effect in this case. When (4.7) hold with strict inequality, we have the usual Poynting effect whereas if these inequalities are reversed, we get a reverse Poynting effect. Since \(d(A) \equiv \sqrt{4 + \tau ^{2}A^{2}}\), the conditions (4.7) can be written as conditions on the total angle of twist \(\tau A\). Such a transition in the Poynting effect depending on the amount of twist was not found to occur for the quadratic-Biot material used in [1]. The critical value of \(\tau A\) for which the transition in the Poynting effect occurs when equality holds in (4.7) which can be shown to occur when

$$ \tau ^{2}A^{2} = \frac{3(7 - \gamma )\left ( \gamma + 5 \right )}{(2 + \gamma )^{2}}, \quad \gamma \ne - 2. $$
(4.8)

In Fig. 4, we plot the dimensionless axial force

$$ \bar{N}=\frac{N}{\mu A^{2}\pi} = - \frac{1}{3\tau^{2} A^{2}} \big[ [2d(A) + 11] + \gamma [d(A) + 1] \big] (d(A)-2)^{2} $$
(4.9)

versus total angle of twist for values of \(\gamma \) in the range \(- 5 \le \gamma \le 0\). The similarity with Fig. 2 for simple shear is evident.

Fig. 4
figure 4

Dimensionless resultant axial force \(\bar{N}\) as a function of the total angle of twist \(\tau A\) for the generalized Varga material (2.2) in the negative range of \(\gamma \). At each fixed sufficiently large \(\tau A\), note the transition from the classic Poynting effect (\(\bar{N} < 0\)) to the reverse Poynting effect (\(\bar{N} > 0\)) as \(\gamma = c_{2}/\mu \) decreases from 0 to −5

Full size image

The analysis of the pure torsion problem is clearly more complex than that for the case of simple shear. Some further progress can be made by considering the special case of slender thin cylinders but we shall not pursue this here.

5 Concluding Remarks

Motivated by the recent paper [1], we have further investigated here the Poynting effect in simple shear and torsion for isotropic incompressible hyperelastic materials by using a stretch-based formulation and focused on the well-known generalized Varga strain-energy density (2.2) as an illustrative example. For the classic plane stress formulation of simple shear, when the two material constants in the model are positive, the lateral normal stress was shown to be always compressive so that one has the classical Poynting effect. When the second constant is negative, two possibilities arose: on nondimensionalizing this constant through division by the shear modulus, it was shown that for a given value of this parameter, the classical Poynting effect occurred for a sufficiently small amount of shear whereas for larger values of shear a reverse Poynting effect was obtained. A similar result was found for the normal traction on the slanted faces of the specimen. For the alternative formulation of simple shear where the hydrostatic pressure was determined by assuming at the outset that the normal traction on the slanted faces vanishes, it was found that the dimensionless lateral normal stress was independent of the material constant ratio and was always tensile so that one has a reverse Poynting effect. Similar results were shown to hold for the problem of pure torsion of a solid circular cylinder where the resultant axial normal force required to maintain pure torsion was found to be compressive for sufficiently small total angle of twist and tensile for larger values of twist. The results obtained here are reminiscent of those described in [13, 15] for anisotropic materials where further references to the literature on Poynting effects may be found.

We have focused attention in this paper on the specific generalized Varga model (2.2) since it is a natural sequel to consider as a complement and contrast to the quadratic-Biot model considered in [1]. Other stretch-based models could of course be examined. An obvious candidate is the celebrated Ogden model [8, 9] with power-law dependence on the principal stretches. Simple shear for the one-term Ogden model has been investigated in the recent paper [16] where it was shown that the classical or reverse Poynting effect can occur depending on the strain-hardening exponent in the model. Results for pure torsion for such models are the subject of a forthcoming paper [17].