1 Introduction

In d-dimensional linear elasticity, the stress components σ ij and the strain components ε kl are related by the constitutive law σ ij =C ijkl ε kl , with the usual symmetry conditions:

Thus any elastic material is characterized by a system of elastic coefficients C=(C ijkl )1≤i,j,k,l≤d but this correspondence is not one-to-one because these coefficients are linked to the choice of a particular orthonormal frame. A changing of proper orthonormal frame, i.e. a rotation matrix r of elements \(r^{p}_{i}\), modifies the components of the elasticity tensor according to the tensorial rule:

(1)

In the modern language of differential geometry, it defines an action of the special orthogonal group \(\mathbb{SO}(d)\) of ℝd on the vector space \(\mathbb{E} (d) = \mathbb{S}^{2} \mathbb{S}^{2} \mathbb {R}^{d}\) of the elastic coefficients systems C. As the assignment (1) of the \(C' = (C'_{ijkl})\) to the C=(C pqmn ) is linear, we said that it is a linear representation of \(\mathbb{SO}(d)\) into \(\mathbb{E} (d)\):

(2)

To a given elasticity tensor corresponds the set of all elastic coefficient systems C′ representing it:

(3)

called the \(\mathbb{SO}(d)\)-orbit of C (or simpler the orbit of C). To each elasticity tensor corresponds an orbit. The space \(\mathbb{EL} (d)\) of the elasticity tensors, that can be assimilated to the orbit space, is often called the quotient space of \(\mathbb{E} (d)\) by the group \(\mathbb{SO}(d)\) and is denoted \(\mathbb{E} (d) / \mathbb {SO}(d)\). We want to study its underlying geometric structure. In the present work, we treat the planar case (d=2) although some results are more general and, as we hope, our method could be generalized to the case d=3. Thus, characterizing the elastic materials amounts to find a convenient parameterization of this set by local charts.

Powerful tools are the theory of linear representation of groups [32] and the theory of invariants [24], particularly the simplest ones, the polynomial invariants. The analysis of the symmetries becomes strongly easier using a matrix presentation of the calculus and a suitable scaling of the components of the elasticity tensor. Voigt notation [41] consists in collecting the stress and strain tensor components into n-column vectors and the elasticity tensor’s ones into a n×n symmetric matrix (n=3 in 2D and n=6 in 3D). Although widely used in the literature, Voigt’s notation is not relevant for an easy study of symmetries. Even if it is older and previous to the modern tensorial calculus, Kelvin’s system [33, 34] must be preferred. It has been introduced and used again by Walpole [42], Rychlewski [29, 30], Mehrabadi and Cowin [19, 20]. This formulation is particularly efficient because it allows recovering the elastic law as a simple product of a matrix by a column vector of ℝn in a way such that the concepts of Euclidean norm and Euclidean scalar product can be transported. The calculations are simplified and the changing of elasticity tensor’s components through a changing of proper orthonormal frame of ℝd is represented by an orthogonal transformation of ℝn. It allows a decomposition into irreductibles [32] of the space \(\mathbb{E} (d)\). The real valued functions that are invariant over each orbit characterize the elasticity tensor in an intrinsic way. Following a fundamental theorem (Hilbert’s basis theorem), the set of polynomial invariants is generated by a finite number of them [17, 18]. The difficulty consists in finding a minimum set of generators (or functional basis), that needs detecting the dependency relations (syzygies). The knowledge of these invariants allows determining to which orbits the system of elastic coefficients belongs. In the 3D case, the decomposition into irreductibles for the orthogonal group is well known and used by many authors. Among them, without being exhaustive, can be quoted Pratz [28], Cowin [9], Boehler, Kirillov Jr. and Onat [5], Ostrasablin [26, 27]. There are 5 irreductibles subspaces, \(\mathbb{E}_{0}\) and \(\mathbb{E}'_{0}\) of dimension 1, \(\mathbb{E}_{5}\) and \(\mathbb{E}'_{5}\) of dimension 5, and \(\mathbb{E}_{9}\) of dimension 9. Finding a systems of generators separating the orbits is a harder task. The minimum number is 18. A strategy followed by some authors [1, 35] consists in building systematically the polynomial invariants of increasing degree p. Moreover, as it will be seen further, this way would require following the method up to degree 10.

Boehler and coworkers paper [5] is probably one of the more achieved insofar as it takes into account the decomposition into irreductibles. To the primary invariants of each subspace, one must add the joint invariants revealing the coupling between them. Embedding the elasticity tensor into a 37-dimensional Euclidian space, Boehler and his coworkers propose 39 generators, among them 15 primary invariants: a linear one for each subspace \(\mathbb{E}_{0}\) and \(\mathbb{E}'_{0}\), two invariants for each subspace \(\mathbb{E}_{5}\) and \(\mathbb{E}'_{5}\), and nine invariants for \(\mathbb{E}_{9}\) of which the degrees run from p=2 to 10. The main breakthrough of this work is the construction of primary invariants of \(\mathbb{E}_{9}\). It remains finding the syzygies because a minimal number of 6 is expected. Concerning the 24 joint invariants, a minimum number of 3 is expected between \(\mathbb{E}_{5}\) and \(\mathbb{E}'_{9}\), 3 between \(\mathbb{E}'_{5}\) and \(\mathbb{E}'_{9}\), and 6 between \(\mathbb{E}_{5}\), \(\mathbb{E}'_{5}\) and \(\mathbb{E}'_{9}\). It remains to determine the numerous syzygies between the 24 joint invariants. Another point of view adopted by Bóna, Bucataru and Slawinski [6] is parameterizing directly the elasticity tensor space with 18 parameters on the ground of Kelvin’s eigendecomposition [34]. Based also on eigenvalue problems, Betten proposed a simple method to obtain easily invariants of the elasticity tensors [4].

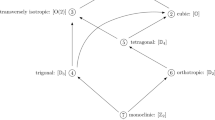
Relatively deconnected from the determination of the invariants, another topics of practical interest is the analysis of the symmetry group of a given anisotropic material, that is the closed subgroup of \(\mathbb{O}(d)\) of the orthogonal transformations leaving invariant all the elastic coefficients. At each symmetry group corresponds a class of materials. As proved again recently in [8, 14], there is only 8 possible symmetry groups in 3D: I for the triclinic materials, ℤ2 for the monoclinic materials, D 2 for the orthotropic materials, D 3 for the trigonal materials, D 4 for the tetragonal materials, \(\mathbb {O}(2)\) for the transversely isotropic materials, O for the cubic materials and \(\mathbb{O}(3)\) for the isotropic materials. Moreover, it is worth noting that the study of the symmetry groups of a second gradient medium was made in [2].

In the literature, the studies are generally made in a basis naturally associated to the symmetry group, that reduces the elasticity tensor to a simple form which renders easier the calculations. An open question is determining the elastic behaviour of an anisotropic material of which the symmetry is not known a priori. It is of great interest for geomaterials, composite and biological materials. Methods to determine the closest class of symmetry of a given material and the distance to it is discussed by Bucataru et al. [7] and François et al. [15]. Other methods of accomplishing this objective has been proposed by Cowin and coworkers in [10, 11] and applied in [43]. Another challenge of the analysis of the elasticity tensor’s invariants concerns the damage models. Indeed, the initiation and propagation of the defects in a material leads generally to a lack of symmetry of the material properties. Thus the damage theories rarely involve the representation of the symmetry group in the modeling, excepted in a few sporadic attempts [15, 16, 25].

If the studies in 3D deserve to be improved, the theoretical analysis of the 2D case, interesting per se, is simpler but nevertheless not trivial. Curiously, not much attention has been paid in the literature to it, except Vannucci et al. [37], Vincenti et al. [40], Vannucci [36] and Vannucci et al. [38], following the polar method proposed by Verchery [39] using \(\mathbb{SU}(2)\). The aim of the present paper is to study the 2D case by an alternative method. It is structured as follows. In Sect. 2, Kelvin’s representation and its advantages are presented. Section 3 recalls the parameterization of the stress tensor space according to Mohr’s circle construction and useful for the sequel. In Sect. 4, the elasticity tensor parameterization inherits from the stress tensor one due to a simple matrix calculus. We recover Weyl’s decomposition in irreductibles [3, 31]. There are 4 irreductible subspaces, \(\mathbb{E}_{0}\) and \(\mathbb{E}'_{0}\) of dimension 1, \(\mathbb{E}_{2}\) and \(\mathbb{E}_{4}\) of dimension 2. We propose 5 generators, among them 4 primary invariants (a linear one for each subspace \(\mathbb{E}_{0}\) and \(\mathbb{E}'_{0}\), a quadratic one for each subspace \(\mathbb{E}_{2}\) and \(\mathbb{E}'_{4}\)) and a joint invariant between \(\mathbb{E}_{2}\) and \(\mathbb{E}'_{4}\). In Sect. 5, the previous invariants allows us to reveal the underlying geometry of the elasticity tensor space \(\mathbb{EL} (2)\), consisting in a 5-dimensional manifold \(\mathbb{EL}_{g}\) (corresponding to the generic orbits) of which the boundary is composed of two volumes \(\mathbb{EL}_{2}\) and \(\mathbb{EL}_{4}\) intersecting following a surface \(\mathbb{EL}_{\mathit{iso}}\) (corresponding to the isotropic elasticity tensors). In Sect. 6, we determine the possible symmetry groups. For each one, we obtain an invariant measure of the lack of symmetry, revealing the physical meaning of the invariants previously determined and providing an original method to determine the elastic behaviour of an anisotropic material of which the symmetry is not known a priori. Conversely to [7], we obtain directly the invariance without minimization. In Sect. 7, we discuss the previous invariant measures in terms of Euclidean geometry and interpret them as length and area. In Sect. 8, we compare the invariants for the actions of ℤ2, \(\mathbb{O}(2)\) and \(\mathbb{SO}(2)\) onto \(\mathbb{E} (2)\). Both orbits for \(\mathbb{SO} (2)\) and \(\mathbb{O} (2)\) are the same but the choice of the generators of their respective invariants depends on the way in which the group acts on the orbit.

2 Kelvin’s Representation

In the planar case, Voigt’s representation of the constitutive law is:

(4)

A more convenient representation, due to Kelvin [33, 34], is:

(5)

According to this representation, the stress component system σ=(σ ij ) will be represented by s∈ℝ3 with s 1=σ 11, s 2=σ 22, \(s_{3} =\sqrt{2} \sigma_{12} \) (and similar representation e∈ℝ3 for the strain component system), while the elastic coefficient system C will be represented by the symmetric 3×3 matrix \(c\in\mathbb{S}^{2} \mathbb{R}^{2}\) such that

(6)

The constitutive law is recast in a matrix relation:

(7)

Generalization to an arbitrary dimension d is obvious with e,s∈ℝd(d+1)/2 and \(c\in\mathbb{S}^{2} \mathbb{R}^{d (d + 1)/2}\), according to the index contraction rule:

(8)

Now, let us show immediately an advantage of this new representation

Theorem 2.1

In Kelvin representation, any orthogonal matrix \(r \in\mathbb{O}(d)\) acts on \(\sigma\in\mathbb{S}^{2} \mathbb{R}^{d}\) as an orthogonal matrix \(R\in\mathbb{O} (d (d + 1)/2 ) \) acting on s∈ℝd(d+1)/2.

Proof

The space \(\mathbb{S}^{2} \mathbb{R}^{d}\) is equipped with the canonical scalar product:

Accounting for the symmetry of the stress tensor, we see that

If \(\sigma, \tau\in\mathbb{S}^{2} \mathbb{R}^{d}\) are respectively represented by s,t∈ℝd(d+1)/2, equipped with the canonical scalar product, one has, owing to the index contraction rule (8):

which defines an isomorphism between the Euclidean spaces \(\mathbb{S}^{2} \mathbb{R}^{d}\) and ℝd(d+1)/2.

For a change of orthonormal frame \(r \in\mathbb{O}(d)\), such that

(9)

it follows that

(10)

which gives

Consequently, the scalar product is conserved:

Because of the isomorphism noted above, this yields

Thus, there exists \(R\in\mathbb{O} (d (d + 1)/2 ) \) such that s′=Rs and t′=Rt. □

3 Parameterization of the Stress Tensor Space

Let us consider a change of orthonormal coordinates \(x' = r^{T}_{\theta}x\) with the rotation matrix

(11)

The geometrical representation of planar symmetric tensors by circles is due to Culmann [12] for the 2D version and to Mohr for the 3D case ([21–23]). The tensorial rule (10) for the stress tensor gives the well known formulas:

that can be stated in the Kelvin representation as the relation s′=Rs:

Theorem 2.1 proves that the transformation R representing r θ is orthogonal. This property appears using well-known formulas expressing trigonometric functions of argument θ into ones of argument 2θ. In matrix form, we have s′=Rs with

(12)

For representing a spatial rotation of angle ϕ and axis defined by the unit vector n, let us recall the Rodrigues formula:

(13)

where I is the identity of ℝ3 and J is the 3×3 skew-symmetric matrix of axial vector n:

(14)

We can verify that R is a rotation of angle 2θ and axial vector:

(15)

Further, the rotation R representing r θ will be denoted R 2θ . Thus, the relation

(16)

gives the harmonic decomposition of s′:

It is limited to terms up to 2θ because representing the tensorial rule for 2-rank tensors. This decomposition suggests to introduce the following scalars:

(17)

and linearly independent vectors of ℝ3:

$$e_1 = n ,\quad e_2 = \frac{1}{\sqrt{2}} \left ( \begin{array}{c} 1 \\[3pt] -1 \\[3pt] 0 \end{array} \right ),\quad e_3 = \left ( \begin{array}{c} 0 \\[3pt] 0 \\[3pt] 1 \end{array} \right ). $$

Thus relation (16) yields

The decomposition of s is obtained by considering the value for θ=0:

In the new orthogonal frame (e 1,e 2,e 3), the tensorial rule becomes

(18)

With this, we have retrieved the irreductible decomposition of the representation of \(\mathbb{SO} (2)\) [32]. On the first irreductible subspace, spanned by e 1=n, the representation is trivial and we find a first invariant, p. On the second one, spanned by e 2 and e 3, the group \(\mathbb{SO} (2)\) acts as r 2θ and it is easy to find an invariant, for instance,

Because of the isomorphism between \(\mathbb{S}^{2} \mathbb{R}^{2}\) and ℝ6 and upon using the index contraction rule (8), we obtained the two invariants of the planar stress tensor (where q is supposed to be non negative):

(19)
(20)

For given values of the constants p and q>0, these two equations define a generic orbit. It is easy to see that the orbit is a circle of radius q and centre given by

(21)

If q=0, Eq. (20) implies σ 11=σ 22 and gives a third invariant σ 12=0. The orbit is non generic and reduced to the point (21). In modern language of differential geometry, the set of the planar stress tensor is the orbit manifold \(\mathbb{S}^{2} \mathbb{R}^{2} / \mathbb {SO} (2)\), union of two parts:

  • the set of the generic orbits, which are circles, is a surface parameterized by local coordinates \((p,s)\in\mathbb{R} \times \mathbb{R}^{*}_{+}\)

  • the set of the singular orbits, which are points, is a straight line (σ 11−σ 22=σ 12=0) parameterized by p∈ℝ.

The orbit manifold is not pure [13], with a local dimension equal to 2 or 1 according to the orbit being generic or not. With this, we have translated into the modern geometrical language the original representation by Mohr of the planar stress tensors by circles in the (σ 11,σ 12) axis, defined by the equation

with \(a = p\ / \sqrt{2}\), obtained by elimination of σ 22 between Eqs. (19) and (20).

4 Decomposition in Irreductibles for the Elasticity Tensor

To reveal the underlying geometric structure of the elasticity tensor space, we shall use the same method as for the stress tensors. The first step consists in finding an irreductible decomposition of the representation ρ(r) of \(\mathbb{SO} (2)\) in the space \(\mathbb {E} (2) = \mathbb{S}^{2} \mathbb{S}^{2} \mathbb{R}^{2}\) of the elastic coefficient systems. Next, we can parameterize the space \(\mathbb{EL} (2) = \mathbb{E} (2) / \mathbb{SO} (2)\) of the elasticity tensors. The key-idea is to work in the new orthogonal frame (e 1,e 2,e 3) because of the change of variable \(\tilde{s} = P^{-1} s\), namely,

(22)

In the new variables \(\tilde{e} = P^{-1} e\) and \(\tilde{s} = P^{-1} s\), the constitutive law has the form

with \(\tilde{c}= P^{-1}\ c\ P\). Owing to (22), we obtain the explicit form of \(\tilde{c}\):

(23)

where:

(24)
(25)
(26)
(27)
(28)
(29)

In order to introduce additional relevant variables, let us observe that in the new variables the tensorial rule, given by (18), can be written as \(\tilde{s}' = \tilde {R}_{2 \theta} \tilde{s} \) with

(30)

For sake of convenience the symmetric matrix \(\tilde{c}\) is decomposed by blocks as:

(31)

where \(\tilde{v}\in\mathbb{R}^{2}\) and \(\tilde{A}\in\mathbb{S}^{2}\mathbb {R}^{2}\). Because of the isomorphism of Theorem 2.1, an elastic coefficient system is represented by the matrix \(\tilde{c}\in\mathbb {S}^{2} \mathbb{R}^{2}\). Combining (7), (16) and \(\tilde{e}' = \tilde{R}_{2 \theta} \tilde{e}\) leads to the tensorial rule of the elasticity tensor in the matrix form:

(32)

Combining (30), (31) and (32) leads to

(33)

The constitutive law is isotropic if \(\tilde{v} = 0\) and \(\tilde{A}\) is an isotropic matrix. In this case, \(\tilde{A}\) is proportional to the identity matrix I:

The isotropic cases are characterized by vanishing values of α, β, η and

(34)

Moreover, introducing the quantity

(35)

the matrix (23) takes the form

(36)

where we define

(37)

Obviously, λ and μ are interpreted as Lamé’s coefficients. The matrix (36) can be additively decomposed into its isotropic part (obtained by putting α=β=γ=η=0):

(38)

and a deviatoric part

(39)

Under the action of \(\mathbb{SO}(2)\), the isotropic part (38) is invariant while the deviatoric one (39) is modified according to the tensorial rule in (33). The relation \(\tilde{v}' = r_{2 \theta} \tilde{v}\) gives

(40)

The relation \(\tilde{A}' = r_{2 \theta} \tilde{A} r_{2 \theta}^{T} \) suggests to represent the symmetric matrix \(\tilde{A}\in\mathbb {S}^{2}\mathbb{R}^{2}\) by a vector \(\tilde{a}\in\mathbb{R}^{3}\) (as the stress tensor \(\sigma\in\mathbb{S}^{2}\mathbb{R}^{2}\) was represented by s∈ℝ3). By analogy with (17), its components are

Theorem 2.1 proves that the transformation R representing r 2θ is orthogonal but, by analogy with Sect. 3, R=R 4θ =exp(4θj(n)) with n given in (15). Replacing 2θ by 4θ and s by \(\tilde{a}\) in (18), we obtain

(41)

In the new variables of \(\mathbb{E}(2)\), the tensorial rule now has the form

(42)

We have obtained the irreductible decomposition of the representation of \(\mathbb{SO} (2)\) into stable subspaces of \(\mathbb{E}(2)\). There are two irreductible subspaces \(\mathbb{E}_{0}\) and \(\mathbb{E}'_{0}\) for which the representation is trivial. For each of them, there is an invariant, λ for \(\mathbb{E}_{0}\) and μ for \(\mathbb{E}'_{0}\). On the third irreductible \(\mathbb{E}_{2}\), the group \(\mathbb{SO} (2)\) acts as r 2θ and it is easy to find an invariant, for instance,

(43)

On the last one \(\mathbb{E}_{4}\), the group \(\mathbb{SO} (2)\) acts as r 4θ and it is easy to find an invariant, for instance,

(44)

If we consider the irreductibles separately, the orbit \(\mathcal{O}_{2}\) in \(\mathbb{E}_{2}\) is the circle of Eq. (43) and the orbit \(\mathcal{O}_{4}\) in \(\mathbb{E}_{4}\) is the circle of Eq. (44). If we consider the angle θ as a time evolution parameter and the corresponding motion of a particle on each circle, we see that the particle on \(\mathcal{O}_{4}\) runs twice as fast as the one on \(\mathcal{O}_{2}\). In fact, the orbits \(\mathcal{O}_{2}\) and \(\mathcal{O}_{4}\) are “coupled”. To take into account this phenomenon, we need another invariant. To find it, it is easier to work with complex numbers z 2=η+iα and z 4=γ+iβ. The group action reads:

Eliminating θ between both relations gives

and leads to the following complex invariant:

(45)

However, this new invariant is not independent of the other ones because

(46)

With the decomposition ζ=ℜζ+iℑζ=ζ r +iζ i , we obtain, in addition to λ,μ,I 2 and I 4, two new invariants:

(47)
(48)

linked to the other ones by the relation

(49)

5 Parameterization of the Elasticity Tensor Space

Using the decomposition in irreductibles, we may characterize the planar elasticity tensors by a system of five invariants, the first four being (where I 2 and I 4 are supposed to be non negative)

(50)
(51)

and the last one chosen among the two following invariants:

(52)
(53)

The knowledge of these invariants is sufficient to determine the elasticity tensor by constructing the orbit in two steps:

  • the elastic coefficients c ij being given in a particular frame of ℝ3 (attached to the experimental testing device), the values of the invariants λ,μ,I 2,I 4 and ζ r or ζ i are calculated by expressions (37), (35), (50), (51) and (52) or (53).

  • In the space of elastic coefficients c ij , the orbit is defined by Eqs. (37), (35), (50), (51) and (52) or (53) with the values of the invariants, λ,μ,I 2,I 4 and ζ r or ζ i determined at the first step.

The set \(\mathbb{EL} (2)\) of the elasticity tensor c is the orbit space \(\mathbb{E} (2) / \mathbb{SO} (2)\), the union of four parts (the first one being the set of the generic orbits):

  • If I 2>0 and I 4>0, the corresponding orbits are closed lines (something like limnescates). Their set is a 5-dimensional manifold \(\mathbb{EL}_{g}\) which can be parameterized by local coordinates (λ,μ,I 2,I 4,ζ r ) or (λ,μ,I 2,I 4,ζ i ).

  • If I 2=0 and I 4>0, then ζ r =ζ i =0 because of (49) and there are two new invariants (γ=β=0) but only five are independent (for instance λ,μ,I 4,β=0 and γ=0). The corresponding orbits are circles of radius I 4. Their set is a volume \(\mathbb{EL}_{4}\) which can be parameterized by local coordinates (λ,μ,I 4) (if we set aside the two null invariants).

  • If I 2>0 and I 4=0, then ζ r =ζ i =0 and there are two new invariants (α=η=0) and a set of five independent invariants. The corresponding orbits are circles of radius I 2. Their set is a volume \(\mathbb{EL}_{2}\) which can be parameterized by local coordinates (λ,μ,I 2).

  • If I 2=I 4=0, there are four new invariants (α=β=γ=η=0) and a set of six independent invariants. The corresponding orbits are points. Their set is a surface \(\mathbb {EL}_{\mathit{iso}}\) which can be parameterized by local coordinates (λ,μ). Physically, each point represents an isotropic elastic constitutive law characterized by Lamé’s coefficients λ and μ.

Using the index contraction rule (6), we see that the five fundamental invariants of the elasticity tensor, expressed in original notations for 4-rank tensors are

(54)
(55)
(56)
(57)

and one chosen among the following two:

(58)
(59)

6 Invariant Measure of the Lack of Symmetry with Respect to Classes of Materials

In the modern language of the theory of invariants, the previous results can be summarized by noting that the algebra \(\mathbb{R} [\mathbb{E} (2)]^{\mathbb{SO}(2)}\) of the invariants of the elasticity tensors is generated by a finite number of polynomials, i.e., \(\mathbb{R} [\mathbb{E} (2)]^{\mathbb{SO}(2)} = \mathbb{R} [\lambda, \mu, I_{2}, I_{4}, \zeta_{i}] = \mathbb{R} [\lambda, \mu, I_{2}, I_{4}, \zeta_{r}]\). From a mathematical viewpoint, the choice of ζ i or ζ r is arbitrary because, together with the four other invariants, they generate the same algebra, according to the existence of the syzygy (46) and there is no relevant argument which prefers one over the other. The aim of the present section is to determine the possible isotropy groups of the elastic materials, usually called symmetry groups in anisotropic elasticity. To each one corresponds a class of material. A symmetry group is a closed subgroup of the Lie group \(\mathbb{O}(2)\), then it is \(\mathbb{O}(2)\) itself or a finite group. While in 2D there are 8 symmetry groups, in 3D it remains only 4: I for the general materials, ℤ2 for the monoclinic materials, D 4 for the tetragonal materials and \(\mathbb {O} (2)\) for the isotropic materials. Indeed, in 3D, when a material has reflexion symmetries about two orthogonal planes, it has a reflexion symmetry about a third plane orthogonal to the two former ones. Similarly, in 2D, when a material has a reflexion symmetry about a straight line, it has a reflexion symmetry about the orthogonal straight line. Thus, if a material is monoclinic, it is orthotropic. Also when passing from 3D to 2D elastic materials, the tetragonal material degenerates into the cubic materials and the transversely isotropic materials into the isotropic ones. No trigonal symmetry is possible in 2D because a monoclinic material is automatically orthotropic. A 2D material is not merely a particular case of a 3D material.

Incidently, we obtain invariant measures of the lack of symmetry with respect to these symmetry groups. One of them is ζ i which is relevant to quantify in an invariant way the lack of orthotropy. This is a good reason to prefer the use of ζ i as generator of the algebra of the invariant of the elasticity tensors rather than ζ r .

6.1 Monoclinic Material

An elastic material for which the isotropy group contains one reflexion about a straight line Δ is said to be monoclinic. In 2D, it is known that it contains also the reflexion about the straight line orthogonal to Δ, then the material is said to be orthotropic (or rhombic). In fact, the concepts of monoclinic and orthotropic materials are identical in 2D. We shall verify this fact latter on. Let a unit vector of inclination angle φ with respect to the x 1-coordinate axis be given by

The reflection about its orthogonal straight line Δ is the orthogonal matrix

Following Theorem 2.1, it is represented in the Kelvin representation by an orthogonal matrix \(M_{\varphi} \in\mathbb{O} (3) \) acting on s∈ℝ3. It is easy to verify that

As in Sect. 4, we work in the new orthogonal frame (e 1,e 2,e 3) because of the change of variable (22). In the new variables \(\tilde{s}' = P^{-1} s'\) and \(\tilde{s} = P^{-1} s\), the reflection has the form

with \(\tilde{M}_{\varphi}= P^{-1}\ M_{\varphi}\ P\). Owing to (22), we obtain the explicit form of \(\tilde{M}_{\varphi}\):

It is worth noting that

(60)

Hence we use the decomposition by blocks (31). As in Sect. 4 for the rotations, the action of the reflexion transforms the elastic tensor into

(61)

Combining (31), (60) and (61) we find

(62)

The elastic material is monoclinic if the elastic coefficients are invariant under a reflection, or equivalently if

(63)
(64)

According to (36), condition (63) may be written as

(65)

or, equivalently,

(66)

According to (36), condition (64) may be written as

(67)

or, equivalently,

(68)

Eliminating φ between (66) and (68) leads to the condition

that is

or

(69)

which is necessary and sufficient for the material to be monoclinic. If this condition is satisfied, the orientation of the unit vector n φ defining the reflexion can be deduced from (65):

6.2 Orthotropic Material

It is worth noting that if (66) and (68) are valid for an angle φ, they are also valid for the angle φ+π/2. In other words, if the material is monoclinic, it is orthotropic. Moreover, as the material is orthotropic when ζ i vanishes, ζ i is an invariant measure of the lack of orthotropy. The larger ζ i becomes, the less the material is orthotropic. This invariant should be considered by the experimentators when intending to identify the symmetries of a material that are not known a priori. We observe that the study of the orthotropic materials reveals the physical meaning of the joint invariant ζ i .

6.3 Tetragonal Material

Let us follow this study of the class of materials by considering an orthotropic material for which the isotropy group contains also the reflection about a third straight line orthogonal to the unit vector n ψ of inclination angle ψ=φ+π/4. Such a material is said to be tetragonal. Applying condition (66) to the angle ψ gives

which implies z 2=0, then α=η=0 or, equivalently, \(I^{2}_{2} = 0\). Taking into account definitions (24) and (25), we conclude that for a tetragonal material

in any coordinate system. For an orthotropic material, I 2 is an invariant measure of the lack of tetragonality. The larger I 2 becomes, the less an orthotropic material is tetragonal.

6.4 Isotropic Material

A tetragonal material for which the isotropy group is \(\mathbb{O}(2)\) itself is said to be isotropic. Thus condition (68) leads to z 4=0, then β=γ=0 or, equivalently, if I 4=0. For a tetragonal material, I 4 is an invariant measure of the lack of isotropy. The larger I 4 becomes, the less a tetragonal material is isotropic.

7 Geometrical Meaning of the Invariant Measures

We would like to discuss the previous invariant measures in terms of Euclidean geometry. It is easy to interpret I 2 in terms of the standard norm of \(\mathbb{E}_{2}\):

and I 4 in terms of the standard norm of the space \(\mathbb{E}_{4}\) of traceless symmetric matrices \(\tilde{A}\):

which are clearly metric notions. The geometric interpretation of ζ i is less obvious. For this aim, let us determine once again at which condition a material is monoclonic. We know that the reflexion m 2φ has two eigenspaces, the straight line along the unit vector n 2φ associated with the eigenvalue −1, and the perpendicular straight line associated with the eigenvalue 1. Condition (63) means that \(\tilde{v}\) is an eigenvector of m 2φ associated with the eigenvalue −1. On the other hand, accounting for the symmetry of matrix m 2φ , condition (64) implies

which, because of (63) yields

which means \(\tilde{A} \tilde{v}\) is an eigenvector of m 2φ associated with the eigenvalue −1. Thus \(\tilde{v}\) and \(\tilde{A} \tilde{v}\) are collinear. By considering them as vectors of ℝ3 with the third component null, this condition may be stated as

In fact, straightforward calculations show that

In short,

  • a material is monoclinic (or orthotropic) if the parallelogram of vertex 0 and adjoining edges \(\tilde{v}\) and \(\tilde{A} \tilde{v}\) becomes flat.

  • an orthotropic material is tetragonal if the circular orbit \(\mathcal{O}_{2}\) degenerates into a point,

  • a tetragonal material is isotropic if the circular orbit \(\mathcal {O}_{4}\) degenerates into a point.

The two latter conditions can be expressed in terms of vector lengths, the former one in terms of area. Hence it is not possible to characterize the lack of symmetry uniquely in terms of invariant norms and distances in 2D and, even more so, in 3D.

8 Comparing the Invariants for the Actions of ℤ2, \(\mathbb{O}(2)\) and \(\mathbb{SO}(2)\) onto \(\mathbb{E} (2)\)

8.1 Parameterization of the Orbit Spaces \(\mathbb{E} (2)/ \mathbb{Z}_{2,\varphi}\)

The symmetry group of an orthotropic material characterized by the unit vector n φ is the cyclic group constituted of the identity and the reflexion m φ . As it is isomorphic to ℤ/2ℤ or, with abbreviated notation ℤ2, we denote it ℤ2,φ . Owing to (62), the action of m φ is

or, in details,

Using the complex framework of Sect. 4, the two last relations may be stated as

(70)

Considering z 2,φ =e −2iφ z 2, a consequence is

Thus independent invariants of the orbit \(\mathcal{O}_{2,\varphi}\) of z 2 under the action of ℤ2,φ onto \(\mathbb{E}_{2}\) are ℜz 2,φ and (ℑz 2,φ )2, or equivalently ℜz 2,φ and \(I^{2}_{2} = (\Re z_{2,\varphi})^{2} + (\Im z_{2,\varphi})^{2}\). Similarly, considering z 4,φ =e −4iφ z 4, we have \(z''_{4,\varphi} = \bar{z}_{4,\varphi}\) and independent invariants of the orbit \(\mathcal{O}_{4,\varphi}\) of z 4 under the action of ℤ2,φ onto \(\mathbb{E}_{4}\) are ℜz 4,φ and (ℑz 4,φ )2, or equivalently ℜz 4,φ and \(I^{2}_{4} = (\Re z_{4,\varphi})^{2} + (\Im z_{4,\varphi})^{2}\).

As the group ℤ2,φ , the orbits are discrete and then defined by the values of six invariants that can be, for instance, λ,μ,I 2,I 4,ℜz 2,φ and ℜz 4,φ . The generic ones are pair of points while for the orthotropic materials characterized by the inclination φ, ℑz 2,φ vanishes and the orbits are singletons.

8.2 Parameterization of the Orbit Space \(\mathbb{E} (2) / \mathbb{O} (2)\)

A straightforward consequence of the previous analysis is the determination of the invariants of the \(\mathbb{O} (2)\)-orbits. The orthogonal group is generated by both rotations and reflexions. The ℤ2,φ -orbits are discrete and in fact contained into the \(\mathbb{SO} (2)\)-orbits so \(\mathbb{O} (2)\)-orbits and \(\mathbb {SO} (2)\)-orbits are identical, that allows the consideration of only the invariants of the previous orbits. Nevertheless, it is worth noting that, unlike the action of rotations, ζ defined by (45) is not invariant for the action of reflexions (70)

(71)

Thus ζ r is a common invariant to the rotations and reflexions while in general ζ i is not so because of its sign inversion in the complex conjugacy occurring in (71). A possible coordinate system to parameterize the \(\mathbb{O} (2)\)-orbits is (λ,μ,I 2,I 4,ζ r ) already introduced in Sect. 5 for parameterizing the \(\mathbb{SO} (2)\)-orbits. Nevertheless, we show in Sect. 6 that a better coordinate system for parameterizing the \(\mathbb{SO} (2)\)-orbits is (λ,μ,I 2,I 4,ζ i ). Finally, both orbits for \(\mathbb{SO} (2)\) and \(\mathbb {O} (2)\) are the same but the choice of the generators of their respective invariants depends on the way in which the group acts on the orbit. The subtleness lies in the sign of ζ i which cannot be inferred of the values of I 2, I 4 and ζ r because it occurs into the syzygy (46) through its square.

9 Conclusions

In 2D, the elastic tensor space is parameterized by 5 coordinates chosen among 6 invariants. It consists in a 5-dimensional manifold, corresponding to the generic orbits, and a “boundary” composed of two volumes intersecting following a surface corresponding to the isotropic elastic tensors. The study is much easier using Kelvin’s representation and the decomposition into irreductibles. There are 4 primary invariants and a joint one which separate the orbits and are invariant measures of the lack of symmetry with respect to the symmetry groups of the elastic tensors. Next, we revealed the physical meaning of these invariants as a measure of the lack of symmetry with respect to the classes of materials and we proposed an original method to determine the elastic behaviour of an anisotropic material of which the symmetry is not known a priori. These measures can be characterized in terms of Euclidean geometry as length or area. It would be very interesting to compare the present method to the one proposed by Cowin and coworkers in [10, 11, 43]. In a next future, we hope to investigate the 3D case with the presently developed tools.