1 Introduction

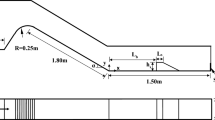
The coexistence of bubbles and turbulence poses a major challenge to both physical and numerical studies of self-aerated free-surface flows. A canonical case is the hydraulic jump taking place at the transition from a supercritical flow to a subcritical flow (Fig. 1) [15]. The air entrainment process in hydraulic jump is a combination of singular aeration at the impingement point (jump toe) and interfacial aeration through the free surface of jump roller [38]. The transport of air bubbles interacts with the development of turbulent structures encompassing large eddies and surface waves [7, 23, 25, 41]. The bubble-turbulence interplay and unsteady flow pattern highlight the complexity of hydraulic jump. A good understanding of the turbulent flow pattern and detailed turbulent structures is essential for advanced experimental and numerical characterisation of two-phase flow properties, flow instabilities and three-dimensional bubbly flow. For instance, the length and time scales of coherent turbulent structures could be crucial information for the determination of grid size (spatial resolution) and time step (temporal resolution) for the CFD modelling of such turbulent air–water flows.

Fig. 1
figure 1

Hydraulic jump in experimental channel; flow from left to right—Flow conditions: Q = 0.0347 m3/s, d1 = 0.0206 m, x1 = 0.83 m, Fr = 7.5, Re = 6.8 × 104

Full size image

In the past decades, large-scale turbulent motions of hydraulic jumps were investigated in terms of free surface fluctuations [4, 29], jump toe oscillations [33, 43], vortex advections [25] and pressure pulsations [1, 24]. The first attempt on velocity turbulence measurement was published by Rouse et al. [35] who modelled hydraulic jump flow using air in a jump-shaped tunnel. To date most efforts on water-phase turbulence quantification were restricted to weak hydraulic jumps with low aeration levels because of the instrumental limitations [17, 20, 22, 32]. Intrusive phase-detecftion techniques were widely used for the characterisation of local air–water flow properties [7, 8, 28, 31], whereas the development of flow imaging, particle tracking and bubble image velocimetry techniques provided approaches to global distributions of void fraction and particle velocity [3, 19, 26, 34, 36]. Chanson and Toombes [11] and Chanson and Carosi [9] derived a series of turbulence statistics from the detection of air–water interfaces in high-speed bubbly flows, including the turbulence intensity and integral turbulent length/time scales. Their techniques were initially developed for self-aerated spillway flows. The application to hydraulic jump was limited (e.g. [6], and the impact of unsteady vortical structures and free-surface deformations need to be addressed [40].

This paper aims to present a series of characteristic turbulent scales for hydraulic jumps. Experiments are conducted to quantify bubbly flow turbulent scales along and perpendicular to the main flow direction for a large Froude number (Fr = 7.5). The longitudinal scales are measured for the first time in the core of hydraulic jumps from the channel bottom to the free surface. The results were preliminarily presented in Wang and Chanson [39]. Herein both longitudinal and transverse bubbly-flow scales are compared with free-surface turbulent scales measured by Murzyn et al. [29] and Chachereau and Chanson [4], as well as with the scales of jump toe perimeter derived from a re-analysis of the instantaneous impingement point position data of Zhang et al. [43]. The results provide a comprehensive depiction of turbulence development in hydraulic jump roller from the internal air–water flow to its fluctuating free surface.

2 Experimental set up and integral turbulent scales

2.1 Experimental facility and set up

The experiments were conducted at the University of Queensland, Australia. Hydraulic jumps are generated in a horizontal rectangular channel (Fig. 1). The channel is 3.2 m long and 0.5 m wide, built with smooth HDPE bed and 0.4 m high glass sidewalls. The horizontal impinging flow is discharged into the flume under a rounded gate of a constant head tank, with a gate opening h. An overshoot gate at the end of flume is used to control the downstream flow conditions and to ensure a time-averaged mean position of the jump toe at x = x1. Here x is the longitudinal distance from the upstream gate, along with y being the vertical distance from the channel bed and z the transverse distance from the centreline. The flow rate Q is measured using a Venturi meter with an accuracy of 2 %. The inflow depth d1 is measured upstream of the jump toe using a pointer gauge, for which the accuracy is largely determined by the inflow surface roughness. Table 1 summarises the flow conditions for the present study and the past data by Chanson [6], Murzyn et al. [29], Chachereau and Chanson [4] and Zhang et al. [43], where the Froude number is defined as Fr = V1 × (g × d1)−0.5 and the Reynolds number Re = ρ × V1 × d1 × μ−1, V1 being the average inflow velocity, g the gravity acceleration, ρ the water density and μ the dynamic viscosity of water. All experimental flows are characterised by partially-developed inflow conditions.

Table 1 Experimental flow conditions and instrumentation for relevant integral turbulent length scale measurements in hydraulic jumps
Full size table

2.2 Integral turbulent scales

A characteristic length scale of turbulent flow structures is the integral turbulent length scale L. The integral length scale is derived from a series of simultaneous measurements of a flow property at two locations separated by a distance Δl. Within the dimension of a coherent turbulent structure, the correlation between the two time series of the flow property decreases with increasing separation distance Δl, and the integral length scale is given by Eq. (1):

$${\text{L}} = \int\limits_{0}^{{\Delta {\text{l}}\left( {({\text{R}}_{\text{ij}} )_{\hbox{max} } =\, 0} \right)}} {({\text{R}}_{\text{ij}} )_{\hbox{max} } \times {\text{d}}(\Delta {\text{l}}} )$$
(1)

where Rij is the cross-correlation function between the signals recorded simultaneously at the locations separated by a distance Δl, with (Rij)max being the maximum cross-correlation coefficient. Note that (Rij)max = 1 for Δl = 0.

A variety of flow properties can be measured and the integral length scales may be deduced for the corresponding turbulent structures. The local void fraction is measured using a phase-detection conductivity probe, and the instantaneous void fraction signal provides the integral length scales of the coherent eddy structures in which air bubbles are advected streamwise [9]. The length scales are obtained in both longitudinal and transverse directions with Δl = Δx and Δz respectively, where Δx is the longitudinal distance between two phase-detection probe sensors and Δz is the transverse sensor separation distance. Figure 2 shows the phase-detection probes used for the longitudinal and transverse length scale measurements, the instrumentation being detailed in Sect. 2.3. Figure 3a shows the cross-correlation functions given by different longitudinal distances Δx at a fixed location in the bubbly flow region. The corresponding maximum correlation coefficients (Rij)max are plotted in Fig. 3b as a function of Δx. The longitudinal integral length scale of the bubbly eddy structures, denoted as Ledd,x, is then given by the shaded area in Fig. 3b. The corresponding transverse length scale is denoted as Ledd,z. Similarly, the instantaneous water elevation signal measured with acoustic displacement meters provides the integral length scales of the coherent free-surface structures, denoted as Lfs,x and Lfs.z in longitudinal and transverse directions, respectively [29]. Lastly, the integral length scale of the jump toe perimeter, Ltoe, is derived from the instantaneous impingement point position data recorded with a video camera. The jump toe perimeter is a two-dimensional structure and Ltoe is a transverse length scale.

Fig. 2
figure 2

Phase-detection probe sensors separated by a longitudinal distance Δx (a) and transverse distance Δz (b). a Dual-tip phase-detection probe with longitudinal separation distance Δx = 29.68 mm between probe tips; flow from bottom left to top right. b Side-by-side phase-detection probes with transverse separation distance Δz = 27.0 mm between probe leading tips; flow from bottom left to top right

Full size image
Fig. 3
figure 3

Variation of correlation function (a) and maximum correlation coefficient (b) between void fraction signals with longitudinal sensor separation distance Δx. Flow conditions: Q = 0.0347 m3/s, d1 = 0.0206 m, x1 = 0.83 m, Fr = 7.5, Re = 6.8 × 104; x − x1 = 0.25 m, y = 0.04 m. a Cross-correlation functions for different longitudinal distances between phase-detection probe sensors. b Maximum correlation coefficient as a function of longitudinal sensor separation distance

Full size image

The integral turbulent time scales are further defined as [9]:

$${\text{T}} = \frac{1}{\text{L}} \times \int\limits_{0}^{{\Delta l(({\text{R}}_{\text{ij}} )_{\hbox{max} } =\,0)}} {({\text{R}}_{\text{ij}} )_{\hbox{max} } \times {\text{T}}_{\text{ij}} \times {\text{d}}(\Delta {\text{l}}} )$$
(2)

where Tij is a correlation time scale of the correlation function Rij(τ) for the given Δl:

$$T_{ij} = \int\limits_{0}^{{\tau ({\text{R}}_{\text{ij}} = \,0)}} {{\text{R}}_{\text{ij}} (\tau ) \times {\text{d}}\tau }$$
(3)

with τ being the correlation time lag. The integral time scales are characteristic time scales reflecting the “life time” of coherent turbulent structures. Table 2 lists the integral turbulent length and time scales investigated in this paper.

Table 2 Integral turbulent length and time scales investigated in the present study
Full size table

2.3 Metrology and instrumentation

The instantaneous void fraction is measured using phase-detection probes equipped with conductivity needle sensors (Fig. 2). The needle sensors are aligned along the main flow direction and designed to pierce bubbles/droplets. The output voltage signals vary with the resistance of air/water detected on the sensor tips [13]. Detailed information of this type of probe is available in Chanson [5]. A series of dual-tip phase-detection probes with different longitudinal sensor tip separations (2.57 mm < Δx < 29.68 mm, Fig. 2a) are used for the characterisation of longitudinal integral turbulent scales Ledd,x and Tedd,x. The transverse integral scales Ledd,z and Tedd,z are derived from measurements with side-by-side probe arrays (0.87 mm < Δz < 92.0 mm, Fig. 2b), except for the small transverse separations achieved with specially-designed dual-tip probes that had sensors of identical lengths (Δx = 0, Δz = 0.87 and 3.57 mm). All sensors are scanned simultaneously at 20 kHz for 45 s at each measurement location.

In their past studies, Murzyn et al. [29] obtained the free-surface elevation using intrusive free-surface wire gauges while Chachereau and Chanson [4] used non-intrusive acoustic displacement meters. The former recorded instantaneous water elevation according to the immersion depth of wire gauges, while the latter worked based upon the acoustic beam travel time between the sensor and detected water surface. Further information and application of the acoustic displacement meters can be found in Kucukali and Chanson [18] and Bung [2]. Two wire gauges or displacement meters were separated by a longitudinal distance Δx or transverse distance Δz for the measurements of corresponding integral turbulent scales (Lfs,x, Tfs,x and Lfs,z, Tfs,z). The wire gauges were scanned at 128 Hz for 5 s, and the acoustic displacement meters were sampled at 50 Hz for 600 s.

For the calculation of jump toe perimeter integral scales, a video camera is used to record the transverse impingement perimeter in a top view above the jump toe. Frame sampling frequency of 25 Hz was employed for 10 s. For each frame, the instantaneous impingement point positions are quantified along the transverse perimeter profile and the transverse distance from the impingement point to the centreline corresponds to the separation length Δl = Δz used to calculate the transverse integral scales Ltoe and Ttoe.

The measurement error associated with the instrumental accuracies is negligible compared to the uncertainties introduced by (a) unsteady jump toe position and (b) limited number of tested Δx and Δz. The jump toe oscillation affects the relative measurement location in jump roller. The limited number of Δx/Δz impacts directly the calculation accuracy of integral turbulent scales, especially when the zero-crossing of correlation function needs to be determined by extrapolation of given points. This is discussed in Sect. 3.2.1 for Fig. 5d when the present data are compared with previous results.

3 Results

3.1 Flow pattern and bubbly flow properties

The hydraulic jump is a turbulent shear flow with the shear layer forming between the high-speed flow in the bottom boundary layer and the recirculating flow next to the free surface [16, 21]. Large vortices develop in the shear layer and interact with the free surface (Fig. 1). The formation and downstream advection of the vortices are coupled with the entrainment of air pockets at the jump toe and diffusive transport of bubbles in the roller [6]. Visual observations highlight three-dimensional structures for these vortices as well as for the deformed roller surface, though most time-averaged flow properties are found to be irrelevant to the transverse position. Figure 4a presents the vertical distributions of time-averaged void fraction C measured with phase-detection probes on the channel centreline. The free surface is outlined at the elevation Y90 where C = 0.9. A typical void fraction profile exhibits a bell-shape distribution in the shear layer and a monotonically increasing void fraction across the free-surface region. The bell-shape profile is predicted by a bubble diffusion equation, with the local maximum void fraction decreasing in the longitudinal direction [7, 12]. The longitudinal evolution of void fraction profile is consistent with the observed enlargement and de-aeration of the largest vortical structures. The air–water exchange through the free surface is an uncontrolled process associated with the highly fluctuating surface motions.

Fig. 4
figure 4

Distributions of time-averaged void fraction and interfacial velocity in jump roller. Flow conditions: Q = 0.0347 m3/s, d1 = 0.0206 m, x1 = 0.83 m, Fr = 7.5, Re = 6.8 × 104; Y90 = y(C = 0.9). a Time-averaged void fraction. b Time-averaged interfacial velocity

Full size image

The time-averaged longitudinal velocity of air–water interfaces V is derived from the mean interfacial travel time Δt over the distance Δx between two phase-detection probe tips, i.e. V = Δx/Δt. Herein Δt is given by the time lag of maximum cross-correlation coefficient between the signals of two probe sensors. Figure 4b shows the distributions of dimensionless longitudinal velocity V/V1 in the jump roller. The positive velocity data demonstrate the boundary layer development next to the channel bed and a marked velocity gradient in the shear layer. While the shear flow decelerates as the water depth increases, the negative velocity of the reversing flow is almost uniform in the free-surface recirculation region. The lack of physical data in a thin layer between the positive and negative flows may be explained by the passage of large vortices which deteriorates the accuracy of the cross-correlation analyses by changing the instantaneous velocity direction frequently. Overall, the time-averaged velocity profile follows a self-similar wall jet equation modified by the average recirculation velocity term [7, 31].

3.2 Integral turbulent length scales

3.2.1 Bubbly flow integral length scales Ledd,x, Ledd,z

Bubbles are carried in coherent three-dimensional large-scale vortical structures in the air–water flow. The length scales of such vortical structures are characterised by the integral turbulent length scales as defined by Eq. (1). Measurements are performed at five cross sections for a given hydraulic jump (Fr = 7.5, Re = 6.8 × 104), and further for other three Froude-similar flows at the same cross section (x − x1)/d1 ≈ 12.5, with Reynolds number ranging from 3.4 × 104 to 1.4 × 105 (Table 1). Figure 5a presents the spatial distributions of dimensionless longitudinal and transverse length scales, Ledd,x/d1 and Ledd,z/d1, in the jump roller. The results are compared between different Reynolds numbers at the given cross section in Fig. 5b, c. The transverse integral length scales are further compared with some previous data in Fig. 5d.

Fig. 5
figure 5

Longitudinal and transverse integral length scales of bubbly flow. a Longitudinal and transverse integral length scales of bubbly flow; Fr = 7.5, Re = 6.8 × 104. b, c Longitudinal (b) and transverse (c) integral length scales of bubbly flow for different Reynolds numbers; (x − x1)/d1 ≈ 12.5. d Comparison of transverse bubbly-flow integral length scales between present data and data of Chanson [6] and Zhang et al. [43]

Full size image

The bubbly-flow length scales are shown typically between 0.2 × d1 and 0.8 × d1 in the shear flow region and between 0.5 × d1 and 2.3 × d1 in the free-surface region. These are about one order of magnitude larger than the typical bubble sizes in the two flow regions respectively [7, 37]. Figure 5a highlights different longitudinal and transverse length scales in the first half of the roller ((x − x1)/d1 < 12.5). Within this region, the results imply that the bubbly vortical structures have a larger longitudinal dimension (Ledd,x > Ledd,z) in the shear flow but a larger transverse dimension (Ledd,x < Ledd,z) in the free-surface region. The longitudinal length scale Ledd,x exhibits a local maximum at some position above the boundary layer and below the path of large-size vortices in the shear layer. The local maximum length scale decreases rapidly along the roller as the shear flow is decelerated and turbulence is dissipated, leading to approximately the same longitudinal and transverse scales at the far end of the roller. By contrary, both integral length scales increase with increasing longitudinal distance in the free-surface region. Maximum length scales are shown close to the positions of 50 % void fraction. These positions are close to the time-averaged water elevations measured by acoustic displacement meters, and might be considered as a pseudo-interface between bubbly flow (C < 0.5) and spray region above (C > 0.5) [42].

Figure 5b, c show little effect of Reynolds number on the bubbly-flow integral length scales except for Re < 4 × 104. For the smallest tested Reynolds number, larger length scales are obtained between y/d1 = 2 and 5, exhibiting quasi-linear increase in Ledd,x and Ledd,z with increasing vertical position instead of a local trough in the data profile. This flow region (2 < y/d1 < 5) is characterised by pseudo-periodic change in instantaneous velocity directions induced by the passage of large-size vortices. Such unsteady recirculating motions are remarkable in hydraulic jumps with large Reynolds numbers, and are responsible for the deterioration of correlation between the phase-detection signals ((Rij)max in Eq. (1)) hence a smaller integral turbulent scales. For a small Reynolds number, few marked vortices form and they are dissipated quickly within a short distance downstream of the toe. Therefore, no decrease in the integral scales is shown at the given position. The criterion for negligible scale effects (Re > 4 × 104) is in agreement with previous findings focusing on void fraction (e.g. [10]). It is emphasised in recent works that the scale effects must be assessed for specified key parameters, whereas no attempt was reported dealing with turbulent length and time scales. The present work supplements the existing assessment criteria by introducing the integral turbulent scales. Further investigations would be worthwhile to cover a broader range of Froude numbers.

In Fig. 5d, the transverse integral length scale data are plotted at relative vertical positions to the characteristic elevation Y90 to facilitate comparison between different flow conditions and longitudinal positions. Good agreement is shown in the shear flow region. In the previous studies, most physical data were missed next to the free-surface (0.7 < y/Y90 < 1.1), and the existing data of Zhang et al. [43] were underestimated in this region. The underestimate of Ledd,z in Zhang et al. [43] was because the tested transverse separation distance was limited to Δz < 35.8 mm, compared to that up to 92 mm in the present study. The narrower range of Δz in the past experiments hindered accurate estimate of the tail shapes of correlation functions. Since the turbulent length scales are different in the shear flow and free-surface regions, different ranges of probe separation distances should be employed accordingly during physical measurements.

3.2.2 Free-surface integral length scales Lfs,x, Lfs,z and impingement perimeter length scale Ltoe

It is demonstrated above that large integral length scales are shown for bubbly flow structures in the free-surface region. The vertical positions of the maximum length scales are close to the time-averaged water elevations where the free-surface integral length scales Lfs,x and Lfs,z were measured by Murzyn et al. [29] and Chachereau and Chanson [4]. Despite different Froude numbers, their data are compared herein with the bubbly-flow length scale data at the elevation y(C = 0.5). The comparisons are shown in Fig. 6a for the longitudinal scales and in Fig. 6b for the transverse scales. The bubbly-flow length scales Ledd,x and Ledd,z characterise the sizes of coherent bubbly structures next to the free surface based on the detection of air–water interfaces, whereas the free-surface length scales Lfs,x and Lfs,z are some typical dimensions of coherent roller surface structures given by the measurement of instantaneous water depth. The results indicate quantitatively comparable integral length scales for the free-surface bubbly flow turbulence and roller surface fluctuations/deformations. Although the maximum water level fluctuations are observed in the first half of jump roller [27, 38], the free-surface integral length scales increase at further downstream positions along the roller as a result of the transition from highly-turbulent breaking surface structures to more organised wavy patterns.

Fig. 6
figure 6

Comparison between bubbly-flow length scales close to mean water elevations and free-surface length scales by Murzyn et al. [29] and Chachereau and Chanson [4]. a Longitudinal length scales. b Transverse length scales

Full size image

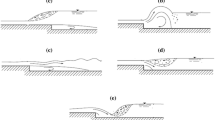
Another characteristic of hydraulic jump that highlights the three-dimensional flow pattern is the unsteady transverse perimeter of the impingement point at jump toe. Figure 7 presents several independent shoots of instantaneous impingement perimeter from a head view. The instantaneous perimeter exhibits wavelike shapes, with the time-averaged shape being a transverse straight line [43]. The impingement perimeter integral length scale Ltoe characterises the typical wave length of the perimeter profile. Table 3 gives the results derived from a re-analysis of the instantaneous impingement point position data of Zhang et al. [43]. The data indicate larger impingement perimeter length scales for a higher Froude number. This is consistent with the visual observations showing more frequent appearance of large wavy patterns in the perimeter profile of stronger hydraulic jump. The impingement point is a locus of large turbulent structures that develop both in the shear flow and at the free surface. Basically, the length scales of impingement perimeter are larger than the transverse bubbly-flow length scales and free-surface length scales, i.e.:

$${\text{L}}_{\text{edd,z}} \le {\text{L}}_{\text{fs,z}} < {\text{L}}_{\text{toe}}$$
(4)
Fig. 7
figure 7

Top view of typical shapes of transverse impingement perimeter; flow from left to right

Full size image
Table 3 Dimensionless integral turbulent length and time scales for transverse impingement perimeter at jump toe
Full size table

3.3 Integral turbulent time scales

The integral turbulent time scale defined by Eq. (2) provides a time scale of turbulent flow structures from being detected to a fully dissipation. Figure 8 presents the distributions of dimensionless bubbly-flow time scales Tedd,x × V1/d1 and Tedd,z × V1/d1 for Fr = 7.5, Re = 6.8 × 104. The data at y(C = 0.5) are compared with the free-surface time scales Tfs,x × V1/d1 and Tfs,z × V1/d1 measured by Chachereau and Chanson [4] in Fig. 9. Figure 8 shows the longitudinal bubbly-flow integral time scales consistently larger than the transverse time scales at the same cross section. The “lifetime” of the coherent vortical structures in the lower shear flow is one order of magnitude smaller than that of the large bubbly structures in the recirculation region. Comparison between the bubbly-flow and free-surface time scales around the positions of average water depth shows relationships:

$${\text{T}}_{\text{edd,x}} \left( {{\text{y}}\left( {{\text{C = 0}} . 5} \right)} \right) > {\text{T}}_{\text{edd,z}} \left( {{\text{y}}\left( {{\text{C = 0}} . 5} \right)} \right) > {\text{T}}_{\text{fs,x}} \approx {\text{T}}_{\text{fs,z}}$$
(5)

where all time scales increase with increasing distance from the jump toe. The integral time scales of impingement perimeter fluctuations Ttoe are given in Table 3, showing larger impingement perimeter time scales than those measured in the air–water flow or at the free surface. It is noteworthy that several past studies indicated a slower motion in horizontal jump toe oscillations than in vertical water depth fluctuations [30, 38].

Fig. 8
figure 8

Longitudinal and transverse integral time scales of bubbly flow; Fr = 7.5, Re = 6.8 × 104

Full size image
Fig. 9
figure 9

Comparison between bubbly-flow time scales close to mean water elevations and free-surface time scales by Chachereau and Chanson [4]

Full size image

4 Discussion: flow instability and turbulent scale characterisation

For an unsteady flow with pseudo-periodic fluctuating motions, the turbulence statistics measured at a fixed location are the superimposition of fast, quasi-random turbulence and relatively slow fluctuating motions (e.g. jump toe oscillations, free surface fluctuations and large vortex advections). The fluctuating motions are often coupled with the formation of large-scale turbulent structures, leading to large values of local turbulent properties [40]. For example, large bubbly-flow integral length and time scales are shown next to the free surface (Figs. 5a, 8). These large turbulent scales are related to the flow instabilities, i.e. oscillation of jump toe position and deformation of free-surface profile, rather than the “true” turbulence of velocity field. A decomposition of the physical measurement signals allows for a quantification of the respective contributions of fast turbulence and slow fluctuations to the characterisation of turbulent properties [14]. Particularly, for the bubbly-flow integral turbulent scales, the phase-detection probe signal is decomposed into a mean component with frequencies smaller than 0.33 Hz, a low-frequency component between 0.33 and 10 Hz corresponding to the slow fluctuating motions, and a high-frequency component above 10 Hz corresponding to the fast turbulent motions. Such frequency thresholds are determined based upon the investigations of characteristic frequencies of fluctuating motions [40]. Since the decomposition of correlation functions between signals can be treated as a linear process (see [14], the integral length and time scales given by the raw signals could be expressed as the sum of the high-frequency integral scales given by the high-frequency signal component (>10 Hz) and the low-frequency integral scales given by the low-frequency signal component (0.33–10 Hz), e.g.

$${\text{L}}_{\text{edd}} \approx {\text{L}}_{\text{edd}}^{\prime } + {\text{L}}_{\text{edd}}^{\prime \prime }$$
(6)

where the symbols of low- and high-frequency components are denoted using (′) and (″) respectively.

Figure 10 compares the high-frequency component of longitudinal bubbly-flow integral length scale Ledd,x″/d1 with the length scale Ledd,x/d1 given by the raw signal (the same data as in Fig. 5a). The decomposed length scale is significantly smaller than the original data in the upper shear layer and entire recirculation region. Next to the roller surface, the presence of large-scale surface fluctuations and recirculating motions leads to a maximum bubbly-flow length scale that is one order of magnitude larger than the length scale truly associated with the fast flow turbulence. The close values of Ledd,x″ and Ledd,x in the lower shear flow above the channel bed imply small impact of fluctuating motions in this region. Wang et al. [41] indicated faint correlation between the fluctuations of water depth and local total pressure in this region. They suggested that the main effect of flow instabilities on the local turbulence properties in the lower shear flow was linked with the longitudinal jump toe oscillations which might influence the development of boundary layer hence the velocity field.

Fig. 10
figure 10

Decomposition of longitudinal integral length scale of bubbly flow—comparison between length scales derived from raw phase-detection signal and high-frequency signal component; Fr = 7.5, Re = 6.8 × 104

Full size image

A decomposition of integral time scales (not shown here) further demonstrates the different turbulent time scales in flow regions with and without the impact of flow instabilities. The high-frequency component of dimensionless longitudinal integral time scales Tedd,x″ × V1/d1 are found consistently between 0.1 and 0.25, compared with the time scales of raw signal Tedd,x × V1/d1 increasing from 0.2 at the bottom to over 3 next to the free surface. The decomposition of integral time scales is a non-linear process, and the experimental data suggest a relationship Tedd ≥ Tedd′ + Tedd″.

5 Conclusion

An experimental investigation of characteristic turbulent scales in hydraulic jumps is presented throughout the air water column up to the free surface. The investigated turbulent scales include the longitudinal and transverse integral length/time scales of the vortical structures in the bubbly flow, the longitudinal and transverse integral length/time scales of the fluctuating surface of jump roller, and the transverse integral length/time scales of the jump toe impingement perimeter. New experiments are performed to measure the bubbly-flow turbulent scales, while further turbulent scales are derived from a re-analysis of the original data of Murzyn et al. [29], Chachereau and Chanson [4] and Zhang et al. [43].

The results highlight the existence of instantaneous three-dimensional turbulent structures from bottom to free surface of the jump roller. The turbulence field is not isotropic, and the turbulent structures exhibit different characteristics in the shear flow region and free-surface region. On the one hand, the vortical structures in which bubbles are carried in the lower shear flow have longer longitudinal dimension and shorter transverse dimension. A local maximum is seen for the longitudinal length scale between the bottom boundary layer and turbulent shear layer but not shown for the transverse scale. The length and time scales decrease in the downstream direction, associated with streamwise de-aeration and dissipation processes. On the other hand, the large bubbly-flow structures in the upper recirculation region show longer transverse dimension than longitudinal dimension. Maximum length and time scales are reached close to the mean elevation of water surface where quantitatively comparable free-surface length and time scales are obtained. The similar bubbly-flow and free-surface length scales in this region (L ~ 0.5 × d1 to 3 × d1) are larger than the scales of vortical structures in the shear flow (L ~ 0.2 × d1 to 0.8 × d1) but smaller than the transverse scales of jump toe impingement perimeter (L ~ 2 × d1 to 5.5 × d1). The large turbulent length and time scales in the free-surface region and at the jump toe are induced by the unsteady fluctuating motions of the roller. Typically, the turbulent time scale related to the relatively slow fluctuations is one order larger than the time scale linked with the fast velocity turbulence. The effects of Reynolds number are minimised with Reynolds numbers no less than 4 × 104. Further investigation can be undertaken in the future to assess the effect of Froude number.