Spatial evolution of coherent motions in finite-length vegetation patch flow

Abstract

A number of experimental studies on submerged canopy flows have focused on fully-developed flow and turbulent characteristics. In many natural rivers, however, aquatic vegetation occurs in patches of finite length. In such vegetated flows, the shear layer is not formed at the upstream edge of the vegetation patch and coherent motions develop downstream. Therefore, more work is neededz to reveal the development process for large-scale coherent structures within vegetation patches. For this work, we considered the effect of a limited length vegetation patch. Turbulence measurements were intensively conducted in open-channel flows with submerged vegetation using Particle Image Velocimetry (PIV). To examine the transition from boundary-layer flow upstream of the vegetation patch to a mixing-layer-type flow within the patch, velocity profiles were measured at 33 positions in a longitudinal direction. A phenomenological model for the development process in the vegetation flow was developed. The model decomposed the entire flow region into four zones. The four zones are the following: (i) the smooth bed zone, (ii) the diverging flow zone, (iii) the developing zone and (iv) the fully-developed zone. The PIV data also confirmed the efficiency of the mixing-layer analogy and provided insight into the spatial evolution of coherent motions.

1 Introduction

The importance of aquatic vegetation as a factor for the improvement of riverine environmental quality has been widely reported. Vegetation reduces suspended sediment transport as a result of the local reduction in bed shear stress. Submerged vegetation generates coherent motions at the vegetation edge and such large-scale eddies control the vertical exchange of mass and momentum both within and above the canopy. The aquatic canopy impacts ecological processes such as the supply of dissolved nutrients and sediment nutrient dynamics. Therefore, understanding flow characteristics for vegetated flows is greatly important.

A number of experimental studies on submerged canopy flows have focused on fully-developed and homogeneous vegetation flows. A key feature of vegetation flow is the generation of a shear layer at the vegetation edge which is similar to the free shear layer. An analogy between the terrestrial canopy flow and the free mixing-layer was first described by Raupach et al. [16]. For aquatic vegetation flow, the flow structure has a range of behaviours depending on the submergence depth ratio. Nepf and Vivoni [10] revealed the transition between submerged canopy flow and emergent canopy flow. By using detailed Laser Doppler anemometry (LDA) measurements, Poggi et al. [15] developed a phenomenological model that described turbulence structure within the canopy shear layer. They divided the entire depth region into three sublayers. The first layer was the lower layer in which the Karman vortices behind vegetation elements were dominant. The second layer was the middle layer in which Kelvin–Helmholtz (K–H) vortices were generated by inflectional instability and the third layer was the upper layer that was similar to boundary layers.

For flexible canopy flow, the passage of the K–H vortex generates the coherent wave motion of the plants, called the ‘Monami’ phenomena. Ghisalberti and Nepf [4] demonstrated the applicability of the mixing-layer analogy to aquatic canopy flow and found that the ‘Monami’ was a forced response to the instability of the mixing-layer. The same conclusion was obtained by Ikeda and Kanazawa [6]. Okamoto and Nezu [14] also investigated the occurrence of the ‘Monami’ phenomena and developed the combined technique of PIV and Particle Tracking Velocimetry (PTV) to examine the interaction between the velocity field and flexible vegetation motion.

In many natural rivers, aquatic vegetation occurs in patches of finite length. In such vegetated flows, flow is diverted away from the vegetation patch at the leading edge of the patch. In these areas, a shear layer is not formed at the vegetation patch edge and longitudinal advection contributes significantly to mass and momentum transport. Folkard [3] made the first step by considering the effect of a limited length vegetation patch on hydrodynamics. Sukhodolov and Sukhdolova [21] and Maltese et al. [7] focused on the spatial pattern of turbulent structure that developed over submerged vegetation patches. To identify spatial sedimentation and erosion patterns within the vegetation patches, Bouma et al. [1] combined field and flume experiments. Nikora et al. [13] examined the effects of aquatic vegetation on hydraulic resistance in a range of characteristic patch patterns.

Based on measurements with a flexible vegetation model, Nepf and Ghisalberti [9] suggested that submerged vegetation flow cannot be considered as the free turbulent mixing-layer because its spatial evolution is limited by the free surface. Nepf and Ghisalberti [9] evaluated the length scales of the transition from boundary-layer flow to mixing-layer-type flow. Zong and Nepf [23] and Rominger and Nepf [18] investigated the wake structure behind a two-dimensional porous obstruction and provided a model for predicting the length scale of the steady wake. These authors indicated that when a porous obstruction has two interfaces parallel to the flow direction, the strength of the vortices is greatly increased relative to the vortices that form at a single interface. Recently, Siniscalchi et al. [19] examined the effect of a finite size vegetation patch on the drag forces exerted on individual plants within the patch. The results suggested the presence of a large three-dimensional coherent structure at the top of the vegetation patch.

As previously mentioned in recent years, mean flow and turbulence characteristics in vegetated open-channel flows have received much attention. However, detailed information regarding the spatial evolution of coherent motions within finite-length vegetation patches is not yet available. Therefore, in the present study, we considered the effect of a limited length vegetation patch. Using PIV, turbulence measurements were intensively conducted in open-channel flows with submerged vegetation. Velocity profiles were measured at 33 positions in the longitudinal direction in order to examine the transition from boundary-layer flow upstream of the vegetation patch to mixing-layer-type flow within the vegetation patch. A new phenomenological model for the developing process of vegetation flow was developed. The model decomposed the entire flow region into four zones. The present PIV data also confirmed the efficiency of the mixing layer analogy and provided insight into spatial evolution of coherent motions.

2 Experimental method

Figure 1a shows the experimental setup and the coordinate system. Experiments were conducted in a 10m long, 40cm wide glass-made flume. The elements of the vegetation model were composed of rigid strip plates. Vegetation elements were attached vertically to the flume bed. The size of these elements was $h = 50.0\text{ mm}$ in height, $b = 8.0\text{ mm}$ in width and $t_{h }= 1.0\text{ mm}$ in thickness. $H$ represents the water depth and $h$ represents the vegetation height. As shown in Fig. 1b, $B_v$ and $L_v$ represent the neighboring vegetation spacing in the spanwise and streamwise directions, respectively. In other words, the vegetation allocation was a square pattern. The $x$-axis is the streamwise direction, and $x=0$ is the leading edge of the patch. The $y$-axis is the vertical direction and $y=0$ is the channel bed. The time-averaged velocity components in each direction are defined as $U$ and $V$, and the turbulent fluctuations are $u$ and $v$, respectively.

Fig. 1

Experimental setup. a PIV measurements. b Allocation pattern of vegetation elements

To measure two-component instantaneous velocities (i.e., $\tilde{u}(t)\equiv U+u(t)$ and $\tilde{v}(t)\equiv V+v(t)$), within and above the canopy, a laser light sheet (LLS) was vertically projected into the water column from the free surface. The 2.0mm thick LLS was generated with a 3.0W Argon-ion laser using a cylindrical lens. The illumination position of the LLS was located at centerline of the vegetation elements, beginning 0.5m upstream of the vegetation patch ($x=-0.5\text{ m}$) and extending 5.0m downstream of the leading edge of the patch ($x=5.0\text{ m}$). Illuminated flow pictures were taken by a high-speed CCD camera ($1024\times 1024$ pixels) with a 500Hz frame-rate and a 60s sampling time. In the present study, the resolution was 0.2mm/pixel. Instantaneous velocity components $(\tilde{u},\;\tilde{v})$ on the $x-y$ plane ($20 \text{ cm}\times 20 \text{ cm})$ were calculated using PIV algorithm over the entire depth region. The reference window size was $25\times 25$ pixels. To examine the evolution mechanism of the coherent structure in submerged vegetation flow, velocity profiles were measured at 33 positions in a longitudinal direction.

Table 1 Hydraulic condition

Table 1 shows the hydraulic condition. Experiments were conducted on the basis of three flow scenarios for submerged vegetation flow, in which the vegetation density, $\lambda _f$, was changed. For all cases, the relative submergence depth, $H/h$, and the bulk mean velocity, $U_m$, were kept constant (i.e.,$H/h=3.0$ and $U_m =20.0\text{ cm/s}$). For this study, the dimensionless vegetation density, $\lambda _f$, was defined as follows:

$$\begin{aligned} \lambda _f =ah=\frac{\sum \limits _i^n {A_i h} }{S\cdot h} \end{aligned}$$

(1)

where, $A_i$ is the frontal area of a vegetation element, $S$ is the referred bed area, and $n$ is the number of elements occupied in $S$. The vegetation density, $a$ (1/m), was defined as the total frontal area per vegetation volume $Vo=S\times h$. Nepf [8] suggested that only canopies with $ah\ge 0.1$ provide sufficient resistance to transform the velocity profile into a mixing-layer profile, with an inflection point at the canopy edge. In the present study, canopy flows with $\lambda _f =ah=0.86$ and $ah=0.38$ are classified as dense canopy flows. In contrast, canopy flows with $\lambda _f =ah=0.0975$ are classified as sparse canopy flows.

3 Results

3.1 Mean-flow structure

Figure 2 shows the vertical profiles of the time-averaged streamwise velocity $U(y)$ at $x/h=0-80$ for $\lambda _f =0.38$. The boundary of the mixing-layer is indicated with a dashed line in Fig. 2. The mixing-layer limits $h_{2}$ (upper) and $h_{1}$ (lower) were estimated as the elevation of 10% of the maximum Reynolds stress $-\overline{uv} _{peak} \left( x \right)$.

Fig. 2

Vertical profiles of mean velocity at various locations within the vegetation patch

Near the leading edge of the vegetation patch ($x/h\ge 0$), the drag effect of the vegetation elements decelerates the streamwise velocity within the canopy layer $(y/h\le 1.0)$. As a result, the inflection-point appears above the vegetation edge and the flow velocity profile resembles a mixing-layer type profile.

This result is in good agreement with that of Ghisalberti and Nepf [4]. Downstream of the leading edge of the vegetation patch $(0\le x/h\le 20)$, the velocity continued to decelerate below the canopy edge and a clear boundary layer with a steep gradient develops at the vegetation edge $(y/h=1.0)$. Further downstream $(x/h\ge 20)$, variations of the velocity profiles in the streamwise direction are relatively small $({\partial U}/{\partial x\approx 0})$.

Figure 3 compares the mean velocity profiles at each location for $\lambda _f =0.38$ with the hyperbolic tangent law of the mixing-layers. The velocity profile of pure mixing-layers is given by the following:

$$\begin{aligned} \frac{U-\overline{{U}}}{\Delta U}=\frac{1}{2}\tanh \left( {\frac{y-\overline{{y}}}{2\theta }} \right) \end{aligned}$$

(2)

The momentum thickness, $\theta$, is defined by the following:

$$\begin{aligned} \theta =\int \limits _0^\infty {\left[ {\frac{1}{4}-\left( {\frac{U-\overline{{U}}}{\Delta U}} \right) ^{2}} \right] dy} \end{aligned}$$

(3)

The velocity difference, $\Delta U$, is defined as follows: $\Delta U=U_2 -U_1$. $U_1$ indicates the constant velocity of the low speed zone within the mixing-layer, and $U_2$ indicates the constant velocity of the high speed zone; $\overline{{U}}={(U_1 +U_2 )}/2$ and $\overline{{y}}={(h_1 +h_2 )}/2$. As seen from Fig. 3, the velocity profiles at each location agree well with the mixing-layer profiles of equation (2). This result confirmed efficiency of the definition of the present mixing-layer in submerged canopy flows.

Fig. 3

Comparison of the present mean velocity profiles with tangent hyperbolic law of mixing layer

Figure 4 shows the mixing-layer thickness, $\delta _{ml} =h_2 -h_1$, obtained from the Reynolds stress distributions. For comparison, Fig. 4 also represents the momentum thickness $\theta$, which is a measure of shear layer growth. It is observed that both $\delta _{ml}$ and $\theta$ increase rapidly, and that a mixing-layer develops downstream. Then, at distances larger than $x/h=30$ from the leading edge of the vegetation patch $(x/h\ge 30)$, the mixing-layer thickness, $\delta _{ml}$, and the momentum thickness, $\theta$, stabilize and remain almost constant within the downstream portion of the patch. This indicates that the upper boundary of the mixing-layer $(y =h_{2})$ reaches the free surface and that the mixing-layer stops growing. In an unobstructed shear-layer, the mixing-layer continually develops downstream. However, for aquatic canopy flow, the development of the mixing-layer is confined by the free surface. Ghisalberti and Nepf [5] also pointed out the stabilization of mixing-layer width, and proposed that the growth of the vegetated shear layer ceases once the production of the shear-layer-scale turbulent kinetic energy is balanced by the drag dissipation.

Fig. 4

a Variations of mixing layer thickness along the vegetation patch. b Variations of momentum thickness along the vegetation patch

Also observed is that the ratio of the mixing-layer thickness $\delta _{ml}$ to the momentum thickness, $\theta$, is similar for all of the flow scenarios $(\delta _{ml} /\theta =7.1)$. These values are consistent with those of Ghisalberti and Nepf [4] and Nezu and Sanjou [11].

3.2 Subdivision of vegetated canopy flow

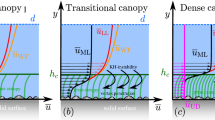
A phenomenological model for the development process of submerged vegetation flow is considered on the basis of the present experimental results and is shown in Fig. 5. The whole flow region is divided into the following four zones.

$$\begin{aligned} {\begin{array}{ll} {x\le x_{SM} }&{\quad \text{ smooth} \text{ bed} \text{ zone}} \\ {x_{SM} \le x\le x_{DF} }&{\quad \text{ diverging} \text{ flow} \text{ zone}} \\ {x_{DF} \le x\le x_{DV} }&{\quad \text{ developing} \text{ zone}} \\ {x\ge x_{DV} }&{\quad \text{ fully}-\text{ developed} \text{ zone}} \\ \end{array} } \end{aligned}$$

Upstream of the vegetation patch $(x\le x_{SM} )$, the flow is unaffected by the canopy and the velocity profile is similar to that found in open channel flow. At the vegetation patch edge ($x/h = 0$), vegetation creates a high flow resistance and the flow velocity begins to decelerate within the vegetation patch. As a result, much of the flow approaching the vegetation patch from the upstream is diverted away from the patch. Zong and Nepf [22] called this phenomenon ‘diverging flow’. The end of the diverging flow zone is denoted by $x_{DF}$. In the diverging flow zone, the shear layer is not yet formed and as compared to the canopy drag turbulent stress is negligibly small.

Fig. 5

Phenomenological model for the developing process of submerged vegetation flow

Downstream of the diverging flow zone $(x\ge x_{DF} )$, the profiles show a constant velocity, $U_{1}$, within the canopy and a constant velocity, $U_{2}$, over the canopy. The velocity difference, $\Delta U=U_2 -U_1$, creates a shear layer at the canopy interface $(y/h=1.0)$, and Kelvin–Helmholtz vortices evolve downstream. The growth of a large-scale vortex can be seen in the distributions of the Reynolds stress and the peak of $-\overline{uv}$ becomes larger.

Beyond $x_{DV}\, (x\ge x_{DV} )$, coherent structures grow to a finite size and reach fixed penetration into the canopy. We define $x\le x_{DV}$ as the ‘developing zone’ and $x\ge x_{DV}$ as the ‘fully-developed zone’. The length of the developing zone, $L_{DV} =x_{DV} -x_{DF}$, varies with the vegetation density. Nepf and Ghisalberti [9] reported that the shear-layer width reaches a fixed scale at approximately $10h$ downstream from the canopy leading edge based on measurements in flexible canopy flow ($a=5.7\, (1/\text{ m})$).

The development of the streamwise velocity, $U$, at several elevations within and above the canopy is shown in Fig. 6. Note that the flow velocity, $U$, decelerated within the canopy $(y/h\le 1.0)$ and accelerated over the canopy $(y/h\ge 1.0)$ downstream of the leading edge of the patch $(x/h\ge 0)$. The data clearly demonstrates the effect of vegetation density. For dense canopy $(\lambda _f =0.86)$, flow was greatly perturbed by the vegetation elements. As a result, the flow velocity, $U$, within the canopy decreases and reaches the constant values faster as vegetation density increases.

Fig. 6

Variations of the time-averaged streamwise velocity along the vegetation patch

Further downstream $(x/h\ge 20)$, the velocity within and above the canopy is fairly uniform $({\partial U}/{\partial x}\approx 0)$.

We consider the vertical velocity to evaluate the diverging flow around the vegetation patch. Figure 7 shows the development of the vertical velocity, $V$, at the vegetation edge ($y/h = 1.0$). It is evident from Fig. 7 that values of $V(h)$ increase rapidly at $-2.0\le x/h\le 0$, indicating that the diverging flow approximate begins at $x/h = 2.0$ upstream of the vegetation patch. After entering the vegetation patch $(x/h\ge 0)$, vertical velocity has large positive values. Here, it should be noted that the deceleration in $U$ is accompanied by an increase in the vertical velocity, $V$, associated with the diverging flow. The diverging flow continues until $x_{DF} /h=8.0$ for $\lambda _f =0.86$.

As the vegetation density, $\lambda _f$, decreases, the vertical velocity, $V$, becomes lower (the flow diversion decreases) and spans a longer distance. This result is consistent with Zong and Nepf [23]. It is useful to define the length-scale of the Diverging flow zone, $L_{DF} =x_{DF}$, as the distance from the leading edge of the patch to the point where the vertical velocity, $V$, is reduced to 0.

Downstream of the diverging flow zone $(x/h\ge 20)$, the values of $V$ become negligibly small and diverging flow ends. Also observed is that the downward flow into the canopy layer ($V < 0$) occurs at $x/h = 12.0$ from the leading edge for $\lambda _f =0.86$. This suggests that high-speed flow over the canopy accelerates low-speed flow within the canopy. Rominger and Nepf [18] also reported that the streamwise velocity reaccelerates subsequent to the diverging flow zone, because the Reynolds stress can penetrate to the canopy layer.

The length-scales of the diverging flow and the developing zones for $\lambda _f =0.86$, 0.38, and 0.095 are summarized in Fig. 8. The data clearly demonstrate the effect of the vegetation density. As the vegetation patch becomes denser, the vertical velocity, $V$, increases and diverging flow ends at shorter distance from the vegetation patch edge (the length of the diverging flow zone, $L_{DF}$, decreases). By the end of the diverging flow zone, the time-averaged flow velocity reaches a fully-developed condition (see Fig. 6).

Fig. 7

Variations of the time-averaged vertical velocity along the vegetation patch

Fig. 8

Length-scales of Diverging flow zone and Developing zone

Downstream of the diverging flow zone, the velocity difference, $\Delta U=U_2 -U_1$, creates a strong shear layer at the canopy interface, and coherent motions evolve downstream. Growth of coherent motions can be measured in values of the Reynolds stress. In this study, the length-scale of the developing zone is defined as the distance from $x=x_{DF}$ (the downstream end of the diverging flow zone) to a point where the growth rate of the Reynolds stress peak value $\frac{1}{-\overline{uv} _{peak} \left( x \right) }\frac{\partial }{\partial x}\left( {-\overline{uv} _{peak} \left( x \right) } \right)$ decayed to 10% (i.e., $L_{DV} =x_{DV} -x_{DF}$).

It is observed that the length of the developing zone, $L_{DV}$, becomes smaller as the vegetation density, $\lambda _f$, increases. This indicates that the flow development of the dense canopy flow is accelerated as compared to that of the sparse canopy flow due to higher resistance. This result is consistent with that of Souliotis and Prinos [20]. They suggested that the vegetation density and the vegetation patch length have a dominant role in flow and turbulence development. As a result, sparse canopy flow requires more length for fully-development as compared to dense canopy flow. In the present study, the $L_{DV}$ for $\lambda _f =0.095$ is approximately 1.3 times the $L_{DV}$ for $\lambda _f =0.86$.

Nepf and Ghisalberti [9] also evaluated the length scales of the transition from boundary-layer flow upstream of the vegetation patch to mixing-layer-type flow within the vegetation patch $L_{T}$ as follows:

$$\begin{aligned} L_T \approx 3.0\left( {\frac{U_h }{U_*}} \right) \left( {C_D a} \right) ^{-1} \end{aligned}$$

(4)

where $U_{h}$ is the velocity at the vegetation edge, $U_{*}$ is the friction velocity, and $C_{D}$ is the drag coefficient for the vegetation elements. The values of $C_{D}$ were calculated using Eq. (5) (see [10]), as follows:

$$\begin{aligned} \frac{\partial }{\partial y}\left( {\frac{-\overline{uv} }{U_*^2 }} \right) \approx \frac{1}{2}C_D a\left( {\frac{U}{U_*}} \right) ^{2} \end{aligned}$$

(5)

For the present study, the length scales of the transition $L_{T}$ evaluated from Eq.(4) are $L_T /h=6.7$ for $\lambda _f =0.86, \,L_T /h=12.4$ for $\lambda _f =0.38$, and $L_T /h=80.5$ for $\lambda _f =0.095$. These values of $L_T /h$ are in good agreement with those of $L_{DF} /h$ (the length-scales of the diverging flow region) for dense canopy flow ($\lambda _f =0.86$ and 0.38). In contrast, for sparse canopy flow $(\lambda _f =0.095)$, the $L_T /h$ overestimates the length scale of the transition, because the transition from turbulent boundary-layer to mixing-layer does not occur for $\lambda _f =0.095$.

3.3 Turbulence structure

Figure 9 shows the vertical distribution of the Reynolds stress $-\overline{uv} (y)$ at $x/h=0-80$ for $\lambda _f =0.38$. The values of $-\overline{uv} (y)$ are normalized by the bulk mean velocity, $U_m$. The boundary of the mixing-layer is indicated by the dashed line in Fig. 9. The lower limit of the mixing-layer is the penetration height $h_\mathrm{p} \left( {=h_1 } \right)$ as defined by Nepf and Vivoni [10].

After entering the vegetation patch $(x/h\ge 0)$, the maximum of the Reynolds stress is located at the vegetation edge $(y/h=1.0)$, which corresponds well to the elevation of the inflection-point as shown in Fig. 2. The values of $-\overline{uv}$ decay downward into the canopy and the distributions are nearly uniform below the lower limit of the mixing-layer $(y<h_1 )$. This rapid decrease is caused by the strong drag force due to the vegetation elements.

Near the leading edge of the vegetation patch $(x/h=4.0)$, the values of the Reynolds stress are relatively small. The result suggests that the transport of the momentum is dominated by longitudinal advection from the leading edge of the vegetation patch in the diverging flow zone $(x/h\le x_{DF} /h=12)$.

Within the developing zone $(x/h\ge x_{DF} /h=12)$, the magnitude of the Reynolds stress becomes larger and the penetration height, $h_{p}$, decreases downstream. This implies that the higher Reynolds stress penetrates into the vegetation layer and that the vertical momentum exchange is promoted more significantly as coherent motions develop along the vegetation patch.

Fig. 9

Vertical distributions of Reynolds stress at various locations within the vegetation patch

Vertical momentum transport due to coherent motions can be described by the magnitude of the Reynolds stress. The downstream distributions of the peak Reynolds stress, $-\overline{uv} _{peak} \left( x \right)$, are shown in Fig. 10. For dense canopy flow ($\lambda _f =0.86$), the variation of $-\overline{uv} _{peak}$ is small within the diverging flow zone $(x/h\le x_{DF} /h)$. A significant increase in $-\overline{uv} _{peak}$ is observed at $x/h\ge x_{DF} /h\, (=12)$ (i.e. the developing zone). This implies that coherent motions evolve downstream and that the organization of the vortices enhances the vertical transport of momentum. Beyond $x_{DV} /h\, (x/h\ge x_{DV} /h)$ the growth rate of $-\overline{uv} _{peak} \left( x \right)$ starts to decrease. This result suggests that the length-scale of coherent motions grow to a fixed scale and that dense canopy flow reaches its fully-developed condition at $x/h=x_{DV} /h\left( {=\text{3}0} \right)$.

Fig. 10

Variations of peak Reynolds stress along the vegetation patch

In contrast, for sparse canopy flow ($\lambda _f =0.095$), the values of $-\overline{uv} _{peak} \left( x \right)$ are lower than those for dense canopy flow. This result is in good agreement with Nepf and Ghisalberti [9]. For $\lambda _f =0.095\, (ah\le 0.1)$, the vegetation density is not sufficient enough to produce a strong shear layer at the vegetation edge and consequently, the vertical momentum transport becomes smaller.

A quadrant analysis was conducted for instantaneous Reynolds stress $-u\left( t \right) v\left( t \right)$. The quadrant Reynolds stress, $RS_i$, is defined as follows:

$$\begin{aligned} RS_i =\mathop {\lim }\limits _{T\rightarrow \infty } \frac{1}{T}\int _0^T {\left( {\frac{uv}{\overline{uv} }} \right) I_i } dt \end{aligned}$$

(6)

If $\left( {u,v} \right)$ exists in a quadrant $i$, then $I_i =1$, otherwise $I_i =0$. Each quadrant of $\left( {u,v} \right)$ corresponds to the following coherent events:

• $i=1\, \left( {u>0,v>0} \right)$ : outward interaction

• $i=2\, \left( {u<0,v>0} \right)$ : ejection

• $i=3\, \left( {u<0,v<0} \right)$ : inward interaction

• $i=4\, \left( {u>0,v<0} \right)$ : sweep

Figure 11 shows the vertical distribution of the quadrant Reynolds stress, ${RS}_{i}$, at each location for $\lambda _f =0.38$. The values are normalized by the bulk mean velocity, $U_{m}$. Near the leading edge of the vegetation patch $(x/h=2.0)$, the contribution of the outward interaction, $RS_1$, and the inward interaction, $RS_3$, becomes larger within the entire canopy layer. This area corresponds to a region of low value Reynolds stress in Fig. 9, indicating that no-organized structure is observed. Siniscalchi et al. [19] also observed negative Reynolds stress regions $(-\overline{uv} <0)$ at the leading edge of the vegetation patch.

Fig. 11

Quadrant Reynolds stress at each location within the vegetation patch $(\lambda _f =0.38)$

In the diverging flow zone $(x/h=6.0)$, the over-canopy region $(y/h\ge 1.0)$ is dominated by ejection, the upward transport of low-speed fluid. This implies that ejection events are pronounced in the same manner as those observed in open-channel flows, as pointed out by Nezu and Nakagawa [12]

In the developing zone $(x/h=18.0)$, the sweep-dominated area, the downward transport of high-speed fluid, is observed at $y/h=1.0$, where the Reynolds stress maximum is located (Fig. 9). The result indicates that the coherent structure is generated near the vegetation edge. The presence of the sweep-dominated area near the vegetation edge agrees with the observations reported by Maltese et al. [7].

In the fully-developed zone $(x/h=68.0)$, the sweep-dominated area expands vertically and appears to cover the whole canopy layer $(0.0\le y/h\le 1.0)$. The shear layers grow wide enough to penetrate into the canopy layer. These data strongly suggest that the momentum transfer between the in-canopy and the above-canopy is mainly carried out by sweep and ejection motions.

3.4 Coherent motion

PIV techniques are much more powerful to examine the trajectory of coherent motions than point measurements such as LDA and acoustic Doppler velocimetry (ADV) (see [17]). Figure 12 shows the instantaneous velocity vectors $(\tilde{u},\;\tilde{v})$ at each location for $\lambda _f =0.38$, which are subtracted by a convection velocity, $U_c \left( h \right)$, at the vegetation edge. The contour of the instantaneous Reynolds stress, $-uv$, is also depicted by the rainbow in Fig. 12. The evolution and development of coherent structures are demonstrated clearly. Within the diverging flow zone ($x/h=4.0-8.0,\, x/h=8.0-12.0$), small-scale turbulent motions, which are indicated by a solid circle, are generated at the vegetation edge. These small-scale eddies die out quickly.

Fig. 12

Contours of the instantaneous Reynolds stress $(\lambda _f =0.38)$

Within the developing zone ($x/h=18.0-22.0$), strong positive regions of $-uv$ are clearly seen near the vegetation edge, where mean flow shear is greatest. Downward vectors, (i.e. the sweep motions ($u>0,\, v<0$)) appear and high-speed parcels are transported into the canopy-layer. These Sweep motions are followed by Ejection motions ($u<0,\, v>0$), upward vectors of low-speed fluid parcels. This result is consistent with the work of Reynolds and Castro [17].

Within the fully-developed zone ($x/h=66.0\text{-}70.0$), turbulent motions are more organized and values of the instantaneous Reynolds stress become larger. The velocity vectors show the cycle of a strong sweep at the front of the vortex followed by a weak ejection at the rear of the vortex. The present PIV data confirm that the K–H vortices extend to around $y/h=2.5$ and that the sweep and ejection motions dominate the entire flow field.

The axial integral length-scale, which is an indication of the largest eddies, can be evaluated from the PIV data, as follows:

$$\begin{aligned} L_x \equiv \int _0^\infty {\frac{\overline{u\left( {x_0 ,y_0 ,t_0 } \right) u\left( {x_0 +x,y_0 ,t_0 } \right) } }{u{\prime }\left( {x_0 ,y_0 } \right) u{\prime }\left( {x_0 +x,y_0 } \right) }} dx \end{aligned}$$

(7)

where $L_x$ represents the length scales in the streamwise direction. The subscript 0 denotes a reference point (i.e. $\left( {x_0 ,y_0 } \right) )$ and $u{\prime }\equiv \sqrt{\overline{u^{2}} }$ indicates the turbulence intensity. Figure 13 shows the vertical distributions of $L_x$ at each location for $\lambda _f =0.86$, 0.38 and 0.095. The present data are compared with the terrestrial canopy data of Brunet et al. [2].

Fig. 13

Vertical distributions of the axial integral length-scale at various locations within the vegetation patch

Within the canopy $(y/h\le 1.0)$, small values of $L_x$ remain almost constant. The length-scales $L_x$ lie within the range of $0.5\text{-}1.0h$ for all 5 positions. The most rapid change is observed near the vegetation edge $(y/h=1.0)$. The values of $L_x$ become larger with an increase of downstream distance from the leading edge ($x/h=0$).

In the fully-developed zone ($x/h=68.0$), coherent motions grow to a finite size and the length scales, $L_x$, are on the order of the vegetation height, $h$, above the vegetation edge ($L_x \approx 1.5\sim 2.0h$). These values are in good agreement with the terrestrial canopy data of Brunet et al. [2].

Notice that, once $y/h\ge 2.0$ (near the free surface), the values of $L_x$ start to decrease. These data confirm the earlier conclusion (Figs. 3, 4) that the development of coherent motions is more confined by the existence of the free surface for the aquatic canopy. For aquatic canopy flow, the free surface is not far above the canopy $(H/h\le 5.0)$ and large-scale boundary turbulence is not present. In contrast, for the terrestrial canopy, the length scale $L_x$ increases from the channel bed up to $y/h\approx 3.0$.

4 Conclusions

In this study, turbulence measurements were conducted in a finite-length vegetation patch flow in order to examine the transition from boundary-layer flow upstream of the patch to mixing-layer-type flow within the patch. The results confirmed the efficiency of the mixing layer analogy and provided insight into spatial evolution of the coherent structure. Present PIV measured data revealed four distinct regions for developing process of the coherent structure in finite-length vegetation patch flow. The main findings are the following:

• 1. The upstream portion of the vegetation patch, called the ‘diverging flow region’ interacts with surrounding water through vertical advection. Flow was diverted away from the vegetation patch. As a result, the flow velocity decelerated within the canopy and accelerated over the canopy after entering the vegetation patch. It is also observed that the vertical velocity has large positive values and that flow diverging continues until $x/h=8.0$ from the leading patch edge for dense canopy flow.

• 2. Mixing-layer thickness increases rapidly and remains almost constant within the fully-developed zone $(x\ge x_{DV} )$. This indicates that the upper boundary of the mixing-layer reaches the free surface and that the mixing-layer stops growing in the submerged vegetation flow.

• 3. The region downstream of the diverging flow region $(x\ge x_{DF} )$ is called the ‘developing region’. In this region, coherent motions develop downstream. The magnitude of the Reynolds stress becomes larger along the vegetation patch and coherent motions enhance the vertical transport of the momentum.

• 4. Using a quadrant analysis we revealed that no-organized structure is observed at the leading edge of the vegetation patch. Within the developing zone, a sweep-dominated area appears near the vegetation edge. Further downstream, the sweep-dominated area expands vertically and covers the whole canopy layer.

• 5. The evolution and development of coherent structures are clearly demonstrated in the present PIV data. The results confirmed that coherent motions extended to the free surface and that sweep and ejection motions dominated the entire flow field. Further downstream, coherent structures grow to a finite size and the integral length-scales are on the order of vegetation height $h$ above the vegetation edge.

• 6. We calculated the length scale of the diverging flow and the developing zones. The growth of coherent structures can be measured with the values of the Reynolds stress. The results revealed that the flow development of the dense canopy flow is accelerated as compared to that of the sparse canopy due to higher resistance. In the present study, the length-scale of the developing region for sparse canopy is approximately 1.3 times that for dense canopy.