1 Introduction

Studies of flow over urban areas have been carried out with two main goals: to characterize and possibly to predict pollutant concentration [5] and to assess the effect of the urban landscape on the local weather/climate [20]. A way of improving numerical models is by means of including more representative aerodynamic parameters. Under neutral stability condition and within the surface layer, the relevant aerodynamic parameters are the friction velocity, \(u_*\), the roughness length, \(z_0\), and the zero-plane displacement height, \(d_0\) [5, 6, 19, 25]. The use of empirical curves in dispersion models frequently implies the knowledge of the lateral and vertical concentration standard deviation. A criticism to these formulas is their applicability to urban areas other than where they were fitted. Thus, the needs for representative urban dispersion models encourages the search for more general parameterizations including both the surface layer and roughness layer [8]. The simulation of urban structures in wind tunnels is often a better option due to the fact that field experiments are much more complex and expensive and they are subjected to the weather variability. Wind tunnel simulations provide the needed flow controllability to avoid the influence of undesirable forcings. The relative ease with which the experimental setup can be changed is also an advantage, making sensitivity studies frequently possible. The flow pattern over several obstacle configurations has been studied by many investigators. A wind-tunnel study of the scalar field in a street canyon was carried out by Kastner-Klein and Plate [11]. They obtained concentration profiles for a range of canyon configurations, and concluded that the position of the tracer source across the canyon is very influential on the concentration, with concentrations close to the upstream wall as higher as ten times of those encountered on the downstream wall. Baik et al. [3] simulated water flow over a canyon with three setups: same height obstacles, upstream obstacle higher, and downstream obstacle higher; the aspect ratio was also changed. Their results showed less concentration on the downstream wall in agreement with Barlow et al. [4], who employed naphthalene sublimation technique to simulate emission from roof, street, and walls. Barlow et al. observed that for each aspect ratio tested, the scalar transfer coefficient reduced monotonically from downstream wall, street and upstream wall. This suggests that the recirculation within the canyon is not like a symmetrical vortex, as the experiment of Baik et al. [3] had indicated. Their data also suggest that the scalar transfer coefficient seems to decrease as the aspect ratio increase. This is likely to be because of trapping effects, usually observed for aspect ratio greater than one. Khan et al. [13] show that the dimensionless horizontal velocity is mainly positive ahead the midway of obstacles for the smallest aspect ratio (\(h/d\) = 1/9) and negative for \(h/d\) = 1/4 and 1/1.5 (they define aspect ratio in the inverse way: \(d/h\) represented by \(s/k\)). The standard deviation of \(u\)- and \(w\)-component at obstacle midway increases as the aspect ratio (\(h/d\)) decreases (their \(s/k\)=\(d/h\) increases). Ricciardelli and Polimeno [26] carried out hot-wire anemometer measurement over an urban canyon model using a 2-D probe. Their results show that both mean and fluctuation characteristics of the flow are rather related to the local geometry.

Dispersion models need aerodynamic parameters as input. For example, mixing-length based models, Gaussian models, or still turbulence second order closure models, all make use of eddy diffusivity coefficients, which in turn are computed from gradient velocity profiles [1, 27]. Gaussian plume model, in particular, must be utilized carefully in urban areas, since many of the assumptions implied in its formulation is not matched within the canopy layer or even in the roughness sublayer. Specifically, Gaussian plume models assume homogeneity and the flow must be sufficiently stationary in order that the time taken for a fluid particle to be displaced from the source to the receptor be much less than the time-scale of wind variability and much greater than the wind velocity [18]. Even so, some improvements on the Gaussian formulation within the canopy layer by means of a proper scaling have been suggested by Pournazeri et al. [23] from water channel experiments.

The reason for which the surface boundary layer (SL) wind profiles, or equivalently \(u_*\), \(z_0\), and \(d_0\), is in the core of dispersion models is that, under neutral stability condition, turbulence is produced by the flow shear: the steeper the velocity gradient, the stronger the shear and thereby the mixing. Hence, accurate assessment of aerodynamic parameters should improve the description of dispersion models and their predictive power.

In this paper a flow past an urban canyon model is studied using a wind tunnel and the hot-wire technique with the objective of understanding the influence of the aspect ratio over the flow profile. The impact of the aspect ratio on the flow and on the urban energy response to natural forcings has been addressed by [4, 15, 22]. We have analyzed wind tunnel results of a flow past a canyon, a typical configuration utilized as urban canopy model (UCM), to obtain robust relationships within the domain we have simulated. Sensitivity tests were carried out by varying the canyon aspect ratio and wind speed.

Our measurements provide \(u_*\), \(z_0\), and \(d_0\), which are needed as inputs in most dispersion model such as AERMOD or even in mesoscale models such as WRF. These parameters will be used, particularly, in a UCM described in [15]. In that work the UCM is based on parallel canyons and is coupled with a 1-D turbulence model based on the Mellor-Yamada model [16, 17]. Nevertheless, the aerodynamic parameters found here could be, in principle, used in any other UCM described by parallel canyons.

2 Experimental setup

A wind tunnel with an open test section located in the Aerodynamics Division at the Instituto de Aeronáutica and Espaço (IAE), São José dos Campos, Brazil, has been deployed to obtain the sequence of simulations presented throughout this paper. The cross-section of the wind tunnel contraction outlet and the diffuser inlet is circular with a diameter of 0.65 m. The turbulence is produced in a controlled way by mean of a screen 1 m upstream. The wind tunnel test section is 1 m long. The turbulence intensity of the free flow with the model in the test section is 1.2 % within the velocity range investigated. This is at least 10 times lower than it is usually observed in the atmosphere. Cases in which the turbulence in the model is different (usually lower) of the prototype have also been addressed by Pournazeri et al. [23]. They developed a scaling method that can be used to correct cases when the turbulence intensity in the model does not match that in the prototype. That new scaling method was also utilized to correct concentration measured in physical models, so that it could be transferred to the real scale. However, the aforementioned study by Ricciadelli and Polinemo [26] show that the flow within the canyon is little sensitive to the turbulence level of the flow above. Thus, the finds discussed in Sect. 3.1 are assumed to be little affected, especially from a qualitatively point of view

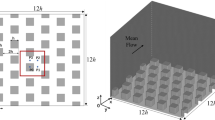
An important point to be considered is that in such a short section test the flow does not have enough fetch to develop a typical wind speed profile as observed in a real field experiment. Our wind tunnel flow profile is rather flat (Fig. 1). However, this is not expected to make much difference in the final results. The reason to think so is that in real scale the flow in equilibrium or not with the ground surface encounters an obstacle (say the upstream building of a street canyon) and a new non-equilibrium internal boundary layer is formed. The flow experiences then a strong shear very close to the new surface, which in turn produces a thin highly-turbulent layer. If there is sufficient fetch, the turbulence provides the needed mixing for the flow to get the equilibrium with this new surface. Since building width are usually not so large, the wind speed profile above them does not meet an equilibrium condition when the flow arrives at the step-down (canyon). This is also what happens in a wind tunnel simulation when either a single canyon is deployed [12], or multiples canyons are deployed [11, 13]. A strong shear in this conditions is also observed in numerical simulations [7]. For example, Kastner-Klein and Plate [11] show that roof shape is more influential on a scalar concentration within the canopy layer than whether there is or there is not other buildings upstream. Furthermore, Ricciardelli and Polinemo [26] results showed that the approaching wind speed profile (smooth or turbulent in their case) is little influential on the mean and fluctuation characteristics of the flow within the canopy layer. Above the canopy layer a smooth profile can produce a higher speed. Based on the qualitative explanation above and on the results of Ricciadelli and Polinemo [26], we assumed that the almost-flat approaching profile used in this work does not affect significantly the main features encountered, in particular, the flow pattern and the general behavior of the speed and variance profiles. The physical model is constituted of one single street canyon with the sides closed by a glass plate to avoid a net air flow along the canyon (\(O\!y\) direction). The model is made of polished wood and was built to permit the variation of the aspect ratios (\(h/d\)) by varying its width, \(d\), and keeping the canyon height, \(h\), constant [2].

Fig. 1
figure 1

Approaching flow above the upstream building top (\(z_\infty = 2.5 h\))

Full size image

In the set of experiments carried out, we obtained the vertical flow profile from positions \(z/h\) = 0.1, 0.3, 0.5, 0.7, 0.9, 1.0, 1.1, 1.5, 2.0, 2.5, and for the horizontal positions (\(x\)) according to Fig. 2. Three canyon aspect ratios were tested, 1/4, 1/6, and 1/8, with the canyon height remained fixed. We investigate flow speed, standard deviation, and turbulence profiles raised at the positions \(x = 1h\) up to \(x = d-h\) with \(1h\) spacing from each other. The nominal flow speeds adopted were 2, 5, and 10 m/s. For nominal flow speed of 10 m/s some non-stationarity has been noticed because the way the fan controller works (feedback controller), but it was not over 1 m/s. Furthermore, since most of data are analyzed in normalized form, such a non-stationarity plays no important role. The Reynolds number based on the canyon width varied from \(2\times 10^4\) to \(2\times 10^5\).

Fig. 2
figure 2

Layout of measurement points for each canyon width. The points in the vertical are \(z/h\) = 0.1, 0.3, 0.5, 0.7, 0.9, 1.0, 1.1, 1.5, 2.0, and 2.5. The flow comes from left

Full size image

Hot-wire anemometry was carried out with a Dantec-Dynamics system constituted of a one-directional probe, a constant temperature anemometer (CTA) bridge on the acquisition board, and an analog-to-digital (A/D) converter board. The calibration was carried out using a Dantec-Dynamics calibration unit, which works based on the control of pressure and temperature of air inside a camera of a known volume and with an outlet of known diameter. These quantities allow the determination of the exiting air flow speed [10]. The sampling rate was 1,000 Hz and the series length was set to contain \(2^{16}\) points so that the corresponding sampling time was about 1 min (65,536 ms). After some previous tests we found that a velocity interval of 0.1–12 m/s for calibration was good enough to include all the possible range of velocities expected during the essays. The relationship between velocity and the bias in the CTA bridge is not linear, and we used a fourth-degree polynomial calibration curve as suggested by the manufacturer:

$$\begin{aligned} U_\mathrm{eff} = a_0 + a_1 E + a_2 E^2 + a_3 E^3 + a_4 E^4, \end{aligned}$$
(1)

where \(E\) is the bias on the bridge and \(U_\mathrm{eff}\) the effective flow speed.

Strictly speaking, \(U_\mathrm{eff}\) is not actually the longitudinal component of the velocity (\(U\)), unless the flow is undisturbed. As it will be shown, a relatively smooth flow is observed above the canyon height and in these cases \(U_\mathrm{eff}\) is very close to \(U\). Below the canyon height, the vertical flow component becomes significant and \(U_\mathrm{eff}\) is, in theses cases, a measure of the magnitude of the flow velocity. The HWA effective speed is a combined effect of the three velocity components given by

$$\begin{aligned} U^2_\mathrm{eff} = U^2 + k^2V^2 + h^2W^2 \end{aligned}$$
(2)

in which \(k=k(\alpha )\) and \(h=h(\theta )\) are functions of the yaw and pitch angles, respectively. As the \(V\) component is along the wire it is practically zero. Originally, Jorgensen [9] performed angle sensitivity tests and found that the value of \(h\) ranges from 1.02 to 1.04 for an angle interval from 20 to 90 degrees. This implies that

$$\begin{aligned} U_\mathrm{eff} \approx \sqrt{U^2 + W^2}. \end{aligned}$$
(3)

Within the canyon we can have \(W\!\sim \! U\). Hence, the profiles presented herein are actually \(U_\mathrm{eff}\) versus \(z\). However, this point will not affect the qualitative aspects of our discussion though it will be important to understand the limitation of the parameterization to be presented in Sect. 3.2. For sake of simplicity, we will use the symbol \(U\) to refer to the flow speed as measured by the HWA after applying the calibration.

Due to the two-dimensionality of our experimental set-up, the results are expected to present some limitations: a model with only a single canyon and bi-dimensionality are the main issues. Three-dimensional effects in an array of cubes during a water channel experiment have been reported by Princevac et al. [24]. The most interesting feature found is a net flow along the canyon perpendicular to the main stream (outer flow), which is intensified when the central cube is replaced by one with double height. This is an effect usually not observed in laboratory experiments, mainly because of 2-D symmetry of structures employed. Thus, when applying the results in this paper one should note that it was performed in a 2-D canyon.

3 Results and discussion

3.1 Flow characteristics

In Fig. 3 is shown plots of flow speed, standard deviation, and turbulence intensity [\(\sigma _u(z)/U(z)\)] for the canyon with width \(4h\). It can be seen that the speed profiles for \(h/d=1/4\) present similar shapes, suggesting that the use of non-dimensional variables can be helpful to formulate some parameterization. The profile position on the \(Ox\) direction is little influential on the profile shape, unless for the closest position to the lee wall and below the canyon height. This can be more clearly seen for the flow speed of 10 m/s: close to the floor we found that the flow speed for the profile at \(x=h\) is about 2 m/s whereas for the other two profiles corresponding to positions \(x=2h\) and \(x=3h\) we found 3 m/s. The speed difference observed above the canyon height is just due to the different speeds of the free flow. However, if we correct the profile with \(U_\infty = 11.3\) m/s, the lower part of it still does not follow the other two profiles, showing the lee wall effect on it.

Fig. 3
figure 3

Flow speed, standard deviation, and turbulence intensity for the canyon width of \(4h\). Each line of the same type corresponds to a probe position on the \(Ox\)-axis (\(x=1, 2,3h\)) for a given flow speed

Full size image

Standard deviation (STD) profiles are shown in Fig. 3b. The highest region above the canyon presents the lowest STD as expected. Toward the canyon floor, a common characteristic observed is that the STD increases until a maximum value around \(z=1h\) and then decreases until \(z=0.5h\), and turns to increase in the region \(z<0.5h\). From this we can distinguish four regions where different processes are probably acting:

  • region I: \(z/h \approx 2.5\) — characterized by full flow speed and low disturbances since the flow does not encounter any obstacle;

  • region II: \(z/h \approx 1.0\) — is the layer where the free stream more strongly interacts with the recirculating flow within the canyon. Also, in this region there is a wake formed upstream due to the abrupt displacement of the wall (up-to-down step). These two processes ensure the highest values of STD as observed;

  • region III: \(z/h \approx 0.5\) — in this region the flow circulation is well developed, making the flow to move in a rather defined eddies. Thus, the “degree of randomness” in the motion is lower;

  • region IV: \(z/h \approx 0.1\) — is the layer where the flow shear is very high due to the influence of the floor, making the STD greater than in region III. Despite of the strong shear close to the floor, the flow speed is relatively low in such a way that STD in this region is not as great as in region II.

In addition to flow speed and STD, a quantity often used in engineering to characterize a turbulent flow is the turbulence intensity, defined as \(\sigma _u(z)/U(z)\). Profiles of turbulence intensity were plotted in Fig. 3c. With exception of a couple of spurious points below \(z=0.5h\), turbulence intensity profiles are all similar. In general, the features just described in Fig. 3a–c do not change significantly in function of the flow speed. This was also observed for the other two canyon aspect ratios (not shown here). However, the flow pattern does change from a canyon width to another. We analyzed dimensionless profiles for the three flow speeds of 2, 5, and 10 m/s, including only the three common dimensionless positions of canyons 4 and \(8h\), namely \(\frac{x}{d}=\frac{1}{4}\, \big (\frac{2}{8}\big )\), \(\frac{x}{d}=\frac{2}{4}\, \big (\frac{4}{8}\big )\), and \(\frac{x}{d}=\frac{3}{4}\, \big (\frac{6}{8}\big )\), thus eliminating absolute positioning. Dependence of position is more apparent for \(x/d=0.25\), that is, the closest profile to the lee wall. In general, the profiles fall onto a same curve with only some spatial variability below \(z/h=0.5\). This suggests that a reliable parameterization of type \(U/U_\infty = f(z/z_\infty )\) can be searched for at least down to the half canyon height. This systematic variation of the flow speed with height when both flow speed and height are written as dimensionless quantities is also observed in the STD profiles. Furthermore, the small differences among normalized profiles at different canyon positions make the process of taking spatial average of the profiles more meaningful. This fact is used in the following discussion on obtaining aerodynamics parameters and in Sect. 3.2, where we will be always using spatially-averaged profiles to seek some parameterization.

A sensitivity test for canyon \(4h\) and \(U=\) 2, 5, 10 m/s was carried out to obtain aerodynamics parameters from flow vertical profiles over the canyon. Results are shown in Table 1. The non-linear problem

$$\begin{aligned} \text{ minimize:}\sum _{k=1}^N \Bigl [\frac{u_*}{\varkappa }\ln \Bigl (\frac{z_k-d_0}{z_0}\Bigr ) - U_k\Bigr ]^2 \end{aligned}$$
(4)

with respect to \(u_*\), \(z_0\), and, \(d_0\) is little sensitive on the initial parameter \(d_0^{(0)}\) once it is appropriately chosen, which guarantees the convergence of \(d_0\). The determination of \(d_0\) from the log-law fit is difficult as it has been reported by [6]. They averaged spatially the profiles and then fitted \(z_0\) and \(d_0\), inputting \(u_*\) computed from \(\sqrt{\overline{u^{\prime } w^{\prime }}}\).

Table 1 Aerodynamic parameters estimated for different flow speeds
Full size table

Since the experimental profiles presented here are not logarithmic, it is necessary to choose points that better represent the log-law. Most of the points measured within the canyon stay apart from a logarithm curve. On the other hand, with only a few points the fit errors are large. A compromise between staying as far as possible of the canyon floor and keeping a reasonable number of points was found using profiles with five or six points (Table 1). Note that \(d_0\) tends to become stable when a six-point profile is chosen. The same statement holds for the two other parameters. An exception is \(z_0\) (= 0.03 mm) obtained from six points and \(d_0^{(0)} = 40\) mm for \(U= 5\) m/s. That value is much less than the 0.26 mm found from the profile fit for \(d_0^{(0)}\) equals 20 and 30 mm. However, those cases are accompanied by a large relative error (14.60). Based on the overall magnitude of the relative error, the two best fits are found choosing six points and \(d_0^{(0)}\) equals 20 or 30 mm. Therefore, we consider the best set of aerodynamic parameters the values in columns 1 and 3 of the fitted parameters in Table 1. For these cases, \(U_\infty \) and \(u_*\) values in the canyon \(4h\) are (2.02, 5.06, 10.71) m/s and (0.15, 0.38, 0.81) m/s, respectively, yielding \(u_*/U_\infty \) = (0.074, 0.075, 0.075) m/s. Such values of \(u_*/U_\infty \) are consistent with those found by [21]—ranging from 0.050 to 0.074—in a related wind tunnel study whose canyon dimension and flow speed employed were comparable with the ones we present in Table 1.

In order to understand how the flow pattern changes as the aspect ratio is varied, the velocity field is shown in Fig. 4 in a unified way. After the normalization the flow fields become all similar regardless of the flow speed or the probe absolute position in the canyon. However, the effect of the canyon width is not negligible. Some features are worth to mention: for the canyon \(d=4h\) (first row in Fig. 4 ‘matrix’) the lowest flow speed region (\(0 < U/U_\infty < 0.1\)) is found as expected close to the lee wall, extending to region between \(x/d = 0.375\) and \(z/h = 0.5\). The second lowest flow speed region (\(0.1 < U/U_\infty < 0.2\)) also presents similar contours for the three flow speed tested. In general, the flow contours are also similar for a given canyon width. As the canyon becomes wider, the region of the lowest speed tends to decrease. Note that the typical circulation pattern is not seen in these figures because we are dealing with a effective velocity that brings information of both horizontal and vertical components (cf. Eq. 3). The standard deviation field (Fig. 5) presents the greatest values around \(z/h = 1\) and downstream of the middle of the canyon for all cases. However, some particular features are seen for each canyon width. For canyon \(4h\) (Fig. 5a–c), the STD increases as the free flow speed (\(U_\infty \)) increases (brighter core). It is interesting to note that, even though STD values are enhanced for higher speeds, the pattern of contour lines does not suffer significant changes. As the canyon aspect ratio is increased the core of highest STD tends to be displaced toward the canyon center.

Fig. 4
figure 4

Flow speed field of hot-wire measurements. Variation in the aspect ratio for a given speed is in the mosaic rows and mosaic columns correspond to the variation in the flow speed for a given canyon width

Full size image
Fig. 5
figure 5

The same as Fig. 4 for the dimensionless standard deviation [\(\sigma _u(z)/U_\infty \)]

Full size image

3.2 Flow parameterization

It has been usual to normalize \(U(z)\) by the flow speed at the canopy top height, that is, \(U(z)/U(h)\) [12, 25]. Kastner-Klein et al. [12], for example, used the canopy top as normalization height because of the needs of comparing laboratory results with field observations, often taken at canopy height. However, they pointed out that a divergence of \(U(h)\) values in their measurements was the main cause of the scattering observed on the mean flow velocity profiles. This suggests that perhaps the canopy height is not a suitable parameter for normalizing flow profiles. In fact, in the present study the normalization by the flow speed at the highest level (reference level = \(2.5h\), also called here by \(U_\infty \)) has shown to be more fruitful. With this procedure, the spatially averaged curves over all position for a given aspect ratio collapse onto a single curve, showing not only that the normalization chosen is appropriated, but also that a general behavior arise from it (Fig. 6a–c).

Fig. 6
figure 6

Profiles of the position-averaged speed and standard deviation (disposed by rows) for each aspect ratio tested (disposed by columns). The dimensionless velocity defect \(\left(\frac{U_\infty - U_{\min }}{U_\infty } = 0.8\right)\) and the dimensionless STD peak \(\left(\frac{\sigma _u}{U_\infty }|_{\max } = 0.15\right)\) are the same for all aspect ratios

Full size image

In Fig. 6 we present spatial mean values of the flow speed and standard deviation. It becomes clear that the normalization by the free flow speed, \(U_\infty \), is more useful for obtaining empirical formulas than the normalization by the flow speed at canopy height, \(U(h)\), once a more regular behavior is observed. Flow speed profiles for each canyon width differ only below \(z/h=0.5\), the highest turbulence level, from where a more pronounced deflection toward greater speeds is observed for increasing aspect ratios. If we define a dimensionless velocity defect as \(\frac{U_\infty - U_{\min }}{U_\infty }\), one gets \(\sim \)0.8 for all aspect ratios. A similar behavior is also found with respect to the standard deviation. In fact, the \(\sigma _u\)-profiles are all similar with a peak value of approximately 0.15 at \(z/h = 1\) for all flow regimes. This means that the ratio of standard deviation to the free flow speed (\(\sigma _u/U_\infty \)) is not dependent on the flow regime, but it is governed only by the canyon aspect ratio. Moreover, the \(\sigma _u/U_\infty \) peak value is not even affected by the aspect ratio.

For parameterizing the speed profiles instead of using a multi-valued function, for example, an exponential describing the flow speed within the canyon and a logarithm above, we have adopted a single-valued function suggested by the speed profile shape. In the case of canyon \(8h\) the function \(\frac{U}{U_\infty } = A + B \arctan \bigl (C \frac{z}{h} + D\bigr )\) showed useful. This would also be consistent with the finds of [14], but it cannot reproduce very well the other two aspect ratios (canyons 4 and \(6h\)) because a ‘turnover’ below \(0.5h\). The difference in the profile shapes is that in [14] a block mesh was employed to simulate the urban landscape while in this work we employed a single canyon. The sheltering of the lee wall gives arise to the ‘turnovers’ of speed and standard deviation profiles. Another suggestion based on the overall profile shape is

$$\begin{aligned} \frac{U}{U_\infty } = A + B\exp \Bigl [-\frac{(z - z_c)^2}{2\sigma ^2}\Bigr ] , \end{aligned}$$
(5)

in which \(z_c\) (dimensionless) is the Gaussian curve center and \(\sigma \) (dimensionless) its standard deviation. (Note that \(\sigma \) has no relation with \(\sigma _u\), the velocity standard deviation). This function can describe quite accurately all cases of velocity profiles of this study. In Table 2 is shown values of the constants \(A\), \(B\), \(z_c\), and \(\sigma \) adjusted by means of a least-square fit. The Gaussian curve presents some limitation for the standard deviation profiles, especially for canyon \(4h\). Attempting to describe \(\sigma _u\) profiles from a detailed model would demand data beyond we have. Thus, we restrict ourselves to the use of the flux-gradient model [18]:

$$\begin{aligned} \overline{u^{\prime }w^{\prime }} = -\nu _e \frac{\partial U}{\partial z} . \end{aligned}$$
(6)

Assuming that the longitudinal and the vertical velocity fluctuations are approximately proportional, we can write \(\overline{u^{\prime }w^{\prime }}\approx -C\overline{u^{\prime }u^{\prime }}=-C\sigma _u^2\). A more precise formulation of this hypothesis would consider the recirculation flow within the canyon so that the fluctuations would be proportional to the eddy sizes, which in turn are on average of the order of the canyon dimensions, that is, \(w^{\prime }/u^{\prime } \sim h/d\), resulting

$$\begin{aligned} \overline{u^{\prime }w^{\prime }}\approx -\frac{h}{d}\overline{u^{\prime }u^{\prime }}. \end{aligned}$$
(7)

The scaling analysis above is supported by laboratory data. For instance, in a wind tunnel experiment, in which several block arrangements were tested, [6] show that \(\sigma _u^2/U_\text{ Ref}^2\) versus \(z/\delta \) (\(\delta \) is the boundary layer height) presents almost the same behavior as \(\overline{u^{\prime }w^{\prime }}/U_\text{ Ref}^2\) versus \(z/\delta \) for all block arrangements studied. Their data are compatible with \(\sigma _u^2/\overline{u^{\prime }w^{\prime }}\) ranging from \(-3\) to \(-5\).

Table 2 Constants obtained from the least-square adjustment of the function \(A + B\exp \bigl [-\frac{(z - z_c)^2}{2\sigma ^2}\bigr ]\)
Full size table

Therefore, Eq. 6 can be be written as

$$\begin{aligned} \sigma _u^2 \approx \frac{d}{h}\nu _e\, \frac{\partial U}{\partial z}. \end{aligned}$$
(8)

By replacing \(U\) as in Eq.5 we obtain

$$\begin{aligned} \frac{\sigma _u}{U_\infty } \approx \sqrt{-\frac{d}{h}\frac{\nu _e}{U_\infty }\frac{z-z_c}{\sigma ^2}B\exp \Bigl [-\frac{(z - z_c)^2}{2\sigma ^2}\Bigr ]} . \end{aligned}$$
(9)

Note that the constant \(B\) is always negative (Table 2) and that this equation is not held for \(z/h<z_c\), so that the parameterization is supposed to work just down to \(z_c\).

The parameterized curves are shown in Fig. 6 as dashed lines. We have remained the same constant values of \(B\), \(z_c\), and \(\sigma \) presented in Table 2 since these constants are from the fit of the speed profiles. The eddy viscosity was found to vary linearly with the aspect ratio as \(\nu _e = 0.027\frac{h}{d}\, \, \mathrm{m^2/s}\), so that the factor \(\frac{d}{h}\nu _e\) in Eq. 9 almost does not change. The single-valued function found here is not accurate enough for the standard deviation profile below \(z/h \approx z_c\). The ‘turnovers’ in canyon \(4h\) (\(z_c = 0.37\)) and \(6h\) (\(z_c = 0.24\)) cannot be explained by Eq. 9. The single term in Eq. 8 is probably the cause since the vertical velocity gradient becomes negative. A more robust model must include other terms derived from the fundamental equations. A complete description of the standard deviation profile was not really expected given the parameterization approximations. Even so, it seems to be appropriate to describe the observations at least down to \(z/h=z_c\). Besides the parameterization approximations, errors can also be attributed to the measuring procedure. As the flow becomes more and more bi-dimensional as it closes the canyon floor, the error in determining the \(U\) increases. We remind that HWA presents pitch sensitivity, and this certainly affects the measurement accuracy, especially in highly turbulent flow [\(\sigma _u/U \ge 0.35\), see Fig. 3c] as reported by [26]. Indeed this is the case for measurements below the canyon half-height.

4 Concluding remarks

In this paper we presented wind tunnel results of a flow past an urban canyon model of different aspect ratios (1/4, 1/6, and 1/8) and flow speeds (2, 5, and 10 m/s). A single-directional hot-wire anemometer was deployed to obtain profiles at several position across the canyon model.

Fields of flow speed and standard deviation, and turbulence intensity present similar patterns. When they are written as dimensionless variable no significant change with the aspect ratio or the free flow speed was observed. Therefore, dimensionless flow profiles are all similar, making the determination of the aerodynamic parameters \(u_*\), \(z_0\), and \(d_0\) more robust. Non-linear fits of flow speed profiles were obtained after a suitable choice of the initial value of \(d_0\), for which all aerodynamic parameters converge. The standard deviation profile reveals four flow regions: free flow, wake flow, well developed recirculation, and wall shear flow. The regular way in which the flow speed and the standard deviation respond to the free flow speed suggested a normalization for which all profiles collapse onto a single dimensionless profile that depends only on the canyon aspect ratio. The quantitative features found are:

  • for the aspect ratio of 1/4 dimensionless speed profiles present a minimum of about 0.2 at \(z/h\approx 0.5\). It is clear that the minimum occurs only for aspect ratios above 1/6;

  • the dimensionless velocity defect was found to be the same for all aspect ratios (\(\frac{U_\infty - U_{\min }}{U_\infty } = 0.8\));

  • the dimensionless standard deviation is independent of the flow speed and presents a peak (\(\frac{\sigma _u}{U_\infty }|_{\max } = 0.15\)) around \(z/h = 1.0\), which is independent of the aspect ratio as well. As the aspect ratio increase there is a trend of the dimensionless standard deviation profile to bend toward increasing values for \(z/h<0.5\), presenting a local minimum of 0.10 at \(z/h\approx 0.4\). It is not clear if this is really a characteristic pattern of dimensionless standard deviation: greater aspect ratios should be tested to check this feature;

  • turbulence intensity profiles follow similar behavior as the standard deviation with a peak value of about 0.5 at \(z/h=0.5\).

We used the free flow speed to normalize the flow speed and the standard deviation. The normalization criterion revealed to be important for obtaining convergent dimensionless profiles. The parameterization of standard deviation profiles via a flux-gradient model demonstrated to be reasonable in describing them quantitatively down to \(z/h=0.25 - 0.50\). Below this value a more detailed model would be needed. Also, the way the HWA acquire the velocities is an intrinsic source of error when the mean flow is not unidirectional.