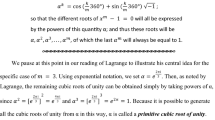Addressing the transition from secondary (high) school to university mathematics is a common challenge in educational systems worldwide. Relevant literature suggests that a common challenge university students may experience is confronting the significant change from a computational to a proof-based view of mathematics (Gueudet, 2008). Pre-service teachers (PSTs), as a university student group, experience additional challenges during their transition between high school and tertiary classrooms. As Felix Klein (1908/1939) described, PSTs experience “double discontinuity” during their forward transition from secondary to university mathematics and when transitioning back from university mathematics to school mathematics when returning to school as teachers. Winsløw and Grønbæk (2014) discussed three dimensions of “double discontinuity”: (a) the institutional context (university vs. high school), (b) the subject’s role within the institution (secondary student vs. university student vs. secondary mathematics teacher), and (c) the difference in mathematical content (scientific vs. elementary). Currently, the research literature has focused on the content dimension through a cognitive lens, offering evidence of teachers’ difficulties with connecting secondary and university mathematics (Wasserman et al., 2018; Zazkis & Leikin, 2010). To address this issue, teacher educators have developed teacher education materials that support teachers’ construction of specific mathematical ideas from an advanced and coherent standpoint (e.g., Carlson et al., 2021; Izsák et al., 2022; Moore et al., 2019; Thompson et al., 2019; Wasserman et al., 2022). However, not much emphasis has been placed on the other two dimensions of double discontinuity, including how PSTs interpret their experience of secondary-university mathematics transition, as well as how this experience is constructive toward their identity and professional development. To study these phenomena around PSTs’ shift from learning mathematics to acculturating as school mathematics teachers, it is necessary to adopt a sociocultural and situated perspective (Holland et al., 1998; Lave, 1991) to investigate how their experience of school–university transition, including the involved institutional context and the PSTs’ role in them, might influence their intended teaching practice.

Situated in Hong Kong, this study offers an added cultural perspective of framing the school–university transition and of observing the double discontinuity phenomenon in mathematics teacher education. Due to its colonial history, Hong Kong has been known for its unique characteristics of being where the Western and Asian cultures meet. According to Seah et al. (2017), Hong Kong students conveyed a mix of conceptions of mathematics learning, such as valuing not only explorations (e.g., problem-solving and learning through mistakes) and applications (e.g., connecting math to real life) but also effort (e.g., practicing with lots of questions) and recall (e.g., memorizing facts). Recently, a large-scale educational reform has taken place in Hong Kong, and a set of new mathematics curriculum standards were introduced to emphasize not only key learning areas (mathematics content) but also generic skills (e.g., problem-solving, critical thinking, communication), values, and attitudes (e.g., learning to learn; CDC, 2017). However, such curriculum reform has not fared well in light of a high-stake Hong Kong Diploma of Secondary Education (DSE) mathematics exam, which is largely procedural, algebraic, and fragmented in content rather than emphasizing problem-solving, representations, and connections (Ng et al., 2022). Local students have been under high pressure by the DSE exam, which is evidenced by their efforts in private tutoring after school to increase their scores. As reflected by Bray’s (2013) survey with 1646 secondary school students on private supplementary tutoring in Hong Kong (also called shadow education), 71.8% of sampled Form 6 (i.e., Grade 12) students received private tutoring, and on average, Form 6 students receive more than 2 hours of mathematics tutoring per week.

Against this sociocultural background, we are motivated to explore questions regarding how Hong Kong PSTs navigate their roles as both university students and prospective teachers of mathematics in the context wherein they themselves and their future students carry a mix of conceptions of learning mathematics. In this study, the PSTs have a dual role as double majors in mathematics and mathematics education. Thus, we are interested in how their roles and experiences figure under a mathematics curricula reform effort, including how they might position themselves to resolve the discontinuities they conceive in an exam-oriented education system in Hong Kong. We also seek to discover whether, behind their conceived discontinuities, any coherent experiences exist and, if so, how such experiences can explain the PSTs’ knowledge and positioning as future mathematics teachers.

Despite the phenomenon of double discontinuity having been well-investigated outside Hong Kong, we consider it significant to further understand how it manifests in the specific (i.e., East Asian) cultural context. This emphasis on culture will not only add to current research on double discontinuity, especially in terms of its contextual and identity dimensions, but also support the thesis of advancing research from underrepresented regions and cultural perspectives (Mesa & Wagner, 2019). It will further examine the specific cultural practice of mathematics (teacher) education by taking on a non-western-centric view of research while shedding light on the opportunities and struggles presented to PSTs with unique experiences of school–university transition during a time of educational reform.

In the following, we first elaborate on the concept of figured worlds and expand it to discuss PSTs’ school–tertiary transition. Then, we present our research questions regarding the PSTs’ figured worlds and how they may influence the PSTs’ knowledge construction and intended teaching practices. Then, we describe the methodology undertaken to establish the profiles of three PST participants. We present the results and conclude by discussing how the PSTs’ profiles contribute to further understandings of the problem of double discontinuity in Hong Kong, as well as the implications in mathematics teacher education.

1 Theoretical framework

We adopt a sociocultural and situated perspective that views learning as “a social phenomenon, constituted in the experienced, lived in world” (Lave, 1991, p. 64). This perspective highlights the interdependency of actor, activity, knowledge, and context. It considers learning to be inherently social and highly situated in practices with taken-for-granted ways of doing and acting (Lave, 1991). Below, we expand on the constructs of figured worlds and attitudes towards mathematics to discuss its relevance to our study.

1.1 Figured worlds

The concept of figured worlds, as proposed by the seminal work of Holland et al. (1998), is a “socially and culturally constructed realm of interpretation in which particular characters and actors are recognized, significance is assigned to certain acts, and particular outcomes are valued over others” (p. 52). The concept has influenced education research, including the work of Urrieta (2007), who explained that figured worlds are formed through classroom interactions, and in them, students figure out who they are in relation to those around them. As he claimed, students “can reconceptualize who they are, or shift who they understand themselves to be” (p. 120) as individuals or members of classroom communities.

According to Ma and Singer-Gabella (2011), the figured world of mathematics classrooms can shape students’ sense of self as mathematics learners through constructing joint meanings for various classroom activities. As Boaler and Greeno (2000) showed, many mathematics classroom environments described by students are dominated by rote learning and ritualized practices—that is, a figured world of “received knowing”—in which students consider their knowledge as primarily dependent upon and derived from an authoritative source other than themselves (p. 174). In contrast, students who participated in a figured world of mathematical talk and project-based learning identified mathematics learning as useful for solving problems outside of school, constructing a sense of “connected knowing” (Boaler, 1998).

The concept of figured worlds is significant to identity construction. The notion of self is always relative to how people act and engage in certain social characteristics and relationships, that is, placing themselves with others in contexts (Holland et al., 1998). For example, Hatt (2007) clarified the meaning of “smartness” by showing how smartness is a sociocultural product embodied through academic identity. This suggests that identity is constructed beyond the application of a label, such as “I am smart” or “I am incompetent,” but through positioning how people participate in their “worlds” and how they relate to others within and outside these worlds (Carlone et al., 2014).

In Hong Kong, traditional teaching practices dominate secondary mathematics classrooms. The local school culture features whole-class instruction and teacher-led activities, giving high priority to memorizing mathematical facts; in turn, students mainly learn by rote (Leung, 2001). Compensating for large class sizes and striving for efficiency, instruction focused on procedures featuring minimal student involvement (Lui & Leung, 2013). While Boaler and Greeno (2000) assert that the school context and teaching approach can significantly impact students’ future participation in mathematics learning, we extend this argument to the impact on PSTs’ intended future teaching practice as schoolteachers. Using figured worlds, we add to the descriptions of current school mathematics classroom practices from the perspectives of three Hong Kong PSTs and address how these PSTs come to understand their ability to “craft their future participation, or agency, in and across figured worlds” (Urrieta, 2007, p. 120) to teach school mathematics. We also expand the use of the notion of figured worlds to research the PSTs’ transition between educational environments (i.e., secondary mathematics vs. tertiary mathematics vs. mathematics education), looking into how they navigate between different figured worlds, including how they shape the sense of self within the sociocultural contexts of the figured worlds and in their intended future teaching.

1.2 Attitudes towards mathematics

In understanding the relationship among teachers’ experiences, dispositions, and practices, it is important to consider teacher knowledge as located in “the lived lives of teachers, in the values, beliefs, and deep convictions enacted in practice, in the social context that encloses such practices, and in the social relationship that enliven the teaching and learning encounter” (Britzman, 1991, p. 50). This is especially true for PSTs who are learning to teach yet have no classroom teaching experience to draw on. Their values, beliefs, and emotions come into play as they make decisions, and they act and reflect on the different purposes, methods, and meanings of teaching (Zembylas, 2005). Relevant to our interests in PSTs’ figured worlds of mathematics, we adopted Di Martino and Zan’s (2011) three-dimensional model of attitude towards mathematics that included (1) emotional disposition towards mathematics; (2) vision of mathematics; and (3) perceived competence in mathematics when describing their relationship with mathematics. We used this model to prompt our investigation and conduct our analysis into the PSTs’ figured worlds of mathematics as mathematics learners. We also chose the autobiographical approach from a sociocultural perspective to evoke events about the PSTs’ past that they identified as important to draw out the close relationships among the three dimensions.

2 Research questions

Informed by the literature, we undertook a case study methodology with two research objectives. Our first objective is to characterize three Hong Kong PSTs’ figured worlds of high school and tertiary classrooms as mathematics learners. Secondly, we aim to understand how those figured worlds influenced their knowledge construction and intended teaching practices from the perspective of future mathematics teachers. Extending from our case study participants to PSTs in Hong Kong, we pay attention to the union of activity and (content) knowledge of the PSTs and how it is constructive in shaping their values and identities associated with school mathematics teaching. Specifically, we pose the following research questions (RQs):

  • RQ1: What dominant practices, interactions, and taken-for-granted meanings populate Hong Kong PSTs’ figured worlds of secondary and tertiary mathematics classrooms, and how do they position themselves in their figured worlds?

  • RQ2:Through participation in their figured worlds and taking the position as secondary school mathematics teachers, (a) what mathematical connections do they make, and (b) what resources do they draw upon to orient their intended teaching practices in addressing the secondary–tertiary mathematics transition?

Regarding RQ2b, we narrow our focus of the broader transition problem to the PSTs’ ability to address secondary–tertiary mathematics transition in their intended teaching. We acknowledge that orienting their teaching to address the school–university transition is likely nontrivial for PSTs in many countries; however, we note that in the context of Hong Kong and many Asian education systems, preparing for postsecondary education is considered one of the ultimate goals of secondary education. Under such context, it is important for mathematics teachers to consider such an orientation, and we are, therefore, intentional in prompting them to do so in this study.

3 Methods

3.1 Participants and context

We recruited and examined the transition experiences of three undergraduate students enrolled in their third year of a five-year double-major (mathematics and mathematics education) Bachelor of Education program. We deem the dual learning experiences of students enrolled in this double-major program—currently the only 5-year B.Ed. program in secondary mathematics education offered in Hong Kong—suitable for the goal of this study, as the participants would have extensive learning experiences in both tertiary mathematics courses and mathematics education courses respectively. At the time of the study, the participants had taken at least four required university-level mathematics courses (advanced calculus, linear algebra, foundation of modern mathematics, and mathematical analysis). In particular, the course named Foundation of Modern Mathematics (MATH1050) was taken in the first year of study and covered basic concepts and techniques relevant to a proof-based view of mathematics. In addition, the participants had completed two mathematics education courses that covered the local mathematics curriculum with introductory theories and concepts on mathematics teaching and learning. Therefore, they were not only mathematics majors but also were beginning to construct their identities as prospective mathematics educators, which aligned with the study’s objective to examine issues relevant to “double discontinuity.”

In order to gain insights into Hong Kong PSTs’ experiences and knowledge, we recruited a purposive sample of three participants—William, Maria, and Sterling (pseudonyms)—from a cohort of 20 PSTs. We selected the three cases based on their genders, secondary and university mathematics academic achievement, and personal backgrounds (local or immigrant) so that they represent a suitable variety of backgrounds in and attitudes towards mathematics.

3.2 Research procedures

Adopting a semi-structured interview and narrative inquiry approach, the interviewers (first and second authors) engaged in dialogues with each participant individually to facilitate their reflection on their transition into university mathematics as students (first interview) and discussion about their intended teaching as mathematics educators (second interview). One of the interviewers (the second author) had established relationships with the participants as a faculty member teaching in the program. In addition to taking field notes and videotaping all interview sessions, the research team collected the PSTs’ written artifacts generated from the interview sessions.

First interview and post-interview task

As mentioned, we adopted Di Martino and Zan’s (2011) three-dimensional model for attitude to prompt the participants to reflect on their experiences and attitudes in school and tertiary mathematics, including significant aspects of their learning and transitions, such as their MATH1050 studies (see Supplementary Material for a detailed interview protocol). The first set of interviews each lasted approximately 1.5 h.

Upon completion of the first interview, we asked each participant to complete a post-interview task in their own time. The task invited the participants to design one or a series of lessons that would address the school–university discontinuity in some ways. We asked them to create a lesson plan electronically, where they could write down any main ideas, instructional goals, task sequences, and mathematical examples. They did not need to implement the lesson in real classrooms but only to discuss their rationale in the second interview. We encouraged them to be creative and to have the freedom to choose what to teach (including content outside the extant school curriculum) and how to teach. This task was meant to stimulate their thinking regarding what content to address and how they might address the secondary–tertiary transition as a mathematics teacher, through which we could examine how their figured worlds of mathematics learning might influence their thinking. We note that although we prompt the PSTs to create a hypothetical, non-conventional lesson, we did not anticipate them as unrealistic for implementation in real classrooms. There are occasions where these lessons could be implemented in Hong Kong, such as shadow education programs (Bray, 2013) and other after-school programs. Indeed, the PSTs did position themselves as the teacher who would implement the lessons to benefit their students and could describe a context in which these lessons could be implemented (e.g., a transition course occurring after school and before college entrance).

Second interview

The second interview consisted of two activities. Firstly, we followed up on the post-interview task by asking each participant to describe their lesson plans and design rationales. We focused the interview questions on (1) how the topic and concepts were chosen, (2) their relevant learning experiences that influenced their design, and (3) why they thought the lesson would be beneficial for their students’ transition (see Supplementary Material for a full list of questions). When asking these questions, we paid particular attention to the PSTs’ responses that reflected their figured worlds as revealed in the first interview, and we prompted for explanation to identify the coherency between their lesson design and their personal transitioning experience. The second interview lasted about 2.5 h.

In the second activity, we asked questions to engender discussion on a specific mathematical topic—inverse function. We were interested in what meanings the PSTs held at both university and secondary levels and whether (and how) their education on inverse functions at the university level had enabled a reconceptualization of related ideas from their high school curricula. By using a specific mathematical context, we aimed to understand what mathematical connections (or lack thereof) the PSTs could make and how they operationalized their attitudes about mathematics and mathematics teaching so as to confirm the figured worlds they reported in the first interview.

We chose inverse function because of two reasons. First, inverse function is present in both secondary and tertiary mathematics curricula, and extant literature has revealed individuals’ diverse meanings for inverse function in both contexts (e.g., Kontorovich, 2017; Paoletti, 2020; Paoletti et al., 2018; Wilson et al., 2016; Zazkis & Kontorovich, 2016). We were interested in whether and how the PSTs could make conceptual connections across the two contexts, especially whether and how their university learning supported such connections. Second and relatedly, in examining the MATH 1050 course materials, we observed that the instructor used non-conventional representations of inverse functions and graphs. A common technique for determining the analytical form of an inverse function is the action of switching the input and output variables of the original function and solving for the dependent variable (also called switching-and-solving). This approach maintains the convention that \(x\) is the input and \(y\) is the output of both functions. Accordingly, due to the same naming of variables of both functions, some writers of curricular materials present graphs of both functions in the same coordinate plane (\(x\) labeled on the horizontal axis and \(y\) labeled on the vertical axis), while in fact, the \(x\) (or \(y\)) does not correspond to the same quantity regarding the two functions.

In contrast to this approach, the MATH 1050 instructor represented an inverse graph by labeling \(y\) on the horizontal axis (Fig. 1). This alternative representation of the inverse graph ensures the two variables of a function and its inverse are consistent, and therefore, the two functions convey equivalent relationships of paired quantities in context (Paoletti, 2020; Paoletti et al., 2018; Wilson et al., 2016). In the interview, we used a series of tasks, prompts, and questions (see Supplementary Material) to gain insights into the PSTs’ meanings for inverse function around this text material. We aimed to examine whether the non-conventional text had triggered meaningful reconstruction and transformation in their content knowledge and perhaps their reflection on relevant secondary concepts.

Fig. 1
figure 1

An excerpt of the MATH1050 course material (written by the course instructor) that introduces the method of finding the graph of an inverse function g (in red), given the graph of the original function f (in blue)

Full size image

3.3 Data analysis

The entire 12 h of video data were transcribed verbatim for data analysis. While reviewing the videos and transcripts, we identified episodes in which the participants narrated socially constructed ways of being, acting, and using language in secondary and tertiary mathematics classrooms. In accordance with the interview protocol, the participants took on positions as high school mathematics students, tertiary mathematics students, and mathematics PSTs. We did not treat these positions as mutually exclusive, understanding that multiple figured worlds were always at play. The three authors first took independent passes through watching the video episodes case-by-case and wrote analytical memos to document their observations and interpretations to generate participant profiles. Then, they met to examine the transcripts collectively to verify the patterns observed. This approach yielded possible figured worlds, positions, and mathematical meanings verified for each participant across the two interviews.

In response to RQ1, we operationalized figured worlds as Discourse (Gee, 1996), following the work of Gonsalves et al. (2019). By a Discourse, with a capital “D,” Gee (1996) refers to a socially accepted association among ways of being, acting, and using language at certain times and places, so as to assume particular “recognizable” identities. Guided by Discourse analysis (Gee, 1999), we examined how the PSTs assumed a recognizable identity, what and how practices were enacted, what significance and relationships were assigned to certain acts, and what kinds of knowledge were more valued than other knowledge in the PSTs’ description of their figured worlds of school and university mathematics. In addition, aiming to understand the PSTs’ positions in their figured worlds, we paid attention to the ways they used multiple materials, linguistic, and social resources to position themselves inside, outside, and peripherally in the classroom community. We also identified instances in which they described themselves as being socially identified by others or being offered positions that they had to accept, reject or negotiate, and make choices in response.

In response to RQ2, we focused our analysis on the second set of interviews. We first identified instances in which the participants explained the design rationale of their hypothetical transition lessons. Then, we reviewed these instances iteratively to identify common themes in their thinking. In doing so, we focused on how they shifted their positioning from mathematics learners to future mathematics teachers to envision their future teaching. Second, we focused on instances in which they made mathematical connections between secondary and tertiary mathematics, including moments when they discussed the mathematical examples in their lesson plans and when they responded to the tasks on inverse function. We iteratively interpreted the mathematical meanings and (or lack thereof) connections conveyed by their utterances, written artifacts, and other actions. Finally, we attended to how the participants’ design rationale and mathematical understandings related to their experiences in secondary and tertiary classrooms. This involved us examining instances across the two interviews to discern how each participant’s different figured worlds mutually influenced or explained each other, which reflected our goal of discerning the continuity and coherency of the PSTs’ experiences behind their experienced double discontinuity.

4 Results

We organize the results around the two research questions. We first narrate the three participants’ figured worlds and positioning from the mathematics learner’s perspective. Then, we discuss their knowledge and intended practices as future mathematics teachers.

4.1 Figured worlds and positioning as a mathematics learnerFootnote 1

The case of William

William positioned himself as one of the stronger mathematics students. He described his secondary school mathematics studies as boring and unstimulating. As he described the role of textbooks, “with the way [the teachers] teach, I didn’t really need them because I could simply read the textbook and learn it myself.” He explained that completing textbook exercises dominated his classroom learning and that he frequently worked ahead of the teacher’s lecture pace because his teacher had to cater to “weaker” students. By contrast, his peers with “lower ability” would not understand the content 90% of the time; they were generally more playful and talkative and did not take mathematics as seriously. William’s descriptions demonstrated his perceived differences in the abilities and characteristics between students who were strong and weak at mathematics in his figured world, and those abilities and characteristics were somewhat fixed.

William attributed his academic success not only to his mathematical competence but also to his ability to imitate as a “copycat” (i.e., copying the solution from one question to another, as if literally “moving symbols between pieces of paper”). He described the content as not intellectually challenging and “not needing to think,” and success could be achieved by “knowing and remembering” mathematical procedures. He critiqued this teaching approach for the lack of hands-on activities and the constraints of the paper-and-pencil medium. For example, when learning about 3D shapes, he would have preferred to learn about 3D shapes by manipulating with 3D visualizations of those shapes. This suggested that despite being a good “copycat,” William had envisioned a world of mathematics learning that could be “interesting and fun.” However, his envisioned world conflicted with his figured world of secondary mathematics, as he had to “resort to being a ‘copycat’ after all.” Therefore, William’s figured world of school mathematics was strongly associated with the practice of rote learning, which was an attribute of mathematical success.

In contrast, William used the metaphor of “burning brain,” as in “burning all your brain cells,” to depict his experience of studying tertiary mathematics. He described his suffering when working with definitions and theorems and applying them to construct proofs in MATH1050. Rather than “knowing and remembering” mathematical procedures, he described the necessity of “understanding what every single step meant” when working on proofs. While he found solving a proof to be intellectually rewarding, he did struggle to solve it, concluding that learning mathematics is “interesting but miserable” simultaneously. Considering himself as a B-range student in tertiary mathematics, William identified himself as not fully committed to “spending time” to understand or to extend his thinking to thrive in tertiary mathematics. He realized that those who obtained better grades did not necessarily have superior abilities but must put in much more effort than he had to prepare for exams. In summary, we argue that, during William’s school–university transition, he had shifted from positioning himself as a strong mathematics student to an average one, from enacting rote to conceptual learning, and from believing that individuals’ mathematical capabilities are fixed to believing that they can be improved by efforts.

The case of Maria

Maria, one of the few female students, was an immigrant student who moved to Hong Kong when she was in lower secondary. She positioned herself as having been an “above average” secondary mathematics student. She shared a vivid memory from her Grade 10 mathematics class, where her teacher called several students (including Maria) to the front of the class and identified them as the students he would nurture toward earning a high grade in their future DSE exam based on their grades in a recent test. She supposed her teacher intended to “motivate” the chosen students and “boost their confidence,” but she did not feel comfortable with this form of recognition. The teacher’s move to call out students caused Maria to consider school mathematics as a venue for competitions. She felt stressed and anxious about making mistakes that would jeopardize how others viewed her. This contributed to her identity work, as she was always conscious of her impression to others by maintaining high test scores.

The teacher’s move also implied to Maria that the goal of learning was to receive a high grade. In this context, drilling and memorizing had been the predominant learning modes since Grade 10. She repeatedly recalled having to “complete many questions” from multiple sources (textbooks, past DSE exams, and other materials by independent publishers). She admitted that she did not conceptually understand what she was doing when completing sets of questions “that weren’t much different at all.” Maria recalled her positive attitude toward mathematics in her junior grades, but it shifted during her senior grades when she was stressed by having the “responsibility” and “obligation” to perform well in the DSE exam. In summary, Maria attributed her secondary mathematics learning from an institutional perspective, where she assumed a sense of responsibility and felt pressure to perform better than others.

As Maria transitioned into tertiary mathematics, she realized the context was drastically different regarding a sense of “competition;” she no longer knew “how other people were doing” and realized she needed to “take care of her [own learning].” Maria said this was the most difficult aspect of her secondary–tertiary mathematics transition. However, she found it a “new and exciting” experience to learn proof and logic, enjoying proving that something is “absolutely true” and learning new techniques to do so. Identifying herself as “not so successful” in tertiary mathematics, she would advise her fellow students to “dig deep” and ask questions in pursuit of conceptual understanding. Maria’s figured world of university mathematics is characterized by students striving to overcome difficulties in understanding and appreciating the beauty of mathematics.

The case of Sterling

Sterling summarized his secondary mathematics studies as learning “a set of tools … to tackle a range of pre-defined mathematical problems.” He had strong memories of dedicating two to three hours daily outside of class to work on DSE exam problems. However, he did not use the word “drilling” negatively as William and Maria did; rather, he considered it a way that prompted him to think about the problems deeply. He described two kinds of exam questions: those pertaining to key steps or patterns to be observed and those deepening one’s mathematical thinking by revealing interesting mathematical relationships in the solution. In turn, Sterling constructed a figured world where learning secondary mathematics was about finding the meanings underlying exam-related problems and becoming more competent in solving them.

However, Sterling’s figured world of high school mathematics did not situate him with a “big picture” of when and why certain methods should be used until attending university (e.g., finding the right method of integrating a very complex function). Therefore, he enjoyed mathematics even more at the tertiary level. Contrasting his view of secondary mathematics that was exclusively contextualized in the DSE exam, his revised view was “about how to approach a problem in general.” He analogized learning mathematics as “putting a puzzle together” to convey his appreciation of the “beautiful,” “amazing,” and “powerful” world of mathematics. Like William and Maria, Sterling expressed a gap in his transition from secondary to tertiary mathematics in doing proofs but noted the gap could be filled by self-learning and practicing thinking thoroughly and conceptually. He realized his peers seemed to find MATH1050 “devastating,” but he positioned himself differently from his peers for both his emotional disposition and perceived competence in tertiary mathematics.

4.2 Knowledge and intended practices as a mathematics educator

Despite the distinctive figured worlds of the three PSTs, our analysis revealed four common themes about their knowledge and intended practices as future mathematics teachers: (1) including difficult but essential ideas, (2) going beyond procedural knowledge, (3) contextualizing tertiary mathematics in secondary contexts, and (4) reconstructing secondary ideas from a higher standpoint.

Including difficult but essential ideas

Echoing their prior descriptions that constructing and comprehending proofs was difficult during the transition, William, Sterling, and Maria commonly included proof and logic in their lesson plans. For example, Sterling designed a lesson to introduce the language of “if and only if” and the logical reasoning behind it, which he thought was lacking in the current secondary mathematics curriculum. Furthermore, he suggested that introducing these precursory concepts is essential, and they are simple enough that secondary students could understand:

I had great difficulty understanding ‘if and only if’ in my transition from secondary to university. As I mentioned earlier, I do not know why those two things are equivalent; namely, the idea that “if A, then B” and” “if B, then A” and the idea that A and B are true or false at the same time are equivalent. And then, I spent a lot of time trying to understand why this was true. And later, I realized that the source of the problem is that logical reasoning is not stressed in the secondary mathematics curriculum. (…) So, I think in this part, first, [the students can] know more about logic; second, this requires time to comprehend but is simple in essence, and I can introduce these ideas in the secondary curriculum. If they are going to study mathematics at university, they will understand those ideas more easily.

Similarly, Maria focused her lesson on the terminology of “if and only if” and the difference between “for any” and “there exist” and that between “and” and “or.” In William’s lesson, he used the Theorem of Division Algorithm to introduce the notions of existence and uniqueness (e.g., “there exists,” “unique”). William described his lesson as a “taste program” that sets the foundation for students’ university study; he also analogized his designed lesson as training Zaku Warriors to become stronger in foundational aspects so that his students could be prepared for more advanced aspects of mathematical work:

[MATH]1050 introduces many kinds of proofs, and many people are stuck in this course. So, I was thinking, if it is possible, teaching students some sense of constructing proofs, giving them examples, and letting them practice. It is like a baby-ness class that allows them to get familiar with these ideas. So, when they transition to 1050, they are not starting from zero; they have a foundation. Using the words of [instructor’s name blinded], he likes to say we are like Zaku Warriors but without the shield, and we will be beaten to death before starting to fly. I think if the students can take this transition course, they would have the shield so that they do not die that fast.

Positioning themselves as future mathematics teachers, the three PSTs had an intention to prepare their students with the essential skills, mindset, and language required to succeed in university mathematics courses so that they would struggle less in university courses.

William and Maria could also draw on their learning experiences to reflect on the gaps between secondary and university content. For example, Maria contrasted her proving experiences in high school and university, saying that high school proof tasks were primarily geometric proofs and required attention to details and measurements of the geometric diagrams, while university proofs required more logical reasoning and had a very different flow than high school proofs. She also recalled her struggles with identifying counterexamples to a proposition in university because her high school teachers “had never offered counterexamples but only examples.” Accordingly, Maria included relevant content in her lesson plan to address these gaps. These results suggested that the PSTs’ university learning had played a role in changing their views of mathematics and content knowledge. As Maria explained, she valued the efforts of introducing proofs in secondary curricula because “teaching proofs is for students to understand that mathematics is rigorous,” and she wanted them to understand that “mathematics is not all about numerical calculation.”

Going beyond procedural understanding

Echoing Maria’s comment, William and Sterling discussed their intention of going beyond teaching procedures and computation in a transition course. As Sterling said:

When I learned these topics, the way of thinking or of how to approach a problem was not emphasized. The teacher usually just demonstrated [a solution] directly. However, the core is the reason for solving the question in this way and why this method is used this time but another method next time.

Being critical about his high school teacher’s teaching focused on procedures, Sterling valued mathematical reasoning and problem-solving in secondary classrooms and considered it important to unpack the thinking behind a solution or a procedure. Regarding why teaching proofs could foster reasoning beyond being a “copycat,” William explained.

Proving always involves a lot of variation.… You must use your brain to think about which theorem you should use and then what the next step is. So, I do not think the [copycat] situation … would happen…memorizing proofs would not work. But I hope students can learn from the definitions, proofs, theorems, and the mindset of proving…Proving is more about logical reasoning. The method can be straightforward, and you can just put the definitions in there; “copying” is, indeed, sufficient for this step. However, if you do not use your brain to consider how to fill in the middle part and merely copy the theorems and do not know what results you can obtain by using which theorem, it is not going to work.

William argued that being a “copycat” would not sufficiently accommodate the variations entailed in proving. By introducing proofs in this transition course, William intended to foster students’ logical reasoning, explaining that such reasoning processes require “using your brain” to figure out a proof beyond memorizing and copying definitions and theorems.

Contextualizing tertiary mathematics in secondary contexts

The third theme that emerged from our analysis was associated with the PSTs’ efforts to balance introducing skills and terminologies essential for learning university mathematics and making them accessible to secondary students. In describing his lesson, William explained that he chose division as the topic because division and numerical calculations were accessible and manageable for most secondary students, saying, “they work with numbers every day at school, so I think their concept of numbers should not be weak. Therefore, I can teach them something deeper…So, I think focusing on numbers is a good starting point.” Likewise, Sterling expressed that he put much effort into finding the appropriate examples to illustrate the notion of if-and-only-of. He eventually chose the Pythagorean Theorem as the context because it is “the first theorem I learned in middle school, which is very easy to understand.” He further explained that “there is no need to teach new stuff,” and the primary goal was to use a simple context to teach something useful in the future. Both William and Sterling based their transition lessons within the framework of the secondary mathematics curriculum. Their focus was not on teaching new concepts but on nurturing the essential mathematical mentality required in university mathematics.

Reconstructing secondary ideas from a higher standpoint

Related to the previous theme but in the opposite direction, we observed the PSTs’ ability to view secondary ideas through the lens of university mathematics. For example, Sterling discussed the example of \({x}^{2}=2\): if \(x=\sqrt{2}\), then \({x}^{2}=2\) is always true; conversely, if a number \(x\) satisfies the equation \({x}^{2}=2\), x is not necessarily \(\sqrt{2}\). He considered that introducing the idea of if-and-only-if could caution students that reversing a true statement does not always produce a true statement, and therefore, proving the equivalence of two statements requires proving both directions to be true. This instance suggested Sterling could view a secondary example from the angle of logic and proof, suggesting he had reconstructed his understandings due to university study.

In contrast, our work with William and Maria suggested that PSTs’ university study sometimes might not transfer or contribute to an improved understanding of secondary content. When asked to explain the material shown in Fig. 1, William struggled to explain why the method of reflecting the blue graph along the line of \(y=x\) works. When asked whether the blue and red graphs are the same, William responded that they are different because one needs to look from \(x\) to \(y\) for the blue graph, which represents the relationship of \(x\) against \(y\), while the red graph represents the relationship of \(y\) against \(x\) which reads from \(y\) to \(x\). He further argued that this was as if the statement “I am my mother’s son” is different from “[my mother] is my mother”—although both statements speak to the relationship of the same pair of variables, one can view one variable in relation to the other and vice versa. William’s conception entailed a commitment to the convention of reading the quantity on the horizontal axis as an input and that on the vertical axis as an output of a function, which was a common practice in the high school curriculum. In responding to the same task, Maria considered the two graphs the same, but she denied that the red graph is a correct representation of the inverse function because an inverse function and its original should be different functions. William and Maria’s responses suggested they did not conceive the equivalent relationship between a function and its inverse as intended by the instructor; their understanding constructed at high schools persisted rather than being transformed by their university study. In comparison, we observed significant reorganization in Sterling’s knowledge about inverse functions during the session. After being prompted, he could conceive equivalence between a function and its inverse in terms of their graphs, symbolic representations, function machine metaphor, and the formal definition in set language.

Another evidence of William’s limited understanding of inverse function was his reserved opinion about the role of inverse function in the secondary curriculum, saying, “inverse is about solving equations. If you teach it as solving equations, it is relevant, but I cannot think of anything else…Inverse function can be an application of solving equations, I would say.” When asked if we could draw on the idea of inverse function to introduce logarithmic and exponential functions, William opined it was not a good option; he explained that students need to know what those functions are before introducing to them inverse as an application.

5 Discussion

Regarding RQ1, our results showed that the three PSTs narrated similar figured worlds of secondary mathematics that were consistent with the exam-driven culture, but they also conveyed differences in their attitude towards mathematics. In particular, regarding the activity of doing repetitive mathematics practices, William saw them as a way of succeeding in the game of exams (by “resorting to being a copycat”); Maria developed a negative attitude towards them, at times having “no clue at all” what she was doing; and Sterling interpreted them as a resource for advancing his mathematical knowledge. In terms of similarity, the participants commonly appreciated the “beauty” behind mathematical proofs despite comprehending the logic and language of proofs to be difficult. These results illuminated the multiple and complex ways identity and positioning could be developed during the school–university transition.

Regarding RQ2a, we have identified evidence that the PSTs could make connections between secondary and tertiary mathematics. Both William and Sterling could recontextualize university mathematics in secondary contexts and attempted to tailor their teaching to meet the knowledge base of secondary school students (e.g., use divisibility as a context for teaching proofs). In comparison, we found it less trivial for the PSTs to reorganize their understandings of secondary concepts from a higher standpoint. Only Sterling demonstrated his understanding of solving a quadratic equation as enriched through the lens of tertiary mathematics (i.e., if-and-only-if). We also considered his ability to make connections during the inverse function task to be nontrivial, which could be explained by his strong mathematical background in both secondary school and university and his persistence in seeking underlying meanings and relationships starting from his secondary studies.

In contrast to the case of Sterling, both Maria and William conveyed difficulties with constructing mathematical connections regarding the concept of inverse function, which echoes the persistent issue of the second discontinuity. William and Maria’s learning of inverse functions at the university level did not seem to support their reconceptualization of related school mathematical topics. William’s reserved opinion about teaching the inverse function at high school reflected his view of doing secondary mathematics as being a “copycat.” Although he attempted to resist the “copycat” practice in his teaching, his mathematical knowledge, which was a product of his school experiences, constrained him from making conceptual connections between university and school mathematics. This implies that the mathematical knowledge William constructed at school was likely not conceptually coherent with university mathematics and, therefore, did not necessitate or support his reorganization of that knowledge. Recall that all three PSTs commonly described their lacking the opportunity to experience and construct mathematical knowledge in conceptual, coherent, and meaningful ways. These findings imply the importance of improving the secondary curriculum so that students’ postsecondary learning is possible and sustained.

Regarding RQ2b, we found the PSTs’ figured worlds of secondary and postsecondary mathematics as learners influenced their intended teaching practices in multiple ways. Their learning experiences in secondary and tertiary mathematics classrooms became critical resources they reflected upon to envision their future mathematics teaching. They reflected on the gaps between secondary and university mathematical content (e.g., proof terminologies and techniques) and intended to respond to the discontinuity by teaching topics that resonated with their learning struggles as a mathematics learner. Meanwhile, they were mindful of situating advanced ideas in contexts accessible to secondary students. They also negotiated between traditional and proof-based views of mathematics teaching and grappled with different teaching paradigms in their professional learning. They were critical about their schoolteachers’ teaching and considered alternative approaches that would benefit their future students’ transitions (e.g., going beyond procedures and computation to teach logic, reasoning, and problem-solving). The PSTs’ resistance to the computation-oriented mathematical norms suggested that their university mathematics learning had transformed their views of mathematics and influenced their thinking about what should be taught in secondary classrooms and what kind of mathematics teacher they wanted to become.

These findings collectively revealed coherency in the PSTs’ experiences behind the issue of double discontinuity (which reflected our title, “seeing the continuity”). That is, the PSTs’ figured worlds of secondary and university mathematics had shaped and were explanatory for their figured worlds of mathematics education. We consider this a novel contribution to the extant literature on double discontinuity as prior researchers often framed discontinuity as a deficit—calling it an issue, a gap, or a struggle from an observer’s perspective—and as something hindering PSTs’ progress or learning. In addition to confirming the existence of double discontinuity, our work here characterized how the PSTs’ current identity, beliefs, and knowledge were formed and shaped by their past experiences, and thereby, their figured worlds of mathematics education were connected to their figured worlds of secondary and tertiary mathematics. Despite the struggles or discontinuities they experienced, the PSTs had sought ways to navigate between the figured worlds of school and tertiary mathematics and had the intention to transform their experienced discontinuity into productive practices and beliefs that would potentially make a difference in their students. These findings justified the affordances of adopting a sociocultural and affective perspective (including the framework of figured worlds) to interpret aspects of PSTs’ experiences, especially in revealing the positive consequences of the double discontinuity that are not necessarily visible when only cognitive factors are considered.

6 Conclusion, implications, and future directions

In conclusion, our findings shed light on the “double discontinuity” faced by PSTs from a situated and sociocultural perspective. This was evident by the differences between the PSTs’ figured worlds of secondary and university mathematics—the first discontinuity, and their difficulties with reconceptualizing high school mathematics based on their university learning—the second discontinuity. Meanwhile, we found that the PSTs’ experiences across the two contexts were coherent (as opposed to “discontinued”) in certain ways. Their experience of procedural and exam-oriented school curricula continued to constrain their ability to reconceptualize school mathematical concepts. More importantly, the double discontinuity became a critical resource that shaped the PSTs’ thinking about mathematics teaching, on which they capitalized to transition to their new role. As informed by the results, we suggest teacher educators’ account for teachers’ prior learning experiences and support them in reflecting on and leveraging those experiences to inform their teaching practices.

We note that one limitation of this study lies in the small number of cases we focused on. We acknowledge that these three PSTs’ experiences might not generalize to other PSTs in Hong Kong or other countries, but the ways they navigated between the figured worlds of university and school mathematics were likely not unique, and future research can continue to test our findings in broader educational contexts. Additionally, more research is called for in the following areas: (1) adopting other qualitative methodologies (e.g., coding and phenomenography) to investigate and generate a bigger picture of the different secondary–tertiary transition experiences held by PSTs in specific cultural contexts; (2) developing a culturally relevant understanding of the phenomenon of “double discontinuity;” (3) studying the role of teacher education programs and interventions on (re-)conceptualizing PSTs’ figured worlds of school mathematics; (4) examining teachers’ (re-)construction of mathematical content knowledge through negotiating their experiences and identities as learners through participating in various figured worlds of mathematics.