1 Introduction

Promoting students’ mathematical creativity is encouraged by several mathematics educators and researchers who have also described the types of tasks that may occasion mathematical creativity in the classroom (Silver, 1997; Tabach & Friedlander, 2013). Yet, in the classroom, it is the teacher who ultimately decides which tasks to implement, a decision that is based not only on knowledge and beliefs, but also on underlying values. In a previous study, I investigated teachers’ knowledge and beliefs related to tasks that may occasion mathematical creativity (Levenson, 2013). Specifically, the findings described task features and cognitive demands noticed by participants when describing a task they believed could occasion mathematical creativity. In that study, the teachers had no formal education regarding mathematical creativity, and values were not investigated.

Values are often implicit, and thus a challenge to explore, but they can surface when decisions must be made (Bishop, 2012). In the current study, participants were teachers who had some familiarity and experience with mathematical creativity in educational settings. To elicit values, they were asked to choose one task from among three tasks that could potentially occasion mathematical creativity in different ways, and state which task they believed had the most potential to occasion mathematical creativity. This is in line with researchers who claimed that it is not mere choice which elicits values, but choosing from alternatives after careful consideration that is inherent to the process of valuing (Raths et al., 1987). The aim of the current study is to investigate teachers’ values related to tasks when the aim is to occasion mathematical creativity in the classroom.

2 Classroom mathematical creativity

In education, we are less concerned with the creativity of a few eminent people (Big-C creativity) and more concerned with everyday creativity (little-c creativity, Kaufman & Beghetto, 2009). This latter type of creativity focuses on the “novel and personally meaningful interpretation of experiences, actions, and events” (Kaufman & Beghetto, 2009, p. 3). In this study, I define mathematical creativity as a disposition that promotes the ability to generate several solutions and solution paths, to change directions of focus, and to produce novel and original solutions. According to Silver (1997), this disposition can be fostered broadly in the general school population.

Generating many ideas, possibilities, and potential approaches to finding solutions to a problem is a mark of fluent thinking (Mann et al., 2017). When solving a mathematics problem, fluency is measured by the number of unduplicated, mathematically correct, and meaningful ideas generated for the problem. Changing focus, trying out different strategies, making use of different representations (e.g., algebraic and graphical representations), and connecting different branches of mathematics are signs of flexibility (Leikin, 2009). Flexibility may also mean overcoming fixation or breaking away from stereotypes (Haylock, 1997; Krutetskii, 1976). Measuring flexibility may be carried out by classifying students’ solutions into categories and then counting the number of categories with correct responses (Kim et al., 2004; Kwon et al., 2006), or by considering the number of different methods used to solve a problem (Leikin, 2009). Originality has been observed and measured by the level of insight and conventionality of a solution based on the learning history of the participants (Leikin, 2009) or it may be novel, in the sense that it is new to the student (Silver, 1997). Taken together, encouraging fluency, flexibility, and originality during mathematical activities can help dispel the notion among students that mathematics is about following rules, and that every problem has exactly one correct answer and one correct solution path.

Considering the centrality of mathematics tasks in the classroom, researchers have described task features and cognitive demands which can occasion mathematical creativity in the classroom. These task features include having many solutions, or multiple methods to reach one solution, or incorporating multiple representations (Kwon et al., 2006; Leikin, 2009). In addition, tasks that may be extended with further questions can also encourage mathematical creativity (Sheffield, 2009). In general, open tasks, which may be open-start (can be approached in different ways), open-ended (have multiple possible outcomes), or a combination thereof, are considered creativity promoting tasks (Klein & Leikin, 2020). Regarding cognitive demands, researchers encourage the use of tasks that entail non-imitative and non-algorithmic thinking (Lithner, 2008), or that require a new (for the learner) way of thinking (Silver, 1997). Tasks that encourage the learner to make connections between different mathematical topics or between mathematical and non-mathematical domains are said to encourage flexibility (Leikin, 2009). Generalization is another cognitive demand sometimes associated with promoting mathematical creativity (Haylock, 1987; Klein & Leikin, 2020). In other words, the higher the cognitive demand, the more likely creativity will emerge.

There is a tenuous relationship between task features and cognitive demands. For example, tasks that may be solved in multiple ways (a task feature) potentially lead to high cognitive demand if students are indeed encouraged to examine different solution paths (Henningsen & Stein, 1997). This in turn can lead to flexibility, an aspect of creativity. Yet, even when a task may be solved in different ways, teachers may lower the cognitive demand by requesting students to solve the task with a particular algorithm. The premise of this study is that if teachers choose a task because they value the fact that it has several solution paths, then they will at least attempt to implement it in such a way that it will lead to, for example, flexibility. Furthermore, mathematical tasks have multiple features and cognitive demands, and teachers must choose which aspects are of more value when aiming to occasion mathematical creativity. Values are discussed next.

3 Values

Over the years, researchers have defined values in different ways (e.g., Kluckhohn, 1951; Rokeach, 1973). Gathering several definitions, Schwartz and Bilsky (1987) found five common features of values definitions and formed their own definition, “Values are: (a) concepts or beliefs, (b) about desirable end states or behaviors, (c) that transcend specific situations, (d) guide selection or evaluation of behavior and events, and (e) are ordered by relative importance” (p. 551). More recently, Chin and Lin (2001) defined values as “personal preferences concerning individual’s standards for considering the importance or worthwhile of something for themselves to think and act” (p. 250, italics in original).

Within mathematics education, several reviews of the study of values were concerned with differentiating between beliefs and values (e.g., Atweh & Seah, 2008; Bishop et al., 2003; Hannula, 2012). DeBellis and Goldin (2006) stated that while beliefs involve attribution of some external truth to a set of propositions, values refer to “personal truths or commitments cherished by individuals. Values help motivate long-term choices and shorter-term priorities” (p. 135). Philipp (2007) stated that while people hold beliefs to be true or false with varying degrees of conviction, values come from the word ‘value,’ meaning the worth of something, and are thus desirable or undesirable. Values are generally context-free, while beliefs are context-dependent; values are more stable than beliefs (Seah, 2002).

In this study, I adopt the notion that values are associated with preference and choice, and that a person may hold many beliefs, but it is their values that determine decisions to be made (Bishop, 2012). Furthermore, in accordance with Seah (2018), this study views values as being both cognitive and affective in nature, where “the process and act of valuing invariably involve reasoning and thinking” (p. 563). Thus, in this study, I determine that an object of attention or an idea is of value when that object is scrutinized, compared to other related objects (or ideas), and held to be more important and more worthy than the others.

While values may surface, it does not mean that they are made explicit, either to an outsider observing actions or to the person making the decisions, posing a methodological challenge for researchers; some have investigated espoused values and others enacted values (Chan & Wong, 2019). Espoused values are the values we tell others we hold. At times, they may be values we want others to believe we hold (Lim & Kor, 2012). Enacted values are values that we practice. Previous studies investigated enacted values by observing classroom lessons. For example, Frade and Machado (2008) observed how a teacher encouraged discussions and debates, which the authors used to infer that the teachers value rationalism and openness.

In addition to individual values, there are social and institutional values. Social values are values shared by members of a community (Hannula, 2012), such as valuing the use of examples, resources, and multimodal representations during effective mathematics lessons (Seah, 2011). Institutional values are those found in official documents, such as national curricula guidelines (Hannula, 2012). In Israel, for example, where this study took place, the mandatory elementary school mathematics curriculum (Department of Education, 2006) specifically recommends having students solve arithmetic problems in their own way and to encourage creativity and a disposition that mathematics is not just about following rules. Thus, encouraging creativity may be said to be an institutional value specifically related to mathematics in the Israeli context. Yet, several studies found that national values may sometimes come in conflict with local educators’, teachers’, and parents’ values, and that even when values are accepted, they may be implemented in diverse ways (MacNab, 2000).

In the current study, the values examined were those enacted by participants when having to choose one mathematical task, among three, with the aim of occasioning mathematical creativity. Because participants did not actually have to implement those choices, this methodology is like those used in studies that engaged participants with hypothetical situations, where they were confronted with a dilemma and a choice had to be made (Chan & Wong, 2019). The research questions are the following: What task features and cognitive demands do teachers value when aiming to occasion mathematical creativity? Are some more valued than others? Do teachers value equally a task’s potential to elicit fluency, flexibility, and originality?

4 Method

4.1 Participants and setting

The setting for this study was an elective course entitled Creativity in Mathematics Education, attended by students working towards their master’s degree in mathematics education. There were 42 participants (labeled P1–P42), eight of whom had completed a first degree in mathematics or a mathematically rich field such as computer science and were concurrently studying towards their secondary mathematics teaching degree. Of the 34 practicing teachers, 26 were secondary teachers, and eight were elementary teachers with a mathematics specialty, meaning that they had taken extra mathematics courses during their professional training, beyond those of generalist teachers. As part of the graduate degree, both elementary and secondary teachers take advanced mathematics content courses. Teachers are also familiar with the mathematics curriculum and the mathematical content taught in different grades. The average years of mathematics teaching experience was six. None of the participants had previously participated in professional development related to creativity.

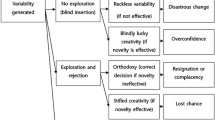
The course took place over a semester and consisted of 14 90-min lessons. The aim of the course was to familiarize participants with relevant theories concerning the development of creativity (e.g., Runco, 1996), thought processes of mathematicians as they create mathematics (Sriraman, 2009), and mathematical creativity manifested in school (Silver, 1997). Participants engaged with mathematical tasks that had some of the features and cognitive demands related to creativity promoting tasks described in the background, and discussed how fluency, flexibility, and originality may be assessed (see for example Fig. 1). In line with Shriki (2010), they worked in pairs to invent a new geometrical concept, examine its properties, and experience the creative work of a mathematician. Participants also implemented activities I had chosen from various studies (Kwon et al., 2006; Levav-Waynberg & Leikin, 2012; Silver & Cai, 2005; Tsamir et al., 2010) with their peers in the course, gaining experience in planning how to implement and evaluate the effectiveness of various tasks in occasioning mathematical creativity. Finally, the framework for analyzing tasks according to task features and cognitive demands from Levenson (2013) (details are given in the next section) was also introduced.

Fig. 1
figure 1

An example of a course activity

Full size image

The assignment investigated in this study was given during the second-to-last lesson. Participants were presented with three tasks, along with the sources of those tasks, and asked to evaluate the potential of each task to occasion mathematical creativity, state which task they believed had the most potential to occasion mathematical creativity, and write the reasons for their choice. They had 2 weeks to complete the assignment.

4.2 Choosing tasks

The method of this study was based on my definition for valued objects and ideas (see Section 3). Accordingly, the first step was to bring task features, cognitive demands, and aspects of creativity to participants’ attention, by having them analyze each of the tasks. This also served to elicit knowledge that participants had gained during the course, and separate that knowledge from values. The second step was to have participants scrutinize these task characteristics and compare them to each other, by having them choose which task had the most potential to occasion mathematical creativity and explain their choice. This prompted participants to compare task characteristics of one task to task characteristics of the other tasks. When explaining their choice, they signified which task characteristics and aspects of creativity were most important to them when the aim was to occasion mathematical creativity. For example, P39 explained why he chose Task 2, “Despite that Task 1 has the most potential to contribute to a student’s original thinking, Task 2 supports all three elements of creativity.” The use of the term ‘despite’ hints at a deliberate choosing of one task, while recognizing that other tasks also have potential.

I considered alternative research methods. I did not interview teachers directly and ask them which task features and/or cognitive demands were most important when promoting creativity, because then participants would have to answer on the spot without enough time to consider all options. Instead, participants were given 2 weeks to complete the assignment, and consider their responses. Likewise, classroom observations were not conducted because those values surface as teachers make quick decisions during a lesson, making it difficult to reflect on the underlying values which may have motivated decisions. Participants were not requested to plan a lesson involving one of the tasks, because when planning a lesson, values related to one issue (e.g., cognitive demands that may support creativity) may compete with other values not necessarily related to tasks (e.g., supporting equity in mathematics classrooms). According to my definition, an object is said to be valued when it is compared to other related objects, in this case comparing task features and cognitive demands to other task features and cognitive demands.

4.2.1 The tasks

The tasks used in this study were chosen for several reasons. First, they were among tasks chosen by teachers with a similar background, but who had no experience with mathematical creativity, as those they believed could occasion mathematical creativity (Levenson, 2013, 2015). This allowed me to investigate if some task features and cognitive demands not necessarily associated with mathematical creativity might still be valued even after participating in professional development. For example, in Levenson’s (2013) study, one participant wrote that a specific task could occasion mathematical creativity because it included several mini-tasks. Task 3 in the current study is such a task. Yet, having several mini-tasks is not a task feature associated with mathematical creativity. To elicit from participants which task features and cognitive demands they valued over others when aiming to occasion creativity, each of the three tasks had the potential to occasion mathematical creativity, but in different ways. For example, Task 1 had a higher cognitive demand than Task 2, but Task 2 had the potential to elicit more solutions (i.e., fluency) than Task 1. Task 3 allowed students to discover a new (for them) rule, in line with Silver’s (1997) vision of classroom mathematical creativity. Finally, to keep the assignment authentic, as well as meaningful, each of the tasks had several features which may give rise to several cognitive demands, as opposed to having each task associated with just one task feature and cognitive demand.

For each task presented below, I first note if that type of task was familiar to participants. Then, I present an a priori analysis carried out in accordance with Levenson’s (2013) framework of task features and cognitive demands previously mentioned by teachers when choosing tasks that may occasion creativity. Some task features and cognitive demands were noted in the background as those which support the occasioning of mathematical creativity (e.g., having several possible solutions or solution methods and non-algorithmic reasoning). Others are not necessarily associated with occasioning mathematical creativity, such as communication requirements (e.g., a demand for students to communicate and justify their procedures, Stein et al., 1996), the source of the task (e.g., classroom textbook, enrichment book, internet site), the length of the task (e.g., one main problem or several mini-tasks, Levenson, 2013), and surface characteristics (e.g., whether the task includes visual aids, manipulatives, or is set in a real-life context, Arbaugh & Brown, 2005).

Task one: Pages in a book

The first task was the following:

To number the pages of a bulky book, the printer used 2989 digits. How many pages does the book have? (Pólya, 1945)

This task was not a typical task participants engaged with during the course, nor was it in line with tasks suggested by researchers discussed in the course (e.g., Leikin, 2009). The task has one correct solution, and from previous experience with students, there are not many ways to solve the problem (task features). In a school context, it is not a standard task (task feature), and thus elicits from the solver new ways of thinking, organizing the information, and coming to some form of generalization, before finding the solution (cognitive demands). Regarding its potential for occasioning creativity, it encourages non-algorithmic thinking, offers no directions or strategies, and thus has the potential to promote flexibility and originality. The teacher in my previous study (Levenson, 2013) who originally suggested this task remarked that it was very challenging.

Task two: Find the area

This task (see Fig. 2) was the most like activities students engaged with and implemented during the course. Furthermore, it was taken from a fifth-grade book to investigate if teachers would be able to see the value of tasks found in their regular textbooks. It was chosen because it explicitly invites the solver to discuss various solutions, a feature associated with fluency, flexibility, and originality. The problem has one correct answer, but several solution paths, and an explicit request to discuss multiple solution methods (task features). The use of the term ‘discuss’ (a task feature), as opposed to ‘explain,’ signifies to the teacher that this task is meant to be discussed with the whole class, in turn leading to the generalization (a cognitive demand) that despite various ways to find the area, the area of the polygon stays the same.

Fig. 2
figure 2

Find the area (The Center for Educational Technology, 2006)

Full size image

Task three: Multiplying signed numbers

Like the second task, this task (see Fig. 3) was taken from a mathematics book, this time from seventh grade. Like the first task, it does not seem to encourage fluency, flexibility, and originality. Instead, in line with other studies of classroom mathematical creativity, it encourages students to come to a new, for them, multiplication rule (a cognitive demand) (Silver, 1997), and to experience the creative work of mathematicians (Shriki, 2010). It also includes different mathematical representations, a task feature associated with creativity (Leikin, 2009). In addition, while the instructions do not specifically ask students to search for different ways when answering the questions, there are several ways to view patterns (a cognitive demand) in the multiplication table (a task feature).

Fig. 3
figure 3

Multiplying signed numbers

Full size image

In summary, the three tasks represent different degrees and types of openness, with Task 1 having no hints at all and thus the most open at the start, Task 2 having some hints but plenty of room for going off in different directions (open-ended), and Task 3 being very directed, with a bit of openness when filling in the table. While all three tasks may occasion mathematical creativity in different ways, my hypothesis was that Task 2 would be chosen as having the most potential to occasion classroom mathematical creativity as it can be solved in many ways, leading to fluency, flexibility, and originality. Indeed, for those reasons, this is the task that I would have chosen. Yet, I was interested to see if participants would value task features and cognitive demands identified with the other two tasks, such as non-algorithmic thinking, or would choose a task because it is different than the norm, or because it would lead to new ways of thinking and possibly flexibility, but not necessarily to fluency or even originality.

4.3 Data analysis

Participants’ responses to both parts of the assignment were analyzed by a combination of directed and inductive content analysis (Patton, 2002). Direct analysis was carried out in accordance with Levenson’s (2013, 2015) framework for analyzing task features and cognitive demands. Inductive content analysis was used to review additional task features and cognitive demands that arose in the current study, but were not mentioned in Levenson’s previous studies. For example, several teachers in the current study mentioned that the first task did not offer any hints. I decided that “not having hints” could be considered a task feature, especially because it might be related to features of creativity such as allowing for flexible thinking. Tables 1 and 2 list the data categorization along with examples for each category. Some examples are “positive examples,” in that the participant identified that task feature or cognitive demand with the task, and some are “negative examples,” in that the participant specifically noted that it was not present or identified with that task. For example, regarding Task 1 and ‘multiple solution methods’ (TF5), P8 wrote: “The task invites many ways for solving it,” while P7 wrote: “This task does not have many ways to reach the solution.”

Table 1 Task features and examples
Full size table
Table 2 Cognitive demands and examples
Full size table

I performed the data analysis and invited a mathematics education researcher to follow the analytical protocol with data from eight participants, representing about a fifth of the whole data set. These participants were chosen because in my analysis, their data gave instances of all the elements in the analytical protocol. For these participants, I found 152 references to task features and cognitive demands, and the second researcher found 124 references. Of these, 93 were identical in that we both found similar evidence for the same feature. In general, the second researcher agreed that perhaps because I was more familiar with the data and the framework, I simply noticed more evidence than she did. There were a few cases where I marked a section as evidence of a task feature or cognitive demand, and the second researcher disagreed with my analysis. For example, regarding Task 2, P6 wrote, “If the instruction would change and it would be possible to use additional ways to calculate the area, and not just by using rectangles, then this task could occasion creativity.” I categorized this as TF8 (extending the task), but the second researcher claimed that P6 was envisioning a different task, and not the one presented. I argued that P6 was essentially saying how the task could be extended. We decided to label it as ‘can be extended’ (TF8) because P6 was acknowledging that the task could be extended and even offering a way to extend the task. There were 21 instances when the second researcher marked a section as evidence of some feature or cognitive demand and I did not, out of which I accepted six. There were six instances where we marked differently the same section of response. For example, regarding Task 1, P31 wrote, “I do not think students will understand what is being asked of them.” I marked this as evidence of CD7 (needs to understand the problem) and the second researcher marked it as TF7 (a non-standard task). We decided to code it CD7 as P31 specifically pertained to what the task was asking. All instances of disagreement were discussed, after which we reached consensus for the assigned code for each instance. Finally, as the terms fluency, flexibility, and originality were key concepts discussed during the course, specific mentions of these terms were also tallied.

To determine what participants valued in a task when aiming to occasion mathematical creativity, and in line with my definition of a valued object or idea, I compared what a participant noticed about the preferred task when it was first analyzed (what came to the attention of that participant), and what was important enough for that participant to mention at the point of choice. For example, P22 preferred Task 2. In her initial analysis, she identified ‘mathematical communication’ (TF2), ‘multiple solution methods’ (TF5), ‘leads to new knowledge’ (CD3), ‘encourages generalization’ (CD4), ‘challenge’ (CD6), fluency, and originality. However, when reasoning why this task had the most potential to occasion mathematical creativity, she pointed to ‘multiple solution methods’ (TF5), ‘leads to new knowledge’ (CD3), ‘challenge’ (CD6), and originality. I infer from this that although she identified ‘communication’ and ‘generalization’ with this task, they were not considered valuable by P22 as a means to occasion mathematical creativity. Furthermore, referring to aspects of mathematical creativity, I infer that P22 valued originality more than fluency. In another example, P34 stated, “Personally, I was most impressed with Silver’s (1997) definition of creativity and therefore, tasks that promote creativity are those that promote all of the measures [fluency, flexibility, and originality] that he proposed.” P34 stated that she was “impressed,” implying that she identified with or valued this definition. Indeed, in her initial analysis, in addition to identifying all three aspects of creativity, she mentioned ‘leads to new knowledge’ (CD3), ‘encourages generalization’ (CD4), and ‘can be extended’ (TF8). At the point of decision, she only mentioned ‘leads to new knowledge’ (CD3) along with fluency, flexibility, and originality. To summarize, as will be seen in the findings, participants were able to point out various task features and cognitive demands associated with each task according to what they had studied and experienced in the course. However, when it came to explaining their preferred task, they did not simply repeat their initial analysis, but pointed only to those task features, cognitive demands, and aspects of creativity that were most important to them when occasioning mathematical creativity; thus, there was nearly always a reduction in the mentions of those task features and cognitive demands.

5 Findings

Of the 42 participants, 17 declared Task 1 as having the most potential to occasion mathematical creativity, 22 declared Task 2, and six declared Task 3 as having the most potential. One participant claimed that all three could equally promote mathematical creativity and one claimed that both Tasks 1 and 2 were equally preferable.

The next sections present findings separately for those who preferred Task 1, Task 2, and Task 3. It analyzes the task features and cognitive demands, as well as specific mentions of fluency, flexibility, and originality, at two points: initial analysis of the task and when participants chose and explained their preference for that task.

5.1 Choosing Task 1

Frequencies of mentions for specific task features and cognitive demands are summed up in Tables 3 and 4 respectively. At the point of initial analysis are frequencies noted for all participants who mentioned these in any way, and in parenthesis are the frequencies of those who positively identified that feature with that task. For example, 12 of the 17 participants raised the issue of being able to solve a task in a number of ways (TF5), but only 10 stated that there were many ways to solve Task 1. At the point of making a choice, only four noted this feature when explaining why they preferred this task.

Table 3 Frequencies of initially mentioned (and positively identified) task features for those who preferred Task 1 (N = 17)
Full size table
Table 4 Frequencies of initially mentioned (and positively identified) cognitive demands for those who preferred Task 1 (N = 17)
Full size table

The most mentioned and positively identified task feature was ‘multiple solutions methods’ (TF5). This feature and being a ‘non-standard task’ (TF7) were the mostly highly noted features when choosing this task as preferred. Task 1 is indeed a non-standard task for participants in this study and their students, but it hardly has several solution methods. Yet, P26 wrote, “This problem has only one solution, but it probably has several ways of getting there (even though I only found one).” P35 wrote, “students can approach the problem in several ways.” Note that both participants did not necessarily find several solution methods, but believed that it could be either solved or at least approached in several ways. Of particular interest is the case of ‘surface characteristics’ (TF3). Although five participants positively acknowledged this feature (saying that the problem was placed in an everyday context), when it came to choosing a preferred task, it was not noted. I infer from this that those who preferred Task 1, ‘surface characteristics’ were not valued as a means to occasion mathematical creativity.

During the initial stage, the most identified cognitive demands for this task were ‘requires non-algorithmic thinking’ (CD2), ‘encourages generalization’ (CD4), and ‘challenge’ (CD6) (see Table 4). Yet, 'generalization' (CD4) was much less mentioned at the point of choice, indicating that even if the task encouraged generalization, for those who preferred this task, it was of less value than ‘challenge’ or ‘non-standard thinking’ when aiming to occasion creativity. Regarding challenge, because it is difficult to know how participants interpreted this notion, we look to see how they related it to other issues. P26 wrote, “Task 1 presents a non-standard and challenging task because in order to solve it you need to use non-algorithmic original thinking which does not appear in standard textbooks.” P26 specifically related ‘challenge’ to ‘non-algorithmic thinking’ and ‘non-standard tasks,’ and to originality. P30 also related ‘non-standard tasks’ to ‘challenge,’ “This is a challenging task, not like most found in regular schoolbooks.” P40 preferred Task 1, and directly related ‘challenge’ to an aspect of creativity, “Because it (Task 1) is challenging, it requires flexible thinking.”

Finally, more participants mentioned flexibility and originality at the point of choosing a task (see Table 5), than fluency. While six participants mentioned fluency in their initial analysis, only three positively identified fluency with this task, and only two reiterated this at the point of choice. For example, P6 specifically wrote “The task has potential to promote flexibility, but not fluency.” Interestingly, even more participants noted flexibility at the point of choice than in their initial analysis. Perhaps their initial analysis led to them realize how this task might promote flexible thinking.

Table 5 Frequencies of initially mentioned (and positively identified) fluency, flexibility, and originality, for those who preferred Task 1 (N = 17)
Full size table

5.2 Choosing Task 2

As can be seen in Table 6, among those who chose Task 2, there was a general trend, as with Task 1, that fewer task features and cognitive demands were mentioned at the point of choosing a preferred task than when initially analyzing the tasks. As with Task 1, ‘multiple solution methods’ (TF5) was the most mentioned feature, both initially and when choosing a task. However, unlike for Task 1, for Task 2, this makes sense. Task 2 has many solution paths, as well as explicit instructions to discuss the various solutions.

Table 6 Frequencies of initially mentioned (and positively identified) task features for those who preferred Task 2 (N = 22)
Full size table

Notice that only three task features were noted at the end stage, while six types of cognitive demands (see Table 7) were noted, inferring more agreement among participants regarding which features they valued, than which cognitive demands they valued. This suggests that if teachers choose a task because they value ‘multiple solutions methods,’ those teachers may implement the task in various ways, promoting different cognitive demands. As for Task 1, ‘challenge’ (CD6) was highly sought after. P4 explained his choice of Task 2 and wrote, “This task… has many solution paths, some even challenging, that few students will think of.” P4 associated ‘challenge’ with originality, in that if a solution path is challenging it will likely be discovered by only a few. An indirect relationship between ‘challenge’ and creativity may also be seen in P15’s statement, “The question is challenging, shakes up the student’s knowledge, and causes him to investigate additional options.” The reference to additional options suggests a relationship to the flexibility aspect of creativity.

Table 7 Frequencies of initially mentioned (and positively identified) cognitive demands for those who preferred Task 2 (N = 22)
Full size table

Mentions and identifications of fluency, flexibility, and originality at both stages were quite similar (see Table 8). Thus, it may be said that participants who chose Task 2 valued a task that could promote all three, and not only one or two recognized dimensions of mathematical creativity.

Table 8 Frequencies of initially mentioned (and positively identified) fluency, flexibility, and originality, for those who preferred Task 2 (N = 22)
Full size table

5.3 Choosing Task 3

Among those who chose Task 3 (see Tables 9 and 10), ‘multiple solution methods’ (TF5) once again was the most frequently mentioned feature at each stage. However, this time, ‘generalization’ (CD4) was the most frequently identified, as well as the most frequently mentioned cognitive demand for preferring this task. Recall that this task was chosen for the study because it was thought to occasion creativity by having students come up with new (for them) rules. Furthermore, both Tasks 1 and 2 also encouraged generalization, but especially among those who preferred Task 2, generalization was not valued. Perhaps for those who greatly valued generalization, more so than other cognitive demands, this task offered the most opportunities for encouraging generalization. This raises a parameter of values, not investigated in this study, regarding the degree to which values are held.

Table 9 Frequencies of initially mentioned (and positively identified) task features for those who preferred Task 3 (N = 6)
Full size table
Table 10 Frequencies of initially mentioned (and positively identified) cognitive demands for those who preferred Task 3 (N = 6)
Full size table

Regarding fluency, flexibility, and originality, two participants noticed and identified fluency with this task, and one participant noticed and identified flexibility and originality with this task. At the point of choosing, three participants each mentioned all three aspects of creativity.

6 Discussion

So, which task features and cognitive demands were of value to participants when aiming to occasion mathematical creativity? Teachers valued having ‘multiple solution paths’ (TF5), over other features, regardless of the task. That is, even for Tasks 1 and 3, which had fewer solution paths than Task 2, some participants still mentioned this as a reason for choosing those tasks. While it might be that those participants essentially preferred those tasks for other reasons, they still deliberately brought up the possibility of different solution paths for those tasks as well, even if they could not find them. Thus, we might say that having multiple solution paths was a valued feature when it came to occasioning mathematical creativity.

Recall that research read by participants in the course (e.g., Silver, 1997) discussed the importance of engaging students with tasks that have multiple solution paths, and that participants engaged with multiple-solution tasks during the course. We might therefore conclude that the value of engaging with multiple solution tasks had become a social value (Hannula, 2012). Although this result is specific to the context of this study, it adds to previous studies (e.g., Levenson, 2015) which exemplified how graduate courses that combine theory with practical experience may impact on teachers’ beliefs, and in this case values. It also shows how new knowledge can shift values. In my previous study of teachers’ naïve choices of tasks that have the potential to occasion mathematical creativity, teachers with similar backgrounds but with no formal knowledge of creativity claimed that ‘surface characteristics’ (TF3) can impact on a task’s potential to occasion creativity (Levenson, 2013). Participants in this study noted surface characteristics for Task 1, but did not mention it as a reason for choosing this task. It was not a value identified with mathematical creativity.

Regarding cognitive demands, ‘generalization’ (CD4) was initially highly identified with all three tasks. Interestingly, generalization is a cognitive demand generally associated with mathematics, and even thought to be the essence of mathematics (e.g., Schoenfeld, 1992; Steen, 1988). Yet, for those who preferred Tasks 1 and 2, it was mentioned much less at the choosing stage, indicating that for those participants, it was not a valued cognitive demand when aiming to promote mathematical creativity. Another cognitive demand associated in general with mathematics is ‘challenge’ (CD6). While some mathematics researchers (e.g., Sullivan et al., 2016) stress the need to offer students challenging tasks, and challenge may be generally associated with “mathematically powerful classrooms” (Schoenfeld, 2014, p. 407), researchers of creativity do not specifically focus on challenge. Yet, at the point of choosing, challenge was overall the most frequently mentioned cognitive demand. As challenge was barely discussed in the course, this finding has ramifications beyond the context of this study. It might be that participants valued challenge as an important aspect of mathematical activity, not necessarily because they associate it with creativity. Yet, as shown in the findings, several participants directly or indirectly related challenge to aspects of creativity such as flexibility and originality. Challenge was also a cognitive demand cited by teachers in my previous study of mathematics teachers’ naïve choices of creativity promoting tasks (Levenson, 2013). Thus, we might conclude that challenge is valued among teachers (i.e., it is a social value), regardless of their experience with creativity. This is in line with Seah (2002) who stated that values are generally context free and manifest themselves in consistent behavior. In the current study, however, participants’ statements specifically related challenge to other task features, cognitive demands, and to creativity, suggesting that knowledge and experience may contribute to a teacher’s recognition of how challenge might contribute to mathematical creativity.

Regarding fluency, flexibility, and originality, findings showed that some participants valued equally all three aspects of creativity, and (as we saw from P34) specifically looked for tasks that would support all three aspects. Others seemed to value flexibility and originality more than fluency, at times noting that one task (usually Task 1) did not promote fluency, but did promote flexibility and originality. This is in line with mathematics education researchers (e.g., Haylock, 1997; Lithner, 2008) who agree that flexibility and originality are of more value than fluency, especially in the context of problem solving.

A note about the context of this study. Because the assignment was given in the context of a course, it might be that teachers were espousing values that they believed the instructor of the course would want to see (Lim & Kor, 2012). This could also explain the frequent mentions of fluency, flexibility, and originality, specifically at the point of choice. For example, recall that P39 explained that he chose Task 2 because it supports all three elements of creativity. Perhaps, he was just quoting what he heard in the course. However, if having multiple solution paths was more of an espoused value than an enacted value, we would expect to find similar findings among cognitive demands. We would expect to find ‘requires non-algorithmic reasoning’ (CD2), ‘leads to new knowledge’ (CD3), and ‘making connections’ (CD5) to be frequently mentioned, because they were the most discussed and experienced during the course. In fact, ‘requires non-algorithmic reasoning’ (CD2) was highly identified and noted at the point of choice for Task 1, but not for the other tasks, while ‘leads to new knowledge’ (CD3) and ‘making connections’ (CD5) were noted less among all tasks. Furthermore, although ‘non-algorithmic reasoning’ was highly valued among those who preferred Task 1, this might be an outcome of valuing ‘non-standard tasks’ (TF7), also identified with Task 1. Thus, it seems less likely that participants were espousing values they believed the instructor would want to hear.

Also related to the context was the method specifically designed to explicate values from participants in a graduate course, separating knowledge possibly gained during the course, from values. In a sense, the first part of the study was about eliciting participants’ knowledge related to task features, cognitive demands, and aspects of mathematical creativity, and in the second part I inferred values by contrasting how frequently participants mentioned features in their own initial analysis to the frequency of those mentions when choosing tasks. This method could be adopted and adapted by teacher educators focusing on other areas of mathematics education.

Many questions remain. While mathematical tasks are important, teachers’ implementations of chosen tasks are equally important (Estrella et al., 2020). Values may manifest themselves in different ways as they are implemented in the classroom (MacNab, 2000). A limitation of this study is that although I attempted to have participants focus only on which task features and cognitive demands they valued when aiming to occasion mathematical creativity, participants might still have envisioned how these tasks would be implemented, implicitly considering other competing values. Thus, we might also ask how teachers’ experiences impact on what they value in a task when aiming to occasion mathematical creativity.

Although not the focus of this study, findings indicated that participants did relate some task features to other features and to cognitive demands, such as a task being non-standard and thus challenging. The relationship between valued task features and cognitive demands could be important. Tasks may have features that were specifically designed to elicit certain cognitive demands, and tasks may have features that were meant to promote various aspects of creativity. However, if a teacher values a task because, for example, it requires communication but does not value encouraging students to explore new strategies, then the classroom discussion might not lead to mathematical creativity. On the other hand, a teacher who values generalization, but also values multiple solutions, may encourage students to seek various ways to reach that generalization, even if it is not an apparent aim of the task (such as in Task 3). Further study is needed to explore how values are related.

We also saw a tentative relationship between the task features, cognitive demands, and aspects of creativity that teachers valued, and their chosen task. When aiming to occasion creativity, teachers who valued the cognitive demand of challenge more than generalization tended to choose the first task, while those who valued having several solution paths tended to choose the second task. What might this say about teachers’ values related to mathematical creativity? Do some teachers value mathematical creativity as a means for encouraging students to consider various strategies? Do they value mathematical creativity as a way to encourage non-algorithmic thinking? Further study might also investigate the task features and cognitive demands teachers value when choosing tasks to promote additional aims of mathematics education, such as supporting collaborative thinking. Might some of the values we saw in this study persist in a different context? In line with Cai and Garber (2012), beyond offering insights into teachers’ or students’ values, studies such as these raise awareness into the need for and challenges of studying values in mathematics education.