1 Introduction

Vocational mathematics: What’s that?

Isn’t is just a limited number of applications based on what students already have been taught in general education?

There’s no mathematics in work—it’s all computerised nowadays, isn’t it? Anyway, it’s just common sense as far as I can see.

How do they decide what to teach? They probably just go and ask a few managers—they would surely know what mathematics is needed by their workers.

This is a selection of typical comments I have heard over a working lifetime of vocational mathematics teaching and workplace mathematics research, emanating from people from all walks of life, including mathematics and other education academics and other vocational teachers. In part, they signify a general lack of awareness of this specialised but important subfield of mathematics education and, in part, a lack of awareness of the complexities of mathematics-containing work undertaken by workers at all skill levels in the current technological environment. Public media attention is generally focused on high-stakes mathematics assessments, nationally and internationally. As discussed below, attempts to map workplace observations onto current school mathematics curricula are likely to miss much of the tacit knowledge involved in work and its richness of context. The naive assumption of direct transfer from school to work also betrays a somewhat simplistic understanding of the relationship between formal mathematics education and work in general.

The articles in this special issue collectively illustrate just some of the complexities, tensions, and contradictions that underpin the field of vocational mathematics education. They are informed by workplace research in general and specifically in relation to people doing mathematics at work (FitzSimons, 2013). They are also informed by research in adult education, vocational education, and mathematics education, while having the potential to contribute to each of these subfields of education and to school, vocational, and higher education policy in general. Vocational mathematics education by definition implies an automatic engagement of mathematics education with the world beyond the institution of formal education. The term vocational is taken to represent paid skilled work in our globalised economy. However, notions of work, mathematics, and education are all in a state of continual evolution, influenced by and in turn influencing the social and cultural, economic and political, and technological developments of our time—as has been the case throughout history (Radford, 2003; Restivo, 1992; Salling Olesen, 2010). Vocational mathematics education encompasses preparation for, or continuing education in, mathematical facets of recognised skilled work, ranging from narrowly specified jobs to broader clusters of occupations to recognised professions. The context of constant change and the increasingly rapid evolution of work affect both the nature of work activity and its organisation, as well as the tools, materials, and the techniques needed.

The evolution of work throughout the ages has seen major changes in the way that vocational knowledge has been developed, communicated, and passed on. Starting from entirely contextualised forms of thinking and communication, and what might now be regarded as informal education, various forms of apprenticeship and formal systems of knowledge sharing in the Middle Ages, education for work has been formalised and increasingly institutionalised in general and vocational education over the last centuries. This institutionalisation is in order to accelerate learning (Salling Olesen, 2010). However, there is also a generally held assumption by policy makers, among others, that the transition from education to work is unproblematic and that formal qualifications alone are sufficient. Policy documents often invoke a naive use of the metaphor of transferable skills, particularly in relation to mathematics. In fact, much research, in this issue and elsewhere, is focused on this transition between the two different institutions of education and work, not least because they are completely different social and cultural activities, with different purposes, goals, and priorities and contrasting means of achieving these, and in very different contextual settings. This is not to overlook the fact that Education is an industry in itself in view of recent trends towards marketisation, particularly in the post-compulsory years (FitzSimons, 2002, 2011).

Another issue of concern to policy makers is the widely publicised perception of employers in some industries that there is a so-called skills gap, where novice workers graduating from formal education across the spectrum, or moving from other occupations, are thought to lack the necessary mathematical knowledge and skills to be “work-ready”. The problem is a complex political, social, and economic one, with responsibilities extending well beyond the education sector. Although it is true that many job applicants of all ages have left school with minimal mathematics qualifications, and lacking in deep conceptual understanding of the mathematics they encountered there, quite possibly accompanied by negative attitudes towards the subject, the issue is more complex and will be discussed further below. However, it needs to be acknowledged that, as identified by the 1982 Cockcroft Report, mathematical selection tests used by employers are not necessarily a valid indicator of the true situation. For example, the content of the tests may bear little resemblance to the work required to be undertaken by the successful applicant, and the tests may be set and marked by people without appropriate training or experience. (See Cockcroft, 1982, pp. 25–26, for further elaboration.) In this technological era, the focus may be on rote-learned procedural skills that are no longer needed nor used, but which are relatively straight forward to assess compared to the higher order mathematical skills that may be less visible but far more important.

In this commentary I will address notions of work, the need for innovation, and the role of workplace mathematics. I will then provide an overview of some of the complex issues that confront the subfield of vocational mathematics education with consequences for current and future workers, drawing in part on the work of Basil Bernstein. Finally, I will address the question of workplace research and offer some possible directions for future research, as well as implications for general mathematics education. Reflections on the articles included in this special issue will frame the discussion.

2 Work, innovation, and workplace mathematics

There is no single definition of work, just as there is no all-encompassing definition of workplace: Work can be carried out by people operating as single traders, employed in, or running small businesses, even as part of large multinational operations. Work to produce material or intellectual goods or services for humans and their environment, local to global and beyond, can be conducted in any physical location as well as virtually. In the context of globalisation and rapid social, economic, and environmental change, especially in relation to relentless technological advances, innovation has a key role to play. Workers are constantly having to learn things that do not currently exist and for which they have no prior experience. They need to produce and use (locally) new forms of knowledge or to recontextualise existing forms.

Ellström (2010) portrayed practice-based learning and innovation at work as a cyclical process of adaptive and developmental learning, driven by contradictions and tensions between the explicit, officially prescribed, work process and the implicit work process as subjectively interpreted and performed in practice on the basis of tacit knowledge. The innovation process “begins with questioning, a disturbance or the emergence of a problematic situation …[which] leads to routinized patterns … being broken and a search for new ways of dealing with the disturbance or the problematic situation at hand” (p. 36). Ellström explains how the interplay between these two operational dimensions (explicit and implicit) takes place in accordance with two complementary processes or logics. The logic of production has an emphasis on the mastering and reproduction of prescribed work processes, with “a focus on establishing and maintaining well learned and routinized action patterns. The aim is to reduce variation so that the task concerned can be performed rapidly and with a low percentage of error” (p. 33). The logic of development is mainly focused on the exploration and reconceptualisation (or reconstruction) of the operations that are performed in practice. This logic requires a “preparedness to question, reflect on and, if necessary, transform established practices in the organisation into new solutions or ways of working” (p. 34). In other words, creativity, an ability to improvise, is essential to finding solutions to unexpected problems that arise as part of normal operations in workplaces of all kinds. The logic of production is exemplified in the article by Coben and Weeks in the development and assessment of the mathematical knowledges and skills required of nurses responsible for administering drug dosages, where they are expected to routinely use these knowledges and skills rapidly, with the highest level of accuracy. Yet, nurses also need to be ready to question possible misunderstandings or conflicts in communication (Pozzi, Noss, & Hoyles, 1998). The logic of development is exemplified by Roth’s article where the electrical conduit benders need to find a solution and “break the rules”. Generalisable innovation relies on conceptual, theoretical knowledge (Muller, 2009), and this has implications for vocational mathematics curricula, as will be discussed below.

Many people from all walks of life, including employers, tend to assume that school mathematics, which they take as proxy for the discipline, is the only mathematics; people also commonly accept that the school-based methods which they personally experienced are the only correct ones (cf. Cockcroft, 1982). Apart from the fact that the mathematical activities undertaken on a daily basis across all occupations remain largely invisible due to the crystallisation of mathematics within technological artefacts (Williams & Wake, 2007a, 2007b), to most outsiders, including prospective and practising mathematics teachers (Nicol, 2002), the mathematics observed in many workplaces appears as low level. The hegemonic legacy of school education makes it difficult to appreciate that mathematics at work, and elsewhere, is completely embedded within a complex and sometimes contradictory set of parameters and constraints regulating the task at hand: for example, available staff, tools and artefacts; various forms of communication, online and offline; work organisation; legal requirements (including safety for workers themselves, also end users); relative priority or urgency; cost minimisation; and so on. Moreover, the answers really matter, mistakes are costly, and meaning is paramount, especially with respect to reasonableness and feasibility of solutions.

When school leavers in the industrialised world eventually enter the world of work, they are likely to find themselves in far less predictable circumstances, with people asking them questions involving mathematical thinking, often requiring urgent decisions. They may be asked to justify and explain their thinking, whether it be in relation to costings, design, production, development, reliability, trouble shooting, repair, and so forth. They are also likely to be confronted with technology-driven programmes for manipulating and recording various quantities, statistically controlling production, storing and locating raw materials and finished goods, programming and machining or manufacturing objects—from the very small to the very large—in three dimensions, and so on (FitzSimons, 2013, 2014). All of these have real, practical inputs and outcomes, and structuring resources which offer contextual support to mathematical activity in the form of constraints and reasonableness of answers. Graphical and spreadsheet outputs in industry may bear little resemblance to the forms experienced in school (Williams & Wake, 2007a, 2007b; see also Wake, 2014). During and after acquiring the necessary qualifications for entry to work, novice workers need to learn how to adapt to the often tacit social and cultural organisation of their particular occupation and place of work. For many, this period of transition can be problematic as there are tensions and contradictions between the familiar student role and the anticipated worker role, often combined with a fledgling adult role. Articles by Bakker and Akkerman, Hahn, Roth, and by Wake focus on this issue of transition, but from several different theoretical perspectives as follows: boundary crossing, forms of rationality, subjectivity, and consequential transitions. In each case, the powerful influences at work have implications for the relative value placed by students on vocational mathematics knowledge.

As noted above, workplace problems are likely to require creative and innovative solutions. At the same time, the consequences of mistakes made by employees can have serious, if not fatal, consequences for humans and their environment, on a local or sometimes global level. In many occupations, workers are given increasing responsibility for decision-making according to their capabilities and experience. Over time, experienced workers may be required to train others while continuing with their own responsibilities. Many people operate their own businesses, or subcontract their labour to others, supplying their own transport, tools, and other materials, along with complying with legal requirements such as insurance and taxation (FitzSimons, 2014). In all of these, theoretical, conceptual mathematical knowledge as well as practical, contextual mathematical knowledge have critical roles to play. In order to provide a theoretical framework for the discussion of some of the issues facing vocational mathematics education, I turn, albeit briefly, to the work of Basil Bernstein.

3 The contribution of Basil Bernstein

In FitzSimons (2012), I drew on the work of Bernstein (2000) in terms of democracy and pedagogic rights, based on a case study which supported giving pharmaceutical manufacturing workers access to powerful theoretical knowledge. Bernstein used the concept of classification to describe and analyse the structure of formal education which generally isolates mathematics, including vocational mathematics in our case, from other curricular subjects. When the boundaries around the subject of mathematics are strong, there is little real interaction between mathematics and other subjects, even though well intentioned, but often naive, attempts may be made at relevance through the insertion of text conveying the simplified aspects of contextual settings into the pedagogy. In vocational mathematics education, context is crucial and attempts may be made to specifically link the physical or virtual knowledge objects with the mathematics, as in the case of articles by LaCroix and by Coben and Weeks; also by Bakker et al. This is in contrast to that of Roth, where the “magic circles” based on theoretical trigonometric knowledge appeared neither conceptually developed nor linked to the artefact actually used in work practice.

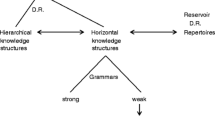
3.1 Vertical discourse/horizontal discourse

Muller (2009) remarked that actual occupational knowledges are a hybrid of conceptual, theoretical knowledge and contextual, procedural knowledge, and Wheelahan (2009) stressed the importance of vocational students having access to theoretical knowledge due to the increasing complexities of the rapidly changing technological and other conditions of work. Bernstein’s (2000) analysis of the structure of knowledge takes two forms: vertical discourse and horizontal discourse. Vertical discourse refers to disciplinary knowledge, such as formal academic mathematics, and is described as being theoretical, conceptual, and generalisable knowledge; coherent, explicit, and systematic, with strong boundaries between itself and other disciplines. As Wheelahan (2009) explained in relation to vocational education:

Theoretical knowledge is general, principled knowledge. It is organised as a vertical discourse which is, to a greater or lesser extent, hierarchically structured. It consists of ‘specialised symbolic structures of explicit knowledge’ in which the integration of knowledge occurs through the integration of meanings and not through relevance to specific contexts (Bernstein 2000, 160). Students need access to the disciplinary system of meaning as a condition for using knowledge in contextually specific applications. For example, students need access to mathematics as a condition for understanding and applying particular formulas, and if they are to use these formulas in different contexts. (p. 230)

Horizontal discourse refers to contextual knowledge, such as the mathematics used and developed in the workplace, which is generally weakly classified and submerged within the goals and objectives of the job. It is practical knowledge, informed by the accumulated mathematical knowledge and experience of workplace over the history of the occupation and the specific worksite, often undertaken in complex and/or contradictory contexts. It may be developed in response to an experienced need or a potential, imagined reality. It is specific, locally useful knowledge; a set of strategies which are local, segmentally organised, and likely to be “oral, local, context-dependent and specific, tacit, multi-layered, and contradictory across but not within contexts” (Bernstein, 2000, p. 157). Compared to school mathematics, there are weak boundaries between workplace mathematics and other workplace knowledges.

Vocational curricula are often strongly contested, with struggles between the perceived industry needs and the academic, social, and civic development of learners (Lauder, 2009). Muller (2009) considered the implications for the structure of vocational curricula, differentiating between those which have conceptual coherence and those which have contextual coherence.

Conceptual coherence curricula … presume a hierarchy of abstraction and conceptual difficulty. Contextual coherence curricula, on the other hand, are segmentally connected, where each segment is adequate to a context, sufficient to a purpose. Here, adequacy is externally guaranteed, often by a profession or professional statutory body, where in the former, adequacy is internally guaranteed.... Conceptual coherence curricula are regulated by adequacy to truth (logic); contextual coherence curricula by contextual adequacy, to a particular specialised form of practice. (p. 216)

The vocational areas addressed by Hahn, Coben and Weeks, Bakker et al., Bakker and Akkerman, and by Swanson and Williams more strongly emphasise conceptually coherent curricula while recontextualising these with meaningful work-related tasks, whereas the articles by LaCroix and by Roth suggest that contextual coherence is more important in these trade-based vocational education. What are the implications of this differentiation?

Following from the work of Bernstein (2000), it is important for vocational mathematics education to address both vertical and horizontal discourses to enable people to transcend their current workplace contexts. In other words, workers at all levels have the right to gain access to what Bernstein terms unthinkable knowledge (FitzSimons, 2002, 2012; see also FitzSimons, 2008), that is, access to alternative possibilities beyond those experienced on an everyday basis. For example, process manufacturing workers need to be able to comprehend the underlying principles (or big ideas) of quality assurance and the importance of their own contribution in routine measurements and other data collection. This is to enable the most valid readings to be obtained for effective process improvement; also because the workers may be held personally responsible for the results obtained. They should be able to engage meaningfully with outputs such as quality control [QC] charts or other statistical graphs, charts, and tables used as tools of management. Access to unthinkable knowledge, or knowledge which transcends that officially prescribed in curriculum documents, of course remains an argument for theoretical knowledge in formal education in general, but has specific salience in the case of vocational education, particularly vocational mathematics education, when the critical question of what counts as valuable knowledge is raised.

4 What is valued vocational mathematics knowledge and who should decide?

At stake are fundamental differences between knowledge that dominates in formal education and knowledge that dominates at work and the respective uses to which knowledge is put—assumptions based on the premise that the social worlds of work and education value knowledge and its use in different ways (Havnes, 2008). Curriculum and assessment frameworks such as the European Qualifications Framework (EQF) serve many political, economic, and social purposes, including the management of the increasing flows of labour in the EU, and the associated need for recognition of diverse qualifications from around the globe, or equivalences in non-certified skills or prior learning. These frameworks, in various ways, determine the possibilities for education pathways which are critical at the post-compulsory level. One crucial factor in vocational mathematics education is whether these pathways are potentially available to all learners or whether the lack of appropriate disciplinary mathematics and other related knowledges offered in lower level qualifications in fact prevents learners from gaining access to higher educational levels. This has implications for the possibility of promotion, either in the areas of management or more senior positions of responsibility, both of which demand more complex knowledge and skills. Hahn provides an illustration of business studies graduates progressing to Master’s level needing more sophisticated statistical knowledge, while Swanson and Williams discuss the example of people choosing to return to study in order to become mathematics teachers, and possibly moving to better paid work or working conditions than previously open to them. The laboratory technicians in articles by Bakker et al. and Bakker and Akkerman, and also the nurses in Coben and Weeks, where scientific reasoning is imperative as part of the repertoire of workers, appear to have vocational pathways open to them enabling them to progress to higher education should the need arise.

A report addressing quality issues in vocational education in the EU (Seyfried, 2007) included priorities such as improving the employability of the labour force, as well as offering a better access to vulnerable groups such as early school leavers, young unemployed people, long-term unemployed people, older people, handicapped people, migrants, and ethnic minorities. One of the stated objectives was to improve “basic skills in literacy and numeracy …” (p. 85). As FitzSimons (2011) observed, the dilemma is that

the conception of “basic skills in numeracy” is almost always taken for granted in documents, such as these—as if there is a well understood and shared agreement about what this means in practice—when this is far from the actual case. (p. 107)

There appears to be a tendency for many official documents to use terms such as basic mathematics without elaboration, on the assumption that there is a shared and unambiguous meaning. In my experience (e.g., FitzSimons, 2002, 2012), the term is likely to comprise arithmetic calculations, mainly the rational numbers, with a focus on pseudo-contextualised applications to measurement, while ignoring the three dimensional world of shape and space, conceptual understanding of the practicalities of quality control, and completely disregarding higher level mathematical skills of reasoning, argumentation, and so forth.

One component of Straehler-Pohl and Gellert’s (2013) three-dimensional model for connecting Bernstein’s concept of classification with classroom discourse drew on Chevallard’s (1999, cited in Straehler-Pohl & Gellert, 2013) Anthropological Theory of Didactics. In relation to types of mathematics problems, Chevallard identified two inseparable facets: (a) the practical (or know-how) level, focusing on problems and the techniques used to solve them; and (b) the discursive environment, including description, explanation, and justification, which constitutes a deeper theoretical level. As noted previously, work of all kinds can demand not only the first level of technique in specialised applications (horizontal discourse) but may also require the second, more highly classified, level of mathematical thinking (vertical discourse). In order to support vocational students to generate and use more powerful knowledge in solving unforeseen problems and in reasoning involving mathematical concepts, vocational mathematics discourse should address both aspects of mathematics, not just the first.

What might hinder the development of coherent conceptual mathematical knowledge which incorporates more than just mechanical skills, or so-called basic mathematics? For many aspiring and current workers, formal mathematics education has left them feeling alienated from the discipline through their inability to make sense of its abstract theoretical concepts and its seeming irrelevance to their current lives and prospective futures (FitzSimons & Godden, 2000). In my experience, they are most unlikely to consider positively any proposal that they should study more mathematics than is absolutely necessary for meeting the minimal qualification requirements.

In the vocational mathematics classroom, tensions are apparent (e.g., in the LaCroix and the Roth articles) between what the mathematics curriculum demands and the mathematics teachers say and do and what the trade/vocational teachers and the workers on-the-job say and do. These relate to authority and the valued uses of knowledge. Roth theorises the boundary crossing, the tensions, and the transition from student to worker in terms of subjectivity, although Swanson and Williams argue that the whole context of the activity of transition goes far beyond the individual. At the university level, Hahn described the three kinds of logic followed by Master’s students in reaction to her teaching experiment on statistical decision-making: (a) scientific (vertical discourse), (b) technical (unreflective rule following, as often found in school), and (c) pragmatic (what works best for novice workers). In the end, most students followed the pragmatic rationality, although a few made attempts at scientific rationality. “What works” (horizontal discourse) appears to be the most valued knowledge in many workplaces (especially trades) and their vocational education programmes where contextual learning plays a significant role. In the article by LaCroix, it appeared that any method was satisfactory as long as the answer was within acceptable limits; and in Roth’s article, trigonometry was taught in order to pass the formal assessment without serious attention to the theoretical underpinning knowledge. Even in professional vocational programmes such as business management, valued knowledge can be a source of tension. Hahn’s article well illustrates the tendencies of her students towards pragmatism, especially under the powerful influence of their ongoing work experience, including the transformation of their identities as workers rather than students (see also Wake, 2014, on identity formation). For vocational mathematics teachers such as Hahn, working in professions outside of the natural and life sciences, their role is made more difficult because their highly educated students do not immediately perceive the value of the disciplinary structure, and this meta-knowledge has to be developed. For teachers working in science-oriented vocations, such as those discussed by Bakker and Akkerman, Bakker et al., and by Coben and Weeks, the vertical discourse of mathematics is the main focus, reflecting its valued knowledge status which is generally accepted by students. However, serious attention must be paid to the horizontal discourse of context in that pragmatic, workable outcomes have to be achieved that are mathematically justifiable, especially in view of the possible tragic consequences of errors.

Given that (a) it cannot be assumed that all school leavers have developed strong theoretical skills and understandings in the discipline of mathematics; (b) many have had negative, and sometimes damaging, experiences of learning mathematics; and (c) the powerful forces of socialisation in many occupational areas eschew formality in favour of on-the-job pragmatism, the question arises: Is there justification for the apparent segregation of some vocational mathematics education programmes that, in practice, focus (almost) entirely on horizontal discourse at the expense of vertical discourse? Also, who should decide?

5 Tensions in vocational mathematics teaching

The question of who will teach vocational mathematics (including statistics) has been debated over many years across the institutional spectrum. There are arguments for staff specialising in the vertical discourse of mathematics and mathematics education on the grounds that they are more suitably qualified in theoretical mathematics and have expertise in specific pedagogical aspects such as pedagogical content knowledge. However, there are likely to be problems if mathematics specialists have no relevant industrial experience nor make any serious effort to comprehend the specific contexts, applications, and problems that students may be confronted with during their studies or after graduation (i.e., the horizontal discourse). On the other hand, teaching staff with relevant trade or professional experience are likely to have extensive contextual experience but limited mathematics subject matter knowledge and pedagogical content knowledge. They may be unable to comprehend mathematical learning difficulties and be limited in their mathematical pedagogic repertoire. The article by LaCroix raises a most interesting new dimension to this debate: Mathematically well-prepared teachers were available to assist students with difficulties, and few required assistance with school-based mathematical calculations. The students’ problems arose mostly from the fact that they were yet to experience the actual practical implementation in the trade classroom of the calculations they were required to perform. LaCroix concluded that they were limited by a lack of contextual knowledge of the trade-based objects and drew on Radford’s Theory of Knowledge Objectification to explain their difficulties. This theory may well be extended to explain the problems of vocational mathematics teachers who have no relevant industrial experience and little or no appreciation of the practical work that is likely to confront students as they begin work in the field, or are already confronting in apprenticeship modes, and suggests an important new avenue of research. The boundary crossing the work of Bakker et al., Bakker and Akkerman, Hahn, and of Coben and Weeks offers a critical area for research in mathematics teacher development. (See Akkerman & Baker, 2011 for an extensive review of boundary crossing as dialogic and a potential resource for professional and identity development.)

6 Assessment and technology

Along with curricular content, the question of assessment is critical, and results can serve many purposes, informing various stakeholders about the performance of individual students or cohorts, nationally and internationally; although not unproblematically, especially in the case of adult learners in the Project for the International Assessment of Adult Competencies (PIAAC) (Tsatsaroni & Evans, 2013). Assessment can be used formatively to assist teachers and students in overcoming difficulties or misconceptions. At present, assessment in vocational mathematics education appears to be under-researched and under-theorised. The contribution by Coben and Weeks, which drew on theories of authentic assessment and involved close collaboration between educators and a peak nursing body in the UK, offers a model for a wide range of occupations in its theoretical and practical aspects; in particular, the potential of electronic technologies to assist students, their teachers, and the industry in general to address the development of critical mathematical skills in meaningful ways with strong, meaningful contextual references to practice. In this significant facet of nurses’ work, Coben and Weeks, together with their extensive inter-disciplinary team, combined the vertical discourse of mathematics and horizontal discourse of authentic context to produce successful outcomes in ways that have eluded nursing educators who have used traditional textbook approaches. One strength of the project is that the technology-based approach opens up the potential for users in less developed countries to adapt the material for their own purposes under their own conditions.

Although initially expensive to develop, high quality educational technology has the potential to provide access to learners and teachers across time and space. Stacey and Wiliam (2013) identified five major ways that technology could change assessment practices: (a) improved item preparation and selection, including adaptive testing based upon on a student’s earlier responses; (b) more sophisticated item presentation which could modify the support required for successful completion of the task; (c) enhanced operation allowing students to engage in tasks in different ways while adhering to constraints, thus expanding authentic assessment possibilities; (d) unobtrusive collection, analysis, and reporting of evidence as well as automated diagnostic analysis of response patterns; and (e) the possibility of multi-dimensional models of student proficiency allowing detailed feedback to students and teachers. The articles by Bakker et al. and Bakker and Akkerman also demonstrate the close inter-relationship between technology as a workplace tool which vocational students need to learn to instrumentate and instrumentalise (Trouche, 2004) for optimal intelligent use, and technology as an educational tool which can isolate critical mathematical features from workplace practice and support students to develop skills and understanding with strong contextual reference, as in the article by Coben and Weeks. In scientific disciplines, where workers such as laboratory technicians will inevitably be confronted with constantly evolving technologies, it is important that they have access to powerful ways of knowing mathematics through the knowledge structures of the vertical discourse. Bakker and Akkerman remind us that mathematical and statistical modelling in these workplaces are far from the straightforward exercises seen in school, in that critical mathematical judgements need to be made that may ultimately concern people’s lives and potential users who are distant in time and space. At the same time, research demonstrates that the optimal mathematical answer is not necessarily the best, or even feasible, answer in practical situations (see, e.g., FitzSimons, 2013).

Havnes (2008) believes that generalisation beyond a given context requires variance across contexts in both the use and valuing of knowledge, and this becomes a resource for learning. He regards assessment in vocational education as a boundary object, involving students, teachers, and workplace supervisors, emphasising the confrontation of the institutional practices of work and of education especially in relation to knowledge use and knowledge valuing. From this perspective, as demonstrated by Bakker and Akkerman, and implicit in the article by Hahn, vocational mathematics assessment can be a useful means to communicate across boundaries in a two-way collaboration between education (students and their teachers) and industry personnel.

One of the goals stressed by many recent mathematics curriculum and assessment frameworks, and an important factor in innovation at work (Ellström, 2010), is creativity. Taking the notion of creativity as involving an activity which is intentional, imaginative, producing locally novel and valued outcomes, Askew (2013) observed that the inclusion of values represents a shift from the traditional view of creativity as an individual attribute to one which is fundamentally and unavoidably social. In terms of mathematics education, he noted that creativity is context-bound; that teachers need to disentangle creativity from content assessment; and that students be encouraged to play and take risks, accepting the inevitable failures or errors; and that they should be encouraged to develop critical judgement. Creativity assessment emphasis, according to Askew, should be formative, and teacher judgement should be supported by reference to a set of desired attributes such as mathematical accuracy, strength of justification, or mathematical elegance. In practice, creativity depends upon a combination of vertical and horizontal discourses. It requires a sound working knowledge of the context in order to perceive a need or to solve an unforeseen problem in an innovative manner, transforming existing knowledge or reconceptualising the problem resulting in a new way of working. As is the case for professional industrial mathematicians (e.g., Nakagawa & Yamamoto, 2013), there must be a respectful understanding of the perspectives of others from different disciplines and with different contextual knowledges in relation to concerns within and beyond the workplace. The mathematical accuracy, reasoning, and argumentation identified by Askew, drawn from the theoretically principled, structural knowledge of the vertical discourse of mathematics, can enable workers to transcend the contextually bound procedural knowledge that is also necessary but not sufficient to support creative, innovative ideas for products and strategies.

7 Why is workplace mathematics research important?

One major problem facing many governments around the globe is skill shortages in particular areas of industry. Research reports into education needs in mathematics, science, and technology commissioned by governments themselves, by industry or employer groups, by education and other trade unions, and by academies of science, all have the potential to inform policy on mathematics education. Many reports stress the need for the mathematics education community at all levels, especially at the post-compulsory level, to work collaboratively with strategic industrial partners in order to attract and maintain student interest in pursuing careers in these areas. The joint ICMI-ICIAM study, Educational interfaces between mathematics and industry (Damlamian, Rodrigues, & Sträßer, 2013), offers strong support for joint research, internships, and various forms of boundary crossing between academic mathematicians, applied mathematicians, industry representatives, mathematics teacher educators, vocational and school mathematics teachers, and their students. Many authors, including Lesh (2010), have criticised contemporary mathematics curricula for failing to engage with the world beyond the education system. Wake’s article addresses the specific issue of informing general mathematics curricula, based on his research experience of working with college students, involving them in making their own workplace observations. However, one major problem appears to be actually persuading significant decision makers in the mathematics education community that the exchange of knowledge between industry and education should be two-way, rather than the implicit one-way—from school to work—respectful collaboration as called for by industrial and academic mathematicians, Nakagawa and Yamamoto (2013), and by Wedege (2013).

LaCroix calls for more research into students’ subjective experiences in undertaking vocational mathematics education. However, it appears that little research, if any, has enquired into the relationship between an individual’s previous formal mathematics education and their current mathematical, or mathematics-containing, practices; that is, research that integrates work as a societal process, the mathematical (and other) knowledge required to do that job, and the individual’s subjective experiences as a learner of mathematics and a person doing a responsible job (Salling Olesen, 2008). Adults’ Mathematics: In Work and for School is a research project which aims at analysing and understanding adults’ mathematics-containing competences from this perspective, emphasising the two-way relationship between mathematics education and the workplace. Adopting a sociomathematical approach (Wedege, 2010), it addresses the societal context of knowing, learning, and teaching mathematics, with the intention of informing future mathematics curriculum and teaching. Building on this model, Björklund Boistrup and Gustafsson (2014) and Johansson (2014) in their analyses of three case studies—lorry loaders in a road-carrier company and nursing aides in an orthopaedic department and a semi-emergency department of a hospital—adopted different theoretical frameworks to study how adults utilise structuring resources in different workplace measuring activities. Focusing on the subjective experiences of the workers and how they perceived mathematics, the findings show that these adults used mathematics in ways that are radically different from typical mathematics textbook and adult numeracy test examples.

8 Conclusion

The articles in this special issue have touched upon many issues common to mathematics education across the spectrum, but have also raised many others which have the potential to inform further debate in mathematics education and in workplace education, and beyond. One major issue, strongly related to motivation, appears to be the perceived relevance of the particular mathematical curricular content to school and vocational students’ current work experience and/or anticipated futures. For all students, this means taking serious account of both the conceptual and the contextual aspects of mathematics curricula.

Bernstein’s (2000) theoretical distinctions between vertical discourse and horizontal discourse have offered a language of description and analysis to take our understanding of vocational mathematics education far beyond the simplistic notion of (school and college) mathematics with applications, reflected in many textbook titles over the last half century. In the workplace, contextual knowledge involves both technical skills, such as knowledge and understanding of equipment (tools, machines, and other artefacts) and work organisation (as a technology of management), and behavioural skills such as cultural and personal knowledges developed in relation to the specific work situation. These skills are critical but take time to develop; a point often overlooked by those demanding “work readiness” in school leavers and university graduates, who may well be proficient in the vertical discourse of mathematics in terms of theoretical and principled knowledge but who appear less than competent on the job. (Furthermore, it is impossible to capture this complexity in a few lines of text in instructional or assessment exercises). In terms of mathematics, the immediate workplace focus, particularly in the trades, is often on “the way we do it here”. That is, following Bernstein’s theorisation of horizontal discourse, the mathematical skills are segmented, focusing on the particular task, and not structurally unified in ways that might allow the worker to transform their knowledge when confronted by novel situations such as unforeseen breakdowns or technological innovations. When vocational mathematics education is focused almost entirely on this horizontal discourse, not only are individual workers disempowered but also the community at large fails to benefit from the potential skill development of its workforce. On the other hand, as emphasised throughout this special issue, vocational mathematics education cannot afford to focus predominantly on the vertical discourse and assume that contextual knowledge will develop more or less automatically. The professional/vocational education of prospective mathematics teachers integrates both vertical and horizontal discourses, supporting future teachers to recontextualise their disciplinary knowledge of mathematics in the context of practice with learners within particular sectors. Vocational mathematics education in general has the same the responsibility to all other workers.

A common issue worldwide, particularly in post-compulsory education, is a shortage of funding, resulting in staff cutbacks and reductions in student contact hours. Research-based technological innovations in mathematics education, in collaboration with industry, as discussed by Bakker et al. and by Coben and Weeks, offer a solution to this problem. They also have the potential to offer vocational and other students in schools experiencing mathematics staff shortages, including those from less developed countries, access to powerful mathematical knowledge. In addition to this, non-judgmental, high-quality technology-based learning resources aimed at developing competence in a given vocational field can do much to overcome issues of mathematics anxiety and lack of confidence in mathematics that are experienced by many school leavers and adults in general.

Finally, the concept of transition is a recurring theme throughout this issue. In fact, at every stage of life, people are undergoing transitions related to ageing, caring relationships, and changing work situations (e.g., quantity, quality, intensity, innovation, redundancy). More research is needed on the role of mathematics education in transitions for school leavers and for vocational students: the transitions between school and workplace as discussed in this issue and also transitions directly between school and university, particularly in science and technology fields, and also in fields such as business studies and social sciences, as students encounter the more theoretical and abstract aspects of mathematics and statistics.

The big question is: What can mathematics education and industry learn from each other through a respectful two-way communication process? Industry managers and representatives of peak bodies (and politicians) can come to understand why new graduates from school and university are not always “work-ready” in mathematics, due in part to the transition process between the two different worlds of education and work. Industry leaders can learn about the intended outcomes of recent curriculum innovations and possibly contribute to these processes, while employers can gain an understanding that the mathematics actually used in the workplace is likely to be far more sophisticated than the so-called basic skills (see, e.g., Damlamian et al., 2013; Hoyles, Noss, Kent, & Bakker, 2010). For its part, the mathematics education community could become more informed about how mathematics is developed and recontextualised by people working across all sectors of industry—primary, secondary, and tertiary—both in relation to production (material and virtual) and to work organisation. Mathematics teachers at school, vocational, and university levels can become informed about their students’ possible career foregrounds through practical interaction with local industry, possibly in partnership with the local mathematics education university faculty (see Damlamian et al., 2013 for examples). Last, but not least, education (and labour) policy makers could ensure that the policies they make are informed by high-quality, independent research and are not internally contradictory in terms of desired outcomes and the conditions of mathematics (and other) teachers’ work in both vocational and general education (FitzSimons, 2002).

In summary, vocational mathematics education has three defining characteristics that set it apart from general mathematics education.

  1. 1.

    It has as its specific purpose the preparation of future workers—or the continuing development or (re) education of qualified workers—for an intended segment of working life, specifically in a certain, sometimes narrow, field of work, or else in a broader range of occupations. (This is alongside citizenship development in many countries.)

  2. 2.

    It has the potential for immediate feedback from a range of stakeholders, including students themselves, other vocational teachers, actual or potential employers, peak industry and employer bodies, trade unions, politicians and bureaucrats, and, of course, from the mathematics education research community itself.

  3. 3.

    The students are generally in a process of transition: moving between school and work, sometimes in a linear fashion, from school to work, and sometimes inhabiting both worlds, moving backwards and forwards between them. This transition has implications for the learner’s identity.

For most people, the goal of having meaningful and satisfying paid work, under reasonable working conditions, ideally in a field of personal interest, is of great importance. The work of the mathematics education community of educators, teachers, and researchers in supporting their students’ vocational aspirations is fundamental.