Joint Production of Food and Wildlife: Uniform Measures or Nature Oases?

Abstract

Intensive agriculture is often bad for wildlife. Does this imply that a goal to boost wildlife on agricultural land is best met through a general reduction in intensity? We argue that such an approach may not be optimal, since cost functions for provision of wildlife on agricultural land may be non-convex, due to fixed costs associated with such provision. This implies that, even when farms are identical, it may be preferable to split them into groups of high providers and low providers. We test our hypothesis in a study of the optimal management of mown grasslands in southern Sweden, where the two products are silage and successful reproduction of ground-nesting birds, and the variable controlled by the farmer is the date of the first mowing. We show that the optimal solution is likely to involve some farmers maintaining profit-maximizing practices while other—identical—farmers delay their first mowing significantly. The superiority of such split solutions may have major implications for agricultural policy.

1 Introduction

There is generally a trade-off between food production and wildlife conservation. Over the course of human history, food production has expanded both in intensity (production per unit of land) and extent (area of land under agriculture), frequently at the expense of wildlife. On the other hand, many wild species have adapted to the agricultural landscape and are dependent on it. However, even these species are threatened today due to the trend towards more intensive agricultural practices. An important example of this is the collapse of Europe’s farmland bird populations (see for instance Donald et al. 2001, 2006). From a policy perspective, two alternative approaches to helping such threatened species may be distinguished: the first is through uniform measures applied to all farms (such as a uniform reduction in intensity), the second is to encourage split solutions under which some farms pursue high-intensity production whereas others make greater compromises in productivity for the sake of nature. In this paper we perform an ecological–economic analysis of the choice between these two approaches. We set up a general problem and explore its properties in theory, then demonstrate its relevance through a discussion of ecological theory, and finally demonstrate the characteristics of the solutions in a numerical example applied to the breeding of ground-nesting birds on mown grasslands.

We begin our discussion of the literature with the influential paper of Green et al. (2005), who build a model with a fixed quantity of homogeneous land, a constraint on total food production from that land, and a production possibility frontier (ppf) for food and nature. It follows straightforwardly that if the ppf is convex it is better to concentrate on either food or nature on any given unit of land, whereas if it is concave then it is better to produce them jointly. They denote the former option land sparing, and the latter wildlife-friendly farming (subsequently this option has been named land sharing).

Subsequent work shows that the solution to the sparing–sharing dilemma depends on the context, and throws the problem formulation into question. Phalan et al. (2011) apply the framework of Green et al. (2005) to the study of wild animals in Ghana and northern India. They conclude that dividing land strictly between food production and nature production is typically the least-cost strategy to achieve given populations of such animals. Consider an animal which needs large areas of forest to survive. Allowing hedgerows or isolated trees to grow on agricultural land may have significant negative effects on food production while doing little to help such an animal; however, as the density of trees increases the marginal benefits to the animal may increase whereas the marginal cost may be constant, thus yielding a concave cost function. On the other hand, they note that some species may thrive on agricultural land—in which case sharing is likely to be superior—while for others the situation may be more complex than the simple sparing/sharing dichotomy allows. Meanwhile, Gutiérrez-Vélez et al. (2011) examine the relationship between palm-oil plantations and deforestation, testing the hypothesis that intensive agriculture will protect forests. They reject the hypothesis since they find that high-intensity palm-oil plantations involve forest conversion while low-intensity plantations do not typically expand into existing forest.

Several papers—such as Hodgson et al. (2010) and Clough et al. (2011)—demonstrate the importance of considering more inputs into agricultural production than land alone. Hodgson et al. (2010) study butterfly populations on organic farms (sharing) and conventional farms $+$ reserves (sparing). Given a restriction on minimum total yield they find that sparing is likely to yield more butterflies than sharing if the spared land is managed as nature reserves, but not if it is simply in the form of extra field margins. Implicitly, creation of nature reserves involves the use of extra inputs (such as labour) compared to field margins, so it is not surprising that their creation can yield greater nature production. Clough et al. (2011) show that species richness and yield do not covary on tropical cocoa plantations, which is not surprising given large variations in the efficiency of plot management; better-managed plots may give higher yields and more biodiversity. On the other hand, Egan and Mortensen (2012) show that the spatial context may also be important; for instance, the relative gains from land sparing may be greatest in landscapes with a low amount of non-crop habitat.

Although authors such as Green et al. and Phalan et al. are performing economic analyses, they have not been picked up in the economics literature, where the sparing–sharing question has received little or no attention. There is a large literature on spatial aspects of optimal exploitation of biological resources (see for instance Sanchirico and Wilen 1999). These articles focus on the heterogeneous spread of biological populations across space, frequently correlated with the heterogeneous nature of space (e.g. land of differing quality). However, the sparing–sharing dilemma—as modelled by Green et al. (2005) and in this paper—concerns a homogeneous land area without spatial interactions between plots. The article which gets closest to ours in approach is perhaps Rauscher and Barbier (2010), although it is focused on a different problem. They set up a two-region global model in which there is a trade-off between agglomeration of productive activity (industry) and preservation of biodiversity. The laissez-faire equilibrium involves dispersion (similar to land sharing in our problem), whereas biodiversity considerations may favour concentration of human settlements into one of the two-regions (land sparing).

We now turn to policy, focusing on the European context.¹ In Europe, mosaic landscapes provide semi-natural habitat for a wide range of species, species that have evolved over centuries in interaction with farming (Benton et al. 2003; Lindborg et al. 2008). As a result, many threatened species are dependent on continuation of traditional management practices—typically low-intensity—for their preservation, including grazing of livestock on arable grassland and semi-natural meadows, keeping woody and herbaceous elements between fields, low inputs of chemicals and mineral fertilizers, and complex crop rotations (Edwards et al. 1999; Billeter et al. 2008; Kleijn et al. 2009). For such species ‘sparing’ in the sense of returning the land to a wild state is not beneficial, hence the policy dilemma is not between sparing and sharing but between uniform and split solutions, where the former involves all agricultural land being managed in a more wildlife-friendly way, and the latter involves a subset of land being managed using low-intensity production for both biodiversity and food production whereas the remainder is managed more intensively.

Agriculture in the EU is heavily influenced by the common agricultural policy (CAP) which has, historically, encouraged intensification with above-market prices at the expense of nature and biodiversity (Donald et al. 2001). In response, voluntary agri-environmental schemes (AES) have been introduced to encourage farmers to adopt more costly, or less profitable, farming practices for environmental protection (Kleijn and Sutherland 2003; Stoate et al. 2009). Some AES have measurable positive effects, whereas others do not, but in many cases little is known about either the efficacy or the efficiency of AES (Kleijn and Sutherland 2003; Stoate et al. 2009). Furthermore, Kleijn et al. (2006) find that some schemes may deliver higher levels of biodiversity in general, without helping threatened species in particular. Since 2005 there has also been a general shift in CAP rationale away from direct support that encourages overproduction to decoupled support with attached environmental obligations that require farmers, particularly those not participating in AES, to take minimal environmental care (Brady et al. 2009). In the impending CAP2013 reform environmental considerations are coming to the fore, with it being marketed as the ‘greening’ of the CAP (EU 2011). Of particular relevance to our research is the plan to make 30 % of direct payments—around €12 billion annually²—contingent upon 7 % of agricultural land being ‘spared’ as field margins, hedges, fallow, etc., denoted ‘ecological focus areas’ (COM 2011, p. 41). In this context, a key question is how agricultural policy in general, and agri-environmental schemes in particular, affect biodiversity, and whether these need to be reformed to yield better outcomes (Phelps 2007). An important question for policy is then under what circumstances uniform measures should be applied to all farms, and under what circumstances split solutions should be encouraged under which some farms concentrate on high-intensity production whereas others make greater compromises in productivity for the sake of nature conservation.

We perform an economic analysis of the choice between uniform measures and split solutions, first in theory and then in a specific case. In order to focus specifically on this choice—and following the ecological literature including Green et al. (2005) and Phalan et al. (2011)—we assume homogeneous land and focus on within-field processes; hence we do not consider dynamic spatial aspects such as movement of individuals over time from one place to another. In our numerical application we build on an ecological model in which agricultural intensification, through advancement of harvest and reduced times between harvest events, decreases habitat quality for some species and may lead to local extinction. In simplified form we can imagine (and model) a homogeneous landscape being used in different ways by different farmers, and habitat quality varying locally depending only on the management of the land in that place.³

We differ from the tradition in the ecological literature—and Green et al. in particular—in two very important respects. Firstly, instead of using a ppf for food and nature, we base our analysis on a cost function for nature production. Secondly, we allow for a third scenario in addition to the two that they analyse—i.e. convexity and concavity—which is that the ppf (or, better, the cost function for nature production) is neither convex nor concave.

The reason for deriving a cost function for nature production is that land is not the sole input to production. Typically, agriculture is a multi-input (and multi-output) production process. In the definition of the ppf physical input use is assumed constant, implying that input costs are also kept constant for any combination of outputs, e.g. food and wildlife, which is a restrictive assumption. The cost function, on the other hand, defines the minimum cost of achieving some target level of nature, where cost is measured in terms of lost profits to farmers from producing food. In the absence of monetary valuation of the benefits of nature, the rational economic goal is to achieve a nature goal at least-cost.

Regarding convexity and concavity, convex cost functions are commonly assumed in economics, corresponding to monotonically rising marginal and average costs; the more nature that is to be produced, the more costly it will be at the margin. Concavity, on the other hand, implies that the marginal cost of production decreases continuously the more is produced. However, both convexity and concavity are special cases, and it is likely in reality that the cost function will be neither convex nor concave. To see how such a cost function may arise, interpret ‘nature’ as the population of a particular species, and assume that that species is not viable on agricultural land managed for maximum profit. Then initial reductions in agricultural intensity, while costly, will give no return in terms of a raised population; marginal returns will only become non-zero at the point at which intensity has already been reduced sufficiently for a viable population to exist. Beyond this point, reductions in agricultural intensity may give high but declining marginal returns. The result is U-shaped average costs. We analyse the case of U-shaped average costs in detail below, and we demonstrate that the policy conclusions which follow are quite different compared to the simple cases of convexity and concavity. Convexity gives uniform solutions, while concavity gives split solutions. On the other hand, given U-shaped average costs the optimal solution depends on the quantity of nature desired: for small quantities it is optimal to split farmers into profit-maximizers who produce no nature and non-profit-maximizers who produce both food and nature, but for large quantities all farmers produce both food and nature and we have a uniform solution.

We go on to develop a specific case in which we combine ecological life-history theory (Perrins and McCleery 1989; Daan et al. 1990; Drent 2006) and economic production theory to describe the trade-offs involved and describe how an optimal solution can be found. The case concerns the management of mown grassland in southern Sweden—and other geographies that have similar ecological conditions—that produces grass for silage and provides habitat for juvenile ground-nesting birds. The process of agricultural intensification has led to earlier mowing of grassland throughout north-western Europe (Smith and Jones 1991; Vickery et al. 2001). However, the shorter gap before the first mowing may prevent successful reproduction of many species, among which are ground-nesting birds Kleijn et al. (2011). This can have implications for many species, and dramatic effects have been shown for at least corn crake (Crex crex) (Green et al. 1997; Tyler et al. 1998), whinchat (Saxicola rubetra) (Broyer 2003, 2009; Grubler et al. 2008), and skylarks (Alauda arvensis) (Vickery et al. 2001). Does the optimal solution involve all farmers delaying first mowing equally, or should a subset of farmers delay mowing for a longer period? In accordance with the general results, we find that the answer depends on the target level of bird recruitment.

The remainder of the paper is organized as follows. In Sect. 2 we set out the model and prove five propositions related to the results explained above. In Sect. 3 we develop and calibrate the model for the specific case of grassland management in southern Sweden. Section 4 concludes.

2 Theory

Here we set up the theoretical model and prove five propositions, to which we refer in the remainder of the paper.

2.1 The Model

We have a unit area of homogeneous agricultural land, on which both agricultural products and nature are produced. Profits are made from agricultural production, but there is a trade-off such that increasing nature production implies lower profits; this loss of profits is treated as a cost. A social planner divides the area into $n+1$ subareas indexed by $i=0, \ldots , n$, each of which is managed differently; we denote the $n+1$ management strategies as treatments.⁴ Subarea $i$ is of size $x_i$, rate of nature production $z_i$ per unit area, and costs are $c(z_i)$ per unit area, where $c$ is an increasing function. Area $x_i$ is restricted to be greater than or equal to zero, while the rate of nature production $z_i$ is restricted to the interval $[z_l, z_h]$, where $z_l$ is nature production on land where profit-maximizing technology is used, and $z_h$ is the maximum attainable rate of nature production. Finally, since we have a unit area of land, $\sum \nolimits _{i=0}^n x_i = 1$.

We assume that the land is always managed, although not necessarily to produce food, since in Europe land which is abandoned will generally produce nature of an inferior type from a conservation perspective. The cost of nature production may take different forms, such as lost food production due to nature-friendly farming practices, or increased input costs. The fact that we assume a social planner implies that we do not consider problems of regulation such as asymmetric information, but simply seek the best solution for society. The problem is also static; we do not consider the dynamics of species decline and recovery, but assume that nature and food production follow directly from input use, which is sufficient given the aims of this paper. In accordance with the static treatment of the problem we do not incorporate spatial externalities or effects of fragmentation.

We set the problem up as a cost minimization, by imposing a restriction that total nature production must be at least $Z$, i.e. $\sum \nolimits _{i=1}^n x_i z_i \ge Z$,⁵ and write the problem as a Lagrangian with the shadow price of nature denoted $\lambda _z$, and the shadow price of land $\mu _z$:

$$\begin{aligned} \min _{\{{z_i, x_i}\}_{i=1}^n} \mathcal L = \sum \limits _{i=0}^n x_i c(z_i) - \lambda _z \left( \sum \limits _{i=0}^n x_i z_i - Z\right) - \mu _z \left( \sum \limits _{i=0}^n x_i - 1 \right) . \end{aligned}$$

(1)

2.2 Solution Part 1: The Principle of Equal Marginal Costs

Now assume an interior solution and take the first-order condition in $z_i$ to yield the well-known principle of equal marginal costs.

Proposition 1

Marginal costs of nature production on all land whose treatment is not at a boundary $(z=z_l$ or $z=z_h)$ must be equal to the shadow price of nature:

$$\begin{aligned} c'(z_i) = \lambda _z\quad {\mathrm{for\,\,all}} \,\, i. \end{aligned}$$

(2)

This is one condition that must be satisfied for an optimal solution. However, to be sure we have a minimum in costs we also need the following condition.

Proposition 2

Assume that the level of nature provision is restricted to a closed interval $[z_l, z_h]$, and that the cost function $c(z)$ is continuously differentiable $(C^1)$. If the cost function is strictly convex across the interval then $n=1$, i.e. there is a unique choice of nature provision $z$ which must be applied to the entire area in order to minimize costs. On the other hand, if the cost function is strictly concave the cost-minimizing solution must be at a corner such that an area $x_1$ is devoted fully to nature production, while $x_0$ is devoted to profit-maximizing farming, and $x_0 z_l + x_1 z_h= Z$.

Proposition 2 follows since (i) when the cost function is convex marginal costs cannot be equal (required by Proposition 1) unless $n=1$, and (ii) the second-order condition for cost minimization is $c''(z_i)>0$, which holds given convexity. It implies that if the cost function is convex across the allowed interval ($z=z_l$ to $z=z_h$) then there is a unique cost-minimizing solution with uniform treatment. On the other hand, if the cost function is concave then an equimarginal solution which satisfies the restriction will lead to a global maximum in costs, and costs are minimized at the corner instead.

Thus far, the results mirror those of Green et al. (2005). The intuition is straightforward. Given convex costs it gets more and more expensive to produce nature on a given plot the more nature there already is, and so if two plots of land have different treatments, it is always possible to reduce costs at constant total nature production by transferring nature production from the land with a lot of nature to the land with less. Given concave costs it gets cheaper and cheaper to produce nature the more there already is on a plot, hence it makes sense to concentrate nature production to the greatest possible extent.

2.3 Solution Part 2: The Extended Equimarginal Principle

The results above do not go far enough: the case in which costs are neither convex nor concave has not been analysed. As we show below, this case is empirically relevant. In order to analyse this case we must consider the possibility of split solutions. Consider two areas under different treatments $i$ and $j$, where at least one of the treatments is internal (not at a corner), and take first-order conditions in $x_i$ and $x_j$ to yield the following proposition.

Proposition 3

When there are two areas of land under different treatments $i$ and $j$, the marginal cost of producing nature by switching land from treatment $i$ to treatment $j$ must be equal to the shadow price of nature, that is

$$\begin{aligned} \lambda _z = \frac{c(z_i) - c(z_j)}{z_i-z_j}. \end{aligned}$$

Note that, in combination with Proposition 1, the proposition implies that the marginal cost of producing nature through increasing $z_i$ must also be equal to the marginal cost of producing nature by switching land between treatments, if treatment $i$ is interior (i.e. not at a boundary such as $z_i=z_l$ or $z_i=z_h$).

Furthermore, note the following special case, obtained when $z_i =z_l$ and $c(z_i) =0$.

Proposition 4

When there are two areas of land under different treatments $i$ and $j$, and treatment $i$ is profit-maximizing $($hence $z_i=z_l)$ while treatment $j$ is internal, the average cost of producing nature additional to $z_l$ through treatment $j$ must be equal to the marginal cost, that is

$$\begin{aligned} \lambda _z = \frac{c(z_j)}{z_j-z_l} = c'(z_j). \end{aligned}$$

So, at the optimum, average costs are equal to marginal costs. Note here that average costs are defined as the average cost of additional nature production over and above that which is produced as a by-product of profit-maximizing farming, $z_l$.

The intuition behind these results is straightforward: if it costs $\lambda _z$ to get an extra unit of nature through a marginal increase in nature production on area $x_i$, at the optimum it should also cost $\lambda _z$ to get an extra unit through switching some land from treatment $i$ to treatment $j$.

Finally, we must consider sufficient conditions for optimality. How do we know when we have found the optimal solution? Recall that the cost function $c(z)$ is defined across the interval $[z_l, z_h]$, that it must be increasing, that it need not be continuous, and that $c(z_l)=0$.

Proposition 5

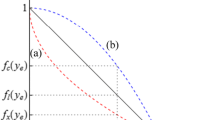
Define the function $f(z)$ as the largest convex function which is less than or equal to $c(z)$. Then $f(z)$ is the cost function for nature production after allowing for the possibility of split solutions. For values of $z$ where $f(z)=c(z)$ we have uniform solutions, and for values of $z$ where $f(z)<c(z)$ we have split solutions. Assume there exist one or more intervals $(z_-,z_+)$ across which $f(z)<c(z)$, where $z_-<z_+$. Across such an interval the optimal treatments are $z_-$ and $z_+$, with the proportion of land under treatment $z_+$ rising as total nature production $z$ rises.

The explanation of the proposition is straightforward: if the cost of achieving nature production $z$ per unit area by uniform treatment is higher than the cost of achieving the same average nature production by combining areas with higher and lower rates of production, then it must be optimal to split production in this way. If not, then it cannot be optimal to split. See Fig. 1.

Fig. 1

Four cost functions for nature production (continuous lines), and the four corresponding functions $f(z)$ (dashed lines where different): a Convex costs, corresponding to Proposition 1; b concave costs, corresponding to Proposition 2; c neither convex nor concave, corresponding to Proposition 3; d neither convex nor concave, special case corresponding to Proposition 4. The dots mark the boundaries of the intervals $z_-$ and $z_+$ across which split solutions are employed

2.4 Fixed Costs

Figure 1d shows that in the presence of fixed costs of nature production a split solution is inevitable for sufficiently low levels of nature production.⁶ Meanwhile, consideration of the ecological–economic problem shows that there may frequently be fixed costs associated with raising nature production per hectare. Specifically, consider the ‘land-use moderated conservation effectiveness hypothesis’ proposed by Kleijn et al. (2011), according to which agricultural practices—such as ploughing, harvesting, or pesticide application—are conceptualized as disturbances, and decreasing gaps between disturbances make it successively harder for individual species to survive and reproduce. When the gaps fall below a critical level—which we denote $\overline{g}$—reproductive success falls to zero and the species is doomed to local extinction. Now combine this with an economic model in which there is a profit-maximizing gap between disturbances $g^*$ which the farmer chooses if unconstrained by nature production targets, while increases in this gap above $g^*$ lead to reductions in profits. Fixed costs arise when $g^*$ is strictly less than $\overline{g}$, since this implies that incremental increases in the disturbance gap generate no benefits for nature while they are costly to the farmer.

A simple class of cases arises if we assume that the marginal costs of nature production are strictly increasing. Fixed costs are then crucial, and three cases can be distinguished. The simplest case is when nature is boosted as soon as the farmer increases the gap from $g^*$, hence there are no fixed costs. In the other extreme, fixed costs are so large (because $\overline{g} \gg g^*$) that average costs are declining across the allowed interval. In the third case $\overline{g} > g^*$, but fixed costs are smaller such that average costs decline first then rise. The three cases are illustrated in Fig. 2, both in terms of total costs and marginal and average costs.

Fig. 2

Total costs, marginal costs, and average costs: a uniform measures—zero fixed costs; b nature oases—large fixed costs; c combination—small fixed costs. Recall that $z_l$ is nature production on land where profit-maximizing technology is used, and $z_h$ is the maximum attainable rate of nature production

In Fig. 2a we have zero fixed costs, hence the cost function is convex and average costs are increasing. Thus, as shown by Propositions 1 and 2, if separate plots are treated differently we must be able to reduce total costs by increasing nature production on the plot with less nature, and reducing production on the other. Hence all farms act uniformly at the optimum.

In Fig. 2b fixed costs are sufficiently large that average costs are decreasing across the entire allowed range of nature production. Since average costs are never equal to marginal costs, Proposition 4 implies that only the boundary points—minimum nature production $z_l$ or maximum nature production $z_h$—are ever chosen. (In terms of Proposition 5, $f(z)$ is always less than $c(z)$.) That is, for any total quantity of nature $Z$ we always have a corner solution with $z_i=z_l$ and $z_j=z_h$, and hence $x_i z_l + x_j z_h = Z$. If $z_l=0$ this implies that we create oases of nature in a landscape otherwise characterized by profit-maximizing agriculture. Intuitively, since average costs of nature production from a given unit of land are declining across the allowed interval, it makes sense to concentrate nature production as much as possible.

Figure 2c is similar to 2b, but fixed costs are smaller and average costs decline initially and then rise. Since marginal costs are strictly increasing, from Proposition 1 a split solution is only possible if at least one of the treatments is at a boundary. Furthermore, the necessary condition in Proposition 4 can only be satisfied given a combination of $z_l$ (profit-maximization) and $z_+$ (minimum average costs). In terms of Proposition 5, $f(z)$ is less than $c(z)$ for $z \in (z_l, z_+)$, hence we have a split solution across that interval; $z_l$ is thus equal to $z_-$. As we increase the shadow price of nature from zero we will shift land from treatment $z_l$ to $z_+$, the point at which average and marginal costs are equal. Once all land is under treatment $z_+$ we are on the increasing section of the average cost curve, $f(z)=c(z)$, and further increases in nature provision are achieved by uniform measures, i.e. all farms increasing their nature production equally.

3 An Application to Bird Reproduction from Mown Grasslands

In this section we build up a model of bird reproduction on mown grassland based on the land-use moderated conservation effectiveness hypothesis of Kleijn et al. (2011). Our case concerns the management of mown grassland in southern Sweden, the products from which are grass (silage) and juvenile ground-nesting birds. Our aim is to characterize the problem and identify the key parameters which determine whether split or uniform solutions are optimal. That is, we must determine whether a given overall rate of bird reproduction can be achieved at least cost by all farmers delaying mowing equally, or if a subset of farmers were to delay their mowing more, while the remainder continue to maximize profits.

The process of agricultural intensification has led to earlier mowing of grassland throughout north-western Europe (Smith and Jones 1991; Vickery et al. 2001). Increased fertilizer application increases grass growth and allows for multiple harvests, and by producing silage rather than hay, earlier mowing is possible because good drying conditions are not necessary (Vickery et al. 2001). Furthermore, grass harvested early has higher protein content, which is beneficial for livestock (Nocera et al. 2005). However, early mowing dates can be detrimental for birds breeding in grass fields (Green et al. 1997; Vickery et al. 2001; Grubler et al. 2008; Roodbergen and Klok 2008; Broyer 2009; Humbert et al. 2009). An early mowing date means that many bird species are still breeding, with incubating parents (Grubler et al. 2008), nests or juveniles (Green et al. 1997) still in the grass.

3.1 The Model

The fundamentals of the model are as follows. Fledgling survival is assumed to be only a function of the date of the first mowing; the more mowing is delayed, the greater the chance for fledglings to fly the nest. On the other hand, for the farmer there is an optimal mowing date, and delaying mowing beyond this date reduces profits due to a reduction in grass quality and the delay in starting the second cycle of grass growth and harvest. In order to solve the problem we need the farmers’ cost function for delayed mowing, and the production function for juvenile birds depending on the mowing date.

In constructing the model we first anchor the time line to the farmers’ profit-maximizing harvest time, by defining time $t=0$ when farmers’ profits $\pi = \pi ^*$, where $\pi ^*$ represents profits when the farmer is unconstrained. We measure time in days, so $t=5$ corresponds to 5 days after the date of profit-maximizing harvest.

The second step is to estimate a function for the cost of harvest delay. The optimal harvest date is chosen based on a range of considerations. Delaying harvest raises the quantity of the fodder crop, but reduces its quality; furthermore, it impacts negatively on the second and third crops in the cycle (Gunnarsson et al. 2009). To approximate the costs of delaying harvest we choose the cost function

$$\begin{aligned} c(t) = c_0 t^2, \end{aligned}$$

(3)

where $c$ is the total cost of delay (in the form of lost profits, €/ha). We set the parameter $c_0 = 0.3$ in order to approximately match the cost function of Gunnarsson et al. (2008, Fig. 9). The function implies that we only ever need to consider cases where $t \ge 0$, since earlier harvest implies both lower profits and lower production of fledglings.

The final—crucial—step is to model fledgling survival as a function of harvest date, or more generally to model the flow rate over time at which fledglings fly the nest. This is a new model of a general form that has strong support in the ecological literature (e.g. Drent 2006). We consider a typical small or medium sized bird that breeds on the ground in spring or early summer. It could be thought of as a corn crake, whinchat, corn bunting, skylark or similar species. For clarity we consider only a single clutch per season, although the model could be extended to incorporate relaying or multi-brooding. Most birds breeding in temperate regions have a declining clutch or brood size with season ; see recent review by Drent (2006). The laying date of an individual female may be a compromise between the offspring’s probability of surviving until reproduction, which is higher for those born early, and the parents’ cost of reproduction which might be lowered by delaying breeding. The result is that the total reproductive value, of parents and offspring combined, decreases over the season (Perrins and McCleery 1989; Drent 2006). Hence, the measurable effect in a natural population is that the number of produced recruits per pair declines over the season.

We propose the following model, which captures essential features of the breeding biology of the above mentioned species, and is in general accordance with ecological life-history theory and a large body of empirical results for birds breeding in temperate regions (e.g. Perrins 1965; Drent 2006). First, there is an earliest possible date for the start of breeding, $\overline{u}$, after which breeding rises steeply to a peak before declining more gradually, according to the following function:

$$\begin{aligned} B(t) = K_1 (t-\overline{u}) [T-(t-\overline{u})]^{\gamma -1}. \end{aligned}$$

(4)

Here $B$ is the breeding rate, $T$ is the length of the breeding season, $\gamma$ is a parameter greater than or equal to $2$ which determines the length of the tail in breeding time (high $\gamma$, long tail), and $K_1$ is a parameter set to normalize total breeding to unity. Note that when $t=\overline{u}$ the breeding rate is zero, and when $t=T+\overline{u}$ the rate is again zero; in between it is positive. The function is illustrated in Fig. 3a, with $\overline{u} = -15$, $T = 45$, $\gamma =3$, and $K_1=3.24 \times 10^{-7}$. So the first breeding occurs just 15 days before the date of profit-maximizing mowing, and only a small fraction of pairs manage to breed before the first mowing. This is an assumption which reflects reality for many grassland breeding birds (e.g. Broyer 2009).

Fig. 3

The model of fledgling survival. a Breeding rate as function of $t$ (area normalized to unity); b fledging rate if all chicks survive, as fn. of $t$; c recruits per brood, as fn. of fledging time; d fledging rate as fn. of fledging time

Second, we assume a fixed time between breeding and fledglings leaving the nest, $U$. We can thus define time $\overline{t}$ as the earliest time at which fledglings can leave the nest, where $\overline{t} = \overline{u} + U$, and ceteris paribus the rate at which birds leave the nest, $G(t)$ will be

$$\begin{aligned} G(t) = K_1 \cdot (t-\overline{t}) [T-(t-\overline{t})]^{\gamma -1}. \end{aligned}$$

(5)

Note that $\overline{t}$ is not restricted to be positive, since it may be the case that the first fledglings leave the nest before the farmers’ profit-maximizing harvest time. On the other hand, we can add the restriction that harvest time $t \le \overline{t} + T$; there is never any reason to delay harvest beyond the time at which the last fledglings have left the nest. This is illustrated in Fig. 3b, with $U=30$. Here we see that the first fledglings fly the nest 15 days after the profit-maximizing mowing date, implying zero survival given profit maximization.

Third, we estimate fecundity $F$—the number of produced offspring which survive until the next year in the absence of mowing—as a function of the time at which they leave the nest, $t$.⁷ Ceteris paribus, fledgling survival is higher the earlier breeding takes place, and we assume an exponential decline over time:

$$\begin{aligned} F(t) = K_2 \cdot \exp [-\alpha (t-\overline{t})]; \quad t\ge \overline{t}. \end{aligned}$$

(6)

Here $K_2$ is the fecundity of parents whose fledglings leave the nest at $\overline{t}$, and $\alpha$ determines the rate of decline in fecundity. In Fig. 3c we set $K_2=2$, implying that $2$ recruits per brood survive (on average) if breeding occurs at the earliest possible date, and the decay rate in fecundity is 5 %/day, so delay in breeding of more than a few days is very costly in terms of survival chances of the juveniles, even in the absence of mowing.

We now have $G(t)$, the normalized rate at which fledglings leave the nest as a function of time, and $F(t)$, fledgling survival as a function of when they leave the nest. The product of these two functions—$G(t) \cdot F(t)$—gives the rate of production of surviving birds as a function of time, ${\mathrm{d}}z / {\mathrm{d}}t$:

$$\begin{aligned} G(t) \cdot F(t) = \frac{{\mathrm{d}}z}{{\mathrm{d}}t} = \frac{K (t-\overline{t}) [T-(t-\overline{t})]^{\gamma -1}}{e^{\alpha (t-\overline{t})}}; \quad t\ge \overline{t}. \end{aligned}$$

(7)

This is illustrated in Fig. 3d.

We now use Eqs. (3) and (7) to derive an expression for marginal costs of fledgling production. From (3) we know the marginal costs of delay, ${\mathrm{d}}c / {\mathrm{d}}t = 2 c_0 t$. Combining this with the rate of nature production (Eq. 7) we obtain the following expression for the marginal cost of nature production:

$$\begin{aligned} \frac{{\mathrm{d}}c}{{\mathrm{d}}z} = \frac{2 c_0 t e^{\alpha (t-\overline{t})}}{K (t-\overline{t}) [T-(t-\overline{t})]^{\gamma -1}} . \end{aligned}$$

(8)

Since $t \ge \overline{t}$, $t \ge 0$, and $t \le T+\overline{t}$ we know that this function is always positive, which is of course to be expected; starting from the profit-maximizing harvest time, the marginal cost of nature production through delaying harvest will always be positive.

3.2 Three Cases

In order to make further progress, we consider three cases in turn. Firstly, the simplest case of $\overline{t}=0$, then $\overline{t} <0$, and finally $\overline{t}>0$. When $\overline{t} =0$, profit-maximizing harvest occurs at exactly the time that birds start to leave the nest. This is of course unlikely, but gives us a simple benchmark case. Use Eq. (8) to write

$$\begin{aligned} \frac{{\mathrm{d}}c}{{\mathrm{d}}z} = \frac{2 c_0}{K} \frac{e^{\alpha t}}{(T-t)^{\gamma -1}}. \end{aligned}$$

(9)

Then when $t=0, {\mathrm{d}}c / {\mathrm{d}}z = (2 c_0/K)/T^{\gamma -1}$, a positive constant. Furthermore, it is straightforward to show that the second derivative is positive, indicating that marginal costs of nature production are positive and strictly increasing.⁸ This case thus corresponds to Fig. 2a from the theoretical model, and a uniform solution is optimal; all farms should delay harvest equally. The intuition is that the marginal costs of delay are initially zero and then increase, whereas the benefits are initially positive and then decrease.

The second case we analyse is $\overline{t} < 0$, implying that profit-maximizing harvest occurs after fledglings have started to leave the nest. Following the intuition of the first case, we know that in this case the marginal cost of delay is initially zero and then rises, whereas the marginal benefit is initially positive and then decreases. We thus expect the same result as above, that a uniform solution is optimal. Assuming $\overline{t} <0$ in Eq. (8) it is straightforward to show that when $t=0$ (the lowest allowed value) ${\mathrm{d}}c/{\mathrm{d}}z =0$, i.e. the marginal cost of nature production for a profit-maximizing farm is zero. Furthermore, by the same method as above it is straightforward to show that ${\mathrm{d}}c/{\mathrm{d}}z$ is increasing in $z$ (the second derivative is positive) so again we have increasing marginal costs, the case corresponds to Fig. 2a, and a uniform solution is optimal.

The third case is $\overline{t} >0$, implying that profit-maximizing harvest occurs before fledglings have started to leave the nest. Thus, no fledglings will survive on land managed this way. Now, rewrite Eq. (8) as follows:

$$\begin{aligned} \frac{{\mathrm{d}}c}{{\mathrm{d}}z} = \frac{2 c_0}{K} \frac{\frac{t}{t-\overline{t}} e^{\alpha (t-\overline{t})}}{[T-(t-\overline{t})]^{\gamma -1}} . \end{aligned}$$

(10)

Based on this equation we wish to demonstrate that there is a single turning point in ${\mathrm{d}}c / {\mathrm{d}}z$ as $z$ increases from $z_l$ to $z_h$. To do so we show first that there is a single turning point in ${\mathrm{d}}c / {\mathrm{d}}z$ as $t$ increases from $\overline{t}$ to $\overline{t} + T$ (the time interval during which fledglings leave the nest), and then we use the fact that $z$ is strictly increasing in $t$.

By inspection, when $t$ approaches $\overline{t}$ from above then marginal costs of nature provision approach infinity. Furthermore, when $t$ approaches $T + \overline{t}$ from below then marginal costs again approach infinity. In between, marginal costs are positive and finite. Finally, $\frac{{\mathrm{d}}}{{\mathrm{d}}t} ({\mathrm{d}}c/{\mathrm{d}}z)$ is monotonically increasing in $t$ (the second derivative is strictly positive). So as harvest time $t$ goes from $\overline{t}$ to $\overline{t} + T$, the marginal cost of nature provision declines from infinity, reaches a minimum, and increases towards infinity again. Finally, since $z$ is strictly increasing in $t$ in the interval $\overline{t}$ to $\overline{t} + T$ this implies that there is a single turning point, a minimum, in marginal costs of nature provision, implying that there is at most a single turning point (a minimum) in average costs.

This case thus corresponds to Fig. 2c from the theoretical model. Denote time of harvest, costs, and nature production at the point of minimum average costs by $(t^{*}, c^{*}, z^{*})$, and recall that we have a target level of nature production $Z$. Then if $Z < z^{*}$ we have a split solution in which harvest is delayed to $t^{*}$ over an area $Z / z^{*}$, and harvest is at $t=0$ on the remainder. On the other hand, if $Z> z^{*}$ we have a uniform solution with harvest delayed to time $t>t^{*}$ over all farms, such that the restriction is satisfied with equality.

3.3 Parameterization

Ideally we would like to solve for the cost function explicitly. To do so, we must integrate the expression for ${\mathrm{d}}z/{\mathrm{d}}t$ in Eq. (7). We can do this analytically, using integration by parts (or commercial software), if $\gamma$ is an integer. Setting $\gamma =3$ (which gives a reasonable shape) we have

$$\begin{aligned} {{\mathrm{d}}z}/{{\mathrm{d}}t} = K e^{-\alpha (t-\overline{t})} (t-\overline{t}) [T-(t-\overline{t})]^2. \end{aligned}$$

(11)

Integrating gives

$$\begin{aligned} z&= K/\alpha ^4 \big \{ e^{-\alpha s} [-6 + \alpha (4 T - 6 s) - \alpha ^3 (T - s)^2 s - \alpha ^2 (T^2 - 4 T s + 3 s^2)]\nonumber \\&\quad \quad \quad \quad + T^2 \alpha ^2-4T \alpha + 6 \big \}, \end{aligned}$$

(12)

where $s = t-\overline{t}$. Given that we also have costs $c= c_0 t^2$ we can substitute for $t$ to find $z$ as a function of $c$, which we know (since it is an increasing function) can also be expressed as $c(z)$. Finally, average costs are simply $c/z$, and we already have marginal costs (Eq. 10).

Since the key equations are (10) and (12), the parameters to be set are $c_0, \alpha , T, \overline{t}$, and $K$. Regarding costs of delay, we have $c = c_0 t^2$ (Eq. 3) and $c_0 = 0.3$ €/ha. This parameter simply scales the costs of raising bird survival, and does not affect the results qualitatively given a restriction on (or target level of) survival. We set $\alpha =0.05$, hence the rate of decline of fecundity is approximately 5 %/day, and the length of the breeding season is 78 days, hence $T=78$. Again, these two parameters affect the results quantitatively but not qualitatively; for instance, with a more concentrated breeding season (higher $\alpha$, lower $T$) returns to delay would increase and hence a given target would be attained at lower cost. The assumption crucial to the qualitative nature of the results is that the first birds leave the nest after the date of profit-maximizing harvest, as explained above. We set $\overline{t} = 15$ to reflect a bird species breeding during the mowing season. Finally we normalize the rate of breeding success to unity given no harvest, hence $K=0.950$.

Having set the parameters we can plot marginal and average costs of bird production per hectare of farmland, Fig. 4a. Figure 4b shows survival as a function of delay, Eq. (12). In both cases we normalize survival as a fraction of the maximum (no mowing).

Fig. 4

a Marginal and average costs of bird production from one hectare of farmland; b bird recruitment (as a fraction of the maximum) as a function of harvest delay

From the figure we see that if the overall target for fledgling survival is less than 51 % of maximum survival, then the optimal solution is split, with some farms delaying to give 51 % survival on their land, and other farms not delaying at all. On the other hand, if the target is above this level then all farms delay equally. The necessary delay can be read of from Fig. 4b; given a split solution, the delay is 34 days. This implies that if total bird production over the entire area is planned to be less than 51 % of the maximum (undisturbed) level, then a split solution should be applied in which some farms harvest at the profit-maximizing time, whereas others delay harvest by 34 days. Put differently, a uniform rule to delay harvest by anything less than 34 days must be inefficient, since it leads to all farmers operating with unnecessarily high average costs of nature production.

Note that the cost per fledgling in Fig. 4a should be interpreted as follows. If the density of breeding pairs is such that an average of 1 bird/ha would successfully fly the nest given no grass cutting, then the average cost of achieving 0.6 survivals/ha (60 %) can be read off as around €700/bird. Note that this high figure results from the above normalization of breeding success (and hence, implicitly, bird numbers). Assume for instance a hectare of land on which 10 fledglings would survive given no grass cutting; on that hectare, the cost per surviving fledgling of achieving 6 survivals would be €70/bird.

The size of the cost saving of adopting a split solution compared to a uniform solution depends on total bird survival aimed for. If total survival is very close to the 51 % level then savings will be small because the difference between the two solutions will be small. However, as total survival approaches zero the cost ratio between the uniform solution and the split solution will approach infinity. The reason is that for small rates of bird survival it is extremely inefficient to incur fixed costs over the entire area; much better to focus production on a few fields. For instance, if we aim to achieve an average survival rate of 20 % over an area of 1,000 ha, the necessary uniform delay would be 25 days (from Eq. 12/Fig.  4b), and the total cost would be €188,000 (Eq. 3). On the other hand, a split solution would involve 39 % of farms delaying first harvest by 34 days (follows since 20/0.51 = 39) at a total cost of €135,000, a saving of 28 %.

3.4 Uncertainty

In the model we assume that all parameters are known, and furthermore that there is no variation from year to year in growing and breeding conditions. In reality quantities which are treated as parameters in the model—such as the timing of the start of the breeding season, the optimal date of first harvest, and the time between breeding and fledglings first leaving the nest—will be stochastic variables, and this may potentially have a major effect on the results.

An extension to explicitly account for uncertainty is beyond the scope of this paper, however we discuss possible effects here. Given stochastic variables, the problem is in principle straightforward; we simply need to calculate expected returns to different policies (split or uniform). In practice the date of profit-maximizing harvest and the date on which breeding starts are likely to covary, hence as long as the social planner (or regulator in a market economy) can change the earliest harvest date from one year to another then variance in these variables will not have a great effect on the results.

If there is stochastic variation in the length of time $U$ between breeding and fledglings leaving the nest then the situation is more complex. Assume that when $U = E[U]$ then $\overline{t}> 0$ so no fledglings survive given profit-maximizing harvest. Then in a year when $U$ is unexpectedly low a uniform solution might be favoured in hindsight, whereas if $U$ is high then a split solution is even more strongly favoured. Hence it is not obvious that the introduction of uncertainty into the model will change the results fundamentally.

When there is uncertainty, we should also allow for risk aversion. Given risk aversion, the risk of unfavourable outcomes weighs more heavily than in the case of risk neutrality. Assuming that the costs of any harvest delay are well-known, and hence that the uncertainty is with regard to the resulting breeding success, an unfavourable outcome is a late or slow breeding such that birds leave the nest later than expected. The result is that split solutions are very likely to be favoured. To see this, consider Fig. 5, where the effect of a bad outcome is illustrated by a shift in ${\mathrm{d}}z/{\mathrm{d}}t$ to the right in the lower panels compared to the upper. Given a split solution in our parameterized model we have a 34-day delay on a subset of farms, and the bad outcome leads to a significant but not catastrophic drop in the number of birds successfully flying the nest. However, given a uniform solution in which a small number of birds are produced on all land then the bad outcome leads to no birds successfully flying the nest.

Fig. 5

Nature production under expected and bad outcomes for $U$, given a a split solution (34-day delay on a subset of land), and b a uniform solution (20-day delay on all land). The area under the curve to the right of harvest date shows birds which have successfully flown the nest

4 Discussion and Conclusions

We show that split solutions may frequently be socially optimal when farmers are to provide nature as well as food. Regulations frequently encourage uniform solutions, for instance regulations which force all farmers to observe the same rules, or input taxes which must be paid at the same rates by all farmers. On the other hand, some regulations encourage split solutions, such as through special support for organic farms. Our analysis shows that environmental and agricultural economists must take seriously the possibility that split solutions may be optimal under a wide range of circumstances, due to non-convexity in the cost function for nature production. We analyse one particular case in detail. Nevertheless, the model is illustrative, and more empirical data is needed to draw definite conclusions in this case. Hence, the main function of our paper is as a call for further empirical research; given the very large potential cost savings, the possibility that split solutions may be optimal should be much more widely recognized when designing agri-environmental policy.⁹

Of particular concern in this respect is the proposal to make 30 % of the EU’s Common Agricultural Policy direct payments after 2013 conditional on observation of specific environmentally friendly management practices, particularly creation of ecological focus areas. Whether this is a cost-efficient use of resources for environmental protection is potentially a major welfare economic issue: could the €39 billion that is being distributed to farmers annually in the EU be reallocated to generate larger environmental benefits? The more precise question our analysis provokes is whether all farmers in the EU should be paid for providing environmental services (since the area-based payment levels are so high that it amounts to an offer that the reasonable farmer could not refuse)? Or should an opening be made for split solutions and the development of specialist environmental providers that give taxpayers more bang for the buck?

Finally, note that the problem as we have formulated it is closely related to the basic microeconomics of production. In that literature, a traditional scenario is one with many symmetric firms producing the same good. A central question is then how much of the good each firm should produce, and hence (given market demand) how many firms there will be in equilibrium. If the average cost curve of a single firm is monotonically increasing (i.e. always upward-sloping) then we will have an infinite number of small firms; if the average cost curve is monotonically decreasing (downward-sloping) then we have a natural monopoly with a single firm; and if the average cost curve is U-shaped (typically due to a combination of fixed costs and increasing marginal costs) then a given quantity of final product will be produced by a finite number of firms, which may be as low as 1 if market demand is satisfied by production of a single firm on the downward-sloping part of its average cost curve.

In our analysis we have a symmetric area of land, and the question is how much nature should be produced on each unit of land. When the average cost function for nature production on a given unit of land is monotonically increasing then nature production is spread as thinly as possible across the available area; the corresponding result in the production problem is that there is an infinite number of small firms. On the other hand, when average cost functions for nature production are monotonically decreasing then production of nature should be concentrated on as small an area as is possible, with farms on the remaining area maximizing profits; the corresponding result is natural monopoly. Finally, when average cost functions for nature production are U-shaped then the nature of the solution depends on the quantity of nature to be produced. For small quantities of nature, production is concentrated on a subset of farms (which each produce nature at minimum long-run average cost) but when the entire region is under such production then further increases in nature production are best achieved by uniform increases in nature production across the region. Again, we can compare to a natural monopoly where, if the demand curve shifts sufficiently to the right, additional firms enter the market.