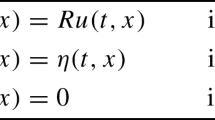An Eulerian–Lagrangian method for optimization problems governed by multidimensional nonlinear hyperbolic PDEs

Abstract

We present a numerical method for solving tracking-type optimal control problems subject to scalar nonlinear hyperbolic balance laws in one and two space dimensions. Our approach is based on the formal optimality system and requires numerical solutions of the hyperbolic balance law forward in time and its nonconservative adjoint equation backward in time. To this end, we develop a hybrid method, which utilizes advantages of both the Eulerian finite-volume central-upwind scheme (for solving the balance law) and the Lagrangian discrete characteristics method (for solving the adjoint transport equation). Experimental convergence rates as well as numerical results for optimization problems with both linear and nonlinear constraints and a duct design problem are presented.

1 Introduction

We are concerned with numerical approaches for optimization problems governed by hyperbolic PDEs in both one and two space dimensions. As a prototype, we consider a tracking type problem for a terminal state $u_d$ prescribed at some given time $t=T$ and the control acts as initial condition $u_0$. A mathematical formulation of this optimal control problem is reduced to minimizing a functional, and, for instance, in the two-dimensional (2-D) case it can be stated as follows:

$$\begin{aligned} \min _{u_0}J(u(\cdot ,\cdot ,T);u_d(\cdot ,\cdot )),\quad \end{aligned}$$

(1.1a)

where $J$ is a given functional and $u$ is the unique entropy solution of the nonlinear scalar balance law

$$\begin{aligned} \begin{aligned} u_t+f(u)_x+g(u)_y&=h(u,x,y,t),\quad (x,y)\in \Omega \subseteq \mathbb {R}^2,\quad t>0,\\ u(x,y,0)&=u_0(x,y),\qquad \quad (x,y)\in \Omega \subseteq \mathbb {R}^2. \end{aligned} \end{aligned}$$

(1.1b)

If $\Omega \ne \mathbb {R}^2$, then (1.1b) is supplemented by appropriate boundary conditions.

In recent years, there has been tremendous progress in both analytical and numerical studies of problems of type (1.1a), (1.1b), see, e.g., [1–3, 8–10, 13, 18, 19, 21–24, 28, 40, 44, 45]. Its solution relies on the property of the evolution operator $\mathcal{S}_t: u_0(\cdot ,\cdot )\rightarrow u(\cdot ,\cdot ,t)=\mathcal{S}_tu_0(\cdot ,\cdot )$ for (1.1b). It is known that the semi-group $\mathcal{S}_t$ generated by a nonlinear hyperbolic conservation/balance law is generically nondifferentiable in $L^1$ even in the scalar one-dimensional (1-D) case (see, e.g., [10, Example 1]). A calculus for the first-order variations of $\mathcal{S}_tu$ with respect to $u_0$ has been established in [10, Theorems 2.2 and 2.3] for general 1-D systems of conservation laws with a piecewise Lipschitz continuous $u_0$ that contains finitely many discontinuities. Therein, the concept of generalized first order tangent vectors has been introduced to characterize the evolution of variations with respect to $u_0,$ see [10, equations (2.16)–(2.18)]. This result has been extended to BV initial data in [3, 8] and lead to the introduction of a differential structure for $u_0\rightarrow \mathcal{S}_tu_0$, called shift-differentiability, see e.g. [3, Definition 5.1]. Related to that equations for the generalized cotangent vectors have been introduced for 1-D systems in [11, Proposition 4]. These equations (also called adjoint equations) consists of a nonconservative transport equation [11, equation (4.2)] and an ordinary differential equation [11, equations (4.3)–(4.5)] for the tangent vector and shift in the positions of possible shocks in $u(x,t)$, respectively. Necessary conditions for a general optimal control problem have been established in [11, Theorem 1]. However, this result was obtained using strong assumptions on $u_0$ (see [11, Remark 4] and [3, Example 5.5]), which in the 1-D scalar case can be relaxed as shown for example in [13, 44, 46]. We note that the nonconservative transport part of the adjoint equation has been intensively studied also independently from the optimal control context. In the scalar case we refer to [4, 5, 6, 13, 36, 44, 46] for a notion of solutions and properties of solutions to those equations. The multidimensional nonconservative transport equation was studied in [7], but without a discussion of optimization issues. Analytical results for optimal control problems in the case of a scalar hyperbolic conservation law with a convex flux have also been developed using a different approach in [44, 46].

Numerical methods for the optimal control problems have been discussed in [2, 20, 22, 44, 46]. In [18, 19], the adjoint equation has been discretized using a Lax–Friedrichs-type scheme, obtained by including conditions along shocks and modifying the Lax–Friedrichs numerical viscosity. Convergence of the modified Lax–Friedrichs scheme has been rigorously proved in the case of a smooth convex flux function. Convergence results have also been obtained in [44] for the class of schemes satisfying the one-sided Lipschitz condition (OSLC) and in [2] for implicit-explicit finite-volume methods.

In [13], analytical and numerical results for the optimal control problem (1.1a) coupled with the 1-D inviscid Burgers equation have been presented in the particular case of a least-square cost functional $J$. Therein, existence of a minimizer $u_0$ was proven, however, uniqueness could not be obtained for discontinuous $u$. This result was also extended to the discretized optimization problem provided that the numerical schemes satisfy either the OSLC or discrete Oleinik’s entropy condition. Furthermore, convergence of numerical schemes was investigated in the case of convex flux functions and with a-priori known shock positions, and numerical resolution of the adjoint equations in both the smooth and nonsmooth cases was studied.

In this paper, we consider the problem (1.1a), (1.1b) with the least-square cost functional,

$$\begin{aligned} J(u(\cdot ,\cdot ,T);u_d(\cdot ,\cdot )):= \frac{1}{2}\int \int \limits _\Omega \bigl (u(x,y,T)-u_d(x,y)\bigr )^2\,dx\,dy, \end{aligned}$$

(1.1c)

and a general nonlinear scalar hyperbolic balance law. To the best of our knowledge, there is no analytical calculus available for the multidimensional problem (1.1a)–(1.1c). We therefore study the problem numerically and focus on designing highly accurate and robust numerical approach for both the forward equation and the nonconservative part of the adjoint equation (leaving aside possible additional conditions necessary to track the variations of shock positions). We treat the forward and adjoint equations separately: The hyperbolic balance law (1.1b) is numerically solved forward in time from $t=0$ to $t=T$, while the corresponding adjoint linear transport equation is integrated backward in time from $t=T$ to $t=0$. Since these two equations are of a different nature, they are attempted by different numerical methods in contrast to [13, 18, 19, 44].

The main source of difficulty one comes across while numerically solving the forward equation is the loss of smoothness, that is, the solution may develop shocks even for infinitely smooth initial data. To accurately resolve the shocks, we apply a high-resolution shock capturing Eulerian finite-volume method to (1.1b), in particular, we use a second-order semi-discrete central-upwind scheme introduced in [31–34], which is a reliable “black-box” solver for general multidimensional (systems of) hyperbolic conservation and balance laws.

The nonconservative part of the arising adjoint equation is a linear transport equation with generically discontinuous coefficients, and thus the adjoint equation is hard to accurately solve by conventional Eulerian methods. We therefore use a Lagrangian approach to numerically trace the solution of the adjoint transport equation along the backward characteristics. The resulting Lagrangian method achieves a superb numerical resolution thanks to its low numerical dissipation.

The paper is organized as follows. In Sect. 2, we briefly revise the formal adjoint calculus and additional interior conditions on the shock position in the 1-D case. Then, in Sect. 3 we present an iterative numerical optimization algorithm followed by the description of our hybrid Eulerian–Lagrangian numerical method, which is applied to a variety of 1-D and 2-D optimal control problems in Sect. 4. Convergence properties of the designed 1-D scheme are discussed in Sect. 5.

2 The adjoint equation

We are interested in solving the optimization problem (1.1a)–(1.1c). Formally, we proceed as follows: We introduce the Lagrangian for this problem as

$$\begin{aligned} L(u,p)&= \frac{1}{2}\int \int \limits _{\mathbb {R}^2} \big (u(x,y,T)-u_d(x,y)\big )^2\,dx\,dy\\&-\int \int \limits _{\mathbb {R}^2} p\big (u_t+f(u)_x+g(u)_y-h(u,x,y,t)\big ) \,dx\,dy. \end{aligned}$$

We integrate by parts and compute the variations with respect to $u$ and $p$. In a strong formulation, the variation with respect to $p$ leads to (1.1b) while the variation with respect to $u$ results in the following adjoint equation:

$$\begin{aligned} -p_t-f'(u)p_x-g'(u)p_y=h_u(u,x,y,t)\,p, \end{aligned}$$

(2.1a)

subject to the terminal condition

$$\begin{aligned} p(x,y,T)= u(x,y,T)-u_d(x,y). \end{aligned}$$

(2.1b)

For sufficiently smooth solutions $u$, the above calculations are exact and the coupled systems (1.1b), (2.1a), (2.1b) together with

$$\begin{aligned} p(x,y,0)=0~\text{ a.e. }~(x,y)\in \mathbb {R}^2 \end{aligned}$$

(2.2)

represent the first-order optimality system for problem (1.1a)–(1.1c), in which (1.1b) should be solved forward in time while the adjoint problem (2.1a), (2.1b) is to be solved backward in time. These computations however have to be seriously modified once the solution $u$ possesses discontinuities. This was demonstrated in [8, 10, 13, 18, 21, 44] and we will now briefly review the relevant results.

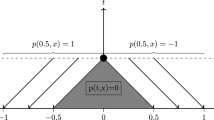
Consider a scalar 1-D conservation law $u_t+f(u)_x=0$ subject to the initial data $u(x,0)=u_0(x)$. Denote its weak solution by $u(\cdot ,t)=\mathcal{S}_t u_0(\cdot ).$ Assume that both the solution $u(x,t)$ and initial data $u_0(x)$ contain a single discontinuity at $x_s(t)$ and $x_s(0)$, respectively, and that $u(x,t)$ is smooth elsewhere. As discussed above, the first-order variation of $\mathcal{S}_t$ with respect to $u_0$ can be computed using, for example, the concept of shift-differentiability, and in the assumed situation, this amounts to considering the corresponding linearized shock position $\hat{x}_s$ given by $\frac{d}{dt}\left( \hat{x}_s(t)[u(\cdot ,t)]\right) = [(f'(u)-\frac{d}{dt}x_s(t)\hat{u})(\cdot ,t)]$, where $[u(\cdot ,t)]=u(x_s(t)+,t)-u(x_s(t)-,t)$. Here, $\hat{u}$ is a solution of the linearized PDE

$$\begin{aligned} \hat{u}_t+(f'(u)\hat{u})_x=0. \end{aligned}$$

Using the variations $(\hat{u},\hat{x})$ shift-differentiability of the nonlinear cost functional $J(u(\cdot ,T),u_d(\cdot ))= J(\mathcal{S}_tu_0(\cdot ),u_d(\cdot ))$ is also obtained, see [13, 21, 25, 44]. It can be shown that the variation $\delta J(\mathcal{S}_tu_0)\hat{u}$ of $J$ with respect to $u_0$ can be also expressed using an adjoint (or cotangent vector) formulation. More precisely, it has been shown in [18] that in the particular setting considered above,

$$\begin{aligned} \delta J(\mathcal{S}_tu_0)(\hat{u})=\int \limits _{\mathbb {R}}p(x,0)\hat{u}(x,0)\,dx, \end{aligned}$$

(2.3)

$p(x,T)=u(x,T)-u_d(x)$ and $p(x_s(t),t)= \frac{1}{2} [\left( u-u_d\right) ^2 ]_T/[u]_T$, where $[u]_T$ represents the jump in u(x,T) across the shock at the final time. This value can be viewed as a finite difference approximation to the derivative $u-u_d$ being the adjoint solution on either side of the shock. The latter condition requires that the adjoint solution is constant on all characteristics leading into the shock. Those rigorous results hold true once the shock position in the solution $u$ is a-priori known. For $u_0$ to be optimal we require the variation on the left-hand side of (2.3) to be equal to zero for all feasible variations $\hat{u}$.

In [19], the above result has been extended to the 1-D scalar convex case with smooth initial data that break down over time. Note that due to the nature of the adjoint equation, the region outside the extremal backwards characteristics emerging at $x_s(T)$ are independent on the value along $x_s(t)$. Hence, neglecting this condition yields nonuniqueness of the solution $p$ in the area leading into the shock, see [2, 10, 13, 44]. A recent numerical approach in [18] is based on an attempt to capture the behavior inside the region leading into the shock by adding a diffusive term to the scheme with a viscosity depending on the grid size. The results show a convergence rate of $(\Delta x)^\alpha$ with $\alpha <1$. However, to the best of our knowledge, no multidimensional extension of the above approach is available.

In this paper, we focus on the development of suitable numerical discretizations of both forward and adjoint equations. The forward equation is solved using a second-order Godunov-type central-upwind scheme [31–34], which is based on the evolution of a piecewise polynomial reconstruction of $u$. The latter is then used to solve the adjoint equation by the method of characteristics applied both outside and inside the region entering shock(s). Similar to [2] we therefore expect convergence of the proposed method outside the region of the backwards shock. We numerically study the behavior of $J$ and demonstrate that even in the case of evolving discontinuities, the desired profile $u_d$ can be recovered using the presented approach.

Since the systems (1.1b) and (2.1a), (2.1b) are fully coupled, an iterative procedure is to be imposed in order to solve the optimization problem. This approach can either be seen as a damped block Gauss-Seidel method for the system or as a gradient descent for the reduced cost functional. The reduced cost functional $\tilde{J}(u_0):=J(\mathcal{S}_tu_0;u_d)$ is obtained when replacing $u$ in (1.1a) by $\mathcal{S}_tu_0$. Then, a straightforward computation shows that $\frac{\delta }{\delta u_0}\tilde{J}(u_0)=p(\cdot ,\cdot ,0)$ if no shocks are present. As discussed above, rigorous results on the linearized cost in the presence of shocks are available only in the 1-D case, see [18, 21] and [13, Proposition 4.1, Remark 4.7 and Proposition 5.1].

3 Numerical method

In this section, we describe the iterative optimization algorithm along with the Eulerian–Lagrangian numerical method used in its implementation.

The underlying optimization problem can be formulated as follows: Given a terminal state $u_d(x,y)$, find an initial datum $u_0(x,y)$ which by time $t=T$ will either evolve into $u(x,y,T)=u_d(x,y)$ or will be as close as possible to $u_d$ in the $L^2$-norm. To solve the problem iteratively, we implement the following algorithm and generate a sequence $\{u_0^{(m)}(x)\},\ m=0,1,2,\ldots$.

Iterative Optimization Algorithm

• 1. Choose an initial guess $u_0^{(0)}(x,y)$ and prescribed tolerance $tol$.

• 2. Solve the problem (1.1b) with $u(x,y,0)=u_0^{(0)}(x,y)$ forward in time from $t=0$ to $t=T$ by an Eulerian finite-volume method (described in Sect. 3.1) to obtain $u^{(0)}(x,y,T)$.

• 3. Iterations for $m=0,1,2,\dots$ while $~\displaystyle {J(u^{(m)};u_d)=\frac{1}{2}\int \int \limits _\Omega \bigl (u^{(m)}(x,y,T)-u_d(x,y)\bigr )^2\,dx\,dy>tol}$ or while $~\displaystyle {|J(u^{(m)};u_d)-J(u^{(m-1)};u_d)|>tol}$

• (a) Solve the linear transport equation (2.1a) subject to the terminal condition $p^{(m)}(x,y,T):=u^{(m)}(x,y,T)-u_d(x,y)$ backward in time from $t=T$ to $t=0$ using the Lagrangian numerical scheme (described in Sect. 3.2) to obtain $p^{(m)}(x,y,0)$.

• (b) Update the control $u_0$ using either a gradient descent or quasi-Newton method [12, 29, 42].

• (c) Solve the problem (1.1b) with $u(x,y,0)=u_0^{(m+1)}(x,y)$ forward in time from $t=0$ to $t=T$ by an Eulerian finite-volume method (described in Sect. 3.1) to obtain $u^{(m+1)}(x,y,T)$.

• (d) Set $m:=m+1$.

Remark 3.1

Note that in the given approach the full solution $u$ needs not to be stored during the iteration.

Remark 3.2

The above algorithm is similar to the continuous approach from [13] though, unlike [13], we focus on the numerical methods in steps 2, 3(a) and 3(c) and thus do not use an approximation to the generalized tangent vectors to improve the gradient descent method.

Remark 3.3

If we use a steepest descent update in step 3(b) for some stepsize $\sigma >0$ as

$$\begin{aligned} u_0^{(m+1)}(x,y):=u_0^{(m)}(x,y)-\sigma p^{(m)}(x,y,0), \end{aligned}$$

then, due to a global finite-volume approximation of $u$ and an appropriate projection of $p$ (see Sect. 3.1), we obtain a piecewise polynomial control $u_0^{(m+1)}$ in this step of the algorithm. The fact that the control $u_0^{(m+1)}$ is always piecewise polynomial prevents the accumulation of discontinuities in the forward solution in our algorithm. Clearly, other (higher-order) gradient-based optimization methods can be used to speed up the convergence, especially in the advance stages of the above iterative procedure, see, e.g., [29, 42] for more details.

Remark 3.4

In [13], a higher number of iterations is reported when the adjoints to the Rankine–Hugoniot condition are neglected. In view of 2-D examples, we opt in this paper for the higher number of optimization steps $m$ compared with the necessity to recompute the shock location and solve for the adjoint linearized Rankine–Hugoniot condition.

3.1 Finite-volume method for (1.1b)

In this section, we briefly describe a second-order semi-discrete central-upwind scheme from [34] (see also [31–33]), which has been applied in steps 2 and 3(c) in our iterative optimization algorithm on page 5.

We start by introducing a uniform spatial grid, which is obtained by dividing the computational domain into finite-volume cells $C_{j,k}:=[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}]\times [y_{k-\frac{1}{2}},y_{k+\frac{1}{2}}]$ with $x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}}=\Delta x,\ \forall j$ and $y_{k+\frac{1}{2}}-y_{k-\frac{1}{2}}=\Delta y,\ \forall k$. We assume that at a certain time $t$, the computed solution is available and realized in terms of its cell averages

$$\begin{aligned} \overline{u}_{j,k}(t)\approx \frac{1}{\Delta x\Delta y}\int \int \limits _{C_{j,k}}u(x,y,t)\,dx\,dy. \end{aligned}$$

according to the central-upwind approach, the cell averages are evolved in time by solving the following system of ODEs:

$$\begin{aligned} \frac{d}{dt}\overline{u}_{j,k}(t)=-\frac{F_{{j+\frac{1}{2}},k}-F_{{j-\frac{1}{2}},k}}{\Delta x}-\frac{G_{j,{k+\frac{1}{2}}}-G_{j,{k-\frac{1}{2}}}}{\Delta y}+ h(\overline{u}_{j,k},x_j,y_k,t), \end{aligned}$$

(3.1)

using an appropriate ODE solver. In this paper, we implement the third-order strong stability preserving Runge–Kutta (SSP RK) method from [26].

The numerical fluxes $F$ and $G$ in (3.1) are given by (see [31, 34] for details):

$$\begin{aligned} \begin{aligned} F_{{j+\frac{1}{2}},k}&=\frac{a^+_{{j+\frac{1}{2}},k}f(u^\mathrm{E}_{j,k})-a^-_{{j+\frac{1}{2}},k}f(u^\mathrm{W}_{j+1,k})}{a^+_{{j+\frac{1}{2}},k}-a^-_{{j+\frac{1}{2}},k}} +\frac{a^+_{{j+\frac{1}{2}},k}a^-_{{j+\frac{1}{2}},k}}{a^+_{{j+\frac{1}{2}},k}-a^-_{{j+\frac{1}{2}},k}}\left[ u^\mathrm{W}_{j+1,k}-u^\mathrm{E}_{j,k}\right] , \\ G_{j,{k+\frac{1}{2}}}&=\frac{b^+_{j,{k+\frac{1}{2}}}g(u^\mathrm{N}_{j,k})-b^-_{j,{k+\frac{1}{2}}}g(u^\mathrm{S}_{j,k+1})}{b^+_{j,{k+\frac{1}{2}}}-b^-_{j,{k+\frac{1}{2}}}} +\frac{b^+_{j,{k+\frac{1}{2}}}b^-_{j,{k+\frac{1}{2}}}}{b^+_{j,{k+\frac{1}{2}}}-b^-_{j,{k+\frac{1}{2}}}}\left[ u^\mathrm{S}_{j,k+1}-u^\mathrm{N}_{j,k}\right] . \end{aligned} \end{aligned}$$

(3.2)

Here, $u^\mathrm{E,W,N,S}_{j,k}$ are the point values of the piecewise linear reconstruction for $u$

$$\begin{aligned} \widetilde{u}(x,y):=\overline{u}_{j,k}+(u_x)_{j,k}(x-x_j)+(u_y)_{j,k}(y-y_k),\quad (x,y)\in C_{j,k}, \end{aligned}$$

(3.3)

at $(x_{{j+\frac{1}{2}}},y_k)$, $(x_{{j-\frac{1}{2}}},y_k)$, $(x_j,y_{{k+\frac{1}{2}}})$, and $(x_j,y_{{k-\frac{1}{2}}})$, respectively. Namely, we have:

$$\begin{aligned} \begin{aligned}&u^\mathrm{E}_{j,k}:=\widetilde{u}(x_{{j+\frac{1}{2}}}-0,y_k)=\overline{u}_{j,k}+\frac{\Delta x}{2}(u_x)_{j,k},\quad u^\mathrm{W}_{j,k}:=\widetilde{u}(x_{{j-\frac{1}{2}}}+0,y_k)=\overline{u}_{j,k}\\&\qquad \qquad -\frac{\Delta x}{2}(u_x)_{j,k},\\&u^\mathrm{N}_{j,k}:=\widetilde{u}(x_j,y_{{k+\frac{1}{2}}}-0)=\overline{u}_{j,k}+\frac{\Delta y}{2}(u_y)_{j,k},\quad u^\mathrm{S}_{j,k}:=\widetilde{u}(x_j,y_{{k-\frac{1}{2}}}+0)=\overline{u}_{j,k}\\&\qquad \qquad -\frac{\Delta y}{2}(u_y)_{j,k}. \end{aligned} \end{aligned}$$

(3.4)

The numerical derivatives $(u_x)_{j,k}$ and $(u_y)_{j,k}$ are (at least) first-order approximations of $u_x(x_j,y_k,t)$ and $u_y(x_j,y_k,t)$, respectively, and are computed using a nonlinear limiter that would ensure a non-oscillatory nature of the reconstruction (3.3). In our numerical experiments, we have used a generalized minmod reconstruction [35, 37, 43, 47]:

$$\begin{aligned} \begin{aligned}&(u_x)_{j,k}=\mathrm{minmod}\left( \theta \frac{\overline{u}_{j,k}-\overline{u}_{j-1,k}}{\Delta x},\, \frac{\overline{u}_{j+1,k}-\overline{u}_{j-1,k}}{2\Delta x},\,\theta \frac{\overline{u}_{j+1,k}- \overline{u}_{j,k}}{\Delta x}\right) ,\\&(u_y)_{j,k}=\mathrm{minmod}\left( \theta \frac{\overline{u}_{j,k}-\overline{u}_{j,k-1}}{\Delta y},\, \frac{\overline{u}_{j,k+1}-\overline{u}_{j,k-1}}{2\Delta y},\,\theta \frac{\overline{u}_{j,k+1}- \overline{u}_{j,k}}{\Delta y}\right) , \end{aligned} \qquad \theta \in [1,2]. \end{aligned}$$

(3.5)

Here, the minmod function is defined as

$$\begin{aligned} \mathrm{minmod}(z_1,z_2,...):=\left\{ \begin{array}{lc} \!\min _j\{z_j\}, &{} ~~\text{ if } ~~z_j>0 ~~\forall j,\\ \!\max _j\{z_j\}, &{} ~~\text{ if } ~~z_j<0 ~~\forall j,\\ \!0, &{}\text{ otherwise }.\end{array}\right. \end{aligned}$$

The parameter $\theta$ is used to control the amount of numerical viscosity present in the resulting scheme: larger values of $\theta$ correspond to less dissipative but, in general, more oscillatory reconstructions. In all of our numerical experiments, we have taken $\theta =1.5$.

The one-sided local speeds in the $x$- and $y$-directions, $a^\pm _{{j+\frac{1}{2}},k}$ and $b^\pm _{j,{k+\frac{1}{2}}}$, are determined as follows:

$$\begin{aligned} \begin{aligned}&a^+_{{j+\frac{1}{2}},k}=\max \left\{ \max \limits _{u\in \left[ \min \{u^\mathrm{E}_{j,k},u^\mathrm{W}_{j+1,k}\}, \max \{u^\mathrm{E}_{j,k},u^\mathrm{W}_{j+1,k}\}\right] }f'(u),0\right\} ,\\&a^-_{{j+\frac{1}{2}},k}=\min \left\{ \min \limits _{u\in \left[ \min \{u^\mathrm{E}_{j,k},u^\mathrm{W}_{j+1,k}\}, \max \{u^\mathrm{E}_{j,k},u^\mathrm{W}_{j+1,k}\}\right] }f'(u),0\right\} ,\\&b^+_{j,{k+\frac{1}{2}}}=\max \left\{ \max \limits _{u\in \left[ \min \{u^\mathrm{N}_{j,k},u^\mathrm{S}_{j,k+1}\}, \max \{u^\mathrm{N}_{j,k},u^\mathrm{S}_{j,k+1}\}\right] }g'(u),0\right\} ,\\&b^-_{j,{k+\frac{1}{2}}}=\min \left\{ \min \limits _{u\in \left[ \min \{u^\mathrm{N}_{j,k},u^\mathrm{S}_{j,k+1}\}, \max \{u^\mathrm{N}_{j,k},u^\mathrm{S}_{j,k+1}\}\right] }g'(u),0\right\} . \end{aligned} \end{aligned}$$

(3.6)

Remark 3.5

In equations (3.1)–(3.6), we suppress the dependence of $\overline{u}_{j,k}$, $F_{{j+\frac{1}{2}},k}$, $G_{j,{k+\frac{1}{2}}}$, $u^\mathrm{E,W,N,S}_{j,k}$, $(u_x)_{j,k}$, $(u_y)_{j,k}$, $a^\pm _{{j+\frac{1}{2}},k}$, and $b^\pm _{j,{k+\frac{1}{2}}}$ on $t$ to simplify the notation.

Remark 3.6

We solve the balance law (1.1b) starting from time $t^0=0$ and compute the solution at time levels $t^n$, $n=1,\ldots ,N_T$, where $t^{N_T}=T$. Since the obtained approximate solution is to be used for solving the adjoint problem backward in time, we store the values of $u$ and its discrete derivatives, $u_x$ and $u_y$, so the piecewise linear approximants (3.3) are available at all of the time levels.

3.2 Discrete method of characteristics for (2.1a), (2.1b)

We finish the description of the proposed Eulerian–Lagrangian numerical method by presenting the Lagrangian method for the backward transport equation (2.1a).

Since equation (2.1a) is linear (with possibly discontinuous coefficients), we follow [14, 15] and solve it using the Lagrangian approach, which is a numerical version of the method of characteristics. In this method, the solution is represented by a certain number of its point values prescribed at time $T$ at the points $(x_i^\mathrm{c}(T),y_i^\mathrm{c}(T))$, which may (or may not) coincide with the uniform grid points $(x_j,y_k)$ used in the numerical solution of the forward problem (1.1b). The location of these characteristics points is tracked backward in time by numerically solving the following system of ODEs:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx_i^\mathrm{c}(t)}{dt}=f'(u(x_i^\mathrm{c}(t),y_i^\mathrm{c}(t),t)),\\&\frac{dy_i^\mathrm{c}(t)}{dt}=g'(u(x_i^\mathrm{c}(t),y_i^\mathrm{c}(t),t)),\\&\frac{dp_i^\mathrm{c}(t)}{dt}=-h_u\big (u(x_i^\mathrm{c}(t),y_i^\mathrm{c}(t),t),x_i^\mathrm{c}(t),y_i^\mathrm{c}(t),t\big ) p_i^\mathrm{c}(t), \end{aligned}\right. \end{aligned}$$

(3.7)

where $x_i^\mathrm{c}(t),y_i^\mathrm{c}(t)$ is a position of the $i$th characteristics point at time $t$ and $p_i^\mathrm{c}(t)$ is a corresponding value of $p$ at that point.

Notice that since the piecewise linear approximants $\widetilde{u}$ are only available at the discrete time levels $t=t^n,\,n=0,\ldots ,N_T$, we solve the system (3.7) using the second-order SSP RK method (the Heun method), see [26]. Unlike the third-order SSP RK method, the Heun method only uses the data from the current time level and the previous one and does not require data from any intermediate time levels. This is the main advantage of the Heun method since the right-hand side of (3.7) can be easily computed at each discrete time level $t=t^n$. To this end, we simply check at which finite-volume cell the characteristics point is located at a given discrete time moment, and then set

$$\begin{aligned} \begin{aligned}&u(x_i^\mathrm{c}(t^n), y_i^\mathrm{c}(t^n),t^n)=\widetilde{u}(x_i^\mathrm{c}(t^n),y_i^\mathrm{c}(t^n),t^n)\\&\quad =\overline{u}_{j,k}^n+(u_x)_{j,k}^n\big (x_i^\mathrm{c}(t^n)-x_j\big )+(u_y)_{j,k}^n\big (y_i^\mathrm{c}(t^n)-y_k\big ), ~~\text{ if }~(x_i^\mathrm{c}(t^n),y_i^\mathrm{c}(t^n)){\in } C_{j,k}. \end{aligned} \end{aligned}$$

(3.8)

Thus, as the time reaches 0, we will have the set of the characteristics points $(x_i^\mathrm{c}(0),y_i^\mathrm{c}(0))$ and the corresponding point values $p_i^\mathrm{c}(0)$. We then obtain the updated initial data (step 3(b) in our iterative optimization algorithm on page 5) by first setting

$$\begin{aligned} u_0^{(m+1)}(x_i^\mathrm{c}(0),y_i^\mathrm{c}(0)):=u_0^{(m)}(x_i^\mathrm{c}(0),y_i^\mathrm{c}(0))-\sigma p_i^\mathrm{c}(0), \end{aligned}$$

(3.9)

where $\sigma =\mathcal{O}(\Delta x)$, and then projecting the resulting set of discrete data onto the uniform grid. The latter is done as follows: For a given grid point $(x_j,y_k)$, we find four characteristics points $(x_{i_1}^\mathrm{c}(0),y_{k_1}^\mathrm{c}(0))$, $(x_{i_2}^\mathrm{c}(0),y_{k_2}^\mathrm{c}(0))$, $(x_{i_3}^\mathrm{c}(0),y_{k_3}^\mathrm{c}(0))$, and $(x_{i_4}^\mathrm{c}(0),y_{k_4}^\mathrm{c}(0))$ such that

$$\begin{aligned} \begin{aligned}&\left( x_{i_1}^\mathrm{c}(0){-}x_j\right) ^2{+}\left( y_{i_1}^\mathrm{c}(0){-}y_k\right) ^2= \min \limits _{i:\ x_{i_1}^\mathrm{c}(0)>x_j,\ y_{i_1}^\mathrm{c}(0)>y_k} \left[ \left( x_i^\mathrm{c}(0){-}x_j\right) ^2{+}\left( y_i^\mathrm{c}(0){-}y_k\right) ^2\right] ,\\&\left( x_{i_2}^\mathrm{c}(0){-}x_j\right) ^2{+}\left( y_{i_2}^\mathrm{c}(0){-}y_k\right) ^2= \min \limits _{i:\ x_{i_2}^\mathrm{c}(0)<x_j,\ y_{i_2}^\mathrm{c}(0)>y_k} \left[ \left( x_i^\mathrm{c}(0){-}x_j\right) ^2{+}\left( y_i^\mathrm{c}(0){-}y_k\right) ^2\right] ,\\&\left( x_{i_3}^\mathrm{c}(0){-}x_j\right) ^2{+}\left( y_{i_3}^\mathrm{c}(0){-}y_k\right) ^2= \min \limits _{i:\ x_{i_3}^\mathrm{c}(0)<x_j,\ y_{i_3}^\mathrm{c}(0)<y_k} \left[ \left( x_i^\mathrm{c}(0){-}x_j\right) ^2{+}\left( y_i^\mathrm{c}(0){-}y_k\right) ^2\right] ,\\&\left( x_{i_4}^\mathrm{c}(0){-}x_j\right) ^2{+}\left( y_{i_4}^\mathrm{c}(0){-}y_k\right) ^2= \min \limits _{i:\ x_{i_4}^\mathrm{c}(0)>x_j,\ y_{i_4}^\mathrm{c}(0)<y_k} \left[ \left( x_i^\mathrm{c}(0){-}x_j\right) ^2{+}\left( y_i^\mathrm{c}(0){-}y_k\right) ^2\right] , \end{aligned} \end{aligned}$$

(3.10)

and then use a bilinear interpolation between these four characteristics points to obtain $u_0^{(m+1)}(x_j,y_k)$.

We are then ready to proceed with the next, $(m+1)$-st iteration.

Remark 3.7

In the 1-D case, the projection procedure from the characteristics points onto the uniform grid simplifies significantly, as one just needs to locate the two characteristics points that are closest to the given grid point from the left and from the right, and then use a linear interpolation.

Remark 3.8

It is well-known that one of the difficulties emerging when Lagrangian methods are applied to linear transport equations with discontinuous coefficients is that the distances between characteristics points constantly change. As a result, characteristics points may either cluster or spread too far from each other. This may lead not only to a poor resolution of the computed solution, but also to an extremely low efficiency of the method. To overcome this difficulties, we either add characteristics points to fill appearing gaps between the points (the solution values at the added points can be obtained using a similar bilinear/linear interpolation) or remove some of the clustered characteristics points.

Remark 3.9

Notice that if $u_d(x,y)$ is discontinuous, the solution of the optimization problem is not unique: Due to the loss of information at the shock, there will be infinitely many different initial data $u_0(x,y)$, which would lead to the same solution of (1.1b).

Remark 3.10

It should be observed that the solution of the adjoint transport equation (2.1a) can be computed back in time using different methods. We refer the reader, e.g., to [25], where several first-order discretizations of the 1-D transport equation without source terms have been presented and analyzed. In the numerical results below, we compare the proposed discrete method of characteristics with an upwind approach from [25] when applied to the 1-D equation (2.1a) (see Example 1 in Sect. 4.1).

4 Numerical results

In this section, we illustrate the performance of the proposed method on a number of numerical examples. We start with a grid convergence study by considering a linear advection equation in (1.1b) as a constraint. We then consider a control problem of the inviscid Burgers equation and demonstrate the non-uniqueness of optimal controls in the case of nonsmooth desired state. Next, we numerically solve a duct design problem modified from [44]. Finally, we apply the proposed method to the 2-D inviscid Burgers equation.

4.1 The one-dimensional case

In this section, we consider the 1-D version of the optimization problem (1.1a)–(1.1c):

$$\begin{aligned} \min _{u_0}J(u(\cdot ,T);u_d(\cdot )),\quad J(u(\cdot ,T);u_d(\cdot )):= \frac{1}{2}\int \limits _I\bigl (u(x,T)-u_d(x)\bigr )^2\,dx, \end{aligned}$$

(4.1a)

where $u$ is a solution of the scalar hyperbolic PDE

$$\begin{aligned} \begin{array}{cl} u_t+f(u)_x=h(u,x,t),&{}\quad x\in I\subseteq \mathbb {R},\quad t>0,\\ u(x,0)=u_0(x),&{}\quad x\in I\subseteq \mathbb {R}. \end{array} \end{aligned}$$

(4.1b)

If $I\ne \mathbb {R}$, then (4.1b) is augmented with appropriate boundary conditions.

The corresponding adjoint problem is

$$\begin{aligned} \begin{aligned} -p_t-f'(u)p_x&=h_u(u,x,t)p,&\quad x\in I\subseteq \mathbb {R},\quad t>0,\\ p(x,T)&=p_T(x):=u(x,T)-u_d(x)&\quad x\in I\subseteq \mathbb {R}. \end{aligned} \end{aligned}$$

(4.2)

4.1.1 Example 1: Linear constraints

We numerically solve the optimization problem (4.1a)–(4.1b) with the terminal state $u_d(x)=e^{-(x-\pi )^2}$ and subject to a linear advection equation as constraint:

$$\begin{aligned} u_t+u_x=0,\quad x\in [0,2\pi ],\quad t>0, \end{aligned}$$

(4.3)

with the periodic boundary conditions. The corresponding adjoint equation is

$$\begin{aligned} -p_t-p_x=0\quad x\in [0,2\pi ],\quad t<T. \end{aligned}$$

(4.4)

Since both (4.3) and (4.4) are linear advection equations with constant coefficients, the exact solution $u_0$ of the studied optimization problem is unique and can be easily obtained:

$$\begin{aligned} u_{0}(x)=u_{d}(x-T). \end{aligned}$$

(4.5)

In this example, we start the iterative optimization algorithm (page 5) with the constant initial condition,

$$\begin{aligned} u_0^{(0)}(x)\equiv 0.5, \end{aligned}$$

and illustrate that the proposed Eulerian–Lagrangian method is second-order accurate. We use spatial grids with $\Delta x=2\pi /100,2\pi /200, 2\pi /400$ and $2\pi /800$ for the Eulerian part of the method and the corresponding number of the characteristics points (100, 200, 400 or 800) for the Lagrangian part. We set $T=2\pi$ and $tol$, and measure the $L^1$-errors for both the control (see (4.5)),

$$\begin{aligned} {\Vert e_0\Vert }_{L^1}:=\Delta x\sum _j\left| u_0^{(m)}(x_j)-u_d(x_j-2\pi )\right| , \end{aligned}$$

and the terminal state,

$$\begin{aligned} {\Vert e_T\Vert }_{L^1}:=\Delta x\sum _j\left| u^{(m)}(x_j,2\pi )-u_d(x_j)\right| . \end{aligned}$$

The results of the numerical grid convergence study displayed in the Table 1 for $tol=(\Delta x)^4$, clearly show that the expected second-order rate of convergence has been achieved.

Table 1 Example 1: $L^1$-convergence study

It should be pointed out that problem (4.1a) does not contain any regularization with respect to $u_0$. In general, this may lead to a deterioration of the iteration numbers within the optimization. In order to quantify this effect, we present, in Table 2, the results obtained for the regularized problem

$$\begin{aligned}&\min _{u_0}J_\mathrm{reg}(u(\cdot ,T);u_d(\cdot )),\nonumber \\&J_\mathrm{reg}(u(\cdot ,T);u_d(\cdot )):=J(u(\cdot ,T);u_d(\cdot ))+\frac{\alpha }{2}\int \limits _I\big (u_0(x)-u^*(x)\big )^2\,dx, \end{aligned}$$

(4.6)

where $u$ is a solution of (4.3), $u^*(x)=e^{-(x-\pi )^2}$, and $\alpha$ is a regularization parameter. Obviously, the gradient computation in (3.9) has to be modified accordingly, but no further changes compared with the previous example are made. As expected, Table 2 shows that increasing value of parameter $\alpha$ leads a decreasing number of iterations while preserving the second order of accuracy of the method.

Table 2 Example 1: $L^1$-convergence study for the regularized cost functional

Furthermore, we compare the performance of the proposed discrete method of characteristics with an upwind approach from [25] for solving the adjoint transport equation (4.4). To this end, we apply a first-order version of the central-upwind scheme (briefly discussed in “Appendix A”) to the forward equation (4.3) and then use either the method of characteristics or the first-order upwind scheme for solving the adjoint equation (4.4). Since in this case, the overall accuracy of the method is one, we chose a much larger $tol=(\Delta x)^2$. Table 3 shows the number of iterations and $L^1$-errors for both cases. We observe that the iteration numbers are slightly better if the adjoint equation is solved by the method of characteristics; they are also lower compared to the corresponding numbers in Table 1 due to the reduced tolerance. As expected, the rate of convergence is approximately one.

Table 3 Example 1: Comparison of the upwind scheme and the method of characteristics for solving (4.4)

4.1.2 Example 2: Nonlinear constraints

In this section, we consider the optimization problem (4.1a)–(4.1b) subject to the nonlinear inviscid Burgers equation,

$$\begin{aligned} \begin{aligned}&u_t+\left( \frac{u^2}{2}\right) _x=0,&\quad x\in [0,2\pi ],\quad t>0,\\&u(x,0)=u_0(x),&\quad x\in [0,2\pi ],\\&u~\text{ is } 2\pi \text{-periodic }, \end{aligned} \end{aligned}$$

(4.7)

as the constraint and use its solution at a certain time as a terminal state for the control problem. We generate this terminal state $u_d$ by solving (4.7) with the initial data given by

$$\begin{aligned} u_0(x)=\frac{1}{2}+\sin x,\quad x\in [0,2\pi ]. \end{aligned}$$

(4.8)

It is easy to show that for $t<\pi /2$ the solution of (4.7), (4.8) is smooth, whereas it breaks down and develops a shock wave at the critical time of $t=\pi /2$ (later on, the shock travels to the right with a constant speed of $s=0.5$). In the following, we will consider both smooth, $u(x,T=\pi /4)$, and nonsmooth, $u(x,T=2)$, solutions of (4.7), (4.8), computed by the 1-D version of the second-order semi-discrete central-upwind scheme (see Sect. 3.1), and use them as terminal states $u_d$ in the optimization problem.

In Figs. 1 and 2, we plot the recovered smooth optimal initial data $u_0^{(m)}(x)$ together with the exact initial data $u_0(x)$ from (4.8) and the computed terminal state $u^{(m)}(x,T=\pi /4)$ together with $u_d(x)$, respectively. The Eulerian part of the computations were performed on a uniform grid with $\Delta x=2\pi /100$. At the beginning of each backward Lagrangian step, the characteristics points were placed at the center of each finite-volume cell. We have also solved the optimization problem on finer grids, namely, with $\Delta x=2\pi /200$ and $2\pi /400$. The plots look very similar to those shown in Figs. 1 and 2 and therefore are not presented here. In all of the computations, the iterations were started with the initial guess $u_0^{(0)}(x)\equiv 0.5$.

Fig. 1

Example 2 (smooth case): Recovered initial data $u_0^{(m)}(x)$ with $m=1, 5, 20, 50, 100$ and $150$ (dashed line) and the exact initial data (4.8) (solid line)

Fig. 2

Example 2 (smooth case): Recovered solution of the optimal control problem, $u^{(m)}(x,T=\pi /4)$ with $m=1, 5, 20, 50, 100$ and $150$ (dashed line) and the terminal state $u_d$ (solid line)

We also perform a numerical grid convergence study, whose results are presented in Table 4. One can clearly see that similarly to the case of linear constraint (Example 1), the expected second-order rate of convergence has been achieved in the smooth nonlinear case with $tol=25(\Delta x)^4$.

Table 4 Example 2: $L^1$-convergence study for smooth solutions

We then proceed with the nonsmooth terminal state $u_d(x)=u(x,T=2)$. In this case, the solution of the studied optimization problem is not unique. Our Eulerian–Lagrangian method recovers just one of the possible solutions, which is presented in Figs. 3 and 4. In Fig. 3, we plot the recovered initial data $u_0^{(m)}(x)$ together with the initial data (4.8), used to generate $u(x,T=2)$ by the central-upwind scheme. In Fig. 4, we show the computed terminal state $u^{(m)}(x,T=2)$ together with $u_d(x)$. The plotted solutions are computed on a uniform grid with $\Delta x=2\pi /100$ and the corresponding number of characteristics points (as before, similar results are obtained on finer grids but not reported here).

Fig. 3

Example 2 (nonsmooth case): Recovered initial data $u_0^{(m)}(x)$ with $m=1, 5, 20, 50, 100$ and $200$ (dashed line) and $u_0(x)$ given by (4.8) (solid line)

Fig. 4

Example 2 (nonsmooth case): Recovered solution of the optimal control problem, $u^{(m)}(x,T=2)$ with $m=1, 5, 20, 50, 100$ and $200$ (plotted with points) and the terminal state $u_d$ (solid line)

Further, we conduct a comparison of the convergence behaviour for the smooth $(T=\pi /4)$ and nonsmooth $(T=2)$ solutions of the optimization problem (4.1a), (4.7). In the nonsmooth case, the terminal state $u_d$ is discontinuous. The discontinuity is located at $\bar{x}=\pi +1$ with the left $u_d(\bar{x}-)=u_l=3/2$ and right $u_d(\bar{x}+)=u_r=-1/2$ states, respectively. The extremal backward characteristics emerging at $\bar{x}$ reach the points $x_l=\bar{x}-3$ and $x_r=1+\bar{x}$ at time $t=0$. In order to avoid the problem of nonuniqueness of the optimal solution in the region $x_l\le x\le x_r$, we compute in the nonsmooth case the $L^1$-error only on the intervals $I_l:=[0,x_l]$ and $I_r:=[x_r,2\pi ]$, that is, in this case we define

$$\begin{aligned} \Vert e_0\Vert _{L^1_\mathrm{loc}}:=\Delta x\sum _j\chi _{I_l\cup I_r}(x_j)|u_0^{(m)}(x_j)-u_0(x_j)|. \end{aligned}$$

Here, $u_0$ is given by equation (4.8) and $\chi _I$ is the characteristic function on the interval $I$. The tolerance for both cases is set to $tol=(\Delta x)^2$ and the results are reported in Table 5.

Table 5 Example 2: Comparison of convergence behavior for $J\le tol=(\Delta x)^2$ and terminal times $T=\pi /4$ and $T=2$, for which the terminal states $u_d$ is smooth and nonsmooth, respectively

We also check the numerical convergence of the computed adjoint solution $p$. Notice that inside the region of the extremal backwards characteristics, $p$ is constant and according to [19], its value is equal to $\frac{1}{2}\frac{\left( u(\bar{x}+,T)-u_d(\bar{x})\right) ^2-\left( u(\bar{x}-,T)-u_d(\bar{x}\right) ^2}{u(\bar{x}+,T)-u(\bar{x}-,T)}=0$. Therefore, $p(x,0)\equiv 0$ everywhere, and we measure the computed $p$ in the maximum norm at time $t=0$. The results are shown in Table 6, where we demonstrate the behavior of $\max |p_j(0)|$ both outside, $\displaystyle {\max _{j: x_j\in I_l\cup I_r}|p_j(0)|}$, and inside, $\displaystyle {\max _{j: x_j\in [x_l,x_r]}|p_j(0)|}$, the shock region. As expected, a pointwise convergence is only observed away from the region of the extremal backwards characteristics.

Table 6 Example 2: Maximum values of the adjoint solution $p$, computed at time $t=0$ outside and inside the region of the extremal backwards characteristics

4.1.3 Example 3: Duct design problem

In this example, we consider a duct design problem from [16] (see also [44, p. 233]).

In the original model in [16], the flow within a duct area $A(x)$ is described by the 1-D Euler equations. Under several simplifying assumptions, this problem can be reduced to an optimization problem for $A$ subject to the following ODE constraint (see [17]):

$$\begin{aligned} f(u)_x=h(u,A),\quad x\in (0,1), \end{aligned}$$

(4.9)

with

$$\begin{aligned} f(u)=u+\frac{H}{u}, \quad h(u,A)=-\frac{A'}{A}\left( \gamma u-\frac{H}{u}\right) , \end{aligned}$$

(4.10)

where $\gamma$ and $H$ are positive constants, and appropriate boundary conditions are supplied.

The boundary conditions for (4.9), (4.10) given in [16] are such that the solution has a discontinuity at some unknown point $x_*$, at which the Rankine–Hugoniot condition holds. The desired profile of $A$ is then obtained by solving a minimization problem for a given state $u_d(x)$ obtained as a solution of (4.9), (4.10) for a prescribed area $A_d(x)$ and the following boundary data $u(0)=u_\ell =1.299$ and $u(1)=u_r=0.506$. The function $A_d$ is defined as the following cubic polynomial:

$$\begin{aligned} A_d(x)=-1.19x^3+1.785x^2+0.1x+1.05. \end{aligned}$$

In [44, Section 7.1], a time dependent version of the original duct design problem has been considered subject to the nonlinear hyperbolic balance law constraint:

$$\begin{aligned} \begin{aligned}&u_t+f(u)_x=h(u,A),&\quad x\in (0,1),\quad t>0,\\&u(x,0)=u_0(x),&\quad x\in (0,1),\\&u(0,t)=u_\ell (1+0.15\sin (4\pi t)),\quad u(1,t)=u_r,&\quad t>0, \end{aligned} \end{aligned}$$

(4.11)

with $f$ and $h$ given by (4.10). The terminal velocity profile $u_d$ is given by the solution of (4.11) with $A=A_d$. The optimization for $A$ is then performed using a tracking-type functional on the full spatial and temporal grid and a regularization of $A$. In this paper, we consider a slightly different optimization problem: For a given $A=A_d$ and a desired flow profile $u_d$ we identify the initial flow condition $u_0$. Hence, we study an optimization problem (4.1a) subject to the constraint (4.11). In our numerical experiments, we choose the parameters $\gamma =\frac{1}{6}$ and $H=1.2$ as in [16]. The terminal state $u_d$ is obtained as the numerical solution of (4.11) (computed by the 1-D version of the second-order semi-discrete central-upwind scheme from Sect. 3.1) at time $T=0.15$ from Riemann initial data with

$$\begin{aligned} u(x,0)=\left\{ \begin{aligned}&u_\ell ,&x<0.5,\\&u_r,&x>0.5. \end{aligned}\right. \end{aligned}$$

(4.12)

The recovered initial condition $u_0^{(m)}(x)$ is shown in Fig. 5. As in the previous nonsmooth example, the recovered initial condition is not unique since the terminal state is discontinuous. In Fig. 6, we plot the obtained solution of the optimal control problem (4.1a), (4.11). As one can see, the convergence in this example is much slower than on the previous ones, but after about 2000 iterations we recover $u^{(2000)}(x,T=0.15)$, which almost coincides with $u_d$.

Fig. 5

Example 3: Recovered initial data of the optimal control problem, $u_0^{(m)}(x,T=0.15)$ with $m=10, 50, 200, 500, 1000$ and $2000$ (dashed line) and $u_0(x)$ given by (4.12) (solid line)

Fig. 6

Example 3: Recovered solution of the optimal control problem, $u^{(m)}(x,T=0.15)$ with $m=10, 50, 200, 500, 1000$ and $2000$ (plotted with points) and the terminal state $u_d$ (solid line)

The presented results were obtained using the initial guess $u_0^{(0)}(x)=u_\ell +(u_r-u_\ell )x$, which satisfies the prescribed boundary condition at time $t=0$. We have used a uniform finite-volume grid with $\Delta x=1/100$ and taken 400 characteristics points, which were placed uniformly in the interval $(0,1)$ at the terminal time $T=0.15$. Notice that some of the traced characteristics curves leave the computational domain at times $t\in (0,T)$. This may lead to appearing and widening gaps at/neat the shock area. We fill these gaps using the linear interpolation technique discussed in Remark 3.8.

4.2 The two-dimensional case

We finally turn to the 2-D example.

4.2.1 Example 4: 2-D Burgers equation

We numerically solve the 2-D optimization problem (1.1a)–(1.1c) subject to the inviscid Burgers equation:

$$\begin{aligned} u_t+\left( \frac{u^2}{2}\right) _x+\left( \frac{u^2}{2}\right) _y=0. \end{aligned}$$

(4.13)

The optimal control problem is solved in the domain $[0,2\pi ]\times [0,2\pi ]$ with the period boundary conditions and the terminal state $u_d$ obtained by a numerically solving (using the second-order semi-discrete central-upwind scheme described in Sect. 3.1) Eq. (4.13) subject to the following initial data:

$$\begin{aligned} u(x,y,0)=\frac{1}{2}+\sin ^2\!\Big (\frac{1}{2}x\Big )\sin ^2\!\Big (\frac{1}{2}y\Big ). \end{aligned}$$

(4.14)

The solution was computed on a uniform finite-volume grid with $\Delta x=\Delta y=2\pi /100$. We have started the Lagrangian method of characteristics with $10^4$ points uniformly distributed throughout the computational domain at time $t=T$. We show 2-D plots of the optimal controls and the corresponding optimal states at times $T=1$ and $T=3$ (both the top view and the 1-D diagonal slice along the line $y=x$). The results for $T=1$ are shown in Figs. 7 and 8, while the results for $T=3$ are presented in Figs. 9 and 10. In the former cases, when the terminal state is smooth, the solution of the optimization problem exhibits quite fast convergence in recovering both the initial data and the terminal state. In the latter case of a nonsmooth terminal state, the convergence is slower, and the control $u_0$ given by (4.14) is not fully recovered due to lack of uniqueness. Nevertheless, the optimal state $u^{(200)}(x,y,T=3)$ in Fig. 10 almost coincides with $u_d$.

Fig. 7

Example 4 ($T=1$): Recovered initial data $u_0^{(m)}(x,y)$ with $m=1,5,20,50$ and $130$ and the exact initial data (4.14) (top left). The bottom part contains the corresponding plots along the diagonal $y=x$

Fig. 8

Example 4: Recovered solution of the optimal control problem, $u^{(m)}(x,y,T=1)$, with $m=1,5,10,20,50$ and $130$ and the terminal state $u_d$ (top left). The bottom part contains the corresponding plots along the diagonal $y=x$

Fig. 9

Example 4 ($T=3$): Recovered initial data $u_0^{(m)}(x,y)$ with $m=1,5,10,50,100$ and $200$ and the exact initial data (4.14) (top left). The bottom part contains the corresponding plots along the diagonal $y=x$

Fig. 10

Example 4: Recovered solution of the optimal control problem, $u^{(m)}(x,y,T=3)$, with $m=1,5,10,50,100$ and $200$ and the terminal state $u_d$ (top left). The bottom part contains the corresponding plots along the diagonal $y=x$

5 A convergence analysis

In this section, we discuss convergence properties of the proposed method in the 1-D case. Here, the derivation closely follows [44] and we apply the results from [44] to the presented scheme in order to proof its convergence.

To this end, we consider the problem (4.1b) in $\mathbb {R}$ with no source term ($h(u,x,t\equiv 0$)):

$$\begin{aligned} \begin{aligned}&u_t+f(u)_x=0,&\quad x\in \mathbb {R},\quad t>0,\\&u(x,0)=u_0(x),&\quad x\in \mathbb {R}, \end{aligned} \end{aligned}$$

(5.1)

and a strictly convex flux function $f\in C^2(\mathbb {R})$, that is,

$$\begin{aligned} f''\ge c>0\quad \text{ for } \text{ some }~~c>0. \end{aligned}$$

(5.2)

The adjoint problem is then of the type

$$\begin{aligned} \begin{aligned}&p_t+v(x,t)p_x=0,&\quad x\in \mathbb {R},\quad t\in (0,T),\\&p(x,T)=p_T(x)&\quad x\in \mathbb {R}, \end{aligned} \end{aligned}$$

(5.3)

where $v(x,t)=f'(u(x,t))$ in the case under consideration. It can be shown that if $p_T$ is Lipschitz continuous and $v\in L^\infty ((0,T)\times \mathbb {R})$ is OSLC, that is, it satisfies,

$$\begin{aligned} v_x(\cdot ,t)\le \alpha (t),\quad \alpha \in L^1(0,T), \end{aligned}$$

(5.4)

then there exists a reversible solution of (5.3). We refer, for instance, to [25, Definition 2.1, Theorem 2.2] and [44, Definition 3.7.2, Theorem 3.7.3] for the notion of reversible solutions. Further results on (5.3) can be found in [4].

Remark 5.1

The adjoint equation (5.3) as well as the assumption (5.4) is well-defined for $v(x,t)=f'(u(x,t))$ only if $u$ does not contain any shocks. Therefore, the following convergence analysis is only applicable where the characteristics are outside the region entering a shock.

Under the above assumptions convergence properties within a general theory were established in [25, 44] for some first-order numerical methods. The assumptions are restrictive but to the best of our knowledge no results for multidimensional problems, general flux functions or higher-order methods are available. Even though our numerical experiments clearly demonstrate the convergence of the proposed second-order Eulerian–Lagrangian method, we have been unable to formally prove this. Instead, we significantly simplify our method by adding a substantial amount of numerical diffusion to both the Eulerian and Lagrangian parts as described below, and prove the convergence for the simplified method only.

We first reduce the order of the method to the first one. The central-upwind scheme then becomes the HLL scheme [27], which can be written in the fully discrete form as

$$\begin{aligned} \overline{u}_j^{n+1}=\overline{u}_j^n-\lambda \left( F_{j+\frac{1}{2}}^n-F_{j-\frac{1}{2}}^n\right) , \end{aligned}$$

(5.5)

where $\overline{u}_j^n\approx \frac{1}{\Delta x} \int _{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}u(x,t^n)\,dx$ are the computed cell averages, $\lambda :=\Delta t/\Delta x$ and the numerical fluxes are given by

$$\begin{aligned} F_{j+\frac{1}{2}}^n=\frac{a_{j+\frac{1}{2}}^+f(\overline{u}_j^n)-a_{j+\frac{1}{2}}^-f(\overline{u}_{j+1}^n)}{a^+_{j+\frac{1}{2}}-a^-_{j+\frac{1}{2}}}+\frac{a_{j+\frac{1}{2}}^+a_{j+\frac{1}{2}}^-}{a^+_{j+\frac{1}{2}}-a^-_{j+\frac{1}{2}}} (\overline{u}_{j+1}^n-\overline{u}_j^n), \end{aligned}$$

(5.6)

with the following one-sided local speeds:

$$\begin{aligned} a^+_{j+\frac{1}{2}}=\max \left\{ {f'}(\overline{u}_j^n),{f'}(\overline{u}_{j+1}^n),0\right\} ,\quad a^-_{j+\frac{1}{2}}=\min \left\{ {f'}(\overline{u}_j^n),{f'}(\overline{u}_{j+1}^n),0\right\} . \end{aligned}$$

(5.7)

The amount of numerical viscosity present in the HLL scheme (5.5)–(5.7) can be reduced by setting

$$\begin{aligned} a^+_{j+\frac{1}{2}}=-a^-_{j+\frac{1}{2}}=a_{j+\frac{1}{2}}:=\max \left\{ |{f'}(\overline{u}_j^n)|,|{f'}(\overline{u}_{j+1}^n)|\right\} , \end{aligned}$$

(5.8)

which leads to the Rusanov scheme [41] with the numerical flux

$$\begin{aligned} F_{j+\frac{1}{2}}^n=\frac{1}{2}\left( f(\overline{u}_j^n)+f(\overline{u}_{j+1}^n)\right) -\frac{a_{j+\frac{1}{2}}}{2}(\overline{u}_{j+1}^n-\overline{u}_j^n). \end{aligned}$$

(5.9)

However, the numerical diffusion in the Rusanov scheme (5.5), (5.8), (5.9) is still not large enough and we thus further reduce it by considering the modified Lax–Friedrichs scheme studied, for instance, in [44, Section 6.5.2]: We replace the local speeds $a_{j+\frac{1}{2}}$ by the global ones, which results in the following numerical flux:

$$\begin{aligned} F_{j+\frac{1}{2}}^n=\frac{1}{2}\left( f(\overline{u}_j^n)+f(\overline{u}_{j+1}^n)\right) -\frac{\gamma }{2\lambda }(\overline{u}_{j+1}^n-\overline{u}_j^n), \quad \gamma =\lambda \max \limits _ja_{j+\frac{1}{2}}. \end{aligned}$$

(5.10)

Assuming that at time $T$ the set of the characteristics points coincides with the finite-volume grid, the 1-D method of characteristics for the adjoint problem (5.3) is

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx_i^\mathrm{c}(t)}{dt}=f'(u(x_i^\mathrm{c}(t),t)),\quad x_i^\mathrm{c}(T)=x_i,\\&\frac{dp_i^\mathrm{c}(t)}{dt}=0,\quad p_i^\mathrm{c}(T)=p_T(x_i^\mathrm{c}(T))=p_i^{N_T}. \end{aligned}\right. \end{aligned}$$

(5.11)

Here, the value of $u(x_i^\mathrm{c}(t),t)$ is obtained from the piecewice constant reconstruction

$$\begin{aligned} \widetilde{u}(x,\cdot )=\sum _j\chi _j(x)\overline{u}_j(\cdot ), \end{aligned}$$

(5.12)

that is,

$$\begin{aligned} u(x_i^\mathrm{c}(t^n),t^n)=\widetilde{u}(x_i^\mathrm{c}(t^n),t^n)=\overline{u}_j^n, \end{aligned}$$

provided the characteristic point $x_i^\mathrm{c}$ is located in cell $j$ at time $t^n$. The ODE system (5.11) is then to be integrated backward in time starting from $t=T$.

In order to establish a convergence result, we modify the method of characteristics as follows. At the end of each time step, the obtained solution is first projected to the finite-volume cell centers $\{x_j\}$ (this procedure adds a substantial amount of a numerical diffusion to the nondiffusive method of characteristics) and then the method is restarted. This way, at time $t=t^{n+1}$ each characteristics will start from the cell center and provided the CFL number is smaller than 1/2, it will stay in the same cell at the end of the time step. Therefore, the new location of the characteristics can be obtained using the Euler method:

$$\begin{aligned} x_j^\mathrm{c}(t^n)=x_j-\Delta t{f'}_j^n,~ \text{ where } \,{f'}_j^n:={f'}(\overline{u}_j^n). \end{aligned}$$

(5.13)

The resulting Lagrangian method then reduces to a first-order Eulerian (finite-difference) one, which can be described as follows:

• If ${f'}_j^n=0$, then

  $$\begin{aligned} p_j^n=p_j^{n+1}; \end{aligned}$$

  (5.14)

• If ${f'}_j^n>0$, then

  $$\begin{aligned} p_j^n=(1-\beta _j^n)\,p_j^{n+1}+\beta _j^n\,p_{j+1}^{n+1}, \end{aligned}$$

  (5.15)

  where

  $$\begin{aligned} \beta _j^n=\frac{\lambda {f'}_j^n}{1-\lambda ({f'}_{j+1}^n-{f'}_j^n)^+}=\frac{\lambda {f'}_j^n}{1-\lambda (\Delta ^+{f'}_j^n)^+}; \end{aligned}$$

  (5.16)

• If ${f'}_j^n<0$, then

  $$\begin{aligned} p_j^n=(1-\gamma _j^n)\,p_j^{n+1}+\gamma _j^n\,p_{j-1}^{n+1}, \end{aligned}$$

  (5.17)

  where

  $$\begin{aligned} \gamma _j^n=\frac{-\lambda {f'}_j^n}{1-\lambda ({f'}_j^n-{f'}_{j-1}^n)^+}=\frac{-\lambda {f'}_j^n}{1-\lambda (\Delta ^+{f'}_{j-1}^n)^+}. \end{aligned}$$

  (5.18)

In (5.16) and (5.18), we have used the standard notations $\Delta ^+\omega _j:=\omega _{j+1}-\omega _j$, $\xi ^+:=\max (\xi ,0)$, and $\xi ^-:=\min (\xi ,0)$.

It should be observed that $\forall j,n$,

$$\begin{aligned} \beta _j^n>0,\quad \gamma _j^n>0,\quad \frac{1}{2}\le 1-\lambda (\Delta ^+{f'}_j^n)^+\le \frac{3}{2},\quad \lambda (\Delta ^+{f'}_j^n)^+\le \frac{1}{2}, \end{aligned}$$

(5.19)

as long as the following CFL condition is imposed:

$$\begin{aligned} \lambda \le \frac{1}{4\max \limits _{j,n}|{f'}_j^n|}. \end{aligned}$$

(5.20)

Remark 5.2

Notice that if ${f'}_{j+1}^n\ge {f'}_j^n$, then (5.15), (5.16) is a result of the linear interpolation between the point values of $p$ at the characteristic points $x_j^\mathrm{c}(t^n)$ and $x_{j+1}^\mathrm{c}(t^n)$, while if ${f'}_{j+1}^n<{f'}_j^n$, then (5.15), (5.16) reduces to a simple first-order upwinding:

$$\begin{aligned} p_j^n=p_j^{n+1}+\lambda {f'}_j^n(p_j^{n+1}-p_{j+1}^{n+1}). \end{aligned}$$

A similar argument holds for (5.17), (5.18).

Next, we reformulate the above cases and rewrite equations (5.14)–(5.18) in the following compact form (see also [44, (6.45)] or [25, (3.9)]):

$$\begin{aligned} p_j^n&= \beta _j^nH({f'}_j^n)p^{n+1}_{j+1}+\gamma _j^nH(-{f'}_j^n)p^{n+1}_{j-1}+\left( 1-\beta _j^nH({f'}_j^n)-\gamma _j^nH(-{f'}_j^n)p_j^n\right) \nonumber \\&= \sum \limits _{l=-1}^1B_j^{n,l}p^{n+1}_{j-l}, \end{aligned}$$

(5.21)

where

$$\begin{aligned} \begin{aligned}&B_j^{n,-1}:=\lambda v_j^{n,0}=\beta _j^nH({f'}_j^n)=\lambda \frac{({f'}_j^n)^+}{1-\lambda (\Delta ^+{f'}_j^n)^+},\\&B_j^{n,1}:=-\lambda v_{j-1}^{n,1}=\gamma _j^nH(-{f'}_j^n)=-\lambda \frac{({f'}_j^n)^-}{1-\lambda (\Delta ^+{f'}_{j-1}^n)^+},\\&B_j^{n,0}:=1+\lambda (v_{j-1}^{n,1}-v_j^{n,0})=1-\gamma _j^nH(-{f'}_j^n)-\beta _j^nH({f'}_j^n), \end{aligned} \end{aligned}$$

(5.22)

and $H$ is the Heaviside function. We also note that the difference $\Delta ^+p_j^n$ can be written as

$$\begin{aligned} \Delta ^+p_j^n=\sum \limits _{l=-1}^1D_j^{n,l}\Delta ^+p^{n+1}_{j-l}, \end{aligned}$$

(5.23)

where

$$\begin{aligned} D_j^{n,-1}:=\lambda v_{j+1}^{n,0},\quad D_j^{n,1}:=-\lambda v_{j-1}^{n,1},\quad D_j^{n,0}:=1+\lambda (v_j^{n,1}-v_j^{n,0}). \end{aligned}$$

(5.24)

Taking into account (5.19) and the CFL condition (5.20), it is easy to check that

$$\begin{aligned} B_j^{n,l}\ge 0,\ D_j^{n,l}\ge 0,\quad \forall j,n\ \text{ and }\ l\in \{-1,0,1\}. \end{aligned}$$

(5.25)

In what follows, we prove the convergence of the discrete scheme (5.21), (5.22) towards the solution of (5.3) with $v=f'(u)$. We follow the lines of [25, 44] and assume that:

(A1):

There exist constants $\Delta _0,M_u>0$ such that for all $\Delta t=\lambda \Delta x\le \Delta _0$, we have

$$\begin{aligned} \Vert \widetilde{u}\Vert _\infty \le M_u,\;\widetilde{u}(\cdot ,t)\rightarrow u(\cdot ,t) \text{ in } L^1_\mathrm{loc}(\mathbb {R})~\forall t\in [0,T], \end{aligned}$$

(5.26)

where $\widetilde{u}$ is given by (5.12) and $u$ is the entropy solution of (5.1), (5.2);

(A2):

There exists a function $\mu \in L^1(0,T)$ such that for all $\Delta t=\lambda \Delta x\le \Delta _0$, the discrete OSLC holds, that is,

$$\begin{aligned} \Delta ^+\overline{u}_j^n\le \lambda \int \limits _{t^n}^{t^{n+1}}\mu (s)\,ds\quad \forall j,n. \end{aligned}$$

(5.27)

It was proved in [44] that solutions obtained by the scheme (5.5), (5.10) satisfy the assumptions (A1) and (A2). The OSLC property and rigorous convergence rate estimates were established for several first-order [38, 39] and second-order [30] schemes. Numerous numerical experiments reported in the literature suggest that solutions of both the HLL (5.5)–(5.7) and Rusanov (5.5), (5.9) schemes also satisfy the assumptions (A1) and (A2). However, to the best of our knowledge, no rigorous proof of this is available.

Equipped with the above assumptions, we apply [44, Theorem 6.3.4] to our scheme. To this end, we verify that the discrete functions $v_j^{n,l}$ in (5.22) fulfill the following conditions which are similar to the assumptions (A1) and (A2) (see [25, Theorem 2.4]):

(A3):

There exist a constant $M_a>0$ such that for all $\Delta t=\lambda \Delta x\le \Delta _0$

$$\begin{aligned} \Vert \widetilde{v}^l\Vert _\infty \le M_a,\quad \widetilde{v}=\sum _{l=0}^1\widetilde{v}^l\rightarrow v=f'(u) \text{ in } L^1_\mathrm{loc}((0,T)\times \mathbb {R}) \text{ as } \Delta x\rightarrow 0. \end{aligned}$$

(5.28)

Here,

$$\begin{aligned} \widetilde{v}^l(x,t):=\sum _{j,n}v_j^{n,l}\chi _{Q_j^n}(x,t), \end{aligned}$$

where $\chi _{Q_j^n}$ is a characteristic function of the space-time volume $Q_j^n:=[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}})\times [t^n,t^{n+1})$;

(A4):

There exists a function $\alpha \in L^1(0,T)$ such that for all $\Delta t=\lambda \Delta x\le \Delta _0$

$$\begin{aligned} \sum \limits _{l=0}^1\Delta ^+v^{n,l}_j\le \lambda \int \limits _{t^n}^{t^{n+1}}\alpha (s)\,ds\quad \forall j,n. \end{aligned}$$

(5.29)

We start by proving (5.28) and note that

$$\begin{aligned} \Vert \widetilde{v}^l\Vert _\infty \le 2\max _{j,n}|{f'}_j^n|=:M_a<\infty , \end{aligned}$$

since $\Vert \widetilde{u}\Vert _\infty$ is bounded, and

$$\begin{aligned} \widetilde{v}(x,t)=\sum \limits _{l=0}^1\widetilde{v}^l(x,t)= \sum _{j,n}\frac{({f'}_j^n)^++({f'}_{j+1}^n)^-}{1-\lambda (\Delta ^+{f'}_j^n)^+}\;\chi _{Q_j^n}(x,t). \end{aligned}$$

Taking into account (5.26), (5.27), we have that for all $R>0$ and all $\Delta t=\lambda \Delta x\le \lambda$

$$\begin{aligned}&\Vert \widetilde{u}(\cdot +\Delta x,\cdot )-u\Vert _{L^1((-R,R)\times (0,T))}\nonumber \\&\quad =\Vert \widetilde{u}(\cdot +\Delta x,\cdot )-u(\cdot +\Delta x,\cdot )+u(\cdot +\Delta x,\cdot )-u\Vert _{L^1((-R,R)\times (0,T))}\nonumber \\&\quad \le \Vert \widetilde{u}-u\Vert _{L^1((-R-1,R+1)\times (0,T))}+\Vert u(\cdot +\Delta x,\cdot )\nonumber \\&\qquad -u\Vert _{L^1((-R,R)\times (0,T))}\rightarrow 0~ \text{ as } \,\Delta x\rightarrow 0. \end{aligned}$$

(5.30)

We also have

$$\begin{aligned} \begin{aligned} \Big |f'(u)-\sum \limits _{l=0}^1\widetilde{v}^l\Big |\le&\sum _{j,n}\Big [\left| (f'(u))^+-v_j^{n,0}\right| + \left| (f'(u))^--v_j^{n,1}\right| \Big ]\chi _{Q_j^n}(x,t)\\ \le&2\sum _{j,n}\Big [\left| (f'(u))^+-({f'}_j^n)^+\right| +\lambda \left| (f'(u))^+(\Delta ^+{f'}_j^n )^+\right| \\&+\left| (f'(u))^--({f'}_{j+1}^n)^-\right| +\lambda \left| (f'(u))^-(\Delta ^+{f'}_j^n)^+\right| \Big ]\chi _{Q_j^n}(x,t) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \left| (f'(u))^+(\Delta ^+{f'}_j^n )^+\right|&+\left| (f'(u))^-(\Delta ^+{f'}_j^n)^+\right| \le 2\Vert f'(u)\Vert _\infty |{f'}_{j+1}^n-{f'}_j^n|\\&\le 2\Vert f'(u)\Vert _\infty \max _{\widetilde{u}}\{|f''(\widetilde{u})|\}\,|\overline{u}_{j+1}^n-\overline{u}_j^n| \end{aligned} \end{aligned}$$

provided $u\in L^\infty (\mathbb {R}\times (0,T))$ and $\widetilde{u}$ satisfies (5.26) and (5.27). We then denote by $M_0{:=}\Vert u\Vert _\infty$, $M_1{:=}\max _{|u|\le \max \{M_0,M_u\}}|f'(u)|$, and $M_2{:=}\max _{|u|\le \max \{M_0,M_u\}}|f''(u)|$ to obtain

$$\begin{aligned} \begin{aligned}&\Big |f'(u)-\sum \limits _{l=0}^1\widetilde{v}^l\Big |\le 4M_2\sum _{j,n}\Big [|u-\overline{u}_j^n| +\lambda M_1|\overline{u}_{j+1}^n-\overline{u}_j^n|\Big ]\chi _{Q_j^n}(x,t). \end{aligned} \end{aligned}$$

The last inequality together with (5.30) lead to (5.28) since $\widetilde{u}(x+\Delta x,t)=\sum _{j,n}\overline{u}_{j+1}^n\chi _{Q_j^n}(x,t)$.

It remains to prove (5.29). Let $\alpha \in L^1(0,T)$, $\Delta _0>0$ such that (5.26) and (5.27) hold with $\mu (t)=\alpha (t)$, and assume without lost of generality that $\alpha (t)\ge 0,~\forall t$. We also denote by

$$\begin{aligned} \Omega :&= \Delta ^+v^{n,0}_j+\Delta ^+v^{n,1}_{j-1}\\&= \frac{({f'}_{j+1}^n)^+}{1-\lambda (\Delta ^+{f'}_{j+1}^n)^+} -\frac{({f'}_{j}^n)^+}{1-\lambda (\Delta ^+{f'}_{j}^n)^+}+\frac{({f'}_{j+1}^n)^-}{1-\lambda (\Delta ^+{f'}_{j}^n)^+}\nonumber \\&-\frac{({f'}_{j}^n)^-}{1-\lambda (\Delta ^+{f'}_{j-1}^n)^+}. \end{aligned}$$

To establish the required estimate, we distinguish between several cases, which are treated using (5.19) and (5.20) to obtain:

• If ${f'}_{j+1}^n\ge 0$ and ${f'}_j^n\le 0$, then

  $$\begin{aligned} \Omega =&\displaystyle \frac{{f'}_{j+1}^n}{1-\lambda (\Delta ^+{f'}_{j+1}^n)^+}-\frac{{f'}_j^n}{1-\lambda (\Delta ^+{f'}_{j-1}^n)^+}\nonumber \\ \le&\displaystyle 2\left( {f'}^n_{j+1}-{f'}_j^n\right) \le 2M_2(\Delta ^+\overline{u}_j^n)^+; \end{aligned}$$

• If ${f'}_{j+1}^n\ge 0,{f'}_j^n>0$ and ${f'}_{j+1}^n>{f'}_j^n$, then

  $$\begin{aligned} \begin{aligned} \Omega =&\frac{{f'}_{j+1}^n}{1-\lambda (\Delta ^+{f'}_{j+1}^n)^+}-\frac{{f'}_j^n}{1-\lambda \Delta ^+{f'}_j^n}\nonumber \\ =&\frac{(1-\lambda {f'}^n_{j+1})\Delta ^+{f'}_j^n+\lambda {f'}^n_j(\Delta ^+{f'}_{j+1}^n)^+}{(1-\lambda \Delta ^+({f'}_{j+1}^n)^+) (1-\lambda \Delta ^+{f'}_j^n)}\\ \le \,\,&M_2\left[ 4(\Delta ^+\overline{u}_j^n)^++(\Delta ^+\overline{u}_{j+1}^n)^+\right] ; \end{aligned} \end{aligned}$$

• If ${f'}_{j+1}^n\ge 0,{f'}_j^n>0$ and ${f'}_{j+1}^n\le {f'}_j^n$, then

  $$\begin{aligned} \Omega =\frac{{f'}_{j+1}^n}{1-\lambda (\Delta ^+{f'}_{j+1}^n)^+}-{f'}_j^n\le \frac{{f'}_j^n}{1-\lambda (\Delta ^+{f'}_{j+1}^n)^+}{-}{f'}_j^n\le \frac{1}{2}M_2(\Delta ^+\overline{u}_{j+1}^n)^+; \end{aligned}$$

• If ${f'}_{j+1}^n<0,{f'}_j^n>0$, then

  $$\begin{aligned} \Omega =\frac{{f'}_{j+1}^n}{1-\lambda (\Delta ^+{f'}_j^n)^+}-\frac{{f'}_j^n}{1-\lambda (\Delta ^+{f'}_j^n)^+}<0; \end{aligned}$$

• If ${f'}_{j+1}^n<0,{f'}_j^n\le 0$ and ${f'}_{j+1}^n\le {f'}_j^n$, then

  $$\begin{aligned} \Omega&= {f'}_{j+1}^n-\frac{{f'}_j^n}{1-\lambda (\Delta ^+{f'}_{j-1}^n)^+}\le {f'}_j^n-\frac{{f'}_j^n}{1-\lambda (\Delta ^+{f'}_{j-1}^n)^+}\nonumber \\&\le \frac{1}{2}M_2(\Delta ^+\overline{u}_{j-1}^n)^+; \end{aligned}$$

• If ${f'}_{j+1}^n<0,{f'}_j^n\le 0$ and ${f'}_{j+1}^n>{f'}_j^n$, then

  $$\begin{aligned} \begin{aligned} \Omega =&\frac{{f'}_{j+1}^n}{1-\lambda \Delta ^+{f'}_j^n}-\frac{{f'}_j^n}{1-\lambda (\Delta ^+{f'}_{j-1}^n)^+}\nonumber \\ =&\frac{(1+\lambda {f'}^n_j)\Delta ^+{f'}_j^n-\lambda {f'}^n_{j+1}(\Delta ^+{f'}_{j-1}^n)^+}{(1-\lambda \Delta ^+{f'}_j^n) (1-\lambda \Delta ^+({f'}_{j-1}^n)^+)}\\ \le \,\,&M_2\left[ 4(\Delta ^+\overline{u}_j^n)^++(\Delta ^+\overline{u}_{j-1}^n)^+\right] ; \end{aligned} \end{aligned}$$

Assuming as before that $u$ and $\widetilde{u}$ satisfy (5.26), (5.27), we conclude that in all of the cases $\Omega$ can be estimated by

$$\begin{aligned} \Omega \le c\lambda \int \limits _{t^n}^{t^{n+1}}\alpha (s)\,ds \end{aligned}$$

with $c=c(M_2)$.

The established estimates together with [44, Theorem 6.3.4] lead to the following convergence result.

Theorem 5.1

Assume that $f\in C^2(\mathbb {R})$ satisfies the assumption (5.2). Let $p_T\in Lip(\mathbb {R})$ and $u\in L^\infty (\mathbb {R}\times (0,T))$ and satisfy (5.26), (5.27). Assume that the discretization of $p_T$ is consistent, that is, there exist constants $M_T>0$ and $L_T>0$ such that

$$\begin{aligned} \begin{aligned}&\Vert \widetilde{p}_T\Vert _\infty \le M_T,\quad \sup \limits _{x\in \mathbb {R}}\left| \frac{\widetilde{p}_T(x+\Delta x)-\widetilde{p}_T(x)}{\Delta x}\right| \le L_T,\\&\widetilde{p}_T\rightarrow p_T \text{ in } [-R,R]~ \text{ for } \text{ all } \;R>0 \text{ as } \Delta x\rightarrow 0. \end{aligned} \end{aligned}$$

(5.31)

Assume also that the CFL condition (5.20) holds. Then, the solution to the adjoint scheme (5.21) converges locally uniformly to the unique reversible solution $p\in Lip(\mathbb {R}\times [0,T])$ of (5.3) with $v=f'(u)$, that is,

$$\begin{aligned} \widetilde{p}\rightarrow p \text{ in } [-R,R]\times [0,T]~ \text{ for } \text{ all } R>0\; \text{ as } \;\Delta t=\lambda \Delta x\rightarrow 0. \end{aligned}$$

Here, $\widetilde{p}_T$ and $\widetilde{p}$ are piecewise constant approximations of $p_T(x)$ and the computed solution $\{p_j^n\}$, respectively.

Remark 5.3

While equations (5.26), (5.27) and (5.31) mimic the assumptions (D2), (D3) and (C1) in [44], it should be observed that (5.27) can be weakened the same way it was done in [44]. Similarly, one could use [25, Theorem 3.7] to establish the convergence result for the adjoint equation.

The previous simplifications allow to state a convergence result for the gradients for a smooth version of the cost functional (1.1c). For a given nonnegative function $\phi _\delta \in {Lip}_0(\mathbb {R})$ with the support in $[-\frac{\delta }{2},\frac{\delta }{2}]$ and $\int _{\mathbb {R}}\phi _\delta (x)\,dx=1$ and $\psi \in C^1_\mathrm{loc}(\mathbb {R}^2)$, let $J_\delta$ be given by

$$\begin{aligned} J_\delta (u_0):=\int \limits _0^1\psi \big ((\phi _\delta *u)(x,T),(\phi _\delta *u_d)(x)\big )\,dx. \end{aligned}$$

(5.32)

Here, $u$ is the entropy solution of the initial value problem (5.1) and $*$ denotes a convolution in $x$. For $J_\delta$ to be well-posed we assume $u_d\in L^\infty (\mathbb {R})$. We discretize $J_\delta$ by

$$\begin{aligned} \widetilde{J}_\delta (\widetilde{u}_0)=\sum \limits _k\psi \big ((\phi _\delta *\widetilde{u})(x_k,T),(\phi _\delta *\widetilde{u}_d)(x_k)\big )\Delta x, \end{aligned}$$

(5.33)

where $(\widetilde{\cdot })$ denotes a corresponding piecewise polynomial (piecewise constant for first-order methods) approximation.

The gradient of $J_\delta$ exists in the sense of Frechet differentials, see [44, Theorem 5.3.1]. Using Theorem 5.1 and [44, Theorem 6.4.8], one may obtain the follwoing convergence result.

Theorem 5.2

Assume that $f\in C^2(\mathbb {R})$ satisfies the assumption (5.2). Let $J_\delta$ be given by (5.32) and assume that $u_0\in L^\infty (\mathbb {R}\times (0,T))$ such that $(u_0)_x\le K$. Let

$$\begin{aligned} \widetilde{p}(x_j,T)=\sum \limits _k\phi _\delta (x_j-x_k)\partial _1\psi \big ((\phi _\delta *\widetilde{u})(x_k,T), (\phi _\delta *\widetilde{u}_d)(x_k)\big )\Delta x, \end{aligned}$$

where $\partial _1\psi$ denotes a partial derivative of $\psi$ with respect to its first component.

Let $\widetilde{u}(x,\cdot )$ be an approximate solution of (5.1) obtained by (5.5), (5.10), (5.12) and $\widetilde{p}$ be a piecewise constant approximation of the solution computed by (5.21). Let the CFL conditions (5.20) and

$$\begin{aligned} \lambda \max \limits _{|u|\le \Vert u_0\Vert _\infty }|f'(u)|\le \min \{(1-\rho )\min (\gamma ,2-2\gamma ),1-\gamma \} \end{aligned}$$

hold for some fixed value of $\rho \in (0,1)$.

Then, $\widetilde{p}(\cdot ,0)$ is an approximation to the Frechet derivative of $J_\delta$ with respect to $u_0$ in the following sense:

$$\begin{aligned} \widetilde{p}(\cdot ,0)\rightarrow p(\cdot ,0)=\nabla J_\delta (u_0) \text{ in } L^r(\mathbb {R})\; \text{ as } \;\Delta t=\lambda \Delta x\rightarrow 0, \end{aligned}$$

for all $r\ge 1$. Herein, $p$ is the reversible solution of (5.3) with the terminal data

$$\begin{aligned} p_T(x)=\int \limits _0^1\phi _\delta (x-z)\partial _1\psi \big ((\phi _\delta *u)(z,T),(\phi _\delta *u_d)(z)\big )\,dz. \end{aligned}$$

Remark 5.4

A similar result holds under the assumption that $(u_0)_x\big |_{\mathbb {R}\backslash E}\le K$ for some closed set $E$, see [44, Chapter 6] for more details.