1 Introduction

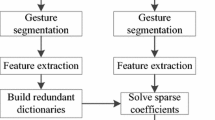
Gesture recognition is widely used in the field of artificial intelligence and pattern recognition as a natural way of interaction, for example, dynamic gesture recognition and pattern recognition of robot multi fingered grasping [1]. Data glove sensors and EMG signal acquisition devices, and cameras are most widely used. Gesture recognition based on data glove has high recognition rate and fast speed. But this method requires users to wear complex data gloves and position tracker, which does not meet the requirements of natural human-computer interaction. The price of data gloves is expensive, and it is not suitable for extensive promotion. Gesture recognition based on EMG signals is mainly to collect multi-channel sEMG signals by sensors, then extract the characteristic parameters of each gesture, and finally realize gesture recognition [2]. The advantage of this method is that EMG signals are not affected by the external environment, so they have better real-time performance. But because of the individual difference, the difficulty of classification is increased, and it needs to be equipped with EMG acquisition device, which brings inconvenience to the application in reality. The gesture recognition based on vision mainly uses camera to capture gesture images and identifies gestures by image processing and related algorithms [3, 4]. The advantage of this method is that the input device is cheap, and the camera is becoming more and more popular in all kinds of consumer electronic products, and it does not add any additional requirements to the manpower, so that the interaction between the computer and the human is more natural. Therefore, more and more researches have been done on vision based hand gesture recognition, and the recognition rate and real-time performance have been greatly improved. It relates to the techniques include gesture detection, gesture segmentation, feature extraction and classification recognition [5] etc. Although these technologies have developed greatly in recent years, the complicated background environment and low performance of classification algorithms are often encountered in acquisition gesture by visual sensors. Therefore, there are still some challenges for accurate gesture recognition [6, 7]. In recent years, the proposition and development of sparse representation theory provide a new approach for the pattern recognition [8, 9]. It shows great development potential and broad application prospect. John, Wright et al. [10] first proposed the sparse representation-based classification (SRC) framework. Redundant dictionary is constructed by training samples for this method [11,12,13]. The test sample is expressed as a sparse linear combination of training samples by the sparse solution algorithm [14,15,16]. Finally, the minimum residual error is classified, and the results show that the method proposed has a good performance.

After the SRC method has been proposed, sparse representation theory is gradually gained the researchers’ attention [17,18,19]. Various approaches are proposed for sparse solution algorithms. The most commonly used sparse solution algorithms are greedy algorithms, which are used to solve approximately the minimization of the norm. The greedy algorithm is easy to implement by selecting the appropriate atoms iteratively, and it is often called orthogonal matching pursuit (OMP) algorithm [20, 21]. Only one atom is selected in iteration, and the times of iterations are too much, the efficiency is lower. What’s more the sparsity needs to be set. Many improved algorithms have appeared to aim at the problem of OMP algorithm. For example, a regularized ROMP (Regularized Orthogonal Matching Pursuit) algorithm [22,23,24] is proposed to select multiple atoms for iteration. Stagewise weak orthogonal matching pursuit (SWOMP) algorithm based on atom selection threshold [25, 26] and subspace pursuit (SP) algorithm based on retrospective thinking [27, 28] are proposed to have reduced the computational complexity, but most of algorithms rely on sparsity. The sparsity adaptive matching pursuit (SAMP) algorithm can approach the sparsity by step size gradually. The method of step size approximation is divided into many stages in iteration. Each stage increases the fixed step size to meet the requirement. Because the step size is fixed, the choice of step size will also affect the performance of the algorithm [29,30,31].

Beginning from sparse representation classification algorithm, this paper introduces sparse estimation and variable step size to aim at the disadvantages of existing greedy algorithms. A modified adaptive orthogonal matching pursuit (MAOMP) algorithm is proposed, and it is validated on the gesture samples. The results show that the performance is better than other algorithms, and the accuracy and efficiency of the algorithm are improved.

2 Sparse representation classification algorithms

The basic idea of sparse representation is that the training samples are constructed as redundant dictionaries, and the test samples can be represented by sparse linear combination of the dictionary elements, then sparse reconstruction algorithm is used to solve the sparse coefficients [32]. Sparse representation classification algorithms are mainly concerned on two aspects: the construction of redundant dictionaries and the solution of sparse coefficients. The framework model of sparse representation classification algorithm is introduced.

2.1 Test samples as linear representations of training samples

Given a sample set containing \(\hbox {C}\) class gestures, and the total sample number is n. Suppose that the \(j\in [1,\ldots ,C]\) class contains the \(n_j \) gesture samples, and the sample is enough. The i gesture of this class can be represented by column vectors \(a_{j,i} \in \mathfrak {R}^{m\times 1}\). The gesture samples are used to form a column vector matrix \(A_j =[a_{j,1} ,a_{j,2} \ldots ,a_{j,n_j } ]\in \mathfrak {R}^{m\times n_j}\). In the column vector matrix, mrepresents the dimension of the matrix. In the theory, a test sample \(y\in \mathfrak {R}^{m}\) belonging to class j is distributed in a linear subspace formed of this class of sample sets. That is that y can be represented linearly by \(A_j\):

$$\begin{aligned} y=A_j v_j =a_{j,1} v_{j,1} +a_{j,2} v_{j,2} +\cdots +a_{j,n_j } v_{j,n_j } \end{aligned}$$
(1)

In the formula (1), \(v_j =[v_{j,1} ,v_{j,2} \ldots ,v_{j,n_j } ]\in \mathfrak {R}^{n_j \times 1}\) is coefficient of linear expression. The categories of the test samples have not been determined. So the whole class C of gesture sample is formed into a redundant dictionary matrix \(A=[A_1 ,\ldots ,A_j ,\ldots ,A_C ]=[a_{1,1} ,\ldots ,a_{j,n_j } ,\ldots ,a_{C,n} ]\in \mathfrak {R}^{m\times n}\). That is that y can be represented by \(\hbox {A}\):

$$\begin{aligned} y=Ax \end{aligned}$$
(2)

In the formula (2), \(x=[0,\ldots 0,v_{j,1} ,v_{j,2} ,\ldots ,v_{j,n_j } ,0,\ldots ,0]\) is a sparse coefficient of test samples, nonzero elements correspond to the classj. If \(S=\left\| x \right\| _0 \) and \(\hbox {S}\le n\), x is sparse and \(\hbox {S}\) is sparsity.

2.2 Sparse computation method for minimizing norm

Because the dimension of the dictionary A is less than the number of samples, that is \(m<n\), the formula (2) belongs to underdetermined equation, and the solution is not unique. But x is a sparse matrix, and A satisfies the 2S order restricted isometry property (RIP). In the dictionary A, any 2S column sample data is linearly independent. For any sample y and constant \(\delta _S \in (0,1)\), the dictionary A satisfies formula (3), and then the unique solution can be guaranteed [33, 34].

$$\begin{aligned} (1-\delta _S )\left\| y \right\| _2^2 \le \left\| {Ay} \right\| _2^2 \le (1+\delta _S )\left\| y \right\| _2^2 \end{aligned}$$
(3)

Formula (2) can be solved by minimizing the \(l_0 \)norm:

$$\begin{aligned} \hat{{x}}=\mathop {\hbox {argmin}}\limits _x \left\| x \right\| _0 \quad s.t.\,\, y=Ax \end{aligned}$$
(4)

The solution of the minimization of the \(l_0 \) norm is a NP-hard problem. The greedy algorithm can only approximately solve the minimization of the \(l_0 \) norm problem. Among them, OMP algorithm is widely adopted, and the greedy algorithm is analyzed and solved in this paper. According to the theory of compressed sensing, when xis enough sparse, the formula (4) can be equivalent to solving the minimization of the \(l_1 \) norm problem [35].

$$\begin{aligned} \hat{{x}}=\mathop {\hbox {argmin}}\limits _x \left\| x \right\| _1 \quad s.t.\,\, y=Ax \end{aligned}$$
(5)

Because of the environmental factors, the actual sample collection will be affected by noise, light etc. The test samples cannot be better represented by linear combination of training samples, and the recognition rate will be affected easily. In order to improve robustness, a noise constraint can be added:

$$\begin{aligned} \hat{{x}}= & {} \mathop {\hbox {argmin}}\limits _x \left\| x \right\| _0 \quad s.t.\,\, \left\| {y-Ax} \right\| _{_2 } \le \varepsilon \end{aligned}$$
(6)
$$\begin{aligned} \hat{{x}}= & {} \mathop {\hbox {argmin}}\limits _x \left\| x \right\| _1 \quad s.t.\,\, \left\| {y-Ax} \right\| _{_2 } \le \varepsilon \end{aligned}$$
(7)

2.3 Classification according to the minimum residual error

The sparse coefficient of linear combination has been obtained, and it can use the sparse coefficient and redundant dictionary to reconstruct the test sample. Then compare the reconstructed samples and test samples of each class. Finally, judge the categories of the test samples according to the minimum residual error.

$$\begin{aligned} \gamma _j (y)= & {} \left\| {y-A\delta _j (\hat{{x}})} \right\| _{\text {2'}} j=1,2,\ldots ,C \end{aligned}$$
(8)
$$\begin{aligned} I(y)= & {} \hbox {argmin}_j r_j (y) \end{aligned}$$
(9)

In the formula (9), \(\gamma _j (y)\)is corresponding to the residual error of the class j sample. In the formula (8), \(\delta _j (\hat{{x}})\) is corresponding to coefficient value of the class j sample. Other location is 0 and I(y) is the categories of testing samples.

The steps of sparse representation classification algorithms are summarized below:

  1. 1

    Input: training sample\(A\in \mathfrak {R}^{m\times n}\), test sample\(y\in \mathfrak {R}^{m\times 1}\), and error threshold \(\varepsilon >0\).

  2. 2

    Each column of the A and y are normalized by the \(l_2 \) norm

  3. 3

    Solve the \(l_0 \) norm of the minimization:

    $$\begin{aligned} \hat{{x}}=\mathop {\hbox {argmin}}\limits _x \left\| x \right\| _0 \qquad s.t.\,\, \left\| {y-Ax} \right\| _2 \le \varepsilon \end{aligned}$$

    Or translate to solve the \(l_1 \) norm of the minimization:

    $$\begin{aligned} \hat{{x}}=\mathop {\hbox {argmin}}\limits _x \left\| x \right\| _1 \qquad s.t.\,\,\left\| {y-Ax} \right\| _{_2 } \le \varepsilon \end{aligned}$$
  4. 4

    Compute the residuals for the each class\(j\in [1,C]\):

    $$\begin{aligned} \gamma _j (y)=\left\| {y-A\delta _j (\hat{{x}})} \right\| _2 \end{aligned}$$
  5. 5

    Outputs: \(I(y)=\arg \min _j r_j (y)\)

3 Modified adaptive orthogonal matching pursuit algorithm

It is very important to solve sparse coefficients for sparse representation theory. That is how to use a small number of atoms in a redundant dictionary to represent the original signal. Aiming at the disadvantages of greedy algorithms, a modified adaptive orthogonal matching pursuit (MAOMP) algorithm is proposed in this paper to improve the accuracy and efficiency of the greedy algorithm. The MAOMP algorithm does not need to input the true sparsity, the initial value of the sparsity is estimated by matching test, and the estimated value to meet condition is taken as the length of the support set. Then, the atom is selected from the projection set, and the index set and the support set are updated. The original signal is estimated by retrospective thinking and least square method, and update residuals. Finally, the number of filtered atoms is adjusted by stages and variable step size. Approach to true sparsity and lead to better sparse representation.

3.1 Sparsity estimation

In this paper, atomic matching test is used to estimate the initial sparsity. The sparsity \(S_0\) is less than the true sparsity S. The set \(\Lambda _0 \) consist of the index before the \(S_0 \) in the \(u=\left| {\left\langle {\gamma _0 ,A_l } \right\rangle } \right| \), corresponding to the A. The reference [35] presents a true proposition that A satisfies the RIP property in terms of parameters \((S,\delta _S ),\delta _S \in (0,1)\).That is if \(S_0 \ge S\), the formulation \(\left\| {A_0^T y} \right\| _2 \ge \frac{1-\delta _S }{\sqrt{1+\delta _S }}\left\| y \right\| _2 \) is right. Then the converse negative proposition of the original proposition should also be right. That is when\(\left\| {A_0^T y} \right\| _2 <\frac{1-\delta _S }{\sqrt{1+\delta _S }}\left\| y \right\| _2 \), \(S_0 <S\)is right. Therefore, the converse negative proposition can be used to estimate the initial sparsity. First, given a smaller value\(S_0 \), when\(\left\| {A_0^T y} \right\| _2 <\frac{1-\delta _S }{\sqrt{1+\delta _S }}\left\| y \right\| _2 \), \(S_0 \)is constantly increased until the condition is not satisfied. \(S_0 \) is the estimated sparsity at this moment.

3.2 Variable step size

Since sparsity is generally unknown, and SAMP algorithm uses smaller step size approximation and step size is fixed, this method decreased the efficiency of the algorithm. Because each iteration error is declining constantly, and just starting to decline rapidly, then the range slows down gradually and tends to be stable finally. Therefore, when set the step size, it should be gradually reduced. The larger step size is adopted to reduce the times of iterations at the beginning, and then gradually reduce the step size and improve the accuracy. In this paper, the method to achieve the variable step size is that the step size coefficient \(\beta \in (0,1)\) is multiplied by the step under the condition to satisfy the variable step size. With the increase of stage, the step is decreased gradually.

$$\begin{aligned} step=\left\lceil {\beta \times step} \right\rceil ,\quad \beta \in (0,1) \end{aligned}$$
(10)

The steps of the whole MAOMP algorithm are:

  1. 1

    Input: training sample \(A\in \mathfrak {R}^{m\times n}\), test sample \(y\in \mathfrak {R}^{m\times 1}\), constant \(\delta _S \) and step coefficient \(\beta \).

  2. 2

    Initialization: sparsity \(S_0 =1\), step size \(step=m/\log _2 n\), residual error \(\gamma _0 =y\), index set \(\Lambda _0 =\varnothing \) and the support set \(A_0 =\varnothing \).

  3. 3

    Compute the projective set \(u=\left\{ {u_j |u_j =\left| {\left\langle {\gamma _0 ,A_l } \right\rangle } \right| ,}{l=1,2,\cdots ,n} \right\} \), and select the \(S_0 \) larger value in u. The index value and the support set are stored \(\Lambda _0 \)and \(A_0 \) separately.

  4. 4

    If \(\left\| {A_0^T y} \right\| _2 <\frac{1-\delta _S }{\sqrt{1+\delta _S }}\left\| y \right\| _2 \), the \(S_0 =S_0 +1\) is confirmed. And then turn on step 3. Or compute the residual error \(\gamma _0 =y-A_0 A_0^+ y\), and set \(L=S_0\), \(stage=1\) and the times of iteration \(t=1\). Turn on step 5.

  5. 5

    Compute the projective set \(u=\left\{ {u_j |u_j =\left| {\left\langle {\gamma _{t-1} ,A_l } \right\rangle } \right| ,}{l=1,2,\cdots ,n} \right\} \), and select the L larger value in u. The corresponding index values form a set \(J_0\).

  6. 6

    Update index sets and support sets:

    $$\begin{aligned} \Lambda _t =\Lambda _{t-1} \cup J_0 ,A_t =A_{t-1} \cup A_l (l\in J_0 ) \end{aligned}$$
  7. 7

    The equation \(y=A_t x_t \) is computed and least square solution is given:

    $$\begin{aligned} \hat{{x}}_t =\mathop {\hbox {argmin}}\limits _{x_t } \left\| {y-A_t x_t } \right\| _2 \end{aligned}$$
  8. 8

    Select the largest L of the absolute value marked as\(\hat{{x}}_{tL} \), and then the L column in corresponding to \(A_t\) is marked as \(A_{tL}\) and the A column ordinal is marked as \(\Lambda _{tL}\).

  9. 9

    Update the residual error \(\gamma _t =y-A_{tL} \hat{{x}}_{tL}\)

  10. 10

    If residual error \(\left\| {\gamma _t } \right\| _2 <\varepsilon \), turn on the step 11. If \(\left\| {\gamma _{new} } \right\| _2 \ge \left\| {\gamma _{t-1} } \right\| _2\), \(stage=stage+1\), \(step=\left\lceil {\beta \times step} \right\rceil L=L+step\) and \(t=t+1\), turn on the step 5. If the two conditions is not satisfied, \(\Lambda _t =\Lambda _{tL} ,t=t+1\), turn on the step 5.

  11. 11

    Output: sparse coefficient \(\hat{{x}}\), and the nonzero items in corresponding to the index set \(\Lambda _t \) are the final iteration \(\hat{{x}}_t\).

The MAOMP algorithm is similar to the SAMP algorithm, and the parameter input does not need to set sparsity. Sparsity is estimated on Step 2 to step 4. The length of the initialization support set is the estimated sparsity \(S_0 \). The algorithm efficiency is improved. In addition, the initial step size is different for different situations, and set \(step=m/\log _2 n\) here. A staged approximation process based on the SAMP algorithm is on step 5 to step 10. The true sparsity can be better approximated by changing the step size gradually. The step 10 shows that the residuals after iteration are constantly decreasing, so the algorithm can converge. In MAOMP algorithm, sparsity estimation and variable step size are adopted to reduce the times of iterations to some extent and improve the accuracy.

4 Experimental simulation

4.1 Establishment of gesture sample

In order to verify the effect of gesture recognition in this method, hand gesture images are collected. Gesture sample library is built to analyze the influence situation of various factors on hand gesture recognition. In the experiment, the appointed gesture samples are selected. In YCbCr color space, the Y component is independent of the Cb and Cr components, so that the skin segmentation is less affected by illumination. It is a linear transformation from YCbCr color space to RGB color space and is easy to segment. Therefore, YCbCr color space is selected to segment the gesture image. The ellipse model is set up in YCbCr color space to segment the gestures, and the Hu invariant moments and HOG features are extracted.

4.1.1 Grab gesture sample library

In this paper, five typical grab gesture samples are collected from five people by camera. The gestures include five fingers grasp, three fingers grasp, two fingers pinch, one finger hook and five fingers open. As is shown in Fig. 1, five kinds of gestures are collected, and collect 20 pictures for each person. That is that each type of gesture collect 100 pictures, a total of 500 images can be used in the experiment. The collection of gestures also takes into account the changes in gesture rotation, scale, illumination and background to make the effect of identification more obvious.

Fig. 1
figure 1

The five kinds of grab gesture samples. a five fingers grasp b three finger grasp c two finger pinch d single finger hook e five fingers open

Full size image
Fig. 2
figure 2

the partial ASL gesture samples

Full size image

4.1.2 ASL sample library

The ASL sample library contains 26 letters of gesture (letters j and z gestures are dynamic, so this article will not be considered). The gesture pictures are collected separately for five people by Kinect in the same light and scene. Each operator and each letter has a color image and a depth image, the color images of 24 letters are collected, and collects 20 pictures for each person. A total of 2400 color images can be used in the experiment, and Fig. 2 is a partial color image.

4.2 The influence of parameter selection on performance of MAOMP algorithm

In order to verify the estimation effect of sparsity, the estimated value of sparsity S are compared when the parameter \(\delta _S\) are taken different values. 50 training samples and ten test samples were randomly selected from each gesture in grab gesture library, and reduce the dimension to 100. 50 training samples and two test samples were randomly selected from each gesture in ASL sample library. The experimental results are shown in Figs. 3 and 4.

As is shown in Figs. 3 and 4, the sparsity estimates \(S_0 \) corresponded to \(\delta _S \) can fluctuate near a certain value. For example, when \(\delta _S =0.2\), the average value of the estimation \(S_0\) is 27 in grab gesture sample library and is 24 in ASL sample library. Because 50 training samples are taken in two gesture libraries, the theoretical sparsity S is 50, which serves as a reference for sparsity estimation. In addition, \(\delta _S \) is smaller, the estimation of the sparsity and the fluctuation are larger. It is closer to the theoretical sparsity, but the estimated value may be greater than the theoretical sparsity. To the contrary, \(\delta _S \) is the larger, the estimation of the sparsity is smaller, and the estimation is more stable. But, when it decreases to a certain extent such as 0.9, the sparsity estimation value is maintained at 1. Because \(\frac{1-\delta _S }{\sqrt{1+\delta _S }}\) is a decreasing function, the range of iterative termination conditions is enlarged with the \(\delta _S \) decreasing. The times of iterative estimation are increased, and the estimation of the sparsity is greater. So \(\delta _S\) have an obvious influence on the times of iterative estimation and the estimation of sparsity, and \(\delta _S =0.2\) is selected to reduce the times of subsequent iterations and avoid over estimation.

Fig. 3
figure 3

the sparsity estimation in grab gesture sample library

Full size image
Fig. 4
figure 4

the sparsity estimation in ASL sample library

Full size image

The algorithm of this paper also adopts the idea of variable step size, and the effect of different values \(\beta \) on the algorithm is verified by experiments. 50 training samples are selected for each class, and the remaining samples are taken as test samples in grab gesture sample library, then the dimension of feature is reduced to 100. 50 training samples are selected for each class, and the remaining samples are taken as test samples in ASL sample library, then the dimension of feature is reduced to 100 and takes \(\delta _S \) as 0.2.

Figure 5 shows the influence of different step size coefficients on the recognition rate. It can be seen that the recognition rate of the two sample library is decreasing gradually with the step size coefficients \(\beta \) increasing. The recognition rate decreased from 93.2 to 79.5% in grab gesture sample library with \(\beta \) increasing. The recognition rate decreased from 94.9% to 80.2% in ASL sample library with \(\beta \) increasing. Moreover, the maximum drop amplitude between \(\beta =0.4\) and \(\beta =0.5\) is about 4%, and other intervals drop by about 2%.

Fig. 5
figure 5

the influence of different step size coefficient on recognition rate

Full size image
Fig. 6
figure 6

the variation of residual error with iterations in grab gesture sample library

Full size image
Fig. 7
figure 7

the variation of residual error with the iterations in ASL sample library

Full size image

The decreasing in recognition rate between \(\beta =0.4\) and \(\beta =0.5\) is greatest. In order to explain the situation better, 100 and 150 iterations are made in the two sample library respectively. The variation curve of the residuals with the times of iterations is plotted, as shown in Figs. 6 and 7.

When the times of iterations increases to a certain value, the residuals converges to a smaller value. When the residuals remain same, the times of iterations are stages. The stages and iterations will decrease with the increasing of step coefficient. The times of iterations are the highest as 88 and the lowest as 9 in grab gesture sample library. The times of iterations are the highest as 103 and the lowest as 14 in ASL sample library. The falling amplitude of the times in iterative convergence between \(\beta =0.4\) and \(\beta =0.5\) is larger than others. Decreasing amplitude is 18 in grab gesture sample library and is 22 in ASL sample library, others is about 10. Because the step size is larger, the selected elements are more. The length of the support set is large and the convergence is fast. But the sparsity is easily overestimated, which reduces the recognition rate. When \(\beta =0.5\), over-estimation has been made. The atom of linear representation in test sample contains too many other atoms, which will reduce the recognition rate. Considering the recognition rate and the times of iterations, \(\beta =0.4\) is more appropriate.

Fig. 8
figure 8

The variation of recognition rate on each algorithm with the dimensionality in grab gesture sample library

Full size image
Fig. 9
figure 9

The variation of average running time on each algorithm with the dimensionality in grab gesture sample library

Full size image
Fig. 10
figure 10

The variation of recognition rate on each algorithm with the dimensionality in ASL sample library

Full size image

4.3 Performance comparison of the algorithms

In the two gesture libraries, the MAOMP algorithm is compared with OMP, ROMP, SWOMP, SP and SAMP algorithms from the two aspects of recognition rate and average running time. In the experiment, 50 samples are selected as training set at random, 50 samples are taken as test set. After the features are extracted, PCA is used to reduce the dimension. In addition, the parameters of each algorithm need to be set. In MAOMP algorithm,\(\delta _S =0.2\) and \(\beta =0.4\) are taken. The sparsity of the SWOMP and SP algorithms is set to 40. The threshold parameter of the SWOMP algorithm is set to 0.5. The step size of the SAMP algorithm is set to 5. The recognition rate and average running time of different matching pursuit algorithms in grab gesture sample library are shown in Figs. 8 and 9 respectively. It can be seen from Fig. 8 that the recognition rate of each algorithm increases with the increase of dimension. In low dimensionality, the recognition rate of MAOMP algorithm can still be more than 85%, and the recognition rate of SAMP, SP and SWOMP is maintained at 80–85%, while the ROMP and OMP algorithms are less than 80%. In high dimensionality, the recognition rate of MAOMP, SAMP, SP and SWOMP is higher than 90%, and the ROMP and OMP algorithms are around 85%. For the whole, the recognition rate of MAOMP algorithm is the highest under the same dimension, the SAMP algorithm is second, and the OMP algorithm is the smallest. As can be seen from Fig. 9, the average running time of each algorithm increases gradually with the increase of dimensionality. In low dimensionality, the average running time of each algorithm is smaller, about 0.001s, and the difference is small. In high dimensionality, the running time of each algorithm is different greatly. When the dimension is 200, the average running time of OMP algorithm is 0.028 s, the SAMP algorithm is 0.019 s, the MAOMP algorithm is 0.012 s, and the other algorithms are almost below 0.010 s. For the whole, the average running time of OMP algorithm is the longest under the same dimension, the SAMP algorithm is second, and the SWOMP algorithm is the shortest.

Fig. 11
figure 11

The variation of average running time on each algorithm with the dimensionality in ASL sample library

Full size image

The recognition rate and average running time of different matching pursuit algorithms in ASL sample library are shown in Figs. 10 and 11 respectively. As can be seen from Figs. 10 and Figure 11, both the recognition rate and the average run time increase with the increase of dimensionality. n the ASL sample library, more samples are selected, so the recognition rate and average computing time are relatively high compared with grab gesture library. In Fig. 10, the recognition rate of the MAOMP, SAMP and SP algorithms is above 85% at low dimensionality, and the recognition rate of SWOMP, ROMP and OMP algorithms is maintained at 80–85%. In high dimensionality, the recognition rates of MAOMP, SAMP, SP and SWOMP are close to 95%, and the ROMP and OMP algorithms are close to 90%. MAOMP algorithm has the highest recognition rate, followed by the SAMP algorithm, and the OMP algorithm is the smallest under the same dimension. In Fig. 11, the average running time of different algorithm is shorter about 0.002 s at low dimensionality. The running time of each algorithm varies greatly at high dimensionality. When the dimension is 200, the average running time of the OMP algorithm is 0.054 s, the SAMP algorithm is 0.034 s, the MAOMP algorithm is 0.025 s, and the other algorithms are below 0.020 s. Under the same dimension, the average running time of OMP algorithm is the longest, then the SAMP algorithm is second, and the ROMP algorithm is the lowest.

To sum up, OMP algorithm selects only one atom at iteration, resulting in lower accuracy and efficiency. SP, SWOMP and ROMP algorithm select more than one atom each time by improve the atomic selection strategy, which simplifies the OMP algorithm and improves the efficiency of OMP algorithm, but the recognition accuracy is easily affected by sparsity or threshold parameters. The SAMP algorithm improves the accuracy and efficiency of OMP algorithm by step size approximation, and the efficiency is higher than that of OMP algorithm. But it depends on the initial step size, and the step size is fixed. The sparsity estimation is not accurate enough, and the recognition rate is lower than the MAOMP algorithm. MAOMP algorithm introduces rough estimation of sparsity in solution, and the subsequent each stage step decreases gradually makes the approximation of sparsity is more accurate, which is higher than other improved OMP algorithms, and the average running time is significantly less than the OMP algorithm and SAMP algorithm. Especially in more samples, when dimension is higher, it has more obvious advantages.

5 Conclusion

Based on sparse representation classification algorithm, an improved adaptive orthogonal matching pursuit algorithm (MAOMP) is proposed to solve the problem of low precision and uncertain parameters of greedy algorithms in sparse solution. MAOMP algorithm introduces the sparsity estimation step. The sparsity initial value is estimated by matching test. The variable step size is added to adjust the filtered atom number by stages, and approaches the true sparsity. Experimental results show that the performance of MAOMP algorithm is better than that of other improved OMP algorithms, especially when there are more samples and higher dimensions. The next step is to add some occluded images to identify the robustness of the algorithm.