Introduction

Cellulose nanocrystals (CNCs) are one type of cellulose-based nanoparticle that can be extracted from various biomass resources, such as trees, plants, bacteria, algae, and tunicates (Moon et al. 2011). The resulting CNCs have a fibril morphology, high aspect ratio (10–100), high surface area-to-volume ratio, high mechanical properties, low coefficient of thermal expansion, and low density. The exposed OH side groups on CNC surfaces can be readily modified to achieve different surface properties, which can effect self-assembly, dispersion within a wide range of matrix polymers, and control of both the particle-particle and particle-matrix bond strength. This unique set of characteristics represents a “building block” with new capabilities that can be used in the development of new advanced composites. CNCs have been used in the development of network composites (Moon et al. 2011; Lin et al. 2012; Eichhorn 2011) as well as the reinforcement phase in polymer matrix composites (Moon et al. 2011; Lin et al. 2012; Eichhorn 2011). For the CNC-polymer composites, generally, both elastic modulus and tensile strength increase with increasing CNC content (Pei et al. 2011; Xu et al. 2013; Siqueira et al. 2009; Lu and Hsieh 2009; Cao et al. 2011), and the strain-at-failure can either increase (Pei et al. 2011; Xu et al. 2013) or decrease (Siqueira et al. 2009; Lu and Hsieh 2009) depending on the properties of the polymer matrices. To better understand how CNCs affect these composite properties, it is important to first understand the properties of individual CNCs.

The elastic modulus of CNCs has been studied using a variety of experimental and simulation methods. Commonly-employed experimental techniques are the in situ tensile test using inelastic X-ray diffraction (Diddens et al. 2008), Raman (Rusli and Eichhorn 2008; Sturcová et al. 2005), three point bending using atomic force microscopy (AFM) (Iwamoto et al. 2009) and indentation using AFM (Lahiji et al. 2010; Wagner et al. 2011; Pakzad et al. 2011). The elastic properties of CNC have been studied using molecular mechanics (MM) (Reiling and Brickmann 1995; Tanaka and Iwata 2006; Eichhorn and Davies 2006; Wu et al. 2013) and molecular dynamics (MD) (Bergenstråhle et al. 2007; Neyertz et al. 2000; Wohlert et al. 2012) simulations of cellulose chains and Iβ crystalline cellulose (cellulose Iβ).

The ultimate properties (i.e. tensile strength and strain-at-failure) of CNCs, however, are less studied. As the typical dimensions of a CNC are 50–500 nm in length and 3–20 nm in diameter depending on its source (Moon et al. 2011), it is difficult to measure ultimate properties using experimental methods (Tan and Lim 2006). The tensile strength typically reported for CNCs, 7.5 GPa, comes from a theoretical approach based on bond energies within cellulose (Mark 1968). To the authors knowledge, there has been only one study of experimentally-measured tensile strengths of cellulose nanomaterials, which was reported to be between 2 and 6 GPa (Saito et al. 2013).

Therefore, despite the significant potential benefit of using CNCs in composite materials, progress in this area is hindered by the lack of available information about the ultimate properties of individual CNCs and the challenge of obtaining such information using experimental methods. We directly address this issue using MD simulations. MD has been successfully used for studying mechanical strength and failure mechanisms of various nanoscale materials, including carbon nanotubes (Liew et al. 2004), metal nanowires (Koh et al. 2005) and composites (Tomar and Zhou 2007), and amorphous polymers (Hossain et al. 2010). Here, we apply it to predict the ultimate properties of cellulose Iβ, which can be used as an estimate for CNC ultimate properties. The simulation captures the stress response of the material to tensile strain in the three orthogonal directions from which we calculate the elastic modulus, Poisson’s ratio, yield stress and strain, and ultimate stress and strain. The effect of strain rate and the direction-dependent nature of these mechanical properties is analyzed. Finally, the fundamental relationships between material properties and atomic structure are discussed.

Simulation

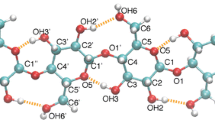
A molecular model of the monoclinic cellulose Iβ unit cell is constructed based on recent X-ray diffraction measurements (Nishiyama et al. 2002). The lattice constants are \(a=0.7784\,\hbox {nm}, \quad b=0.8201\,\hbox {nm},\quad c=1.0380\,\hbox {nm},\quad \alpha =\beta =90^{\circ }\), and \(\gamma =96.5^\circ\). The unit cell is expanded \(4\times 4\times 8\) times in the three orthogonal directions to obtain a simulation system (Fig. 1). Periodic boundary conditions are applied in all directions.

Although use of periodic boundary conditions precludes the model from capturing surface effects, we apply them here for three reasons. First, periodic boundary conditions provide a means of partially overcoming the size limitations of an atomistic model. This size limitation is particularly stringent for the reactive force field that is necessarily used in this work to describe the breaking of covalent bonds. As a result, the model is relatively small: ~5 nm in the transverse directions and ~10 nm in the chain direction. Although the former is consistent with that of naturally occurring CNCs (3–20 nm), the latter is much shorter than the 50–500 nm length of most crystal (Moon et al. 2011). Periodic boundary conditions enable us to effectively model a much larger system. Second, periodic boundary conditions provide a numerical means of applying strain without imposing artificial constraints on the chains themselves. With non-periodic boundaries, strain can only be applied by applying an external force or displacement to the chains at the perimeter of the crystal. Therefore, although there are model surfaces, they are constrained in such a way that they do not respond ‘naturally’ to the strain or to interactions with the interior of the crystal. This issue is avoided in a periodic system where the boundaries themselves can be changed to apply strain. Thus, the use of periodic boundary conditions provides a physically-realistic means of applying strain to the largest possible model crystal. Lastly, the periodic model is used because it is relatively simple and enables us to isolate the bulk material response from that due to the crystal surfaces. The effect of surfaces on a CNC’s mechanical properties depends on its surface-to-volume ratio, which in turn depends on the source of the crystal and it is not straightforward to measure experimentally. Studying these uncharacterized and variable surface effects necessarily requires that we know the bulk material response for reference; this is achieved through the use of periodic boundary conditions in this study. For reference, however, select simulations are performed with finite boundaries and strain applied direction to the chains at the perimeter of the crystal.

Fig. 1
figure 1

Molecular model of cellulose \(\hbox {I}\beta\) shown a in perspective view and b in the \(x\)-\(y\) plane. The three orthogonal deformation directions are \(x, y\) and \(z\) where the \(z\)-direction is in the direction of the cellulose chains. b The \(x\)- and \(y\)-directions are parallel and perpendicular to the hydrogen bonding plane, respectively. The three lattice parameters that describe the cross section of the cellulose unit cell are labeled, \(a=0.7784\,\hbox{nm}, b=0.8201\,\hbox{nm}\) and \(\gamma =96.5^\circ\) (Nishiyama et al. 2002)

Full size image

The first stage of the simulation is equilibration. The simulation cell is equilibrated in the NPT (constant number of atoms, pressure and temperature) ensemble for 300 ps with timestep 0.5 fs to reach its equilibrium state at 300 K and 1 atmosphere. Afterwards, energy minimization is performed to allow the system reach its lowest energy state. The simulation cell dimensions after minimization are recorded as initial lengths \(\hbox {L}_{x0}, \hbox {L}_{y0}\) and \(\hbox {L}_{z0}\).

To apply strain, the simulation system is deformed in the three orthogonal directions labeled in Fig. 1: the \(x\)-direction is parallel to the (200) hydrogen bonding plane, the \(y\)-direction is perpendicular to the (200) lattice plane, and the \(z\)-direction is parallel to the longitudinal axis of the cellulose chains. Deformation in each direction is performed independently. Tensile strain is applied in each direction by elongating the simulation cell by a small increment \(\delta\)L = L0 × 0.25 %. The system is then re-equilibrated in the NPT ensemble for time \(\hbox {t}_{eql}\) with 1 atmosphere of pressure applied in the two non-deformed directions in order to allow their dimensions to change according to the Poisson effect. The system is strained and equilibrated repeatedly until 100 % strain is reached. By modeling large strain, i.e. beyond the initial elastic and plastic deformation, we obtain the full strain response of the material with which we can analyze failure mechanisms. The strain rate of the tensile deformation is controlled by changing the equilibration time \(\hbox {t}_{eql}\) from 0.25 to 2,500 ps to achieve strain rates from \(10^{-2}\) to \(10^{-6}/\hbox {ps}\).

The stress and strain in the deformation direction are recorded to calculate the mechanical properties. The lengths of the two non-deformed directions after each equilibration are used to calculate the corresponding Poisson’s ratios. The atomic positions are also obtained for analysis. All the acquired data are values averaged over the last 10 % of simulation time at each equilibration step. The simulations are performed using LAMMPS software and the ReaxFF force field (Mattsson et al. 2010) is used to describe the atomic interactions. This force field was previously used to accurately predict the elastic modulus of cellulose \(\hbox {I}\beta\) using molecular mechanics (Wu et al. 2013). Note that a reactive force field is necessary for this work to enable the model to capture the breaking (and potentially formation) of covalent bonds due to strain. The ReaxFF is one of only two available reactive force fields that is currently parameterized for all the atom types in cellulose (Liang et al. 2013).

Results

Stress–strain behavior

The stress–strain behavior of the model cellulose \(\hbox {I}\beta\) subject \(y\)-direction strain at a rate of \(10^{-3}/\hbox {ps}\) is shown in Fig. 2. We will use this result to explain generally-observed trends, introduce terminology and explain how mechanical properties are calculated from simulation data. First, we identify the ultimate point as the maximum stress and corresponding strain. In this example, the ultimate point occurs at stress 0.44 GPa and strain 8.6 %, labeled U in Fig. 2. Strains higher than point U are identified as large deformation, where permanent changes of material structure and failure can occur. Strains smaller than U correspond to small deformation, from which we calculate mechanical properties. Second, we find the yield point by fitting a second order polynomial from the origin point O (0 % strain) to the ultimate point U. The second derivative of the polynomial is the curvature of the fitted line. Then, we fit the polynomial again using the data from O to strains smaller than U. As the strain decreases, the curvature of the polynomial decreases. When the curvature approaches zero, the second order polynomial curve approaches a straight line. We repeat the fitting process until we find the point at which further decreasing the strain will not decrease the curvature, i.e. the curvature reaches its minimum value and the polynomial can be considered linear. This is identified as the yield point that separates the linear elastic and nonlinear plastic deformation regimes and is labeled Y in Fig. 2. In this example, the yield point is at stress 0.29 GPa and strain 4.1 %. Finally, a straight line is fitted from point O to Y, and its slope is the elastic modulus; in this example \(\hbox {E}_y=7.08\,\hbox {GPa}\).

Fig. 2
figure 2

Stress–strain behavior of the model cellulose \(\hbox {I}\beta\) deformed in the \(y\)-direction at strain rate \(10^{-3}/\hbox {ps}\) (open circles), and the corresponding strain in the \(x\)-direction (solid lines) and the \(z\)-direction (dotted lines). The origin, yield and ultimate points, and the various deformation regimes are labeled

Full size image

Figure 2 also shows the strain in the other two orthogonal directions (i.e. \(x\) and \(z\)). The slopes of linear fits to the strain data in the elastic deformation regime (straight lines) provide the corresponding Poisson’s ratios. In this example, they are \(\nu _{x/y}=0.10\) and \(\nu _{z/y}=0.02\).

The full set of stress–strain data (in the small deformation region only) for the three orthogonal directions and at different strain rates (\(10^{-4}, 10^{-3}\) and \(10^{-2}/\hbox {ps}\)) is given in Fig. 3. The stress and strain at the ultimate point and the yield point, elastic modulus and Poisson’s ratio are calculated for each deformation direction and strain rate combination. The magnitudes of these properties are reported in Fig. 4 and Tables 1 and 2. For reference, Fig. 4 also reports the elastic modulus and ultimate properties for a single cellulose chain strained in the chain (\(z\)) direction.

Fig. 3
figure 3

Stress–strain behavior during tensile deformation in the a \(x\)-, b \(y\)- and c \(z\)-direction at strain rates of 10\(^{-4}\) (solid squares), \(10^{-3}\) (open circles) and \(10^{-2}/\hbox {ps}\) (crossed triangles). The corresponding strain in the non-deformed directions is also reported for the \(x\)- (solid lines), \(y\)- (dashed lines) and \(z\)-direction (dotted lines)

Full size image
Fig. 4
figure 4

Model-predicted mechanical properties: a elastic modulus, b yield stress, c yield strain, d ultimate stress and e ultimate strain, and their dependence on strain rate. Tensile deformation of the cellulose \(\hbox {I}\beta\) in the \(x\)-direction (squares), \(y\)-direction (circles) and \(z\)-direction (triangles) at strain rates from \(10^{-4}\) to \(10^{-2}/\hbox {ps}\). The deformation of a single cellulose chain in the \(z\)-direction (stars) in shown in a, d and e at strain rates from \(10^{-6}\) to \(10^{-2}/\hbox {ps}\)

Full size image
Table 1 Mechanical properties of a cellulose \(\hbox {I}\beta\) calculated from the response to deformation in the \(x\), \(y\) and \(x\)-directions at strain rates of \(10^{-4}, 10^{-3}\) and \(10^{-2}/\hbox {ps}\) predicted by the MD simulation
Full size table

Effect of deformation direction

To understand the effect of the deformation direction on mechanical properties, we initially focus on results obtained at one strain rate, \(10^{-4}/\hbox {ps}\). The elastic modulus is reported in Fig. 4a and the first row of Table 1. We observe that the axial modulus (i.e. in the \(z\)-direction) is 107.8 GPa; this is consistent with values reported in previous experimental studies, which fall in the range of 105–220 GPa (Sturcová et al. 2005; Rusli and Eichhorn 2008; Diddens et al. 2008; Iwamoto et al. 2009; Dri et al. 2013). The transverse moduli (i.e. in the \(x\)- and \(y\)-directions) are 21.6 and 7.6 GPa, respectively. They also fall into the range of values reported in the literature from experiments, 2–50 GPa (Diddens et al. 2008; Lahiji et al. 2010; Wagner et al. 2011; Pakzad et al. 2011). It is notable that most previous simulation predictions of the elastic modulus were obtained using the MM method, in which there is no dynamics and so corresponds effectively to 0 K. The previously-reported values using MM are 111–156 GPa in the \(z\)-direction (Neyertz et al. 2000; Tanaka and Iwata 2006; Eichhorn and Davies 2006; Wu et al. 2013) and 7–47 GPa in the transverse directions (Eichhorn and Davies 2006; Wu et al. 2013). The MD method used in this paper incorporates atomic motion and so enables calculation of the elastic modulus at a finite temperature 300 K. Increased temperature is expected to decrease the elastic modulus predicted by a simulation (Koh et al. 2005). This is consistent with the observation that the finite temperature approach (MD) used here predicts the elastic modulus in the \(z\)-direction to be slightly lower than previously-reported values from MM. In the transverse directions, the moduli predicted here using MD and previously using MM are comparable. Lastly, we observe that the axial modulus of the crystal is slightly larger than that of the single chain indicating that inter-chain interactions do contribute to the crystal’s resistance to elastic deformation in the chain direction, consistent with previous observations that inter-chain hydrogen bonds affect axial elasticity (Eichhorn and Davies 2006; Wu et al. 2013).

The Poisson’s ratios are reported in Table 2. The only experimental value available for comparison in the literature is \(\nu _{(100/001)}=0.38\) which was obtained using X-ray diffraction (Nakamura et al. 2004). The [001] orientation is along the \(z\)-direction and the [100] orientation is comparable to the \(y\)-direction (\(6.5^{\circ }\) difference between the [100] and \(y\) directions). Therefore, we can compare the model predicted Poisson’s ratio \(\nu _{y/z}=0.46\) to the experimental value and observe good agreement. There is also one previous study of Poisson’s ratios predicted using density functional theory with a semi-empirical correction for van der Waals interactions; that work reported \(\nu _{y/x}=0.560\pm 0.026, \nu _{z/x}=0.025\pm 0.001, \nu _{x/y}=0.111\pm 0.003\), and \(\nu _{z/y}=0.046\pm 0.002\) (Dri et al. 2013). These values are comparable to the results in Table 2, although previously-reported \(\nu _{y/x}\), \(\nu _{x/y}\) and \(\nu _{z/y}\) are slightly larger and \(\nu _{z/x}\) is slightly smaller than the Poisson’s ratios reported in this paper. Comparison of the Poisson’s ratio in the different directions in Table 2 reveals that the largest Poisson effects are observed in the \(y\)-direction in response to either \(x\)- or \(z\)-direction strains (\(\nu _{y/x}=0.37\) and \(\nu _{y/z}=0.46\)). This may be attributable to the fact that the \(y\)-direction is perpendicular to the hydrogen bonding plane and therefore there is little resistance to Poisson contraction. We also observe there is only a small amount of contraction in the \(z\)-direction in response to strain in either the \(x\)- or \(y\)-direction (\(\nu _{z/x}=0.04\) and \(\nu _{z/y}=0.01\)). This may be due to the fact that there are covalent bonds within the chains that are able to resist contraction.

Table 2 Poisson’s ratios at strain rate \(10^{-4}/\hbox {ps}\)
Full size table

The yield stress and strain are given in Fig. 4b and c, and the second and third rows of Table 1, respectively. The yield stress in the \(z\)-direction (4.6 GPa) is significantly larger than in either the \(x\)-direction (0.3 GPa) or \(y\)-direction (0.2 GPa), which exhibit similar yield stress. The strain at yield is also largest in the \(z\)-direction (4.3 %), but the difference between the \(z\)-direction and the other two directions is not as significant as that exhibited by the stress. Comparison of the \(x\)- and \(y\)-directions reveals that, although the yield stresses are comparable, the strain at yield in the \(y\)-direction (2.3 %) is larger than that in the \(x\)-direction (1.3 %). This may be attributed to the fact that hydrogen bonding dominates the response of the crystal to strain in the \(x\)-direction and hydrogen bonds are very short range. That is, at small strain the hydrogen bonds are very strong but the strength of those bonds falls off quickly with increasing strain, resulting in the strain at yield in the \(x\)-direction being the smallest of the three directions.

The ultimate stress and strain are given in Fig. 4d, e, and the fourth and fifth rows of Table 1, respectively. Like the yield stress, the ultimate stress in the \(z\)-direction (5.4 GPa) is over an order of magnitude larger than those in either the \(x\)-direction (0.4 GPa) or \(y\)-direction (0.3 GPa), which exhibit similar ultimate stress. The ultimate stress in the \(z\)-direction is comparable to the previous theoretical estimate of 7.5 GPa (Mark 1968). Also, the strength of cellulose nanofibrils has been measured and reported to be 1.6–3 GPa for wood-derived nanofibrils and 3–6 GPa for tunicate-derived nanofibrils (Saito et al. 2013). Our model prediction of 5.4 GPa agrees well with these values, even though the cellulose \(\hbox {I}\beta\) structure used in this study is idealized and so will differ from the real CNC materials which have surfaces and defects and are not 100 % crystalline. In addition, as discussed in the next section, the model strain rates are likely to be much faster than those used in the measurement of the properties, precluding direct comparison. The ultimate strain in the \(z\)-direction (5.1 %) is in between those in the \(x\)-direction (3.0 %) and \(y\)-direction (7.5 %). Although the \(z\)-direction ultimate stress is much larger than those in the other two directions, the \(y\)-direction ultimate strain is the largest of the three. This may be due to the fact that, as will be discussed later, the deformation mechanism in the \(y\)-direction occurs through a more gradual process of chain redistribution, while the crystal fails in the \(z\)-direction through fast fracture. Comparison of the \(x\)- and \(y\)-direction ultimate properties reveals a similar trend to that observed at the yield points. Specifically, the ultimate stresses are comparable while the ultimate strain in the \(y\)-direction is larger than that in the \(x\)-direction. Like the yield behavior, this may be attributed to the strong, yet short ranged nature of the hydrogen bonds resisting tension in the \(x\)-direction.

Lastly, we also observe that the ultimate stress and strain of the crystal in the \(z\)-direction are comparable to those of the single chain indicating that the failure of the crystal is attributable primarily to interactions and bonding within the cellulose chains. For both the single chain and the cellulose \(\hbox {I}\beta\), the covalent bonds within the chains are strong, resulting in very large ultimate stress.

Effect of strain rate

We observe from Fig. 4a that the elastic modulus of both the \(\hbox {I}\beta\) crystal and the single cellulose chain are not significantly affected by strain rate. This is in agreement with a previous study of the tensile deformation of metals (Liang and Zhou 2004). Although the data is not shown here, the Possions ratios are also unaffected by strain rate. However, as shown in Fig. 4b–e, we observe that the yield and ultimate properties increase with strain rate, which is in agreement with previous simulation of various nanomaterials (Wei et al. 2003; Liang and Zhou 2004; Koh et al. 2005; Wu 2006). To ensure these trends are applicable more broadly, we simulate the single cellulose chain deformation at strain rates from \(10^{-6}\) to \(10^{-2}/\hbox {ps}\). Consistent with the observations for the cellulose \(\hbox {I}\beta\), we observe an increase of ultimate properties with strain rate. However, the rate of that increase appears to be lower at smaller strain rates, indicating the results are approaching constant, low strain rate values.

It is important to note that the magnitude of the strain rates applied in these simulations is large compared to those accessible to typical experiments. For example, the upper limit available to experimental dynamic testing methods \(10^7/\hbox {s} \,(10^{-5}/\hbox {ps}\)) (Ramesh 2008), while the strain rates investigated here are \(10^6\) to \(10^{10}/\hbox {s} \, (10^{-6}\) to \(10^{-2}/\hbox {ps}\)) and \(10^8\) to \(10^{10}/\hbox {s} \, (10^{-4}\) to \(10^{-2}/\hbox {ps}\)), for the single cellulose chain and cellulose \(\hbox {I}\beta\) crystal, respectively. The strain rates accessible to an MD simulation are limited by the necessarily small time step of the model (Liang and Zhou 2004; Koh et al. 2005; Koh and Lee 2006; Wu 2006; Hossain et al. 2010) and, as a result, model predictions cannot be compared directly to most experimental measurements, particularly those based on quasi-static methods. Regardless, the strain rate dependence observed here may have implications for interpreting experimentally-measured properties of CNC-based composites for several reasons. First, as mentioned above, elastic properties appear to be relatively independent of strain rate. Second, high strain rate simulations have been shown to successfully capture some of the large deformation mechanisms of nanomaterials observed in experiments (Yamakov et al. 2004) which suggests that some of the mechanisms discussed in the next section may also be exhibited at smaller strain rates. Finally, dynamic properties of cellulose \(\hbox {I}\beta\) are relevant for these materials to be implemented in armor/ballistic applications, in particular as fillers within polymer matrix composites or for transparent armor applications.

Discussion

The mechanical properties of cellulose \(\hbox {I}\beta\) were shown in the previous section to depend on tensile direction and, in some cases, strain rate. By correlating key points within the stress–strain behavior to the evolution of the crystals’ atomic configuration during deformation it is possible to identify relationships between mechanical properties and atomic scale structures, and to characterize deformation mechanisms. In this section, the stress–strain behavior of the cellulose \(\hbox {I}\beta\) in response to strain in the \(x\)-, \(y\)-, or \(z\)-direction from 0 to 100 % is shown. Specific points on the stress–strain plot (maximums, minimums, inflections, etc.) are identified for further analysis. At each of these points the corresponding atomic structures from the MD simulations are used to assess the configuration of the cellulose chains within the cellulose \(\hbox {I}\beta\). Note that these analyses consider only the bulk material response to strain; simulation predictions for a finite crystal model are reported in the Online Resource for reference. In the following, results are discussed in the order of increasing complexity: the \(z\)-direction is discussed first, followed by the \(y\)-direction and then finally the \(x\)-direction.

\(z\)-direction

The stress–strain behavior of the cellulose \(\hbox {I}\beta\) model in response to \(z\)-direction strain is shown in Fig. 5a. There are four specific points on the stress–strain plot identified at each strain rate: the origin (0), the ultimate point (1), the strain at which stress falls to zero (2) and 100 % strain (3). The corresponding atomic structures viewed from the \(y\)-direction at each of these points are shown in Fig. 5b. Only four cellulose chains are included in each snapshot to facilitate visualization of the breaking of covalent bonds. The crystal fails within 7 % strain. Data from 10 to 95 % is not shown because the stress remains around zero and thus provides little additional information.

Fig. 5
figure 5

a Stress–strain behavior in the \(z\)-direction. b Snapshots of atomic structures viewed from the \(y\)-direction at the points identified in a at three strain rates. Four chains within the same hydrogen bonding plane are included in each snapshot to highlight the breaking of individual covalent bonds. Scale bars are above the topmost snapshots, where the figures in the first three columns correspond to the left scale bar, and those in the last column correspond to the smaller scale indicated by the right scale bar. The arrows indicate the deformation direction

Full size image

The stress increases with strain from point 0 to 1, during which time the cellulose molecules are stretched without breaking. This stress may be due to stretching of covalent bonds, distortion of the glucose rings, and possibly other interactions such as van der Waals or hydrogen bonding. After the ultimate point 1, the stress decreases suddenly, and at least one of the molecules breaks at any strain rate. At point 2, the total stress falls to zero, corresponding to the breaking of all the cellulose chains. This observation indicates a strain response where, once the first chain fails, the other chains fail without much additional strain, which suggests a limited deformation mechanism that is indicative of brittle failure and fast fracture. We can also infer from this result that, although inter-chain interactions play a role in the \(z\)-direction deformation response, their role is small compared to the intra-chain interactions. After point 2, the distance between the two separate parts of the crystal grows larger. This separation continues until 100 % strain at point 3. Similar behavior is exhibited by the finite model (without periodic boundary conditions) as discussed in the Online Resource.

The effect of strain rate on the response of cellulose \(\hbox {I}\beta\) to strain in the \(z\)-direction is relatively small. As described in the previous section, both the stress and strain at the ultimate point decrease with increasing strain rate. We also observe in Fig. 5a that the rate of the decrease in stress after failure (the slope of a line connecting points 1 and 2) is larger at the faster strain rate (i.e. 3.7, 4.3 and 6.5 GPa/% at \(10^{-2}, 10^{-3}\) and \(10^{-4}\), respectively). This is likely due to the fact that there is less time for the material to recover at the faster strain rate. In general, however, the shape of the \(z\)-direction stress–strain curves and the atomic structures are consistent with brittle failure of the cellulose \(\hbox {I}\beta\) at all strain rates. This same failure mode applies to the deformation of the single cellulose chains and, as a result, the ultimate properties of the single chain and the crystal are similar (Fig. 4d, e).

Note that, at the largest strains, we observe negative stress. Negative stress typically corresponds to compression. However, in this case the result is somewhat misleading since it occurs after the crystal has broken into two halves. Specifically, we find that there is local compression (up to ~1 % strain) within the two halves as they are pulled away from each other. This local compressive strain leads to negative stress, despite the fact that the overall strain (calculated from the size of the simulation cell) is tensile.

\(y\)-direction

The stress–strain behavior of the cellulose \(\hbox {I}\beta\) due to deformation in the \(y\)-direction is shown in Fig. 6a. Corresponding snapshots of the crystal as viewed from the \(x\)- and \(z\)-directions are shown in Fig. 6b. In these images, the solid spheres represent atoms explicitly modeled in the simulation system and the transparent spheres represented their images present due to the periodic boundary conditions. The periodic images are included in the snapshots to help visualize the structural changes. These snapshots clearly show that the crystal responds quite differently to \(y\)-direction strain than to strain in the \(z\)-direction because there are no covalent bonds. The key features of this behavior are described here and a more detailed analysis of the subtle behaviors exhibited at each strain rate is available in the Online Resource.

Fig. 6
figure 6

a Stress–strain behavior in the \(y\)-direction. b Snapshots of atomic structures at the points identified in a at three strain rates. For each strain rate, the images in the upper row are viewed from the \(x\)-direction and in the lower row from the \(z\)-direction. All the figures are on the same length scale as shown by the scale bar. The solid rectangles represent atoms explicitly modeled in the system and the transparent spheres represented their periodic images. The arrows indicate the deformation direction

Full size image

At all three strain rates, the stress increases elastically then plastically from the origin 0 to the ultimate point 1. The atomic structure does not change significantly during this process, although there is an increase in the lattice spacing. After point 1, the stress decreases gradually to near zero at point 3 (~20 % strain) with a bump at point 2, where the snapshots indicate slight rearrangement of the cellulose chains occurs.

The response of the crystal after point 3, however, is dependent on strain rate. Specifically, at \(10^{-2}/\hbox {ps}\) we observe void nucleation that starts at point 2 and the voids continuing to grow at point 3. After point 3, the two voids increase in size until the chains completely separate and the crystal breaks into two parts at point 4. This point also corresponds to a negative stress which, as discussed in the previous section, is due to local compressive strain in the two halves of the crystal. With additional strain (until point 5 at 100 %) the distance between the two halves of the crystal increases. At strain rate \(10^{-3}/\hbox {ps}\), after point 3, instead of breaking into two parts, the voids in the crystal increase in size while the stress slowly decreases until, by point 4, the stress is zero. At this strain rate, the chains remain connected to each other throughout the strain process, even at 100 % strain. Then, at \(10^{-4}/\hbox {ps}\), we do not observe void formation within the crystal at any strain. The evolution of the material in response to strain is instead accommodated through reorganization of the cellulose chains. Therefore, strain rate not only affects the magnitude of material properties but also the deformation and failure mechanisms due to strain in the \(y\)-direction.

\(x\)-direction

The stress–strain behavior of cellulose \(\hbox {I}\beta\) in the \(x\)-direction is shown in Fig. 7a. Snapshots of the crystal viewed from the \(z\)-direction are shown in Fig. 7b for each point identified on the stress–strain curve. For all strain rates, multiple peaks are observed within the first 45 % of tensile deformation where the number, positions and magnitudes of the peaks vary with strain rate. In general, the number of discrete events (peaks and valleys in the stress–strain plot) increases with decreasing strain rate. This is likely because at faster strain rates there is less time for the crystal to response so intermediate deformation modes either do not occur or are too insignificant to detect.

Fig. 7
figure 7

a Stress–strain in the \(x\)-direction. b Snapshots of the atomic structures viewed from the \(z\)-direction at the points identified in a at three strain rates. The solid rectangles represent atoms explicitly modeled in the system and the transparent spheres represented their periodic images. All the figures are on the same length scale as shown by the scale bar. The arrows indicate the deformation direction

Full size image

Like the \(y\)-direction strain response, there are no covalent bonds to accommodate \(x\)-direction strain. However, unlike the \(y\)-direction, we do not observe the formation or growth of voids at any strain rate. All strain is accommodated by combinations of slip, reorientation and localized displacement of the cellulose chains, ultimately leading to an evaluation from a crystalline to an amorphous structure. The most significant, quantifiable observation are the slips that occur along the (\(1\bar{1}0\)) plane. This is consistent with the mechanism of plastic deformation in metals where the most active slip planes for dislocation motion act \(\sim 45 ^{\circ }\) to the applied load direction (for cellulose \(\hbox {I}\beta\) the load is applied in the [100] direction which is \(\sim 45 ^{\circ }\) to the (\(1\bar{1}0\)) plane). These slips result in local relaxation of the stress (e.g. after point 1 in Fig. 7). The stress then increases with further strain as deformation occurs through localized displacement of the chains. At the slowest strain rate, we observe a second slip occur along the (\(1\bar{1}0\)) plane from points 5 to 6. In all cases, continued strain ultimately leads to a transition from crystalline to amorphous. A more detailed analysis of this behavior is available in the Online Resource.

Conclusion

MD simulations are used to model uniaxial tensile deformation of \(\hbox {I}\beta\) crystalline cellulose in three orthogonal directions and at three strain rates. The stress–strain response for each deformation direction/strain rate case is analyzed. From the stress–strain data, we calculate the elastic modulus, Poisson’s ratio, yield stress and strain, and ultimate stress and strain. To the best of our knowledge, this is the first report of the entire set of yield and ultimate properties of cellulose \(\hbox {I}\beta\).

Comparison of the mechanical properties in the three orthogonal directions shows that the chain direction corresponds to the largest elasticity, and yield and ultimate stress by an order of magnitude. Comparison between single chain and crystal properties reveals that the covalent bonds within chains provide the crystals’ mechanical strength in the chain direction. However, the strains at yield and failure are more similar to each other, a trend attributable to the difference between gradual deformation in \(x\) and \(y\) as compared to fast fracture in \(z\). The effect of strain rate is also evaluated. We find that the elastic modulus and Poisson’s ratio exhibit little variation with strain rate and their values are in agreement with previously reported experimental and simulation results. However, the yield and ultimate stress and strain depend on strain rate, as do the failure mechanisms associated with those properties. Finally, the atomic structure of cellulose \(\hbox {I}\beta\) during tensile deformation is analyzed, revealing direct relationships between structure, stress–strain behavior, and mechanical properties.

The model predictions presented here should be considered as a first step towards understanding the response of CNCs to strain. However, it is important to reiterate the differences between the model cellulose \(\hbox {I}\beta\) analyzed here and a CNC. The most significant factors are likely to be the small model size, periodic boundary conditions, and the lack of surfaces or defects. First, the model crystal is significantly shorter and may have a smaller cross-sectional area than a typical CNC (cross-sectional area depends on source). The size issue is partially address through the use of periodic boundary conditions which enable us to effectively model a much larger system. However, a periodic model has its own limitations as it cannot capture the role of surfaces in the crystal’s strain response. CNCs from some sources have large surface-to-volume ratios, in which case the surfaces themselves can determine properties, an effect not captured by the model presented here. Also, any CNC is likely to have defects that can be expected to affect properties, where the magnitude of that effect will depend on defect density. We have not attempted to incorporate defects into these simulations as it is specifically designed to be a reference, i.e. future studies in which defects are explicitly modeled can analyze results in the context of differences between mechanical properties (and deformation modes) predicted for a perfect crystal and one with specific defects. Therefore, the model predictions presented here are idealized and represent the limiting behavior of the material. In this context, however, the results are relevant as they form a baseline for future studies in which more complexity is introduced. In addition, we expect that the strain dependence and anisotropy of deformation mechanisms revealed here, e.g. fast fracture vs. void nucleation and growth vs. chain reorganization, are relevant to the material response in general. Ultimately, this study should lead to and enable a fundamental understanding of the mechanical properties of CNCs and in turn their role in determining the properties of cellulose-based composite materials.