Long term stability of Earth Trojans

Abstract

We explore the long-term stability of Earth Trojans by using a chaos indicator, the Frequency Map Analysis. We find that there is an extended stability region at low eccentricity and for inclinations lower than about $50^{\circ }$ even if the most stable orbits are found at $i \le 40^{\circ }$. This region is not limited in libration amplitude, contrary to what found for Trojan orbits around outer planets. We also investigate how the stability properties are affected by the tidal force of the Earth–Moon system and by the Yarkovsky force. The tidal field of the Earth–Moon system reduces the stability of the Earth Trojans at high inclinations while the Yarkovsky force, at least for bodies larger than 10 m in diameter, does not seem to strongly influence the long-term stability. Earth Trojan orbits with the lowest diffusion rate survive on timescales of the order of $10^9$ years but their evolution is chaotic. Their behaviour is similar to that of Mars Trojans even if Earth Trojans appear to have shorter lifetimes.

1 Introduction

The archival search performed on the infrared data taken by the NASAs Wide-field Infrared Survey Explorer (WISE) mission has recently lead to the discovery of the first Earth Trojan, asteroid 2010 TK7 (Connors et al. 2011). It is a small body 300 m in diameter orbiting at the leading Lagrange triangular point L4. Its orbit is chaotic on a short timescale, of the order of few $10^4$ years, so it is almost certainly a recently captured body. Its discovery has, however, reawaken the interest on the stability of a potential long living population of Earth Trojans. Small asteroids could indeed orbit in stable islands around the Earth L4 and L5 Lagrangian points without being discovered yet.

Mikkola and Innanen (1990) studied with short term numerical integrations the stability of Earth Trojans over a few $10^4$ years and found stable orbits, in particular at low inclination respect to the ecliptic. Tabachnik and Evans (2000) performed a limited number of long term numerical simulations over 50 Myr showing the existence of some stable tadpole orbits on this timescale. A longer term numerical integration of Earth Trojan orbits was performed over 700 Myr by Ćuk et al. (2012) finding a limited number of stable tadpole orbits over this timescale. Dvorak et al. (2012) explored the Earth Trojan phase space in more details within a truncated planetary system from Venus to Saturn and checked the stability over a timescale of the order of $10^7$ years using as stability indicator an eccentricity lower than 0.3.

In this paper we take advantage of the FMA (Frequency Map Analysis) (Laskar 1990), a tool to detect chaotic behaviour on short term numerical integrations, to measure the stability properties of the phase space at the Earth Lagrangian points in a numerical model that includes all planets of the solar system. The FMA method computes the diffusion speed of the orbits and allows a fast and detailed sampling of the stability properties of a large number of orbits. The most stable regions can be quickly outlined and focused long-term numerical simulations can be used to explore the lifetime of the most stable orbits.

While exploring the stability properties of Earth Trojans we also studied the influence of the tidal force of the Earth–Moon systems on the dynamics of Trojans. In addition, during the investigation of the long-term evolution of the most stable orbits, we also included in the dynamical model the Yarkovsky force. Earth Trojans are expected to be small objects and the Yarkovsky effect can play a relevant role in destabilizing their orbits.

2 The numerical algorithm

The FMA method and its implementation to analyse the stability of Trojan orbits is described in detail in Marzari et al. (2002). To explore in details the phase space we need to study a large number of virtual Trojan orbits. The FMA method allows us to test their stability properties with a short-term numerical integration. From the outcome of each integration we analyse the behaviour of the the libration frequency $f_l$ of the angle $l = \lambda _T - \lambda _E$ where $\lambda _T$ is the mean longitude of the Trojans and $\lambda _E$ that of the Earth. Each virtual Trojan is integrated over $10^5$ years and the whole timespan is then covered by running windows. On each of this window, $f_l$ is computed with the high precision numerical method described in Šidlichovský and Nesvorný (1996) and Marzari et al. (2002). From the final set of $f_l$ values, the standard deviation $\sigma _l$ is computed and its logarithm is adopted as diffusion index. The WHM integrator, implemented in the swift software package (Levison and Duncan 1994), is used to calculate the orbits of the putative Trojan and of all the planets (including Pluto) whose orbits are derived from the JPL ephemeris. The initial orbital elements of all the test Trojan orbits are computed randomly within reasonable boundaries and the FMA is applied only on those cases where the critical argument $l$ is still librating at the end of the $10^5$ years integration. The timespan is long enough to measure the diffusion of the orbits in the phase space and detect the most stable trajectories. Since FMA measures the diffusion speed, it is not necessary to cover a timespan comparable to the secular frequencies potentially responsible for their instability (Dvorak et al. 2012).

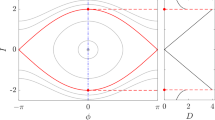
The orbit of each stable virtual Trojan is labeled by its initial semimajor axis, an averaged libration amplitude $D$ calculated over the first running window, a proper eccentricity $e_p$ and an averaged inclination $i$ over the whole integration timespan. The value of $e_p$ is computed by applying the FMA method to the non-singular variables $h$ and $k$ defined as $h = e\, \mathrm{cos}\, \bar{\omega }$ and $k = e\, \mathrm{sin}\, \bar{\omega }$ where $\bar{\omega }$ is the pericenter longitude of the Trojan orbit. Its value can also be directly computed from the eccentricity evolution during the numerical integration. The libration amplitude $D$ can instead be computed either from the difference between the Trojan longitude and that of the Earth or from the oscillation amplitude of the semimajor axis $\varDelta a$ which is directly correlated to $D$ via the formula ${{\varDelta a} \over {D}} \sim \sqrt{3 \mu } \cdot a_E \sim 0.003$ where $\mu$ is ratio of the mass of the Earth over the mass of the sun and $a_E$ the semimajor axis of the Earth (Érdi 1987; Milani 1993). Unfortunately, this formula is a first order linear approximation and it is inaccurate for large values of the libration amplitude $D$. This is clearly shown in Fig. 1 where the relation between $D$ and $\varDelta a$ is derived from a large number of numerical simulations of Trojan-type orbits. The linear trend is good only for $D$ lower than about $70^{\circ }$ while, beyond that value, it overestimates $\varDelta a$. A better relation between $D$ and $\varDelta a$ can be derived by a least squares fit of the numerical data leading to the following higher order formula

$$\begin{aligned} {\varDelta a} \sim \sqrt{3 \mu } \cdot a_E \cdot D - {\sqrt{3 \mu } \over {21}} \cdot a_E \cdot D^3. \end{aligned}$$

(1)

The behaviour predicted by this equation is illustrated in Fig. 1 and it well approximates ${\varDelta a}$ even for $D$ close to $150^{\circ }$. This extension of the formula is important in our study since we find that stable Earth Trojans can have values of $D$ as large as $150^{\circ }$. A residual weak dependence of ${\varDelta a}$ on the orbital eccentricity and inclination explains the scattering of the data around the analytical fit.

Fig. 1

Amplitude of the semimajor axis oscillations ${\varDelta a}$, computed as difference between the maximum and minimum value, as a function of the libration amplitude $D$. The scattered points are derived from a large number of Trojan orbits numerically computed over a short timespan (5,000 years). The linear trend predicted by the formula of Érdi (1987) ${\varDelta a} \sim \sqrt{3 \mu } \cdot a_E \cdot D$ (dotted line) overestimates for large $D$ the real value of ${\varDelta a}$. A semi-empirical formula derived from a least squares fitting of the numerical data: ${\varDelta a} \sim \sqrt{3 \mu } \cdot a_E \cdot D - {\sqrt{3 \mu } \over {21}} \cdot a_E \cdot D^3$ (continuous line) matches ${\varDelta a}$ even for $D$ larger than $70^{\circ }$

The method used to compute the proper eccentricity cannot be applied to compute a proper inclination since the circulation period of the node longitude is comparable or even longer than the integration timespan, preventing a meaningful estimate of its frequency and variation. When using the FMA analysis we need to find a good balancing between the number of numerical integrations to be performed and the informations we need to extract from them. For this reason we adopt an average inclination to mark each orbit.

2.1 Trojan stability maps and influence of the Earth–Moon tidal force

For a Trojan type orbit, the tidal force of the Earth–Moon system may affect the long term stability properties. Dvorak et al. (2012) explored the influence of this perturbing effect on the trajectory of asteroid 2010 TK7 finding that its orbit is not very affected by the presence of the Moon. However, the orbit of this asteroid is highly chaotic and it may not show the true nature of the influence of the Earth–Moon system on the overall Trojan stability. We decided to test the perturbative effect of the Earth–Moon system on all orbits explored with the FMA method. For this reason, we used a second N-body model where the motion of the Moon and Earth around their baricenter is computed. A simplified model is adopted with the Moon moving on a fixed Keplerian orbit around the Earth with orbital elements equal to the mean observed ones. The two bodies move around the baricenter of the system whose orbit is derived from the JPL ephemeris and the independent gravitational attraction of the two bodies is computed both on the other planets and on the putative Trojans. The FMA analysis is then applied also to the outcome of this N-body model which is rather rough since it neglects the influence of the Sun and the other planets on the Moon’s orbit and the $J_2$ contribution is also not considered. However, a more refined model would required too much computational time, nullifying the advantage of the FMA algorithm.

2.2 The Yarkovsky effect

The Yarkovsky effect is a thermal radiation force related to the anisotropic re-emission of the absorbed solar radiation in the infrared. It is known to cause a semimajor axis drift whose rate is, on average, inversely proportional to the body size (Bottke et al. 2002). To study how Earth Trojans evolve under the Yarkovsky perturbing force, we performed a limited number of long-term numerical integrations of the most stable orbits identified with the FMA method. To evolve this potentially stable orbits we have used the package swift-rmvs3 upgraded by M. Broz to include the Yarkovsky effect (http://sirrah.troja.mff.cuni.cz/mira/mp/). Some parameters are required to tune the Yarkovsky force and we adopted for them reasonable values found in literature. We use for the virtual Earth Trojans a bulk density of 2.5 g/cm$^3$, a surface density of 1.5 g/cm$^3$, a surface conductivity of $K = 0.001$ W/(mK) and an emissivity of 0.9 (Nesvorný et al. 2002; Scholl et al. 2005). We neglect in the model any collisional spin reorientation since the impact probability of Earth Trojans with other asteroids is very low. For the albedo, we use an average value of 0.18 computed from the albedos of the 4 asteroids co-orbital with the Earth measured by the NEOWISE survey (Mainzer et al. 2012).

Fig. 2

Diffusion maps showing the stability properties of Trojan orbits as a function of the libration amplitude $D$, proper eccentricity $e_p$ and averaged inclination $i$. The smaller is the diffusion index, the more stable is the orbit. The top panel shows the diffusion map in 3D while the middle and bottom panels are slices of the 3D plot for inclinations ranging from $0^{\circ }$–$15^{\circ }$ (middle panel) and $15^{\circ }$–$30^{\circ }$ (bottom panel)

3 Stability portraits

In Fig. 2 we show a 3-D plot of the diffusion index around L4 and two 2-D slices for inclinations ranging from $0^{\circ }$ to $15^{\circ }$ (middle panel) and from $15^{\circ }$ to $30^{\circ }$ (bottom panel). We plot only those cases where the diffusion index is lower than $-2$ (i.e. $\sigma _l < 10^{-2}$ and we neglect all other orbits since the diffusion index shows they are highly chaotic. We assume there is no asymmetry between the dynamics around L4 and L5 so we computed $1 \times 10^5$ orbits around L4 and about $2 \times 10^4$ were still librating at the end of the simulation. The most stable orbits, having a lower value of the diffusion index $\mathrm{log}(\sigma _l)$, are located at low values of eccentricity, lower than 0.1, and there is no preference for low libration amplitude orbits as observed for Jupiter Trojans (Marzari et al. 2003; Robutel and Gabern 2006) since the libration amplitude of stable orbits extend up to $\sim$150$^{\circ }$. This means that stable Trojans can be found also for semimajor axis as large as ${\sim }(1 \pm 0.003) a_E$, a range comparable to that found by Ćuk et al. (2012). This behaviour may favor the capture into Trojan orbits of bodies previously moving on horseshoe orbits and then perturbed into tadpole trajectories. However, Schwarz and Dvorak (2012) have shown that the capture of asteroids as Earth Trojans is possible but the newly trapped Trojans have eccentricities larger than 0.15, placing them in the unstable region of the phase space. A dissipative force is then needed to trap objects into stable Earth Trojan orbits. The stability portraits of Fig. 2 show that orbits are more chaotic at high inclinations, as already suggested in Dvorak et al. (2012). The stability region in the $(D-e)$ plane considerably shrinks at higher inclinations (Fig. 2 bottom panel) and only orbits with eccentricity lower than 0.05 have low diffusion index.

Fig. 3

Diffusion map in the $(D-i)$ plane for any value of eccentricity. Fine structures can be observed possibly related to secular resonances

In Fig. 3 we plot the diffusion index of all our putative Trojans in the $(D-i)$ plane. There are structures in the phase space that may be related to secular resonances. Dvorak et al. (2012) showed that indeed the $\nu _2, \nu _3, \nu _4$ and $\nu _5$ secular resonances are located within the Earth Trojan phase space, with the $\nu _3$ and $\nu _5$ affecting more frequently the dynamical evolution of Trojans. Unfortunately, our numerical integrations were too short to reliably identify which secular frequencies are responsible for the structures in Fig. 3 but our guess is that those found in Dvorak et al. (2012) are responsible for the unstable arc starting from $D \sim 90^{\circ }$ and $i \sim 0^{\circ }$ and shifting to $D \sim 30^{\circ }$ and $i \sim 40^{\circ }$–$50^{\circ }$. The extent of the stability region in inclination is similar to that outlined in Dvorak et al. (2012) with stable orbits extending up to $\sim$50$^{\circ }$ in inclination but with the highest stability properties observed for $i < 40^{\circ }$ where low values of $\mathrm{log}10(\sigma _l)$ (“blue” dots) can still be found. There are also two vertical structures with stable orbits in the distribution with large libration amplitude and high inclination, but their number is limited.

Fig. 4

Libration period as a function of the libration amplitude. There is a functional dependence between these two variables already predicted by Érdi (1987). The spreading is mostly due to a dependence of the libration frequency also on the eccentricity and inclination

In Fig. 4 the dependence of the libration period $T_l$ on the libration amplitude is clearly illustrated. It is interesting to note that the dynamical signature of the 3 structures identified in Fig. 3 for $D \sim 90^{\circ },\,130^{\circ }$ and $140^{\circ }$ appears also in Fig. 4 where the dependence of $T_l$ on $D$ is partly destroyed.

3.1 Influence of the Earth–Moon tidal force on stability

In the model where the Earth and the Moon move around the common baricenter, the stability regions are slightly less extended and populated, possibly because of the tidal force of the system. In Fig. 5 we show the corresponding diffusion maps for Earth Trojans when the Moon is included as a separate body. If we compare Figs. 2 and 5 we notice that the stability region is slightly less extended in eccentricity in the model with the Moon orbiting the Earth and the total number of stable tadpole orbits is lower. There are instead no significant differences in the stability properties along the libration amplitude $D$. The tidal force of the E–M system acts as an additional perturbing force able to accelerate the diffusion speed of chaotic orbits and it is then reasonable to expect differences in the stability properties of Earth Trojans.

Fig. 5

Diffusion maps for Earth Trojans in the model with the Earth and Moon considered as separate bodies and moving around their common center of mass. The top panel shows the stability index for all orbits with inclination ranging from $0^{\circ }$ to $15^{\circ }$ while the bottom panel those orbits with inclinations in the range $15^{\circ }$–$30^{\circ }$

4 Long term stability

To test the survival of putative Trojans in stable orbits we selected 10 cases with the lowest value of chaos indicator and we integrated their trajectory over a long timespan. We then selected the most stable one (surviving longer) and re-compute its orbit including the Yarkovsky effect. Four different values of diameter have been adopted in the numerical model: 10 m, 100 m, 1 km and 10 km. For each size we integrated 10 different orbits characterized by different values of the obliquity $\epsilon$, randomly selected for each body. In this way we computed 40 independent orbits characterized by different values of the Yarkovsky force. Sampling $\epsilon$ is in effect equivalent to have different contributions of the seasonal component (which depends on $\mathrm{sin}(\epsilon )^2$) and of the diurnal one (depending on $\mathrm{cos}(\epsilon )$).

Fig. 6

Number of surviving Trojans as a function of time for 4 different diameters (10, 100 m, 1, 10 km) and 10 random values of obliquity for each size

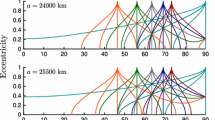
In Fig. 6 we show the lifetimes of the different samples of orbits. A few orbits survive more than 1 Gyr showing a diffusion rate similar to that of Mars Trojans (Scholl et al. 2005). It appears also that the Yarkovsky effect is not a destabilizing force. The fact that smaller bodies 10–100 m in diameter seem to have longer lifetimes is possibly a small number effect. The Yarkovsky force slightly moves the initial orbit and it can drag it in a region of lower diffusion speed respect to the original one. This might also explain why the longest lifetime is obtained for a body 10 m in size. Its chaotic wandering coupled to the Yarkovsky force makes its path towards escape longer than usual. This does not imply that in a larger sample this would happen on average.

In Fig. 7 we illustrate the time evolution of eccentricity and libration amplitude of the body surviving almost 4 Gyr. Its orbit has an initial libration amplitude $D = 1.68$ rad ($\varDelta a \sim 0.0047$ AU), inclination $i=8^{\circ }$ and eccentricity $e = 0.08$. Its evolution is clearly chaotic but the random changes in both the orbital parameters act in different directions keeping the body trapped in the tadpole orbit for a long timespan.

According to our simulations, it is possible that a population of small Trojans, captured at the time of the planet formation, might have survived till present. However, only a very tiny fraction of them would have lasted till now.

Fig. 7

Orbital evolution (eccentricity and libration amplitude) of a 10 m size putative Trojan surviving almost 4 Gyr

5 Conclusions

We have analysed the stability properties of Earth Trojans by using the Laskar’s Frequency Map Analysis. We find that their behaviour is in some aspects similar to that of Mars Trojans since the most stable tadpole orbits are found at low eccentricities and also at large libration amplitude. However, while Mars Trojans are stable only over a stripe in inclination located around $20^{\circ }$, Earth Trojans are stable over a wide range of inclination starting from $0^{\circ }$ up to about $50^{\circ }$. The inclusion of the tidal force due to the orbit of the Moon around the Earth, even if with a rough model, shows that the extent of stability in inclination is reduced. The inclusion of the Yarkovsky effect does not seem to affect the long term evolution of Trojans. By inspecting the evolution of the potentially most stable initial conditions with the inclusion of the Yarkovsky force we find trajectories surviving as Earth Trojans for a few Gyr. As a consequence, if some mechanism was able to cause the capture of Trojans in the earliest phase of the Earth evolution, a tiny fraction of these bodies may still be trapped at present. This raises the question whether the recently found Earth Trojan 2010 TK7 is a temporary trapped body or the fragment of a collision between two long-living Earth Trojans and injected in an unstable orbit.