Reynolds-Number Dependence of Gas Dispersion Over a Wavy Wall

Abstract

Large-eddy simulation is used to investigate the Reynolds-number dependence of gas dispersion over a wavy wall, because the Reynolds-number dependence is important for reproducing normal flow and gas dispersion in a wind tunnel. The ratio of amplitude to wavelength of the wavy surface is set to 0.1, and the Reynolds number based on the bulk velocity and the channel height is varied from $6.67\times 10^{3}$ to $6.67\times 10^{4}$. Two tracer gases are emitted from point sources located at a single crest and trough of the wavy wall. For the lowest Reynolds number, the flow over the wavy wall separates behind the crest and reattaches to the upslope. A recirculation zone is observed near the trough, and the gas emitted from the trough is transported upwind by the recirculating reverse flow. Some gas is discharged from the valley by intermittent velocity bursts that originate in the recirculation zone. As the Reynolds number is increased, the recirculation zone shrinks and the flow increasingly follows the wavy wall. The gas generally disperses in the forward direction and is discharged by the advective flow. As for the gas emitted from the crest, this disperses with the separating flow, while some gas is trapped within the recirculation zone at the lower Reynolds number. As the Reynolds number is increased, the gas advection increasingly follows the wavy wall and the height of the peak concentration approaches the wavy wall. In addition, the accumulated concentration within the valley in both sources depends strongly on the Reynolds number.

1 Introduction

Understanding gas dispersion in the atmospheric boundary layer is important for improving air quality and predicting the spread of chemical, biological, radiological or nuclear agents. Gas dispersion in an urban area is affected mainly by roughness elements such as buildings, structures and trees. Various researchers have investigated the mechanisms for gas dispersion within urban canyons (e.g. Liu and Barth 2002; Liu et al. 2004, 2005; Cai et al. 2008; Cheng and Liu 2011; Michioka et al. 2011; Michioka and Sato 2012; Michioka et al. 2014, 2016). In contrast, gas dispersion over complex terrain (such as mountains) is affected mainly by atmospheric stability and topology such as hills and mountains. Gas dispersion is also affected by flow separation, streamline curvature and complex interactions between the turbulent flow and the terrain. However, the effects of terrain and atmospheric stability on gas dispersion remain an unsolved problem.

As for flow fields, a three-dimensional turbulent flow over a two-dimensional wavy wall, which is the simplest complex terrain, has been investigated in detail. The bottom geometry is defined mathematically by

$$\begin{aligned} z_w \left( x \right) =a\sin \left( {\frac{2\pi x}{\lambda }} \right) , \end{aligned}$$

(1)

where a is the wave amplitude, $\lambda$ is the wavelength, the x-coordinate is directed parallel to the mean flow, and the z-coordinate is in the vertical direction. The geometry of a wavy wall is characterized by the parameter $\alpha$, where

$$\begin{aligned} \alpha =\frac{2a}{\lambda }. \end{aligned}$$

(2)

Zilker et al. (1977) pointed out that the pressure variation and velocity field outside the viscous wall region in the non-separated flow for smaller values of $\alpha$ can be approximated by linear theory, but that linear theory eventually becomes inappropriate as $\alpha$ is increased. The flow separates from the downslope of the wavy wall when $\alpha > 0.03$ and the Reynolds number $Re_h$, based on the half-width of the channel and the bulk velocity, ${<}1.92\times 10^{4}$. Zilker and Hanratty (1979) and Kuzan et al. (1989) showed a flow region map spanned by $\alpha$ and Reynolds number $Re_{\alpha }$ (based on the friction velocity and wave amplitude) that shows the border between separated and non-separated flows. The separated flow over a wavy wall is classified into four zones: an outer flow, a shear layer, a separated region and a thin boundary layer. The separated region is bounded by the streamwise function of zero, and the fluid flows intermittently in the forward and backward directions. Above the separated region, a shear layer (which resembles a mixing layer) is generated that contains an inflection point and has a large velocity gradient (Hudson et al. 1996). Hudson et al. (1996) pointed out that turbulence production near the wavy wall is associated mainly with shear-layer separation from the wavy wall, and that the maximum turbulence intensity occurs close to the inflection point. Cherukat et al. (1998) showed that the intermittent velocity bursts originating in the separated region can be detected at large distances from the wavy wall. Yoon et al. (2009) used direct numerical simulation (DNS) to observe velocity bursts clearly, which they described as large eruptions from the trough. De Angelis et al. (1997) showed that large spanwise fluctuations occur at the upslope of the wavy wall. These are related to the Görtler vortices of streamwise-oriented coherent structures, which are observed in boundary-layer flow over a concave surface (Henn and Sykes 1999). The formation, development and destruction of Görtler vortices was visualized by Tseng and Ferziger (2004) using large-eddy simulation (LES). A thin accelerating boundary layer forms after reattachment of the flow downstream of the trough until the next crest, and in the region very large velocity gradients are observed close to the wall. In the outer layer above the shear layer, the flow is not affected appreciably by the wave-induced turbulence. The turbulent statistics are based on the friction velocity, as in a turbulent flow over a flat plate.

As the Reynolds number increases, the recirculation zone decreases in size and finally disappears. For $\alpha = 0.05$, a recirculation zone has been observed for $Re_h =5.0\times 10^{3}$ and $1.5\times 10^{4}$ but not for $Re_h =3.0\times 10^{4}$ in water-channel experiments (Zilker and Hanratty 1979). Wagner et al. (2010) indicated that, for a higher Reynolds number, the recirculation zone shrinks and the mean velocity gradient becomes larger than that for a lower Reynolds number. The existence of the recirculation zone depends strongly on the Reynolds number.

As for scalar fields, various researchers have focused on the temperature field (e.g., Calhoun et al. 2001; Günther and von Rohr 2002; Choi and Suzuki 2005; Errico and Stalio 2014), but the concentration field has not been investigated in detail. Zilker and Hanratty (1979) used traces of dye streamers originating from injection points on the downslope, near the separation point, downstream of the separation point and in the trough, and investigated the basic trajectories of the dyes. However, the concentration statistics were not obtained. Wagner et al. (2007) measured the velocity and concentration of a trace dye for a turbulent flow over a wavy wall in a water channel. A point source was located at the crest of a wavy wall with $\alpha = 0.05$. The wavy wall was found to enhance the turbulence and the spreading rate of a scalar plume, compared with plumes over the flat wall. Rossi and Iaccarino (2009) implemented DNS for scalar mixing from a point source over a wavy wall to confirm the validity of algebraic flux models. Rossi (2010) pointed out that the algebraic models are able to predict the scalar field in complex flows when the mean velocities and the Reynolds stress tensor are accurately represented. These previous studies paid less attention to the detailed gas-dispersion behaviour over a wavy wall. To understand gas dispersion over complex terrain, it is important to evaluate the amount of gas that accumulates within valleys and the mechanism by which the gas is removed.

In order to reproduce flow and gas dispersion over the terrain using scaled models in a wind tunnel or a detailed numerical simulation, the Reynolds-number independence of flow and gas dispersion is demanded. Castro and Robins (1977) and Snyder and Castro (2002) suggested that the Reynolds-number dependence for flows over sharp-edged obstacles is weak. In contrast, the Reynolds-number dependence for flows over terrain such as hills and mountains remains less well-defined. The Reynolds-number dependence is normally quantified using the roughness Reynolds number (e.g. Teunissen et al. 1987; Ishihara et al. 1999; Ayotte and Hughes 2004), but the roughness Reynolds number does not ensure Reynolds-number independence (e.g. Uehara et al. 2003). For simulating a stable boundary layer or plume rise from a stack and a cooling tower using the wind tunnel, a low wind-tunnel speed is demanded (Ohya 2001; Michioka et al. 2007), resulting in lower Reynolds-number flow. In addition, if the bottom surface at the real-scale wavy wall is smooth, a recirculation zone is not formed because of the high Reynolds number, but is formed in a wind tunnel at low wind speeds. Thus, the Reynolds-number dependence is important, subject to reproducing the flow and gas dispersion over the terrain, but the Reynolds-number dependence of flow and gas dispersion over a wavy wall is also an unsolved problem. To investigate the Reynolds-number dependence using numerical simulations, DNS or LES should be implemented to estimate the exact locations of the separation point and reattachment point over a wavy wall.

The present study uses LES to investigate the Reynolds-number dependence of scalar dispersion over a wavy boundary. Point sources are located at a single crest and a trough of the wave. To confirm the validity of the present LES, the turbulent statistics obtained by the present LES are compared to the DNS results of Maaß and Schumann (1996). The computational conditions and numerical set-up are described in Sect. 2, and using the LES results, we then discuss the mechanism of gas dispersion within the trough in Sect. 3.

2 Large-Eddy Simulation

The filtered continuity, momentum and mass conservation equations can be written, respectively, as

$$\begin{aligned} \frac{\partial {\overline{U_i}} }{\partial x_i }= & {} 0, \end{aligned}$$

(3)

$$\begin{aligned} \frac{\partial {\overline{U_i}} }{\partial t}+\frac{\partial {\overline{U_j}}\, {\overline{U_i}} }{\partial x_j}= & {} -\frac{1}{\rho }\frac{\partial {\overline{P}} }{\partial x_i }+\left( {\nu +\nu _t } \right) \frac{\partial }{\partial x_j }\left( {\frac{\partial {\overline{U_i}} }{\partial x_j }+\frac{\partial {\overline{U_j}} }{\partial x_i }} \right) , \end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial {\overline{C_i}} }{\partial t}+\frac{\partial {\overline{U_j}} \,{\overline{C_i}} }{\partial x_j }= & {} \left( {D+\frac{\nu _t }{Sc_t }} \right) \frac{\partial ^{2}{\overline{C_i}} }{\partial x_j \partial x_j }+S_{i,q} , \end{aligned}$$

(5)

where values with an overbar are filtered, $U_{i}$ is a velocity component, $C_{i}$ is the concentration of tracer gas i, P is the pressure, $\rho$ is the density, $\nu$ is the kinetic viscosity of air ($=1.5\times 10^{-5}\,\hbox {m}^{2}\,\hbox {s}^{-1}$), D is the molecular diffusion coefficient of gas in the air ($=1.5\times 10^{-5}\, \hbox {m}^{2}\,\hbox {s}^{-1}$) and $S_{i},_{q}$ is the source term of tracer gas i. The turbulent Schmidt number ($S_{ct}$) is set to 0.5 (Antonopoulos-Domis 1981), and the eddy viscosity $\nu _{t}$ is modelled by using the dynamic Smagorinsky model (Lilly 1992). The governing equations were solved directly by using OpenFOAM (OpenFOAM 2012), which uses a finite volume method with an unstructured grid.

Fig. 1

Schematics of a computational domains, and b geometry of a wavy wall

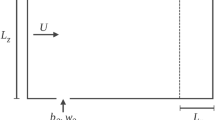
Figure 1 shows a schematic diagram of the computational domain of size $4\lambda \times 1.5 \lambda \times 1.05 \lambda$ for the $x \times y\times z$ grid, where $\lambda = 1.0\,\hbox {m}$ is the wavelength. The domain size is equivalent to or larger than the domain size used in previous studies (Maaß and Schumann 1996; Cherukat et al. 1998; Tseng and Ferziger 2004; Yoon et al. 2009; Chang et al. 2012). The two-dimensional wave profile is given by Eq. 1 with $a = 0.05\lambda$. The streamwise, spanwise and vertical directions are taken as the x, y and z axes, respectively, and the origin of the coordinate axis is the x–y centre of the computational domain at $z/\lambda = 0.05$ from the crest, as shown in Fig. 1. The computational grid system consisted of hexahedral meshes in all regions; the numbers of grid points for all simulations were $170\,(x) \times 128\,(y) \times 128\,(z)$. Uniform meshes with grid spacings of $0.024 \lambda \,(x)$ and $0.012\lambda \, (y)$ were used in the streamwise and spanwise directions, while the smallest grid spacing in the vertical direction near the bottom surface is $0.0027\lambda \,(y^{+}=u_*y/\upsilon = 0.029 - 6.35$ for Case 1–5) and the grid in the vertical direction was geometrically stretched away from both the top and bottom walls towards the centre. The superscript ‘+’ denotes normalization by the friction velocity $u_*$ and $\upsilon$.

No-slip boundary conditions were applied to the boundaries at the top and bottom walls, while periodic boundary conditions were imposed on velocity components in the streamwise and spanwise directions. The flows were driven by a height-independent streamwise pressure gradient, and the chosen values of the Reynolds number $Re=U_b \lambda /\upsilon$ (based on the channel width and the bulk velocity) are listed in Table 1. The bulk velocity is defined as the cross-sectional averaged mean streamwise velocity component.

Table 1 Computational conditions, and the relative contribution of the turbulent mass fluxes to the net mass fluxes at $z^{*}= 0.05 ({<}w^{*}c_1^*{>}_s{/}{<}{\overline{W^{*}}}\, {{\overline{C_1^*}}}{>}_s)$

Two tracer gases were released simultaneously from ground-level continuous point sources. One point source (Source 1) was placed at a single trough of the wavy wall ($x/\lambda = 0, y= 0, z/\lambda = -0.045$), and the other one (Source 2) was placed at a wave crest ($x/\lambda = -0.5, y= 0, z/\lambda = 0.055$). Each tracer gas was released at a steady emission rate Q. The release of tracer gas i was simulated by adding the source term $S_{i,q}$ to Eq. 5. Periodic boundary conditions were imposed on the scalar transfer in only the spanwise direction. Neumann boundary conditions (i.e., zero normal derivative) were imposed on the scalar transfer at the top, bottom, outlet and wall boundaries, and the condition $C_{i} = 0$ was imposed on the upstream boundaries of the domain.

The convection term in the momentum equation was discretized using a second-order central differencing scheme. The convection term in the mass conservation equation was discretized using a total-variation-diminishing scheme because the second-order central differencing scheme produces a large negative concentration. The other terms were estimated using a second-order central differencing scheme. First-order Euler implicit temporal discretization was used for the first time-derivative term. The algorithm used for solving the governing equations was based on the pressure-implicit splitting-of-operators method (Issa 1986).

3 Results

3.1 Normalized Variables

Since the bulk velocities in each case are different, as seen in Table 1, the velocity and concentration statistics are not directly comparable with each other. To absorb the effect of the velocity difference, the normalized velocity, velocity fluctuation, length, time, pressure, kinematic viscosity and concentration are defined as

$$\begin{aligned} {\overline{U_i^*}}= & {} \frac{{\overline{U_i}} }{U_b },\quad u_i^*=\frac{u_i }{U_b},\quad x_i^*=\frac{x_i }{\lambda },\quad t^{*}=\frac{tU_b}{\lambda },\quad {\overline{P^{*}}} =\frac{{\overline{P}} }{\rho U_b^2 },\nonumber \\ \nu _t^*= & {} \frac{\nu _t}{U_b \lambda },\quad {\overline{C_i^*}} =\frac{{\overline{C_i}} U_b \lambda ^{2}}{Q}. \end{aligned}$$

(6)

The momentum and mass conservation equations in Eqs. 4 and 5 are modified by using these normalized variables:

$$\begin{aligned} \frac{\partial {\overline{U_i^*}} }{\partial t^{*}}+\frac{\partial {\overline{U_j^*}} \,{\overline{U_i^*}} }{\partial x_j^*}= & {} -\frac{\partial {\overline{P^{*}}} }{\partial x_i^*}+\left( {\frac{1}{Re}+\nu _t^*} \right) \frac{\partial }{\partial x_j^*}\left( {\frac{\partial {\overline{U_i^*}} }{\partial x_j^*}+\frac{\partial {\overline{U_j^*}} }{\partial x_i^*}} \right) , \end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial {\overline{C_i^*}} }{\partial t^{*}}+\frac{\partial {\overline{U_j^*}} \,{\overline{C_i^*}} }{\partial x_j^*}= & {} \left( {\frac{Sc}{Re}+\frac{\nu _t^*}{Sc_t }} \right) \frac{\partial ^{2}{\overline{C_i^*}} }{\partial x_j^*\partial x_j^*}+S_{i,q}^*, \end{aligned}$$

(8)

where the Schmidt number Sc is 1 and $S_{i,q}^*$ is the normalized source term, which was set to the same value in every case. It is found that in Eq. 7 the viscosity term becomes weak as the Reynolds number increases. In all simulations, the normalized bulk velocity (the cross-sectional averaged velocity) = 1 and all boundary conditions and values of $S_{i,q}^*$ remain the same. Hence, the normalized mass conservation equation (Eq. 8) indicates that the normalized concentration is mainly dominated by the Reynolds number, provided that the normalized eddy viscosity $\nu _t^*$ is not changed significally between cases. Therefore, the normalized variables were used to assess the effect of the Reynolds number on the flow and the concentration field.

3.2 Velocity Statistics

Figure 2 shows the mean velocity vectors and the contours of the mean streamwise velocity component at the central vertical cross-section. In Case 1, the flow over the wavy wall separates behind the crest at $x^{*} = -0.36$ because of an adverse pressure gradient (Yoon et al. 2009), and the flow reattaches at the upslope of the wavy wall at $x^{*} = 0.12$. The locations of the separation and reattachment points are in good agreement with DNS at $Re = 6.76\times 10^{3}$ (Maaß and Schumann 1996; Yoon et al. 2009). The streamwise extent of the recirculation zone is strongly dependent on the Reynolds number. Zilker et al. (1977) showed that a transition from separated to non-separated flow can be induced by increasing the flow rate, which is associated with the Reynolds number. As the Reynolds number increases, the location of the reattachment point shifts upwind and the recirculation zone becomes smaller. This trend was confirmed by the water-channel experiments of Wagner et al. (2007) and the DNS of Wagner et al. (2010). For the highest Reynolds number (Case 5), flow separation is not observed in the mean vector field, as shown in Fig. 2e. The water-channel experiments of Zilker and Hanratty (1979) also indicated the absence of flow reversal for $Re = 6.0\times 10^{4}$. In the present simulations, the instantaneous flow is reversed occasionally in the trough, and instantaneous flow separation is infrequently observed.

Fig. 2

Mean velocity vector and mean streamwise velocity contours for the x-z cross-section: a Case 1, b Case 2, c Case 3, d Case 4, e Case 5

Fig. 3

Vertical distributions of the mean streamwise and vertical velocity components. Open circle DNS by Maaß and Schumann (1996); black line Case 1, red line Case 2, blue line Case 3, green line Case 4, orange line Case 5

Figure 3 shows the vertical distributions of the mean streamwise and vertical velocity components at $x^{*}= -0.3, -0.1, 0.1, 0.3$ and 0.5. Mean quantities are indicated in angled brackets. Both the streamwise and vertical mean velocities obtained by LES in Case 1 are in good agreement with DNS at $Re = 6.76\times 10^{3}$ (Maaß and Schumann 1996). In Case 1, a negative mean streamwise velocity component and a positive mean vertical velocity component are observed near the wavy wall at $x^{*}= -0.1$, which corresponds to recirculating flow. As the Reynolds number is increased, the mean streamwise velocity component near the wavy wall increases, and the vertical mean velocity component becomes negative at the downslope and positive at the upslope. This implies that the flow follows the wavy wall smoothly at the highest Reynolds number.

Fig. 4

Vertical distributions of the standard deviations of the normalized streamwise, spanwise and vertical velocity fluctuations at $x^* = -0.3, -0.1, 0.1, 0.3$ and 0.5. Symbols as in Fig. 3

Fig. 5

Vertical distributions of the Reynolds shear stress at $x^* = -0.3, -0.1, 0.1, 0.3$ and 0.5. Symbols as in Fig. 3

Figure 4 shows the vertical distributions of the standard deviations of the normalized streamwise, spanwise and vertical velocity fluctuation components $\sigma _u^*$, $\sigma _v^*$ and $\sigma _w^*$, respectively, and Fig. 5 shows the vertical distributions of the Reynolds shear stress ${<}u^{*}w^{*}{>}$ (where $u^{*}={\overline{U^{*}}}-\left\langle {{\overline{U^{*}}} } \right\rangle ,w^{*}={\overline{W^{*}}} -\left\langle {{\overline{W^{*}}} } \right\rangle$). The shapes of $\sigma _u^*$, $\sigma _v^*$, $\sigma _w^*$ and ${<}u^{*}w^{*}{>}$ in Case 1 are also in good agreement with the DNS results (Maaß and Schumann 1996). The peaks of $\sigma _u^*$ in Case 1 for $-0.3\le x^{*}\le 0.3$ are located near the level of the crest tops ($z^{*} = 0.05$), which is roughly at the inflection point of the mean streamwise velocity profiles in the free shear layer. The peaks gradually decay for $x^{*}\ge 0.1$ and the values of $\sigma _u^*$ near the wavy wall gradually increase for $x^{*}\ge 0.1$, the location at which the turbulent boundary layer develops downwind of the reattachment point. As the Reynolds number increases, the location of these peaks for $-0.3\le x^{*}\le 0.3$ shifts towards the wavy wall because of the decreasing recirculation zone. The values of $\sigma _v^*$ near the wavy wall for $0.1\le x^{*}\le 0.3$ are almost equal to or larger than the values of $\sigma _u^*$; De Angelis et al. (1997) showed that large spanwise fluctuations occur at the upslope of the wavy wall and that the detached shear layer at the upslope generates strong turbulence. This does not necessarily apply to the high Reynolds-number cases. A possible mechanism for this fluctuation is the Taylor–Görtler instability that produces streamwise vortices such as those observed in boundary-layer flows over concave surfaces (Henn and Sykes 1999). The values of $\sigma _u^*$, $\sigma _v^*$ and $\sigma _w^*$ at the upslope become smaller with an increase in the Reynolds number because the flow is mainly dominated by forward flow and the velocity gradients normal to the wavy wall decrease near the wavy wall.

The location of the peak of ${<}u^{*}w^{*}{>}$ in Case 1 is very close to that of $\sigma _{u }$in Case 1 for $-0.3\le x^{*}\le 0.3$, which is associated with the separated shear layer, and the values of ${<}u^{*}w^{*}{>}$ are small within the recirculation zone. The negative values of ${<}u^{*}w^{*}{>}$ at $x^{*}=0.3$ are artefacts of the calculation in a Cartesian coordinate system. As shown by Hudson (1993), Reynolds shear stresses assume positive values if they are calculated in a boundary-layer coordinate system. Wagner (2007) showed that the normalized Reynolds stresses do not depend significantly on Reynolds number for $5.6\times 10^{3}\le Re\le 2.24\times 10^{4}$. In the present simulations, the vertical profiles of ${<}u^{*}w^{*}{>}$ at the upslope of the wavy wall do not depend significantly on Reynolds number. However, the profiles at the downslope are sharply changed with Reynolds number, and the momentum transfer is quite different.

Fig. 6

Cospectra of the Reynolds shear stress at $(x^{*},y^{*},z^{*}) = (-0.1, 0, 0.05)$. Black line Case 1, red line Case 2, blue line Case 3, green line Case 4, orange line Case 5

Figure 6 shows the cospectra of Reynolds shear stress at $(x^{*}, y^{*}, z^{*}) = (-0.1, 0, 0.05)$ where a nearly maximum Reynolds shear stress is observed in Case 1. The cospectrm $Co_{u^{*}w^{*}}$ of the Reynolds stress is defined as

$$\begin{aligned} {<}u^{*}w^{*}{>}\,=\int _0^\infty {Co_{u^{*}w^{*}} (f^{*})\mathrm{d}f^{*}} , \end{aligned}$$

(9)

where $f^{*}=f\lambda /U_b$. Peak values of $f^{*}Co_{u^{*} w^{*}}$ in Cases 1 and 2 are observed at $f^*= 1$, which corresponds to the wavenumber of the wavy wall $k^{*}\left( {=f^{*}}\right)$. As the Reynolds number increases, the peak values shift towards higher frequencies, with a second peak appearing at $f^*= 1$ for the highest Reynolds number. The peak at $f^*= 1$ suggests that the wavelength of the wavy wall affects the momentum transfer. In addition, the peak of $f^*= 1$ decreases with the increase of the Reynolds number, which is why the shear layer at the downslop shifts towards the bottom surface and the velocity gradient of the mean streamwise velocity component at $z^{*}= 0.05$ becomes smaller. As for the lower frequency of $f^*<0.1$, the values of $f^{*} Co_{u^{*} w^{*}}$ in Cases 1 and 2 are not zero, implying that large-scale turbulent motion also affects the instantaneous momentum transfer. Cherukat et al. (1998) pointed out that, for lower Reynolds number, intermittent velocity bursts are generated in the recirculation zone and extend for large distances away from the wavy wall. The frequencies of these bursts influence $f^{*}Co_{u^{*} w^{*}}$ at the lower frequency, which affects the gas dispersion, as discussed later. In Cases 3, 4 and 5, the values of $f^{*}Co_{u^{*} w^{*}}$ for $f^*< 0.1$ are nearly zero, and larger-scale turbulent motion does not affect the momentum transfer.

Fig. 7

Mean velocity vector and mean concentration contour of tracer gas 1 for the x-z cross-section: a Case 1, b Case 2, c Case 3, d Case 4, e Case 5

Fig. 8

Vertical distributions of the mean concentration of tracer gas 1 and the root-mean-square values of the concertation fluctuation at $x^* = -0.3, -0.1, 0.1, 0.3$ and 0.5. Black line Case 1, red line Case 2, blue line Case 3, green line Case 4, orange line Case 5

3.3 Concentration Statistics (Source at Wave Trough)

Figure 7 shows the mean velocity vectors and the contours of the mean concentration of the gas emitted from the source at the wave trough at the central vertical cross-section. Figure 8 shows the vertical distributions of the mean concentration and the squared values of the concentration fluctuations at $x^{*} = -0.3, -0.1, 0.1, 0.3$ and 0.5. The root-mean-square values of the concentration fluctuation $c_{i,rms}$ are normalized by the bulk velocity $U_{b}$, wavelength $\lambda$ and total emission Q as follows,

$$\begin{aligned} c_{i,rms}^*=\frac{c_{i,rms} U_b \lambda ^{2}}{Q}. \end{aligned}$$

(10)

The values for $\left\langle {{\overline{C_i^*}} } \right\rangle \ge 1.0$ are displayed in Fig. 7. Since the source is located within the recirculation zone in Case 1, the recirculating reverse flow transports tracer gas towards the downslope of the wavy wall until near the separation point, where the gas is dispersed downwind by the separating flow. However, a portion of the gas is again trapped by the recirculating reverse flow, and the peak concentration is observed within the recirculation zone as shown in Fig. 8a. In Case 2, the source is located near the reattachment point, and some tracer gas is transported upwind by the recirculating reverse flow while the other part is dispersed downwind by fluid flowing along the wavy wall. Since the sources in Cases 3, 4 and 5 are outside the recirculation zone, the tracer gas is generally dispersed towards the upslope of the wavy wall. Forward flow dominates at the upslope, hence the peak concentration appears near the wavy wall and the mean concentration gradually decreases in the vertical direction. The instantaneous flow in the trough reverses intermittently, and some tracer gas is transported upwind by the instantaneous reversed flow. However, the frequency of instantaneous reversal decreases with the Reynolds number, causing most of the gas to be dispersed downwind. In addition, the vertical spread becomes smaller and the maximum concentration increases for $x^{*} > 0.1$ with increase of the Reynolds number because the values of $\sigma _v^*$ and $\sigma _w^*$ decrease as shown in Fig. 4. Note that the values of $\sigma _v^*$ and $\sigma _w^*$ are obtained by the velocity fluctuations normalized by $U_{b}$.

The vertical profiles of $c_{1,rms}^*$ as shown in Fig. 8b have almost the same shape as those of $\left\langle {\overline{C_1^*}}\right\rangle$. In Cases 1 and 2, since high values of $c_{1,rms}^*$ are observed within the recirculation zone, the recirculating flow mixes air with high concentrations of gas. The smaller values of $c_{1,rms}^*$ for $x^{*} > 0.1$ indicate that the tracer gas is moderately mixed above the upslope of the wavy wall. In contrast, in Cases 3, 4 and 5, high values of $c_{1,rms}^*$ are observed near the upslope of the wavy wall; the values decrease gradually away from the source, indicating that the high turbulence intensity at the upslope aids in mixing the tracer gas with clear air.

To investigate the mechanism for removing tracer gas from the valley, Fig. 9 shows the streamwise distributions of the vertical advective mass fluxes ${<}{\overline{{W^{*}}}}{>} {<} {\overline{C_1^*}}{>}$, turbulent mass fluxes ${<} {w^{*}c_1^*}{>}$ and total mass fluxes ${<} {{\overline{W^{*}}}\,{{\overline{C_1^*}}}}{>} (={<} {{\overline{W^{*}}} }{>} {<}{\overline{C_1^*}}{>} + {<} {w^{*}c_1^*}{>})$ at $z^{*}=0.05$, which is the level of the crest tops. The relative contributions of ${<}w^{*}c_1^*{>}_{S}$ to ${<}{\overline{W^{*}}}\,{{\overline{C_1^*}}}{>}_{S}$ are listed in Table 1, noting that the subscript s represents the spatially-averaged values at $z^{*}=0.05$. The advective mass fluxes in Case 1 are positive for $x^{*}\ge 0.19$, and the tracer gas is emitted from the valley by advective flow; the advective mass fluxes are negative for $x^{*}<0.19$ because of the moderate downward flow as shown in Fig. 3b. The turbulent mass fluxes in Case 1 are positive or zero in all regions; the tracer gas transported towards the downslope of the wavy wall is trapped within the recirculation zone, and some gas is then removed upwards by the turbulent motion. Therefore, for the lowest Reynolds number, it is turbulent motion that mainly affects the gas removal from the valley. As the Reynolds number is increased, the peak of the turbulent mass flux shifts downwind and decreases, whereas the advective mass fluxes increase for $x^{*}\ge 0.25$, as shown in Fig. 9. In addition, the relative contribution of ${<}w^{*}c_1^*{>}_s{/}{<}{{\overline{W^{*}}}\,{{\overline{C_1^*}}}}{>}$ becomes smaller as the Reynolds number increases. This implies that it is the advective mass flux that dominates gas removal, and most of the gas is removed from the upslope by the upward flow along the wavy wall.

Fig. 9

Streamwise distributions of turbulent, advective and total vertical mass fluxes at $y^* = 0$ and $z^* = 0.05$. Symbols as in Fig. 8

Figure 10 shows the cospectra of vertical turbulent mass fluxes at $(x^{*}, y^{*}, z^{*}) = (-0.1, 0, 0.05)$, where the turbulent mass flux for the lowest Reynolds number is large. The cospectrum $Co_{w^{*}c_1^*}$ is defined as

$$\begin{aligned} {<}w^{*}c_1^*{>}\,=\int _0^\infty {Co_{w^{*}c_1^*} (f^{*})\mathrm{d}f^{*}} , \end{aligned}$$

(11)

where the peak of $Co_{w^{*}c_1^*}$ in Cases 1 and 2 is observed at $f^*= 1$, which is equivalent to the peak of $f^{*}Co_{u^{*} w^{*}}$. The turbulent motion corresponding to the wavenumber of the wavy wall is the main effect on gas removal from the valley. The values of $Co_{w^{*}c_1^*}$ for $f^*< 0.1$ are not zero, and large-scale turbulent motion (i.e. the intermittent velocity bursts) contributes partly to the gas removal. This trend is somewhat similar to pollutant removal from two- and three-dimensional street canyons (Michioka et al. 2011; Michioka and Sato 2012; Michioka et al. 2014, 2016). For the higher Reynolds-number cases, the values of $f^{*}Co_{w^{*}c_1^*}$ are almost zero because instantaneous flow reversal near the source becomes less frequent.

Fig. 10

Cospectra of the vertical turbulent mass fluxes at $(x^{*},y^{*},z^{*}) = (-0.1, 0, 0.05)$. Symbols as in Fig. 8

Fig. 11

Accumulated concentration within the valley: Filled circle Tracer gas 1, filled rectangular Tracer gas 2

To investigate the accumulated concentration within the valley, the spatially-averaged concentration $\left\langle {{\overline{C_i^*}}}\right\rangle _S$ within the target valley, defined as

$$\begin{aligned} \left\langle {{\overline{C_i^*}} } \right\rangle _S =\frac{1}{V_{{\textit{valley}}} }\int _{-0.05}^{0.05} {\int _{-0.75}^{0.75} {\int _{-0.5}^{0.5} {\left\langle {{\overline{C_i^*}} } \right\rangle \mathrm{d}{x}^{*}\mathrm{d}{y}^{*}\mathrm{d}{z}^{*},} } } \end{aligned}$$

(12)

is shown in Fig. 11. Here, $V_{valley}$ is the volume of the target valley and $\left\langle {{\overline{C_1^*}} } \right\rangle _S$ is normalized by the spatially-averaged concentration in Case 1, $\left\langle {{\overline{C_1^*}} } \right\rangle _{S,1}$. As the Reynolds number is increased, the value of $\left\langle {{\overline{C_1^*}} } \right\rangle _S /\left\langle {{\overline{C_1^*}} } \right\rangle _{S,1}$ decreases considerably until $Re \approx 3 \times 10^{4}$. This is because the amount of highly concentrated gas trapped within the recirculation zone decreases as the recirculation zone shrinks. For $Re>3\times 10^{4}$, the value of $\left\langle {{\overline{C_1^*}} } \right\rangle _S /\left\langle {{\overline{C_1^*}} } \right\rangle _{S,1}$ becomes nearly constant at 0.2, and the highly concentrated gas emitted from the source is mostly dispersed in the forward direction and is discharged from the valley by the advective flow. Thus, the accumulated concentration within the valley also depends strongly on the Reynolds number.

Fig. 12

Mean velocity vector and mean concentration contour of tracer gas 2 for x-z cross section: a Case 1, b Case 2, c Case 3, d Case 4, e Case 5

Fig. 13

Vertical distributions of the mean concentration of tracer gas 2 and the root-mean-square values of the concertation fluctuation at $x^* = -0.3, -0.1, 0.1, 0.3$ and 0.5. Black line Case 1, red line Case 2, blue line Case 3, green line Case 4, orange line Case 5

3.4 Concentration Statistics (Source at Crest)

Figure 12 shows the mean velocity vectors and the contours of the mean concentration emitted from the source at the crest at the central vertical cross-section. Figure 13 shows the vertical distributions of the mean concentration and the squared values of the concentration fluctuations at $x^* = -0.3, -0.1, 0.1, 0.3$ and 0.5. In Case 1, a high concentration appears at the level of the wave crests at $z^* = 0.05$ for $x^* < -0.1$ because the gas is transported by the separated flow. Some gas is trapped within in the recirculation zone. The vertical width of the root-mean-square values of the concentration fluctuation in Case 1 becomes wider compared with the values for the higher Reynolds-number case. This is attributed to the fact that the intermittent velocity bursts transport gas upwards. Wagner et al. (2007) showed a snapshot of scalar bursts associated with strong upward motion in a water-channel experiment, but these did not dramatically affect the vertical distributions of the mean concentration fields since the burst frequency was very low. As the Reynolds number is increased, gas increasingly follows the wavy wall and the height of the peak concentration at the downslope approaches the wavy wall. However, even for the highest Reynolds number, the location of the peak concentration at $x^{*} = -0.3$ is not on the wavy wall. Because weak, instantaneously reversed, flow is generated near the wavy wall at the downslope, the fluid does not flow completely along the downslope. At the upslope, the high concentration disappears suddenly because spanwise turbulent motions of high intensity (as shown in Fig. 4b) disperse the gas in the spanwise direction. In addition, the peak concentration at the upslope increases with the Reynolds number because of the decreasing turbulence intensity, as shown in Fig. 4. High values of $c_{2,rms}^*$ are observed within the valley, and a moderate decrease in $c_{2,rms}^*$ in the vertical direction is found compared with the mean concentration. Not only is the gas transported by advective flow, it is also affected by the vertical turbulent motion; the turbulent flow mixes the highly concentrated gas with clean air within the valley. However, for gas removal from the valley, the upward advective flow near the downwind crest is dominant (not shown in the figure).

The accumulated concentration $\left\langle {{\overline{C_2^*}} } \right\rangle _S$ within the target trough is shown in Fig. 11; these values are estimated using Eq. 12, and $\left\langle {{\overline{C_2^*}} } \right\rangle _S$ is normalized by the spatially-averaged concentration in Case 1, namely $\left\langle {{\overline{C_2^*}} } \right\rangle _{S,1}$. As the Reynolds number is increased, the peak concentration near the wavy wall increases as shown in Fig. 13a. Hence, the accumulated concentration within the valley probably increases, but the accumulated concentration gradually decreases as the Reynolds number increases. The difference in mean velocity in the valley strongly affects the accumulated concentration; fluid with a higher positive streamwise velocity component transports the gas in the forward direction by advective flow, causing the gas to be emitted from the valley more rapidly. In other words, the normalized streamwise velocity component within the valley increases with Reynolds number, as shown in Fig. 3, and the higher streamwise velocity component dilutes the accumulated concentration.

4 Summary and Conclusions

Large-eddy simulation is used to investigate the Reynolds-number dependence of scalar dispersion above a two-dimensional wavy wall, with wavelength $\lambda = 1.0\,\hbox {m}$ and wave amplitude = $0.05\lambda$. The Reynolds number (based on the bulk velocity and $\lambda$) was varied from $6.67\times 10^{3}$ to $6.67\times 10^{4}$, with two tracer gases emitted from point sources located at a single wave crest and trough.

The mean velocity, turbulence intensity and Reynolds stress calculated using LES for the lowest Reynolds number ($Re =6.67\times 10^{3})$ are in good agreement with DNS results for $Re =6.76\times 10^{3}$ (Maaß and Schumann 1996). For a lower Reynolds number, the flow over the wavy wall separates behind the crest and re-attaches to the upslope, and a recirculation zone is observed in the trough. As the Reynolds number increases, the recirculation zone shrinks and the flow increasingly follows the wavy wall.

Gas emitted in the trough is transported upwind by the recirculating reverse flow, and some gas is emitted from the trough by the intermittent velocity bursts that originate in the recirculation zone for the lower Reynolds number. With increase in the Reynolds number, the gas generally disperses in the forward direction and is exhausted from the valley by the advective flow. Gas emitted from the crest disperses with the separating flow, and some gas is trapped within the recirculation zone. As the Reynolds number increases, the advection of gas increasingly follows the wavy wall and the height of the peak gas concentration approaches the wavy wall. In addition, the accumulated concentration within the valley from both sources depends strongly on the Reynolds number.