Dispersion of a Passive Scalar Fluctuating Plume in a Turbulent Boundary Layer. Part I: Velocity and Concentration Measurements

Abstract

The prediction of the probability density function (PDF) of a pollutant concentration within atmospheric flows is of primary importance in estimating the hazard related to accidental releases of toxic or flammable substances and their effects on human health. This need motivates studies devoted to the characterization of concentration statistics of pollutants dispersion in the lower atmosphere, and their dependence on the parameters controlling their emissions. As is known from previous experimental results, concentration fluctuations are significantly influenced by the diameter of the source and its elevation. In this study, we aim to further investigate the dependence of the dispersion process on the source configuration, including source size, elevation and emission velocity. To that end we study experimentally the influence of these parameters on the statistics of the concentration of a passive scalar, measured at several distances downwind of the source. We analyze the spatial distribution of the first four moments of the concentration PDFs, with a focus on the variance, its dissipation and production and its spectral density. The information provided by the dataset, completed by estimates of the intermittency factors, allow us to discuss the role of the main mechanisms controlling the scalar dispersion and their link to the form of the PDF. The latter is shown to be very well approximated by a Gamma distribution, irrespective of the emission conditions and the distance from the source. Concentration measurements are complemented by a detailed description of the velocity statistics, including direct estimates of the Eulerian integral length scales from two-point correlations, a measurement that has been rarely presented to date.

1 Introduction

The assessment of chronic and accidental risks related to the atmospheric dispersion of contaminants requires the statistical characterization of its concentration. For chronic risks, estimates of mean concentrations are sufficient. Conversely, when considering the accidental risk due to releases of flammable and explosive substances, what matters is the occurrence of instantaneous concentrations within flammability (or explosivity) limits. Similarly, studies on the exposure and dosages of hazardous materials require estimates of the peak-to-mean ratios. In all those cases, the need to characterize the concentration probability density function (PDF) of the concentration arises. To this purpose, a variety of modelling strategies have been adopted in the literature.

With the aim of modelling the PDF by inverting a limited number of moments, several authors have tried to capture the bulk characteristics of the PDF inferring some functional dependence between the higher-order moments of the concentration PDF. This information is then intended to be used when running simple operational dispersion models, which provide mean values only, so as to approximately estimate the statistical variability of the concentration about its mean. With this aim Chatwin and Sullivan (1990) sought simple relationships between the mean concentration $\overline{c}$ and the standard deviation $\sigma _\mathrm{c}$ of a dispersing scalar in statistically steady self-similar turbulent shear flows. Their analysis was further extended by Mole and Clarke (1995), who demonstrated the existence of simple functional dependencies between second-order, third-order and fourth-order moments of the concentration PDF. Similar analyses were also conducted by Lewis et al. (1997) using field data in varying stability conditions, and, more recently, by Schopflocher and Sullivan (2005) using wind-tunnel experimental data.

Other authors focused directly on the form of the PDF of the concentration. In the case of high intermittent plumes, Yee and Chan (1997) proposed to model the concentration as a clipped-Gamma distribution depending on three parameters that reduce to two as the intermittency becomes negligible. This model was subsequently tested against experimental results by Yee (2009), Klein and Young (2011), and Klein et al. (2011). In the case of confined mixtures, Villermaux and Duplat (2003) showed that the concentration PDF could be well described by a simple Gamma distribution in the whole domain (see also Duplat and Villermaux 2008). More recently, Yee and Skvortsov (2011) showed that a simple Gamma PDF could be used also to reliably model the concentration within a plume emitted from a ground-level point source within a neutral boundary layer.

A more general approach relies on the development of models aiming to directly compute the concentration PDF (or its lower order moments). This has been so far achieved by means of meandering models (Gifford 1959; Yee et al. 1994; Luhar et al. 2000; Franzese 2003), pair-of-particles Lagrangian stochastic models (Durbin 1980; Sawford and Hunt 1986), numerical models resolving the concentration variance balance equation (Andronopoulos et al. 2002; Milliez and Carissimo 2008), micro-mixing Lagrangian models (Sawford 2004; Cassiani et al. 2005a, b; Leuzzi et al. 2012; Amicarelli et al. 2012) and large-eddy simulations (Xie et al. 2004; Vinkovic et al. 2006; Philips et al. 2013).

The reliability of any of these modelling approaches has to be tested against experimental data collected in field or laboratory experiments. Regarding concentration fluctuations of passive scalar plumes in the turbulent boundary layer, two wind-tunnel studies have been hitherto widely adopted as references. These are the pioneering works of Raupach and Coppin (1983) for a line source and Fackrell and Robins (1982a) for point sources. The latter, in particular, has represented a benchmark for more than two generations of authors, who presented several successful predictions of the experimental results using a variety of modelling approaches (Fackrell and Robins 1982b; Sykes et al. 1984; Cassiani et al. 2005a; Vinkovic et al. 2006).

Since the early 1980s, the experimental characterization of the statistical properties of a fluctuating plume has been rarely tackled. More recent experimental work was performed by Yee and Biltof (2004), who studied the concentration fluctuation within an obstacle array, and Hilderman and Wilson (2007), who directly measured the meandering of a plume dispersing in a water channel by using laser-induced fluorescence.

It is worth noting that these studies mainly focus on the second-order statistics and on the correlation between velocity and concentration fluctuations. Relatively little information is available concerning higher order concentration moments. There is therefore a lack of information for assessment of the modelling of the spatial evolution of the concentration PDFs. The objective of this study is to contribute a much needed set of experimental results, by extending the work on source size and elevation conducted by Fackrell and Robins (1982a) to higher order concentration moments, with a detailed definition of the plume structure in its initial phase of growth. To that purpose we have conducted a series of wind-tunnel experiments on the dispersion of a passive scalar emitted by a source of varying size and height, within a turbulent boundary layer. We also investigate the role of the emission velocity at the source that is likely to influence the near-field concentration statistics. The experimental dataset is completed by a detailed description of the statistics of the velocity field. This further information is essential in order to be able to dissociate errors induced by a specific modelling approach to uncertainties introduced by parametrizations used to substitute missing velocity data. In particular, considerable effort has been devoted here to obtaining direct measurements of the Eulerian integral length scales from two-point velocity statistics. The dataset is subsequently used in the second part of this study Marro et al. (2015) to further investigate the dynamics of the dispersion process by adopting the conceptual framework of a meandering plume model (Gifford 1959; Yee et al. 1994). In what follows Sect. 2 discusses the role of the parameters that mainly control the dispersion process, and Sect. 3 presents our experimental set-up and the measurement techniques. Section 4 presents the velocity statistics and concentration measurements are presented in Sect. 5. Throughout, our data are systematically compared to data of Fackrell and Robins (1982a).¹

2 Governing Parameters

We consider the atmospheric dispersion of a passive scalar (with molecular diffusivity $D$ and with same kinematic viscosity $\nu$ and density $\rho$ of ambient air) emitted by a localized source, placed at a height $h_\mathrm{s}$ from the ground, with a diameter $\sigma _0$ and an ejection velocity $u_\mathrm{s}$, so that its mass flow rate is $M_q=\frac{\pi }{4} \sigma _0^2 \, \rho \, u_\mathrm{s}$. The release takes place within a turbulent boundary layer with free-stream velocity $u_{\infty }$, and which is assumed to be fully characterized by self-similar relations, obtained by rescaling profiles of velocity statistics on the friction velocity $u_*$ and the boundary-layer depth $\delta$. Given these assumptions, the moments of the concentration $c$ about its mean $\overline{c}$ at a given position $(x,y,z)$ can be expressed as,

$$\begin{aligned} \overline{(c-\overline{c})^n} = f \left( \sigma _0, h_\mathrm{s}, u_\mathrm{s}, M_q, u_*, u_{\infty }, \delta , D, \nu \right) \end{aligned}$$

(1)

or, equivalently, in non-dimensional form as,

$$\begin{aligned} \frac{\overline{(c-\overline{c})^n}}{\Delta c^n} = f \left( \frac{u_*}{u_{\infty }}, \frac{u_\mathrm{s}}{u_{\infty }}, \frac{h_\mathrm{s}}{\delta }, \frac{\sigma _0}{\delta }, Re, Sc \right) \end{aligned}$$

(2)

where $Re=u_{\infty }\delta /\nu$ and $Sc = \nu /D$ are the Reynolds and the Schmidt numbers, respectively, and $\Delta c= M_q / (u_{\infty } \delta ^2)$ represents a scale of the concentration variations.

In our experimental campaign we aim at studying the influence of three parameters, $\sigma _0/\delta$, $h_\mathrm{s}/\delta$, and $u_\mathrm{s}/u_{\infty }$ (for a fixed $Re$, $Sc$ and ${u_*}/{u_{\infty }}$), whose general effect on the dispersion process is briefly described hereafter.

The diameter of the source is not effective in significantly altering the mean concentration field, unless very close to the emission point. This can be evidenced by Taylor’s (1921) formulation (adapted to an anisotropic velocity field) of the plume vertical $\sigma _z$, and transversal $\sigma _y$ spreads

$$\begin{aligned} \sigma _y^2= & {} \frac{\sigma _0^2}{6} + 2\sigma _v^2T_{\mathrm{L}v}\left\{ t-T_{\mathrm{L}v} \left[ 1-\exp \left( \displaystyle {-\frac{t}{T_{\mathrm{L}v}}}\right) \right] \right\} , \end{aligned}$$

(3)

$$\begin{aligned} \sigma _z^2= & {} \frac{\sigma _0^2}{6} + 2\sigma _w^2T_{\mathrm{L}w}\left\{ t-T_{\mathrm{L}w} \left[ 1-\exp \left( \displaystyle {-\frac{t}{T_{\mathrm{L}w}}}\right) \right] \right\} , \end{aligned}$$

(4)

where $t$ is the flight time, $T_{\mathrm{L}v}$ and $T_{\mathrm{L}w}$ are the Lagrangian time scales and $\sigma _v$ and $\sigma _w$ are the standard deviations of the lateral and vertical velocity components, respectively. According to Eqs. 3 and 4, the influence of $\sigma _0$ is non-negligible only for $t\ll T_\mathrm{L}$. Conversely, variations of the source size have significant effects on the concentration fluctuation for larger distances from the source, provided that its size $\sigma _0$ is much smaller than that of the large eddies of the atmospheric turbulence. To sketch these effects it is useful to refer to the conceptual framework developed by Gifford (1959), who considered the concentration fluctuations to be governed by two distinct phenomena: a meandering movement of the instantaneous plume, causing the displacement of the mass centre, and the relative dispersion of the plume particles relative to the mass centre position. The smaller the source, the larger the range of scales contributing to the meandering motion that displaces the plume centre of mass, therefore producing higher fluctuations around the mean concentration value.

The source elevation $h_\mathrm{s}/\delta$ has an influence on both the mean and the fluctuating concentration fields. The effect on the mean can be again well explained by Eqs. 3 and 4, since, in a turbulent boundary-layer flow, the parameters $T_{\mathrm{L}v}$, $T_{\mathrm{L}w}$, $\sigma _v$ and $\sigma _w$ are highly dependent on the distance from the ground. Concerning the influence on concentration fluctuations, the role of the source elevation $h_\mathrm{s}/\delta$ can be explained by similar arguments to those used for the influence of $\sigma _0/\delta$. For a fixed $\sigma _0/\delta$, the emitted plume is subjected to a range of turbulence scales that decreases as $h_\mathrm{s}/\delta$ decreases, since the source size approaches the size of the larger eddies at the source height. This results in a damping of the contribution of the meandering large-scale motion to the concentration fluctuations. As pointed out by Fackrell and Robins (1982a, (1982b) we may therefore expect that the influence of $\sigma _0/\delta$ vanishes in the limit $h_\mathrm{s}/\delta \rightarrow 0$, i.e. for a ground level source.

Finally, we consider the influence of $u_\mathrm{s}/u_{\infty }$, which is the sole parameter characterizing the dynamical conditions of the flow particles emitted at the source, according to the formulation of the problem given by Eq. 1. It is usually supposed, even if not explicitly proved, that if the outlet velocity $u_\mathrm{s}$ at the source equals the average velocity of the flow $\overline{u}_\mathrm{s}$ over its height (Fackrell and Robins 1982b) the influence of the emission conditions on the particle trajectories is minimized since, once ejected, the flow particles rapidly adopt the statistics of the external velocity field. Since $\overline{u}_\mathrm{s}/u_{\infty } = f(h_\mathrm{s}/\delta )$, this isokinetic condition corresponds to a value $u_\mathrm{s}/u_{\infty }$ that depends in turn on $h_\mathrm{s}/\delta$ only (for a fixed $u_{*}/u_{\infty }$). We expect a varying $u_\mathrm{s}/u_{\infty }$ to alter the plume dynamics in a near-source region, whose extent is however undefined. Furthermore, we expect this extent to be significantly different when analyzing the spatial distribution of different moments of the scalar concentration.

3 Experimental Set-Up and Techniques

3.1 Wind-Tunnel Set-Up

The experiments were performed in the atmospheric wind tunnel of the Laboratoire de Mécanique des Fluides et d’Acoustique at the Ecole Centrale de Lyon in France. This is a recirculating wind tunnel with a working section measuring 14 m long and 3.7 m wide. To control the longitudinal pressure gradients the ceiling slope can be adjusted. In the present configuration the ceiling has a positive slope, so that its height varies from 2 m at the entrance to 2.2 m at a distance of 7 m, and up to 2.5 m at its end. The air temperature in the wind tunnel is regulated so that its variations during a 1-day experiment can be maintained in the range $\pm$0.5 $^{\circ }$C.

The wind-tunnel set-up is sketched in Fig. 1. A neutrally-stratified boundary layer was generated by combining the effect of a grid turbulence and a row of spires, placed at the beginning of the test section, and roughness elements on the floor. The presence of a turbulence grid is not a usual feature of a boundary-layer simulation system, and is used here since it assists in minimizing the inhomogeneities of the flow in the transverse direction. The spires were of the Irwin (1981) type with a height $H= 0.5$ m, spaced by a distance $H/2$. The entire working section floor was overlaid with cubes of side $h=0.02$ m acting as roughness elements. The cubes were placed in a staggered array and covered approximately $1.8$ % of the tunnel floor surface. This experimental set-up allowed us to reproduce a boundary layer of depth $\delta = 0.8$ m. Imposing a free-stream velocity $u_{\infty }=5$ m s$^{-1}$, the Reynolds number $Re=\delta u_{\infty }/\nu \approx 2.6 \times 10^5$ ($\nu$ is the kinematic viscosity of air) was sufficiently high to ensure the adequate simulation of a fully turbulent flow (Jimènez 2004).

Fig. 1

Sketch of the wind-tunnel set-up showing the vortex generators and the turbulence grid at the entrance of the test section, the roughness elements on the floor and the design of the lower-level source (LLS) and the elevated source (ES) configurations

Ethane ($\hbox {C}_2 \hbox {H}_6$) was used as tracer in the experiments, since it has a density similar to air, and was continuously discharged from a source of varying diameter and elevation. Three source configurations were chosen:

ES 3:

Elevated source at $h_\mathrm{s}/\delta =0.19$ and with $\sigma _0/\delta =0.00375$ ($h_\mathrm{s}=152$ mm and $\sigma _0=3$ mm),

ES 6:

Elevated source at $h_\mathrm{s}/\delta =0.19$ and with $\sigma _0/\delta =0.0075$ ($h_\mathrm{s}=152$ mm and $\sigma _0=6$ mm),

LLS:

Lower-level source at $h_\mathrm{s}/\delta =0.06$ and with $\sigma _0/\delta =0.00375$ ($h_\mathrm{s}=48$ mm and $\sigma _0=3$ mm).

The sources consisted of a metallic L-shaped tube (Fig. 1) and were placed at a distance of $7.5\delta$ from the beginning of the test section, where the boundary layer can be considered as fully developed (see Sect. 4). The horizontal side was approximately 30 times the source diameter in order to reduce the influence of the vertical bar on the tracer dispersion. The parameter $\sigma _0$ refers to the internal diameter of the tube. The external diameter was equal to 4 mm for the $\sigma _0= 3$ mm source and to 8 mm for the $\sigma _0= 6$ mm source.

For most of the experiments, the outlet (spatially-averaged) velocity $u_\mathrm{s}$ of the ethane–air mixture was equal to that in the surrounding flow at the source height $\overline{u}_\mathrm{s}=\overline{u}(z=h_\mathrm{s})$, a condition that is hereafter referred to as ‘isokinetic’. Experiments were also performed by imposing a slower outlet velocity $u_\mathrm{s}/\overline{u}_\mathrm{s} = 0.03$ (approximating the condition $u_\mathrm{s}/\overline{u}_\mathrm{s} \rightarrow 0$), hereafter referred to as ‘hypokinetic’ condition.

In what follows $y$ and $z$ denote the transversal and vertical direction, respectively. We consider two different origins of the longitudinal axis: the $x'$-coordinate has its origin at the beginning of the test section whereas the $x$-coordinate has its origin at the source location (see Fig. 1).

3.2 Velocity Measurements

The flow dynamics were investigated by means of hot-wire anemometry, providing information about the spectral characteristics of the velocity and supported by a series of measurements with stereo particle image velocimetry (stereo-PIV), which allowed a knowledge of its spatial structure. The spatial distribution of velocity statistics measured with the two techniques are generally in good agreement. For a detailed comparative analysis of these results, see Nironi (2013).

3.2.1 Hot-Wire Anemometry

The hot-wire constant temperature anemometer was equipped with a X-wire probe with a velocity-vector acceptance angle of $\pm$45$^{\circ }$, allowing for the simultaneous measurements of two velocity components. Calibration was carried out in the wind tunnel using a pitot tube to measure a reference velocity. The probe was not calibrated in yaw. In order to decompose the calibration velocities from the X-probe into the longitudinal and transversal velocity components (Jorgensen 2002), we adopted a yaw correction with constant coefficients $k_1^2=k_2^2=0.0225$. We acquired transversal and vertical profiles of the velocity statistics at varying distances from the entrance of the test section, from $x'=4\delta$ up to $x'=14 \delta$. For each measurement point we recorded a 120 s time series with a sampling frequency of 5000 Hz. The experimental error, estimated by repeating the measurements in a fixed reference location, was approximately $\pm$2 % for the mean and the standard deviation.

3.2.2 Particle Image Velocimetry

A second series of velocity measurements was made with a stereo-PIV system. The ambient air was seeded using a stage smoke generator, with approximately spherical 1 $\mu$m polyethylene glycol particles. A planar region of the flow was illuminated with a pulsed laser and the tracer position was recorded as a function of time in doubly exposed photographs.

Stereo-PIV planes were collected at $x'=7.5\delta$. Velocities were recorded on two planes: a $yz$-plane perpendicular to the flow direction and a $xz$-plane parallel to the flow, allowing for the measurement of the three velocity components. The image resolution was $1280\times 1024$ pixels and the observation field measured approximately $150\times 100$ mm for $xz$-planes and $215\times 150$ mm for $yz$-planes. Several planes were recorded at different heights to cover most of the boundary-layer vertical extent. Images were processed using a cross-correlation algorithm. The interrogation window for the correlation cells was fixed to $32\times 32$ pixels with a round form and a standard 50 % overlap, providing a spatial resolution of about 2 mm for $xz$-planes and 2.5 mm for $yz$-planes. A total set of 10000 image pairs was acquired sequentially for time-averaged computations. The sampling frequency was 4 Hz.

3.3 Concentration Measurements

Concentration measurements were performed with a fast flame ionization detector (Fackrell 1980) with a sampling tube 0.3 m long, permitting a frequency response of the instrument to about 400 Hz. Vertical and transversal profiles of concentration statistics were recorded at various distances downwind, from $x=0.312\delta$ ($x=250$ mm) up to $x=5 \delta$ ($x=4000$ mm). Concentration statistics extracted from each time series recorded in a measurement point include the mean, the standard deviation, the third and the fourth moments.

The calibration was carried out using ethane–air mixtures with concentrations equal to 0, 500, 1000 and 5000 ppm. Generally calibration was performed twice a day, as long as the flame temperature of the flame ionization detector (which was continuously monitored) was constant. When the flame temperature showed variations of more than 2 $^{\circ }$C from its value at the beginning of the experiment, calibration was repeated. The relation between ethane concentration and tension response was linear, with a slope (representing the sensitivity of the instrument) whose variations could reach $\pm$3 %, depending on the ambient conditions.

The flow control system at the source was composed of two lines, ethane and air, each of them equipped with a mass flow controller. The two lines then converged through a valve and the ethane–air mixture was directed to the source. The ethane mass rate was kept constant by the mass flow controller, working in the range 0.2 to 2 Nl min$^{-1}$ and used within 10 and 100 % of its nominal range. Depending on ambient pressure and temperature (that were continuously monitored and recorded), the airflow was regulated by the second mass flow controller, in order to maintain the total volume flow rate at the source (and therefore the outlet velocity $u_\mathrm{s}$).

The error on the ethane–air flow rate was estimated by systematic comparison with measurements provided by a volumetric counter. The maximal difference between measurements of the two instruments did not exceed $\pm$3 %. It should be noted that the maximal error was reached for measurements close to the source, where measuring concentration within the calibration range (0–5000 ppm) required ethane flow rates of about 0.05 Nl min$^{-1}$, i.e. outside of the mass flow controller working range. Conversely, for mass flow rates within the instrument working range the uncertainty was reduced to about 1 %.

Recirculation of air in the wind tunnel implies background concentration increasing with time. To take into account the contribution of this drift, the background concentrations were recorded before and after acquiring any of the concentration time series. The background concentration, which was assumed to evolve linearly with time from its initial to its final value, was then subtracted from the signals.

While performing several measurement campaigns over two years, we observed that the higher order statistics were affected by larger experimental error when measured in spring and summer rather than in autumn and winter. This feature can be explained by the effect of the sampling of atmospheric aerosol (Hall and Emmott 1991) that can induce anomalous peaks in the signals. Due to seasonal changes in continental source strengths and in the removal rate for atmospheric particles, this effect is at its highest in spring and summer (Bergametti et al. 1989). Therefore, the data presented herein all refer to measurement campaigns in autumn and winter, when the disturbance produced by the atmospheric aerosol is minimal.

An averaging time of 300 s was chosen, allowing the stochastic uncertainty of the concentration statistics calculated from finite length time series to be of order 0.1 %, so that its contribution to the experimental error was negligible. The main sources of experimental errors were instead related to the calibration, the sampling of atmospheric aerosols and the flow rate at the source. The relative influence of each of these factors is however difficult to estimate a priori. Therefore, in order to quantify a global experimental error, during our campaign we collected a sample of 20 measurements in each of four fixed locations with respect to the source. These measurements were performed on different days with a time interval of several weeks one to the other. The delay between calibration and measurement was variable (up to four hours). Therefore the statistics extracted from these signals were affected by all the uncertainties due to the experimental chain. The error was then estimated as twice the standard deviation computed over the 20 values collected for each point. The results show that, in the far field, the first two moments of the concentration are affected by an error of 2 % whereas the error rises up to 4.5 % for third- and fourth-order moments. In the near field, the error in the third- and fourth-order moments remained similar to that estimated in the far field. However, due to the higher uncertainty affecting the source flow control system in the near-field measurements, the error in the first two moments, the mean and the standard deviation, reached $\pm$3 %.

4 Velocity Field

We begin by presenting vertical profiles of one-point velocity statistics and spectra, measured by hot-wire anemometry in the flow within which the scalar dispersion takes place. This is a boundary-layer flow over a rough wall with light adverse longitudinal pressure gradient ${\approx }-\!0.095$ Pa m$^{-1}$ (as estimated from the measurements of the free-stream velocity $u_{\infty }$ for varying distances from the entrance of the test section). Further on, the focus is on the estimates of the integral length scales from PIV two-point correlations, and on the derived estimates of the Lagrangian time scales.

4.1 Vertical Profiles of One-Point Velocity Statistics

In order to compare our results to equivalent data by Fackrell and Robins (1982a), we adopted the typical scalings indicated by the similarity theory (Tennekes and Lumley 1972). Based on this theory, the turbulent boundary layer consists, in the simplest view, of an outer and an inner region, the latter including the inertial region and the underlying roughness sublayer (Raupach et al. 1980), extending for a few roughness heights away from the wall. According to the theory, the surface geometry is seen as a boundary condition affecting the flow field as a wall distributed drag, quantified by the roughness length $z_0$, except close to the wall, in the roughness sublayer.

It is generally assumed that, if a proper set of scales is chosen, each region can be described by some form of similarity solution. These are the friction velocity $u_*$, the roughness length $z_0$ and boundary-layer depth $\delta$, representing an inner and an outer length scale, respectively. The bulk properties of the mean velocity distribution in the inertial region $\overline{u}(z)$ are derived by a classical asymptotic matching procedure (in the double limit $z/z_0 \rightarrow \infty$ and $z/\delta \rightarrow 0$), yielding to the familiar logarithmic law (Tennekes 1982),

$$\begin{aligned} \frac{ \overline{u}(z)}{u_*}=\frac{1}{\kappa } \ln \left( \frac{z-d}{z_0}\right) , \end{aligned}$$

(5)

where $\kappa = 0.4$ is the Von Kármán constant and $d$ is the displacement height (Thom 1971; Jackson 1981). In order to quantify the three parameters $u_*$, $d$ and $z_0$, we have adopted the same procedure as Salizzoni et al. (2008). Firstly we have estimated the friction velocity from the Reynolds stress $\overline{u'w'}$ profile as $u_*=\sqrt{-\overline{u'w'}}$, by averaging the ${\overline{u'w'}}$ data in the lower part of the flow field, where these vary only slightly with respect to their average value (Fig. 2f). The two other parameters, $z_0$ and $d$, are then estimated by a best fit of the mean velocity profile with a logarithmic law (Fig. 2b), assuming the computed value of $u_*$. From our measurements we obtained $u_* = 0.185$ m s$^{-1}$, $z_0=1.1 \times 10^{-4}$ m and $d=0.013$ m. A value of $\delta = 0.8 \pm 0.05$ m was estimated by the ${\overline{u'w'}}$ profile, as the height at which $\hbox {d}\left( {\overline{u'w'}}\right) /\hbox {d}z \approx 0$. In principle, the effective value of the outer scale should be taken as $\delta - d$. However, since $d$ is here smaller than the uncertainty in the estimate of $\delta$, we will use the latter as the reference length scale to normalize velocity profiles.

A comparison between boundary-layer parameters in our flow and those of the experiments of Fackrell and Robins (1982a) is given in Table 1. As predicted by the theory, and as shown in Fig. 2b, Eq. 5 fits the velocity profile in a region that slightly exceeds the extent on the inertial region, for $0.025 \le z/\delta \le 0.25$. Conversely, a good fit of the mean velocity profile in the whole turbulent boundary layer extent can be obtained by a power law of the form,

$$\begin{aligned} \frac{\overline{u}(z)}{u_{\infty }}=\left( \frac{z}{\delta }\right) ^n, \end{aligned}$$

(6)

with the exponent $n=0.23$ (Fig. 2a).

Fig. 2

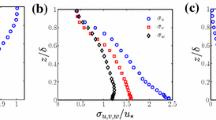
Vertical profiles of non-dimensional velocity statistics and comparison with literature data from Fackrell and Robins (1982a). a Mean longitudinal velocity component; b mean longitudinal velocity component rescaled on inner scaling; standard deviations of the c longitudinal, d lateral component, and e vertical velocity component; f Reynolds stress $\overline{u'w'}$ (opens symbols) and $\overline{u'v'}$ (filled symbols); g estimates of the dissipation rate $\varepsilon$ and production $P$ of TKE

Table 1 Boundary-layer characteristics: comparison with data from Fackrell and Robins (1982a) (F&R)

Profiles of the velocity statistics plotted in Fig. 2 show limited development with increasing $x'$. Therefore, as a first approximation, we consider that from $x'/\delta =7.5$ the flow is homogeneous in the horizontal plane, since the development of coherent structures in the wake of the vortex generators has already reached an equilibrium condition (Salizzoni et al. 2008).

Due to a different wall roughness $z_0$, our profile of $\overline{u}/u_{\infty }$ differs from that of Fackrell and Robins (1982a) (Fig. 2a). However the two profiles collapse, in the lower part of the velocity field, when normalized by an inner scaling (Fig. 2b). Similarly, vertical profiles of higher order velocity statistics tend to collapse on a single curve when normalized with $u_*$ and $\delta$ (Fig. 2c–f). The only relevant discrepancies are observed in the $\sigma _v/u_*$ profiles (Fig. 2d).

General good agreement (Fig. 2g) is also observed in the profiles of the non-dimensional turbulent kinetic energy (TKE) mean dissipation rate, referred to as $\varepsilon$. Two estimates of $\varepsilon$ were obtained here by means of the hot-wire anemometer data and employing the common isotropic approximation and Taylor’s hypothesis of frozen turbulence to convert spatial gradients to temporal gradients, a procedure that may induce non-negligible errors close to the wall, as the turbulent intensity $\sigma _u / \overline{u}$ exceeds $0.3$. The first estimate is computed as (Hinze 1975) $\varepsilon _{iso} =\displaystyle { \frac{15\nu }{\overline{u}^2}\overline{\left( \frac{\partial u'}{\partial t}^2 \right) }}$ whereas the second, referred to as $\varepsilon _{sp}$ is obtained by fitting the one-dimensional spectra (Sect. 4.2) of the longitudinal velocity component in the inertial region adopting the relation $E(k)=\alpha _1 \varepsilon _{sp}^{2/3} k^{-5/3}$, where $k=2 \pi f/\overline{u}$ is the wavenumber, $f$ is the frequency and $\alpha _1=0.5$ (Pope 2000). The two estimates of $\varepsilon$ agree well one with the other and they are also very close to those of TKE production $P\approx \overline{u'w'}\displaystyle {\frac{\partial \overline{u}}{\partial z}}$ (Fig. 2g), showing that, in most of the boundary layer, we can reasonably assume a condition of local equilibrium between production and dissipation of TKE.

Finally, we note that our velocity field is characterized by slight inhomogeneities in the mean longitudinal velocity along the $y$-direction. This implies non-null values of the $\overline{u'v'}$ Reynolds stress component (Fig. 2f) and a non-null lateral component of the mean transversal velocity $\overline{v}$, whose intensity is about 1 % of that of the longitudinal component $\overline{u}$.

4.2 Spectra

Spectra for the three velocity components derived from hot-wire anemometry are shown in Fig. 3, for increasing distances from the wall. These are normalized using the distance $z$ as a length scale and the friction velocity $u_*$ as a velocity scale, and plotted against the dimensionless frequency $n=fz/\overline{u}$.

Fig. 3

Velocity spectra of the three velocity components for growing distances from the wall, $z/\delta$. Comparison with a model extrapolated from field data (Kaimal et al. 1972). a longitudinal component $S_u$, b lateral component $S_v$, and c vertical component $S_w$

The measured spectra for $u$, $v$ and $w$ are compared to the model proposed by Kaimal et al. (1972), based on the Kansas field experiments,

$$\begin{aligned} \frac{n S_u(n)}{u_*^2}= & {} \frac{102 n}{(1+33n)^{5/3}}, \end{aligned}$$

(7)

$$\begin{aligned} \frac{n S_v(n)}{u_*^2}= & {} \frac{17 n}{(1+9.5n)^{5/3}}, \end{aligned}$$

(8)

$$\begin{aligned} \frac{n S_w(n)}{u_*^2}= & {} \frac{2.1 n}{1+5.3n^{5/3}}. \end{aligned}$$

(9)

The measured spectra show good agreement with Kaimal’s model in both the production and the inertial subrange (Fig. 3). This comparison allows us to evidence the similarity between the spectral energy distribution in our simulated flow with that observed in the atmospheric boundary layer. The extension of the inertial subrange in our velocity field is smaller than that occurring in a real atmosphere (due to a reduced Reynolds number). However, the existence of inertial subrange extending over one (or more, depending on the distance from the wall) decade of non-dimensional frequencies (Fig. 3), demonstrates a clear separation between the larger scale energetic eddies and the dissipative scale.

4.3 Integral Length and Time Scales

The characterization of the structure of the large-scale fluctuating motion in an inhomogeneous and anisotropic shear turbulent flow requires the evaluation of a variety of length scales (Carlotti and Drobinski 2004). These can be conveniently estimated from two-point spatial correlation coefficients, defined as,

$$\begin{aligned} \rho _{ii}(\mathbf {x},\mathbf {r})= \frac{\overline{u'_i(\mathbf {x})u'_i(\mathbf {x}+\mathbf {r})}}{\overline{{u'_i}^2}}, \end{aligned}$$

(10)

where $u'_i$ represents the velocity fluctuations of $u$, $v$ and $w$, $\mathbf{x}$ is a fixed point and $\mathbf{r}$ is a generic vector. In this study, correlation coefficients were estimated by stereo-PIV measurements, made at a distance of approximately $8 \delta$ from the beginning of the test section. Measurements in the $xz$-plane allowed the measurements of the coefficients $\rho _{uu}$ and $\rho _{ww}$ whereas measurements on the $yz$-plane provided information on the coefficient $\rho _{vv}$. As an example of our results, we report in Fig. 4 the correlation maps obtained for the $xz$-plane within the inertial region. On the same plots we show the profiles of the correlation coefficient extracted along the $x$ and $z$ axes. A rapid examination of the plot on Fig. 4 reveals the strong anisotropy characterizing the large-scale flow in the lower part of the boundary layer. The spatial extent of the correlation $\rho _{uu}(x,z)$ is considerably wider than that of $\rho _{ww}(x,z)$, and the topology of the iso-contours is highly different for the two functions.

Fig. 4

Two-point spatial correlations in the lower part of the velocity field measurements on the $xz$-plane: a and b $\rho _{uu}$; c and d $\rho _{ww}$

The iso-correlation of $\rho _{ww}(x,z)$ can be well approximated by an ellipse with a major axis aligned in the $z$-direction that is slightly larger than that longed in the $x$-direction. Conversely, the iso-lines of $\rho _{uu}(x,z)$ are elongated in the $x$-direction and are tilted of about $15^{\circ }$ with respect to the $x$-axis due to the shear produced by the wall roughness (Krogstad and Antonia 1994).

As well as allowing a qualitative description of the flow structure, the correlation fields can be used to extract estimates of characteristic length scales, usually referred to as Eulerian integral length scales, defined as

$$\begin{aligned} \Lambda _{ii,j}(\mathbf {x}) = \int _0^{\infty } {\rho _{ii}(\mathbf {x}, r, \mathbf {e}_j) } \hbox {d}r. \end{aligned}$$

(11)

where $\mathbf {e}_j$ is the unit vector in the $j=x,y,z$ directions.

The numerical computation of the integral in Eq. 11 from experimental data can be affected by non-negligible errors. Therefore the estimate of the Eulerian integral length scales is generally calculated as the distance at which the correlation function falls below a threshold value. For example Bewley et al. (2012) assumed a value of 0.5 whereas Takimoto et al. (2013) adopted 0.4. Note that this method may be problematic when computing scales associated to the $\rho _{uu}$ functions, since the extent of the iso-correlation lines corresponding to the threshold value may not be fully captured by the PIV field (see Fig. 4). Similar problems can be encountered for any of the three functions $\rho _{ii}$ at larger distances from the wall as the size of the eddies is at its highest.

In order to avoid these inconveniences, we assume here that the correlation coefficient is an exponential function of the type,

$$\begin{aligned} \rho _{ii,j}(\mathbf {x},r,\mathbf {e}_j) = \exp \left( -\frac{r}{L_{ii,\mathbf {e}_j}}\right) , \end{aligned}$$

(12)

and we adopt the lengths ${L_{ii,\mathbf {e}_j}}$ as a measure of ${\Lambda _{ii,j}}$ [this corresponds to the distance at which $\rho _{ii,j} = e^{-1} \approx 0.37$ (Tritton 1988)]. The choice of a negative exponential is motivated by the shape of the correlation functions profiles (see Fig. 4b and d), characterized by a sharp peak at $\mathbf{{r}\rightarrow 0}$, that hides the presence of any horizontal asymptote of the curves for $\mathbf{{r}=0}$. This evidences that the influence of viscous effects is limited to a tiny region, smaller than the PIV measuring volume. To simplify the notation, the three scales $L_{uu,e_x}$, $L_{vv,e_y}$, $L_{ww,e_z}$, obtained by fitting Eq. 12 to the data in the $x$, $y$, $z$ directions will be hereafter referred to as $L_{uu}$, $L_{vv}$, $L_{ww}$.

The dependence of these three scales on the distance from the wall is depicted in Fig. 5a. The longitudinal length scale $L_{uu}$ is by far the longest and is almost double the transversal scale $L_{vv}$. As expected, $L_{ww}$ is the smallest, even though only slightly smaller (of order 25 %) than $L_{vv}$. Figure 5a also shows that, as predicted by similarity theory, in the lower part of the turbulent boundary layer, $L_{ww}$ scales as $\kappa z$ to about $z/ \delta \approx 0.15$, which represents approximately the upper limit of the inertial layer.

Fig. 5

a Vertical profiles of the Eulerian integral length scales from PIV measurements. Integral length scales, b $L_{vv}$ and c $L_{ww}$ compared to estimates provided by Eqs. 13 and 14 where the proportionality constant $\alpha _v$ and $\alpha _w$ varies in the range 0.2–0.8

We stress here the importance of the scales $L_{vv}$ and $L_{ww}$ in the overall dispersion phenomenon of a passive scalar plume. Nonetheless their determination in dispersion studies is mostly based on indirect procedures, based on dimensional analysis or similarity considerations. These estimates are therefore affected by unpredictable errors, especially that of $L_{vv}$. Indeed, unlike $L_{ww}$, whose upper bound can be evaluated as a fraction of $\delta$, the amplitude of $L_{vv}$ cannot be evaluated by a simple ‘rule of thumb’, which could provide at least a rough estimate of it.

In the modelling of the mass and momentum transfer across the boundary layer, the scales ${L}_{vv}$ and ${L}_{ww}$ can be parametrized assuming the stationarity of the energy cascade as (Sawford and Stapountzis 1986),

$$\begin{aligned} L_{vv}\approx & {} \alpha _v \frac{\sigma _v^3}{\varepsilon }, \end{aligned}$$

(13)

$$\begin{aligned} L_{ww}\approx & {} \alpha _w \frac{\sigma _w^3}{\varepsilon }, \end{aligned}$$

(14)

where $\alpha _v$ and $\alpha _w$ are proportionality constants (in these cases $\sigma _v$, $\sigma _w$ and ${\varepsilon }$ are usually calculated from similarity relations). Since we have direct estimates of these velocity statistics, we can test here the reliability of the parametrizations given by Eqs. 13 and 14 and determine appropriate values for $\alpha _v$ and $\alpha _w$. These parameters are generally assumed in the literature to be free parameters, whose determination mainly rely on matching of numerical results with experimental data rather than on making reference to previous experimental estimates (that are lacking as far as we are aware). As shown in Fig. 5b and c, Eqs. 13 and 14 provide excellent estimates of $L_{vv}$ and $L_{ww}$ assuming $\alpha _v \approx 0.4$ and $\alpha _w \approx 0.6$, respectively. Note that both values are significantly lower than those currently adopted in the literature, which vary between a minimum of 0.8 (Sawford and Stapountzis 1986) and a maximum of 1.8 (Postma et al. 2011).

The direct measurements of the Eulerian integral length scales can be further used to estimate the characteristic ‘life time’ of the larger scale flow structures as (Tennekes and Lumley 1972; Frisch 1995),

$$\begin{aligned} T_{\mathrm{L}v1}\approx & {} \frac{L_{vv}}{\sigma _v} , \end{aligned}$$

(15)

$$\begin{aligned} T_{\mathrm{L}w1}\approx & {} \frac{L_{ww}}{\sigma _w}. \end{aligned}$$

(16)

They can be used as a measure of the Lagrangian time scales, referred to here as $T_{\mathrm{L}v}$ and $T_{\mathrm{L}w}$, which are key parameters in the modelling of pollutant dispersion. As the measurement of the Lagrangian time scales $T_{\mathrm{L}v}$ and $T_{\mathrm{L}w}$ is extremely difficult to achieve, for dispersion modelling purposes, they are usually parametrized as (Tennekes 1982),

$$\begin{aligned} T_{\mathrm{L}v2}= & {} \frac{2 \sigma _v^2}{C_0 \varepsilon } \end{aligned}$$

(17)

$$\begin{aligned} T_{\mathrm{L}w2}= & {} \frac{2 \sigma _w^2}{C_0 \varepsilon }, \end{aligned}$$

(18)

where $C_0$ is the Kolmogorov constant, introduced as a universal constant when referring to a homogeneous and isotropic turbulent flow. However, there is no experimental evidence of the universality of $C_0$ in inhomogeneous and anisotropic turbulence, and its estimate in the literature is in the range $2 \le C_0 \le 8$ (Du et al. 1995; Lien and D’Asaro 2002; Rizza et al. 2006). Given this variability, in most pollutant dispersion studies $C_0$ is usually considered a flow dependent parameter and its value estimated a posteriori, as that providing the best agreement between experimental and numerical concentration results.

A first estimate of $C_0$ can be achieved here by taking advantage of the experimental profiles of $\varepsilon$, $L_{ww}$ and $L_{vv}$. By injecting Eqs. 13 and 14 into Eqs. 15 and 16 and assuming $T_{\mathrm{L}v1}= T_{\mathrm{L}v2}$ and $T_{\mathrm{L}w1}=T_{\mathrm{L}w2}$ we obtain $C_0=\displaystyle {{2}/{\alpha _{v,w}}}$. The two equalities provide slightly different values of the Kolmogorov constant that lie in the range $3.5 \le C_0 \le 5$. Further discussion of the values of $C_0$ is provided in Sect. 5.1.1 where we analyze the vertical and lateral spreading of the passive scalar plume.

5 Concentration Field

We begin by the analysis of the influence of the size and elevation of the source on the first two moments of the concentration PDF (Sect. 5.1). As a second step, we focus on the role of varying emission conditions (Sect. 5.2) and consider the longitudinal evolution of the intermittency factor for all the cases considered (Sect. 5.3). We discuss then the modelling of the concentration PDF (Sect. 5.4) and its physical significance, in particular regarding the dynamics of the dispersion phenomenon. In the light of this discussion, we conclude by presenting the profiles of the third and four moments of the concentration PDF.

The mean is computed as $\overline{c}^* = \frac{1}{N}{\sum _{j=1}^N c_j^* }$ whereas the higher order moments are computed as $m_{nc}^* = \left[ \frac{1}{N}\sum _{j=1}^N(c_j^*-\overline{c}^*)^n\right] ^{1/n}$ (for $n=2,3,4$), $N$ being the number of samples in the time series and $c^*$ the non-dimensional instantaneous concentration. In what follows, the second-order moment $m_{2c}^*$ is denoted as $\sigma _\mathrm{c}^*$.

In normalizing the concentration data we have expressly avoided adopting local scales, such as the maximal mean concentration or standard deviation and we have adopted $\Delta c$ as unique concentration scale (Sect. 2). This is motivated by the need to preserve the information on both the form of the profiles and the magnitude of the peaks, for increasing distances from the source. Note that, due to the transversal flow inhomogeneities discussed in Sect. 4.1 that tend to induce a deviation in the plume axis with respect to the wind-tunnel axis, the mean concentration maxima tend to be shifted to the right of the source. However, in plotting the results, we have included a slight lateral offset in the transversal profiles of the concentration moments, so that the concentration maxima occur at $y=0$.

5.1 Influence of Source Height and Size

As discussed in Sect. 2, the effect of varying source size and elevation on the concentration moments is related to the interaction of the plume with the eddies having characteristic dimensions exceeding the local plume width. We have therefore chosen the size of the two sources ($\sigma _0=3$ mm and $\sigma _0=6$ mm) so that both were significantly smaller than the Eulerian integral length scale, as estimated from the PIV measurements. For similar reasons, the ES and LLS were placed in regions of the flow characterized by marked differences in the values of the Eulerian integral length scales. Note that the non-dimensional height $h_\mathrm{s}/\delta = 0.19$ and size $\sigma _0/\delta = 0.0075$ of the ES is the same as that of the elevated source used in the experiments of Fackrell and Robins (1982a). This feature allows us to compare our results with their dataset.

5.1.1 Mean Concentration Field

Transversal and vertical profiles of the mean concentration downwind from the source are plotted in Fig. 6a–d. Profiles of the ES and different $\sigma _0$ do not show any particular difference (Fig. 6a, b), except very close to the source ($x/\delta = 0.3125$). Conversely, the effect of source elevation is evident. Since the LLS emits closer to the ground, the wall reflection rapidly alters the plume structure. As the distance from the source increases, the mean concentrations for the LLS plume become larger than those measured for the ES, with a maximum that is about two times the value reached by the ES plume (Fig. 6c, d).

Fig. 6

Mean concentration field for ES and LLS. a–d transversal and vertical profiles of $\overline{c}^*$ at various distances downwind: a and b $x/\delta =0.625$; c and d $x/\delta =3.75$. Transversal profiles were measured at the source height and vertical profiles were measured on the plume axis. e ES and f LLS plume spreads $\sigma _y$ and $\sigma _z$

For both ES and LLS, transverse profiles measured at the source height are satisfactorily reproduced by a Gaussian distribution of the form,

$$\begin{aligned} \overline{c}(x,y) = \frac{M_q}{2\pi \sigma _y\sigma _z\overline{u}_\mathrm{adv}} \exp \left( -\frac{y^2}{2 \sigma _y ^2} \right) . \end{aligned}$$

(19)

Concerning the vertical profiles, the Gaussian distribution with total reflection on the ground is the most suited to the reproduction of the mean concentration distribution in the vertical direction (Arya 1999),

$$\begin{aligned} \overline{c}(x,z) = \frac{M_q}{2\pi \sigma _y\sigma _z\overline{u}_\mathrm{adv}} \left[ \exp \left( -\frac{(z+h_\mathrm{s})^2}{2 \sigma _z ^2} \right) + \exp \left( -\frac{(z-h_\mathrm{s})^2}{2 \sigma _z ^2} \right) \right] , \end{aligned}$$

(20)

where $\overline{u}_\mathrm{adv}$ is the mean longitudinal velocity taken at the plume centre of mass.

Experimental mean concentrations were fitted by the simple and reflected Gaussian distributions, i.e. Eqs. 19 and 20, adopting $\sigma _y$ and $\sigma _z$ as free parameters. The resulting values of the vertical and transversal plume spreading are shown in Fig. 6e, f, where no distinction is made between smaller and larger ES sources, since their mean concentration fields are not distinguishable one from the other. For both the ES and the LLS, in the near field as well as in the far field, the vertical spreading was observed to be less than the lateral one.

Plume spreads $\sigma _y$ and $\sigma _z$ are modelled according to Taylor’s statistical theory from Eqs. 3 and 4. In order to take into account the effects of the inhomogeneity of the velocity field, parameters $\sigma _v$ and ${T_{\mathrm{L}v}}$ (as well as $\sigma _w$ and ${T_{\mathrm{L}w}}$) are estimated at the height of the plume centre of mass, whose elevation evolves with the distance from the source. For the same reasons, the flight time is estimated as $t=x/\overline{u}_\mathrm{adv}$.

Equations 3 and 4 were fitted to the experimental values of $\sigma _y$ and $\sigma _z$ expressing $T_{\mathrm{L}v}$ and $T_{\mathrm{L}w}$ from Eqs. 17 and 18 and adopting $C_0$ as a free parameter. It is worth noting that the best agreement between experimental and modeled plume spreads is obtained for $C_0 =4.5$ (Fig. 6e, f), a value that falls in the range $3.5 \le C_0 \le 5$ identified by the analysis of the integral length and times scales (Sect. 4.3). For the ES, the model agrees well with experimental data. A satisfactory agreement for $\sigma _z$ is also found for the LLS, while $\sigma _y$ is overestimated starting from $x/\delta =1.25$.

5.1.2 Standard Deviation

Unlike the mean, the standard deviation $\sigma _\mathrm{c}^*$ shows a strong dependence on the source size, extending to a considerable distance away from the source. Transverse profiles of $\sigma _\mathrm{c}^*$ downwind of the source for the elevated sources are presented in Fig. 7a, c, e, while the vertical profiles of ES and LLS are shown in Fig. 7b, d, f. A strong dependence on the source size is visible near the source: the $\sigma _\mathrm{c}^*$ field from the smaller source is characterized by significantly higher values. The difference between the two fields diminishes moving downwind and finally vanishes in the far field for $x/\delta =3.75$. As discussed in Sect. 2, this effect can be explained by the larger range of scales that act on the plume generated by the smaller source, resulting in an enhanced meandering motion.

Fig. 7

Transversal profiles (at the source height) and vertical profiles (at the plume centre) of $\sigma _\mathrm{c}^*$ for the ES and LLS, at various distances downwind: a and b $x/\delta =0.625$; c and d $x/\delta =1.25$; e and f $x/\delta =3.75$

Source elevation also has a strong influence, as shown in Fig. 7b, d, f. The ES emission results in a higher concentration standard deviation. Even in this case, this difference can be attributed to the different scales of motion that are effective in dispersing the plume. As evidenced in Sect. 4.3, the Eulerian integral length scales are reduced significantly approaching the ground. Therefore, for the LLS emission, the amplitude of the meandering motion acting on the plume is smaller compared to the ES case, thus generating less intense concentration fluctuations. These slight differences between ES and LLS plumes persist until the latest measurement station. The variation of the source height is also reflected on the shape of the profiles of $\sigma _\mathrm{c}^*$. While the $\sigma _\mathrm{c}^*$ profiles from the ES always have a Gaussian form, those produced by the LLS gradually lose their Gaussian shape moving downstream, and level off at the plume centreline (Yee and Wilson 2000).

The variable role of meandering can be conveniently enlightened by analyzing one-dimensional spectra of concentration $E(k)$ measured on the centreline at various distances from the source. These are presented in Fig. 8 in non-dimensional form, normalized as $E^* = E\delta /\sigma _\mathrm{c}^2$ and as a function of $k\delta$. In the near field of the ES plumes, the more intense meandering motion acting on the small source ($\sigma _0 = 3$ mm) produces larger scale concentration fluctuations compared to the larger one ($\sigma _0=$ 6 mm), that are reflected in a higher spectral density for small wavenumbers. The differences between the two spectra are progressively reduced for higher wavenumbers, or fine length scales, at which relative dispersion is predominant. Figure 8a also helps explain the effect on the plume fluctuations due to a source of varying height and constant diameter ($\sigma _0=3$ mm). The large-scale fluctuations in the LLS are significantly reduced compared to the ES, since the plume is submitted to the dispersive action of eddies that are smaller than those experienced by the ES (Sect. 4.3). It is also worth noting how the smaller scale fluctuations appear to be more intense along the centreline of the LLS plume, which is much more sensitive to the small-scale turbulence generated close to the wall. In the far field (Fig. 8b), the lateral and vertical dimensions of the ES plumes exceed those of the bigger structures in the flow (Sect. 4.3). In these conditions, the meandering motion is suppressed and the concentration spectra of the two ES plumes superpose. These are however still different from the spectrum recorded at the LLS plume centreline, which shows reduced large-scale fluctuations and a more prominent role of the smaller eddies in the inertial range.

Fig. 8

Spectra of concentration fluctuations on the plume centreline, at two distances from the source. Comparison between the spectra from the ES with 3 and 6 mm diameter (measured at $z/\delta = 0.19$) and the LLS (measured at $z/\delta = 0.06$). a $x/\delta =0.625$, b $x/\delta =3.75$. For a cut-off frequency of about $400$ Hz, the non-dimensional cut-off wavenumber is in the range $600 < k \delta < 700$. Dotted line represents $-5/3$ dependence on $k \delta$

Further insight into the influence of source size on the plume dynamics can be gained by considering the spatial distribution of the production $P=\overline{u'_jc'} \displaystyle {\frac{\partial \overline{c}}{\partial x_j}}$ ($\overline{u'_jc'}$ is the correlation between velocity and concentration fluctuations) and dissipation $\varepsilon _\mathrm{c} = D \left( \displaystyle {\overline{\frac{{\partial c'}}{{\partial x_j}}\frac{{\partial c'}}{{\partial x_j}}}}\right)$ of the concentration variance at varying distances from the source. Following Fackrell and Robins (1982a) we deduced $\varepsilon _\mathrm{c}$ from the measured spectra of concentration $E(k)$ by means of the relation $E(k)={\alpha _\mathrm{c}} 2\varepsilon _\mathrm{c} \varepsilon ^{-\frac{1}{3}} k^{-\frac{5}{3}}$, with $\alpha _\mathrm{c} = 0.6$. Even though the $- 5/3$ slope inertial region in the concentration spectra is narrow compared to velocity spectra, this estimate was shown to be quite accurate compared to estimates of $\varepsilon _\mathrm{c}$ obtained as the residual of the concentration variance balance equations. Nevertheless, ‘quite accurate’ here involves errors that can reach $\pm$25 %.

The production term is estimated adopting a simple gradient law closure model as $P \approx D_{ty} \displaystyle {\left( \frac{\partial \overline{c}}{\partial y} \right) ^2} + D_{tz} \displaystyle {\left( \frac{\partial \overline{c}}{\partial z} \right) ^2}$, where the turbulent diffusivities are computed as $\displaystyle {D_{ty}(x) = 2 \overline{u}_\mathrm{adv} \frac{\hbox {d} \sigma _y^2}{\hbox {d}x}}$ and $\displaystyle {D_{tz}(x) = 2 \overline{u}_\mathrm{adv} \frac{\hbox {d}\sigma _z^2}{\hbox {d}x}}$.

Fig. 9

Vertical profiles of the non dimensional production and dissipation of concentration fluctuations at a growing distance from the source. Comparison between the elevated sources with $\sigma _0=3$ mm and $\sigma _0=6$ mm: a $x/\delta =0.625$, b $x/\delta =3.75$

Vertical profiles of the variance production and dissipation (in non-dimensional form) for the two ES plumes are shown in Fig. 9 for two distances from the source. As expected, in the far field ($x/\delta =3.75$) profiles of $P$ and $\varepsilon _\mathrm{c}$ do not show any significant difference depending on the source size. In the near field ($x/\delta =0.625$) the dissipation rate is higher for the small 3 mm source. At both locations, the production term for the two cases is several orders of magnitude lower than $\varepsilon _\mathrm{c}$. This means that the higher $\sigma _\mathrm{c}^*$ observed for the $\sigma _0=3$ mm source (compared to the $\sigma _0=6$ mm one) has to be attributed to an enhanced production occurring very close to the source location (over a distance smaller than $x/\delta \approx 0.3$). Unfortunately, our experimental set-up does not allow us to investigate the plume for $x/\delta < 0.3125$. This would require a considerable reduction in the ethane flow rate at the source, in order to perform measurements in the FID calibration range. As discussed in Sect. 3.3, the main limitations for this are imposed by the mass-flow controller, whose error rises significantly for flow rates $<$ 0.05 Nl min$^{-1}$. Further experiments are therefore needed to investigate the dynamics of the plume in this very near-field region.

5.1.3 Comparisons with Fackrell and Robins (1982a)

Passive scalar dispersion experiments performed in this study took place in a velocity field (Sect. 4) that is different than that presented in Fackrell and Robins (1982a), since it develops under the forcing action of a different free-stream velocity $u_{\infty }$ and over a different wall roughness $z_0$, both of which result in a different ratio ${u_*}/ u_{\infty }$ (see Table 1). However, as discussed in Sect. 4.1, the two velocity fields can be considered similar, as a first approximation, since non-dimensional profiles of the velocity statistics of the two datasets show a generally good agreement. Therefore, so long as the source parameters ${h_\mathrm{s}}/{\delta }$ and ${\sigma _0}/{\delta }$ remain constant, we expect the non-dimensional profiles of concentration statistics to collapse onto common curves. To that purpose it is however necessary to convert the longitudinal distances from the source to a non-dimensional time, computed as the ratio between the flight time $t=x/\overline{u}_\mathrm{adv}$ and a characteristic turbulent scale $\tau = \delta /u_*$.

The comparison shown in Fig. 10, concerns longitudinal profiles of three parameters, originally plotted in Fackrell and Robins (1982a). These are the non-dimensional maximal mean concentration $\max (\overline{c})$, the plume half-widths $s_y$ and $s_z$ (an alternative measure of the plume spread, defined as the distance at which the mean concentration falls to half its maximum), and the intensity of concentration fluctuations computed as the ratio of the maximum r.m.s., $\max (\sigma _\mathrm{c})$, to $\max (\overline{c})$.

Fig. 10

Comparison with the Fackrell and Robins (1982a) results (F&R in the legend); a maximum concentrations at varying downwind positions $\displaystyle {\max (\overline{c})\frac{u_\infty \delta ^2}{Q}}$ vs $\displaystyle {\frac{u_*}{\overline{u}(h_\mathrm{s})}\,\frac{x}{\delta }}$, b vertical and lateral plume half-widths $\displaystyle {\frac{s_y}{\delta }}$, $\displaystyle {\frac{s_z}{\delta }}$ vs $\displaystyle {\frac{u_*}{\overline{u}(h_\mathrm{s})}\,\frac{x}{\delta }}$, and c intensity of concentration fluctuation $\displaystyle {\frac{\max (\sigma _\mathrm{c})}{\max (\overline{c})}}$ vs $\displaystyle {\frac{u_*}{\overline{u}(h_\mathrm{s})}\,\frac{x}{\delta }}$

The longitudinal evolution of $\max (\overline{c})$ and of $s_y$ and $s_z$ for the ES plumes are indeed in very good agreement with those presented in Fackrell and Robins (1982a). Conversely, data of $\max (\sigma _\mathrm{c})/ \max (\overline{c})$ for the ES show non-negligible differences. Even though the general tendency of the two profiles is the same, our data exhibit a lower peak value occurring closer to the source. The rate at which $\max (\sigma _\mathrm{c})/ \max (\overline{c})$ decreases once the peak is reached appears more pronounced in our experiments. The reasons for these differences are not self-evident since they cannot be simply linked to differences in the velocity statistics. A possible explanation concerns different conditions very close to the source, where almost all of the production of $\sigma _\mathrm{c}$ occurs. There, a different source design can induce different outlet velocity profiles or different dynamics within the source wake that may significantly alter the process of variance production.

Finally we also report a comparison of $\max (\sigma _\mathrm{c})/ \max (\overline{c})$ between our LLS and the ground-level source (GLS) of Fackrell and Robins (1982a). It should be noted that the two plumes tend to a same constant value of fluctuation intensity $\approx$0.4, except for a near-field region in which, as expected, the fluctuation intensity of our LLS is higher than that of their GLS.

5.2 Influence of the Emission Conditions

The evidence that most of the concentration variance is produced in a relatively limited region very close to the source emphasizes the need to analyze the effect on the concentration field of varying emission conditions (Sect. 5.1.2), which are here assumed to be fully governed by the parameter $u_\mathrm{s}/\overline{u}_\mathrm{s}$. The interest is focused on two emission conditions (see Sect. 3): $u_\mathrm{s}/\overline{u}_\mathrm{s}=1$, i.e. isokinetic conditions, and $u_\mathrm{s}/\overline{u}_\mathrm{s}=0.03$ (approximating the condition $u_\mathrm{s}/\overline{u}_\mathrm{s} \rightarrow 0$) referred to as hypokinetic conditions. Investigating the effect of a highly forced source condition, i.e. $u_\mathrm{s}/\overline{u}_\mathrm{s} \gg 1$, is conversely beyond the aim of this study.

Concentration profiles were measured close to the source, at stations $x/\delta =0.3125$ and $x/\delta =0.625$ (Fig. 11). Measurements show that the differences between the hypokinetic and isokinetic conditions for the $\sigma _0=3$ mm source are negligible at both distances. Conversely for the ES with $\sigma _0=6$ mm the emission conditions produce non-negligible differences in the concentration statistics at $x/\delta =0.3125$ that are then no longer detectable at $x/\delta =0.625$. We can therefore conclude that this effect extends over a distance $x < 80 \sigma _0$, and is therefore significantly reduced compared to that induced by a variation in the source diameter.

Fig. 11

Comparison between isokinetic and hypokinetic conditions: transversal profiles at $x/\delta =0.3125$ of a mean concentration $\overline{c}^*$, and b standard deviation $\sigma _\mathrm{c}^*$

For ES 6 mm, the hypokinetic emission produces a smaller mean concentration and standard deviation than the isokinetic emission. In a sense, we can say that generally the hypokinetic emission results in a reduced effective source, which produces therefore enhanced concentration fluctuations. In most of the studies on passive scalar dispersion in turbulent boundary layers, it is implicitly assumed that the particles emitted at the source take the statistics of the external velocity field almost instantaneously, so that there is no difference between Lagrangian statistics of the fluid particles injected at the source and those in the ambient fluid passing close to it. However it is worth noting that we do not have any information to identify which of the two conditions (isokinetic or hypokinetic) induce a concentration field that is closer to the one generated by these ideal source conditions. This is a feature that certainly deserves to be further analyzed, by comparing our experimental data with numerical results of computational fluid dynamics models or Lagrangian stochastic models obtained by varying the emission conditions at the source.

5.3 Intermittency Factor

To further investigate the role of the large-scale meandering motion on the concentration fluctuation, we focus on the intermittency factor $\gamma _\mathrm{c}$ of the concentration signals. This is defined as the percentage of time for which the plume is experienced at a given point, i.e. the probability that at a position $\mathbf x$ and time $t$ the concentration $c$ is non-zero,

$$\begin{aligned} \gamma _\mathrm{c}(\mathbf x ,t)=\hbox {prob} \{ c(\mathbf x ,t)>0 \}. \end{aligned}$$

(21)

A reliable determination of the intermittency depends on the fine-scale structure of turbulence, whose temporal and spatial resolutions are invariably accompanied by random instrumental noise, whose amplitude depends also on the setting of the gain with which the fluctuations of the measured signal are amplified. Given these limitations due to the instrumentation, in order to quantify $\gamma _\mathrm{c}$ we fixed a threshold value of non-dimensional concentration, referred to as $\Gamma _\mathrm{t}$, so that

$$\begin{aligned} \gamma _\mathrm{c}(\mathbf x ,t)=\hbox {prob} \{ c^*(\mathbf x ,t)>\Gamma _\mathrm{t} \}. \end{aligned}$$

(22)

Since the need for this threshold is due to the measurement errors affecting the zero concentration values, $\Gamma _\mathrm{t}$ has to be a small constant value independent of the downwind distance. For all stations, $\Gamma _\mathrm{t}=1$ was chosen, an arbitrary value that allowed us to efficiently distinguish the moments when the plume is experienced by the probe and the moments of zero concentration.

Profiles of intermittency factor at the plume centreline are plotted in Fig. 12 and show that the emission conditions have an important influence on the intermittency. The channeling of the plume, produced by the isokinetic condition at the source, results in a reduced meandering and therefore in a lower intermittency of the signal (and $\gamma _\mathrm{c}$ values closer to unity). If the tracer is released hypokinetically, the plume is easily captured by the ambient eddies, which engulf the plume in a meandering motion resulting in a higher intermittency of the signal. This effect can be further amplified by the action of the unsteady wake of the source, whose effect extends up to several tens of source diameters (Nironi 2013). As already observed in Sect. 5.2, in both cases—hypokinetic and isokinetic conditions—the higher the source, the greater the influence of the emission velocity on the concentration field.

Fig. 12

Longitudinal profiles of the intermittency factor at the source height for different source conditions

The ground-level emission is less intermittent than the elevated ones and $\gamma _\mathrm{c}$ attains unity as $x/\delta \ge 2.5$. It can be noted that, independently of the source configuration, the intermittency factor approaches unity when the plumes reach the ground and are efficiently mixed by the small-scale surface-generated turbulence that acts by suppressing concentration fluctuations.

5.4 Higher Order Moments and Concentration PDFs

With the aim of seeking a suitable model for the concentration PDF, and defining its dependence on the distance from the source and the emission conditions, following Mole and Clarke (1995), we began by verifying the consistency of our dataset with simple functional dependencies between moments of the concentration PDF of the form

$$\begin{aligned} Sk= & {} a_1 \, (i_\mathrm{c})^{a_2}, \end{aligned}$$

(23)

$$\begin{aligned} Ku= & {} b_1 \,(Sk)^{b_2}+b_3, \end{aligned}$$

(24)

where $i_\mathrm{c}=\sigma _\mathrm{c}/ \overline{c}$ is the intensity of the concentration fluctuations, $Sk = \displaystyle {\frac{m_{3c}^{*3}}{\sigma _\mathrm{c}^{*3}}}$ is the skewness, $Ku = \displaystyle {\frac{m_{4c}^{*4}}{\sigma _\mathrm{c}^{*4}}}$ is the kurtosis and $a_1$, $a_2$, $b_1$, $b_2$, and $b_3$ are free parameters. These latter were determined by fitting Eqs. 23 and 24 to the data (Fig. 13). This preliminary analysis showed two main features: firstly, the values of the parameters did not show any clear dependence on the source dimension, elevation and emission velocity. Secondly, the values of the parameters provided by the best fit $a_1=2.01$, $a_2=0.98$, $b_1=1.67$, $b_2=1.97$, and $b_3=2.99$ were in excellent agreement with the relations $Sk = 2\,i_\mathrm{c}$ and $Ku = 1.5 \,Sk^2 + 3$ that correspond to a Gamma distribution of the form

$$\begin{aligned} p(\chi )=\frac{k^k}{\Gamma (k)}\chi ^{k-1} \exp (-k\chi ), \end{aligned}$$

(25)

with $\Gamma (k)$ the Gamma function, $k = i_\mathrm{c}^{-2}$ and $\chi \equiv c/\overline{c}$ ($c$ being the sample space variable and $\overline{c}$ the mean value). These findings clearly support the existence of a universal function for the PDF of the concentration that can be suitably modelled by a family of one-parameter Gamma distributions (Villermaux and Duplat 2003; Duplat and Villermaux 2008; Yee and Skvortsov 2011).

Fig. 13

a Skewness against intensity, b Kurtosis against skewness. The relations $Sk = a_1\,(i_\mathrm{c})^{a_2}$ and $Ku = b_1\,(Sk)^{b_2} + b_3$ are fitted to the data using least squares

PDFs measured on the plume centreline at various distances from the source location are plotted in Fig. 14, enlightening their link to the intensity of the concentration fluctuations $i_\mathrm{c}$ (Fig. 14a). The Gamma distribution (Eq. 25) is rather efficient in reproducing the changing in the shape of the PDF while increasing the distance from the source: from an exponential-like distribution in the near field, a log-normal-like distribution with short tail in the intermediate field and a Gaussian-like distribution in the far field. It is worth noting that, mathematically, these transitions are fully regulated by the value of $i_\mathrm{c}$ only, and specifically to its value relative to unity. Physically, these transitions can be fully interpreted by an analysis of the intermittency factors $\gamma _\mathrm{c}$.

Fig. 14

Relation between the concentration fluctuation intensity $i_\mathrm{c}$ and the concentration PDF. Results are recorded on the plume centreline at a growing distance from the source for the three source configurations at isokinetic conditions: a $i_\mathrm{c}$ vs $x/\delta$ for ES and LLS cases. Concentration PDF $p$ for b $i_\mathrm{c}>1$, c $i_\mathrm{c} \approx 1$, d $i_\mathrm{c}<1$, e $i_\mathrm{c} \approx 0.4$

In the near field, the plume exhibits large-scale fluctuations due to its meandering motions that result in high intermittency of the signals, i.e. low $\gamma _\mathrm{c}$, and values of $i_\mathrm{c} > 1$ (Fig. 14b). The maximal value of $i_\mathrm{c}$, and its location with respect to the source, depend on $h_\mathrm{s}/\delta$ and $\sigma _0 / \delta$. As the meandering motion is damped, due to the progressive growth of the instantaneous plume caused by relative dispersion, the intermittency is reduced ($\gamma _\mathrm{c}$ increases) and $i_\mathrm{c}$ decreases to reach unity (Fig. 14c), with a rate that is again significantly dependent on $h_\mathrm{s}/\delta$ and $\sigma _0/\delta$. From hereafter, meandering is suppressed and relative dispersion becomes the only mechanism controlling the turbulent transfer. The intermittency factor $\gamma _\mathrm{c}$ tends asymptotically to unity and $i_\mathrm{c}$ falls below one (Fig. 14d). In the very far field, as $i_\mathrm{c}$ tend to its asymptotic value $\approx$0.4, the concentration PDF tends to an invariant form, which approaches a clipped-Gaussian (Fig. 14e).

5.4.1 Third- and Fourth-Order Moments

In the light of the previous discussion on the form of the concentration PDF, we finally turn to the third and fourth moments of concentration. Transversal profiles of the third and fourth moments downwind from the source are presented in Fig. 15a, c, e, and in 16a, c, e for the transversal profiles, while the vertical profiles are shown in Figs. 15b, d, f, and in 16b, d, f. Third-order and fourth-order moments are shown to be very sensitive to both the source size and the source elevation. As observed for $\sigma _\mathrm{c}^*$, the smaller source generates higher moments, due to the enhanced role of the meandering in the near field. Moving downwind, the difference between the concentration field generated by the two releases is progressively reduced (Figs. 15a, c, e, 16a, c, e) and consequently the profiles gradually approach one to the other and finally collapse at $x/\delta = 3.75$.

Fig. 15

Transversal profiles (at the source height) and vertical profiles (at the plume centre) of $m_{3c}^*$ for the ES and LLS, at various distances downwind: a and b $x/\delta =0.625$, c and d $x/\delta =1.25$, e and f $x/\delta =3.75$

Fig. 16

Transversal profiles (at the source height) and vertical profiles (at the plume centre) of $m_{4c}^*$ for the ES and LLS, at various distances downwind: a and b $x/\delta =0.625$, c and d $x/\delta =1.25$, e and f $x/\delta =3.75$

It is remarkable how a small difference in the source size, whose diameter varied by a factor of 2 (from 3 to 6 mm), is reflected in significant variations of higher-order moments of the concentration fluctuations, which persist up to a distance of about 3 m, i.e. in the range $500\sigma _0 < x < 1000\sigma _0$.

The source elevation is even more determinant in shaping the moment profiles. While profiles from the ES emission have a Gaussian shape, in the LLS plume the shape changes quickly in the downwind direction. At $x/\delta = 1.25$ the profiles are already characterized by a plateau at the plume centre. Further away from the source (from $x/\delta = 3.75$), as the values of both $m_{3c}^*$ and $m_{4c}^*$ become almost two orders of magnitude smaller than that in the near field, their profiles exhibit off-centreline peaks, showing how the intermittency is progressively reduced in the core of the plume, as the pollutant is well mixed. The third moment is the most affected by off-centreline peaks, which however appear also on $m_{4c}^*$ profiles. Finally, we note how the plots for $m_{3c}^*$ and $m_{4c}^*$ show generally more scatter in the profiles compared to those of lower order moments. This is due to the undesired spikes recorded in the signals due to aerosol sampling, whose effect becomes evident as the order of the moments of the concentration PDF increases (Sect. 3.3).

Finally, we discuss the reliability of the estimates of higher order moments evaluated adopting the model provided by a simple Gamma distribution (Eq. 25) and using the experimental estimates of the concentration fluctuations $i_\mathrm{c}$. Predictions of $m_{3c}^*$ and $m_{4c}^*$ as estimated from Eq. 25, i.e. $m_{3c \Gamma }^* = \left( \frac{2}{\sqrt{k}} \right) ^{1/3} \sigma _\mathrm{c}^{*}$ and $m_{4c \Gamma }^* = \left( \frac{6}{k } +3 \right) ^{1/4} \sigma _\mathrm{c}^{*}$, turn out to be very accurate close to the source (see Figs. 15a–d, 16a–d). Conversely, in the far field (Figs. 15e, f, 16e, f), we observe discrepancies between the Gamma distribution predictions and experiments. At the plume core, for the ES case, $m_{3c \Gamma }^*$ and $m_{4c \Gamma }^*$ tend to underestimate experimental data, especially the fourth-order moments, whereas the estimates of $m_{3c}^*$ still present a good accuracy. These discrepancies are particularly evident in the far field for the LLS case, where the third-order and fourth-order moments exhibit off-centreline peaks and the Gamma distribution provides a substantial overestimate of the experimental data. A possible explanation of this lost of accuracy is that in the far field the concentration PDF (at the plume centreline) of the LLS relaxes towards a normal distribution (Fig. 14e) and then Eq. 25 provides solutions that are less reliable. However, these comparisons clearly show that a simple Gamma PDF can be assumed as a suitable model to compute the high order moments in the whole domain.

6 Conclusions

We have investigated experimentally the dispersion of a passive scalar emitted within a turbulent boundary layer from a localized source with varying configurations. With the aim of extending the work of Fackrell and Robins (1982a) on concentration fluctuations, we characterized the spatial evolution of the concentration statistics with a focus of the first four moments of the concentration PDF. The experimental results also include a detailed description of the structure of the turbulent boundary layer within which the dispersion process takes place, which is shown to be similar to that reproduced by Fackrell and Robins (1982a) in their experiments. The investigation of the velocity field is performed by analyzing the vertical profiles of one- and two-point velocity statistics. In particular, the latter allowed us to provide a direct estimate of the integral length scales of the flow. These were subsequently used to infer the characteristic integral time scale, which represents a key parameter for the modelling of atmospheric pollutant dispersion.

We discussed the influence of the source configuration on the dispersion by analyzing three main aspects: the source elevation, the source size and the gas emission velocity. Our results show that the source size and elevation have a major influence on the spatial distribution of the higher moments of the concentration PDF. This can be explained by an interaction of the plume during its initial stage of growth with the different scales of motion in the surrounding atmospheric flow. These effects are more and more evident as the moments of the PDF increase, and persist over a distance that is almost three orders of magnitude larger than the source size.

The production of turbulent fluctuations occurs in a region very close to the source, and is therefore likely to be highly influenced by the emission condition and the design of the source. The variation of the emission conditions at the source from isokinetic to hypokinetic can affect the concentration field over a distance of a few tens of source diameters, therefore lower than that in the case of a varying diameter. Decreasing the velocity of the emission results in a reduced effective source size, which implies an increased intermittency of the plume.

Our experimental data generally confirm the results of Fackrell and Robins (1982a) on the effects of source size and elevation on the concentration field. Considering an elevated source, the spatial distribution of the mean concentrations agrees very well with their data, whereas discrepancies are observed in the longitudinal profiles of the intensity of the concentration fluctuations. The reasons for these differences are not fully clear. It is suggested that these may be related to the influence of a slightly different source design on the plume dynamics in its initial phase of growth.

Finally, the experimental non-dimensional PDF is shown to be very well modelled by a Gamma distribution for any of the source configuration considered, irrespective of the source conditions. This implies that the higher order concentration moments can be fully expressed as a function of only one parameter, the intensity of the concentration fluctuation $i_\mathrm{c}=\sigma _\mathrm{c}/\overline{c}$.