1 Introduction

The variability and parametrization of the scalar flux over heterogeneous surfaces has been extensively studied experimentally and numerically (Wieringa 1971; Pasquill 1972; Brutsaert and Kustas 1985; Wieringa 1986; Mason 1988; Parlange and Brutsaert 1989; Brutsaert and Sugita 1990; Parlange and Katul 1995; Brutsaert 1998; Bou-Zeid et al. 2004; 2007). Whereas variances of the turbulent variables (such as \(\overline{w^{\prime }w^{\prime }}\), \(\overline{\theta ^{\prime }\theta ^{\prime }}\) and \(\overline{q^{\prime }q^{\prime }}\)) have been shown to be sensitive to the nature and the scales of the surface variability, mean profiles of the atmospheric flow velocity, temperature or specific humidity are not quite as sensitive to the characteristic spacings of the surface variability, and they show some similarity above a certain blending height (Brutsaert 1998). This characteristic height was defined by Wieringa (1986) as the level inside the planetary boundary layer above which the flow becomes horizontally homogeneous in the absence of other influences. The blending height has been shown to be variable, and it is highly dependent on the nature and amplitude of the surface roughness elements, the atmospheric stability, and the horizontal scale of the heterogeneities (Mason 1988; Claussen 1991; Parlange and Katul 1995; Raupach and Finnigan 1995; Brutsaert 1998). Mahrt (1996) and later Mahrt (2000) presented complete surveys of blending height estimates under different atmospheric conditions. Asanuma and Brutsaert (1999) also showed how the gradients and variances were altered by the surface heterogeneity, but more importantly they presented a dissimilarity between the passive and active scalars. This dissimilarity in the blending for the passive scalar (water vapor) and the active scalar (temperature) was later argued by Albertson and Parlange (1999a) to be due to the role of temperature fluctuations in forcing the vertical velocity fluctuations, through buoyancy. Analytical parametrizations of the blending height above a complex heterogeneous surface have been formulated (Bou-Zeid et al. 2004, 2007; Stoll and Porte-Agel 2008). Overall it has been shown that surface heterogeneity (changes in patch roughness, size, temperature and humidity) plays a relevant role in determining the mean surface scalar flux.

Given the rising demand for clean energy, tapping into a new mix of renewable energy sources such as solar, wind, and geothermal is increasingly attractive. About \(20\,\%\) of the electrical power in countries like Denmark or Spain is provided by wind harvesting. However, for wind energy to be profitable, large arrays of wind turbines must be installed. Thus, there is an increasing interest in better understanding the potential impact of large wind farms on the micrometeorology of the placement site: their effect on fluxes of heat and humidity, and their effect on the surface temperature and scalar concentration. Recent experimental work of Roy and Traiteur (2010), Rajewski et al. (2013), Smith et al. (2013) and numerical studies of Lu and Porte-Agel (2011), Calaf et al. (2011), and Roy (2011) have reported an increase in the surface temperature downwind a large wind farm, an increase of about \(10\,\%\) in the surface flux of passive scalar, and a decrease in the sensible heat flux in stable atmospheric stratification. The experimental work of Rajewski et al. (2013) (the Crop Wind Energy Experiment (CWEX) study) represents a realistic farmland with complex surface heterogeneity and multiple surface roughness transitions, and the study involves multiple factors – atmospheric stability, wind direction, variable atmospheric conditions and temporal surface heterogeneity evolution. Because of this complexity, it is difficult to understand the role and relevance of these factors individually.

The present work aims at expanding current understanding of the effect of large wind farms on the atmospheric boundary layer and to assess the change that large aggregations of turbines might induce on the scalar flux when installed over a heterogeneous surface, characterized by a variety of surface roughness elements. By considering two surface patches of varying lengths and surface roughnesses, results provide additional wind-farm scenarios to those previously presented in Calaf et al. (2011), in which the land surface was considered uniform. The idealized numerical simulations will allow the problem to remain tractable, such that the interplay between internal boundary layer development and the additional turbulent mixing induced by wind turbines can be investigated for the first time.

In Sect. 2 a concise theoretical review of the concepts of a surface-heterogeneity-induced internal boundary layer (IBL) and a wind-turbine-array boundary layer (WTABL) are presented. In Sect. 3 the large-eddy simulation (LES) is introduced, together with the numerical model used to represent the wind turbines and the study cases considered. Section 4 presents the numerical results with a complementary analytical analysis, and finally, Sect. 5 presents the conclusions.

2 The Surface-Heterogeneity-Induced Boundary Layer and the Wind-Turbine-Array Boundary Layer: A Review of Theory

2.1 The Surface-Heterogeneity-Induced Boundary Layer

The study of atmospheric flows over heterogeneous and complex surfaces has been actively developed over the past decades. The precise determination of local-scale surface fluxes of momentum and heat are fundamental for understanding and predicting the local hydrology and meteorology. At present, Monin–Obukhov (MO) similarity theory (Monin and Obukhov 1954) is widely used for the numerical computation and experimental measurement of momentum and scalar fluxes. Although this formulation was originally developed for homogenous flat surfaces and averaged quantities, it has been widely applied in a local sense, and over heterogeneous surfaces. According to Brutsaert (1998) the use of MO similarity theory is appropriate over heterogeneous surfaces when the surface patches are long enough for the flow to reach a local equilibrium within the local patch. This equilibrium is largely induced by the enhanced mixing resulting from atmospheric turbulence: above a characteristic height, the so-called ‘blending height’, the heterogeneities induced by the changing surface are diffused and MO formulation can be used (Wieringa 1971). Yet, the question remains: how to properly determine this blending height a priori, such that similarity theory can be appropriately used. An earlier numerical work of Bou-Zeid et al. (2004) developed an analytical formulation that implicitly determines the theoretical blending height, as well as the equivalent surface roughness that the airflow above the heterogeneous surface would reflect. Bou-Zeid et al. (2004) postulated that the downstream change in the IBL induced by a ‘patchy’ surface is related to the upward diffusion velocity component and the streamwise convective velocity component such that,

$$\begin{aligned} \frac{\text {d} \delta _\mathrm{IBL}}{\text {d}x} \sim \frac{w_\mathrm{rms}}{\langle u(\delta _\mathrm{IBL}) \rangle }. \end{aligned}$$
(1)

From LES data, it was inferred that the standard deviation of the vertical velocity fluctuations \((w_\mathrm{rms}\)) could be approximated by \(w_\mathrm{rms} \approx 0.95u_*\), and the mean streamwise velocity component could be approximated using an equivalent logarithmic profile \(\langle u(\delta _\mathrm{IBL}) \rangle /u_* = (1/\kappa )\,\hbox {ln}(\delta _\mathrm{IBL}/z_{0,\mathrm{eqv}})\), where \(u_*\) is the resultant non-dimensionalized friction velocity at the top of the IBL. Therefore,

$$\begin{aligned} \frac{\text {d}\delta _\mathrm{IBL}}{\text {d}x} = C \frac{\kappa }{\mathrm {ln}(\delta _\mathrm{IBL}/z_{0,\mathrm{eqv}})}, \end{aligned}$$
(2)

with \(z_{0,\mathrm{eqv}}\) being the equivalent surface roughness over the patchy landscape, and \(C\) an adjustable proportionality constant that was determined with the aid of the numerical data, such that \(C=0.85\). Integration and simplification yields

$$\begin{aligned} \delta _\mathrm{IBL} \Big [\mathrm {ln}\Big (\frac{\delta _\mathrm{IBL}}{z_{0,\mathrm{eqv}}}\Big ) -1\Big ] = C\kappa x. \end{aligned}$$
(3)

The LES results further suggested that the blending height is equivalent to the IBL height when \(x \approx 2L_\mathrm{p}\), with \(L_\mathrm{p}\) being the patch length. Therefore, one can write a final analytical equation that determines the blending height,

$$\begin{aligned} h_\mathrm{b} \Big [\mathrm {ln}\Big (\frac{h_\mathrm{b}}{z_{0,\mathrm{eqv}}}\Big ) -1\Big ] = 0.85\,\kappa \, (2L_\mathrm{p}). \end{aligned}$$
(4)

Note that the equivalent surface roughness \((z_{0,\mathrm{eqv}})\) remains unknown; thus a second equation is needed. By equating the total surface force acting on the overall heterogeneous surface as a summation of the individual surface forces acting on each different surface patch \((A_\mathrm{total}\tau _\mathrm{total}=\sum _{i=1}^N A_i\tau _i)\), Bou-Zeid et al. (2004) developed an additional equation relating the blending height and the resultant equivalent surface roughness,

$$\begin{aligned} \frac{1}{\Big ( \mathrm {ln}\frac{h_\mathrm{b}}{z_{0,\mathrm{eqv}}}\Big )^2} = \sum _{i = 1}^N f_i \frac{1}{\Big ( \mathrm {ln}\frac{h_\mathrm{b}}{z_{0,i}}\Big )^2} \end{aligned}$$
(5)

with \(f_i=A_i/A_\mathrm{total}\). Combining both equations it is possible to determine implicitly the blending height \((h_\mathrm{b})\),

$$\begin{aligned} \Big (\frac{h_\mathrm{b}}{1.7\kappa L_\mathrm{p} + h_\mathrm{b}}\Big )^2 = \sum _{i = 1}^N f_i \frac{1}{\Big ( \mathrm {ln}\frac{h_\mathrm{b}}{z_{0,i}}\Big )^2}, \end{aligned}$$
(6)

and the equivalent surface roughness \((z_{0.eqv})\),

$$\begin{aligned} z_{0,\mathrm{eqv}} = h_\mathrm{b} \mathrm {\,exp} \Big [-\frac{1.7 \kappa L_\mathrm{p}}{h_\mathrm{b}} -1\Big ]. \end{aligned}$$
(7)

These two analytical formulations are extensively used in the present work, and its fundamental basis is further exploited for determining the blending height when a large array of wind turbines is installed over a heterogeneous surface. Also, it is important to note that for the present purposes \(L_\mathrm{p}\) is interpreted as \(L_x/2\), following Bou-Zeid et al. (2007). Finer details of the mathematical development and physical reasoning behind the presented formulation can be found in Bou-Zeid et al. (2004; 2007).

2.2 The Wind-Turbine-Array Boundary Layer

Because the turbulent flow over a patch of canopy can be considered statistically fully developed when the patch’s horizontal extent \((L_\mathrm{p})\) is much larger than the height of the elements present in the patch \((h),\,L_\mathrm{p} \gg 10h\) (Albertson and Parlange 1999b), the flow in current large wind farms can be considered to approach a statistically fully-developed regime. Therefore it is possible to define a wind-turbine-array boundary layer (WTABL) in which the flow is fully developed. This concept was first introduced by Frandsen (1992), where it was theoretically hypothesized that the fully-developed flow found in the middle of a large cluster of wind turbines would have a mean velocity profile with a double logarithmic shape. It was considered that under neutral conditions, the flow would develop a logarithmic profile beneath the wind turbine rotor disk characterized by the ground surface roughness \((z_{0,\mathrm{lo}}),\,\overline{u}(z)/u_{*,\mathrm{lo}} = (1/\kappa )\,\hbox {ln}(z/z_{0,\mathrm{lo}})\), and the flow above the wind turbines would develop a second logarithmic profile driven by the geostrophic forcing of the upper boundary layer, \(\overline{u}(z)/u_{*,\mathrm{hi}}=(1/\kappa )\,\hbox {ln}(z/z_{0,\mathrm{hi}})\). In addition, by imposing the continuity of these two logarithmic profiles at the wind turbine hub-height \((z_h)\), Frandsen (1992) deduced the induced surface roughness \((z_{0,\mathrm{hi}})\) that the airflow above the farm would reflect. Where \(u_{*,\mathrm{lo}}\) and \(u_{*,\mathrm{hi}}\) are not ‘proper’ friction velocities per se, but velocity scales related to the square root of the negative shear stress beneath \((u_{*,\mathrm{lo}}=\sqrt{-\tau _{(z_{h}-D/2)}})\) and above the wind turbines (\(u_{*,\mathrm{hi}} = \sqrt{-\tau _{(z_{h} + D/2)}}\), with \(D\) the wind turbine’s rotor diameter). This new characteristic surface roughness made it possible to parametrize the overall effect of the wind turbines and ground surface on the boundary-layer flow above the turbines. It has been proven invaluable in parametrizing large wind farms in atmospheric mesoscale models. This concept was later extended by means of a detailed LES study that showed that the continuity of both logarithmic profiles did not occur directly at hub-height, but through the existence of a connecting ‘buffer’ layer at the turbine rotor height (Calaf et al. 2010; Meneveau 2012). As a result, a new \(z_{0,\mathrm{hi}}\) parametrization was deduced, such that

$$\begin{aligned} z_{0,\mathrm{hi}} = z_{h} \left( 1+\frac{D}{2z_h}\right) ^{\beta } \mathrm {\exp }\Bigg (- \left[ \frac{c_\mathrm{{ft}}}{2\kappa ^2} + \left( \mathrm {ln} \left[ \frac{z_h}{z_{0,\mathrm{lo}}}\left( 1-\frac{D}{2z_h}\right) ^{\beta } \right] \right) ^{-2} \right] ^{-1/2} \Bigg ), \end{aligned}$$
(8)

where the exponent \(\beta =\nu _\mathrm{w}^*/(1+\nu _\mathrm{w}^*)\) was introduced to simplify the notation and where \(\nu ^*_\mathrm{w}\) defines an additional wake eddy viscosity, which is to a first approximation parametrized as a function of the overall wind-farm loading,

$$\begin{aligned} \nu ^*_\mathrm{w} = \nu _\mathrm{w}/(\kappa u_* z) \sim \sqrt{\frac{1}{2}c_\mathrm{ft}} \langle \overline{u}(z_h) \rangle D / (\kappa u_* z_h) \sim 28 \sqrt{\frac{1}{2}c_\mathrm{ft}}. \end{aligned}$$
(9)

Here \(c_\mathrm{ft}\) is expressed as \(c_\mathrm{ft}={\pi C_\mathrm{T}}/{(4 s_x s_y)}\), with \(C_\mathrm{T}\) being the wind-turbine thrust coefficient, \(s_x\) and \(s_y\) the corresponding turbine spacing, and \(z_h\) the turbine hub-height. This induced surface roughness (Eq. 8) is used in the present paper, and thus its expression has been presented here for the sake of completeness. For further details on the theoretical basis and mathematical development see Calaf et al. (2010).

For the sake of clarity, Table 1 presents a summary of the notation used for the various surface roughnesses appearing hereafter.

Table 1 Summary of the notation used for the different surface roughnesses appearing in this work
Full size table

3 The LES and the Wind-Turbine Model

3.1 The LES: Equations and Boundary Conditions

A pressure-gradient driven three-dimensional inviscid and incompressible flow field is mathematically represented by the LES filtered Navier–Stokes equation,

$$\begin{aligned} \partial _\mathrm{t} \tilde{u}_i + \partial _j(\tilde{u}_i\tilde{u}_j) = -\partial _i p^* -\partial _j \tau _{ij} + \delta _{i1}f_1 -\delta _{i1}\,\partial _1p_{\infty }/\rho , \end{aligned}$$
(10)

together with the constraint of conservation of mass,

$$\begin{aligned} \partial _i \tilde{u}_i = 0. \end{aligned}$$
(11)

Because we are interested in numerically reproducing an atmospheric flow field, where the Reynolds number is very high, the molecular viscous effects are neglected in the previous equations. Here \(\tilde{u}_i\) represents the implicitly filtered three-dimensional flow field component, \(\partial _1 p_{\infty }/\rho \) is the imposed constant pressure gradient, and \(p^*\) is the filtered corrected pressure term to which the trace of the subgrid-scale (SGS) stress tensor has been added, \(p^*=\tilde{p}/\rho +\tau _{ii}/3-p_{\infty }/\rho \). The resultant trace-free SGS stress tensor, \(\tau _{ij}\), which represents the explicitly unresolved turbulent structures due to grid resolution, is modelled here with the Lagrangian scale-dependent model of Bou-Zeid et al. (2005). In addition, \(f_1\) represents the additional force per unit mass exerted by the wind turbines in the streamwise direction of the flow field. The force is locally applied at the wind-turbine locations, see Sect. 3.2 for further details.

Following Moeng (1984) and Albertson and Parlange (1999b) the equations are solved by means of a pseudo-spectral discretization using a staggered grid in the vertical direction, with Fourier-based spectral methods used in the horizontal directions and second-order finite differences in the vertical. Time is integrated with a second-order Adams-Bashforth scheme. Further, the non-linear terms in the momentum and scalar equations are de-aliased with the 3/2 rule (Canuto et al. 1988). The code is decomposed into horizontal slices and parallelized with the Message Passing Interface (MPI, Frigo and Johnson 2005).

Due to the horizontal spectral scheme, the flow field is periodic in the horizontal direction, eliminating the need for lateral boundary conditions, and making the physical domain horizontally infinite in a practical sense. In the vertical direction, a zero vertical velocity together with a zero shear stress is imposed at the top (\(z=H\), where \(H\) is the height of the numerical domain as well as the height of the neutrally stratified boundary layer).

For the bottom boundary, the non-slip condition is imposed for the vertical velocity component, while the horizontal components have no formal non-slip condition due to the staggered grid. Additionally, a value for the near-wall limit of the subgrid stress tensor is needed at the first grid point of the staggered grid (at \(z_1=\Delta z/2\)), which is computed with a locally-averaged version of Monin–Obukhov (MO) similarity theory (Bou-Zeid et al. 2005),

$$\begin{aligned} \tau _{i,3} (x,y,z_1)= -\left[ \frac{k\sqrt{\left( {\hat{\tilde{u}}}_1^2 + {\hat{\tilde{u}}}_2^2\right) }}{\mathrm {ln} \, (z_1/z_{0,\mathrm{lo}})} \right] ^2 \, n_i, \end{aligned}$$
(12)

where \({\hat{\tilde{u}}}_i\) represents the double filtered (at \(2\Delta \) grid spacing) horizontal components of the flow. This is equivalent to a local average, see Bou-Zeid et al. (2005), and Hultmark et al. (2013) for further details in this filtering. Further, sub-index i is the direction of interest in the plane parallel to the surface (1 or 2) with \(n_i={\hat{\tilde{u}}}_i/ \sqrt{{\hat{\tilde{u}}}_1^2+{\hat{\tilde{u}}}_2^2}\) representing a unitary direction vector. The velocities are evaluated at \(z_1=\Delta z/2\) given the staggered grid, and the surface roughness (\(z_{0,\mathrm{lo}}\), where lo stands for low, see Sect. 2) is set equal to \(10^{-4}H\) or \(10^{-6}H\), depending on the study case (presented later). The vertical derivatives of the horizontal components of the filtered velocity field are also needed for the subgrid stress model and for computing the convective term at the first grid point above the wall. Following Moeng (1984) the gradients are inferred from MO theory at the first staggered grid point, namely

$$\begin{aligned} \partial _3{\tilde{u}}_i (x,y,z_1)= \Bigg (\frac{\sqrt{\tau }}{\kappa z}\Bigg )n_i \end{aligned}$$
(13)

with \(\tau =\sqrt{\tau _{1,3}^2+\tau _{2,3}^2}\). The scalar transport is modelled as an extra advection-diffusion equation. Similar to Calaf et al. (2011) this transport process is considered passive, that is, buoyancy effects are neglected,

$$\begin{aligned} \partial _\mathrm{t} \tilde{s} + \tilde{u}_i \partial _i \tilde{s} = -\partial _i \pi _j. \end{aligned}$$
(14)

Here \(\tilde{s}\) represents the filtered passive scalar, and \(\pi _j\) the SGS flux term of the scalar field \(\pi _j=\widetilde{S_ju_j}-\widetilde{S}_j\widetilde{u}_j\). Mirroring the approach taken for the momentum equations, \(\pi _j\) is parametrized in a similar dynamic fashion to the SGS stress (see Calaf et al. 2011 for reference). Similar to the momentum equation, here the molecular diffusive effects are neglected. A zero flux condition is imposed at the upper boundary, while the bottom boundary is once again prescribed at the surface using the scalar difference between the surface and the first grid point of the staggered grid with MO similarity theory,

$$\begin{aligned} q_\mathrm{s} (x,y,z_1)= \frac{ \kappa ^2 [s_0 - \tilde{s}(x,y,z_1)] \Big ( \sqrt{ \hat{\tilde{u}}_1^2 + \hat{\tilde{u}}_2^2} \Big ) }{\mathrm {ln} \Big ( \frac{z_1}{z_{0,\mathrm{lo}}}\Big ) \mathrm {ln} \Big ( \frac{z_1}{z_{0,s}}.\Big )}. \end{aligned}$$
(15)

Ideally one would couple a land-surface model to the LES model to properly solve for the surface scalar concentration and the corresponding scalar flux. However, for the sake of simplicity and numerical resources available, a fixed surface scalar concentration \((s_0)\) is alternatively imposed. This is a reasonable approximation if one is only interested in studying the induced changes in the scalar flux. Additionally, a scalar surface roughness \(z_{0,s}\) taken to be \(z_{0,\mathrm{lo}}/10\), is also imposed. The scalar field is initialized with a vertical logarithmic concentration such that the first grid point above the ground has a smaller scalar value than that imposed at the surface.

Here, the flow is driven by an imposed horizontal pressure gradient, with no Coriolis turning effects, such that the main flow is always aligned in the streamwise direction, perpendicular to the wind farm. This has become a standard approach in LES of flow over wind turbines, and it has been used in previous studies such as Calaf et al. (2010, 2011), Lu and Porte-Agel (2011) and Wu and Porte-Agel (2011). The imposed pressure gradient \(\partial _1 p_{\infty }/\rho \) defines an equivalent friction velocity such that \(u_{*,\mathrm{hi}}^{2} = H\partial _1 p_{\infty }/\rho \), which can be related to an external geostrophic wind,

$$\begin{aligned} u_\mathrm{G} = \frac{u_{*,\mathrm{hi}}}{\kappa } \Bigg [ \mathrm {ln}\Bigg (Ro_h\frac{z_h}{z_{0,\mathrm{hi}}}\Bigg ) - C_* \Bigg ], \end{aligned}$$
(16)

where \(C_*\) is an empirical value determined previously (Frandsen et al. 2006) and is found to be equal to 4. The hub-height Rossby number is here defined as \(Ro_h = u_\mathrm{G}/fz_h\), and here, a fixed value of \(Ro_h\) = 1,000 is used corresponding to an imposed geostrophic wind of \(10\,\hbox {m}\,\hbox {s}^{-1}\), a mid-latitude frequency of \(f = 10^{-4}\) s\(^{-1}\) and a wind-turbine hub height, \(z_h = 100\) m. The wind-farm induced surface roughness \((z_{0,\mathrm{hi}})\) is wind-farm dependent, and changes according to the wind-farm configuration as shown earlier in Sect. 2. Here, \(u_{*,\mathrm{hi}}\) is the wind-farm induced friction velocity above the wind-turbine rotor height (also described in Sect. 2). Thus, for a fixed pressure gradient (or equivalently, \(u_{*,\mathrm{hi}}\)) the induced surface roughness (see Eq. 8) changes according to the wind-farm configuration, and the ratio \(u_{*,\mathrm{hi}}/u_\mathrm{G}\) also varies accordingly. Therefore, one must properly normalize results with the global and common external driving mechanism, in this case \(u_\mathrm{G}\). Further, the scalar concentration results will be properly normalized with the total scalar concentration difference between the ground surface \(s_0\), and the top of the atmospheric boundary layer (ABL), \(s_{\infty } = s(H)\). The scalar flux is therefore normalized with the above mentioned total scalar difference between the surface and the top of the ABL multiplied by the driving geostrophic forcing \((q/(s_0-s_{\infty })u_\mathrm{G})\). Given that both the scalar flux and the scalar concentration vary with time and at different rates according to the enhanced mixing by the wind-farm configurations and terrain roughness set-up, it is convenient to normalize the results with the total scalar difference concentration in the ABL, since this drives the overall scalar flux. It is relevant to remark here that \(s_{\infty }\) varies slowly in time.

3.2 The Wind-Farm Model

It has become standard in LES of large wind farms (Wu and Porte-Agel 2011; Lu and Porte-Agel 2011; Yang et al. 2012), to model wind turbines with an actuator (drag) disk model. This has been shown to be an appropiate approximation if one is not interested in the near wake region (first diameter downstream of the wind-turbine rotor disk) (Wu and Porte-Agel 2011). The standard drag disk model is written as,

$$\begin{aligned} f_1 = -\frac{1}{2}\rho C_\mathrm{t}\, A\,u_{\infty }^2, \end{aligned}$$
(17)

which corresponds to a standard drag force model in the streamwise direction. Here \(A\) is the frontal area of the wind turbine rotor, \(A = \pi D^2/4,\,C_\mathrm{t}\) is the thrust coefficient, and \(u_{\infty }\) is the unperturbed incoming wind velocity at hub height. The thrust coefficient \((C_\mathrm{t}=4a(1-a))\) represents the normalized force on the actuator disk caused by the pressure drop taking place in a wind turbine, where \(a\) is the so-called induction factor that is variable, with a maximum value of \(1/3\) at the so-called Betz limit (Burton et al. 2001). Because we are interested in modelling a full wind farm, it is not possible to define an upstream unperturbed incoming flow field \((u_{\infty })\), and so a local velocity at the rotor disk \((u_\mathrm{d})\) is used. This velocity is nonetheless related to the unperturbed velocity by means of the actuator-disk theory, \(u_\mathrm{d}=(1-a)u_{\infty }\). Further, a rotor-disk plane average velocity \((\langle u_\mathrm{d} \rangle )\) is used to avoid spurious fluctuations of the drag force on a single wind turbine. Therefore, the implemented thrust force per unit mass at a given position takes the form

$$\begin{aligned} f_1(x_i,y_j,z_k) = \frac{1}{2}C_\mathrm{t}' \langle u_\mathrm{d} \rangle ^2\frac{\gamma _{j,k}}{\Delta _x}, \end{aligned}$$
(18)

where, \(C_\mathrm{t}'\) is a modified thrust coefficient, \(C_\mathrm{t}^{\prime }=C_\mathrm{t}/(1-a)^2\) resultant of using the incoming velocity at the disk \((u_\mathrm{d})\), and \(\gamma _{j,k}\) is the fraction of overlap area between the wind-turbine rotor and each grid point \((j,k)\). Therefore, for a grid point completely inside the wind-turbine rotor area, \(\gamma _{j,k} = 1\), and for one that it is completely outside, \(\gamma _{j,k} = 0\). For those grid points in between, the appropriate fraction of overlap area is computed.

3.3 Study Cases

Our main purpose is to elucidate the coupled influences of large wind farms and a variable land surface on transport processes. For this reason, study cases have been constructed by varying the thrust coefficients of the wind turbines, thereby increasing or decreasing the actual loading of the wind farm, and by considering several degrees of surface heterogeneity, by adjusting surface-patch lengths. The thrust coefficient has been varied from a very lightly loaded wind-farm case \((C_\mathrm{t}' = 0.6)\), to a case matching the Betz limit \((C_\mathrm{t}' = 2)\). The surface heterogeneity is represented by a successive change in the equivalent surface roughness across the simulation domain. This is achieved by changing the respective sizes of the two surface patches, into which the domain surface is divided, with corresponding different surface roughness. The rough patch is assigned a surface roughness \(z_{0,\mathrm{lo}_\mathrm{r}}/H = 10^{-4}\), and the smooth patch \(z_{0,\mathrm{lo}_\mathrm{s}}/H = 10^{-6}\). The corresponding patch lengths (\(L_\mathrm{r}\) and \(L_\mathrm{s}\)) are also varied. The length of the rough patch \((L_\mathrm{r})\) varies from \(L_x/4\) up to the full domain length \((L_x)\) by increments of \(L_x/4\), and the length of the smooth patch varies inversely. In the cross-stream direction, the patch lengths are kept constant and match the full width of the numerical domain, \(L_y\). A set of three additional simulations with uniform surface roughness with a value equivalent to the corresponding overall respective patchy configurations \((z_0^{homog}=z_{0,\mathrm{eqv}}^{patch})\), and identical wind-farm configuration, have also been considered to better explore the effect of the actual patches. Table 2 summarizes the 15 different study cases containing a wind farm, organized by common changing elements. Table 3 summarizes the four different study cases without wind turbines.

Table 2 Synthesis of the 15 different study cases with wind turbines. The first block consists of cases with a uniform surface and changing wind-turbine loading. The second block maintains the wind-turbine loading constant, and different surface patch lengths are implemented. The third block has the same wind-farm configuration as the second, but with a uniform surface roughness of value equal to the overall equivalent surface roughness of the second block cases. In the last block, the wind-turbine loadings are again changed and the surface patch lengths remain constant: half rough \(-\) half smooth
Full size table
Table 3 Synthesis of the four different study cases without wind turbines
Full size table

The additional physical parameters describing either the numerical domain or the wind-farm configuration have been prescribed as constants. The wind turbines considered in this study have a hub-height \(z_h/D=1\), where \(D\) is the wind-turbine diameter, taken here to be \(100\,\hbox {m}\). Further, the wind-turbine spacing \((s_x,s_y)\) is also kept constant over all study cases, with \(s_x/D=7.85\), and \(s_y/D=s_x/1.5\), which are typical values (Yang et al. 2012). The numerical domain has the following normalized dimensions \(L_x,L_y,L_z=(\pi ,\pi ,1)\), and it is uniformly distributed over \(N_x,N_y,N_z=(128,128,128)\) grid points. Here, the height of the ABL, \(H\) = 1,000 m, is the normalizing length scale. Simulations were run for 800 non-dimensional time units \(t^{*}=t/(H/u_\mathrm{G})\), and results were time averaged over the last 200 non-dimensional time units.

4 Numerical Results and Analytical Analysis

4.1 How does Surface Roughness Variability Affect the Scalar Flux?

In Bou-Zeid et al. (2004) and Albertson and Parlange (1999a), the impact of surface heterogeneities on the scalar flux close to the ground was studied in detail. In this section, the potential relationship between the scalar flux and characteristic variables such as the equivalent surface roughness (\(z_{0,\mathrm{eqv}}\), see Sect. 2), the near-surface friction velocity \(u_{*,\mathrm{lo}}\), and the vertical gradients of the scalar concentration is explored using an eddy viscosity approach. The eddy viscosity approximation has been extensively used in problems related to turbulent boundary-layer flows, and it is recognized for its simplicity and reasonable accuracy.

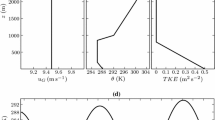
Here we use the eddy viscosity approach for the no wind-turbine case of flow over a heterogeneously rough surface as an illustrative example. Figure 1 presents the relationship between the characteristic variables (\(\overline{q}_\mathrm{s}\), \(z_{0,\mathrm{eqv}}\), \(u_{*,\mathrm{lo}}\) and \(\partial _z (s_0-\overline{s})\,\)) for the study cases \(s_1 - s_4\). The first (a), second (b) and third (c) plots show the increase of \(u_{*,\mathrm{lo}},\,q_\mathrm{s}^\mathrm{noWT}\) and \(\partial _z(s_0-s(z_1))\) (properly normalized) as a function of the equivalent surface roughness \((z_{{0,\mathrm eqv}})\). The presented variables used for the analysis have been horizontally averaged over the full numerical domain; however, the corresponding \(\langle \,\,\rangle _{xy}\) symbols have not been used to simplify the notation. From these three plots it can be observed that, while the surface scalar flux increases by about \(\approx \)56 %, the near-surface friction velocity increases by only \(\approx \)27 % and the scalar gradient near the surface increases by \(25\,\%\). If these changes are now explored in the context of the eddy viscosity, assuming that the average scalar flux close to the ground is in equilibrium with the averaged vertical gradient, the scalar flux can be expressed as,

$$\begin{aligned} \overline{q}_\mathrm{s}^\mathrm{noWT} = \nu _\mathrm{s} \frac{\partial (s_0 - \overline{s(z)})}{\partial z}, \end{aligned}$$
(19)
Fig. 1
figure 1

Surface friction velocity, surface scalar flux and scalar gradient near the surface for study cases \(s_1 - s_4\). Plots a, b, and c show the change in near-surface friction velocity, surface scalar flux and surface scalar gradient (correspondingly normalized) as a function of the normalized equivalent surface roughness \((z_{0,\mathrm{eqv}}/H)\). The lower plot shows the change in the surface scalar flux as a function of the surface friction velocity, illustrating the quasi-linear relationship between the surface flux and the surface friction velocity

Full size image

where \(\nu _\mathrm{s}\sim \kappa \,l \,u_{*,\mathrm{lo}}/Sc\) is proportional to \(u_{*,\mathrm{lo}}\) and a characteristic length scale \(l\), and inversely proportional to the Schmidt number. As a first approximation the Schmidt number has been assumed to remain constant, and thus removed from the analysis. The mixing length scale is assumed to weakly change with the varying surface configuration. This working hypothesis is reinforced by the fact that the blending is not very sensitive to changing surface characteristics. Therefore, the measured increase in the scalar flux could be explained by the change in the surface friction velocity and scalar gradient, \(\Delta q \sim \Delta u_{*,\mathrm{lo}} \Delta (\partial _z s)\), if the eddy viscosity approach is to hold. By substituting the above measured values, we obtain \(\Delta u_{*,\mathrm{lo}} \Delta (\partial _z s) \approx 59\,\%\), which is very close to the measured \(57\,\%\) scalar flux increase. This leads to the first relevant point, which is that the eddy viscosity approach seems to reproduce the measured changes in scalar flux between the different cases with changing surface conditions.

Finally, Fig. 1d shows an existing quasi-linear relationship between \(q_\mathrm{s}^\mathrm{noWT}/u_\mathrm{G}(s_0-s_{\infty })\) and \(u_{*,\mathrm{lo}}/u_\mathrm{G}\). It can be observed that the surface scalar flux increases quasi-linearly, with a slope \(\approx 2\), with the increase in friction velocity close to the surface. This constant slope is explained by the \(27\,\%\) increase in \(u_{*,\mathrm{lo}}\) compared to the \(57\,\%\) increase in \(q_\mathrm{s}^\mathrm{noWT}\) reported above.

4.2 The Wind-Turbine-Array Boundary Layer

The main goal is to analyze the effect that large wind farms might have on the scalar flux when built over a heterogeneously rough (or “patchy”) land surface. However, the change induced by large wind farms on the IBL resulting from the rough-to-smooth transition is investigated first. This phenomenon is clearly illustrated in Fig. 2, where the difference between the time- and cross-stream-averaged velocity with respect to the fully horizontal and time-averaged velocity, is presented in a \(``x-z\hbox {''}\) format. This representation allows a clear visualization of the extent of the IBL development due to the surface heterogeneities (see Fig. 2a). The flow above this IBL is well mixed, and the spatial differences smear out. The characteristic height at which this transition takes place is known as the blending height (\(h_\mathrm{b}\), see Albertson and Parlange 1999a and Bou-Zeid et al. 2004).

Fig. 2
figure 2

Difference of the time- and cross-stream-averaged velocity with respect to the fully horizontal and time-averaged velocity, \((\langle u\rangle _{y,t} - \langle u\rangle _{x,y,t})/u_\mathrm{G}\). The upper plot represents study case \(s_2\) and the lower represents the case with wind turbines \(s_2c\). In the lower plot, the black vertical lines represent the wind-turbine locations

Full size image

The upper plot in Fig. 2 corresponds to the \(s_2\) scenario with no-wind turbines present; the corresponding blending height is represented by the white line. Here, the blending height has been computed with Bou-Zeid et al. (2004)’s formulation presented in Eq. 6. The same surface variability scenario but with wind turbines \((s_2c)\) is presented in the lower plot of Fig. 2. In this case the wind-turbine wakes have a clear influence on the IBL development. Once the IBL is fully perturbed by the wind turbine wakes, it is subsequently entrained into a larger boundary layer, the so-called wind-turbine-array boundary layer (WTABL, see Calaf et al. 2010). The height of this new WTABL can be approximated analytically (see Sect. 4.2.1), and it is also represented in the lower plot with a white line. The analytical expression for the blending height in the presence of wind turbines is developed below.

4.2.1 The Induced WTABL Height: An Analytical Approach

A similar approach to that used by Bou-Zeid et al. (2004) for analytically describing the blending height above a heterogeneous surface, will be used. However, heterogeneities are now induced by the surface and a large array of wind turbines. Initially, it can be assumed that the downstream development of the WTABL is related to an upward or vertical diffusion velocity \((w_\mathrm{rms})\) and a driving streamwise convective velocity component \((\langle u_\mathrm{WTABL}\rangle )\) such that,

$$\begin{aligned} \frac{\text {d}\delta _\mathrm{WTABL}}{\text {d}x} \sim \frac{w_\mathrm{rms}}{\langle u_\mathrm{WTABL}\rangle }, \end{aligned}$$
(20)

where \(\delta _\mathrm{WTABL}\) is the WTABL height. By assuming that \(w_\mathrm{rms} \sim Cu_{*,\mathrm{hi}}\), where \(C\) is an adjustable proportionality constant taken here as 0.95 (as in Bou-Zeid et al. 2004), and \(u_{*,\mathrm{hi}}\) is the friction velocity above the wind-turbine rotor disk, together with \(\langle u_\mathrm{WTABL}\rangle =(u_{*,\mathrm{hi}}/\kappa )\hbox {ln}\Big (\frac{z}{z_{0,\mathrm{hi}}}\Big )\), Eq. 20 can be rewritten as,

$$\begin{aligned} \frac{\text {d}\delta _\mathrm{WFABL}}{\text {d}x} \sim C\frac{\kappa }{{\mathrm {ln}}\displaystyle \left( \frac{z}{z_{0,\mathrm{hi}}}\right) }. \end{aligned}$$
(21)

This can now be integrated between \(z_{0,\mathrm{hi}}\) and \(\delta _\mathrm{WTABL}\) in the vertical direction, and between zero and \(x\), in the streamwise direction, where \(x\) is the downstream distance in which the WTABL develops. Therefore,

$$\begin{aligned} \frac{\delta _\mathrm{WTABL}}{z_{0,\mathrm{hi}}}\Bigg [\mathrm {ln}\Bigg (\frac{\delta _\mathrm{WTABL}}{z_{0,\mathrm{hi}}}\Bigg ) -1\Bigg ] +1= \frac{\kappa \,C\,x}{z_{0,\mathrm{hi}}} \end{aligned}$$
(22)

and because \(\frac{\delta _\mathrm{WTABL}}{z_{0,\mathrm{hi}}} \gg 1\) it can be further simplified to

$$\begin{aligned} \delta _\mathrm{WTABL}\Bigg [\mathrm {ln}\Bigg (\frac{\delta _\mathrm{WTABL}}{z_{0,\mathrm{hi}}}\Bigg ) -1\Bigg ] = \kappa \,C\,x. \end{aligned}$$
(23)

In this equation, \(\delta _\mathrm{WTABL}\) is the unknown for which an analytical expression is sought, \(z_{0,\mathrm{hi}}\) is the induced WTABL surface roughness and for which the formulation of Calaf et al. (2010) introduced in Sect. 2 is used. By substituting the downstream distance beyond which the WTABL ceases to grow vertically, it can be assumed that the WTABL has reached the corresponding blending height. Above the blending height, the flow is fully developed, and spatial differences tend to smear out. This downstream distance, although having an a priori unknown value, can be extracted indirectly and in an approximate manner by using the power deficit curves of well-known large wind farms, such as Horns Rev in Denmark (Barthelemie et al. 2007). Considering the case of Barthelemie et al. (2007), where the mean flow is oriented perpendicular to the wind turbines, coinciding with a wind-turbine separation similar to the present work, it can be extracted that the decay in the power deficit after the fifth wind-turbine row is greatly diminished. This means that, by \(x\approx 5\,s_x\), the WTABL is developed or close to developed in the vertical direction. Therefore, upon substitution and rearrangement of Eq. 23, the final expression for the WTABL blending height can be approximated as follows,

$$\begin{aligned} \frac{h_\mathrm{b}^\mathrm{WTABL}}{D} = \frac{\kappa \,C^*}{\Bigg [\mathrm {ln}\Bigg (\frac{h_\mathrm{b}^\mathrm{WTABL}}{z_{0,\mathrm{hi}}}\Bigg ) -1\Bigg ]}. \end{aligned}$$
(24)

Here \(h_\mathrm{b}^\mathrm{WTABL}\) represents the blending height in the presence of wind turbines and \(C^*\) is a new parameter defined as \(C^* \approx 5 \,C\, s_x/D\). Interestingly, the WTABL blending height mainly depends on the spatial geometry of the wind farm, its loading and the surface heterogeneity, embedded through \(z_{0,\mathrm{hi}}\).

The performance of this new analytical approach for computing the blending height in a WTABL can be assessed with vertical profiles of the horizontal standard deviation of time-averaged variables (generically represented as \(\Delta A\)). This provides a measure of the spatial variability of the variable as a function of height (Albertson and Parlange 1999a). The blending height is determined as the height at which the induced variability first tends to zero. If \(\langle \overline{A(x,z)}\rangle _y\) is the time (indicated by the overline) and cross-stream average (indicated by \(\langle \,\,\rangle _y\)) of a given variable, the horizontal standard deviation of the time-averaged variable is defined as,

$$\begin{aligned} \Delta A = \Bigg (\frac{1}{L_x}\int \Bigg [\langle \overline{A(x,z)}\rangle _y - \langle \overline{A(z)}\rangle _{xy}\Bigg ]^2 \text {d}x\Bigg )^{1/2}, \end{aligned}$$
(25)

with \( \langle \overline{A(z)}\rangle _{xy} = \frac{1}{L_x}\int {\langle \overline{A(x,z)}\rangle _y \text {d}x}\) the fully horizontally and time-averaged value of the specific ‘\(A\)’ variable. Therefore, by applying this to the velocity field, its vertical derivatives and the momentum and scalar flux, it is possible to qualitatively assess the wellness of Eq. 24. An example of the horizontal standard deviation of the time averages is presented in Fig. 3, for case \(s_{2}c\). The horizontal solid line represents the theoretical blending height computed with Eq. 24. The wind-turbine case results are represented by the vertical solid lines, and the no-wind turbine scenario with the dashed lines. It is worth mentioning that there is no standard approach for extracting the blending height from the LES data, and published techniques remain rather imprecise. Here, it has been extracted from the vertical profiles of the horizontal standard deviation of the shear stress, time-averaged \((\Delta \tau _{xz})\), taking the first point where the vertical variability tends to zero. Plotting the positive and negative sign of the standard deviation helps to identify the characteristic height. Given the current limitations, it can be observed that Eq. 24 predicts reasonably well the \(h_\mathrm{b}^\mathrm{WTABL}\), represented in Fig. 3, as the first point where the vertical variability tends to zero. At this characteristic height, the spatial differences induced by the surface heterogeneity and the wind turbines have vanished, and the effect of wind turbines is negligible from this height upwards.

Fig. 3
figure 3

Study case \(s_2c\) in solid lines and \(s_2\) in dashed lines. Vertical profiles of the horizontal standard deviation \((\pm )\) of time-averaged velocity field, its vertical derivatives and the momentum and scalar flux. The horizontal solid line represents the theoretical blending height

Full size image

4.2.2 Dependence of the \(h_\mathrm{b}^\mathrm{WTABL}\) on the Wind Farm Loading and the Surface Heterogeneity

A large wind farm placed over a heterogeneous surface entangles the surface IBL induced by the surface variability. As a result a new complex mixed boundary layer is developed with new characteristics. The goal of this section is to shed light on the relationship between the WTABL created above the wind turbines, the original surface IBL created by the surface complexity, and their joint response to changes in the wind-farm loading and surface patchiness.

Figure 4 presents three plots of the blending height as a function of the equivalent induced wind-farm surface roughness, \(z_{0,\mathrm{hi}}\). The upper plot presents LES data for cases \(s_1c\) to \(s_4c\), where the ratio of the rough patch length with respect to the smooth patch length \((L_\mathrm{r}/L_\mathrm{s})\) was varied. Correspondingly, \(z_{0,\mathrm{hi}}\) increases as a function of the rough patch length, because of the overall increase in \(z_{0,\mathrm{eqv}}\). It is interesting to note that the blending height increases as a function of \(z_{0,\mathrm{hi}}\) (or equivalently \(z_{0,\mathrm{eqv}}\)) up to the threshold where there exists only a single patch, and therefore there is no IBL induced by the patch transitions. This result suggests that the shallow boundary layer developed as a consequence of the surface heterogeneity might entangle in the larger WTABL inducing a change in the overall resultant boundary layer (this point is further explored below). With respect to Fig. 4a, while it would have been clearer to present the results directly as a function of \(z_{0,\mathrm{eqv}}\) instead of \(z_{0,\mathrm{hi}}\), we have presented the results this way so the plots can be compared with Fig. 4b, for which \(z_{0,\mathrm{eqv}}\) is constant and \(z_{0,\mathrm{hi}}\) varies because of changes in the effective turbine thrust coefficient. Figure 4b presents similar blending-height measurements for cases \(s_4a\) to \(s_4e\), where the surface roughness is homogeneous over the entire domain (hence with equal \(z_{0,\mathrm{eqv}}\)), and just the wind-turbine thrust coefficients are varied. In this case, it can be observed that the WTABL grows quasi-linearly with increasing thrust coefficient up to a certain threshold, where it appears to saturate. Finally, the new WTABL blending-height model is compared to the LES results (Fig. 4c), where we observe that the model tends to underestimate the blending height in the LES data by almost \(20\,\%\). However, the model captures the growing trend for the blending height as a function of \(z_{0,\mathrm{hi}}\) fairly well, except for the saturation regions. The discrepancies of the model can be due to its high dependency on the downstream distance at which the WTABL is considered to be developed \((x\sim 5s_x)\), which still remains a rather imprecise measure. In addition, the lack of precision in the technique used to extract the boundary-layer height from the LES data could also explain some of the discrepancies. It is nonetheless relevant to note the overall growing trend of the WTABL height as a function of increasing thrust coefficient and as a function of the overall equivalent surface roughness.

Fig. 4
figure 4

Study cases \(s_1c-s_4c\) (upper plot), cases \(s_4a-s_4e\) (middle plot), and all cases together in the lower plot. The upper and middle plot present blending heights as a function of the equivalent induced wind-farm surface roughness, and the lower plot compares the analytical WTABL height with the LES data also as a function of \(z_{0,\mathrm{hi}}\), which has been computed using Eq. 8

Full size image

Figure 5 provides a more detailed view of the changes induced by the IBL developed by the flow over patches with different surface roughnesses. The vertical profiles of the horizontal standard deviation earlier presented in Fig. 3 for the wind-turbine cases are presented again as a dot-dashed line, so they can be compared to the vertical profiles of the same corresponding standard deviations for the set of simulations \(s_1c^\mathrm{eqv}-s_3c^\mathrm{eqv}\). These last simulations are configured with a homogeneous surface roughness with value equal to the equivalent overall roughness from the patchy cases \((s_1c - s_3c)\), meaning that \(z_0 = z_{0,\mathrm{eqv}}\). This last special set of simulations \((s_1c^\mathrm{eqv}-s_3c^\mathrm{eqv})\) produce the same surface drag to the flow as cases \(s_1c-s_3c\), with the difference that no IBL is developed because of the lack of patches. Therefore one can better explore the effect of the IBL on the overall development of the WTABL. From Fig. 5a–c it is observed that the effect of the IBL seems to be limited to the region beneath the wind-turbine rotor disk \((z/H = 0.05)\). Thus no changes are transmitted above the rotor disk region. However for the scalar flux case (Fig. 5d), it can be observed that differences extend further up the rotor disk, with larger horizontal variations propagating to \(z/H \approx 0.25\). Because the blending height was effectively extracted from the shear stress horizontal standard deviation, no changes can therefore be effectively measured. If the scalar flux profiles had been used, a slight change in the blending height induced by the actual presence of the surface patches would have been observed. In conclusion, it is observed that the IBL developed over the patch transitions has a very limited effect on the average WTABL blending height, if any. However, it does have an impact on the topology of the boundary layer developed, being mostly entangled and diffused through the turbine wake region. Also, as expected, the existence of actual patches induces a noticeable local effect on the spatial variability of the studied variables near the surface.

Fig. 5
figure 5

Vertical profiles of the horizontal standard deviation of time-averaged variables \(u,\,\partial _z u,\,\tau _{xz}\) and \(q\), for cases\(s_1c-s_4c\) (dot-dashed lines) and \(s_1c^\mathrm{eqv}-s_4c^\mathrm{eqv}\) (solid lines). The horizontal solid line represents the theoretical blending height

Full size image

4.3 How does A Wind Farm Change the Scalar Flux Over A Homogeneously Rough Surface? (Revisiting Results with an Eddy Viscosity Approach)

The change in scalar flux induced by the presence of wind turbines installed on a homogeneously rough surface was previously studied in Calaf et al. (2011) for the case of a passive scalar and by Roy and Traiteur (2010) and Lu and Porte-Agel (2011) for the specific case of sensible heat. In Calaf et al. (2011) it was shown how the scalar flux increases by an average value of \(10\,\%\) in the presence of wind turbines. Here, those results are revisited using a different approach that will further help assess the combined effect of surface variability and large wind farms on the scalar flux in Sect. 4.4. As a validation step, this new methodology is first applied for the known case of a wind farm on a homogeneously rough surface. Figure 6a presents the scalar flux ratio between the wind farm case and the non-wind farm scenario together with the friction velocity above the wind farm (b) and close to the surface (c) for cases \(s_4a\) to \(s_4e\), where the surface roughness is homogeneous. As in Calaf et al. (2011), the scalar flux increases with increasing thrust coefficient, peaks, and then begins to decrease. For the reduced number of cases presented here, the average increase of scalar flux is close to \(5\,\%\). It is interesting to note, however, that while the friction velocity above the wind turbines increases by \(19\,\%\), the friction velocity close to the surface decreases by about \(9\,\%\). The increase in shear above the wind turbines due to the increased drag within the turbine field considerably enhances overall mixing above the wind turbine rotors. Correspondingly, a decrease below the wind turbines induced by the reduction of wind speed close to the surface is also a consequence of the increasing thrust coefficient. These apparently contradictory results indicate that considering only \(u_{*,\mathrm{lo}},\,u_{*,\mathrm{hi}}\) and \(q_\mathrm{s}\), is insufficient, and thus additional variables are needed to fully explain the change in the scalar flux. The additional variables to be considered are the vertical gradient of the averaged scalar concentration \((\partial _z \,\overline{s(z)})\), the Schmidt number \((Sc)\) and the overall wind-farm-induced eddy diffusivity \((\nu _\mathrm{s}^\mathrm{WT})\). By invoking an equivalent eddy diffusivity approach, (see Sect. 4.1) the scalar flux can be written as proportional to the vertical gradient of the averaged scalar concentration, such that

$$\begin{aligned} q_\mathrm{s}^\mathrm{WT} = \nu _\mathrm{s}^\mathrm{WT}\,\frac{\partial (s_0 - \overline{s(z)})}{\partial z} = -\nu _\mathrm{s}^\mathrm{WT}\,\frac{\partial \overline{s(z)}}{\partial z}, \end{aligned}$$
(26)
Fig. 6
figure 6

Scalar flux ratio between the wind-farm case and the no-wind farm scenario for study cases \(s_4a-s_4e\). The friction velocity above the wind farm, and also beneath, near the surface

Full size image

where \(\nu _\mathrm{s}^\mathrm{WT}\) represents the wind turbine wake augmented eddy diffusivity. This can be further expressed as,

$$\begin{aligned} \nu _\mathrm{s}^\mathrm{WT} = \frac{\nu _m^\mathrm{WT}}{Sc} \sim \frac{1}{Sc}\Big (\kappa z u_* + \sqrt{\frac{c_\mathrm{ft}}{2}} \langle {\overline{u}}\rangle D\Big ) = \frac{\kappa z u_* }{Sc}\Big (1+ \nu _\mathrm{w}^* \Big ), \end{aligned}$$
(27)

with \(\nu _\mathrm{w}^*=(c_\mathrm{ft}/{2})^{1/2} \langle {\overline{u}}\rangle D/(\kappa l u_*)\) defining the augmented eddy viscosity induced by the wind farm. From vertical profiles of the scalar flux (see Fig. 7a) the wind-farm-induced change in the surface flux can be determined. For the specific \(s_4c\) case, shown in Fig. 7a, the scalar flux increases by a factor \(\approx 1.22\) just beneath the wind-turbine rotor disk height. This increase results from the increase in scalar eddy diffusivity by a factor \(\approx 1.8\) (Fig. 7b) and a small decrease in the scalar vertical gradient by a factor \(\approx 0.68\) (Fig. 7c). That is, there exists an internal balance between the vertical scalar gradients and the scalar eddy diffusivity in the presence of wind turbines, as one would expect. However, the question remains: how can the scalar eddy diffusivity increase by a factor \(\approx 1.8\) when the friction velocity \((u_{*,\mathrm{lo}})\) correspondingly decreases by a factor of 0.93 ? This divergence can be explained by a wake-augmented eddy viscosity and the effect of a non-constant Schmidt number, as suggested by Eq. 27. The existence of an augmented eddy viscosity (already considered in Calaf et al. 2010), can be directly assessed with the LES results. Figure 7d shows vertical profiles of the momentum flux, the eddy viscosity (e) and the vertical gradient of the mean velocity (f) for both scenarios: with and without wind turbines. Using the momentum-flux and eddy viscosity data, and considering that \(\nu _m \sim \kappa z u_* (1+ \nu _\mathrm{w}^* )\), one can extract a vertical profile for the wind-farm-augmented eddy viscosity \((\nu _\mathrm{w}^*)\). Thus, the additional factor \((1+\nu _\mathrm{w}^*)\) in Eq. 27 can be extracted and has an average value of 1.6 (averaged over the wind turbine rotor area). The augmented eddy viscosity is of greatest importance in the vicinity of the wind-turbine disk, which is an indication of the limited range of influence of the wind turbines. If the changes in Schmidt number are neglected as a first approximation, the increase of the eddy diffusivity by a factor of 1.8 can now be assessed,

$$\begin{aligned} 1.8 = \frac{\nu _\mathrm{s}^\mathrm{WT}}{\nu _\mathrm{s}}\Big |_{z_{h}-D/2} \sim \frac{\nu _m^\mathrm{WT}}{\nu _m}\Big |_{z_{h}-D/2} \sim \frac{k\,z\,u_{*,\mathrm{lo}}^\mathrm{WT}}{k\,z\,u_{*,\mathrm{lo}}}(1+\nu _\mathrm{w}^{*})= \frac{u_{*,\mathrm{lo}}^\mathrm{WT}}{u_{*,\mathrm{lo}}}(1+\nu _\mathrm{w}^{*}). \end{aligned}$$
(28)

Using specific values from the example \(s_4c\) case, \(u_{*,\mathrm{lo}}^\mathrm{WT} = 0.039u_\mathrm{G},\,u_{*,\mathrm{lo}} = 0.04u_\mathrm{G}\) and \((1+\nu _\mathrm{w}^*) = 1.61\), gives \(\nu _\mathrm{s}^\mathrm{WT}/\nu _\mathrm{s} = 1.57\), which is close to the earlier expected value (1.8) for the ratio of the eddy diffusivities \((\nu _\mathrm{s}^\mathrm{WT}/\nu _\mathrm{s})\). Therefore, it has been shown that, while the friction velocity beneath the wind-turbine disks is reduced when wind turbines are present, there exists an additional augmented eddy viscosity, \((\nu _\mathrm{w}^*)\) also induced by the wind turbines that opposes this trend and results in an overall increase of the scalar flux.

Fig. 7
figure 7

Vertical profiles of the scalar flux, the scalar eddy diffusivity, and the scalar vertical gradients together with the vertical momentum flux, the eddy viscosity and the mean velocity vertical gradients for study cases \(s_4c\) and \(s_4\). The case with wind turbines \((s_4c)\) is represented with line-hollow circles, the case without wind turbines \((s_4)\) with line-hollow squares

Full size image

4.4 How does a Wind Farm Change the Scalar Flux Over A Heterogeneously Rough Surface?

Here, the change in scalar flux induced by a wind farm installed over a heterogeneous landscape is studied. Figure 8 presents the normalized scalar flux, \(u_{*,\mathrm{lo}}\) and \(u_{*,\mathrm{hi}}\) for the cases where the surface roughness is composed of sequential rough-to-smooth patches and changes in the wind-farm loading are considered (meaning \(L_\mathrm{r}/L_\mathrm{s} = 1/2\), study cases \(s_2a\) to \(s_2e\)). Compare Figs. 8 to 6, the homogeneous surface case: now, the ratio of the scalar flux for the wind-turbine, no wind-turbine cases, increases without reaching a saturation region (see Fig. 8a). This can be explained by the fact that, given the existing patch transition, the ratio \(u_{*,\mathrm{hi}}/u_{*,\mathrm{lo}}\) increases by \(\approx \)5 %. This increase is induced by a larger increase in \(u_{*,\mathrm{hi}}\) (Fig. 8b) relative to \(u_{*,\mathrm{lo}}\) (Fig. 8c), which now has a weaker contribution induced by the overall reduction in surface roughness. The change in scalar flux has also been studied for the case with a fixed farm loading and a heterogeneous rough surface (study cases \(s_{1}c\) to \(s_4c\)). In this case, Fig. 9a shows a slight decrease in the ratio of scalar fluxes as the rough patch length \((L_\mathrm{r})\) is increased. This gentle decreasing tendency can be explained once more due to the ratio of variables \(u_{*,\mathrm{hi}}\) and \(u_{*,\mathrm{lo}}\), both presented in Fig. 9a, c, correspondingly. For these cases, \(u_{*,\mathrm{hi}}\) remains quasi-invariant, and \(u_{*,\mathrm{lo}}\) increases considerably. This result adds to the previous evidence that showed the effect of surface heterogeneity to be limited to heights below the turbine rotor disk. As shown earlier, the surface IBL induced by the surface patches is entangled with the WTABL, and its effect above the WTABL becomes limited. An interesting result from Fig. 9a is that, although the overall scalar flux slightly decreases as a function of the rough patch length (or \(z_{0,\mathrm{eqv}}\)), the scalar flux increases at a faster rate when no wind turbine is present for a given degree of surface heterogeneity. This result is better represented in Fig. 10, where the hollow circles represent the scalar flux for the wind-farm cases and the hollow squares for the cases without turbines. When no wind turbine is present, a small change in the surface roughness has a more noticeable impact on the atmospheric flow. In the presence of wind turbines, the atmospheric flow is perturbed, a WTABL develops, and the near-surface phenomena are isolated from the upper ABL. Thus, when wind turbines are present, changes in the land surface have a weaker effect over the large-scale atmospheric flow. Also the negative feedback of the wind turbines on the near-surface shear enhances this layering phenomenon. It is also remarkable that, for a heterogeneous surface with \(L_\mathrm{r}/L_\mathrm{s} \ge 3/4\), the overall scalar flux induced by the surface heterogeneity is equal to or larger than the scalar flux induced by the combination of a large wind farm and a surface heterogeneity with \(L_\mathrm{r}/L_\mathrm{s} = 1/4\). This implies that the impact of large wind farms is relatively limited when compared to the increase of scalar flux induced by changes in surface roughness alone.

Fig. 8
figure 8

Study cases \(s_2a-s_2e\). Scalar flux ratio between the wind-farm case and the no-wind-farm scenario, the friction velocity above the wind farm, and also near the surface

Full size image
Fig. 9
figure 9

Study cases \(s_1c-s_4c\). Scalar flux ratio between the wind-farm case and the no-wind-farm scenario, the friction velocity above the wind farm, and also near the surface. Here results are represented as a function of \(z_{0,\mathrm{eqv}}/H\) instead of \(c_\mathrm{ft}\), because all cases have the same \(c_\mathrm{ft}\) value

Full size image
Fig. 10
figure 10

Study cases \(s_1c - s_4c\). Scalar flux as a function of the equivalent surface roughness induced by the surface heterogeneity. Circles represent the case with wind turbines, and squares the case without

Full size image

Finally, to illustrate the effects of the surface patchiness, one can look at the evolution of the scalar flux at the first grid point (near the surface) as a function of the downstream distance (see Fig. 11) for the cases with and without wind turbines \((s_1c-s_4c)\). Here we can see the local effects of the patch transitions and the wind turbines. In Fig. 11, the smooth-to-rough transition for all cases occurs at \(x/h=0\), and the rough-to-smooth transition occurs at the apparent discontinuity in each line respectively. As expected, the largest fluxes occur at the smooth-to-rough transition. Here the wind-turbine cases have a proportionately larger surface flux. As the IBL develops and equilibrates with the rough surface condition, the absolute magnitude of the fluxes diminishes to a representative value for the rough surface. It appears that this equilibrium length scale is determined by the relative position of the smooth-to-rough transition and the actual wind turbines. Thus, by analogy with Brutsaert (1998) we can see that the presence of the wind turbines contributes to atmospheric mixing, and accelerates the local IBL equilibrium development. A similar, though less distinct trend, can be seen in the rough-to-smooth transition.

Fig. 11
figure 11

The normalized surface fluxes as a function of position for the patchy land surface (four cases) in the presence of (solid lines) and without (dashed lines) wind turbines. The \(x/H=0\) position corresponds to the smooth-rough transition position. Apparent is the length scale of the scalar flux associated with the surface roughness transitions

Full size image

5 Conclusion

Previous results of Calaf et al. (2011) have been revisited, and a new perspective on the flux increases beneath a wind turbine has been presented. An approximate analytical formulation for the WTABL has also been introduced, compared with LES data and found to yield satisfactory results. The change in the WTABL height as a function of the loading and the surface roughness heterogeneity was also analyzed. It has been shown that, although surface patches do not vary the blending height when determined using ‘momentum variables’, the internal structure of the surface layer is largely modified by being entangled in a deeper boundary layer induced by the wind turbines. It has also been shown that the equilibrium length scale characteristic of surface roughness transitions is determined by the relative position of the smooth-to-rough transition and the actual wind turbines. The reason is that wind turbines accelerate the local IBL equilibrium development.

Finally, it has been shown that, even though the scalar flux is increased in the presence of a large array of wind turbines over a heterogeneous surface with \(L_\mathrm{r}/L_\mathrm{s} = 1/4\), this increase is comparable to the increase induced by a variable surface with \(L_\mathrm{r}/L_\mathrm{s} \ge 3/4\) having no wind turbines. That is, the impact that large wind farms have over complex farmlands is of the same order of magnitude as that induced by increasing the farmland equivalent roughness. Past studies have shown that surface patchiness effects are weaker under stronger background wind conditions. Thus future work should also explore the link between external forcing and surface variability.