1 Introduction

The seismic design of structures has experienced significant advances during the last 30 years or so. One of the most important has been the introduction of the concept of performance-based seismic design (Bozorgnia and Bertero 2004) for designing a structure for various design levels, each one corresponding to a specific seismic intensity and specific performance requirements. These performance requirements are usually defined either deterministically in terms of structural and non-structural deformation and/or damage (Vision 2000; FEMA-356 2000) or probabilistically in terms of direct interests of various stakeholders, such as losses and casualties (Günay and Mosalam 2013; Žižmond and Dolšek 2019; O’Reilly and Calvi 2019).

Current seismic design codes for building structures, such as EC8 (2004), employ the force-based design (FBD) method, which uses forces as the main design parameters. This method performs design in two steps: the first step involves a strength checking, while the second one a displacement checking, usually accomplished iteratively. During the last 25 years or so, the displacement-based design (DBD) method has emerged as a viable alternative of the FBD method. The DBD uses displacements as the main design parameters and since displacements are more intimately related to damage than forces, can more effectively control damage. Besides, DBD requires only one step during the design process, i.e., a strength checking, because the displacement checking is automatically satisfied.

Among the most important proposed DBD methods, one can mention those of Moehle (1992), Panagiotakos and Fardis (1999, 2001), Chopra and Goel (2001), Priestley et al. (2007), Calvi and Sullivan (2008) and Sullivan et al. (2012). The DBD method of Priestley et al. (2007), Calvi and Sullivan (2008) and Sullivan et al. (2012), called the direct displacement-based design (DDBD) method, is the most well-known and highly developed seismic design method. Indeed, a whole book (Priestley et al. 2007), two model codes (Calvi and Sullivan 2008; Sullivan et al. 2012) and a large number of articles (Priestley 1993, 2000; Priestley and Kowalsky 2000; Sullivan et al. 2006, 2008; Priestley et al. 2008; Pennucci et al. 2009; Roldán et al. 2016; O’Reilly and Sullivan 2016) have been published on this method including works not only on reinforced concrete structures but on steel structures as well (Roldán et al. 2016; O’Reilly and Sullivan 2016). Comparisons of the DDBD method against other DBD methods (Sullivan et al. 2003) and the FBD method (Sullivan 2013) have been also published, revealing its advantages and limitations over the other methods.

The most important problem with the DDBD method is the replacement of the original nonlinear multi-degree-of-freedom (MDOF) structure by an equivalent linear single-degree-of-freedom (SDOF) structure in accordance with the substitute structure concept of Shibata and Sozen (1976). This replacement simplifies considerably the method at the expense of losing modeling accuracy as one goes from the MDOF system to the equivalent SDOF one. Thus, higher mode effects and P-Δ effects are lost because of this simplification, which is based on an assumed first mode displacement profile of the structure. These problems have been detected by the developers of the DDBD method and corrected later on in a rather artificial way by adding correction terms in the proposed expressions for the lateral displacement profile and the design base shear and its distribution to take into account P-Δ and higher mode effects (Calvi and Sullivan 2008; Sullivan et al. 2012).

In this work, an improved version of the DDBD method is presented, which takes into account in a rational manner all the aforementioned problems. In this approach, the original nonlinear MDOF structure is replaced by an equivalent linear MDOF structure with the same mass and elastic stiffness as the original structure with the aid of the deformation dependent equivalent modal damping ratios concept developed by the present authors in connection with the seismic design of steel and reinforced concrete (R/C) plane moment resisting frames (MRF) (Papagiannopoulos and Beskos 2010; Muho et al. 2020). The two MDOF systems are equivalent in the sense that the work of dissipation due to hysteretic forces in the nonlinear system is equal to the work of dissipation due to viscous forces in the linear system. Thus, this work equivalence concept can be thought of as an extension of that of Jacobsen (1930) from a SDOF system under harmonic excitation to a MDOF system under seismic excitation.

According to the theory of linear systems, the modulus of the transfer function versus frequency curve for a linear system with viscous damping is smooth with local maxima at the resonant frequencies, while it attains a distorted shape with many and no clearly visible peaks when the system becomes nonlinear. Thus, for a given nonlinear MDOF system under a seismic excitation, one has to feed it progressively with viscous damping until the modulus of its transfer function versus frequency curve becomes smooth. At that instant, the original MDOF nonlinear system has become an equivalent linear MDOF system with equivalent modal damping ratios.

During the employment of the proposed DDBD method, one determines from the displacement spectrum with high amounts of viscous damping the required modal periods for known values of the design modal displacements. From those modal periods the corresponding required modal stiffness and hence the modal base shears can be obtained. The final required base shear is obtained by a combination rule, like the SRSS rule. The aforementioned design modal displacements are obtained on the basis of target inter-storey drift ratios defined for every performance level and the first few modes significantly contributing to the structural response.

Thus, it is apparent that the proposed DDBD method aims to combine advantages and to eliminate or reduce disadvantages of both the FBD and the original DDBD method. More specifically, the proposed DDBD method (1) incorporates a displacement spectrum instead of an acceleration spectrum and thus better controls displacements and hence damage, (2) utilizes deformation and period dependent equivalent modal damping ratios to account for inelastic energy dissipation instead of the single constant behavior (or strength reduction) factor q (or R) adopted by the FBD method and thus, the deformation check of the FBD method is automatically satisfied; (3) replaces the original nonlinear MDOF structure by an equivalent linear MDOF structure instead of the substitute SDOF structure employed by the original DDBD method and thus, takes more rationally and with higher accuracy into account the higher mode and P-Δ effects than the original DDBD method. However, because the proposed DDBD method requires modal information of the structure, it is apparent that in contrast to the original DDBD, the proposed DDBD method requires a numerical model for modal analysis.

Closing this introduction, it should be mentioned here that while this method focuses on displacements, simplified verification methods like the recently proposed in O’Reilly and Calvi (2020) could be implemented in future work. Numerical examples involving the seismic design of five and sixteen storey R/C MRFs are presented for illustration purposes. The merits of the proposed method over the conventional DDBD method (Sullivan et al. 2012) as well as the FBD method of EC8 (2004) are demonstrated and further research activities on the subject are discussed.

2 The original DDBD method

Before proceeding to the proposed improved version of the DDBD, a brief introduction to the original method following the model code (Sullivan et al. 2012) is given in this section for reasons of completeness.

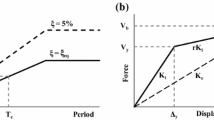
Consider a plane moment resting frame of \({\text{n}}\) stories under a horizontal seismic motion that has to be designed by the DDBD method, as shown in Fig. 1a. The basic idea of the method is to determine the required seismic design base shear \(V_{d}\) for this frame that will ensure that its displacements will not exceed the target displacements. This is accomplished by constructing an equivalent linear SDOF system to the MDOF frame under consideration as it is shown in Fig. 1b. To this end, one has to determine the design displacement \(u_{d}\), the effective mass \(m_{e}\) and the equivalent viscous damping \(\xi_{eq}\) of this equivalent SDOF system.

Fig. 1
figure 1

The MDOF structure (a) and its SDOF representation in the original DDBD (Sullivan et al. 2012) method (b)

Full size image

Assuming a target or limit design inter-storey drift ratio \(\left( {IDR_{T} } \right)\) and that the inelastic displacement profile corresponds to the fundamental mode, the lateral displacement \(u_{i}\) at the storey \(i\)\(\left( {i = 1,2, \ldots ,n} \right)\) can be obtained from the expression

$$u_{i} = \omega_{\theta } IDR_{T} h_{i} \frac{{\left( {4H_{n} - h_{i} } \right)}}{{\left( {4H_{n} - h_{1} } \right)}}$$
(1)

where \(\omega_{\theta }\) is a reduction factor (taking values from 1 to 0.85 decreasing gradually from a frame of 6 stories to one of 16 stories) introduced to take into account higher mode effects and \(H_{n}\) and \(h_{i}\) are the total height of the frame and the height at storey i, respectively.

The effective mass \(m_{e}\) of the equivalent SDOF system is evaluated from

$$m_{e} = \mathop \sum \limits_{i = 1}^{n} \left( {m_{i} u_{i} } \right)/u_{d}$$
(2)

where \(m_{i}\) is the total mass at storey \(i\) and \(u_{d}\) is the characteristic or design displacement shown in Fig. 2a and given by

$$u_{d} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {m_{i} u_{i}^{2} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {m_{i} u_{i} } \right)}}$$
(3)
Fig. 2
figure 2

The effective stiffness at the design target displacement \(u_{d}\) (a) and the design displacement spectra for equivalent damping \(\xi_{eq}\) (b)

Full size image

The estimation of the equivalent damping \(\xi_{eq}\) for the case of R/C MRFs can be obtained from the relation

$$\xi_{eq} = 0.05 + 0.565\left( {\frac{\mu - 1}{\mu \pi }} \right)$$
(4)

where \(\mu\) is the displacement ductility, i.e., \(\mu = u_{d} /{\text{u}}_{y}\), with \({\text{u}}_{y}\) being the yield displacement shown in Fig. 2a. The yield displacement can be approximated as \(u_{y} = H_{e} {\text{IDR}}_{\text{y}}\), where \(H_{e}\) and \(IDR_{y}\) are the effective height (see Fig. 1b) and yield drift of the SDOF structure, respectively, expressed as

$$H_{e} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (m_{i} u_{i} h_{i} ) }}{{\mathop \sum \nolimits_{i = 1}^{n} (m_{i} u_{i} )}}$$
(5)
$$IDR_{y} = 0.5\varepsilon_{y} \frac{{L_{b} }}{{h_{b} }}$$
(6)

In the above, Eq. (6) is valid for R/C framed structures, \(\varepsilon_{y}\) is the material yield strain and \(L_{b}\) and \(h_{b}\) are the length of the beams between column centerlines and the depth of beam sections of the frames considered, respectively.

For known values of \(u_{d}\) and \(\xi_{eq}\) one can calculate with the aid of a displacement design spectrum like the one shown in Fig. 2b, the corresponding damped design displacement \(u_{D,\xi }\) and then the effective period \(T_{e}\) as

$$T_{e} = \frac{{u_{d} }}{{u_{D,\xi } }}T_{D}$$
(7)

where \(T_{D}\) and \(u_{D,\xi }\) are the corner period of the displacement design spectrum and the design displacement with damping \(\xi\) = \(\xi_{eq}\) at \(T_{D}\), respectively.

Then, the effective stiffness is determined by

$$K_{e} = 4\pi^{2} m_{e} /T_{e}^{2}$$
(8)

and finally, the deformation dependent design base shear by

$$V_{d} = K_{e} u_{d} + c \mathop \sum \limits_{i = 1}^{n} P_{i} u_{i} /H_{e}$$
(9)

where the second term takes care of P-Δ effects with \(P_{i}\) denoting the total gravity load on storey level \(i\) and \(c = 0.5\) for R/C structures.

The above design base shear can be distributed to the floor masses of the frame by using the relations

$$\begin{aligned} & {\text{Floors }}1 {\text{ to n}} - 1{:}\quad F_{i} = k V_{d} \left( {m_{i} u_{i} } \right)/\mathop \sum \limits_{i = 1}^{n} (m_{i} u_{i} ) \\ & {\text{Roof }}\left( {\text{Floor n}} \right){:}\quad F_{n} = \left( {1 - k} \right)V_{d} + kV_{d} \left( {m_{n} u_{n} } \right)/\mathop \sum \limits_{i = 1}^{n} (m_{i} u_{i} ) \\ \end{aligned}$$
(10)

where for framed structures \(k = 0.9\). The above force distribution assumes that 10% of the base shear is additionally applied at roof level in order to take care of higher-modes effects.

Using the above lateral forces, one can dimension the frame members. It is apparent, that the DDBD method is a one-step method as requiring only a strength check and not two checks for strength and deformation as it is the case with the FBD method and this is because in the former method deformation requirements are automatically satisfied.

3 Equivalent modal damping ratios

For reasons of completeness, this section, mainly taken from a previous work of the present authors (Muho et al. 2020), presents the theory of calculating the equivalent modal damping ratios for R/C plane frames.

Consider first the transfer function R(ω) for a viscously damped linear elastic MDOF plane frame defined in the frequency domain as the ratio of the absolute roof acceleration \(\overline{{{\ddot{\text{U}}}}}_{\text{r}} \left(\upomega \right)\) of the frame over the acceleration \(\overline{{{\ddot{\text{u}}}}}_{\text{g}} \left(\upomega \right)\) at its base, i.e.,

$${\text{R}}\left(\upomega \right) = \frac{{\overline{{{\ddot{\text{U}}}}}_{\text{r}} \left(\upomega \right)}}{{\overline{{{\ddot{\text{u}}}}}_{\text{g}} \left(\upomega \right)}}$$
(11)

where \(\overline{{{\ddot{\text{U}}}}}_{\text{r}} \left(\upomega \right) = \overline{{{\ddot{\text{u}}}}}_{\text{g}} \left(\upomega \right) + \overline{{{\ddot{\text{u}}}}}_{\text{r}} \left(\upomega \right)\) with \(\overline{{{\ddot{\text{u}}}}}_{\text{g}} \left(\upomega \right)\) and \(\overline{{{\ddot{\text{u}}}}}_{\text{r}} \left(\upomega \right)\) being the earthquake motion and roof relative motion, respectively, in the frequency domain, ω is the frequency and overbars denote Fourier transformation.

The squared modulus \(\left| {{\text{R}}\left(\upomega \right)} \right|^{2}\) of this transfer function \(R\left( \omega \right)\) can be written in the form

$$\begin{aligned} \left| {{\text{R}}\left(\upomega \right)} \right|^{2} & = 1 + 2\mathop \sum \limits_{{{\text{j}} = 1}}^{\text{N}} \frac{{{\varphi }_{\text{rj}}\Gamma _{\text{j}} \omega^{2} \left( {\upomega_{\text{j}}^{2} - \omega^{2} } \right)}}{{\left( {\upomega_{\text{j}}^{2} - \omega^{2} } \right)^{2} + \left( {2\upxi_{\text{j}}\upomega_{\text{j}}\upomega} \right)^{2} }} + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{N}} \frac{{{\varphi }_{\text{rj}}^{2}\Gamma _{\text{j}}^{2} \omega^{4} \left( {\upomega_{\text{j}}^{2} - \omega^{2} } \right)^{2} + 4\upxi_{\text{j}}^{2}\upomega_{\text{j}}^{2} \omega^{2} }}{{\left[ {\left( {\upomega_{\text{j}}^{2} - \omega^{2} } \right)^{2} + \left( {2\upxi_{\text{j}}\upomega_{\text{j}}\upomega} \right)^{2} } \right]^{2} }} \\ & \quad + 2\mathop \sum \limits_{{{\text{j}} \ne {\text{m }}, {\text{m}} > j}}^{\text{N}} \frac{{{\varphi }_{\text{rj}}\Gamma _{\text{j}} {\varphi }_{\text{rm}}\Gamma _{\text{m}} \omega^{4} \left[ {\left( {\upomega_{\text{j}}^{2} - \omega^{2} } \right)\left( {\upomega_{\text{m}}^{2} - \omega^{2} } \right) + 4\upxi_{\text{j}}\upxi_{\text{m}}\upomega_{\text{j}}\upomega_{\text{m}} \omega^{2} } \right]}}{{\left[ {\left( {\upomega_{\text{j}}^{2} - \omega^{2} } \right)^{2} + \left( {2\upxi_{\text{j}}\upomega_{\text{j}}\upomega} \right)^{2} } \right]\left[ {\left( {\upomega_{\text{m}}^{2} - \omega^{2} } \right)^{2} + \left( {2\upxi_{\text{m}}\upomega_{\text{m}}\upomega} \right)^{2} } \right]}} \\ \end{aligned}$$
(12)

where \(\xi_{j}\), \(\xi_{m}\) and \(\varGamma_{j}\), \(\varGamma_{m}\) are the damping ratio and the corresponding participating factor at mode j or m, respectively, \(\varphi_{rj}\) or \(\varphi_{rm}\) is the \(j_{th}\) or \(m_{th}\) modal shape at the top storey (roof) r, \(\omega_{j}\) and \(\omega_{m}\) are the natural frequencies corresponding to the eigenvalue problem with \(m > j\). This form of the transfer function corresponds to a real number and not to a complex number as it is the case with \(R\left( \omega \right)\).

Consider now a nonlinear MDOF plane frame to be replaced by an equivalent linear MDOF plane frame with high amounts of viscous damping. These two MDOF frames are equivalent in the sense that the work of dissipation due to hysteretic forces in the nonlinear system is equal to the work of dissipation due to viscous forces in the linear structure. Thus, this work equivalence concept can be thought of as an extension of that of Jacobsen (1930) from a SDOF system under harmonic excitation to a MDOF system under seismic excitation.

According to the theory of linear systems, the modulus of the transfer function versus frequency curve for a linear system with viscous damping is smooth with local maxima at the resonant frequencies. When the distorted shape with many and no clearly visible peaks of that curve for the nonlinear structure, becomes smooth with clearly visible peaks for the first few modes, this curve represents the equivalent linear structure. By providing Rayleigh type viscous damping progressively to the nonlinear structure, one succeeds in obtaining smoother and smoother \(\left| {{\text{R}}\left(\upomega \right)} \right|^{2}\) versus ω curves for that structure until for some value of damping the curve becomes completely smooth with clearly visible peaks.

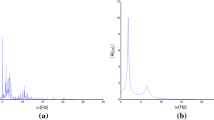
Taking as examples a five and a sixteen storey R/C frame (sectional dimensions and reinforcement values given later in Tables 3, 4, respectively) and applying the above procedure one obtains the curves shown in Fig. 3a, b, respectively, for the nonlinear (dashed red line) and linear (continuous blue line) structure. The distorted modulus of the transfer function versus frequency curve shown by the dashed red lines in Fig. 3a, b, represents the nonlinear response of the five and sixteen storey structure with 5% viscous damping, respectively, obtained by applying the aforementioned procedure in conjunction with nonlinear time history (NLTH) analysis and an accelerogram appropriately scaled so that the frame would reach a target IDR = 2.50%. The above distorted shapes of the five and sixteen storey frames become completely smooth with visible peaks for 24.5 and 36.5% damping values, respectively, as shown by the continuous blue lines in Fig. 3a, b.

Fig. 3
figure 3

Transfer function modulus versus frequency for a nonlinear structure and its equivalent linear structure with damping for a a 5-storey and b 16-storey R/C MRF at 2.50% target IDR

Full size image

The curve smoothening procedure is done sequentially from the first to the last significant mode, while damping is being continuously fed to the system, by employing some smoothness mathematical criteria. Thus, one can obtain the resonance frequencies \(\omega_{k}\) and the corresponding values \(\left| {{\text{R}}\left( {\upomega_{k} } \right)} \right|\) of the completely smoothed curve. Once the \(\left| {{\text{R}}\left(\upomega \right)} \right|^{2}\) versus \(\omega\) curve for all modes has become completely smooth, e.g., as shown in Fig. 3 (blue line), the structure is just below its first yield point (first plastic hinge) and hence, the originally nonlinear structure has become an equivalent linear. At that moment, Eq. (12) is applicable and one can evaluate \({\text{R}}\left(\upomega \right)\) for a sequence of values of the resonant frequencies of \(\omega = \omega_{k}\)\(\left( {k = 1,2, \ldots ,N} \right)\), with \(N\) being the number of the first significant modes and thus, create a system of \(N\) nonlinear algebraic equations to be solved for the modal hysteretic damping ratios \(\xi_{k}\), provided that \({\varphi }_{\text{rj}}\), \(\upomega_{\text{j}}\), \(\varGamma_{\text{j}}\) and \({\text{R}}\left( {\upomega_{\text{k}} } \right)\) are known.

Thus, for a large number of plane frames under a large number of far-fault earthquake motions one determines structural seismic response in the time domain by NLTH analyses involving large displacement and P-Δ effects. This response is then brought to the frequency domain by a Fourier transform for the construction of the transfer function R(ω) from which the equivalent modal damping ratios \(\xi_{k}\) can be calculated. NLTH analyses are conducted many times for every seismic motion by progressively scaling that motion in order to capture all the target deformation values. Thus, the resulting \(\xi_{k}\) turn out to be deformation dependent, while due to the way they have been derived, include higher mode and P-Δ effects.

For this purpose, a large number of R/C framed structures (2–20 storeys) was first seismically designed according to EC8 (2004) and then subjected to a large number of seismic motions. The above structures were designed assuming a peak ground acceleration equal to 0.30g, soil type B and the same capacity design and ductility detailing standards as those in EC8 (2004) for medium ductility class. The design in all cases considered a three-dimensional (3-D) model of each building regular in plan and elevation with three bays of 6 m length, in both horizontal directions, and a height of 3 m for each storey. The middle two-dimensional (2-D) frame was isolated for the purposes of this work and appropriately loaded using influence surfaces. Use of NLTH analyses was then employed on detailed models of these structures with the aid of Ruaumoko 2D software (Carr 2006). All structural elements were modeled using a component (Giberson) beam element with concentrated hinges described by the modified Takeda hysteresis rule at both their ends. The interaction between axial force and bending moment was considered for columns. The stiffness and strength deterioration were considered for all members The above NLTH analyses were conducted using a set of 100 far-fault earthquake accelerograms recorded worldwide, selected from the Pacific Earthquake Engineering Research Center ground motion database (PEER 2013), 25 for each one of the four soil types A, B, C and D as categorized by EC8 (2004). More information about the modeling adopted here and the selected motions can be found in Muho et al. (2020) and Muho (2017).

Tables 1 and 2, taken from Muho et al. (2020), provide explicit empirical expressions of \(\xi_{k}\) as functions of period T for the first four modes (k = 1, 2, 3, 4) and four values of \(IDR_{T}\) (performance levels) only for the cases of soil types B and C. Expressions for soil types A and D can be found in Muho (2017). It should be noted here that all the aforementioned \(\xi_{k}\) values have been determined on the assumption that they correspond to hysteretic dissipation ignoring the viscous damping \(\xi_{v}\) values of elastic deformation. Thus, in order to obtain the total equivalent modal damping \(\xi_{eq,k}\), one has to add those modal values, i.e., \(\xi_{eq,k} = \xi_{k} + \xi_{v}\), where \(\xi_{v}\) for simplicity reasons is assumed here to be constant for each mode and equal to 5% (for RC structures).

Table 1 Equivalent modal damping ratios (\(\xi_{k}\)%) for R/C MRFs for different performance levels, soil type B and various values of \(IDR_{T}\)
Full size table
Table 2 Equivalent modal damping ratios (\(\xi_{k}\)%) for R/C MRFs for different performance levels, soil type C and various values of \(IDR_{T}\)
Full size table

Closing this section, one should make clear that the equivalent modal damping ratios presented here are applicable not only to the frames for which they were constructed, but to any plane R/C MRF for which its three basic characteristics, \(T_{1}\), the first natural period in seconds, \(\rho\), the stiffness and a, the strength ratio defined in Chopra (2011) have values within the ranges 0.55 ≤  \(T_{1}\) ≤ 4.42 s, 0.151 ≤  \(\rho\)  ≤ 0.887 and 2.252 ≤  \(a\)  ≤ 6.623, respectively (Muho et al. 2020).

4 The proposed DDBD method

This section presents in detail the proposed improved DDBD method, which utilizes an equivalent linear MDOF system with viscous damping instead of the corresponding SDOF system employed by the original DDBD (Sullivan et al. 2012) method. Thus, in here one has modal lateral displacements \(u_{i,j}\) at the storey i for the mode j instead of the lateral displacements \(u_{i}\) of the original DDBD (Sullivan et al. 2012) method. Index \(i = 1,2, \ldots ,n\), where \(n\) is the total number of stories of the frame and index \(j = 1,2 \ldots ,N\), where \(N\) identifies the first \(N\) modes significantly contributing to the seismic structural response. Furthermore, here one has equivalent modal damping ratios \(\xi_{eq,j}\) instead of one value of \(\xi_{eq}\) for the SDOF system.

The modal displacement profiles \(u_{i,j}\) for a target inter-storey drift ratio \(IDR_{T}\) are estimated here based on the first four modal shapes resulting from modal analysis. In order to achieve this, the modal inter-storey drift ratio \(IDR_{Tj}\) for each mode j is first introduced here and defined as

$$IDR_{Tj} = f_{j} IDR_{T}$$
(13)

where \(f_{j}\) is the mass participation factor for mode j. The modal target displacements \(u_{i,j}\) corresponding to the \(IDR_{Tj}\) can be expressed in terms of the modal shapes \(\phi_{i,j}\) of the frame (normalized, e.g., to the roof displacement) in the form

$$u_{i,j} = x_{j} \phi_{i,j}$$
(14)

where \(x_{j}\) is a modal multiplication factor with dimensions of length to be determined.

One can easily obtain from Eq. (14) the relation

$$\left( {\frac{{u_{i + 1,j} - u_{i,j} }}{{h_{i + 1} - h_{i} }}} \right) = x_{j} \left( {\frac{{\phi_{i + 1,j} - \phi_{i,j} }}{{h_{i + 1} - h_{i} }}} \right)$$
(15)

and observing that

$$IDR_{Tj} = { \hbox{max} }\left( {\frac{{u_{i + 1,j} - u_{i,j} }}{{h_{i + 1} - h_{i} }}} \right)_{j}$$
(16)

he can have from Eq. (15) the expression

$$IDR_{Tj} = \hbox{max} \left( {\frac{{\phi_{i + 1,j} - \phi_{i,j} }}{{h_{i + 1} - h_{i} }}} \right)_{j} x_{j}$$
(17)

which can be solved for \(x_{j}\) and provide

$$x_{j} = IDR_{Tj} /\hbox{max} \left( {\frac{{\phi_{i + 1,j} - \phi_{i,j} }}{{h_{i + 1} - h_{i} }}} \right)_{j}$$
(18)

By substituting Eq. (18) in (14), one can finally express the modal target displacement \(u_{i,j}\) in terms of the modal \(IDR_{Tj}\) in the form

$$u_{i,j} = \frac{{IDR_{Tj} }}{{\hbox{max} \left( {\frac{{\phi_{i + 1,j} - \phi_{i,j} }}{{h_{i + 1} - h_{i} }}} \right) _{j} }} \phi_{i,j}$$
(19)

Having found the modal target displacements \(u_{i,j}\) one can proceed to the calculation of the characteristic or design modal displacements \(u_{d,j}\) from a relation analogous to Eq. (3), which reads

$$u_{d,j} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (m_{i,j} u_{i,j}^{2} ) }}{{\mathop \sum \nolimits_{i = 1}^{n} (m_{i,j} u_{i,j} )}}$$
(20)

where \(m_{i,j}\) is the modal mass (\(m_{i}\) × \(f_{j}\)) at mode j and storey i.

The equivalent modal damping ratios \(\xi_{eq,j} = \xi_{j} + 5\%\) can be determined by the method briefly described in Sect. 3, where mode index k is used instead of the present index j. One can find there (Tables 1, 2) explicit expressions of \(\xi_{j}\) for the first four significant modes \(\left( {j = 1,2,3,4} \right)\) of the structure, soil types B and C and various values of \(IDR_{T}\).

Using the design modal displacements \(u_{d,j}\) of Eq. (20) in conjunction with values of the equivalent modal damping ratios \(\xi_{eq,j}\) obtained from Tables 1 and 2, one can easily determine with the aid of a design displacement spectrum like the one shown in Fig. 4, the corresponding damped design modal displacements \(u_{\xi ,j}\) and thus, the effective modal periods \(T_{e,j}\) of the frame as

$$T_{e,j} = \frac{{u_{d,j} }}{{u_{D,\xi } }}T_{D}$$
(21)

where \(T_{D}\) and \(u_{D,\xi }\) are the corner period of the displacement design spectrum and the displacement with damping \(\xi = \xi_{eq,j}\) at \(T_{D}\), respectively (Fig. 2b).

Fig. 4
figure 4

The design displacement spectrum for equivalent modal damping ratios \(\xi_{eq,j}\)

Full size image

Hence, the modal effective stiffness \(K_{e,j}\) can be obtained by

$$K_{e,j} = \frac{{4\pi^{2} m_{e,j} }}{{T_{e,j}^{2} }}$$
(22)

where the modal mass \(m_{e,j}\), in view of Eq. (2), is equal to

$$m_{e,j} = \mathop \sum \limits_{i = 1}^{n} \left( {m_{i,j} u_{i,j} } \right)/u_{d,j}$$
(23)

Thus, the modal design base shear \(V_{d,j}\) can be obtained by

$$V_{d,j} = K_{e,j} u_{d,j}$$
(24)

The above modal design base shear \(V_{d,j}\) is distributed to the floor masses of the frame in the form of lateral modal design forces \(F_{i,j}\) reading as (Chopra 2011)

$$F_{i,j} = V_{d,j} \frac{{m_{i,j} u_{i,j} }}{{\mathop \sum \nolimits_{i = 1}^{n} m_{i,j} u_{i,j} }}$$
(25)

Finally, the maximum lateral design force \(F_{i}\) at every storey i (Fig. 1) can be obtained by a modal combination rule, such as the SSRS rule, in the form

$$F_{i} = \sqrt {\mathop \sum \limits_{j = 1}^{N} F_{i,j}^{2} }$$
(26)

The above maximum lateral design forces can be used to design an R/C frame through static analysis. It should be noted here that since the proposed method works on the basis of a MDOF representation of the structural system, it takes into account, by default, both P-Δ and higher mode effects without the need of an artificial increase of the lateral forces as is the case of the original DDBD (Sullivan et al. 2012) method.

It should be pointed out that since the modal design displacements in Eq. (20) are based on the modal shapes of the structure, in order to obtain better modal analysis results, one has to use reasonable values of the effective flexural stiffness \(EI_{eff} = c EI_{g}\) of the members of the structure, where E is the modulus of elasticity, the subscripts “eff” and “g” stand for “effective” and “gross” sectional moment of inertia, respectively and c is a reduction coefficient accounting for the presence of cracks in concrete. EC8 (2004) recommends a value of c = 0.5. A much better approximation for c, employed here for elastic modal analysis, can be obtained from the empirical expression (Muho et al. 2019; ATC72-1 2010)

$$c = \frac{{EI_{eff} }}{{EI_{g} }} = - 0.07 + 0.59\left( {\frac{P}{{A_{g} f_{c} }}} \right) + 0.07\left( {\frac{{L_{s} }}{H}} \right), {\text{where}} \,\,0.2 \le c \le 0.6$$
(27)

where P denotes the axial force (positive for compression), \(A_{g}\) the member cross section area, \(f_{c}\) the concrete compression strength, \(L_{s}\) the shear span (assumed to be half of the clear member length) and H is the member’s cross section height. However, the most realistic value of \(EI_{eff}\) can be obtained by the secant to yield expression \(EI_{eff} = M_{y} /\phi_{y}\), where \(M_{y}\) and \(\phi_{y}\) are the member moment and curvature at yield, respectively (Muho et al. 2020; ATC72-1 2010). This expression requires knowledge of the steel reinforcement and is, in general, very time consuming for design purposes. It is usually reserved for structural assessment through dynamic nonlinear analysis.

Moreover, in order to take into account the possibility of a sway collapse mechanism, expected, e.g., in the top storey, it is suggested the modal shapes to be calculated after assigning to that storey half of the stiffness reduction of the storey below. Finally, since it is expected that the base of the columns of the first storey to yield, it is also suggested the modal shapes to be calculated after assigning pinned connections at the base of these columns.

5 Design examples

The proposed DDBD method is illustrated here through two design examples involving one five and one sixteen storey R/C MRFs. For comparison purposes these frames are also designed on the basis of the original DDBD (Sullivan et al. 2012) and the FBD method of EC8 (2004), while the responses of all three kinds of design are compared on the basis of NLTH analyses.

Because there are two decisions to be made during the design of framed R/C structures, i.e., one concerning the selection of the sectional dimensions of the members and one concerning the selection of the required reinforcing steel of those members, in order to simplify the design comparisons, it was decided that those comparisons of the two DDBD methods (proposed and original) to be based only on the required reinforcing steel of the same member sectional dimensions.

To achieve this, all frames were first designed based on EC2 (2004) and EC8 (2004) and all sectional dimensions produced by these codes were used as starting sections for the frames to be designed by both the proposed and the original DDBD (Sullivan et al. 2012) methods. Thus, all frames were first designed based on the EC8 (2004) design spectrum for peak ground acceleration (\(PGA\)) equal to 0.36 g, soil type B and a behavior factor q = 3.9. The vertical load was assumed to be the same for all frames with values \(g_{d}\) = 21 kN/m and \(q_{d}\) = 3 kN/m distributed on beams and \(g_{c}\) = 60 kN, \(q_{c}\) = 9 kN and \(g_{c}\) = 70 kN, \(q_{c}\) = 18 kN concentrated on the outer and middle columns, respectively, where \(g\) and \(q\) denote dead and live loads, respectively. The combinations of 1.35 \(g\) + 1.5 \(q\) and \(g\) + 0.3 \(q\) ± seismic forces were used for the design. Concrete and steel material properties were assumed to be those for C25/30 and S500, respectively. The design was accomplished with the aid of SAP2000 (2016).

The deformation checks on IDR for damage limitation and second order (P-Δ) effects through the stability sensitivity coefficient \(\theta\), were both done with the aid of the equal displacement rule (EC8 2004). For frames without non-structural elements, EC8 (2004) limits the maximum IDR value to 1.00% under the frequent earthquake, which here is taken as the design seismic action multiplied by 0.5. Moreover, \(\theta\) should be less than 0.2 for the design seismic action in order to avoid a second order analysis. Satisfaction of the above deformation restrictions had as a result the increase of the external and internal column and beam section heights and reinforcement over those resulting from strength checking. The final IDR values at each storey under the frequent earthquake were found to be 0.71, 0.74, 0.61, 0.45 and 0.26%, for the five storey frame, while the maximum IDR value for the sixteen storey frame was found to be 0.67%. The final \(\theta\) values at each storey were found to be 0.13, 0.12, 0.08, 0.05 and 0.02 with a maximum value of 0.13 for the five storey frame, while the maximum \(\theta\) value for the sixteen storey frame was found to be 0.19. Thus, according to EC8 (2004), the design seismic actions were multiplied by \(1/\left( {1 - \theta } \right)\) = 1.15 and 1.23, for the five and sixteen storey frames, respectively, to account for second order effects.

The geometry of the above designed frames is summarized in Fig. 5 and the required sectional dimensions with the corresponding reinforcing steel ratios are given in Tables 3 and 4 for the five and sixteen storey frames, respectively, where only results for the first three and the last two storeys of the sixteen storey frame are presented due to space limitations.

Fig. 5
figure 5

Frame geometry, section and reinforcing steel numbering for the design examples of the five and sixteen storey frames

Full size image
Table 3 Sectional dimensions and steel reinforcing ratios of the five storey frame designed by the EC2 (2004) and the EC8 (2004)
Full size table
Table 4 Sectional dimensions and reinforcing steel ratios of the sixteen storey frame designed by the EC2 (2004) and the EC8 (2004)
Full size table

Symbols used in Fig. 5 and Tables 3, 4 and all subsequent ones, are as follows: h is the cross-section height of columns and beams, ρ is the reinforcement ratio, i.e., the reinforcement area normalized to the cross-sectional area bd, where b is the width, h is the height and d = h − 4 cm; the symbol \(\rho_{tot}\) indicates the total reinforcement ratio of columns and \(\rho_{1A} , \rho_{2A} , \rho_{1B}\) and \(\rho_{2B}\) indicate the reinforcement ratios at the left and right ends of the beams. In these tables, only the necessary geometric sizes and reinforcement of the members of the frame are shown. Frames are symmetric, i.e., with reference to Fig. 5, outer (1,4) and middle (2,3) columns have the same geometry and reinforcement, beams No. 5 and No. 7 also have the same geometry and reinforcement, and so on.

Next, the above two frames are re-designed by the proposed and the original DDBD method in terms of the required reinforcing steel for the purpose of illustrating the proposed DDBD method and comparing it against the original one and the FBD method of EC8 (2004).

First, the five and sixteen storey frames are designed by the proposed DDBD method starting with the sectional dimensions of Tables 3 and 4, respectively, produced by EC8 (2004). Since the modal target displacements \(u_{i,j}\) are based on the modal shapes of the frame, one has to first make a good estimation of the effective stiffness of the members. Thus, instead of the constant value of 0.5 \(EI_{g}\) of EC8 (2004), more realistic member stiffness values are assumed here based on Eq. (27).

Thus, based on the above effective stiffnesses, one can calculate the modal shapes \(\phi_{i,j}\) from modal analysis. The periods corresponding to the first four modes were found to be 1.61, 0.56, 0.31 and 0.20 s, and 3.33, 1.27, 0.76 and 0.56 s, for the five and the sixteen storey frames, respectively. The corresponding modal damping ratios from Table 1 (also adding \(\xi_{v}\) = 5%) for \(IDR_{T}\) = 2.50% were found to be \(\xi_{eq,j}\) = 23.0, 18.2, 15.5 and 28.2% and \(\xi_{eq,j}\) = 25.6, 14.0, 11.1 and 11.0%, for the five and the sixteen storey frames, respectively.

The mass participation factors \(f_{j}\) for the first four modes were found to be equal to 95.6, 3.5, 0.7 and 0.2% and 72, 14, 5 and 3% for the five and the sixteen storey frames, respectively. Thus, following Eq. (13), the target modal \(IDR_{Tj}\) values corresponding to the first four modes were found to be equal to 2.39, 0.09, 0.02 and 5·10−5 % and 1.81, 0.31, 0.11 and 0.06% for the five and sixteen storey frames, respectively.

From the calculated modal shape values and \(IDR_{Tj}\), one can proceed to estimate the modal target displacements \(u_{i,j}\) from Eq. (19) and then to calculate the characteristic or design modal displacement \(u_{d,j}\) from Eq. (20).

Based on the equivalent modal damping ratios \(\xi_{eq,j}\) found above, one can determine the corresponding damped displacements using the EC8 (2004) design displacement spectrum constructed for soil type B, \(PGA = 0.36g\), corner period \(T_{D}\) = 2.0 s and various values of damping (\(\xi_{eq}\) = 5–30%), as shown in Fig. 6. Then, from Eq. (21) one can calculate the modal effective periods \(T_{e,j}\) with the value of design displacement (\(u_{D,\xi }\)) with damping \(\xi = \xi_{eq,j}\) easily found from Fig. 6 at \(T = T_{D}\) = 2.0 s. Using Eq. (22) one can calculate the modal effective stiffness \(K_{e,j}\). Finally, the modal design base shear \(V_{d,j}\) can be found from Eq. (24) and can be distributed to each storey following Eq. (25), while the maximum design lateral forces are obtained using the SSRS rule following Eq. (26).

Fig. 6
figure 6

EC8 (2004) displacement spectrum for various values of damping for soil B and PGA = 0.36 g

Full size image

The total mass \(M_{i}\), modal mass \(m_{i,j}\), modal shapes \(\phi_{i,j}\), modal target displacement \(u_{i,j}\), modal lateral forces \(F_{i,j}\) and the final maximum resulting design lateral force \(F_{i}\) for each storey i are given in Tables 5 and 7 for the five and sixteen storey frames, respectively. The period \(T_{j}\), effective mass \(m_{e,j}\), mass participation factor \(f_{j}\), inter-storey drift ratio \(IDR_{Tj}\), characteristic displacement \(u_{d,j}\), equivalent damping \(\xi_{eq,j}\), effective period \(T_{e,j}\), effective stiffness \(K_{e,j}\) and the base shear \(V_{b,j}\) for each mode j are given in Tables 6 and 8 for the five and sixteen storey frames, respectively. One can easily observe in Table 6 that the contribution of higher modes is negligible which is expected considering the height of the frame. On the other hand, in Table 8, corresponding to the sixteen storey frame, the significant contribution of the higher modes is very clear.

Table 5 Storey characteristic structural and design force values for the five storey frame designed by the proposed DDBD method
Full size table
Table 6 Modal characteristic structural and design force values for the five storey frame designed by the proposed DDBD method
Full size table
Table 7 Storey characteristic structural and design force values for the sixteen storey frame designed by the proposed DDBD method
Full size table
Table 8 Modal characteristic structural and design force values for the sixteen storey frame designed by the proposed DDBD method
Full size table
Table 9 Storey characteristic structural and design force values for the five storey frame designed by the original DDBD method (Sullivan et al. 2012)
Full size table
Table 10 Storey characteristic structural and design force values for the sixteen storey frame designed by the original DDBD (Sullivan et al. 2012) method
Full size table

The above lateral forces \(F_{i}\) given in Tables 5 and 7 are assigned to each storey i of the five and sixteen storey frames, respectively. A static analysis in accordance with the EC2 (2004) design code, resulted in the required reinforcing steel given in Tables 11 and 12, for the five and sixteen storey frames, respectively, for each column and beam member following the symbolism of Fig. 5.

Table 11 Reinforcing steel ratios of the five storey frame designed by the proposed (P-DDBD) and the original DDBD (Sullivan et al. 2012) (O-DDBD) method
Full size table
Table 12 Reinforcing steel ratios of the sixteen storey frame designed by the proposed (P-DDBD) and the original DDBD (Sullivan et al. 2012) (O-DDBD) method
Full size table

Next, the above five and sixteen storey frames are re-designed by the original DDBD method (Sullivan et al. 2012) using the same sectional dimensions of Table 3 and 4, respectively. All the procedural information is summarized in Tables 9 and 10 for the five and sixteen storey frames, respectively. The final reinforcing steel ratios of the five and sixteen storey frames are shown in Tables 11 and 12, respectively. A comparison between the target displacement, total design base shear and the design lateral forces as well as between the required reinforcing steel as resulted from the above DDBD methods is given in Figs. 7, 8, 9 and Table 13, respectively.

Fig. 7
figure 7

Comparison of the target lateral displacement profile of the proposed DDBD and the original DDBD (Sullivan et al. 2012) method for the a five and b sixteen storey frame

Full size image
Fig. 8
figure 8

Comparison of the total design base shear of the proposed DDBD, original DDBD (Sullivan et al. 2012) and the FBD method of EC8 (2004) for the a five and b sixteen storey frame

Full size image
Fig. 9
figure 9

Comparison of the design lateral forces of the proposed DDBD, original DDBD (Sullivan et al. 2012) and the FBD method of EC8 (2004) for the a five and b sixteen storey frame

Full size image
Table 13 Required reinforcing steel of the frames designed by the original DDBD method (Sullivan et al. 2012) and the FBD method of EC8 (2004) normalized to the required reinforcing steel of the frames designed by the proposed DDBD method
Full size table

The lateral target displacement profile produced by the original DDBD method is higher than the one produced by the proposed DDBD for both five and sixteen storey frames as it is shown in Fig. 7a, b, respectively.

For the five storey frame, the proposed and the FBD method of EC8 (2004) resulted in similar values of design base shear and lateral design forces, as it is shown in Figs. 8a and 9a, respectively, and hence to the same amount of required reinforcing steel, as it is indicated in Table 13. For comparison purposes, Figs. 8a and 9a show two cases of the design forces of the original DDBD (Sullivan et al. 2012) method, i.e., including Ρ-Δ effects [c = 0.5 in Eq. (9)] and without including these effects [c = 0 in Eq. (9)]. Higher-modes effects modifications, i.e., \(\omega_{\theta }\) in Eq. (1) and k in Eq. (10), are not taken into account by default according to Sullivan et al. (2012) for a five storey frame. One can observe that the original DDBD method resulted in much higher values of the design base shear lateral forces and hence higher amounts of the required reinforcing steel. This may be due to the empirical and very approximate nature of Eq. (6), which is used in the original DDBD method (Sullivan et al. 2012) to approximate the \(IDR_{y}\) and thus, the displacement ductility and the equivalent damping \(\xi_{eq}\). Using Eq. (6), one can find \(IDR_{y}\) = 1.67% and hence a displacement ductility \(\mu\) = 1.27 and an equivalent damping \(\xi_{eq}\) = 8.83%, which leads to a final base shear of 611 kN. However, due to the very approximate nature of Eq. (6) for predicting the \(IDR_{y}\) and the sensitivity of \(\xi_{eq}\) to the input value of \(\mu\), one may obtain different values of the design base shear than the real ones. For example, using NLTH analysis one can find a more accurate prediction of \(IDR_{y}\) = 1.15% and hence \(\mu\) = 1.84 and \(\xi_{eq}\) = 13.22%, which leads to a final base shear value of 398 kN, which is very different from the previously calculated base shear of 611 kN. On the other hand, the proposed method inherently includes the effect of \(IDR_{y}\) or \(\mu\) and one does not have to calculate them since the used equivalent modal damping ratio values are directly related to \(IDR_{T}\) and the elastic natural periods \(T\) of the frame.

Considering the sixteen storey frame, the comparison of total design base shear and design lateral force profiles as obtained by the proposed DDBD, original DDBD (Sullivan et al. 2012) and the FBD method of EC8 (2004) is given in Figs. 8b and 9b, respectively. All methods resulted in similar values of design base shear and lateral forces, and hence to the same ammount of required reinfocing steel, as it is indicated in Table 13. Figures 8b and 9b contain two cases of the design forces of the original DDBD (Sullivan et al. 2012) method, i.e., including Ρ-Δ effects [c = 0.5 in Eq. (9)] and higher-modes effects modifications [\(\omega_{\theta } = 0.85\) in Eq. (1) and k = 0.9 in Eq. (10)] and without including these effects and modifications. It is evident that in the original DDBD (Sullivan et al. 2012) method the inclusion of these effects is done in a rather artificial way. Without the inclusion of these effects, the design lateral force of the original DDBD (Sullivan et al. 2012) method results in a much lower value than the one produced by the proposed method as it is shown in Figs. 8b and 9b.

The proposed method takes into account these effects in a rather rational way, since it works on the basis of the MDOF representation of the structure in contrast to the original DDBD (Sullivan et al. 2012) method which works with a SDOF representation of the building. By including P-Δ and higher modes effects, one can observe in Figs. 8b and 9b that the response of the original method approaches the one produced by the proposed method. However, even though the total base shear produced by the proposed and the original DDBD (Sullivan et al. 2012) method resulted in being almost the same, the lateral force profiles are different.

Next, the above five and sixteen storey frames designed by the EC8 (2004), the proposed and the original DDBD method are compared through NLTH analyses. Twenty real accelerograms, compatible to the EC8 (2004) design spectrum as shown in Fig. 10, were used in order to evaluate the deformation response of these frames and compare it with the target one. For this purpose, the Ruaumoko 2D software (Carr 2006) was used. All structural elements were modeled as described in Sect. 3 and in Muho et al. (2020) and Muho et al. (2019) assuming effective stiffness equal to the secant to yield \(EI_{eff} = M_{y} /\phi_{y}\), where \(M_{y}\) and \(\phi_{y}\) denote bending moment and curvature at yield.

Fig. 10
figure 10

Earthquakes compatible to the design acceleration spectra of EC8 (2004) for soil B and PGA = 0.36 g

Full size image

The mean IDR response results as obtained from the 20 compatible to EC8 (2004) design spectrum accelerograms are summarized in Fig. 11 for the frame designs obtained by the proposed DDBD, the original DDBD (Sullivan et al. 2012) and the FBD method of EC8 (2004). Regarding the five storey frames, one can observe that all of them result in having a response below the target value of \(IDR_{T}\) = 2.50% with the frame designed by the proposed DDBD method better approaching the design target \(IDR_{T}\). The proposed DDBD method resulted in a much more economically designed frame (with respect to reinforcing steel) than the original DDBD method (Sullivan et al. 2012) and to an almost the same designed frame with that by the FBD of EC8 (2004). However, in this example, higher mode effects were found to be practically negligible due to the rather small number of the stories of the frame.

Fig. 11
figure 11

Comparison of the IDR response profiles of the a five and b sixteen storey frame designed by the proposed DDBD, the original DDBD (Sullivan et al. 2012) and the FBD of EC8 (2004) method

Full size image

Similar to the five story, the sixteen storey frame designed by the proposed DDBD method resulted in having maximum IDR response much closer to the design target \(IDR_{T}\) than the other two methods. Thus, one can conclude here that the proposed method, based on a rather rational approach, results in excellent performance also for the cases of tall frames, where higher mode and P-Δ effects are significant. This is done without any rather artificial modification of the lateral forces and the displacement profile, as it is the case with the original DDBD (Sullivan et al. 2012).

As a final example, the proposed and the original DDBD methods are used to design the five-storey frame of the first example for four performance levels: immediate occupancy (IO) with IDR = 1.0% under the frequently occurred earthquake, damage control (DC) with IDR = 1.5% under the occasional occured earthquake, life safety (LS) with IDR = 2.5% under the design basis earthquake and collapse prevention (CP) with IDR = 4.0% under the maximum considered earthquake. In order to produce the corresponding forces for the CP, DC and IO levels, the design seismic forces of the LS performance level are multiplied by 1.50, 0.50 and 0.30, respectively (Vision 2000). For each performance level described above, use is made of the corresponding lateral forces as resulted by the two methods. Thus, the performance level resulting in the highest base shear is the one that controls the design and hence the one for which the frame has to be finally designed. In Fig. 12 the resulting base shear values for each performance level produced by the proposed and the original DDBD method are shown. One can observe that for both methods the design is controlled by the LS level. Since the five-storey frame has been already designed for the LS performance level (or \(IDR_{T} = 2.5\%\)) in the first example using both the proposed and the original DDBD methods, it remains here only to evaluate the above two designs under the four performance levels. This is done through NLTH analysis, using the accelerograms for the LS level after appropriate scaling with the factor corresponding to each performance level. One can observe in Figs. 13 and 14, that both methods result in safe designs for all performance levels considered here, since the IDR response of both frames does not exceed any of the target \(IDR_{T}\) values of the corresponding performance levels. Moreover, one can observe that the frame designed by the proposed method resulted in having a response with the maximum IDR much closer to the design target \(IDR_{T}\) of the corresponding performance levels.

Fig. 12
figure 12

Comparison of the total design base shear forces for each performance level as obtained by the proposed and the original DDBD (Sullivan et al. 2012) method

Full size image
Fig. 13
figure 13

Comparison of the IDR response profiles at a immediate occupancy and b damage control, for the five storey frame designed by the proposed DDBD and the original DDBD method for four performance levels

Full size image
Fig. 14
figure 14

Comparison of the IDR response profiles at a life safety and b collapse prevention for the five storey frame designed by the proposed DDBD and the original DDBD method for four performance levels

Full size image

To sum up, in this section it has been shown the consistency of the proposed method to produce frames with deformation responses closer to the target response and hence with more predictable behavior and with less required steel material. Moreover, it has been shown the ability of the proposed method to handle in an excellent way the design of very tall frames with high P-Δ and higher mode effects without using any artificial factor. Thus, the proposed DDBD method proved to be a more rational and improved DDBD method, which employs a MDOF equivalent system instead of a SDOF one. Further research is needed to study the application of the proposed DDBD method to other cases than MRFs, such as infilled frames or frame-wall dual systems and to further extend the method to cases of the more realistic three-dimensional building frames.

Some additional differences between the proposed and original DDBD method (Sullivan et al. 2012) which can be stated here are (1) the proposed method uses the natural periods of the frame in order to determine the equivalent modal damping values directly defined for the target \(IDR_{T}\) in contrast to the original DDBD method (Sullivan et al. 2012) which uses an \(IDR_{y}\) and the resulting displacement ductility to determine equivalent damping taking the target \(IDR_{T}\) indirectly into account, (2) the proposed method provides equivalent modal damping ratios for soil types A, B, C and D, as categorized by EC8 (2004), which is not the case with the original DDBD method (Sullivan et al. 2012) and (3) the proposed method requires determination of natural frequencies and modal shapes for the first few modes by elastic modal analysis, which is not the case with the original DDBD method (Sullivan et al. 2012).

6 Conclusions

From the preceding developments and examples, the following conclusions can be drawn:

  1. 1.

    An improved direct displacement-based design (DDBD) method has been proposed for plane R/C MRFs, which employs a multi-degree-of-freedom equivalent system instead of the single-degree-of-freedom system used by the original method. The method can be used on the basis of either two performance levels (as in current codes) or four performance levels.

  2. 2.

    The method uses the concept of deformation dependent equivalent modal damping ratios previously developed by the present authors for other purposes and the concept of the design modal displacements developed herein. The design modal displacements are determined on the basis of target inter-storey displacement ratios for every performance level and the first few modes significantly contributing to the structural response.

  3. 3.

    The proposed method by its nature can take more rationally and with higher accuracy into account P-Δ and higher mode effects than the original one. However, the proposed method requires an elastic modal analysis for the determination of natural frequencies and modal shapes of the first few modes. Both original and proposed DDBD methods perform the design in one step (strength checking) and not in two steps (strength and deformation checking) as it is the case with the FBD method of EC8.

  4. 4.

    Numerical examples involving the seismic design of two R/C moment resisting plane frames were used to illustrate the proposed DDBD method and demonstrate its ability to successfully handle the design of both short and tall frames. Comparisons with the original DDBD and the FBD method of EC8 on the assumption of members designed to have the same concrete cross-sections showed that all methods result in safely designed frames with the proposed method to produce frames with deformation responses closer to the target response and hence with a better use of the required material. Comparisons of the three methods with respect to the amount of reinforcing steel, showed that the proposed and the FBD method of EC8 resulted in much lower demands than the original DDBD method for the case of the five storey frame, while the differences among the methods for the case of the sixteen storey frame were negligible.