High-slope terrain locomotion for torque-controlled quadruped robots

Abstract

Research into legged robotics is primarily motivated by the prospects of building machines that are able to navigate in challenging and complex environments that are predominantly non-flat. In this context, control of contact forces is fundamental to ensure stable contacts and equilibrium of the robot. In this paper we propose a planning/control framework for quasi-static walking of quadrupedal robots, implemented for a demanding application in which regulation of ground reaction forces is crucial. Experimental results demonstrate that our 75-kg quadruped robot is able to walk inside two high-slope ($50^\circ$) V-shaped walls; an achievement that to the authors’ best knowledge has never been presented before. The robot distributes its weight among the stance legs so as to optimize user-defined criteria. We compute joint torques that result in no foot slippage, fulfillment of the unilateral constraints of the contact forces and minimization of the actuators effort. The presented study is an experimental validation of the effectiveness and robustness of QP-based force distributions methods for quasi-static locomotion on challenging terrain.

1 Introduction

Current research on legged robots is motivated by their potential impact in real-world scenarios such as disaster recovery scenes. Such environments require systems capable of robustly negotiating uneven and sloped terrains. In recent years the field has seen remarkable advances in the theoretical tools, which have allowed legged robots to tackle challenging and possibly dynamic tasks in simulation (Macchietto and Shelton 2009a; Lee and Goswami 2012). It is especially the introduction of Quadratic Programming (QP) solvers that strongly affected the field. The efficiency of these solvers coupled with the computational power of modern CPUs allow the resolution of small-medium size QP inside fast control loop (i.e., 1–10 ms). However, to this date, experimental results have been limited to few platforms and tasks, still not matching the complexity of the real world. Righetti et al. (2013) experimented with walking up a slope of $26^\circ$ with the Little Dog quadruped robot. On the quadruped robot StarlETH (Gehring et al. 2013; Hutter et al. 2012) used a contact-force optimization method to achieve static walking on a surface with approximately $40^\circ$ inclination. Regarding contact force control in humanoid robots, research had mainly focused on balancing experiments on flat ground (Hyon et al. 2007; Ott et al. 2011; Stephens and Atkeson 2010) and walking on even terrain (Nishiwaki et al. 2002; Kajita et al. 2003). It is only recently, mainly in the context of the Darpa Robotics Challenge (DRC), that we have seen humanoids walking on uneven terrain and climbing stairs (Feng et al. 2015; Kuindersma et al. 2015; Johnson et al. 2015). Even though these results are impressive, the high number of falls during the DRC finals proved the lack of robustness of these controllers.

Fig. 1

HyQ quadruped robot walking inside a $50^\circ$-inclined groove. Desired wrench (force, moments) at the CoM is depicted in white. Ground reaction forces are in brown friction while cone constraints are indicated in shaded red. The wall inclination is $\theta$ (Color figure online)

Fig. 2

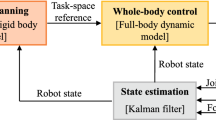
Block diagram of our framework. The motion generation block (yellow) computes the input trajectories for CoM and joints, while the motion control block (green) computes the reference torques for the low-level controller (grey). Light-red blocks indicate user-defined input parameters. Each block is detailed in the sections indicated in parenthesis (Color figure online)

This substantial gap between simulation and reality is due to a number of different factors. The lack of high-fidelity joint torque control is probably the first difficulty (Hutter et al. 2012; Cheng et al. 2008; Boaventura et al. 2012). Moreover, the identification of inertial and geometric parameters of these high-DoF multi-body systems is usually cumbersome (Mistry et al. 2009), and errors in the identified dynamical models introduce unknown disturbances in the control actions. Furthermore, the estimation of the system state is typically a complex procedure that merges multiple sensor data in order to exploit all the available information (Bloesch et al. 2012).

The main contribution of this work are the experimental results that showed a 75-kg torque-controlled quadruped robot walking in between two high-slope ($50^\circ$) V-shaped walls (Fig. 1). A video of the experiments is available at youtu.be/qOvtbPryygs. To achieve them we had to tackle all the above-mentioned issues, combining different ideas from planning to control and applying them to such challenging test case. To the best of our knowledge this is the first implementation of such a task on a real robot. Such a scenario is ideal for testing the capabilities of our controller, because it allows large slope inclinations, and therefore it requires greater rotations of the ground reaction forces (GRFs) compared to walking on a flat or inclined surface. For instance, a static walk on a single slope of $50^{{\circ }}$ would not be possible with a friction coefficient of 1 or less. Nonetheless, our QP force-optimization approach is applicable to any kind of sloped terrains, similar to previous methods. Figure 2 presents the building blocks of our control framework. The motion control block presented in Sect. 2 is a QP-based controller. It is very similar to the one used to balance on flat ground the DLR-Biped (Ott et al. 2011) and the one used to achieve static walk and trot on flat ground with the quadruped StarlETH (Gehring et al. 2013). Differently from previous works (Ott et al. 2011; Gehring et al. 2013) we derive our controller starting from the centroidal dynamics of the robot. we explicitly state the simplifying assumptions leading to the relationship between the contact forces and the angular acceleration of the robot’s base. Moreover, we extend the method to avoid joint-torque discontinuities when breaking and making contacts. The motion generation block presented in Sect. 3 computes desired trajectories for the CoM, the base orientation and the swing foot to achieve a static walking pattern. The latter adapts to the geometry of the terrain to achieve a stable foothold and to ensure physical feasibility (e.g. not to violate the constraints of the stance feet). Section 4 introduces our robotic platform and reports the experimental results obtained, along with the values used for all the parameters of the algorithm. Moreover, it empirically demonstrates the necessity of controlling the contact forces by showing the failures when trying to achieve this task using control strategies that do not optimize the contact forces. Section 5 discusses some practical issues that are often overlooked when working in simulation. Similarly to Ott et al. (2011) we show how to use the cost function of the QP to reduce the joint torques and so avoid violating the torque limits. We then present a simple procedure to identify the position of the CoM of the robot (which was crucial for the success of our experiments) and estimate the contact friction. Finally, Sect. 6 draws the conclusions and discusses future work directions.

1.1 Contributions

We believe that the main contribution of this work lies in the experimental results: the high slope of the terrain makes the task extremely challenging, which is probably the reason why previous works (Righetti et al. 2013; Hutter et al. 2012) have focused on lower slopes.

On top of the experimental contribution, the paper presents several other contributions, some of which have been fundamental for the success of the experiments:

• We present a strategy to avoid discontinuity in the contact forces computed by the QP-based controller when breaking or making a contact (see Sect. 3.2).

• We discuss a simple method to identify the position of the CoM of the robot that only requires knowledge of the contact forces and the position of the feet with respect to the base of the robot (see Sect. 5.2).

2 Whole body controller with optimization of ground reaction forces

This section describes the control architecture developed for quadrupedal robot walking on inclined terrain. The controller computes desired joint torques, that are tracked by the low-level torque controllers (Boaventura et al. 2012). Our objectives are to regulate (i) the position of the center of mass (CoM) and (ii) the orientation of the base of the robot. We do this by computing Ground Reaction Forces (GRFs) at the stance feet that result in the desired (i) acceleration of the CoM and (ii) angular acceleration of the robot’s base. At the same time, we take into account the constraints imposed by the friction cones.

2.1 Centroidal robot dynamics

The design of the controller is based on the following assumptions. First, we assume that Coriolis and centrifugal forces are negligible: this is reasonable because in our experiments the robot moves slowly. Second, since most of the robot’s mass is located in its base (i.e., 47 out of 75 kg), we approximate the CoM ($x_{com}$) and the average angular velocity of the whole robot (Orin et al. 2013) with the CoM of the base $x_{com-base}$ ¹ and the angular velocity of the base $\omega _b$. Third, since our platform has nearly point-like feet, we assume that it cannot generate moments at the contacts. Fourth, we assume that the GRFs are the only external forces acting on the system. Under these assumptions, we can express the linear acceleration of the CoM $\ddot{x}_{com}$ and the angular acceleration of the base $\dot{\omega }_b$ as functions of the c GRFs (i.e., $f_1, \dots , f_c \in \mathbb {R}^3$, where c is the number of stance feet):

$$\begin{aligned}&m (\ddot{x}_{com} + g) = \sum _{i=1}^c f_i \end{aligned}$$

(1)

$$\begin{aligned}&I_G \dot{\omega }_b \simeq \sum _{i=1}^c (p_{com,i} \times f_i), \end{aligned}$$

(2)

where $m \in \mathbb {R}$ is the total robot’s mass, $g\in \mathbb {R}^3$ is the gravity acceleration vector, $I_G \in \mathbb {R}^{3\times 3}$ is the centroidal rotational inertia (Orin et al. 2013), $p_{com,i} \in \mathbb {R}^3$ is a vector going from the CoM to the position of the $i^\text {th}$ foot defined in an inertial world frame $\mathscr {W}$ (see Fig. 3).

Fig. 3

Summary of the nomenclature used in the paper. Leg labels: left front (LF), right front (RF), left hind (LH) and right hind (RH). The world frame $\mathcal {W}$; the base frame $\mathcal {B}$ (attached to the geometric center of the robot body). Left subscripts indicate the reference frame, for instance ${}_Bx_{com}$ is the location of the CoM w.r.t. the base frame. In case of no left subscript, quantities are expressed w.r.t. $\mathcal {W}$

These two equations are the base of our control design because they describe how the GRFs affect the acceleration of the CoM and the angular acceleration of the robot’s base. We now design two proportional-derivative control laws to compute the desired values of $\ddot{x}_{com}$ and $\dot{\omega }_b$. Then, we will find the GRFs that allow us to achieve these desired accelerations.

2.2 Control of CoM’s position and base’s orientation

We compute the desired acceleration of the CoM $\ddot{x}_{com}^d \in \mathbb {R}^3$ using a PD control law:

$$\begin{aligned} \ddot{x}_{com}^d = K_{pcom} (x_{com}^d - x_{com}) + K_{dcom} (\dot{x}_{com}^d - \dot{x}_{com}), \end{aligned}$$

(3)

where $x_{com}^d\in \mathbb {R}^3$ is the desired position of the CoM, whereas $K_{pcom} \in \mathbb {R}^{3\times 3}$ and $K_{dcom} \in \mathbb {R}^{3\times 3}$ are positive-define diagonal matrices of proportional and derivative gains, respectively. Similarly, we compute the desired angular acceleration of the robot’s base $\dot{\omega }_b^d \in \mathbb {R}^3$ as:

$$\begin{aligned} \dot{\omega }_b^d = K_{pbase} e(R_b^d R_b^\top ) + K_{dbase} (\omega _b^d - \omega _{b}), \end{aligned}$$

(4)

where $R_b\in \mathbb {R}^{3\times 3}$ and $R_b^d\in \mathbb {R}^{3\times 3}$ are rotation matrices representing the actual and desired orientation of the base w.r.t. the world reference frame, respectively, $e(.): \mathbb {R}^{3\times 3} \rightarrow \mathbb {R}^3$ is a mapping from a rotation matrix to the associated rotation vector, $\omega _b \in \mathbb {R}^3$ is the angular velocity of the base, whereas $K_{pbase} \in \mathbb {R}^{3\times 3}$ and $K_{dbase} \in \mathbb {R}^{3\times 3}$ are positive-define diagonal matrices of proportional and derivative gains, respectively.

2.3 Computation of the desired GRFs

Given a desired value of the acceleration of the CoM and the angular acceleration of the robot’s base, we want to compute the desired GRFs f. We rewrite (1) and (2) in matrix form as:

$$\begin{aligned} \underbrace{\begin{bmatrix}I&\quad \dots&\quad I \\ [p_{com,1}\times ]&\quad \dots&\quad [p_{com,c}\times ]\end{bmatrix}}_A \underbrace{\begin{bmatrix}f_1\\\dots \\f_c\end{bmatrix}}_f = \underbrace{\begin{bmatrix}m (\ddot{x}_{com}^d+g) \\ I_g \dot{\omega }_b^d\end{bmatrix}}_b, \end{aligned}$$

(5)

where we replaced the actual accelerations with the desired accelerations. This system has 6 equations and $k=3c$ unknowns; since in our experiments $3\le c \le 4$, typically the system has infinite solutions. We exploit this redundancy to satisfy the inequality constraints imposed by the friction cones. At every control loop we solve the following quadratic program:

$$\begin{aligned} \begin{aligned} f^d&= \mathop {\hbox {arg min}}_{f \in \mathbb {R}^k} (Af-b)^\top S (Af-b) + \alpha f^\top W f\\&\quad {{\mathrm{s.t.}}}\quad \underline{d}< C f < \bar{d},\\ \end{aligned} \end{aligned}$$

(6)

where $S \in \mathbb {R}^{6\times 6}$ and $W \in \mathbb {R}^{k\times k}$ are positive-definite weight matrices, $\alpha \in \mathbb {R}$ weighs the secondary objective, $C \in \mathbb {R}^{p \times k}$ is the inequality constraint matrix, $\underline{d}, \bar{d}\in \mathbb {R}^{p}$ the lower/upper bound respectively, with p being the number of inequality constraints. These ensure that (i) the GRFs lie inside the friction cones and (ii) the normal components of the GRFs stay within some user-defined values.

We approximate friction cones with square pyramids to express them with linear constraints. We then define $C, \underline{d}$ and $\bar{d}$ as:

$$\begin{aligned} C = \begin{bmatrix}C_0&\quad \dots&\quad 0 \\ \vdots&\quad \ddots&\quad \vdots \\ 0&\quad \dots&\quad C_c\end{bmatrix} \quad \underline{d} = \begin{bmatrix} \underline{d}_0 \\ \vdots \\ \underline{d}_c\end{bmatrix} \quad \bar{d} = \begin{bmatrix}\bar{d}_0 \\ \vdots \\ \bar{d}_c\end{bmatrix}, \end{aligned}$$

(7)

with:

$$\begin{aligned} C_i = \left[ \begin{matrix} (-\mu _i n_i + t_{1_i})^\top \\ (-\mu _i n_i + t_{2_i})^\top \\ (\mu _i n_i + t_{2_i})^\top \\ (\mu _i n_i + t_{1_i})^\top \\ n_i^\top \\ \end{matrix}\right] \quad \underline{d}_i = \left[ \begin{matrix} -\infty \\ -\infty \\ 0 \\ 0 \\ f_{{min}_i} \end{matrix}\right] \quad \bar{d}_i = \left[ \begin{matrix} 0 \\ 0 \\ \infty \\ \infty \\ f_{{max}_i}\\ \end{matrix}\right] , \end{aligned}$$

(8)

where $n_i\in \mathbb {R}^3$ is the direction normal to the surface, $t_{1_i}$, $t_{2_i}\in \mathbb {R}^3$ are the tangential directions, $\mu _i\in \mathbb {R}$ is the coefficient of friction, and $f_{min_i}, f_{max_i}\in \mathbb {R}$ are the minimum and maximum allowed values for the $i^\text {th}$normal force, respectively; all these values are relative to the $i^\text {th}$contact. In this work we suppose to know the direction normal to the surface. In the future we could integrate vision or haptic perception to estimate the contact surface online. In the cost function of (6) the term $f^\top W f$ regularizes the solution by trading-off the tracking of $\ddot{x}_{com}$ and $\dot{\omega }_b$ with small-magnitude GRFs. We can use the weight matrix W to penalize certain force directions (e.g. to penalize tangential forces). Actually, in our experiments we found more useful to penalize high joint torques rather than high GRFs (see Sect. 5.3).

Fig. 4

Logic diagram of the state machine used in the static walking algorithm. Rectangles represent states, arrows represent transitions, and rounded boxes represent actions associated to transitions

Remark 1

According to our robotic-platform specificities, the presented controller is sufficient to control the whole system. The robot has 18 DoFs (12 joints plus 6 DoFs of the floating base), but as long as it stands on four feet it is subject to 12 rigid-contact constraints. This leaves only 6 unconstrained DoFs, which are exactly the number of DoFs controlled by the presented method. When the robot stands on three feet it has instead 9 unconstrained DoFs: in this phase the 3 additional DoFs are compensated by the control of the position of the swinging foot. However, for systems with more DoFs (e.g. humanoid robots) it is necessary to control the remaining redundancy.

Remark 2

Although this paper focuses on quadruped locomotion, the presented method can accommodate for any number of contact points. For instance we could use virtual models (Pratt et al. 2001) to generate virtual forces at the end-effectors to achieve motion-force tasks. In case of physical interaction, we have to incorporate the effect of the additional contact forces on the centroidal dynamics (i.e., on the vector b in (6)). This would enable to include manipulation tasks to physically interact with the environment.

Remark 3

The weights of the two conflicting terms in the objective function of (6) must be carefully tuned through the parameter $\alpha$. A too strong regularization causes big tracking errors, thus negatively affecting the robot equilibrium.

Remark 4

Problem (6) always has a solution. Nonetheless, if the desired accelerations require GRFs that violate the inequality constraints, the controller does “the best that it can” in the least-squares sense. Therefore, it is crucial to plan trajectories that are coherent with friction constraints.

2.4 Mapping of GRFs to joint torques

We compute the desired joint torques $\tau ^d \in \mathbb {R}^n$ (where n is the number of joints) by superimposing two control actions. First, mapping the desired GRFs $f^d$ into joint space we get the feedforward torques $\tau _{ff}$:

$$\begin{aligned} \tau _{ff} = -S J_c^\top f^d, \end{aligned}$$

(9)

where $J_c \in \mathbb {R}^{k\times n+6}$ is the stacked Jacobian of the contact points and $S =[ 0_{n \times 6}~ I_{n \times n}]$ is a selection matrix that selects the actuated DoFs. This same mapping was used by Ott et al. (2011) and it is valid only for quasi-static motion.

The second part consists of a proportional-derivative (PD) joint-position controller with low gains, which on average contributed only to $\approx$18 $\%$ of $\tau ^d$. This second term is motivated by safety reasons—hydraulic actuators can generate fast and powerful movements—and it is also used to move the swing leg. During the swing motion we increase the PD gains of the swing leg joints to improve tracking capabilities. Overall, we compute the desired torques $\tau ^d$ that we command to the underlying joint-torque controllers (Boaventura et al. 2012) as:

$$\begin{aligned} \begin{aligned} \tau ^d = \tau _{ ff } + PD(q^d,\dot{q}^d, c_{st}), \end{aligned} \end{aligned}$$

(10)

where $q^d \in \mathbb {R}^n, \dot{q}^d\in \mathbb {R}^n$ are the desired joint positions and velocities, respectively, and $c_{st}\in \mathbb {R}^4$ is the vector of boolean variables representing the stance condition of the legs.

3 Static-walking algorithm for quadrupeds

Our static-walking algorithm is a sequential repetition of the following phases: move CoM, unload leg, swing leg, load leg. Each phase is a state of the state machine depicted in Fig. 4. The gait sequence that we used in our climbing experiments is an input parameter of the walking algorithm and it is described in the Appendix. We assume that the robot starts with all four legs in contact with the terrain. A boolean flag $c_{st}$ represents the contact state; changes in the contact state are triggered either by the walking algorithm or by the sensor feedback, depending on the walking phase.

In the move-CoM phase the robot moves its CoM such that its vertical projection intersects the support triangle formed by the three future stance legs (i.e., those that are not about to swing, see Sect. 3.1). This ensures static equilibrium when breaking the contact. A timer regulates the duration $t_{mcom}$ of the move-CoM phase. Then the unload phase starts, which consists in gradually reducing to zero the load on the swing leg (Sect. 3.2). When the time $t_{load}$ has elapsed, the swing phase begins with the computation of the desired foot placement for the swing foot (Sect. 3.3). The foot swings first away from the surface, to achieve step clearance, and then towards it (see Fig. 5). If during the pre-touchdown motion the foot reaches the ground earlier than predicted the swing phase terminates. Otherwise the leg keeps moving (searching motion, see Sect. 3.3) until the foot makes contact. Finally, during the load phase, the number of stance legs is reset to four and the last swing leg is gradually loaded, redistributing the weight equally on all four legs. At the same time the robot’s height is corrected (see Sect. 3.4). After the load phase the next swing leg is taken from the gait sequence and the cycle repeats. The input parameters for the static-walking algorithm (Fig. 2) are: the surface normal $n_i$ for each contact point, the gait sequence GaitS, the step-length offset $stepLoff$, the step height $stepH$, and the time duration of each phase ($t_{mcom}$, $t_{load}$, $t_{sw}$) (see Table 1).

Fig. 5

HyQ robot walking inside a $50^{\circ }$-inclined groove. The CoM is depicted in black and white. The wall inclination is $\theta$. The red dot represents the projection $P_{xy} x_{com}^d(t_{mcom})$ of the desired CoM position $x_{com}^d(t_{mcom})$ on the polygonal approximation of the next support region T, projected on a plane orthogonal to gravity (light blue). The desired trajectory of the swing leg lies on a plane normal to the ground surface, and it depends on the step height ($stepH$) and length ($stepL$) (Color figure online)

3.1 CoM’s trajectory generation

We estimate the CoM position $x_{com}$ w.r.t. an inertial frame $\mathcal {W}$ through leg odometry (Lin et al. 2005). To do this we use joint-angle measurements and the model of the robot kinematics; under the assumption that the stance feet do not move (i.e., no slip), and given that there are always at least three stance feet, the position/orientation of the robot can always be uniquely determined. Since during the load and unload phases a foot may slightly slip, we did not use it for the odometry during these phases.

Table 1 Parameters of the controller

In the move CoM phase the desired CoM trajectory is generated as a 5th-order minimum-jerk spline. The trajectory starts from the current CoM position ($x_{com}^d(0)$) and it ends at the target CoM $x_{com}^d(t_{mcom})$. The target CoM is computed so that $P_{xy}x_{com}^d(t_{mcom})$ lies inside a conservative polygonal approximation of the next support region T, computed using a polytope projection method (Bretl and Lall 2008). $P_{xy}\in \mathbb {R}^{3 \times 3}$ is a projector into a plane perpendicular to gravity (see Fig. 5). Since the steps are adapted to the terrain geometry during the walking, the support triangle can change its inclination w.r.t. gravity, because the feet may not be exactly at the same height. Therefore, to ensure static equilibrium, we consider a projection of the triangle $P_{xy}T$. The position of $P_{xy}x_{com}^d(t_{mcom})$ inside $P_{xy}T$ can be tuned by changing the parameter d, which is the distance from the midpoint of the largest edge of the triangle. The smaller d, the smaller the static-equilibrium margin, but the bigger the walking velocity, because the amplitude of backward motions is reduced (Buchli et al. 2009).

While we generate the desired trajectory of the CoM, we also need to compute the desired trajectories for the joint-level PD controllers of the stance legs. These joint trajectories must of course prevent the PD controllers from “fighting” against the whole-body controller. Since the legs of the robot have only 3 DoFs, we can analytically compute the joint trajectories from the foot trajectories. The trajectories of the feet can in turn be computed from the desired CoM and base orientation. In the following the left subscript indicates the frame in which vectors are represented. Assuming that the stance feet do not move w.r.t. the inertial frame $\mathcal {W}$ (i.e., ${}_{w}\dot{p}_i=0, \forall i \in StanceFeet$), we compute the velocity of the $i^\text {th}$ foot w.r.t. the base frame $\mathcal {B}$ (i.e., ${}_{b}\dot{p}_i$) as a function of the CoM’s velocity ${}_w\dot{x}_{com}$ and the base angular velocity ${}_w\omega _b$:

$$\begin{aligned} {}_{b}\dot{p}_i = R ( {}_{w}\dot{x}_{com} - \begin{bmatrix}R^T {}_{b}p_i\end{bmatrix}_{\times } {}_w\omega _b), \end{aligned}$$

(11)

where $R\in \mathbb {R}^{3\times 3}$ is the rotation matrix from $\mathcal {W}$ to $\mathcal {B}$. Using ${}_w\dot{\omega }^d_{b}(t)$ and ${}_w\dot{x}^d_{com}(t)$ generated by the spliner (in world coordinates), we can then compute ${}_{b}p_i^d$ by integrating ${}_{b}\dot{p}_i^d$. Finally, we compute the desired joint angles for each stance leg to (with inverse kinematics) use as references for the joint PD controllers.

3.2 Leg loading/unloading

The loading/unloading phases are fundamental to prevent discontinuities in the joint torques any time that the number of stance legs changes. We achieve the loading/unloading by splining the upper bound $f_{max,i}$ on the normal force of the leg i, from the current value to 10m/0, where m is the mass of the robot. In particular, we update the $\bar{d}$ vector (inequality constraints) at each time step during these phases.

3.3 Swing leg

At the beginning of the swing phase we compute the step length $stepL_i$ as a fixed offset $stepLoff$ in the forward direction w.r.t. the hip shoulder. Computing the footstep locations w.r.t. to the shoulder—rather than w.r.t. the actual foot position—ensures no drift in the distance between the feet. Then the swing leg trajectory $p_i^d(t)$ is generated on a plane normal to the ground surface, as a function of the user-defined step height $stepH$ and step length $stepL$ (see Fig. 5). The first part of the swing motion is a spline through a via point to achieve step clearance; the second part consists of a surface-approaching motion (pre-touchdown) towards the desired foot placement. During the downward motion, if the contact is made before the planned foothold is reached, the leg stops. Conversely, if the step ends before making contact, the foot keeps moving at constant velocity along the ground normal direction (searching motion) until it either makes contact or reaches the workspace limits. The lowest singular value of the foot Jacobian matrix is monitored to stop the leg motion before getting close to a singularity (e.g. leg completely extended).

3.4 Height correction

Whenever the swing foot makes contact before/after expected the foot-shoulder distance gets smaller/larger, and this affects the height of the robot. Thus, to prevent the robot from gradually “squatting”/“rising” during the walk, we correct the leg’s length. During the load phase, while changing the limit of the normal force, we also move the desired foot position—and the relative desired joint positions—of $\Delta p_i(Z)$:

$$\begin{aligned} \Delta p_i = - \left[ h^d - e_3^\top {}_Bx_{com} - (- e_3^\top p_i(t_{sw})\right] , \end{aligned}$$

(12)

where $h^d \in \mathbb {R}$ is the desired robot height computed at the CoM (see Table 1), ${}_Bx_{com}$ is the position of the CoM in the frame $\mathcal {B}$ (identified as explained in Sect. 5.2) and $e_3^\mathrm{\top }\in \mathbb {R}^{1\times 3}$ is a vector selecting the z component.

4 Experiments

Before carrying out experiments on the real robot we extensively tested the framework in simulation with the SL software package (Schaal 2001). (see attached video). However, for the sake of brevity, we report only the results obtained on the real robot.

4.1 HyQ platform

The experimental platform used in this work is a quadruped robot (Semini et al. 2011) (Fig. 5). The robot weighs 75 kg, it is $1m\times 0.5\times 1m$ ($L\times W\times H$) dimensions and it is equipped with 12 actuated DoFs   i.e., 3 DoFs for each leg. The hip abduction-adduction ($\textit{HAA}$) joints (see Fig. 3) connect the legs to the robot’s torso, creating the lateral leg’s motion, while the hip and knee flexion/extension ($\textit{HFE}$ and $\textit{KFE}$, respectively) create the motion in the sagittal plane. Linear hydraulic cylinders actuate the hip and knee flexion/extension ($\textit{HFE}$ and $\textit{KFE}$, respectively), while the $\textit{HAA}$ are rotary hydraulic actuators. Load-cells, located at the end of the piston rods, measure the force of the hydraulic cylinders. By kinematic transformations, considering the lever arm between the piston attachment and the joint axis, the joints’ torques are computed. Similarly, a custom torque sensor, embedded in the $\textit{HAA}$ joint, provides direct measurements of the torque. An off-board pump brings the pressurized oil to the system through tethered hoses. An inertial measurement unit (IMU) provides measurements of orientation and angular velocity of the robot’s base. Since most of the torque at the joints is due to the GRFs, we estimate the force at the ith foot as: $f_i \simeq -J_i^{-\top } \tau _{leg_i}$, where $J_i\in \mathbb {R}^{3\times 3}$ is the ith leg’s Jacobian and $\tau _{leg_i}\in \mathbb {R}^3$ are the torques of the ith leg’s joints. All the joints of the robot are torque controlled with a high-performance low-level controller (Boaventura et al. 2012). To verify the contact status of the feet we use a threshold on the normal component of the GRFs. We computed all the kinematic transformations using efficient automatically-generated C++ code (Frigerio et al. 2012).

4.2 Groove

A good template to test the capability of our framework is the “horizontal groove” (see Fig. 5). In this experiment the robot must actively push against the wall of the chimney to keep the GRFs inside the friction cones, so preventing slips and consequent falls. For practical reasons we built a horizontal chimney (groove) instead of a vertical one, which has been equivalently good for the proof of the concept. The robot has successfully walked through the entire length (2.5 m) of the groove, with a wall inclination of $\theta =50^{\circ }$. A video of the experiments is available at youtu.be/qOvtbPryygs. Before starting the controller the robot is already inside the groove, with all four feet in contact with the walls. We repeated the experiments six times in a row using the same parameters of the algorithm, and the robot succeeded five times. A video of the six experimental trials is enclosed, showing the failure in trial 2. The failure seems due the fact that when the robot lifted the right-front foot its CoM vertical projection was not inside the support triangle. This may happen because we are neglecting the weight of the legs in the computation of the CoM. The data reported in the following are relative to one of the five successful experiments, in which the robot exhibited similar performances.

4.2.1 Implementation details

The control of the base’s orientation aims to maintain the robot’s base horizontal during the walk. Table 1 reports the values of the parameters used in the experiments. To be conservative we used a friction coefficient ($\mu = 0.5$) lower than the one that we estimated ($\mu =1$) (see Sect. 5.1). This is important to improve the robustness w.r.t. the friction coefficient and terrain topology (i.e., inclination). Indeed, by using a conservative friction coefficient in the optimization problem, uncertainties in the estimation of the terrain’s normal direction are well tolerated. For example, in our experimental trials this ensured a tolerance to slope estimation errors of up to $18^{\circ }$.

The identification of the CoM position (see Sect. 5.2) was crucial for the success of the experiments. Despite having only 2.7 cm of error (in the xy plane) w.r.t. the CoM computed from the CAD model, this was enough to make the robot fall after half a cycle.

The control loop for the low-level torque controller ran at 1 kHz, whereas the whole-body controller ran at 133 Hz. We solved the optimization problem (6) in real-time using the open-source software OOQP (Gertz and Wright 2001). On the onboard pentium PC104 1GHz computer, running under a real-time Linux operating system, the resolution of (6) with $3c=12$ variables ($c=4$ contact points) and $5c=20$ inequality constraints took on average 6.34 ms. Higher control rates could be achieved by using faster QP solvers such as qpOases (Ferreau et al. 2013) of EigQuadProg (Guennebaud et al. 2011), but this did not seem necessary for our application. Using a faster QP solver is however an interesting future direction because it would free computational resources that we could allocate to planning and estimation.

Fig. 6

Experimental results. Tracking of the center of mass during the walking

Fig. 7

Experimental results. Tracking of the base’s orientation during the walking

Fig. 8

Cartesian components of the contact forces in the left-front leg. Red plots are the desired forces generated by the optimizer, while blue plots are the actual contact forces (estimated from joint torques). The difference is due to the action of the PD controller, whose overall influence is on average lower than 18 $\%$ (Color figure online)

4.2.2 Results

Figures 6 and 7 present the tracking of the CoM’s position and the base’s orientation, respectively. Figure 8 plots the tracking of the contact forces of the left-front foot. The feedback ratio $\int { \vert \tau _{PD}\vert dt} / \int {\vert \tau \vert dt }$ is a good metric to determine how accurate our kinematic/dynamic model (e.g. body inertia and estimation of the CoM) of the robot is. In particular the feedback ratio represents the contribution of the PD controller relative to the total commanded torque. The feedback ratio computed for the experimental data of Fig. 8 is $18\,\%$ Fig. 9 shows the distribution of the GRFs on all the legs for the same groove experiments. The GRFs are always inside the friction-pyramid boundaries. Note that the unilateral constraints on the contact forces implicitly restrict the CoP inside the convex hull of the contact points.

Fig. 9

Distribution of the contact forces at the four feet. The plots show the forces along the ground normal direction as a function of the norm of the tangential forces. The green lines represent the estimated boundaries of the friction cones, which correspond to a friction coefficient $\mu = 1$, while the red line represent the conservative friction coefficient of $\mu = 0.5$ set in the controller (Color figure online)

4.2.3 Torque limits

During the walk the robot reached configurations in which the torques needed at the ${\textit{HFE}}$ joints exceeds their limits. Indeed for the sagittal joints the available torque depends on the joints’ positions because the lever arm of the piston varies (nonlinearly) with the joint angle (Semini et al. 2011). We therefore tuned the matrix $W_{\tau }$ to penalize torques at the ${\textit{HFE}}$ joints. We also tried to repeat the experiment with a steeper wall inclination $\theta = 60^{\circ }$, both in simulation and on the robot. The experiment failed because both ${\textit{HFE}}$ and ${\textit{HAA}}$ reached their torque limits and the problem could not be solved by tuning $W_{\tau }$ (see Sect. 5.3). Conversely in simulation, where the torque limitations were absent, the test succeeded.

4.2.4 Comparison with other approaches.

We implemented three other algorithms to compare them with our approach on the same experimental conditions:

• 1. a high-gain joint PD position controller (with $K=500$ Nm/rad and $D=6$ Nms/rad);

• 2. our controller, but without considering the terrain inclination (i.e., $\theta =0^{\circ }$);

• 3. a low-gain PD controller ($K=150$ Nm/rad and $D=3$ Nms/rad) superimposed to a floating-base gravity compensation Righetti et al. (2011).

We computed the floating-base gravity compensation as:

$$\begin{aligned} \tau _{ff} = (N_c S^T)^{\sharp }N_c g, \end{aligned}$$

(13)

where $N_c = {I} - J_c^{\sharp }J_c$ is the null-space projector of the contact Jacobian $J_c \in \mathbb {R}^{k\times (n+6)}$, which is a stack of the stance feet’s Jacobians $J_{c_i} = \begin{bmatrix} J_{B_i}&J_{q_i} \end{bmatrix}$, $(.)^\sharp$ is the Moore-Penrose pseudoinverse, and $g\in \mathbb {R}^{n+6}$ are the generalized forces due to gravity. With all these controllers the robot has lost the traction with the surface when moving the body, demonstrating the importance, for this kind of task, of controlling the GRFs. The first controller does not have an optimization stage and so the feet quickly start to slip. The second controller directs the GRFs on the vertical axis (Z), so once the GRFs leave their friction cones the robot slips and falls. The last controller compensates for gravity using a Moore-Penrose pseudoinverse, which generates a minimum-norm torque vector. This generally corresponds to GRFs pointing through the hip-joint axis. Even though the GRFs could possibly lie inside the friction cones, the lack of an explicit optimization results in the robot slipping and falling when the robot’s base starts moving.

5 Practical issues

Here we present a number of steps taken to ensure the robustness of the robot’s behavior in a real-world environment.

5.1 Friction cone estimation

Before performing the walking experiments we estimated the friction coefficient $\mu$ at the contact between the rubber coating of the robot’s feet and the wall surface. We laid one of the groove walls flat on the ground, with the robot standing statically on top of it. Then we made the robot exert horizontal GRFs, increasing up to the point at which one of the feet slipped. Finally, we chose $\mu = \sqrt{f_x^2 + f_y^2}/f_z)$, where $f_x, f_y$ and $f_z$ are respectively the two tangential components and the normal component of the contact force at the foot, right before slipping.

5.2 Identification of the CoM with static poses

In order to improve the estimation of the center of mass of the robot we identified its location. Since most of the mass of the robot is located in the base, we assumed that the CoM does not depend on the configuration of the legs—as we did in the controller design. This allows us to consider just a lower dimensional model of the robot (e.g. the rigid body of the base). When the robot is still (i.e., $\dot{q} = \ddot{q} = 0$) the net moment at the CoM is zero:

$$\begin{aligned} \Gamma _{com} = \sum _{i=0}^3 (p_{com,i} \times f_i)= \sum _{i=0}^3 (p_i - x_{com}) \times f_i = 0, \end{aligned}$$

(14)

where $f_i \in \mathbb {R}^{3}$ is the GRF at the ith foot and $p_{com,i} \in \mathbb {R}^3$ is the distance from the CoM to the ith foot. The only unknown in this equation is the CoM position $x_{com}$. By collecting force and position measurements over T seconds while the robot was in a set of manually designed static poses, we could write the overconstrained system of equations:

$$\begin{aligned} \underbrace{\begin{bmatrix}[\sum _{i=0}^3 f_i(0)]_{\times } \\ \vdots \\ [\sum _{i=0}^3 f_i(T)]_{\times }\end{bmatrix}}_A x_{com} = \underbrace{\begin{bmatrix}\sum _{i=0}^3 (f_i(0) \times p_i(0)) \\ \vdots \\ \sum _{i=0}^3 (f_i(T) \times p_i(T))\end{bmatrix}}_b \end{aligned}$$

(15)

We designed the static poses to obtain a sufficiently rich regression matrix A. We then estimated the CoM’s position as $\hat{x}_{com} = (A^\top A)^{-1}A^\top b$. The estimated CoM lied at about 2.7 cm (in the xy plane) from the CoM computed from the CAD model. Moreover, by performing a recursive least-squares estimation with forgetting factor, we measured how much the CoM’s estimation varied through all the static poses due to the influence of the mass of the legs. The variations were of $\approx$1 cm; this suggested that approximating the robot’s CoM with the base’s CoM was acceptable for our quasi-static movements. Such an error could be relavant for humanoids but can be tolerated for a quadruped robots (since they have support areas bigger than humanoids in relation to body size). The advantage of this approach over more general methods (Schumacher et al. 2009) is that it requires very little data to perform the identification. Indeed, identifying the CoM of each link of the robot is typically a time-consuming process. Some of the legs parameters (when the robot is standing on the ground) are partially observable (Gautier 1991a). This requires many carefully designed trajectories for the robot body (e.g. to ensure persistent excitation condition (Armstrong 1989; Jovic et al. 2015). Conversely, to identify the robot CoM we just need to set few poses with a non-zero roll and pitch orientation to have the CoM always observable.

5.3 Torque minimization

The joint torque limits proved to be a crucial issue during our experiments. The respect of the joint-torque limits can be achieved in (6) through either the cost function or the inequality constraints. Even though this allows constraint violations, we used the first method because the second one was computationally too expensive. The regularization term $f^\top W f$ can be defined in order to penalize joint torques rather than GRFs. This can be achieved by knowing the relationship between feet forces and torques: $\tau = -S^{\top }J_c^\top f$. Therefore to minimize $\tau ^\top W_{\tau } \tau$, with $W_{\tau }\in \mathbb {R}^{3c\times 3c}$ being a diagonal positive-definite matrix, we set

$$\begin{aligned} W = J_c S^\top W_{\tau } S J_c^\top \end{aligned}$$

This results in implicitly minimizing the torques of the stance-legs’ joints.

5.4 Robustness to friction coefficient

Looking at Fig. 9 it can be noted that GRFs are always close to the cone boundaries. This is expected because, due to the quasi-static motions, gravitational components (mainly vertical) dominates in the body wrench, and using a regularization that minimizes the norm of the torques or of the forces leads to solutions that are close to the cone boundaries (for the actual task). To improve robustness it would be preferable to have a solution where forces are close to the cones’ normals. This is equivalent to penalizing the norms of the feet’s forces in frames that are aligned with the contacts’ normals. To achieve this we could set the following block-diagonal weight matrix (Righetti et al. 2013):

$$\begin{aligned} W = \begin{bmatrix} T_0W_{n_0}T_0^T&\dots&0 \\ \vdots&\ddots&\vdots \\ 0&\dots&T_cW_{n_c} T_c^T\end{bmatrix}, \end{aligned}$$

(16)

where $T_i=\begin{bmatrix}t_{1_i}&t_{2_i}&n_i\end{bmatrix}$ is a rotation matrix whose columns are the coordinate axis of a frame aligned with the contact surface i. The weight matrix for each stance leg i is $W_{n_i} = diag(K_{t_1}, K_{t_2}, 1)$, where $K_{t_1}$ and $K_{t_2}$ are the weights used to penalize the tangential forces in the $t_{1_i}$ and $t_{2_i}$ directions. Despite this regularization would be preferable for the robustness of the controller, due to the torques’ limitations we used the regularization described in Sect. 5.3 in the real experiments.

6 Conclusions and future work

We presented a self-contained planning/control framework for quadrupedal quasi-static walking on high-sloped terrain, reporting experimental results on a torque-controlled quadruped robot. By direct control of the GRFs we could avoid slippage despite the high terrain inclination (i.e., $50^{\circ }$). Similar theoretical control architectures have been presented in recent years (de Lasa et al. 2010; Lee and Goswami 2010; Gehring et al. 2013; Macchietto and Shelton 2009a), but to the best of our knowledge, the few demonstrations on torque-controlled platforms have been limited to humanoid balancing (Hyon et al. 2007; Stephens and Atkeson 2010; Ott et al. 2011) and quadruped locomotion on terrains with low slope ($\le$40$^{\circ }$) (Righetti et al. 2013; Hutter et al. 2012). The presented experiments show that the recent trend of force-based control frameworks can be used to perform locomotion on high-slope terrain. We believe that this capability is essential for the deployment of robots in adverse environments, such as mountains or disaster-recovery scenarios.

In the controller we assumed that the CoM does not depend on the configuration of the legs, though their mass is far from negligible. Despite this simplifying assumption, the use of a lower-dimensional model was sufficient to perform the task. Furthermore, we have shown that a simple procedure is adequate to estimate the few inertial parameters used in our simplified model.

In the near future we plan to relax the simplifying assumptions undertaken in this work (quasi-staticity, lower-dimensional model) and develop a whole-body control framework with optimization of GRFs, joint torques and joint limits. This framework will be suitable to perform more dynamic tasks. Indeed, relaxing the quasi-static assumption (i.e., computing the whole-body dynamics) would allow for more aggressive movements, hence faster locomotion. We want to speed up the controller in order to solve the optimization in real-time, despite the increased computational burden (due to more inequalities and variables).

We plan to perform more challenging tasks like locomotion on different groove shapes (e.g. diverging walls, irregular slopes, turns), on ice and slippery slopes (low friction) and on a moving platform (keep balance).

The framework will also be extended to our Centaur robot (a quadruped base with two arms on top) in order to perform whole-body manipulation tasks. In this scenario the legs can provide assistance to pull or push an object. Furthermore, a body-posture optimization will be implemented with the purpose to increase stability and be more effective to exert a force in a desired direction, while minimizing the torques at the legs’s joints. This is a strategy, to reduce the overall energy expenditure, which is very common for humans.

Fig. 10

(top) Top view of two different support triangles $T_1$ and $T_2$. Relative to $T_1$ we report also the three contact forces $f_1,f_2,f_3$, the distance between the contact points $p_{12}, p_{13}, p_{23}$ and the friction cone of $f_3$. (bottom) Gait sequence for the groove walk experiments

More advanced techniques for the estimation of the base’s position/orientation (Bloesch et al. 2012) could improve the performances of the controller. Finally, we plan to incorporate more information on the geometry of the environment, possibly combining vision and active haptic exploration (e.g. touching three points on the terrain and fitting a plane).

Appendix

1.1 Intuitive justification of foot placement

This section explains our choices regarding foot positioning for quadrupedal walking on v-shaped terrain. We show that, when the robot stands on three feet, having an acute support triangle is convenient for maintaining the robot in equilibrium. We know that the robot is in equilibrium when the net external force and moment (about any point) acting on it are zero. We define a reference frame $O_1$ located at foot 1 (see Fig. 10), with the axis $z_1$ aligned with gravity and the axis $x_1$ pointing towards foot 2 (which we assume to be approximately aligned with foot 1). At the equilibrium, the net moment $m\in \mathbb {R}^3$ about $z_1$ has to be zero, that is:

$$\begin{aligned} P_z m = (P_{xy} p_{12})\times (P_{xy} f_2) + (P_{xy} p_{13}) \times (P_{xy} f_3) = 0,\nonumber \\ \end{aligned}$$

(17)

where $P_{xy}\in \mathbb {R}^{3\times 3}$ projects onto the $x_1y_1$ plane, $P_z\in \mathbb {R}^{3\times 3}$ projects onto the $z_1$ axis, $f_2 (f_3)\in \mathbb {R}^3$ is the GRF at the foot 2 (3), and $p_{12}, p_{13} \in \mathbb {R}^3$ are the lever arms from foot 1 to foot 2 and 3, respectively. The first term of (17) always generates a positive moment about $z_1$ because of the unilaterality constraints, i.e., $f_{2y}>0$. To have equilibrium then we need $f_3$ (i.e., the second term) to generate a negative moment about $z_1$. In other words $(P_{xy}f_3)$ must lie in the right halfspace delimited by the line passing through feet 1 and 3. Similarly, computing the net moment about $z_2$ (i.e., the z axis of the frame $O_2$), we can infer that to have equilibrium $(P_{xy}f_3)$ must lie in the left halfspace delimited by the line passing through feet 2 and 3. This implies that $(P_{xy}f_3)$ must lie—not only inside the friction cone, but also—inside the support cone, that is the cone originating in $O_3$ and delimitated by two sides of the support triangle (green cone in Fig. 10). We can then state that having an acute support triangle leaves more freedom in the choice of $f_3$ because it results in a bigger area of intersection between the friction cone and the support cone. If $p_3$ gets too close to $p_1$ or $p_2$, a part of the friction cone of $f_3$ stops intersecting the support cone, leaving less freedom for the choice of $f_3$ (e.g. red support triangle in Fig. 10).

Taking advantage of these insights we planned contact configurations that generate acute support triangles. A gait sequence that satisfies this requirement is RH, RF, LH, LF, in which we set an initial offset positions for the feet along the x direction (see Fig.10 (bottom)).