Energy-optimal trajectory planning for car-like robots

Abstract

When a battery-powered robot needs to operate for a long period of time, optimizing its energy consumption becomes critical. Driving motors are a major source of power consumption for mobile robots. In this paper, we study the problem of finding optimal paths and velocity profiles for car-like robots so as to minimize the energy consumed during motion. We start with an established model for energy consumption of DC motors. We first study the problem of finding the energy optimal velocity profiles, given a path for the robot. We present closed form solutions for the unconstrained case and for the case where there is a bound on maximum velocity. We then study a general problem of finding an energy optimal path along with a velocity profile, given a starting and goal position and orientation for the robot. Along the path, the instantaneous velocity of the robot may be bounded as a function of its turning radius, which in turn affects the energy consumption. Unlike minimum length paths, minimum energy paths may contain circular segments of varying radii. We show how to efficiently construct a graph which generalizes Dubins’ paths by including segments with arbitrary radii. Our algorithm uses the closed-form solution for the optimal velocity profiles as a subroutine to find the minimum energy trajectories, up to a fine discretization. We investigate the structure of energy-optimal paths and highlight instances where these paths deviate from the minimum length Dubins’ curves. In addition, we present a calibration method to find energy model parameters. Finally, we present results from experiments conducted on a custom-built robot for following optimal velocity profiles.

1 Introduction

Energy optimization is a fundamental requirement to achieve long term autonomous deployments of mobile robots. One of the main bottlenecks for robots is the limited lifetime of on-board batteries. To extend the system lifetime, it is critical to optimize the energy consumption of the robot, in addition to harvesting additional energy. Motion is a major source of energy consumption. In this work, we study the problem of minimizing the energy consumption by optimizing the motion of the robots.

In particular, we focus on car-like robots powered by direct current (DC) motors. It is well-known that the energy consumption of a DC motor depends on its angular speed and acceleration [19]. The angular speed and acceleration of the driving DC motor in turn controls the translational velocity and acceleration of a car-like robot. We study the problem of computing a path and the corresponding velocity profile of a robot so that it consumes a minimum amount of energy to travel.

The classical problem of optimizing the path and velocity profiles for mobile robots while satisfying velocity and/or acceleration constraints is known as kinodynamic planning [5]. The pioneering work for finding minimum length paths for a forward-only car-like robot was done by Dubins [6]. Reed and Shepps [20] extended this work for a car that can go forward and backward. Balkcom and Mason [1] used an optimal control formulation to derive the time optimal trajectories for bounded velocity differential drives. Recently, Chitsaz et al. [3] used similar techniques to give the complete characterization for minimum wheel rotation paths for differential drive robots. As we will show, the minimum length or time paths are not the same as the minimum energy paths. Figure 1 shows one such instance where the energy optimal path deviates from the minimum length (Dubins’) paths.

Fig. 1

The minimum length path consists of 3 circular segments, whereas the minimum energy path consists of a straight line segment and 5 circular segments of varying radii. The optimal velocity profile along the path is given by the color in the heat map along the path. The straight line and circular segments with higher turning radius allow the robot to move at a higher speed and thus for a lesser time leading to lower energy consumption (despite being longer). We explore this trade-off between velocity, turning radius, path length and energy in this paper

Existing literature of finding minimum energy paths for robots includes the work of Sun and Reif [22] who consider the problem of computing the optimal path for robots traversing a terrain. Under the assumption that the friction coefficients are known across the terrain, they show how to compute a path that requires minimum energy to overcome frictional forces. This work generates the path but does not yield an optimal velocity and acceleration profile. Furthermore, the paths found are piecewise linear which cannot be directly applied for car-like robots.

With recent advancements in hybrid and electric vehicles technology, power management and optimization has received considerable interest in the automotive sector (see e.g. [10]). Research studies in this area target power optimization based on the users’ input and driving profiles. However, there has been little work on finding energy efficient trajectories for vehicles that navigate autonomously. Energy optimal trajectory planning has also been studied for robotic manipulators. Gregory et al. [9] studied the problem of finding energy-optimal control inputs for a manipulator with two revolute joints to follow a prescribed path. Wigstrom et al. [25] studied the problem of scheduling jobs for possibly multiple industrial robots, where each job requires the robot to optimize its control profile with respect to energy and follow a prescribed path. Our work differs from this literature in that we use the kinematic and energy model for a car-like robot. In addition, we focus on simultaneously computing the energy optimal path and velocity profile along this path.

In order to compute velocity profiles, the power consumption needs to be modeled. Mei et al. [18] model the power consumption as a sixth-degree polynomial of the robot’s speed using experimentally collected data. However, their model does not incorporate acceleration. More importantly, they use this model to compare velocity profiles but do not address the problem of computing an optimal profile.

Kim and Kim [14] find the optimal velocity profile for a robot moving on a straight line, when the total time to travel is fixed. However, this solution does not incorporate any bound on maximum velocity of the robot. In [13], they propose a rotational trajectory planner that minimizes the energy consumption. They do not present a systematic method to combine the solutions for translational and rotational trajectories. Thus, it is not clear if this approach yields an optimal solution. Wang et al. [24] studied the problem of finding a minimum energy trapezoidal velocity profile. As we will show shortly, trapezoidal profile itself is not optimal in terms of total energy consumption. In addition, they do not consider any upper bound on the velocity of the robot. Further, their technique is only applicable for turn-in-place-move-forward type of motion for differential drives, and is not experimentally verified.

Broderick [2] et al. studied the problem of computing energy-efficient velocity profiles for a tracked robot. The path of the robot was computed using a boustrophedon coverage pattern and decomposed into straight-line segments and turns. The goal was to compute the velocity profile for the left and right tracked wheels along each segment. The cost function for each segment penalized a linear combination of the control inputs, efficiency of the motors, and the fraction of area not covered by the trajectories before the start of the current segment. Based on this cost-function, the paper presented trade-offs between the control inputs and the area covered by the robots.

In this paper, we study the problem of computing paths and velocity profiles for forward-only car-like robot that minimizes the energy consumption in a flat, obstacle-free environment. First, we focus on the case of finding the energy optimal velocity profile when the path is given. Depending on the application, a high-level planner can specify the exact path to be followed by the robot. However, often the velocity along the path is free to be arbitrarily set. For such situations, we present a closed form solution for the velocity and acceleration profile that minimizes the energy consumption, based on our model. Next, we consider the problem of computing the minimum energy path itself, given a start and goal position and orientation (pose) for the robot.

Dubins [6] first showed that the minimum length paths between two poses for car-like robots consists of at most three segments. Furthermore, each segment is one of three types: straight line, left turn with minimum turning radius, and right turn with minimum turning radius. As we discuss in detail in this paper, for minimum energy paths there is a trade-off between the length of the paths, turning radius, frictional forces, velocity and acceleration of the robot. Unlike minimum length paths, a minimum energy path may contain segments with varying turning radius (Fig. 1). To accommodate this, we present a graph (termed Energy Roadmap) which generalizes the notion of Dubins’ paths by including turns with arbitrary radii on a discrete set of poses. The Energy Roadmap also incorporates the closed-form solution for optimal velocity profiles. We show how to build this structure efficiently, and present details of an implementation. Finally, we investigate the structure of minimum energy paths found using our algorithm, and highlight instances when these paths deviate from the Dubins’ paths.

The rest of the paper is organized as follows: The energy model and the formal problem statement are presented in Sect. 2. We derive the optimal velocity profiles with and without a maximum velocity bound for a path with single segment in Sects. 3 and 4 respectively and for multiple segments in Sect. 5. The application of these results to simultaneously compute the minimum energy path and velocity profiles is presented in Sect. 6. Experiments on our custom-robot are presented in Sect. 7 along with a calibration procedure for estimating the parameters of the energy model in Sect. 7.1. We conclude with a discussion on the utility of our results in Sect. 8.

2 Problem formulation

First consider the problem of computing the optimal velocity profile when given a path $\mathcal {\tau }\$on which the robot will move. The instantaneous position of the robot along $\mathcal {\tau }\$is represented by a single variable of time $x(t)$. The linear velocity and acceleration of the robot along this path are represented by $v(t)$ and $a(t)$ respectively. We define the state of the robot by $\mathbf {X}(t) = \left[ x(t),v(t) \right] ^T$. The state transition equation can be written as,

$$\begin{aligned} \dot{\mathbf {X}}(t) = \left[ \begin{array}{l} \dot{x}(t)\\ \dot{v}(t) \end{array}\right] = \left[ \begin{array}{l} v(t)\\ a(t) \end{array}\right] \end{aligned}$$

(1)

where $a(t)$  is the control input.

We first describe the energy consumption model for the robot, before formally stating the problem.

2.1 Energy model

Consider a robot with car-like steering, with forward, translational velocity provided by a DC motor. We use the model described in [19] for energy consumption in a brushed DC motor. This detailed model takes into account the energy dissipated in the resistive winding, the energy required to overcome internal and load friction and the mechanical power delivered to the output shaft. The instantaneous current $i(t)$ in the motors is given by,

$$\begin{aligned} i(t) = \frac{1}{K_T}\left[ T_F + T_L + D_f\omega (t) + (J_M + J_L)\frac{d\omega (t)}{dt}\right] \end{aligned}$$

(2)

and the voltage $e(t)$ across the motor is given by,

$$\begin{aligned} e(t) = i(t) R + K_E \omega (t) \end{aligned}$$

(3)

where $\omega (t)$ is the angular velocity of the motor, $K_E$ and $K_T$ are back-electromotive force and torque constants, $T_F$ and $T_L$ are internal and load frictional torques, $D_f$ is the internal damping, and $J_M$ and $J_L$ are motor and load moments of inertia.

Since linear velocity of the robot and angular velocity of the motor for a car-like robot are proportional to each other, we can rewrite Eqs. 2 and 3 to yield the energy consumption for traveling from $t=0$ to $t=t_f$ as,

$$\begin{aligned} E&= \int \limits _{0}^{t_{f}} \Big [ e(t)i(t) \Big ]dt.\nonumber \\&= \int \limits _{0}^{t_{f}} \Big [ c_1a^2(t) + c_2v^2(t) + c_3v(t) + c_4 + c_5a(t)\nonumber \\&\quad + c_6v(t)a(t) \Big ]dt . \end{aligned}$$

(4)

where constants $c_1, \ldots , c_6$ are combinations of the motor parameters, and $v(t)$ and $a(t)$ are the linear velocity and acceleration of the robot obtained from $\omega (t)$ and the radius of the wheel. When the initial and final velocity values are the same for $\tau$, the net contribution by the terms corresponding to $c_5$ and $c_6$ is zero and can be ignored [19]. Hence, we can rewrite the energy model as,

$$\begin{aligned} E = \int \limits _{0}^{t_{f}} \left[ c_1 a^2(t) + c_2 v^2(t) + c_3 v(t) + c_4 \right] dt. \end{aligned}$$

(5)

The constants $c_1, \ldots , c_4$ depend on the motor parameters which in turn depend on the robot design and the surface on which the robot is moving. These parameters can be obtained using the calibration procedure presented in Sect. 7.1.

The robot’s wheels may slip when it is making a sharp turn at a high speed. The maximum speed with which the robot can move along $\mathcal {\tau }\$is a function of the instantaneous turning radius, the inertia of the robot and the frictional forces with the surface. We assume the maximum centrifugal force without slipping can be specified by a parameter $F_{\text {max}}$. Thus the maximum safe translational speed without slipping will be,

$$\begin{aligned} v_m(t) = \sqrt{\frac{F_\text {max}r(t)}{m}}, \end{aligned}$$

(6)

where $r(t)$ is turning radius and $m$ is the mass of the robot. Any other function of the form $v_m(t) = f(r(t))$ can be easily incorporated in our algorithm.

2.2 Problem statement

Let $D$ be the total length of $\tau$. The energy consumption for a velocity profile $v(t)$ traversing $\mathcal {\tau }\$is given by Eq. 5. The final time $t_f$ can be fixed or kept free. The robot starts from and returns to rest over $\tau$. This gives us the following boundary conditions,

$$\begin{aligned} v(0) = 0, \;v(t_f) = 0,\; x(0) = 0,\; x(t_f) = D \end{aligned}$$

(7)

We study four problems of increasing generality. For the first three problems, the objective is to find a velocity profile $v(t)$ to minimize $E$, subject to the constraints given below:

Problem 1

$\mathcal {\tau }\$consists of a single segment. There is no bound on the maximum velocity of the robot, i.e., $v(t)\ge 0$ for ${0 \le t \le t_f}$. Find the optimal velocity profile $v^*(t)$ minimizing Eq. 5 subject to state transition and boundary constraints given by Eqs. 1 and 7.

Problem 2

$\mathcal {\tau }\$consists of a single segment. The maximum velocity of the robot over $\mathcal {\tau }\$is bounded by constant $v_{m}$, i.e., ${0 \le v(t) \le v_m}$ for ${0 \le t \le t_f}$. Find the optimal velocity profile $v^*(t)$ minimizing Eq. 5 subject to state transition and boundary constraints given by Eqs. 1 and 7.

Problem 3

$\mathcal {\tau }\$consists of $N$ segments composed of straight lines and curves. There is a separate velocity bound for each segment $i$ given by $v_m(i)$. $v_m(i)$ is constant over the $i^{th}$ segment. Let $D(i)$ be the distance to travel for each $1 \le i \le N$. Find the optimal velocity profile $v^*(t)$ minimizing Eq. 5 subject to state transition and boundary constraints given by Eqs. 1 and 7.

Finally, we consider the problem of computing the path $\mathcal {\tau }\$itself. $\mathcal {\tau }\$is specified by the steering control input $\phi (t)$ and the translational velocity $v(t)$. The robot starts at and returns to rest. We do not consider the cost of steering, and assume for simplicity that the robot can instantaneously switch the steering input. There are existing techniques [7, 16] to compute continuous trajectories for car-like robots where the rate of change of the steering input is bounded. The physical interaction between the surface and the steering wheel has also been extensively studied [4]. Since our algorithm first computes a graph (as presented in Sect. 6), smoothness constraints and the steering cost can be included while searching for the optimal solution in the graph. We assume that there are no obstacles in the environment. Many sampling-based planning algorithms that consider obstacles often require a subroutine that computes the optimal cost and path between two poses in an obstacle-free environment (see e.g. [12, 17]). Hence, we focus on the fundamental case of finding energy-optimal paths without considering obstacles, which can be used as subroutines for the general case.

Problem 4

Given start and goal poses, compute a path $\mathcal {\tau }\$ and a velocity profile along this path for a car-like robot to minimize Eq. 5. The velocity at all times must obey the constraint given by Eq. 6. The robot starts at and returns to rest.

The solutions for Problems 1, 2, 3 and 4 are presented in Sects. 3, 4, 5 and 6 respectively. Problems 1 and 2 form special cases of the last two problems and provide insight into the structure of general optimal velocity profiles. We use the generalized solutions of the first two problems, with non-zero boundary conditions, as subroutines for solving Problems 3 and 4.

3 Optimal velocity profile without bounds

In this section, we present the solution to Problem 1, when the path $\mathcal {\tau }\$ consists of a single section with no bound on the maximum velocity of the robot. We first state the necessary conditions and present the closed form solution for the optimal velocity profile. Then, we discuss and provide insights for the structure of the optimal profile. Finally, we compare the optimal profile with the commonly-used trapezoidal velocity profile.

3.1 Solution to problem 1

When there is no bound on the maximum velocity, the Hamiltonian [15] for this problem can be obtained as,

$$\begin{aligned} H(\mathbf {X}(t), a(t), \varvec{\lambda }(t),t)&= c_1 a^2(t) + c_2 v^2(t) + c_3 v(t) \nonumber \\&+\, c_4 + \lambda _1(t) v(t) + \lambda _2(t) a(t) \end{aligned}$$

(8)

where $\lambda _1(t)$ and $\lambda _2(t)$ are the Lagrange multipliers and acceleration $a(t)$ is the control.

The three necessary conditions for $a^*(t)$ to optimize the Hamiltonian for all time $t \in [0, t_f]$ are given as,

$$\begin{aligned} \dot{\mathbf {X}}^*(t) = \frac{\partial H}{\partial \varvec{\lambda }}, \;\;\; \varvec{\dot{\lambda }}^*(t) = -\frac{\partial H}{\partial \mathbf {X}},\;\;\; 0 = \frac{\partial H}{\partial a} \end{aligned}$$

(9)

Applying these necessary conditions, we can solve the resulting partial differential equations for the optimal control and states to get,

$$\begin{aligned} a^*(t)&= k s_1 e^{k t} - k s_2 e^{-k t} \end{aligned}$$

(10)

$$\begin{aligned} v^*(t)&= s_1 e^{k t} + s_2 e^{-k t} - \left( \frac{c_3 + s_3}{2 c_1}\right) \end{aligned}$$

(11)

$$\begin{aligned} x^*(t)&= \frac{s_1 e^{k t}}{k} - \frac{s_2 e^{-k t}}{k} - \left( \frac{c_3 + s_3}{2 c_1}\right) t + s_4. \end{aligned}$$

(12)

where $k = \sqrt{\frac{c_2}{c_1}}$ and $s_1,\ldots ,s_4$ are constants.

We can solve for $s_1,\ldots ,s_4$ in terms of the final time $t_f$ by substituting the boundary conditions given in Eq. 7 for $v^*(t)$ and $x^*(t)$. We obtain,

$$\begin{aligned} s_1&= - \frac{D k}{kt_f + e^{kt_f}(kt_f-2) + 2}, \nonumber \\ s_2&= s_1 e^{kt_f}, \quad s_3 = 2c_1(s_1 + s_2) - c_3\nonumber \\ s_4&= - \frac{s_1-s_2}{k}. \end{aligned}$$

(13)

By substituting in Eqs. 10–12 we obtain,

$$\begin{aligned} a^*(t)&= D\left( \frac{c_2}{c_1}\right) \left( \frac{e^{k(t_f-t)} - e^{kt}}{kt_f + e^{kt_f}(kt_f-2) + 2}\right) , \nonumber \\ v^*(t)&= D\sqrt{\frac{c_2}{c_1}} \left( \frac{(1+e^{kt_f} - (e^{k(t_f-t)}+e^{kt}))}{kt_f + e^{kt_f}(kt_f-2) + 2}\right) , \nonumber \\ x^*(t)&= D\left( \! \frac{(e^{k(t_f-t)}-e^{kt}) - (e^{kt_f}-1) + kt(e^{kt_f}+1)}{kt_f + e^{kt_f}(kt_f-2) + 2}\! \right) \!. \end{aligned}$$

(14)

Since the final time is free, it can be solved for using the additional boundary condition (known as the transversality condition) given by,

$$\begin{aligned} H(\mathbf {X^*}(t_f), a^*(t_f), \varvec{\lambda }^*(t_f),t_f) = 0. \end{aligned}$$

(15)

Substituting Eqs. 10–13 above results in,

$$\begin{aligned} \left( D\frac{c_2}{c_1}+2\right) \big (1-e^{kt_f}\big ) + \sqrt{\frac{c_4}{c_1}}kt_f\big (1+e^{kt_f}\big ) = 0, \end{aligned}$$

(16)

which is an equation in a single variable $t_f$ (all other terms are constant) and can be solved using any existing solver for transcendental equations. (We used MATLAB’s fzero function). Alternatively, if the final time is fixed, we can directly substitute this given value in Eq. 14 to find $v^*(t)$.

Figure 2 shows the optimal velocity profile obtained for traveling a distance of $50$ m using Eq. 14. It can be observed that the profile consists of symmetric acceleration and deceleration curves with an almost-constant velocity region in the middle. From Eqs. 14 and 16, we can show that the peak velocity is reached at $t=t_f/2$ and is given by, $v^*\left( \frac{t_f}{2}\right) = \sqrt{\frac{c_4}{c_2}} \frac{\left( e^{\frac{k}{2}t_f}-1\right) }{\left( e^{\frac{k}{2}t_f}+1\right) }$. The corresponding optimal control profile $a^*(t)$ is shown in Fig. 3. The acceleration profile is a smooth exponentially decreasing function. The acceleration is almost zero in the middle region (exactly zero at $t=t_f/2$).

Fig. 2

The optimal velocity profile $v^*(t)$ for a distance $D=50$ m using $c_1,\ldots ,c_4$ obtained during calibration in Sect. 7.1. The optimal profile consists of symmetric exponential curves, reaching a maximum velocity at $t=t_f/2$

Fig. 3

Optimal control $a^*(t)$ obtained for traveling a distance of $D=50$ m corresponding to the optimal velocity profile shown in Fig. 2

3.2 Structure of the optimal profile

The optimal velocity profile shows similar structure when the distance to travel $D$ varies. Figure 4 shows the optimal velocity profiles for traveling four different distances. The optimal profile reaches the same peak velocity and does not go faster even if the distance to travel increases.

Fig. 4

Optimal Velocity $v^*(t)$ profiles obtained for traveling distances $D=5, 35, 70, 100$ m follow a similar structure

From the cost function (Eq. 5), we see that both higher velocities (through terms $c_2$ and $c_3$) and longer times (through $c_4$) are penalized by higher energy cost. Consider a time-optimal trajectory where the solution would be to move as fast as possible, subject to maximum acceleration and deceleration. Such a trajectory would pay a much higher instantaenous cost (through terms $c_1,c_2,c_3$) but integrated over a shorter time. The energy-optimal trajectory, on the other hand, achieves the optimal energy trade-off between moving faster (and consequently for a lesser time) and moving slower (and for longer times). In constrast to a time-optimal trajectory, the solution for the energy-optimal trajectory does not exceed the peak velocity of $\sqrt{\frac{c_4}{c_2}}$. The following lemma sheds light on this underlying structure for the optimal velocity profiles.

Lemma 1

Consider an arbitrary velocity profile $v(t)$ traveling a distance $D$. Let the total energy consumption of $v(t)$ be $E$. If the given profile crosses $\sqrt{\frac{c_4}{c_2}}$ at times $t_i$ and $t_{i+1}$, we can replace this section of $v(t)$, $t_i \le t \le t_{i+1}$ by a constant velocity section of ${v_c = \sqrt{\frac{c_4}{c_2}}}$, so that the resulting velocity profile covers the same distance and consumes energy less than $v(t)$.

3.3 Comparisons with trapezoidal velocity profile

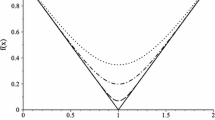
A trapezoidal velocity profile is commonly used for its ease of implementation. A trapezoidal velocity profile (see Fig. 5) consists of a constant acceleration section, followed by a constant velocity section, followed by a constant deceleration section. In [24], Wang et al. computed the optimal trapezoidal velocity profile for traveling a given distance $D$. However, their result is only applicable in the case when there is no bound on the maximum velocity of the robot. Figure 5 shows the general optimal profile and optimal trapezoidal profile computed for traveling a distance of $D=50$ m, with no maximum velocity constraints.

Fig. 5

Optimal trapezoidal profile computed using the same energy function shown together with the general optimal profile for traveling $D=50$ m. The general optimal profile we compute gains higher savings with respect to the trapezoidal profile while accelerating and decelerating. This yields higher energy savings when the total distance to travel is less, a scenario commonly seen when the robot has to frequently start and stop

The general optimal profile we compute gains higher savings with respect to the trapezoidal profile while accelerating and decelerating. For example, the optimal profile yields $1.94~\%$ savings when traveling $1$ m, while the savings drop to $0.32~\%$ when $D=100$ m for the parameters calculated on our custom robot. In situations where the robot has to frequently stop, following an optimal profile would result in more energy savings and a longer lifetime. In addition, these figures are highly system-specific. The velocity profile computed in this work is guaranteed to minimize the energy consumption for the stated assumptions.

4 General solution incorporating maximum velocity bound

The optimal profile given in Sect. 3 does not satisfy any bound on the maximum velocity imposed by the physical limitations of the robot. In this section, we solve for the optimal velocity profile for Problem 2, with a bound on the maximum velocity $v(t)\le v_m$. We now derive the analytical solution for Problem 2 by first discussing the possible structures of an optimal profile. Depending on the value of $v_m$ and $D$, the optimal velocity profile can belong to one of the following two cases.

4.1 Unconstrained optimal profile does not violate bound ${v(t) \le v_m}$

In the case that the optimal velocity profile computed in Sect. 3 does not exceed the bound $v_m$, then this profile is a valid solution for the constrained case too. This happens when $v_m \ge \sqrt{\frac{c_4}{c_2}}$. Additionally, in the case when the distance to travel $D$ is small, the optimal velocity profile may not have enough time to reach $v_m$ or $\sqrt{\frac{c_4}{c_2}}$. We can observe this situation in Fig. 4 when $D=5$ m.

4.2 Unconstrained optimal profile violates the bound ${v(t) \le v_m}$

If the unconstrained optimal profile violates the bound $v_m$, the constrained optimal velocity profile will consist of unconstrained $\mathbf {U}$ ($v(t) < v_m$) and constrained arcs $\mathbf {C}$ ($v(t)=v_m$) joined together at corner points. We show that there exists an optimal profile with a $\mathbf {U}-\mathbf {C}{-}\mathbf {U}$ sequence (or one of its degenerate cases $\{\mathbf {U}{-}\mathbf {C},\mathbf {C}{-}\mathbf {U},\mathbf {C}\}$) having corner points at times $t=t_1$ and $t=t_f-t_2$ (degeneracy occurs when either or both of $t_1$ and $t_2$ equal to 0).

By definition, there cannot be any $\mathbf {U}{-}\mathbf {U}$ or $\mathbf {C}{-}\mathbf {C}$ sequence, as these do not include any corner points. Combining this observation with the following lemma, we show that the constrained velocity profile is limited to a ${\mathbf {U}{-}\mathbf {C}{-}\mathbf {U}}$ sequence or one of its degenerate case.

Lemma 2

The optimal velocity profile cannot consist any sequence of the form $\mathbf {C}{-}\mathbf {U}{-}\mathbf {C}$.

The proof follows a process similar to that in Lemma 1. We show that any ${\mathbf {C}{-}\mathbf {U}{-}\mathbf {C}}$ sequence can be replaced by a single $\mathbf {C}$ segment to reduce the energy consumption.

We now show how to obtain the solution for this case in closed form. Specifically, we show how to obtain $v^*(t)$ for the unconstrained and constrained arcs and compute the corner points $t_1$ and $t_2$.

We begin by writing the velocity constraint in the form of state inequality $\bar{S} = (v(t) - v_m) \le 0$. We convert the state inequality $\bar{S}$ into a control equality $\bar{S}^{(1)}$ and interior point constraint $G$ by differentiating $\bar{S}$ once, leading to $\bar{S}^{(1)} = \dot{v}(t) = u$ and $G = \xi (v(t) - v_m)$. The Hamiltonian is augmented with the control equality constraint between $[t_1, t_f-t_2]$ and is given by $\hat{H} = H + \mu (t)a(t)$. Here, $\mu (t)$ is the slack variable associated with the control constraint and $H$ is given by Eq. 8.

We use the three necessary conditions given in Eq. 9 to obtain the optimal profile in the time interval $[0, t_1]$ and $[t_f-t_2,t_f]$. On the constraint boundary, i.e., $t \in [t_1, t_f-t_2]$, the following necessary conditions must hold [11],

$$\begin{aligned} \dot{\mathbf {X}}^*(t) = \frac{\partial \hat{H}}{\partial \varvec{\lambda }} \;\;\; \varvec{\dot{\lambda }}^*(t) = \frac{\partial \hat{H}}{\partial \mathbf {X}}\;\;\; 0 = \frac{\partial \hat{H}}{\partial a} \end{aligned}$$

(17)

Additionally, on the two corners ($t = t_1$, $t = t_f -t_2$), the following conditions must hold for the optimal solution,

$$\begin{aligned}&\!\!\!H(t_1^{+}) = H(t_1^{-}) {+} \left[ \frac{\partial G}{\partial t}\right] _{t_1}, \varvec{\lambda }(t_1^{+}) = \varvec{\lambda }(t_1^{-}) {-} \left[ \frac{\partial G}{\partial \mathbf {X}}\right] ^T_{t_1} \nonumber \\&\!\!\!H((t_f-t_2)^+) = H((t_f-t_2)^-) \nonumber \\&\!\!\!\varvec{\lambda }((t_f-t_2)^+)= \varvec{\lambda }((t_f-t_2)^-) \end{aligned}$$

Using the conditions given above, we can solve for the optimal control and velocity profile in terms of the constants for the off-boundary exponential curves, and times $t_1$, $t_2$ and $t_f$. The optimal velocity profile in this case is given by,

$$\begin{aligned} v^*(t) = {\left\{ \begin{array}{ll} s_1 \left( e^{kt} + e^{k(2t_1-t)} -(1+e^{2kt_1})\right) , \quad 0 \le t \le t_1 \\ v_m, t_1 \le t \le t_f - t_2 \\ s_2 \left( e^{-k(t_f-t-2t_2)} + e^{k(t_f-t)} - (1 + e^{2kt_2}) \right) ,\\ t_f-t_2 \le t \le t_f. \end{array}\right. } \end{aligned}$$

(18)

We can obtain the values of these constants and times using the initial and final conditions, the transversality condition given in Eq. 15, and the interior point constraint $v^*(t) = v_m, \quad t_1 \le t \le t_f-t_2$ as,

$$\begin{aligned} s_1&= -\frac{v_m}{(e^{kt_1} - 1)^2},\nonumber \\ s_2&= -\frac{v_m}{(e^{kt_2} - 1)^2},\nonumber \\ t_1&= t_2 = \frac{1}{k} \ln \left[ \frac{\sqrt{\frac{c_4}{c_2}} + v_m}{\sqrt{\frac{c_4}{c_2}} - v_m} \right] . \end{aligned}$$

(19)

The final time can then be calculated by using the total distance to travel and the distances traveled in the two exponential curves.

$$\begin{aligned} t_f = t_1 + t_2 + \frac{x^*(t_f-t_2)-x^*(t_1)}{v_m}. \end{aligned}$$

(20)

Figure 6 shows the optimal velocity profile obtained for traveling a distance of $25$ m with the maximum velocity bound set to $v_m = 1$ m/s. Observe that the optimal velocity profile follows an exponential curve till it hits the boundary at $t_1 = 4.06$ s and then stays on the constraint boundary, before following a symmetric exponential curve to zero. However, this profile is not the same as that obtained from the unconstrained solution by setting velocity equal to $v_m$ wherever it exceeds. This unconstrained optimal velocity profile obtained from Sect. 3 is also shown in Fig. 6. The corresponding optimal control $a(t)$ is shown in Fig. 7. The acceleration is zero when $v(t)$ is on the constraint boundary, and follows exponential curves otherwise.

Fig. 6

Optimal velocity ($v^*(t)$) profile obtained for maximum velocity bound $v_m = 1$ m/s. The constrained velocity profile consists of exponential acceleration and deceleration curves with the constraint boundary in the middle. This profile is not the same as that obtained from unconstrained solution by setting velocity to $v_m$ wherever it exceeds

Fig. 7

Optimal control for the case with bound on maximum velocity. Note that the control is zero whenever the velocity is on the constraint boundary (see Fig. 6)

5 Optimal profile over multiple segments

In many applications, a high level task planner is used to find the exact path to be followed by the robot. However, the velocity profile of the robot along this path is free to be optimized. We use the solution from the preceding sections to solve for the problem of finding the optimal velocity profile when the given path consists of $N$ segments (see Fig. 8). We restrict our attention to the case when the paths are composed of straight-line segments and constant curvature turns with possibly different turning radii. For each segment, we are given maximum allowable velocity for the robot $v_{m}(i)$ (see Eq. 6) and the distance to travel $D(i)$, $1 \le i \le N$.

Fig. 8

Typical path for a robot composed of two straight line segments and two turns of different radii. Segments have different maximum allowable velocities, depending on their radii

The robot initially starts at and returns to rest, however the initial and final velocity for the intermediate segments is not constrained to zero. Let $v_0(i)$ and $v_f(i)$ be the initial and final velocities for segment $i$. Thus, $v_0(1) = 0$ and $v_f(N) = 0$. The velocities $v_0(i)$ and $v_f(i)$ can be non-zero for all other intermediate segments. If we know the $v_0(i)$ and $v_f(i)$ that the optimal uses, we can find the entire velocity profile.

5.1 Velocity profile subroutines

While solving for the optimal profiles in Sects. 3 and 4, we considered only zero initial and final velocity boundary conditions. Here, we extend this result for possibly non-zero $v_0$ and $v_f$ as initial and final velocities, and use this extension as a subroutine for solving Problem 3. Note that in Problem 3, the first and the last segments have zero initial and final velocities respectively, and hence the energy model (which ignores the terms $c_5$ and $c_6$ because they cancel-out) remains valid (see proof in appendix).

For segments with no bound on the maximum velocity, by following a process similar to that described in Sect. 3 we get,

$$\begin{aligned} s_1&= \frac{(v_0-v_f)(1-e^{-kt_f}-kt_f) + D k (1-e^{-kt_f})}{e^{kt_f}(2-kt_f)+e^{-kt_f}(2+kt_f)-4}, \nonumber \\ s_2&= \frac{(v_0-v_f)(1-e^{kt_f}+kt_f) - D k (1-e^{kt_f})}{e^{kt_f}(2-kt_f)+e^{-kt_f}(2+kt_f)-4}, \nonumber \\ s_3&= 2c_1(s_1 + s_2) - c_3 -v_0, \nonumber \\ s_4&= - \frac{s_1-s_2}{k}. \end{aligned}$$

(21)

The resulting profiles can be obtained by substituting the above in Eqs. 10–12.

Similarly for segments with a maximum velocity bound $v_m$, the optimal velocity profile is given by,

$$\begin{aligned} v^*(t) = {\left\{ \begin{array}{ll} s_1 \left( e^{kt} + e^{k(2t_1-t)} -(1+e^{2kt_1})\right) + v_0, \quad 0 \le t \le t_1 \\ v_m, t_1 \le t \le t_f - t_2 \\ s_2 \left( e^{-k(t_f-t-2t_2)} + e^{k(t_f-t)} - (1 + e^{2kt_2}) \right) + v_f,\\ t_f-t_2 \le t \le t_f. \\ \end{array}\right. } \end{aligned}$$

(22)

where,

$$\begin{aligned} s_1&= -\frac{(v_m - v_0)}{(e^{kt_1} - 1)^2}, \quad s_2 = -\frac{v_m - v_f}{(e^{kt_2} - 1)^2}, \nonumber \\ t_1&= \frac{1}{k}\ln \left( \frac{c_4 + c_2v_m^2 - 2c_2v_0v_m}{c_4-c_2v_m^2} + \right. \nonumber \\&\left. \frac{2(c_2v_m(c_4-c_2v_0v_m)(v_m-v_0))^{\frac{1}{2}}}{c_4-c_2v_m^2}\right) ,\nonumber \\ t_2&= \frac{1}{k}\ln \left( \frac{c_4 + c_2v_m^2 - ca_2v_fv_m}{c_4-c_2v_m^2} + \right. \nonumber \\&\left. \frac{2(c_2v_m(c_4-c_2v_fv_m)(v_m-v_f))^{\frac{1}{2}}}{c_4-c_2v_m^2}\right) . \end{aligned}$$

(23)

Figure 9 shows the optimal velocity profile obtained for traveling a distance of $30$ m, with velocity bound $v_m = 0.4$ m/s and initial and final velocities $v_0 = 0.3$ m/s and $v_f = 0.1$ m/s respectively. Note that the acceleration and deceleration times are different in this case.

Fig. 9

Optimal velocity profile with $v_0 = 0.3$ m/s, $v_m = 0.4$ m/s and $v_f = 0.1$ m/s for traveling $30$ m

The following theorem summarizes the results for all the cases considered.

Theorem 1

The optimal velocity profile that minimizes the energy consumption given by Eq. 5 for a segment with distance $D$ is given by,

• Equations 13 and 14 when there is no maximum velocity bound or if $v_m > \sqrt{\frac{c_4}{c_2}}$, and initial and final velocities for the segment are both zero. The final time $t_f$ is obtained from Eq. 15.

• Equations 21 and 14 when there is no maximum velocity bound or if $v_m > \sqrt{\frac{c_4}{c_2}}$, and at least one of initial or final velocities for the segment is non-zero. The final time $t_f$ is obtained from Eq. 15.

• Equations 18 and 19 when the maximum velocity bound $v_m \le \sqrt{\frac{c_4}{c_2}}$ and initial and final velocities are both zero for the segment. The final time $t_f$ is obtained from Eq. 20.

• Equations 22 and 23 when the maximum velocity bound $v_m \le \sqrt{\frac{c_4}{c_2}}$, and initial or final velocity is non-zero for the segment. The final time $t_f$ is obtained from Eq. 20. The initial and final velocity for the first and last segment respectively is zero.

We can use the separate cases of this theorem as subroutines to compute the optimal velocity profile for multiple segments using dynamic programming. Note that the last case is only valid when the initial and final velocity of the first and the last segment is zero (i.e., the net effect of $c_5$ and $c_6$ is zero).

5.2 Dynamic programming

Let $V_{max} = \max \{v_m(1),v_m(2),\dots ,v_{m}(i),\dots ,v_m(N)\}$. We then discretize the velocity space at the segment boundary into $M+1$ equal partitions ${v^{(k)}=\frac{k}{M}V_{max}, 0 \le k \le M}$. Let $C(v^{(k)}, i)$ be the cost to reach velocity $v^{(k)}$ at the $i^{th}$ segment boundary. Let $E(v_0,v_m,v_f)$ be a function which gives the energy consumption for an optimal velocity profile in a segment starting with $v_0$ and ending with $v_f$, using the solution in Theorem 1. If either $v_0 > v_m$ or $v_f > v_m$ then the function returns the cost as $E(v_0,v_m,v_f) = \infty$.

We can then use the following recurrence for the $i^{th}$ segment boundary:

$$\begin{aligned} C(v^{(k)}, i)&= \min _{0\le j\le M}\left( C\left( v^{(j)},i\!-\!1) \!+\! E(v^{(j)}, v_{m}(i), v^{(k)}\right) \right) \!,\\&1\le k\le M. \end{aligned}$$

Since the robot initially starts from rest, we have the following,

$$\begin{aligned} C(v^{(k)}, 0) = {\left\{ \begin{array}{ll} 0 &{} k = 0,\\ \infty &{} 1 \le k \le M. \end{array}\right. } \end{aligned}$$

The solution can be obtained by backtracking from $C(v^{(0)}, N)$ and finding optimal segment boundary velocity values. The optimal velocity profile can then be constructed using these optimal boundary velocity values to find individual segment profiles using Theorem 1.

Figure 10 shows the optimal velocity profile obtained for a path consisting of 4 segments. The velocity bounds for these segments are ${v_m=\{0.8, 0.2, 0.8, 0.4\}}$ m/s and the distances ${D = \{6,0.5,6,1\}}$ m respectively. By discretizing velocity at the junction boundaries, we obtain the set of transition velocities using the recurrence given above as,

$$\begin{aligned}&v_0(1) = v_f(4) = 0~\mathrm{m/s},&v_f(1) = v_0(2) = 0.2~\mathrm{m/s},\\&v_f(2) = v_0(3) = 0.2~\mathrm{m/s},&v_f(3) = v_0(4) = 0.4~\mathrm{m/s}. \end{aligned}$$

The profiles between the boundaries are computed using Theorem 1.

Fig. 10

Optimal velocity profile with different bounds for different segments. The given path consists of 4 segments with bounds ${v_m=\{0.8, 0.2, 0.8, 0.4\}}$ m/s and distances ${D=\{6, 0.5, 6, 1\}}$ m

For building the table $C$, we consider $M+1$ discretized velocities at transition boundaries of $N$ segments. The table has size $O(MN)$ and can be constructed in time $O(M^2N)$. This discretization can be avoided when a segment is sufficiently long so that the robot can accelerate (or decelerate) to the bound for the next segment. In this case a greedy approach which chooses the transition velocity at the $i^{th}$ segment boundary using the following rule suffices:

$$\begin{aligned} v(i) = \left\{ \begin{array}{ll} 0, &{} i=0,\\ \min {\{v_m(i-1), v_m(i)\}}, &{} 0<i<N,\\ 0, &{} i=N. \end{array}\right. \end{aligned}$$

We can then use Theorem 1 to compute velocity profiles for each segment $i$ using $v_0(i) = v(i-1)$ and $v_f(i) = v(i)$.

Using a procedure similar to that in Lemma 1 we can show that at any segment boundary, if a velocity profile decelerates further than ${\min \{v_m(i),v_m(i+1)\}}$, it consumes more energy than another profile that only decelerates up to ${\min \{v_m(i),v_m(i+1)\}}$. It can also be shown that the complete velocity profile obtained by combining profiles for each segment is optimal, when each distance $D(i)$ is large. However, when the distances are small, this strategy forces the velocity profile to achieve ${v_f(i) = v(i)}$ leading to higher energy consumption. The optimal solution on the other hand will reach a much lower value for $v_f(i)$. The dynamic programming solution presented here covers this possibility by incorporating all boundary velocity values.

6 Energy optimal paths

In this section, we study the problem of finding an energy optimal path and a velocity profile along this path, given a start and goal poses for a car-like robot (refer Problem 4). Dubins [6] first showed that the minimum length curves between two poses consists of at most three segments. Each segment is either a left or a right turn of minimum turning radius or a straight line path, and no other type. The maximum feasible speed along a curve depends on the turning radius of the robot (Eq. 6). In the absence of any constraints on the maximum speed, we know from the discussion in Sect. 3 that the energy consumption is a monotonically increasing function of the length of the paths. This suggests that for a car-like robot capable of traveling at more than $\sqrt{\frac{c_4}{c_2}}$ at the minimum turning radius, the minimum length paths are also the minimum energy paths. The optimal profile for such paths will be those given in Sect. 3.

In general, computing the energy optimal paths cannot be decoupled from finding the velocity profiles. The structure of the minimum energy paths will depend on the trade-off between turning radii $r(t)$, maximum feasible speed as a function of turning radii $v_m(t)$, the length of the path and the energy parameters. While finding a general solution where the turning radius varies continuously in time seems difficult, we find an approximate solution by restricting the robot to move along a sequence of constant curvature paths.

To find such a path, we build a weighted graph (which we term as the Energy Roadmap) $\mathbf {G}(\mathbf {V},\mathbf {E})$, where each vertex represents a discretized pose and velocity, i.e. $\mathbf {V} = \{(x,y,\theta ,v)\}$.¹ We add an edge between two vertices $\mathbf {v_i}=(x_i,y_i,\theta _i,v_i)$ and $\mathbf {v_j}=(x_j,y_j,\theta _j,v_j)$ if (i) there exists a (directed) circular arc (or straight line) from $(x_i,y_i,\theta _i)$ to $(x_j,y_j,\theta _j)$, and (ii) $v_i$ and $v_j$ are both less than or equal to the maximum feasible speed along this circular arc. The weight on the edge from $\mathbf {v_i}$ to $\mathbf {v_j}$ is set to the energy for the minimum energy velocity profile along this circular arc with start and end speeds set to $v_i$ and $v_j$. The energy is computed using the result in Theorem 1.

The minimum energy path from the start and goal vertex can then be computed by any shortest path algorithm on $\mathbf {G}$, e.g. A* search. The shortest (minimum energy) path will be a sequence of poses and discretized velocities; the entire robot path can be obtained by connecting the sequence of poses with circular arcs or straight line segments and the optimal profile along the path can be obtained by applying Theorem 1 to the corresponding sequence of velocities.

In the Energy Roadmap, although the poses are discretized, we allow connecting any two poses with a circular arc (Fig. 11). Note that we do not impose any grid connectivity or fixed radius turns. Further, although we discretize velocities at a pose, we use the optimal energy profiles leveraging Theorem 1 to interpolate the velocity between two vertices (as opposed to enforcing any fixed profile).

Fig. 11

In the Energy Roadmap we connect any two discretized poses by a circular path, if it exists. a All possible circular paths starting from $(0,0,0)$. The minimum turning radius is set to $1$ m. A total of 2254 paths exists from $(0,0,0)$ using side resolution of $0.1$ m and orientation resolution of $\frac{\pi }{64}$. b Paths starting from $(0,0,0)$ reaching all discretized vertices with $(x,3,\theta )$. There exists a unique circular path starting from a given pose reaching a given position

The complete algorithm is presented in Algorithm 1. The main subroutines GetMinEnergy and GetMinEnergy Profile are applications of Theorem 1. The subroutine GetPath finds the directed circular arc or straight line path. The rest of the subroutines are obvious from their names.

If $|X|$, $|\Theta |$, $|V|$ are the number of discretized positions, orientations and velocities respectively, then the Energy Roadmap has $|\mathbf {V}|=|X|\cdot |\Theta |\cdot |V|$ vertices. Checking for a feasible path between every pair of vertices would require $O(|X|^2|\Theta |^2|V|^2)$ checks. Instead we can reduce the number of checks to $O(|X|^2|\Theta |)$ by observing that there is exactly one circular arc or line from a given pose $(x_i,y_i,\theta _i)$ to a position $(x_j,y_j)$ as shown in Fig. 12. Hence, we only check each pose with every other position for a feasible path (Lines 4–6 in Algorithm 1). Looking up a vertex from a pose or position while adding the edge (FindVertex in Lines 12–13) can be done in constant time by maintaining a map of pointers.

Fig. 12

There exists only one circle passing through a pose $(x_i,y_i,\theta _i)$ and a position $(x_j,y_j)$. All other circular arcs (shown dashed) passing through the same pair of points will not have a tangent aligned along $\theta _i$ at $(x_i,y_i)$. Hence, in building the Energy Roadmap, instead of searching over all pairs of poses ($O(|X|^2\cdot |\Theta |^2)$), we search over pairs of poses and positions ($O(|X|^2\cdot |\Theta |)$)

6.1 Implementation

We implemented² the algorithm in . We used the GNU Scientific Library [8] to perform numerical integration in computing energy and for solving the transversality condition given in Eq. 15. To find the Dubins’ paths, we used the Open Motion Planning Library [21]. Our implementation makes the following optimizations to reduce the runtime and storage requirements:

• In general, the number of edges in $\mathbf {G}$ can be $O(|X|^2|\Theta | |V|^2)$. For a fine discretization, the storage can become prohibitively high. We reduce the storage requirement to $O(|X||\Theta ||V|^2)$ by observing that the paths between two poses are invariant to rotation and translation in the plane. Hence, instead of computing and storing edges between all possible pairs of vertices, we initially create a lookup table consisting of outgoing edges from $(0,0,\theta ,v_0)$, for all $\theta \in \Theta$ and $v_0\in \mathbf {V}$ to all other vertices. While finding the shortest path using A* search, each time a new vertex, say $(x,y,\theta ,v)$, is discovered, we first transform all other vertices in the relative coordinate frame centered at $(x,y)$. We can then extract its neighbors by looking up the relative coordinates in the table. This approach trades the running time of the search phase with the running time for building the Energy Roadmap (Lines 4–18) and the storage required for the Energy Roadmap.

• To further speed up the A* search, we use a lower bound on the energy as a heuristic function. For any vertex $(x_i,y_i,\theta _i,v_i)$, a lower bound on the energy to reach the goal $(x_t,y_t,\theta _t,v_t)$ can be computed as $c_4 \frac{d}{v_m}$ where $d$ is the Euclidean distance between $(x_i,y_i)$ and $(x_t,y_t)$.

A discretization of $0.1~m, \frac{\pi }{64}\text {rad}$ and $0.5$ m/s was used for finding minimum energy trajectories. Energy parameters $c_1,\ldots ,c_4$ were set to 1, $F_{\text {max}} = 0.05$, $\mathrm{m}=1$ and minimum turning radius was set to $1$ m for each instance. The graph, thus created consisted of 6.4 M vertices. The lookup table to store potential edges (as described above) used 10 GB memory. Computing the minimum energy path typically took under 15 mins on a 3.0 GHz computer. To find the optimal velocity profile along the Dubins’ path a resolution of $0.02$ m/s was used for dynamic programming.

6.2 Comparison with Dubins’ paths

Figure 13 shows the energy-optimal paths and velocity profiles obtained using Algorithm 1 for four start and goal poses. These four instances are representative of the trade-off between the turning radius, maximum velocity and energy. Figure 13a shows an instance where the Dubins’ path consisted of three consecutive circular segments of minimum turning radius. The maximum allowable speeds along turns of minimum radii using Eq. 6 was $0.22$ m/s. Hence, the optimal velocity profile along the Dubins’ path (right column) was forced to move at a slower speed, for a longer time consequently paying a higher energy cost. On the other hand, the optimal path consisted of a straight line segment and turns with greater turning radii, allowing the robot to move at a higher velocity. The resulting path, although longer than the Dubins’ path, takes a lesser amount of time to travel and pays a lower energy cost.

Fig. 13

The left column shows the energy-optimal paths found using Algorithm 1. The color profile along the path indicates the optimal velocity profile, also shown in the middle column. The dashed path is the minimum length Dubins’ paths. The energy-optimal velocity profiles along the Dubins’ paths (using the dynamic programming presented in Sect. 5) are shown in the right column. Energy parameters $c_1,\ldots ,c_4$ were set to 1, $F_{\text {max}} = 0.05$, $m=1$ and minimum turning radius was set to $1$ m for each instance. A discretization of $0.1~\mathrm{m}, \frac{\pi }{64}\text {rad}$ and $0.5$ m/s was used for finding minimum energy trajectories. Resolution of $0.02$ m/s was used for dynamic programming

Figure 13b shows an instance where the minimum energy path does not contain a straight line segment, whereas the Dubins’ path does. Both paths begin and end with circular segments of minimum turning radius. The minimum energy path, however, spends lesser time on the minimum turning radius segments and switches to segments with higher turning radius (consequently lower energy) in the middle. We can observe that one of the characteristics of minimum energy paths is to avoid turns with minimum turning radius. Figure 13c shows an instance where the minimum energy path does not contain any segment of minimum turning radius.

We observed that as the length of the minimum radius turns becomes smaller than length of the straight line segment of the Dubins’ path, the energy overhead of traveling at slower speeds decreases. Figure 13d shows one such instance.

It must be noted that these observations are a function of the system parameters. For example, if the robot is capable of moving at very high speeds at minimum turning radius, then the minimum energy path will coincide with the minimum length paths. Nevertheless, Algorithm 1 will find the minimum energy path, subject to the discretization.

7 Calibration and experiments

To test the validity of our results, we performed experiments using our custom robot. We first describe a simple procedure to find the energy model (Eq. 5) of the robot for a given flat surface.

7.1 Calibration

We use a custom-built robot (see Fig. 14) for experiments. Two DC motors with their output shafts coupled together through a gearbox drive the robot. The robot has car-like steering controlled by a servo motor through a fixed steering rod (unlike Ackermann steering). We use separate batteries to drive the DC motors and power the rest of the electronics on the robot.

Fig. 14

Left custom-built robot used in our experiments. Right attopilot voltage and current measurement circuit from SparkFun Electronics

Our method utilizes a simple current and voltage measurement circuit (Fig. 14) connected between the output of the motor and the motor driver circuit. This circuit measures the current flowing through and the voltage across the motor. An optical encoder installed on one of the robot’s wheels measures its linear velocity. In the calibration procedure described next, we fix the steering of the robot so that it drives in a straight line.

We can write Eqs. 2 and 3 as,

$$\begin{aligned} i(t) = b_1 + b_2v(t) + b_3a(t),\nonumber \\ e(t) = b_4 + b_5v(t) + b_6a(t) \end{aligned}$$

(24)

where $b_1,\ldots ,b_6$ are linear combinations of the internal parameters of the motors. The calibration procedure to obtain the energy parameters consists of the following steps:

STEP 1 Drive the robot at a constant velocity ($v_{set}$) for some time interval (we used $10$ s in our calibration experiments). Log the current and voltage across the motor. Repeat for different $v_{set}$ values ranging from the minimum to the maximum achievable velocity for the robot. Figure 15a shows some of the actual profiles obtained during calibration for $v_{set}$ from 0.5 to 2.5 m/s.

Fig. 15

Figures obtained during calibration on the corridor surface. Left to right: a The robot initially accelerates from rest to various set velocity values. We compute the average current and voltage for the region where the robot moves at $v_{set}$ (STEP 1). b Current consumption as a linear function of the velocity, when the motor is not accelerating (STEP 2), c voltage applied to the motor as a linear function of the velocity, when the motor is not accelerating (STEP 2). d Calibration procedure to determine the parameter $c_1$ in the energy model. We accelerate the robot with various set acceleration values $a_{set}$ while logging current and voltage values (STEPS 3 and 4)

STEP 2 Compute the average current and voltage for each of the above trials disregarding the initial acceleration phase. Using Eq. 24, we can find the parameters $b_1$, $b_2$, $b_4$ and $b_5$ using least-squares linear fitting to the data (see Fig. 15b, c).

STEP 3 To find the remaining two terms $b_3$ and $b_6$ in the model, program the robot to drive from rest at various set acceleration values $a_{set}$ to reach some velocity value (we used $1.6$ m/s for our system, see Fig. 15d).

STEP 4 Compute the values of $b_3$ and $b_6$ by substituting $a_{set}$ and $b_1,b_2,b_4$ and $b_5$ values obtained above in Eq. 24 and taking the average of all the readings.

STEP 5 Finally, calculate the required parameters $c_1,\ldots ,c_4$ in Eq. 5 using $c_1 = b_3b_6$, $c_2 = b_2b_5$, $c_3 = b_1b_5 +$ $b_2b_4$, and ${c_4 = b_1b_4}$.

Using the above procedure, we calibrated our robot on three surfaces: indoors on a corridor and outdoors on concrete and grass. The corridor surface was flat whereas the two outdoor surfaces had uneven terrain, the grassy area more so. Figure 15 shows plots for the complete calibration procedure with the corridor surface. Figure 16 shows the current and voltage plots for the grass surface. The current consumption and voltage required for driving the robot are higher for grass than for the corridor surface. Since the surfaces outdoors are uneven, the plots contain more noise than those for corridor. The model parameters computed for all surfaces are shown in Table 1.

Fig. 16

Current and voltage as a function of velocity, for the grass surface outdoors. Since the surface outdoors is not flat, the plots contain more noise than the corridor surface (Fig. 15b, c)

Table 1 Energy model parameters (SI units) obtained using the calibration procedure

7.2 Experiments

We conducted experiments on the smooth corridor surface to experimentally validate the optimal velocity profiles found in Sect. 5 and compared with two other profiles. We first computed the analytical solution for the velocity profile to travel the given distance. We then sampled this profile at $10$ Hz and stored the values in a look-up table.

Figure 17 shows the optimal profile computed using the dynamic programming solution presented in Sect. 5, for a given path three segments with distances ${D=\{10, 3, 10\}}$ m and maximum velocity constraints as ${v_m = \{1, 0.2, 1\}}$ m/s. The computed velocity profile is shown as a dashed curve. The total energy consumed over the entire profile was $595$ J. The actual profile executed has small deviations arising due to noise and disturbances on the surface. In this work, we pre-compute the optimal trajectory for the robot. A useful extension to this could be to design an optimal velocity feedback controller which minimizes the energy consumption.

Fig. 17

Optimal velocity profile executed by the robot for multiple segments. The dashed curve shows the optimal profile computed using the dynamic programming solution for segments with ${D = \{10, 3, 10\}}$ m and maximum velocity constraints ${v_m = 1, 0.2, 1}$ m/s

We compare the energy consumption of our optimal profile with two commonly-used trapezoidal profiles. We chose the maximum speeds for these profiles as 1 and 2 m/s, so that the robot covers the same distance taking more and less time than the optimal respectively. We perform these comparisons for $D=20$ m and $D=45$ m.

Figure 18 shows the optimal, slower and faster velocity profiles executed by the robot in the corridor. The optimal profile computed is also shown in Fig. 18 as dashed. Table 2 shows the comparison of the energy consumption for all the trials conducted. As we can observe, the optimal profile consumes lesser energy than the two sub-optimal profiles. Also, the energy savings become more significant as the distance traveled increases.

Fig. 18

Left optimal velocity profile executed by the robot for traveling $20$ m in $18.4$ s while consuming $296$ J energy. The optimal profile is shown as dashed. Right sub-optimal velocity profiles executed by the robot for traveling $20$ m at maximum set velocities of 1 and 2 m/s. The energy consumption for these profiles is 303 and 319 J

Table 2 Energy consumption during experiments

8 Conclusion

In this work, we studied the problem of computing trajectories for a car-like robot so as to minimize the energy consumed while traveling on a flat surface. We separately considered the problem of computing the energy optimal velocity profiles, and that of simultaneously computing the energy optimal paths and velocity profiles. We presented closed form solutions for the velocity profiles for two cases: no constraints on the robot’s speed, and a single upper-bound on the speed. For the general problem of computing both paths and trajectories, a discretized graph search algorithm that leverages our closed form solution for optimal velocity profiles was presented. Using an implementation of this algorithm, we investigated the structure exhibited by minimum energy paths and highlighted instances when these paths differ from the minimum length (Dubins’) paths. The closed-form velocity profiles and the obstacle-free trajectories can be used as subroutines by sampling-based planners for computing trajectories in the presence of obstacles.

In addition, we presented a calibration procedure for obtaining robot’s internal parameters related to energy consumption. We demonstrated the utility of the calibration procedure and the algorithms presented in the paper with experiments performed on a custom-built robot.

Appendices

Appendix 1: Proof: unconstrained solution

The state transition equation can be written as,

$$\begin{aligned} \dot{\mathbf {X}}(t) = \left[ \begin{array}{l} \dot{x}(t) \\ \dot{v}(t)\end{array}\right] = \left[ \begin{array}{l} v(t) \\ a(t) \end{array}\right] \end{aligned}$$

(25)

The objective is to find a velocity profile $v^*(t)$ which minimizes the total energy required for motion given by the following cost functional,

$$\begin{aligned} J = \int \limits _{0}^{t_{f}} \Big [ c_1 a^2(t) + c_2 v^2(t) + c_3 v(t) + c_4 \Big ] dt, \end{aligned}$$

(26)

where the final time $t_f$ is kept a free variable. The initial boundary conditions are given as,

$$\begin{aligned} x(0) = 0,\quad v(0) = 0, \end{aligned}$$

(27)

and the final boundary conditions are given as,

$$\begin{aligned} x(t_f) = D,\quad v(t_f) = 0. \end{aligned}$$

(28)

1.1 Hamiltonian

The hamiltonian $H(\mathbf {X},\varvec{\lambda },u,t)$ is defined as,

$$\begin{aligned} H(\mathbf {X},\varvec{\lambda },u,t) = J + \lambda _1(t) \dot{x}(t) + \lambda _2(t) \dot{v(t)}, \end{aligned}$$

(29)

where $\lambda _1(t)$ and $\lambda _2(t)$ are the Lagrange multipliers, also called the co-state variables which include the state transition equations as a constraint to the objective.

When there is no bound on the maximum velocity, the Hamiltonian for this problem can be obtained using Eqs. 25 and 26 as,

$$\begin{aligned} H(\mathbf {X}(t), a(t), \varvec{\lambda }(t),t)&= c_1 a^2(t) + c_2 v^2(t) + c_3 v(t) \nonumber \\&+\, c_4 + \lambda _1(t) v(t) + \lambda _2(t) a(t) \end{aligned}$$

(30)

where the acceleration $a(t)$ is the control.

The three necessary conditions for $a^*(t)$ to optimize the Hamiltonian [15] for all time $t \in [0, t_f]$ are given as,

$$\begin{aligned} \dot{\mathbf {X}}^*(t) = \frac{\partial H}{\partial \varvec{\lambda }}, \;\;\; \varvec{\dot{\lambda }}^*(t) = -\frac{\partial H}{\partial \mathbf {X}},\;\;\; 0 = \frac{\partial H}{\partial a} \end{aligned}$$

(31)

By substituting we get,

$$\begin{aligned} \dot{x}(t)&= v(t),\\ \dot{v}(t)&= a(t),\\ \dot{\lambda _1}(t)&= 0,\\ \dot{\lambda _2}(t)&= 2c_2v(t)+c_3+\lambda _1,\\ \lambda _2(t)&= -2c_1a(t), \\ \therefore \lambda _2(t)&= -2c_1\dot{v}(t). \end{aligned}$$

Using the last two equations, we can write,

$$\begin{aligned} -2c_1\ddot{v}(t)&= 2c_2v(t)+c_3+\lambda _1, 2c_1\ddot{v}(t) \\&+\, 2c_2v(t)+c_3+\lambda _1 = 0. \end{aligned}$$

We can solve for this second order differential equation to yield,

$$\begin{aligned} v^*(t) = s_1 e^{k t} + s_2 e^{-k t} - \left( \frac{c_3 + s_3}{2 c_1}\right) \end{aligned}$$

(32)

where $k = \sqrt{\frac{c_2}{c_1}}$ and $s_1 - s_4$ are constants and $\lambda _1 = s_3$.

Applying the state transition equations, we can get the optimal control and states given as,

$$\begin{aligned} a^*(t)&= k s_1 e^{k t} - k s_2 e^{-k t} \end{aligned}$$

(33)

$$\begin{aligned} x^*(t)&= \frac{s_1 e^{k t}}{k} - \frac{s_2 e^{-k t}}{k} - \left( \frac{c_3 + s_3}{2 c_1}\right) t + s_4. \end{aligned}$$

(34)

We can solve for $s_1-s_4$ in terms of the final time $t_f$ by substituting the boundary conditions given in Eqs. 27 and 28 for $v^*(t)$ and $x^*(t)$. We obtain,

$$\begin{aligned} s_1&= - \frac{D k}{kt_f + e^{kt_f}(kt_f-2) + 2}, \nonumber \\ s_2&= s_1 e^{kt_f},\nonumber \\ s_3&= 2c_1(s_1 + s_2) - c_3, \nonumber \\ s_4&= - \frac{s_1-s_2}{k}. \end{aligned}$$

(35)

By substituting in Eqs. 33–34 we obtain,

$$\begin{aligned} a^*(t)&= D\left( \frac{c_2}{c_1}\right) \left( \frac{e^{k(t_f-t)} - e^{kt}}{kt_f + e^{kt_f}(kt_f-2) + 2}\right) , \nonumber \\ v^*(t)&= D\sqrt{\frac{c_2}{c_1}} \left( \frac{(1+e^{kt_f} - (e^{k(t_f-t)}+e^{kt}))}{kt_f + e^{kt_f}(kt_f-2) + 2}\right) , \nonumber \\ x^*(t)&= D\left( \! \frac{(e^{k(t_f-t)}-e^{kt}) - (e^{kt_f}-1) + kt(e^{kt_f}+1)}{kt_f + e^{kt_f}(kt_f-2) + 2} \!\right) \!. \end{aligned}$$

(36)

Since the final time is free, it can be solved for using the additional boundary condition (known as the transversality condition) given by,

$$\begin{aligned} H(\mathbf {X^*}(t_f), a^*(t_f), \varvec{\lambda }^*(t_f),t_f) = 0. \end{aligned}$$

(37)

Substituting Eqs. 33–34 and 35 above results in,

$$\begin{aligned} \left( D\frac{c_2}{c_1}+2\right) \left( 1-e^{kt_f}\right) + \sqrt{\frac{c_4}{c_1}}kt_f\left( 1+e^{kt_f}\right) = 0, \end{aligned}$$

(38)

which is an equation in single variable $t_f$ and can be solved using existing solvers. (We used MATLAB’s solve function). Alternatively, if the final time is fixed, we can directly substitute this given value in Eq. 36 to find $v^*(t)$.

Appendix 2: Proof for Lemma 1

Proof

Consider any velocity profile $v(t)$ shown in Fig. 19. Let $D$ and $E$ be the total distance covered and energy consumed by $v(t)$. This profile crosses $\sqrt{\frac{c_4}{c_2}}$ between times $[t_1,t_2]$ and $[t_3, t_4]$. Let $d_{12}$ and $d_{34}$ be the distances covered by $v(t)$ in these sections. The total energy consumption of $v(t)$ is given by,

$$\begin{aligned} E = E_{01} + E_{12} + E_{23} + E_{34} + E_{45}, \end{aligned}$$

(39)

where $E_{ij}$ refers to the energy consumption to cover the distance $d_{ij}$.

Fig. 19

Sections of this velocity profile crossing ($v_c=\sqrt{\frac{c_4}{c_2}}$) between $[t_1,t_2]$ and $[t_3,t_4]$ can be replaced by constant velocity ($v_c$) sections resulting in a velocity profile that consumes lesser energy to travel the same distance

We construct another velocity profile $v'(t)$ by replacing the sections $[t_1,t_2]$ and $[t_3, t_4]$ by constant velocity $v_c = \sqrt{\frac{c_4}{c_2}}$ sections for time $\frac{d_{12}}{v_c}$ and $\frac{d_{34}}{v_c}$ respectively. The total distance traveled by $v'(t)$ is $D$, same as $v(t)$. The total energy consumption of $v'(t)$ is given by,

$$\begin{aligned} E' = E_{01} + E_{12}' + E_{23} + E_{34}'+E_{45}, \end{aligned}$$

(40)

since $v'(t)$ is the same as $v(t)$ everywhere except $t\in [t_1,t_2]$ and $t\in [t_3,t_4]$.

We now show that $E' \le E$ by proving both $E_{12}' \le E_{12}$ and $E_{34}' \le E_{34}$. This result can then be generalized to velocity profiles with any number of crossing sections in either directions.

First, consider the energy consumption $E_{12}$ for $v(t)$,

$$\begin{aligned} E_{12} = \int _{t_{1}}^{t_{2}} \Big [ c_1 a^2(t) + c_2 v^2(t) + c_4 \Big ] dt + c_3d_{12}. \end{aligned}$$

(41)

Now, let us consider $E_{12}'$. The time taken in this case would be $t_c =\frac{d_{12}}{v_{c}}$. The energy consumption is,

$$\begin{aligned} E_{12}'&= \int _{t_{1}}^{t_{c}} \Big [ c_1 a^2(t) + c_2 v^2(t) + c_3 v(t) + c_4 \Big ] dt, \nonumber \\&= c_2 v_{c} d_{12} + c_3 d_{12} + c_4 \frac{d_{12}}{v_{c}}. \end{aligned}$$

(42)

The distance $d_{12}$ can also be written as,

$$\begin{aligned} d_{12} = \int _{t_{1}}^{t_{2}} \left[ v(t) dt \right] . \end{aligned}$$

(43)

Substituting Eq. 43 in 42, we obtain,

$$\begin{aligned} E_{12}' = c_2 \int _{t_1}^{t_2} v_c v(t) dt + c_3 d_{12} + c_4 \int _{t_1}^{t_2} \frac{v(t)}{v_c} dt. \end{aligned}$$

(44)

Using Eqs. 41 and 44, we can write,

$$\begin{aligned}&\!\!\!E_{12} - E_{12}'= c_1 \int _{t_1}^{t_2} a^2(t) dt \\&\qquad \qquad \qquad + \frac{c_2}{v_c}\int _{t_1}^{t_2} \left[ v_c(t) - v(t) \right] \left[ \frac{c_4}{c_2} - v(t) v_c\right] dt\\&\!\!\!\therefore E_{12} - E_{12}' \ge 0, \end{aligned}$$

since $v(t) \le v_{c} \le \sqrt{\frac{c_4}{c_2}}$. For the section between $t_3$ and $t_4$, we can show that $E_{34}-E_{34}' \ge 0$.

In general we can replace any number of such sections crossing $\sqrt{\frac{c_4}{c_2}}$ to yield another velocity profile with lower energy covering the same distance moving at $\sqrt{\frac{c_4}{c_2}}$. Hence, once the velocity profile hits $\sqrt{\frac{c_4}{c_2}}$, there is no reason to deviate from this value except at the boundary (initial and final conditions). $\square$

Appendix 3: Proof: constrained solution

We begin by writing the velocity constraint in the form of state inequality $\bar{S} = (v(t) - v_m) \le 0$. The state inequality $\bar{S}$ is converted into a control equality and interior point constraint by differentiating $\bar{S}$ once leading to,

$$\begin{aligned}&\bar{S}^{(1)} = \dot{v}(t) = u. \nonumber \\&v(t_1) = v_m \end{aligned}$$

(45)

Along the unconstrained arc, the state transition is governed by Eq. 25. On the constrained arc, the state transition is given by,

$$\begin{aligned} \dot{\mathbf {X}}(t) = \left[ \begin{array}{l} \dot{x}(t) \\ \dot{v}(t)\end{array}\right] = \left[ \begin{array}{l} v_m \\ 0 \end{array}\right] \end{aligned}$$

(46)

The Hamiltonian is augmented with the control equality constraint in $[t_1, t_f-t_2]$ and is given by,

$$\begin{aligned} \hat{H}&= c_1 a^2(t) + c_2 v^2(t) + c_3 v(t) + c_4 \nonumber \\&+\, \lambda _1(t) v(t) + \lambda _2(t) a(t) + \mu (t) a(t) \end{aligned}$$

(47)

where $\mu$ is the slack variable associated with the control constraint. In the interval $[0, t_1]$ and $[t_f-t_2, t_f]$, the Hamiltonian is given by,

$$\begin{aligned} H&= c_1 a^2(t) + c_2 v^2(t) + c_3 v(t) \nonumber \\&+\, c_4 + \lambda _1(t) v(t) + \lambda _2(t) a(t) \end{aligned}$$

(48)

The interior point constraint is given by,

$$\begin{aligned} G = \xi (t) (v(t) - v_m). \end{aligned}$$

(49)

1.1 $0 \le t \le t_1$

Using the necessary condition $\dot{\lambda } = - \frac{\partial H}{\partial x}$ we get,

$$\begin{aligned} \dot{\lambda _1}&= 0,\\ \therefore \quad \lambda _1&= s_3. \end{aligned}$$

and,

$$\begin{aligned} \dot{\lambda _2}&= -\frac{\partial H}{\partial x},\end{aligned}$$

(50)

$$\begin{aligned} \therefore \quad \dot{\lambda _2}&= -\left[ 2c_2 v(t) + c_3 + s_3\right] . \end{aligned}$$

(51)

Applying the third necessary condition, $0 = \frac{\partial H}{\partial a}$ we get,

$$\begin{aligned} 0&= 2c_1a(t) + \lambda _2(t),\\ \therefore \quad \lambda _2(t)&= -2c_1 a(t). \end{aligned}$$

Differentiating the above equation we get,

$$\begin{aligned} \dot{\lambda _2(t)} = -2c_1 \ddot{v}(t). \end{aligned}$$

From Eq. 51 we can write,

$$\begin{aligned}&2c_1\ddot{v(t)} = 2c_2 v(t) + c_3 + s_3,\\&\quad \therefore \quad \ddot{v}(t) - \frac{c_2}{c_1} v(t) - \frac{c_3+s_3}{2c_1} = 0. \end{aligned}$$

The solution for the above differential equation is given as,

$$\begin{aligned} v^*(t)&= s_1 e^{kt} + s_2 e^{-kt} - \frac{c_3+s_3}{2c_1},\\ a^*(t)&= s_1 k e^{kt} - s_2 k e^{-kt},\\ x^*(t)&= \frac{s_1}{k} e^{kt} - \frac{s_2}{k} e^{-kt} - \frac{c_3+s_3}{2c_1}t + s_4,\\ \lambda _1^*(t)&= s_3,\\ \lambda _2^*(t)&= -2c_1 a^*(t). \end{aligned}$$

Using initial conditions $x(0) = 0$ and $v(0) = v_0$, we get,

$$\begin{aligned} s_4&= - \frac{s_1-s_2}{k},\\ \frac{c_3 + s_3}{2c_1}&= s_1 + s_2 - v_0. \end{aligned}$$

Putting these together we get,

$$\begin{aligned} v^*(t)&= s_1 e^{kt} + s_2 e^{-kt} - (s_1+s_2 - v_0),\\ a^*(t)&= s_1 k e^{kt} - s_2 k e^{-kt},\\ x^*(t)&= \frac{s_1}{k} e^{kt} - \frac{s_2}{k} e^{-kt} - (s_1+s_2-v_0)t - \frac{s_1-s_2}{k},\\ \lambda _1^*(t)&= 2c_1{s_1+s_2-v_0} - c_3,\\ \lambda _2^*(t)&= -2c_1 a^*(t), \end{aligned}$$

where $s_1$ and $s_2$ are two constants left to be evaluated.

1.2 $t_f-t_2 \le t \le t_f$

In this section, the system is governed by the same state equation as in the interval $0 \le t \le t_1$. Hence, we get a similar form for the optimal state and control given by,

$$\begin{aligned} v^*(t)&= s_1' e^{-kt_f} e^{kt} + s_2' e^{kt_f} e^{-kt} - \frac{c_3+s_3'}{2c_1},\\ a^*(t)&= s_1' k e^{-kt_f} e^{kt} - s_2' k e^{kt_f} e^{-kt},\\ x^*(t)&= \frac{s_1'}{k} e^{-kt_f} e^{kt} - \frac{s_2'}{k} e^{kt_f} e^{-kt} - \frac{c_3+s_3'}{2c_1}t + s_4',\\ \lambda _1^*(t)&= s_3',\\ \lambda _2^*(t)&= -2c_1 a^*(t). \end{aligned}$$

where $s_1'\ldots s_4'$ are the new constants to be solved for. Using the final condition, $x(t_f) = D$, we get

$$\begin{aligned} D&= \frac{s_1'}{k} - \frac{s_2'}{k} - \frac{c_3+s_3'}{2c_1}t_f+s_4',\\ \therefore \quad s_4'&= D - \left[ \frac{s_1'}{k} - \frac{s_2'}{k} - \frac{c_3+s_3'}{2c_1}t_f \right] . \end{aligned}$$

Using the second final condition, $v(t_f) = v_f$ we get,

$$\begin{aligned} v_f&= s_1' + s_2' - \frac{c_3+s_3'}{2c_1},\\ \therefore \quad s_3'&= 2c_1(s_1'+s_2'-v_f) - c_3. \end{aligned}$$

The equations can then be written as,

$$\begin{aligned} v^*(t)&= s_1' e^{-k(t_f-t)} + s_2' e^{k(t_f-t)} - (s_1' + s_2' - v_f),\\ a^*(t)&= s_1' k e^{-k(t_f-t)} - s_2' k e^{k(t_f-t)},\\ \lambda _1^*(t)&= 2c_1(s_1'+s_2'-v_f) - c_3,\\ \lambda _2^*(t)&= -2c_1 a^*(t). \end{aligned}$$

1.3 Corner conditions

We can now use the corner conditions to determine the unknown constants $s_1, s_2, s_1', s_2'$. The corner conditions state that $\lambda ((t_f-t_2)^+) = \lambda ((t_f-t_2)^-)$ and $v((t_f-t_2)^+) = v((t_f-t_2)^-)$ and $\mu ((t_f-t_2)^+) = 0$,

$$\begin{aligned}&H(t_2^+) = H(t_2^-),\\&\therefore \quad a(t_f-t_2) = 0,\\&\therefore \quad s_2' = s_1' e^{-2kt_2}. \end{aligned}$$

Using the other corner condition $v((t_f-t_2)^+) = v((t_f-t_2)^-)$ we have,

$$\begin{aligned}&v(t_f-t_2) = v_m,\\&\quad \therefore \quad s_1' e^{-kt_2} + s_1' e^{-kt_2} - (s_1' + s_1' e^{-2kt_2} - v_f) = v_m,\\&\quad \therefore \quad s_1' = -\frac{v_m - v_f}{(e^{-kt_2}-1)^2}. \end{aligned}$$

Using similar arguments at the other corner $t=t_1$ we get the final form for the optimal velocity profile as,

$$\begin{aligned} v^*(t) = {\left\{ \begin{array}{ll} s_1 \left( e^{kt} + e^{k(2t_1-t)} -(1+e^{2kt_1})\right) + v_0, \\ 0 \le t \le t_1 \\ v_m, t_1 \le t \le t_f - t_2 \\ s_2 \left( e^{-k(t_f-t-2t_2)} + e^{k(t_f-t)} - (1 + e^{2kt_2}) \right) + v_f,\\ t_f-t_2 \le t \le t_f. \\ \end{array}\right. } \end{aligned}$$

where,

$$\begin{aligned}&s_1 = -\frac{(v_m - v_0)}{(e^{kt_1} - 1)^2},\nonumber \\&s_2 = -\frac{v_m - v_f}{(e^{kt_2} - 1)^2},\nonumber \end{aligned}$$

Using the transversality condition $H(t_f) = 0$, we can determine the times $t_1$ and $t_2$ as,

$$\begin{aligned} t_1 = \frac{1}{k}\ln&\left( \frac{c_4 + c_2v_m^2 - 2c_2v_0v_m}{c_4-c_2v_m^2} + \right. \nonumber \\&\quad \left. \frac{2(c_2v_m(c_4-c_2v_0v_m)(v_m-v_0))^{\frac{1}{2}}}{c_4-c_2v_m^2}\right) , \nonumber \\ t_2 = \frac{1}{k}\ln&\left( \frac{c_4 + c_2v_m^2 - ca_2v_fv_m}{c_4-c_2v_m^2} + \right. \nonumber \\&\quad \left. \frac{2(c_2v_m(c_4-c_2v_fv_m)(v_m-v_f))^{\frac{1}{2}}}{c_4-c_2v_m^2}\right) . \end{aligned}$$

(52)

and the final time can then be calculated by using the total distance to travel and the distances traveled in the two exponential curves. It is easy to see that if $v_0$ or $v_f$ is equal to $v_m$, then $t_1 =0$ or $t_2 = 0$ respectively.

Appendix 4: Proof for Lemma 2

Proof

Consider any velocity profile consisting of a $\mathbf {C}-\mathbf {U}{-}\mathbf {C}$ sequence covering distance $D$. We can replace this ${\mathbf {C}{-}\mathbf {U}{-}\mathbf {C}}$ sequence with a single $\mathbf {C}$ section, so that the resulting velocity profile covers the same distance and consumes energy less than the original profile.

Let $v(t)$ be any velocity profile that contains a ${\mathbf {C}{-}\mathbf {U}{-}\mathbf {C}}$ sequence. That is, ${v(t) = v_m(t)}$ for ${t_0 \le t \le t_1}$ and ${t_2 {\le } t {\le } t_3}$ and ${v(t) < v_m}$ between ${t_1 \le t \le t_2}$. The energy consumption of this profile for traveling a distance ${D = d_{01} + d_{12} + d_{23}}$ is ${E = E_{01} + E_{12} + E_{23}}$, where $E_{ij}$ is the energy spent in traveling $d_{ij}$ for $v(t)$. We construct another velocity profile that is identical to $v(t)$ in ${[t_0,t_1]}$ and ${[t_2,t_3]}$ but covers the section $d_{12}$ at ${v(t) = v_m}$. The energy consumption for this new profile differs only in the $d_{12}$ section.

By following a process similar to that in Lemma 1, we can show that ${E_{12}' \le E_{12}}$ leading to ${E' \le E}$. Hence, any ${\mathbf {C}{-}\mathbf {U}{-}\mathbf {C}}$ sequence can be replaced by a single $\mathbf {C}$ segment to reduce the energy consumption. Hence, the optimal velocity profile will never consist of a ${\mathbf {C}{-}\mathbf {U}{-}\mathbf {C}}$ sequence. $\square$

Appendix 5: Proof of energy model for non-zero initial and final velocities

Lemma 3

Let $\mathcal {\tau }\$be a path with $N$ segments starting and returning to rest, i.e., $v_0(1) = 0$ and $v_f(N) = 0$. Let $E_{14}(i)$ and $E_{16}(i)$ be the minimum energy obtained for the $i^{th}$ segment using Eqs. 5 and 4 respectively. Then $\sum _i E_{14}(i) = \sum _i E_{16}(i)$.

Proof

First, consider the energy obtained using Eq. 4. For each segment, we have

$$\begin{aligned} E_{16}(i)&= \int _{0}^{t_{f}} \Big [ c_1a^2(t) + c_2v^2(t) + c_3v(t) \\&\quad + c_4 + c_5a(t) + c_6v(t)a(t) \Big ]dt\\&= \int _0^{t_f} \Big [ c_1a^2(t) + c_2v^2(t) + c_3v(t) + c_4\Big ]dt\\&\quad + \int _0^{t_f}\Big [c_5a(t) + c_6v(t)a(t) \Big ]dt\\&= E_{16}^{14}(i) + E_{16}^{56}(i). \end{aligned}$$

Now we have,

$$\begin{aligned} \sum _i E_{16}(i)&= \sum _i E_{16}^{14}(i) + \sum _i E_{16}^{56}(i)\\&= \sum _i E_{16}^{14}(i)\\&= \sum _i E_{14}(i). \end{aligned}$$

The second statement follows since $\sum _i E_{16}^{56}(i)=0$ when $v_0(0) = v_f(N) = 0$ as given by [19]. That is, the net effect of $c_5$ and $c_6$ is zero when the robot starts and returns to rest. $\square$