Performance benchmarking of quadrotor systems using time-optimal control

Abstract

Frequently hailed for their dynamical capabilities, quadrotor vehicles are often employed as experimental platforms. However, questions surrounding achievable performance, influence of design parameters, and performance assessment of control strategies have remained largely unanswered. This paper presents an algorithm that allows the computation of quadrotor maneuvers that satisfy Pontryagin’s minimum principle with respect to time-optimality. Such maneuvers provide a useful lower bound on the duration of maneuvers, which can be used to assess performance of controllers and vehicle design parameters. Computations are based on a two-dimensional first-principles quadrotor model. The minimum principle is applied to this model to find that time-optimal trajectories are bang-bang in the thrust command, and bang-singular in the rotational rate control. This paper presents a procedure allowing the computation of time-optimal maneuvers for arbitrary initial and final states by solving the boundary value problem induced by the minimum principle. The usage of the computed maneuvers as a benchmark is demonstrated by evaluating quadrotor design parameters, and a linear feedback control law as an example of a control strategy. Computed maneuvers are verified experimentally by applying them to quadrocopters in the ETH Zurich Flying Machine Arena testbed.

1 Introduction

Quadrotor vehicles are an increasingly popular aerial vehicle platform. Advantages compared to other micro unmanned aerial vehicle (UAV) platforms are the ability to hover, robustness and straightforwardness of design due to mechanical simplicity (Pounds et al. 2006), and safety benefits due to smaller rotor sizes compared to most other hover-capable UAVs (Hoffmann et al. 2007).

Most early research on quadrocopter control focused on near-hover operation. This operation was commonly achieved using linear controllers, which were tuned through various strategies (see, for example, Bouabdallah et al. 2004, and references therein). Trajectories are typically generated by connecting waypoints by lines or circles, and choosing flight velocity sufficiently low to satisfy near-hover assumptions (e.g. How et al. 2008).

With the above advantages making quadrocopters attractive platforms for numerous research fields, another key strength of these vehicles is increasingly being exploited: They offer exceptional agility in the rotational degrees of freedom due to the off-center mounting of the propellers, which allows the generation of large torques. Most platforms also provide high thrust-to-weight ratios, allowing fast translational dynamics. This has lead to numerous more complex control strategies that leverage these capabilities by explicitly considering the feasibility of trajectories. Examples include fast translations (Mellinger et al. 2010; Purwin and D’Andrea 2011; Hehn and D’Andrea 2011), flips (Lupashin et al. 2010), and dancing motions (Schoellig et al. 2011). Several authors have also introduced algorithms that generate trajectories from a class of motion primitives (lines, polynomials, or splines) and respect the dynamic constraints of quadrocopters (Hoffmann et al. 2008; Cowling et al. 2007; Bouktir et al. 2008). These algorithms enforce dynamic feasibility by designing trajectories in a two-step process, first determining the shape of the trajectory and subsequently determining an appropriate speed profile such that feasibility constraints are not violated.

While this work has lead to impressive results, it has not answered one key question: Given the specifications of a quadrotor vehicle, how fast can a certain maneuver be completed? More formally, this can be stated as: What is the time-optimal trajectory for given initial and final states? The ability to compute accurate answers to this question offers insight that may be helpful for many performance-related topics: How much of the theoretical speed potential does a certain control strategy utilize? Are there specific maneuvers for which there exists a large improvement potential for a given controller? How do the physical parameters of the vehicle, such as mass or maximum thrust, influence performance?

The computation of time-optimal trajectories provides a useful tool to answer these questions: The duration of such trajectories provides an absolute lower bound, which may be used for comparisons. Several approaches have been proposed to compute time-optimal trajectories: Lai et al. (2006) proposed a direct method using control inputs discretized in time, and solved the resulting optimization problem using genetic algorithms and nonlinear programming. Bouktir et al. (2008) presented a different direct method, exploiting the differential flatness of the system dynamics and parameterizing the output trajectory by a set of control points, which are then connected by B-spline functions. While both methods have been successfully demonstrated, the optimality of solutions remained unanswered.

In this paper, we present an algorithm that allows the computation of state and input trajectories between two states. Pontryagin’s minimum principle is employed to determine the structure of time-optimal trajectories, and computed trajectories can be verified to satisfy the minimum principle conditions. While these conditions are necessary—but not sufficient—for optimality, they do provide a strong argument for the found trajectories.

The computation of maneuvers that satisfy the minimum principle using the algorithm presented herein requires considerable computational effort. This makes it an unattractive proposition in real-time scenarios. However, the off-line computation of a selection of maneuvers, chosen to be representative for the motion of the vehicle in a specific application, provides a lower bound on the maneuver duration, to which real-time capable controllers may be compared as a means of benchmarking their performance. If certain motions are expected to be carried out repeatedly, this method may be used to design nominal trajectories, for which stabilizing controllers could then be designed.

We base our calculations on a two-dimensional first-principles model of the quadrotor vehicle. Because the algorithm presented herein is meant as a benchmarking tool rather than a control algorithm, the choice of a two-dimensional model provides a reasonable trade-off: The omission of the third dimension makes the problem tractable by reducing its dimensionality. At the same time, two-dimensional problems cover a large class of maneuvers that are interesting to benchmark. Through rotations of the coordinate system, all maneuvers that start and end at rest may be treated as two-dimensional problems, as well as maneuvers where initial and final velocities and rotations are aligned with the rotated coordinate system. This provides a large number of control scenarios that may be benchmarked, such that the benchmarking results can be considered representative of the performance.

The quadrotor model is presented in Sect. 2. The structure of time-optimal trajectories is determined in Sect. 3, and the algorithm used to solve the induced boundary value problem is presented in Sect. 4. Numerous sample maneuvers have been computed with this algorithm, a selection of which are shown in Sect. 5. The application of time-optimal maneuvers as a benchmarking tool is demonstrated by computing the influence of model parameters and evaluating the performance of a linear controller (Sect. 6). The computed trajectories are validated in actual flight tests, with the experimental results (Sect. 7) demonstrating their validity.

2 Modeling of vehicle dynamics

This section introduces the two-dimensional first-principles model, on which we base our calculations. Furthermore, a non-dimensionalizing coordinate transformation is employed to reduce the number of model parameters to two.

2.1 First-principles model

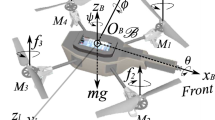
The two-dimensional model has three degrees of freedom: the horizontal position x, the vertical position z, and the pitch angle θ, as shown in Fig. 1.

Fig. 1

Coordinate system and control inputs of the quadrotor model

The quadrocopter is controlled by two inputs: the total thrust force F _T and the pitch rate ω, shown in Fig. 1. The control inputs are subject to saturation. In particular, the pitch rate is limited to a maximum allowable magnitude $\overline {\omega }$, and the thrust is constrained to be between $\underline {F_{T}}$ and $\overline {F_{T}}$:

(1)

(2)

The pitch rate is limited by the range of the gyroscopic on-board sensors, and the maximum collective thrust is determined by the maximum thrust each propeller can produce. Because commonly available motor drivers do not allow changes of the direction of rotation mid-flight, and because the propellers are of fixed-pitch type, it is assumed that the collective thrust is always positive: $\underline {F_{T}}>0$.

The equations of motion are

(3)

(4)

(5)

where g denotes the gravitational acceleration and m is the mass of the quadrocopter.

We assume that the angular velocity $\dot{\theta }$ can be set directly without dynamics and delay. This is motivated by the very high angular accelerations that quadrotors can reach (typically on the order of several hundred rad/s²), while the angular velocity is usually limited by the gyroscopic sensors used for feedback control on the vehicle (Lupashin et al. 2010). This means that aggressive maneuvering is often more severely limited by the achievable rotational rate than the available angular acceleration. The simplification of the model to a constrained rotational rate makes the derivations and numerical computations in this paper tractable.

It should be noted that the first-principles model presented above not only assumes there is direct control of the rotational rate, but also neglects numerous dynamic effects, such as propeller speed change dynamics (Lupashin et al. 2010), blade flapping (Pounds et al. 2006), changes in the angle of attack of the propellers (Huang et al. 2009), and drag forces. Considering that we seek to compute very fast maneuvers, it is to be expected that such effects are significant. However, the purpose of the method presented herein is to allow the benchmarking of quadrotor performance. Because such benchmarks typically serve comparative purposes, modeling inaccuracies play a less significant role than in other applications: As long as the model captures the dominant dynamics, one can expect relative comparisons based on the model to provide meaningful answers. Differences of results based on different models, for example between simulative and experimental results, highlight that the model does not capture all effects; however, when comparing results obtained using the same dynamics, one can expect the neglected effects to, for the most part, cancel out. We therefore believe the trade-off between modeling complexity (and therefore tractability of the optimal control problem) and accuracy to be reasonable. This is further supported by the comparison of numerical and experimental results, which show a reasonable qualitative match with some quantitative discrepancies between simulations and reality (see Sect. 7).

2.2 Non-dimensional model

In order to allow simple comparisons between different configurations, it is beneficial to describe the quadrotor model with as few parameters as possible. We therefore introduce a non-dimensionalizing transformation:

(6)

(7)

(8)

In the transformed coordinates and time, the gravitational acceleration is unity. Defining the state vector

(9)

and the transformed control input vector

(10)

the quadrotor dynamics may be written as

(11)

It is important to note that in the above equations, the derivative $\dot{\mathbf {x}}$ is taken with respect to the transformed time $\hat{t}$.

The transformed control inputs are bounded by the minimum and maximum thrust in units of gravitational acceleration, and unit allowable rotational rate:

$$\underline {u_T} = \frac{\underline {F_{T}}}{m g} \leq u_T\leq \overline {u_T} = \frac{\overline {F_{T}}}{m g},\quad \vert u_R\vert \leq1. $$

(12)

The dimensionless model contains two model parameters: The lower and upper limit of the collective thrust input ($\underline {u_{T}}$ and $\overline {u_{T}}$).

For the remainder of the paper, the hat notation will be omitted. It is understood that calculations are carried out using the dimensionless coordinates, but could equivalently be done in the original system.

3 Minimum principle for time-optimal maneuvers

This section demonstrates how Pontryagin’s minimum principle for time-optimality is applied to the vehicle dynamics. It is shown that the thrust input is bang-bang and that the rotational control is bang-singular, meaning that the control input is always at full positive or negative saturation, except during singular arcs. The system is augmented by the switching function of the rotational rate input, leading to a boundary value problem containing five unknowns. The existence of optimal trajectories is shown.

The time-optimal quadrocopter trajectory between the initial state x ₀ and the final state x _T is characterized by its state trajectory x ^∗(t),t∈[0,T], or equivalently by the corresponding control inputs u ^∗(t),t∈[0,T]. It is the solution to the optimization problem

$$\begin{aligned}&\underset{\mathbf {u}\in \mathbf {U}}{\text{minimize}} & & {T}\\&\text{subject to} & & \dot{\mathbf {x}} = f(\mathbf {x},\mathbf{u}),\\& & & \mathbf {x}(0) = \mathbf {x}_0,\\& & & \mathbf {x}({T}) = \mathbf {x}_T,\end{aligned} $$

(13)

where U denotes the set of all attainable control vectors, as defined by (12).

Minima to this problem may be found using Pontryagin’s minimum principle, which provides necessary conditions for optimality (Bertsekas 2005; Geering 2007). With a cost function equal to 1, i.e., g(x,u)=1, the Hamiltonian for the problem yields

(14)

where p _i denotes the elements of the costate vector p. Note that, because the terminal time of the maneuver is free, the Hamiltonian is always zero along an optimal trajectory (Bertsekas 2005):

$$H\bigl(\mathbf {x}^*,\mathbf{u}^*,\mathbf{p}\bigr) \equiv0 . $$

(15)

Applying the adjoint equation to the Hamiltonian

$$\dot{\mathbf{p}} = -\nabla_\textbf{x}H\bigl(\mathbf{x}^*,\mathbf{u}^*,\mathbf{p}\bigr), $$

(16)

the first four costates may be expressed explicitly as

$$\begin{array}{rcl}\dot{p}_1 = 0&\quad \Rightarrow\quad& p_1 = c_1, \\[3pt]\dot{p}_2 = -p_1&\quad \Rightarrow\quad& p_2 = c_2 - c_1 {t}, \\[3pt]\dot{p}_3 = 0 &\quad \Rightarrow\quad& p_3 = c_3, \\[3pt]\dot{p}_4 = -p_3 &\quad \Rightarrow\quad& p_4 = c_4 - c_3 {t},\end{array} $$

(17)

where the constants c=(c ₁,c ₂,c ₃,c ₄) remain to be determined.

The last element of the costate vector, p ₅, is given by the adjoint (16) to be

$$\dot{p}_5 = -p_2 u_T^* \cos{\theta ^*} + p_4 u_T^* \sin{ \theta ^*}. $$

(18)

The above equation depends on the control input u _T , the trajectory of which is not known a priori. It is therefore not easily possible to express p ₅ explicitly.

3.1 Optimal control inputs

The minimum principle states that the optimal control input trajectory minimizes the Hamiltonian (14) over all possible values of u. Since the two control inputs do not appear in the same summand in the Hamiltonian, it can be minimized separately for u _R and u _T :

3.1.1 Optimal control input $u_{R}^{*}$

For the rotational control input u _R , minimizing (14) results in

$$u_R^* =\underset{u_R\in[-1,+1]}{\operatorname{argmin}}\{ p_5 u_R\}. $$

(19)

If p ₅ changes sign, then $u_{R}^{*}$ switches from −1 to +1 or vice versa. We define

$$\Phi_R := p_5 $$

(20)

as the switching function of $u_{R}^{*}$. If Φ _R is zero for a nontrivial interval of time, then the minimum condition (19) is insufficient to determine $u_{R}^{*}$. In these intervals, which are called singular arcs, $u_{R}^{*}$ is determined using the condition that Φ _R remains zero: It follows that $\dot{\Phi}_{R}$ vanishes, which results in the condition

$$\dot{\Phi}_R = -p_2 u_T^* \cos{\theta ^*} + p_4 u_T^* \sin{ \theta ^*} = 0. $$

(21)

Solving for θ ^∗ using $u_{T}^{*}>0$ (as discussed in Sect. 2.1) and the costate equations (17) yields

$$\theta ^* = \arctan{ \biggl(\frac{p_2}{p_4} \biggr)} = \arctan{\biggl(\frac{c_2 - c_1 {t}}{c_4 - c_3 {t}} \biggr)}. $$

(22)

Differentiating (22) with respect to time gives the trajectory of the control input ${u_{R}^{*}=\dot{\theta }^{*}}$ in a singular arc:

$$u^*_{R,\mathit{sing}} = \frac{c_2 c_3 - c_1 c_4}{(c^2_1 + c^2_3) {t}^2 - 2(c_1 c_2 + c_3 c_4) {t} + c^2_2 + c^2_4}. $$

(23)

The rotational control input $u_{R}^{*}$ of a time-optimal maneuver of the quadrocopter can be written as:

$$u_R^* = \left \{\begin{array}{l@{\quad}l}+1 & \text{if $\Phi_{R} < 0$}, \\[3pt]u^*_{R,\mathit{sing}} & \text{if $\Phi_{R} = 0$}, \\[3pt]-1 & \text{if $\Phi_{R} > 0$}.\end{array}\right . $$

(24)

This type of optimal control trajectory is referred to as bang-bang singular control or bang-singular control (Bertsekas 2005; Ledzewicz et al. 2009).

3.1.2 Optimal control input $u_{T}^{*}$

To compute the optimal control trajectory for the thrust input $u_{T}^{*}$, the sum of all terms of the Hamiltonian containing u _T must be minimized:

$$u_T^* = \underset{u_T\in[\underline {u_T},\overline {u_T}]}{\operatorname {argmin}}\bigl\{p_2 u_T\sin{ \theta ^*} + p_4u_T\cos{ \theta ^*} \bigr\}. $$

(25)

Again, we define a switching function

$$\Phi_T := p_2 \sin{ \theta ^*} + p_4\cos{ \theta ^*}. $$

(26)

For a singular arc to exist, Φ _T must be zero for a nontrivial interval of time. Setting Φ _T to zero and solving for θ ^∗ yields

$$\theta ^* = \arctan \biggl(-\frac{p_4}{p_2} \biggr) =\arctan\biggl(\frac{c_3 {t} - c_4}{c_2 - c_1 {t}} \biggr). $$

(27)

The pitch angle θ ^∗ is determined by the rotational control input $u_{R}^{*}$. If $u_{R}^{*}$ is in a regular interval, then the pitch angle is an affine function of time, and (27) can not be satisfied over a nontrivial time interval. It can therefore be concluded that $u_{T}^{*}$ cannot be in a singular arc when $u_{R}^{*}$ is regular. If $u_{R}^{*}$ is singular, θ ^∗ is given by (22). It follows that, for a singular arc of $u_{T}^{*}$ to exist, the pitch angle trajectory defined by (22) and by (27) must be identical:

$$\arctan \biggl(\frac{c_2 - c_1 {t}}{c_4 - c_3 {t}} \biggr) =\arctan \biggl(\frac{c_3 {t} - c_4}{c_2 - c_1 {t}}\biggr). $$

(28)

Taking the tangent of both sides and multiplying the constraint out yields

$$\bigl(c^2_1 + c^2_3\bigr){t}^2 - 2 (c_1 c_2 + c_3c_4) {t} + c^2_2 + c^2_4= 0. $$

(29)

Neglecting the trivial case c=(0,0,0,0), condition (29) cannot hold for a nontrivial interval of time. The thrust control input $u_{T}^{*}$ therefore does not contain singular arcs and can be written as

$$u_T^* = \left \{\begin{array}{l@{\quad}l}\overline {u_T} & \text{if $\Phi_{T} \leq0$}, \\[3pt]\underline {u_T} & \text{if $\Phi_{T} > 0$}.\end{array}\right . $$

(30)

3.2 Augmented system

Because only the derivative of the switching function Φ _R is given, we augment the system equations (11) with an additional state, representing the switching function Φ _R . We define ${\mathbf {x_{a}}=(\mathbf{\mathbf {x}}^{*},\Phi_{R})}$, resulting in the augmented system dynamics

(31)

where the control inputs $u_{R}^{*}$ and $u_{T}^{*}$ are given by the control laws (24) and (30). A quadrotor maneuver from x ₀ to x _T that satisfies the minimum principle solves the boundary value problem (BVP)

$$\begin{array}{l}\dot{\mathbf{x}}_a = f_a({t},\mathbf {x_a}), \\[3pt]\mathbf{x}^*(0) = \mathbf {x}_0, \\[3pt]\mathbf{x}^*({T}) = \mathbf {x}_T.\end{array} $$

(32)

The BVP (32) contains six unknowns: The final time T, the four unknown constants c, and the initial value of the switching function Φ _R (t=0). However, the initial value of the switching function may not be chosen freely, but must satisfy (15).¹

3.3 Existence of optimal trajectories

While Pontryagin’s minimum principle provides necessary conditions for optimality, it is useful to verify the existence of optimal trajectories. We apply Roxin’s theorem (Roxin 1962) in order to show this.

We note that all assumptions on the system dynamics of Roxin’s theorem hold, guaranteeing the existence and uniqueness of a solution to the system dynamics and the convexity of the system differential equation (11) with respect to the control inputs u (because the control inputs appear linearly, this is straightforward to see). All that remains is to show the reachability of the target state from the initial state.

We show that there is always a trajectory between two arbitrary states. We note that it is sufficient to find a trajectory from an arbitrary state to the origin. A possible maneuver between two states is then the motion from the initial state to the origin, and the reverse of the motion from the final state to the origin. A strategy to drive the system to the origin can easily be found, for example by successively applying the following steps:

• 1. Apply $\mathbf {u}= (\overline {u_{R}}, \overline {u_{T}})$ or $\mathbf {u}= (\underline {u_{R}},\overline {u_{T}})$ until the pitch angle θ is zero. Thrust commands now influence only the vertical dynamics.

• 2. Use the commands $\mathbf {u}= (0, \overline {u_{T}})$ and $\mathbf {u}= (0, \underline {u_{T}})$ to drive the states z and $\dot{z}$ to zero using a bang-bang strategy.

• 3. Apply rotational rate commands to drive the horizontal degree of freedom to zero, while adjusting the thrust such that the vertical degree of freedom remains at rest. The corresponding control inputs will be $\mathbf {u}= (\overline {u_{R}}, g/ \cos {\theta })$, $\mathbf {u}= (\underline {u_{R}}, g/ \cos{ \theta })$, and u=(0,g/cosθ). The allowable pitch angle during this step is limited by the available thrust, as $g/ \cos{ \theta } \leq \overline {u_{T}}$ must hold.

As shown in Roxin (1962), the existence of the minimum follows from the existence of an arbitrary trajectory to the target state.

4 Algorithm for calculation of time-optimal maneuvers

This section introduces a numerical algorithm that solves the boundary value problem for the augmented system (BVP (32)) between arbitrary initial and final states. The resulting maneuvers satisfy the minimum principle with respect to time-optimality. An implementation of the algorithm in Matlab for free use is available on the first author’s website, and is submitted along with this article. This section aims to provide the reader with a high-level overview of the algorithm used. A more detailed discussion of the individual steps may be found in the Appendix.

Finding a solution to the boundary value problem (32) is generally difficult: The state at the end of the maneuver is a non-convex function of the six unknowns, with many local minima and strongly varying sensitivities. With common boundary value problem solvers providing only local convergence under these conditions, it is necessary to provide a good initial guess for the unknowns or the solution trajectory x _a . However, with no straightforward physical interpretation of the constant vector c and the switching function Φ _R , it is difficult to provide such an initial guess. The application of BVP solvers showed that convergence to the correct solution could only be achieved from initial guesses very close to the correct values, making it almost impossible to initialize the algorithm correctly. The problem is further aggravated by the fact that the numerical integration is highly sensitive to numerical errors when entering or leaving singular arcs, as will be discussed in Sect. 4.4.

The algorithm presented herein relaxes these problems by using more robust optimization methods to produce a good initial guess for the BVP solver. For this, we exploit the known bang-singular structure of maneuvers and parametrize a maneuver by the times at which the control inputs switch, and by the terminal time. This approach, commonly referred to as switching time optimization (STO, Zandvliet et al. 2007), provides the significant advantage of requiring no initial guess of x _a or c. Instead of requiring an initial guess of x _a or c, it requires a guess of the switching times, which are easier to obtain, and which can lead to convergence from a much larger range of initial guesses.

The finding of a solution to the STO problem does not necessarily imply a solution to the conditions derived from the minimum principle. Therefore, the STO is used only as a first step of the algorithm. In a second step, the result of it is used to extract an initial guess of c, which typically lies close enough to the correct values to allow a BVP solver to solve the boundary value problem as a third step, and therefore compute a maneuver that satisfies the minimum principle.

If it is assumed that the maneuver has no singular arcs, the algorithm is less complex and more intuitive. Therefore, an algorithm assuming maneuvers with pure bang-bang behavior is introduced first, and then the modifications necessary for the computation of maneuvers with singular arcs are presented.

4.1 Switching time optimization

Under the assumption that the optimal solution is a pure bang-bang maneuver, the entire maneuver can be characterized by the initial values of the two control inputs, the times at which they switch, and the total duration of the maneuver. The switching time optimization algorithm optimizes over the switching times and maneuver duration, using the weighted sum of square state errors at the end of the maneuver as an objective function.

4.2 Parameter extraction

The result of the switching time optimization is a bang-bang maneuver between the initial and the final state. It is necessary to verify that this maneuver does indeed satisfy the conditions of the minimum principle, as they were derived in Sect. 3. To do this, the constants c=(c ₁,c ₂,c ₃,c ₄) are computed based on the result of the STO, and then used as a starting point for a BVP solver.

To compute the constants, a set of equations is obtained from the known switching times: If the maneuver is to satisfy the minimum principle, the switching functions Φ _R and Φ _T must be zero when a switching time in the control inputs u _T and u _R occurs, respectively.

The thrust switching function Φ _T is known explicitly (26), and it is straightforward to generate constraints from it. The trajectory of Φ _R , on the other hand, is not known explicitly (as shown in Sect. 3, only the derivative $\dot{\Phi}_{R}$ of the switching function is known a priori). However, once the state trajectories are known from the STO, the condition H≡0 (which must hold if the maneuver is time-optimal) can be used to compute Φ _R .

Additional constraints are obtained from the fact that the switching function trajectory Φ _R must be a solution to the differential equation (18), which can be evaluated by numerically integrating the differential equation over time intervals, for example between two switching times.

As shown in the Appendix, all of the resulting constraints are linear in the constants c. The resulting overconstrained system of equations can then be solved for the least-squares solution. If this solution does not satisfy all constraints to an acceptable accuracy, the found maneuver does not satisfy the minimum principle. Reasons for this may be an inappropriate choice of the number of switches in the control inputs, failure of the STO to converge to the correct maneuver, or the existence of singular arcs in the optimal maneuver.

4.3 BVP solver

The constants extracted from the solution of the STO and the corresponding maneuver duration are used as initial guesses in a final step. Using the weighted sum of square final state errors as an objective function, the constants and the maneuver duration are optimized. In this step, the control inputs are determined from the control laws defined by the minimum principle (24) and (30), which ensures that the maneuver indeed satisfies the minimum principle. Because the initial guess is typically very close to the optimal values, the BVP solver converges quickly in most cases.

4.4 Modified algorithm for bang-singular maneuvers

For maneuvers containing singular arcs, the switching time optimization is modified. In addition to the times at which the control inputs switch, the durations for which the rotational control input remains in a singular arc after each switching time are also introduced as optimization variables. It is no longer possible to optimize the switching times without knowledge of the constants c, as they define the control input trajectory in singular arcs. The STO algorithm therefore optimizes over the switching times, the singular arc durations, and the values of the constants c. While this overconstrains the optimization problem (the constants c as well as the switching times and singular arc durations define the times at which control inputs switch), the optimization was seen to be significantly more robust when using this parametrization.

Assuming that the thrust input u _T does not switch at the edges of the singular intervals,² $\dot {\Phi}_{R}$ is continuous over the border of the singular arcs, as can be seen from (21). Consequently, the switching function Φ _R enters and leaves a singular arc tangentially. This makes the maneuver highly sensitive to numerical integration errors, and makes it difficult to determine the singular arc entry and exit points from the numerically integrated switching function. The switching times and singular arc durations are therefore retained as optimization variables in the BVP solver step. This makes it necessary to verify the match between the switching function and these optimization variables after convergence of the BVP solver.

5 Numerical results

In this section, we present a selection of quadrotor maneuvers that were computed using the algorithm introduced in Sect. 4. While the algorithm allows the computation of motions between arbitrary states, the results presented herein focus on position changes where the quadrocopter is at rest at the beginning and at the end of the maneuver.

The quadrotor parameters for which the maneuvers have been computed are based on the ETH Zurich Flying Machine Arena vehicles, as described in Lupashin et al. (2010). Table 1 shows the used numerical model parameters in the dimensional form ($\underline {F_{T}}/m,\overline {F_{T}}/m,\overline {\omega}$). The non-dimensional parameters ($\underline {u_{T}},\overline {u_{T}}$) can easily be calculated from these using the control input transformation (12). While computations were carried out in the dimensionless coordinate system, the maneuvers presented herein have been transformed back to the state variables representing physical dimensions, allowing a more intuitive interpretation.

Table 1 Numerical parameters of the quadrotor model

5.1 Vertical displacements

First, the special case of maneuvers with a purely vertical displacement is considered. At the beginning of the maneuver, the quadrotor is at rest and at a pitch angle of zero, and without loss of generality, the initial position of the quadrotor can be set to the origin:

$$\mathbf{x}_0 = \bigl(x(0),\dot{x}(0),z(0),\dot{z}(0),\theta (0)\bigr) = (0,0,0,0,0).$$

At the end of the vertical displacement maneuver, the quadrotor is at rest again, with no overall horizontal displacement, and a final pitch angle that is a multiple of 2π:

$$\mathbf{x}_T = \bigl(x(T),\dot{x}(T),z(T),\dot{z}(T),\theta (T)\bigr) = (0,0,z_T,0,N 2\pi).$$

To determine time-optimal maneuvers, it is necessary to compare maneuvers for different values of full rotations N, as the equivalence of corresponding terminal states is not included in the maneuver description. The terminal times of these different maneuvers are then compared to determine the fastest one.

We limit the results shown herein to maneuvers with a positive z _T value. Maneuvers have been computed for vertical displacements z _T of 0.1 m to 10 m, with a step size of 0.1 m. In Fig. 2, the maneuver duration T is plotted as a function of the vertical displacement z _T . Furthermore, it shows the switching times for each maneuver. For a particular displacement z _T , the maneuver starts at the bottom of the graph (t=0 s) and, as time passes, moves up in the positive direction of the t-axis. Every time a switching line is crossed, the corresponding control input switches to the value specified in the diagram. The maneuver is finished when the T-curve is reached.

Fig. 2

Maneuver duration T as function of the final vertical displacement z _T for rest-to-rest maneuvers with no horizontal displacement. Additionally, the switching times of u _R are drawn in the plot on the top, and the switching times of u _T in the plot on the bottom. The vertical solid line denotes where the structure of the minimum principle solution changes: on the left the solution without a flip, which is faster for small z _T , and on the right the solution where the quadrocopter performs a flip, which is faster for large z _T . The line with the arrows denotes the example maneuver of Fig. 4

If the desired vertical displacement is small, i.e. for z _T ≤2.4 m, the quadrocopter is within a singular arc during the entire maneuver. The pitch angle remains at exactly θ=0. The thrust is at its maximum at the beginning and switches to its minimum at a time such that the quadrocopter comes to rest due to gravity at the desired height z _T . For z _T ≥2.5 m, it is beneficial to perform a flip and to make use of the thrust for braking while the pitch is around θ≈±π. For z _T ≥6.3 m, a singular arc (which keeps the pitch near θ≈±π for a particular time) appears, as can be seen in Fig. 2. Thus, the flip is stopped for an interval of deceleration. A selection of maneuvers is depicted in Fig. 3, showing the different maneuver shapes for varying displacements.

Fig. 3

Illustration of maneuvers for a purely vertical displacement of 1 m, 3 m, and 5 m. The maneuvers satisfy the minimum principle and for each maneuver, a quadrotor is plotted every 0.04 s or every 0.01 s in the zoom box, respectively

The arrow line in the plots of Fig. 2 denotes an example maneuver with a vertical displacement of z _T =5 m. The state, input and switching function trajectories of this maneuver are shown in Fig. 4. The switches in the control input trajectories in Fig. 4 can be depicted by following the arrow line from t=0 s towards t=T in Fig. 2.

Fig. 4

Input and state trajectories of a vertical displacement maneuver with z _T =5 m. In the plot of the control inputs, the switching functions are also drawn, but note that they are scaled to fit into the plot. The switches of the control input trajectories can be obtained by following the arrow line from t=0 s towards t=T in Fig. 2

5.2 Horizontal displacements

We now consider maneuvers that lead to a purely horizontal displacement. For this case, the initial and final state are

$$\mathbf{x}_0 = (0,0,0,0,0), \qquad \mathbf{x}_T =(x_T,0,0,0,0) .$$

Considerations of symmetry lead to the conclusion that, for purely horizontal displacements, the switching times are symmetric about the half-time of the maneuver. This consideration is not proven here, but has shown to always be correct for the computed horizontal maneuvers, with the resulting symmetric maneuvers satisfying the minimum principle. Using this assumption during the STO, the number of optimization variables can be reduced and the computation of horizontal displacements becomes particularly simple.

Maneuvers have been computed for a displacement x _T ranging from 0.1 m to 15 m, with a step size of 0.1 m. Figure 5 shows the maneuver duration T and the switching times as a function of x _T .

Fig. 5

Maneuver duration T as function of the final displacement x _T for purely horizontal rest-to-rest maneuvers. Additionally, the switching times of u _R are drawn in the plot on the top, and the switching times of u _T in the plot on the bottom

For x _T ≤1.5 m, the maneuver is bang-bang with no singular arcs. At the beginning the quadrotor turns at maximum rate, and around the maximum pitch angle the thrust is switched to its maximum for acceleration. Then it turns in the negative direction to decelerate around the minimum peak of θ, before it goes back to θ=0. At x _T =1.6 m, two singular arcs appear. Roughly speaking, the pitch angle is kept at θ≈±π/2 for acceleration and deceleration, respectively. Because a trade-off between fast acceleration in x and maintaining altitude in z is necessary, the pitch angle is not exactly θ=±π/2 within the singular arcs, and is not constant. For x _T ≥7.9 m, the two singular arcs merge: The quadrotor turns smoothly to a negative θ for deceleration, instead of a sharp turn in the middle of the maneuver. For maneuvers with x _T ≥2.4 m, the thrust control input is always at its maximum value. Figure 6 shows an illustration of some selected maneuvers.

Fig. 6

Illustration of maneuvers for a purely horizontal displacement between 3 m and 15 m. The maneuvers satisfy the minimum principle and for each maneuver, a quadrotor is plotted every 0.02 s

5.3 General displacements

For general two-dimensional displacements, the initial and final states are

$$\mathbf{x}_0 = (0,0,0,0,0), \qquad \mathbf{x}_T =(x_T,0,z_T,0,0).$$

Since the final state of a general displacement contains two variables (x _T and z _T ), the maneuver duration T cannot be easily plotted in a two-dimensional figure. As an example, a maneuver with a displacement of 5 m in horizontal and vertical direction, i.e. a maneuver with x _T =5 m and z _T =5 m, is illustrated here. Figure 7 shows the resulting input, state, and switching function trajectories of this example maneuver. Note that the control inputs and the switching functions indeed fulfill the control laws (24) and (30). This implies that the minimum principle for time-optimality is satisfied.

Fig. 7

Input and state trajectories of an example maneuver with x _T =5 m and z _T =5 m. The scaled switching functions are also drawn in the plot of the control inputs

6 Benchmarking of quadrotor designs and controllers

This section demonstrates the usage of computed time-optimal maneuvers as a benchmarking tool for quadrotor designs and controllers.

6.1 Variation of the quadrotor design parameters

The computation of time-optimal maneuvers allows the analysis of the impact of varying quadrotor parameters. These maneuvers allow the separation of effects of the physical parameters of the vehicle, from those of the control strategy by providing the achievable performance for a control law that fully utilizes the capabilities of the vehicle.

For a varying maximum pitch rate $\overline {\omega }$, the adjusted quadrotor performance can be obtained very easily: As the computations are done in the dimensionless coordinate system where the maximum pitch rate is normalized to unity, a changing $\overline {\omega }$ impacts only the back-transformation to the dimensional coordinates. Consequently, no recomputation of maneuvers is necessary and the structure of the switching times, as plotted in Figs. 2 and 5, does not change.

For varying thrust limits $\underline {F_{T}}$ and $\overline {F_{T}}$ (or equivalently $\underline {u_{T}}$ and $\overline {u_{T}}$), the impact of the changing parameters is not straight-forward. Since $\underline {u_{T}}$ and $\overline {u_{T}}$ are used during the computation of the maneuvers, a complete recalculation is required and the structure of the switching time evolution in Figs. 2 and 5 may change. As an example, maneuvers for a horizontal displacement of x _T =5 m have been computed with a maximum mass-normalized thrust $\overline {F_{T}}/m$ between 10 m/s² and 30 m/s² at a step size of 0.5 m/s², while the minimum thrust $\underline {F_{T}}/m$ was kept constant at 1 m/s². The resulting maneuver duration T and the switching times are shown in Fig. 8.

Fig. 8

Maneuver duration T as function of the mass-normalized thrust $\overline {F_{T}}/m$ for a horizontal maneuver with a displacement of x _T =5 m. The switching times of u _R are drawn in the plot on the top, and the switching times of u _T in the plot on the bottom

The gravitational acceleration g poses a lower limit: If the mass-normalized thrust $\overline {F_{T}}/m$ approaches g, the maneuver duration approaches infinity because the quadrotor needs all the available thrust force to maintain hover, and no horizontal displacement can be achieved without height loss. As $\overline {F_{T}}/m$ increases, the slope of the T-curve decreases, which means that the performance gain per additional thrust becomes smaller. It follows that for large thrust-to-weight ratios, an increase of the available thrust force does not lead to significantly better performance with respect to the maneuver duration, with respect to horizontal displacements. To achieve faster displacements, the maximum pitch rate $\overline {\omega }$ would have to be increased as well.

6.2 Benchmarking of a linear controller

To demonstrate the use of time-optimal maneuvers as a controller benchmark, the performance of a linear controller, as commonly found in quadrotor literature, is evaluated. The time-optimal maneuvers provide a lower bound on the achievable maneuver duration, against which the maneuver duration using the linear controller is compared.

The linear controller consists of cascaded position and attitude control loops, as often used in quadrotor control (see, for example, How et al. (2008), Michael et al. (2010), and references therein).

The two-dimensional model presented in Sect. 2 can be linearized around the hover point F _T =mg,θ=0, yielding the linearized dynamics

(33)

(34)

(35)

The pitch angle is straightforward to control using a proportional controller:

(36)

where θ _d is the desired pitch angle that is computed by the position control loop, and τ _θ is the time constant of the attitude control loop.

The two translational degrees of freedom decouple entirely in the linearization, allowing straightforward controller designs for each of them:

(37)

(38)

In the above equations, τ _x and τ _z are the respective closed loop time constants, and ζ _x and ζ _z are the respective damping ratios.

The saturations of the control inputs ω and F _T are applied with the same values as for the computation of time-optimal maneuvers. Additionally, the desired pitch angle θ _d is limited to |θ _d |≤π/2.

It is important to note that this controller is not designed for optimal performance, and performance cannot be expected to match the many more sophisticated controllers that have been presented (see, for example, Hoffmann et al. 2008; Cowling et al. 2007; Bouktir et al. 2008; Mellinger et al. 2010; Purwin and D’Andrea 2011; Lupashin et al. 2010). It is, however, a useful demonstration of the benchmarking of common ‘everyday’ controllers, and their performance.

The parameters of the controller are shown in Table 2, and are based on the parameters of controllers used in the Flying Machine Arena test bed. These parameters are based on manual tuning for all-round usability in the testbed, rather than optimizing simulated performance.

Table 2 Parameters of the linear controller

We compare the performance of the linear controller to the achievable performance when using the model dynamics (3)–(5) and performing translations that start and end at rest. To evaluate the performance of the linear controller, the target translation is provided as a setpoint x _d and z _d , and the closed-loop dynamics are simulated until the state settles. The duration of the maneuver is taken to be the time until the position error remains within 1% of the translation distance.

Figure 9 shows the duration of purely horizontal maneuvers as a function of the translation distance. The results show that this linear controller achieves maneuver times that, depending on the translation distance, are between approximately 175% and 880% of the minimal achievable time. As one expects, the maneuver duration is approximately constant for small translations, but varies significantly for large translations where model nonlinearities become more dominant. The non-monotonicity of the maneuver duration is caused by position oscillations that either lie within the 1% band defining the end of the maneuver, or slightly exceed it.

Fig. 9

Comparison of maneuver times for purely horizontal maneuvers. The maneuver using the linear controller is considered finished when the position error remains within 1% of the desired translation

Figure 10 demonstrates the same comparison between the linear controller and time-optimal maneuvers, this time demonstrating the performance for purely vertical maneuvers. When using the linear controller, the pitch angle θ always remains at 0. The system dynamics are therefore fully linear, except for control input saturations. This is represented in the three distinct regions in the plot: Initially, the maneuver duration is constant. In a second region, the upper thrust constraint is reached, increasing the maneuver duration. In the third section, both upper and lower constraints are active during the maneuver, and the maneuver duration rises faster. The maneuver duration using the linear controller is between 155% and 1100% of the minimal time.

Fig. 10

Comparison of maneuver times for purely vertical maneuvers. The maneuver using the linear controller is considered finished when the position error remains within 1% of the desired translation

The above results show that the linear controller with saturations leaves considerable room for improvement. The highest performance gains are achievable for very small translations, which take approximately constant time with the linear controller.

7 Experimental results

Selected numerical results were experimentally validated by applying them on quadrotor vehicles in the ETH Zurich Flying Machine Arena. The vehicles are based on Ascending Technologies ‘Humminbird’ quadrocopters (Gurdan et al. 2007), but have been modified with custom electronics providing additional communications interfaces, sensors with higher dynamic range, and access to low-level control functions (Lupashin et al. 2010).

Trajectories were recorded using an infrared motion tracking system. Using retro-reflective markers mounted to the vehicle, position and attitude were measured at a rate of 200 Hz. The vehicle velocity was obtained through differentiation of non-causally filtered position measurements.

The control input trajectories are transfered to the quadrotor vehicle ahead of the start of the experiment. A hover controller is employed to stabilize the vehicle at the initial state. The maneuver is triggered and the vehicle executes the control input trajectories, using only feedback from the on board gyroscopes to control its rotational rates. The trajectory is sampled and executed by the on-board microcontroller at 800 Hz.

Considering that the numerical results were obtained using a first-principles model that, as discussed in Sect. 2.1, neglects a number of known effects, executing the numerically computed input trajectories directly is not sufficient to achieve a maneuver that is comparable to the simulation results. In order to adapt the input trajectories to modeling inaccuracies, a model-based policy gradient learning algorithm was applied. This algorithm was presented in Lupashin et al. (2010) and Lupashin and D’Andrea (2011), and minimizes the final state error over multiple iterations of the maneuver. The results shown here were obtained after convergence of the learning algorithm.

A video of the experiments presented herein is available on the first author’s website, and as Electronic Supplementary Material to this article.

Figure 11 shows the state trajectories of two maneuvers after convergence of the policy gradient learning algorithm. The upper graph shows the state trajectories of a purely vertical translation of 5 m, the numerical results of which were shown in Fig. 4. The lower graph shows a translation of 5 m in both coordinates, for which the numerical results were shown in Sect. 5.3 (Fig. 7).

Fig. 11

Measured state trajectories for two example maneuvers: Final state x _T =0 and z _T =5 m (top), x _T =5 m and z _T =5 m (bottom). The numerical results for these maneuvers are shown in Figs. 4 and 7, respectively. It can be seen that the measured trajectories are similar to the numerical ones, with unmodeled dynamics apparent at high speeds and around switching times

For both experiments, the total duration of the maneuver was longer than the calculated duration (approximately 17% for the vertical translation, and approximately 20% for the translation in both coordinates). Multiple reasons for this can be seen in the state trajectories:

The pitch angle trajectories θ show inaccuracies, which can be explained by unmodeled rotational accelerations and propeller dynamics. This is particularly obvious around the switching times of the rotational rate input (e.g. around t=0.9 s in the upper graph, and around t=1.4 s in the lower graph. This highlights the limitations of the dynamical model introduced in Sect. 2: The shape of the trajectory is similar, but with significant differences when large changes in the pitch rate occur.

The velocity trajectories show a loss of acceleration at high speeds. This is very clearly visible in the purely vertical displacement (upper plot), where the rate of increase of vertical velocity $\dot{z}$ reduces as the velocity increases (t=0.2 s to 0.9 s). Well-known aerodynamic effects on propellers (Huang et al. 2009) provide a plausible explanation for this behavior: For a given propeller shaft power, the thrust produced by the propeller decreases significantly as the flight speed increases.

Inspecting the velocity trajectories more closely, it also becomes apparent that sudden changes of acceleration, such as at the beginning of both maneuvers, are not achieved in the experiment. This behavior can be explained by examining the underlying propeller dynamics: For a sudden thrust change, the propeller speed must be increased or decreased instantaneously. The true propeller speed change dynamics are dictated by the available current and by the motor controllers.

The differences between the trajectories are further highlighted in Fig. 12, where experimental and simulative results are superimposed. While the direct comparison highlights the longer duration of the maneuver, it is also clearly visible that the general shape of the simulation results is matched well by the experiments. With the ability to transfer maneuvers from simulation to the experimental platform, it is possible to perform comparative studies not only in simulation, but also in reality. For accurate benchmarks, care should be taken to compare results from similar sources (for example, obtained using the same simulation, as shown in Sect. 6). If, when assessing performance, numerical results for time-optimal maneuvers are to be compared to experimental results, it may be important to account for differences between experimental and simulative results.

Fig. 12

Overlay of trajectories from simulation and experiment: Final state x _T =5 m and z _T =5 m. The direct comparison highlights the longer duration of the experimental trajectory, with peak velocities about 16% and 40% lower in x and z, respectively

8 Conclusion and future work

In this paper, a benchmarking methodology for quadrocopters was presented. Using a two-dimensional first-principles model, the algorithm presented herein computes maneuvers that satisfy Pontryagin’s minimum principle with respect to time-optimality. Using a non-dimensionalized model, the quadrotor vehicle is characterized by two parameters.

Resulting maneuvers for selected initial and final states were illustrated, highlighting the structure of time-optimal maneuvers. The use of this method to quantify performance gains through changes of physical quadrotor parameters was demonstrated, and the benchmarking of a control algorithm was demonstrated by benchmarking a linear controller as it might be used for relatively simple control tasks.

We expect that this method will enable performance benchmarking of quadrotor controllers and quadrotor design decisions. Furthermore, the insights gained into the structure of time-optimal quadrotor maneuvers may be useful in the development of more advanced control strategies.

To confirm the validity of computed maneuvers, and to demonstrate the transferability to real quadrocopters, the maneuvers were successfully demonstrated in the ETH Zurich Flying Machine Arena testbed. A possible extension would be the experimental benchmarking of control strategies. While the optimality conditions apply only to the first-principles model, the experimental results may still serve as a useful reference point that experimental results of other controllers can be compared to.

In tasks that require specific point-to-point motions, the trajectories computed with this algorithm could be applied, as demonstrated by the experimental results. While the computation of time-optimal trajectories is not fast enough to be performed on-line, a precomputed set of trajectories could be stored and applied for specific motions.

An interesting extension of this work would be the computation of time-optimal maneuvers in three dimensions. While the coordinate system can be appropriately transformed to compute all maneuvers starting and ending at standstill using the two-dimensional model, additional insight may be gained through the ability to compute arbitrary maneuvers.

A further possible extension of the work herein could be the development of algorithms that permit significantly faster computation of time-optimal maneuvers, allowing such maneuvers to be computed at timescales that make them useful in on-line planning scenarios.

Appendix: Algorithm for calculation of time-optimal maneuvers

This appendix discusses the numerical algorithm presented in Sect. 4 in more detail, with a focus on how the individual steps were implemented. This implementation (in Matlab) of the algorithm is available for free use on the first author’s website, and is submitted along with this article.

This appendix follows the outline of Sect. 4, first introducing maneuvers containing no singular arcs in Sects. 9.1–9.3, and then showing modifications for bang-singular maneuvers in Sect. 9.4.

Figure 13 shows a flowchart diagram of the algorithm for bang-bang maneuvers, and in the following, the three steps are introduced in detail.

Fig. 13

Flowchart diagram of the algorithm that computes bang-bang maneuvers satisfying the minimum principle. The three steps are presented in detail in Sects. 9.1–9.3. In this graph, ≈ is used to denote that the equation must be solved to acceptable accuracy

1.1 9.1 Switching time optimization

Due to the assumption that the optimal solution is a bang-bang maneuver, the control trajectory u can be efficiently parameterized by the initial control vector u(t=0) and the switching times of the two control inputs, denoted by the sets

$$\begin{array}{l@{\quad}l}\{{T}_{u_R}\} = {T}_{u_R}^i & \hspace {7mm} \text{for}~i = 1,2,\dots,N_R, \\[3pt]\{{T}_{u_T}\} = {T}_{u_T}^j &\hspace{7mm} \text{for}~j = 1,2,\dots,N_T.\end{array} $$

(39)

N _R and N _T are the number of switches of the rotational control input and the thrust input, respectively. The principle of STO is to choose N _R and N _T , and to then improve an initial choice of the switching times $\{{T}_{u_{R}}\}_{\mathit{ini}}$ and $\{{T}_{u_{T}}\}_{\mathit{ini}}$, until a control trajectory is found that guides the quadrotor from x ₀ to x _T with an acceptable accuracy. The final state error is measured using the scalar final state residual function

$$P_{\mathit{res}}\bigl(\{{T}_{u_R}\},\{{T}_{u_T}\},{T}\bigr) = \bigl(\mathbf {x}({T}) - \mathbf {x}_T\bigr)^T W \bigl(\mathbf {x}({T}) - \mathbf {x}_T\bigr), $$

(40)

where the matrix W=diag(w ₁,w ₂,w ₃,w ₄,w ₅) contains the weights of the different state errors. The final state x(T) resulting from the chosen switching times can be obtained by numerically integrating the system dynamics f(x,u) over the interval [0,T], where u is defined by the initial control inputs u(t=0) and the switching times $\{{T}_{u_{R}}\}$ and $\{{T}_{u_{T}}\}$. The maneuver duration T is not known a priori and we seek the minimum T for which P _res =0 can be obtained. The problem can be written as

$$\begin{array}{l@{\quad}l}\multicolumn{2}{l}{\text{find} \quad \{{T}_{u_R}\}, \{{T}_{u_T}\}, {T}} \\[3pt]\text{subject to} & P_{\mathit{res}}\bigl(\{{T}_{u_R}\},\{{T}_{u_T}\},{T}\bigr) = 0, \\[3pt]& {T} \leq\{{T}\}_{ach},\end{array} $$

(41)

where {T} _ach is the set of all T for which P _res =0 is achievable, implying that the maneuver to be found is the one with the shortest possible duration.

The solution of (41) is computed by a two-step algorithm: For an initially small, fixed maneuver duration T, the state residual P _res is minimized by varying the switching times $\{{T}_{u_{R}}\}$ and $\{{T}_{u_{T}}\}$ using a simplex search method (this choice was based on the observation that derivative-free optimization algorithms have shown to perform significantly better in this optimization). After the minimization, T is increased using the secant method

$${T}_{i+1} = {T}_i + \frac{{T}_i-{T}_{i-1}}{(P_{\mathit{res},i-1}/P_{\mathit{res},i})-1}, $$

(42)

or by a constant value if convergence of the secant method is not assumed, see Dahlquist and Björck (2003). These two steps are repeated until P _res =0 is achieved. Since the initial value of T is chosen to be too small to complete the maneuver, and since T is successively increased, the algorithm delivers a value close to the smallest T for which P _res =0 is achievable.

The choice of the number of switches is based on the user’s intuition and experience from the computation of other maneuvers. If the number is chosen too high, the algorithm can converge to the correct result by producing dispensable switching times, as discussed below. The initial guess for the duration of the maneuver T must be chosen to be too short to complete the maneuver, and can be obtained from a guess based on the vehicle’s translational acceleration capabilities, or on similar maneuvers.

1.2 9.2 Parameter extraction

After having found a bang-bang trajectory that brings the quadrotor from the initial state x ₀ to the desired final state x _T , it is necessary to verify that it is a solution to BVP (32). Therefore, the constant vector c=(c ₁,c ₂,c ₃,c ₄) must be determined, based on the trajectories resulting from the STO.

1.2.1 9.2.1 Dispensable switching times

If the number of switches N _R and N _T was chosen too high, then the STO may converge to a solution containing dispensable switching times, which in fact do not represent switches. Therefore, before the constant vector c is computed, all switches at t=0 and t=T are removed, and the initial control vector u(0) is adjusted accordingly. Furthermore, two switches of the same control input, which occur at the same time, are dispensable as well and must, consequently, also be removed.

1.2.2 9.2.2 Conditions on the trajectory of Φ _R

The switching function Φ _R must be zero whenever the control input u _R switches. From the STO, the set of switching times $\{{T}_{u_{R}}\}$ is given, and for each element of this set, Φ _R must vanish. This leads to the conditions

$$\Phi_R\bigl({T}_{u_R}^i\bigr) = 0 \quad \text{for}~i =1,2,\dots,N_R. $$

(43)

As shown in Sect. 3, only the derivative $\dot{\Phi}_{R}$ of the switching function is known a priori. However, once the state trajectories are known from the STO, the condition H≡0 (which must hold if the maneuver is time-optimal) can be used to compute Φ _R . Recalling the Hamiltonian (14) and using the definition Φ _R =p ₅ yields

$$\Phi_R = \frac{1 + p_1 \dot{{x}} + p_2 u_T\sin{\theta } + p_3 \dot{{z}} + p_4 (u_T\cos{\theta} - 1)}{ -u_R}. $$

(44)

As shown in (17), the first four costates p _i are all linear in c. The above equation can therefore be written as a linear function of c:

(45)

Given the linear form of Φ _R , (43) states N _R linear conditions on the constant vector c.

The derivative $\dot{\Phi}_{R}$ is given by (31). For a trajectory that satisfies the minimum principle, the integral of $\dot{\Phi}_{R}$ must coincide with the trajectory of Φ _R given by (45). Hence, for an arbitrary interval [t ₁,t ₂]∈[0,T],

(46)

must hold, where the left side of the equation is computed using H≡0, i.e. by (45). The costates p ₂ and p ₄ are linear functions of c, and the above equation can be written as

(47)

To set up conditions on c based on (47), the maneuver interval [0,T] is divided into N _R +1 subintervals that are separated by the switching times $\{{T}_{u_{R}}\}$, i.e.

$$[0,{T}] = \bigcup\bigl\{\bigl[0,{T}_{u_R}^1\bigr],\bigl[{T}_{u_R}^1,{T}_{u_R}^2\bigr],\dots,\bigl[{T}_{u_R}^{N_R},T\bigr] \bigr\}. $$

(48)

This choice is beneficial with respect to the computational effort, because the switching function Φ _R must vanish at the switching times; the left side of (47) can be set to zero for all intervals, except for the first and the last one. The N _R +1 intervals describe N _R +1 additional linear conditions on the constant vector c.

1.2.3 9.2.3 Conditions on the trajectory of Φ _T

Since the thrust switching function Φ _T is known explicitly, the conditions resulting from $\{{T}_{u_{T}}\}$ are straightforward. From the fact that Φ _T must vanish at each switch of u _T , the condition

$$\Phi_T\bigl({T}_{u_T}^i\bigr) = 0 \quad \text{for}~i =1,2,\dots,N_T $$

(49)

must be satisfied, where the set $\{{T}_{u_{T}}\}$ is given by the STO. The thrust switching function (26) is a linear function of the costates p ₂ and p ₄, and again linear in c:

$$\Phi_T = -c_1 t \sin{\theta} + c_2 \sin{\theta} - c_3 t \cos{\theta} + c_4 \cos{\theta}. $$

(50)

This linear form of the thrust switching function Φ _T allows one to define N _T additional linear conditions on the elements of the constant vector c, based on the conditions from (49).

1.2.4 9.2.4 Condition matrix equation

For the minimum principle to be satisfied, a constant vector c that fulfills all the linear conditions to an acceptable accuracy must exist. The conditions on c derived above are therefore combined into a matrix equation, which we denote as

$$A \mathbf{c} = r. $$

(51)

The matrix A is of size (N _c ×4) and the vector r has the length N _c , where N _c is the total number of linear conditions:

$$N_c = 2N_R + N_T + 1. $$

(52)

For all maneuvers considered here, the system of (51) is overdetermined, permitting no exact solution. Therefore, the least squares solution of (51) is computed (Bernstein 2005), which is given by

$$\mathbf{c}^* = \bigl(A^T A\bigr)^{-1} A^T r. $$

(53)

To verify that a solution to the overdetermined system of equations exists, c ^∗ is substituted back into (51). If the error vector exceeds the expected numerical discrepancies,³ then the solution is considered to be invalid. In the context of the optimal control problem, this implies that there exists no constant vector c for which the minimum principle is fulfilled, and consequently the trajectories x and u resulting from the STO do not satisfy the minimum principle. A possible reason is that the chosen number of switches N _R and N _T and the initial values $\{{T}_{u_{R}}\}_{ini}$ and $\{{T}_{u_{T}}\}_{ini}$ did not cause the STO to converge to the desired maneuver. This may be corrected by varying these parameters. Another reason for the lack of a solution could be that the time-optimal maneuver for the given boundary conditions contains singular arcs, a case that will be discussed in Sect. 9.4.

If the condition matrix equation is satisfied to an acceptable accuracy, then a valid parameter vector c has been found and the parameter extraction step is complete.

1.3 9.3 BVP solver

To verify that BVP (32) is fulfilled and to minimize numerical errors, a last step is performed where the BVP is solved numerically: The state residual P _res is minimized by varying the constant vector c and the maneuver duration T. The problem can be written as

$$\begin{array}{l@{\quad}l}\multicolumn{2}{l}{\text{minimize} \quad P_{\mathit{res}}(\mathbf{c},{T})} \\[3pt]\text{subject to} & \dot{\mathbf{x}}_a = f_a({t},\mathbf{x}_a), \\[3pt]& \mathbf{x}_a(0) = \bigl(\mathbf {x}_0,\Phi_R(0)\bigr). \\\end{array} $$

(54)

The constants c resulting from the parameter extraction and the maneuver duration T obtained by the STO are used as initial values. The optimization over the constants c and the terminal time T is carried out using a simplex algorithm. As these initial values are close to the exact solution, the BVP solver converges quickly, provided that the solution resulting from the STO is indeed a solution to the minimum principle. The initial value of the switching function Φ _R (0) can be obtained by the condition H≡0, i.e. by (45), evaluated at t=0. If P _res is sufficiently small after the minimization, the maneuver satisfies the boundary conditions of the final state being reached, and the algorithm has terminated successfully.

1.4 9.4 Modified algorithm for bang-singular maneuvers

The algorithm described above is able to solve BVP (32), provided that the resulting maneuver does not contain singular arcs. In the general case, however, the time-optimal maneuver is bang-singular, and the algorithm needs to be modified to take possible singular arcs into account.

Within a singular arc, the trajectory of u _R is given by (23) and depends on the constants c. Due to this dependency, computing the constants c after the STO is no longer sufficient, since they determine the singular input and have an impact on the maneuver trajectory. The parameter extraction is therefore embedded into the STO, and the resulting algorithm consists of two successive steps:

• 1. Applying STO, a maneuver that brings the quadrotor to the desired final state is found, and in parallel, a constant vector c that fulfills the condition matrix equation resulting from the parameter extraction is computed.

• 2. Having a reasonable initial guess of the switching times, of the maneuver duration T, and of the constant vector c, a BVP solver that computes a solution to BVP (32) is applied.

Figure 14 shows a flowchart diagram of the algorithm to find bang-singular solutions.

Fig. 14

Flowchart diagram of the algorithm to compute bang-singular maneuvers that satisfy the minimum principle. The symbol ≈ is used to denote that the equation must be solved to acceptable accuracy

1.4.1 9.4.1 Switching time optimization with embedded parameter extraction

For bang-singular maneuvers, u _R may stay within a singular arc for a particular duration each time it switches. We introduce a new set of parameters that describes the durations of the singular arcs, and denote the duration within the singular arc at the switching time ${T}_{u_{R}}^{i}$ as ${D}_{s,u_{R}}^{i}$. At the time ${T}_{u_{R}}^{i}$ the control input u _R enters the singular arc, and at time ${{T}_{u_{R}}^{i}+{D}_{s,u_{R}}^{i}}$ the singular arc is left and u _R switches to −1 or +1.⁴ A bang-singular maneuver is characterized by the sets

$$\begin{array}{l@{\quad}l}\{{T}_{u_R}\} = {T}_{u_R}^i &\text{for}~i = 1,2,\dots,N_R, \\[3pt]\{{D}_{s,u_R}\} = {D}_{s,u_R}^i&\text{for}~i = 1,2,\dots,N_R, \\[2pt]\{{T}_{u_T}\} = {T}_{u_T}^j &\text{for}~j = 1,2,\dots,N_T.\end{array} $$

(55)

Within a singular arc, u _R is given by (23) and its trajectory depends on the constants c. The final state residual P _res is therefore not only a function of the maneuver duration T and of the sets of the switching times, but also of the constant vector c. Accordingly, the state residual may be written as

(56)

The new parameter set $\{{D}_{s,u_{R}}\}$ and the constant vector c are additional optimization variables during the STO.

If the solution is to satisfy the minimum principle, the optimization variables overconstrain the problem: For the solution to satisfy the optimality conditions, the control inputs must be the optimal control inputs, as specified by (24) and (30). These optimal inputs could be found using c to compute the switching functions. This is avoided, however, because the separate optimization of the switching times and c has shown to be more robust.

Because only constants c that satisfy the condition matrix equation A c=r from the parameter extraction are a valid choice, we define the condition residual to be

$$C_{\mathit{res}}\bigl(\{{T}_{u_R}\},\{{T}_{u_T}\},\{{D}_{s,u_R}\},\mathbf{c},{T}\bigr) = (A \mathbf{c} -r)^T W_c (A \mathbf{c} - r), $$

(57)

where W _c is a diagonal matrix containing the weights of the different linear conditions. It is important to note that the matrix A and the vector r are functions of the switching times $\{{T}_{u_{R}}\}$ and $\{{T}_{u_{T}}\}$, of the singular arc durations $\{{D}_{s,u_{R}}\}$, of the maneuver duration T, and of the constants c. For a maneuver that satisfies the minimum principle, the condition residual C _res must vanish. Consequently, the STO problem for bang-singular maneuvers can be written as

$$\begin{array}{l@{\quad}l}\multicolumn{2}{l}{\text{find} \quad \{{T}_{u_R}\}, \{{T}_{u_T}\}, \{{D}_{s,u_R}\}, \mathbf{c},{T}} \\[3pt]\text{subject to} & P_{\mathit{res}}(\{{T}_{u_R}\},\{{T}_{u_T}\},\{{D}_{s,u_R}\},\mathbf {c},{T}) = 0, \\[3pt]& C_{\mathit{res}}(\{{T}_{u_R}\},\{{T}_{u_T}\},\{{D}_{s,u_R}\},\mathbf{c},{T}) = 0, \\[3pt]& {T} \leq\{{T}\}_{ach},\end{array} $$

(58)

where {T} _ach denotes the set of all T for which P _res =0 and C _res =0 is achievable.

For bang-singular maneuvers, the sum of the state and the condition residual P _res +C _res is minimized during the STO. For the computation of C _res , the matrix A and the vector r are required: The parameter extraction is no longer an isolated step, but needs to be performed for each evaluation of C _res within the STO minimization. The parameter extraction is not used to compute the constants c (which are optimization variables), but to compute A and r.

1.4.2 9.4.2 Additional linear conditions for bang-singular maneuvers

For the parameter extraction of bang-singular maneuvers, which is needed to obtain A and r, there exist additional linear conditions that take the requirements on the switching functions within singular arcs into account.

Additional conditions on the trajectory of Φ _R

Considering bang-singular maneuvers, the rotational switching function Φ _R must not only have a zero-crossing at each ${T}_{u_{R}}^{i}$, but it must also stay at zero for the duration of the corresponding singular arc ${D}_{s,u_{R}}^{i}$. An additional set of constraints is introduced, requiring that Φ _R is zero at the beginning and at the end of the singular arcs:

$$\begin{array}{l@{\quad}l}\Phi_R\bigl({T}_{u_R}^i\bigr) = 0 & \text{for}~i =1,2,\dots,N_R, \\[3pt]\Phi_R\bigl({T}_{u_R}^i+{D}_{s,u_R}^i\bigr) = 0 &\text{for}~i = 1,2,\dots,N_R.\end{array} $$

(59)

Because these conditions do not imply that Φ _R is zero during the entire singular arc, it is necessary to verify the trajectory of Φ _R after the computation. If a switch ${T}_{u_{R}}^{i}$ has no singular arc, i.e. if ${D}_{s,u_{R}}^{i}=0$, then the corresponding two conditions in (59) are identical. From this it follows that one additional condition results for each singular arc. We denote the number of singular arcs as N _s , hence (59) describes N _R +N _s conditions. This means that N _s additional conditions have been identified, compared to the bang-bang case. As derived in Sect. 9.2, these conditions are linear with respect to c.

As the derivative of the rotational switching function $\dot{\Phi}_{R}$ is known explicitly, we demand that the integration value of $\dot{\Phi }_{R}$ between two switches of u _R is zero for bang-bang maneuvers. For bang-singular maneuvers, we pose similar conditions, but extra time intervals over the singular arcs are created. An integration value of zero does not imply that Φ _R stays at zero during the whole singular arc, but constant drifts of Φ _R are penalized. Hence, the intervals over which $\dot{\Phi}_{R}$ is integrated are

$$\begin{array}{rcl}[0,{T}] & = & \bigcup\bigl\{\bigl[0,{T}_{u_R}^1\bigr],\bigl[{T}_{u_R}^1,T_{s,u_R}^1\bigr],\bigl[T_{s,u_R}^1,{T}_{u_R}^2\bigr],\dots\\[6pt]& & \hphantom{\bigcup\bigl\{} \dots,\bigl[T_{s,u_R}^{N_R-1},{T}_{u_R}^{N_R}\bigr],\bigl[{T}_{u_R}^{N_R},T_{s,u_R}^{N_R}\bigr],\bigl[T_{s,u_R}^{N_R},T\bigr] \bigr\},\end{array} $$

(60)

where $T_{s,u_{R}}^{i}={T}_{u_{R}}^{i}+{D}_{s,u_{R}}^{i}$ is used for a more compact notation. Analogously to the bang-bang case, a linear condition for each of these intervals can be constructed using (47). If a switch has no singular arc, then ${{D}_{s,u_{R}}^{i}=0}$ and the corresponding interval vanishes. Hence, for bang-singular maneuvers, N _R +N _s +1 linear conditions on the constant vector c result. Compared to a bang-bang maneuver, N _s additional conditions are introduced.

Assuming that the thrust input u _T does not switch at the edges of the singular intervals, $\dot{\Phi}_{R}$ is continuous over the border of the singular arcs, as can be seen from (21). Consequently, the switching function Φ _R enters and leaves a singular arc tangentially. We therefore impose the conditions that the derivative $\dot{\Phi}_{R}$ is zero at the edges of every singular arc. For each singular arc, i.e. for each ${D}_{s,u_{R}}^{i}>0$, two additional conditions result:

$$\begin{array}{l@{\quad}l}\dot{\Phi}_R\bigl({T}_{u_R}^i\bigr) = 0 &\text{for}~i = 1,2,\dots,N_s, \\[3pt]\dot{\Phi}_R\bigl({T}_{u_R}^i+{D}_{s,u_R}^i\bigr)= 0 & \text{for}~i = 1,2,\dots,N_s .\end{array} $$

(61)

The derivative of the rotational switching function is given by

$$\dot{\Phi}_R = (c_1 {t} - c_2)u_T\cos{\theta} + (c_4 - c_3 {t})u_T\sin{\theta}, $$

(62)

which has been derived in Sect. 3. This is a linear function of the constants c, and yields 2N _s additional conditions.

General condition matrix equation

In total, 4N _s additional conditions have been identified. It follows that in the case of a bang-singular maneuver, the condition matrix equation

$$A \mathbf{c} = r $$

(63)

has N _c rows, with a total number of conditions of

$$N_c = 2N_R + N_T + 4N_s + 1. $$

(64)

The condition matrix equation is overdetermined as soon as the maneuver has at least one singular arc.

1.4.3 9.4.3 BVP solver for bang-singular maneuvers

Similar to the algorithm for bang-bang maneuvers, the final step is the reduction of errors through the application of a BVP solver. If the maneuver contains singular arcs, Φ _R stays at zero for a nontrivial interval of time. Since the system is integrated numerically, Φ _R is near zero during the singular arcs, but does not vanish completely due to numerical inaccuracies. As Φ _R enters and leaves the singular arcs tangentially, defining a threshold value below which Φ _R is considered to be zero is not a straightforward task. For this reason, the rotational control trajectory u _R is not determined using the optimal control law (i.e. based on its switching function Φ _R ), but is based on the sets $\{{T}_{u_{R}}\}$ and $\{{D}_{s,u_{R}}\}$. Consequently, $\{{T}_{u_{R}}\}$ and $\{{D}_{s,u_{R}}\}$ are optimizing variables during the BVP minimization, because they impact the control trajectory u. Further, since the switching times of u _R are not determined based on the constants c, the optimal control laws are not implicitly satisfied. One must thus ensure that the condition matrix equation is fulfilled, which is the case if C _res vanishes. Thus, as during the switching time optimization, the sum of the state residual P _res and the condition residual C _res is minimized. The BVP solver problem for bang-singular maneuvers becomes

$$\begin{array}{l@{\quad}l}\multicolumn{2}{l}{\text{minimize}\quad P_{\mathit{res}} + C_{\mathit{res}}} \\[3pt]\text{subject to} & \dot{\mathbf{x}} = f(\mathbf {x},\mathbf {u}), \\[3pt]& \mathbf {x}(0) = \mathbf {x}_0,\end{array} $$

(65)

where the control trajectory u _R is computed according to the switching times and singular arc durations, and u _T according to the optimal control law (30). Note that the arguments $(\{{T}_{u_{R}}\},\{{D}_{s,u_{R}}\},\mathbf{c},{T})$ of P _res and C _res have been omitted for reasons of clarity.

In the BVP Solver step, the N _T linear conditions resulting from the thrust input are trivially satisfied, because u _T is computed based on its switching function Φ _T . Hence, when the matrix condition equation is computed for the evaluation of C _res during the BVP minimization, it has only

$$N_{c,u_R} = 2N_R + 4N_s + 1 $$

(66)

rows, since the conditions resulting from u _T can be neglected.

For bang-singular maneuvers, the BVP solver is similar to the STO. The only differences are that the thrust input u _T is determined based on its control law (30), and that the maneuver duration T is an optimization variable, too, and not kept constant during the minimization of P _res +C _res .

Because u _R is not determined by its control law, and since a vanishing condition residual C _res does not guarantee that the control law holds, it is necessary to verify that the control law (24) is satisfied by inspecting the switching function Φ _R .

If the residuals P _res and C _res are sufficiently small after the minimization, and if the control law for the rotational input u _R is fulfilled, then the maneuver is a solution to BVP (32), and therefore satisfies the minimum principle with respect to time-optimality.