The 3D numerical modeling of the solar modulation of galactic protons and helium nuclei related to observations by PAMELA between 2006 and 2009

Abstract

The global features of the modulation of galactic cosmic ray protons and helium nuclei in a very quiet heliosphere are studied with a comprehensive, three-dimensional, drift model and compared to proton and helium observations measured by PAMELA from 2006 to 2009. Combined with accurate very local interstellar spectra (VLIS) for protons and helium nuclei, this provides the opportunity to study in detail how differently cosmic ray species with dissimilar mass-to-charge ratio ($A/Z$) are modulated down to a few GV. The effects at Earth of the difference in their VLIS’s and those caused by the main modulation mechanisms are illustrated. We find that both the PAMELA proton and helium spectra are reproduced well with the numerical model, assuming the same set of modulation parameters and diffusion coefficients. A comparative study of ³He₂ (He-3) and ⁴He₂ (He-4) modulated spectra reveals that they do not undergo identical spectral changes below 3 GV mainly due to differences in their VLIS’s. This result is important to uncover and investigate the effects on the proton to total helium ratio ($p$/He) caused by the difference in their VLIS’s and those by $A/Z$. The computed $p$/He displays three modulation regimes, reflecting the complex interplay of modulation processes in the heliosphere. At rigidities above ∼3 GV, the $p$/He ratio at the Earth is found to deviate modestly from a value of ∼5.5, largely independent of the assumed modulation conditions. This result indicates that the PAMELA measurement of $p$/He reveals at these rigidities the shapes of their VLIS’s. Below ∼0.6 GV, $p$/He increases with decreasing rigidity from 2006 to 2009 and significant variations are predicted depending on the assumed solar modulation conditions. This result indicates that as modulation levels decreased from 2006 to 2009, the contribution of adiabatic energy changes dissipated faster for protons than for helium nuclei at the same rigidity mainly due to different slopes of their VLIS’s. The differences between modulation effects for protons and helium are found to be the consequence of how the combined interplaying modulation mechanisms in the heliosphere affect the modulated spectra based on their $A/Z$ and particularly on their VLIS’s.

1 Introduction

The interest in modulation of galactic cosmic rays (GCRs) at the Earth has leaped forward when it has become apparent that the solar minimum period of 2006 to 2009 was significantly different than the previous $A < 0$ solar minimum periods (see e.g. Heber et al. 2009; Mewaldt et al. 2010; Kóta 2013; Krainev et al. 2018). Observations of GCRs made by the PAMELA space experiment at the Earth during this period (Adriani et al. 2011, 2013, 2017; Boezio et al. 2017, and references therein) have indeed revealed that solar activity decreased to its lowest level since the beginning of the space exploration era. This magnetic epoch was characterized by a much weaker heliospheric magnetic field (HMF) and the tilt angle of the heliospheric current sheet (HCS) not decreasing as rapidly as the magnitude of the HMF at the Earth, but reaching a minimum value at the end of 2009. Essentially, these observations have sparked several modulation modeling investigations (e.g. Potgieter et al. 2014, 2015; Zhao et al. 2014; Qin and Shen 2017; Aslam et al. 2019a, 2019b, 2019c) as to what adjustments should be made to the elements of the diffusion and drift tensors as solar activity decreases from 2006 to 2009 during this $A < 0$ solar magnetic polarity cycle by establishing compatibility with observations of protons, electrons and positrons. During this magnetic polarity cycle, the HMF is pointing inward in the northern and outward in the southern hemisphere, causing positively charged GCRs to drift inward mostly along the HCS. In addition to the HCS drifts, GCRs undergo convection, diffusion, adiabatic energy changes and global gradient and curvature drifts. Combined, these interplaying processes cause the intensity of GCRs to decrease in the heliosphere toward the Sun and to change significantly over its 11-year solar activity cycle. The mentioned modeling studies established that all modulation processes contributed to the observed changes in intensity spectra from 2006 to 2009, not particularly dominated by one of these processes. The question of how differently helium nuclei (³He₂ and ⁴He₂ indicated below as He-3 and He-4, respectively) may be modulated than protons during such a quiet heliosphere is the main motivation to address in this report.

Protons and helium nuclei are the most abundant CR species, above about 10 MeV, and knowledge of the exact shape of their spectra as it relates to the unusual solar minimum of 2006 to 2009 is of particular importance to heliospheric modulation studies. This is in part because their spectral shapes at the Earth are indicators of the fundamental properties of the solar wind (SW) and the magnetic turbulence throughout the heliosphere. Fortunately, precise information about their very local interstellar spectra (VLIS) based on Voyager 1 (V1), and now also Voyager 2 (V2), observations are available at energies below ∼500 MeV (Stone et al. 2013; Cummings et al. 2016; Stone et al. 2019). Combining the V1 and PAMELA observations over a wide energy range together with sophisticated models for the propagation of GCRs in the Galaxy (GALPROP; see Vladimirov et al. 2011), improved VLIS’s can be constructed at energies of interest to modulation. Such a comprehensive approach to the determination of the VLIS for various GCR species has been recently published by Bisschoff et al. (2019). These reliable VLIS make it possible to study what adjustments should be made to the diffusion and drift tensors even at low energies where solar modulation has significant effects; previously, this could not be done accurately enough because the assumed VLIS’s were inexact, if not unknown, at these low energies. In this context, see also Potgieter (2014), Cummings et al. (2016), Boschini et al. (2017), Bisschoff et al. (2019), and Corti et al. (2019a).

In this paper a full three-dimensional (3D) numerical model is applied to study the helium spectra observed by PAMELA for the mentioned unusual solar minimum period, as was done for protons. This numerical model, and modeling approach, is similar to what was used by Potgieter and Vos (2017), Aslam et al. (2019a), and Bisschoff et al. (2019). Because the helium spectra at the same rigidity as protons can now be obtained (Marcelli et al. 2020), a study is also made about how the proton to helium ratio changed from 2006 to 2009 down to a few GVs. This provides an opportunity to study modulation in detail on how differently GCR species with a different mass-to-charge ratio ($A/Z$) are modulated during a very quiet solar minimum (Munini et al. 2019). From a solar modulation point of view, two distinguishing factors between protons and helium nuclei are their $A/Z$ and VLIS’s (for protons $A/Z = 1.0$, while helium nuclei consists of two isotopes, He-4 with $A/Z = 2.0$ and He-3 with $A/Z = 1.5$). This directly affects the conversion of rigidity to kinetic energy (KE) for these GCRs, and subsequently also the values of the diffusion coefficients and drift coefficient in terms of rigidity and KE. However, as a general assumption for modulation studies of different GCR nuclei, the mean free paths of these particles remain the same as a function of rigidity in the heliosphere, but not necessarily with time. This study specifically aims to further clarify the effects of the different shapes and slopes of their VLIS’s because this influences how adiabatic energy losses shape their modulated spectra deep in the inner heliosphere.

2 Numerical model and very local interstellar spectra

2.1 Model

The numerical model used in this study is based on solving the transport equation (TPE) derived by Parker (1965):

$$ \frac{\partial f}{\partial t} = - \bigl(\mathbf{V} + \langle \boldsymbol{v}_{D} \rangle \bigr).\boldsymbol{\nabla } f + \boldsymbol{\nabla } .( \boldsymbol{K}_{s}.\boldsymbol{\nabla } f) + \frac{1}{3}( \boldsymbol{\nabla } .\mathbf{V})\frac{\partial f}{\partial \mathit{lnp}}, $$

(1)

where $f(\boldsymbol{r}, p, t)$ is the omnidirectional GCR distribution function, $p$ is particle momentum, $\boldsymbol{r}$ is the heliocentric position vector, and $t$ is time, with $\mathbf{V}(r,\theta ) = V(r, \theta )\boldsymbol{e}_{r}$ the radial SW velocity. The terms on the right-hand side represent convection, gradient and curvature drifts, diffusion, and adiabatic energy changes in the form of adiabatic energy losses ($\nabla .\mathbf{V} > 0$) or gains ($\nabla .\mathbf{V} < 0$), respectively. The diffusion tensor $\boldsymbol{K}_{S}$ consists of a diffusion coefficient $K_{\parallel}$ that is parallel to the average HMF, a radial perpendicular diffusion coefficient $K_{\bot r}$ and a polar perpendicular diffusion coefficient $K_{\bot \theta }$ (e.g., Ferreira et al. 2000; Potgieter 2000, 2013). The averaged guiding centre drift velocity for a near isotropic CR distribution is given by $\langle \boldsymbol{v}_{D} \rangle = \boldsymbol{\nabla } \times ( K_{A}\boldsymbol{e}_{B} )$, with $\boldsymbol{e}_{B} = \boldsymbol{B}$/$B$, where $B$ is the magnitude of the background HMF assumed to have a basic Parkerian geometry in the equatorial plane but modified in the polar regions similar to the approach of Smith and Bieber (1991) but adapted to assure that $\nabla .B = 0$. Here, $K_{A}$ is the coefficient specified by the off-diagonal elements of the generalized tensor $\boldsymbol{K}_{S}$, that describes gradient and curvature drifts in the large-scale HMF. All details of the comprehensive 3D model used in this study were published by Potgieter et al. (2014, 2015), Potgieter and Vos (2017), Aslam et al. (2019a) and Bisschoff et al. (2019). We therefore repeat below only essential assumptions and basic parameters concerning the aim and purpose of this work.

The diffusion coefficients ($K$), in general, are related to the particle mean free paths (MFPs), $\lambda$, through

$$ K = \frac{v}{3}\lambda , $$

(2)

with $v = \beta c$ the particle speed; here $c$ is the speed of light so that $\beta$ is the corresponding ratio. Therefore the relationship between $\lambda _{\parallel}$ and $K_{\parallel}$, similarly for $K_{\bot r}$ and $K_{\bot \theta }$, is given by

$$ K_{\parallel } = \frac{v}{3}\lambda _{\parallel } = \frac{\beta c}{3}\lambda _{\parallel }, $$

(3)

illustrating the dependence of $K_{\parallel}$ on $\beta$. In this work the expression for $K_{\parallel}$ is approximated by two power-laws with a smooth transition of slopes given by

$$ K_{\parallel } = ( K_{\parallel } )_{0}\beta \biggl( \frac{B_{0}}{B} \biggr) \biggl( \frac{P}{P_{0}} \biggr)^{c_{1}}D^{\parallel } (P), $$

(4)

where

$$ D^{\parallel } (P) = \biggl[ \frac{ ( \frac{P}{P_{0}} )^{c_{3}} + ( \frac{P_{k}}{P_{0}} )^{c_{3}}}{1 + ( \frac{P_{k}}{P_{0}} )^{c_{3}}} \biggr]^{\frac{c_{2\parallel } - c_{1}}{c_{3}}}, $$

(5)

with $P$ rigidity, $(K_{\parallel})_{0}$ a scaling constant in units of $10^{22}$ cm² s⁻¹, $P_{0} = 1$ GV, $B_{0} = 1$ nT and $P_{k} = 4$ GV is the rigidity at which the transition between the two power laws occurs. The dimensionless quantities $c_{2\parallel} = 1.20$ and $c_{3}= 2.50$ are kept constant, while $c_{1}$ changes from 0.83 to 0.78 between 2006 and 2009 as required by comparison with experimental data. It follows that below 1 GV the function $D^{\parallel}$, given by Eq. (5), is almost rigidity independent and approaches a constant value of ∼1.0. As a result the shape of the rigidity dependence of $K_{\parallel}$ is determined by the combination of the rigidity power law index $c_{1}$ and the rigidity dependence of $\beta$. (Thus the slope of the rigidity dependence of $\lambda _{\parallel}$ below 1 GV hinges only on the power law index $c_{1}$.) At higher rigidities $\beta \sim 1.0$ and the rigidity dependence of $K_{\parallel}$ is determined by a combination of the rigidity power indices $c_{1}$ and $c_{2\parallel}$. It has become evident in the studies done by Potgieter et al. (2015) and Potgieter and Vos (2017) that $\lambda _{\parallel}$ remains independent of rigidity at low rigidities when $c_{1} = 0$ is assumed in Eq. (4). This is required in particular for low rigidity electron modulation in the inner heliosphere (e.g., Dröge 2000). Consequently, the electron rigidity dependence of $\lambda _{\parallel}$ at low rigidities is determined by $D^{\parallel}$ and approximates the effects of the dissipation range, similar to expressions of $\lambda _{\parallel}$ derived by Teufel and Schlickeiser (2003). As such, $c_{1}$, $c_{2\parallel}$ and c₃ approximate the rigidity dependence of $\lambda _{\parallel}$ for the heliospheric turbulence. It follows from Eqs. (3) and (4) that $K_{\parallel}$ displays a somewhat different rigidity dependence than $\lambda _{\parallel}$ at low rigidities because of $\beta$. Because the focus of this work is based on proton and helium nuclei modulation, the effect of $\beta$ on the diffusion and drift coefficients is investigated further and illustrated below in Figs. 3 and 4.

The rigidity and spatial dependences of $K_{\bot r}$ and $K_{\bot \theta }$ are given respectively as:

$$ K_{\bot r} = 0.02 \biggl( \frac{D^{ \bot }}{D^{\parallel }} \biggr)K_{\parallel }, $$

(6)

and

$$ K_{ \bot \theta } = 0.02F_{ \bot \theta } \biggl( \frac{D^{ \bot }}{D^{\parallel }} \biggr)K_{\parallel } = F_{ \bot \theta } K_{ \bot r}, $$

(7)

where

$$ D^{ \bot } (P) = \biggl[ \frac{ ( \frac{P}{P_{0}} )^{c_{3}} + ( \frac{P_{k}}{P_{0}} )^{c_{3}}}{1 + ( \frac{P_{k}}{P_{0}} )^{c_{3}}} \biggr]^{\frac{c_{2 \bot } - c_{1}}{c_{3}}}, $$

(8)

and

$$ F_{ \bot \theta } (\theta ) = A^{ +} \mp A^{ -} \tanh \bigl[ 8\bigl(\theta _{A} - 90^{ \circ } \bigr) \pm \theta _{F} \bigr]. $$

(9)

Here $A^{\pm } = (d_{\bot \theta } \pm 1)/2$, $\theta _{F} = 35^{\circ}$, $\theta _{A} = \theta$ for $\theta \leq 90^{\circ}$ but $\theta _{A} = 180^{\circ} - \theta$ for $\theta \geq 90^{\circ}$, and the dimensionless quantities $d_{\bot \theta } = 6.0$ and $c_{2\bot }= 0.84$. The ratio $D^{\bot }/D^{\parallel}$ is the quantity that changes the rigidity dependence of $K_{\bot \theta }$ and $K_{\bot r}$ with respect to that of $K_{\parallel}$, and the function $F_{\bot \theta }(\theta )$ enhances $K_{\bot \theta }$ by a factor 6.0 towards the polar regions with respect to its value in the equatorial plane. The physical argument for the enhancement of $K_{\bot \theta }$ is based on Ulysses measurements that showed the variance in the transverse and normal directions of the HMF increasing more than in the radial direction (Kóta and Jokipii 1995). Below 1 GV the ratio $D^{\bot }/D^{\parallel} \sim 1.0$ indicating that the assumed $K_{\bot \theta }$ and $K_{\bot r}$ have the same rigidity dependences as $K_{\parallel}$ at these rigidities. However, above 1 GV the ratio $D^{\bot }/D^{\parallel}$ decreases substantially with increasing rigidity to reach a minimum value at the highest rigidity. This indicates that the assumed rigidity dependences of $K_{\bot \theta }$ and $K_{\bot r}$ are flatter than for $K_{\parallel}$ above 1 GV. The motivation for the use of these expressions to represent diffusion coefficients in the heliosphere is given by Potgieter et al. (2014, 2015).

The drift coefficient in this work takes into account that drifts in the heliosphere are reduced by the presence of turbulence as established by direct numerical simulations (e.g., Giacalone et al. 1999; Minnie et al. 2007). However, the functional form of the drift reduction factor is not yet established, probably owing to the lack of proper knowledge about how the HMF turbulence develops throughout the heliosphere in all directions, but progress has been made (see e.g., Tautz and Shalchi 2012; Ngobeni and Potgieter 2015; Engelbrecht et al. 2017). For a modified Parker-type HMF, such as the mentioned Smith-Bieber modification (see also Raath et al. 2016) assumed in this work, $\boldsymbol{B}$ is replaced by $\boldsymbol{B}_{m}$ with magnitude $B_{m}$. Therefore the drift coefficient, expressed as a function of a simple drift reduction factor that depends only on rigidity, is then given by

$$ K_{A} = \frac{\beta P}{3B_{m}}f_{s} = k_{A0}\frac{\beta P}{3B_{m}}\frac{ ( P/P_{A0} )^{2}}{1 + ( P/P_{A0} )^{2}}, $$

(10)

where $f_{s}$ is the drift reduction factor due to diffusive scattering, with $P_{A0} = 0.75$ GV and a dimensionless quantity $k_{A0} = 0.90$. The essence of Eq. (10) is that below 1 GV drifts are reduced with respect to the weak scattering case to account for the small latitudinal gradients of CRs observed by Ulysses (Heber and Potgieter 2006). For detailed explanations of reduction factors, see e.g. Ngobeni and Potgieter (2015), Nndanganeni and Potgieter (2016) and Ngobeni et al. (2019).

The tilt angle $\alpha$ of the HCS and the magnitude of the HMF at Earth both changed from 2006 to 2009 as indicated in Fig. 1. The top panel shows $\alpha$ at the Earth from 2006 to 2010 taken from http://wso.stanford.edu. Also shown in this panel is the calculated ∼15 months moving average values of $\alpha$, as used in the model, for seven semesters indicated as blue open circles. The observed magnitude of the HMF at the Earth is shown in the bottom panel of Fig. 1 for the same period as $\alpha$, taken from http://omniweb.gsfc.nasa.gov. The corresponding calculated ∼10 months moving average values of the HMF used in the model is shown as green open circles. The $\alpha$ and the magnitude of the HMF at the Earth are considered good proxies for solar activity with their lowest and highest values assumed to represent solar minimum and solar maximum conditions, respectively. It is clearly noted in Fig. 1 that $\alpha$ and the HMF magnitude respectively dropped below 10° and 4 nT in 2009, indicating increasing diffusion and drift coefficients from 2006 to 2009. For a similar approach, see Aslam et al. (2019a, 2019b, 2019c).

Fig. 1

Top panel: Tilt angle $\alpha$ of the HCS (blue line) at the Earth from 2006 to 2010 taken from http://wso.stanford.edu. The average values of $\alpha$ used in the model for each semester are indicated as open circles. Bottom panel: Magnitude of the HMF (green line) at the Earth, for the same period, taken from http://omniweb.gsfc.nasa.gov; the corresponding average values of HMF are indicated as open circles

Concerning the global latitudinal dependence of the solar wind speed, it is assumed that $V$ changes from 430 km s⁻¹ in the equatorial plane to 750 km s⁻¹ in the polar regions as described by e.g. Ferreira et al. (2000) and Moeketsi et al. (2005). These adjustments are considered optimal and in accordance with the latitudinal dependence of $V$ observed by Ulysses (McComas et al. 2002; see also the review by Heber and Potgieter 2006).

When considering the influences of both the interstellar magnetic field and the HMF, Magnetohydrodynamic models predicted the heliopause (HP) to be somewhat closer to the Sun in the southern hemisphere when compared to the northern hemisphere in the nose direction of the heliosphere (see e.g., Luo et al. 2013, and references therein). In general, this prediction has been confirmed by V1 and V2 observation of the HP; V1 crossed the HP in August 2012 at a radial distance of ∼122 AU from the Sun and at a polar angle of $\theta = {\sim} 55^{\circ}$ (Stone et al. 2013); in November 2018, V2 also crossed the HP at a radial distance of ∼119 AU and at $\theta = {\sim} 125^{\circ}$ (Stone et al. 2019; Richardson et al. 2019). The HP is relevant because it is assumed to be a heliospheric boundary, the position where modulation commences i.e. where the VLIS of GCR species, described below in Sect. 2.2, must be specified in a model. However, the effects of the asymmetrical position of the HP on GCR modulation have been found to be insignificant in the innermost heliosphere (e.g., Langner and Potgieter 2005; Ngobeni and Potgieter 2011). Therefore the heliosphere in the present model is assumed symmetrical with the HP placed at 122 AU while the solar wind termination shock (TS) position changed, in a time-varying manner, from 88 AU in 2006 to 80 AU in 2009 responding to the varying solar activity (Richardson and Wang 2011). The shock compression ratio of 2.5 is assumed for the TS consistent with V1 and V2 observations (Stone et al. 2005; Richardson et al. 2008) in order to account for the drop in the solar wind speed beyond the TS as assumed in the model. For details on this approach, see also Vos and Potgieter (2016).

The TPE in Eq. (1) is written in terms of $p$ but it is usually solved in terms of rigidity $P$. The well-known relationship between $p$ and $P$ is given as

$$ P = \frac{\mathit{pc}}{ \vert q \vert }, $$

(11)

where $|q| = Ze$ is the particle charge with $e$ the elementary charge and $Z$ the number of such charges. Using the energy-momentum relationship, Eq. (11) can be expressed in terms of the total kinetic energy per nucleon, $E$, as

$$ P = \biggl( \frac{A}{Z} \biggr)\sqrt{E ( E + 2E_{0} )}. $$

(12)

Here, $A$ is the mass number and $E_{0}$ is the particle’s rest-mass-energy. For protons and helium nuclei $E_{0} = 0.9383\text{ GeV}$ is assumed. Equation (12) shows how the conversion of $P$ to $E$ depends on $A/Z$. Thus, the dependence of $\beta$ on $A/Z$ and $P$ can be written explicitly as

$$ \beta = \frac{v}{c} = \frac{P}{\sqrt{P^{2} + ( \frac{A}{Z} )^{2}E_{0}^{2}}} . $$

(13)

As a departure point and purely for explanatory and illustrative purposes, it is relevant to show the dependence of the diffusion and drift coefficients on $\beta$ when studying modulation for GCRs with different $A/Z$. Figure 2 shows $\beta$, given by Eq. (13), as a function of rigidity for different values of $A/Z$, e.g. $A/Z =1$ for protons, $A/Z = 1.5$ for He-3 and $A/Z = 2$ for He-4. Note the differences below $P \approx 5$ GV, whereas above this rigidity the three curves of $\beta$ become progressively similar, approaching 1.0 with increasing rigidity as particles become relativistic.

Fig. 2

The ratio of particle speed to light speed ($\beta$), as given by Eq. (13), as a function of rigidity shown for GCR species with different $A/Z$

The left panel of Fig. 3 depicts the computed rigidity dependence of $K_{\parallel}$, as given by Eq. (4), at the Earth (1 AU in the equatorial plane) for the assumed modulation between 2006 (solid lines) and 2009 (dashed lines). Evidently, $K_{\parallel}$ decreases with increasing $A/Z$ with $P < {\sim} 4$ GV, whereas above this rigidity $K_{\parallel}$ remains independent of $A/Z$ for a given modulation period. The right panel of Fig. 3 depicts the ratio $K_{\parallel} / \beta$ as a function of rigidity, with $K_{\parallel} \propto \beta \lambda _{\parallel}$ as in Eq. (3). As such the dependence of $\lambda _{\parallel}$ on $A/Z$ is eliminated at all rigidities for a given modulation period.

Fig. 3

Left panel: Rigidity dependence of $K_{\parallel}$, as given by Eq. (4), at 1 AU (Earth) between 2006 and 2009 for GCR species with different $A/Z$ as indicated. Right panel: Corresponding $K_{\parallel}/\beta$ ratio is shown as a function of rigidity; here $K_{\parallel}$ is in units of $6.0 \times 10^{22}\text{ cm}^{2}\,\mbox{s}^{-1}$

Figure 4 is similar to Fig. 3 but with the drift coefficient $K_{A}$ shown; again $K_{A}/\beta$ is independent of $A/Z$. Figures 3 and 4 illustrate that the effects of $\beta$, caused by $A/Z$, on both the diffusion and drift coefficients become increasingly significant the lower the rigidity. However, all mean free paths (MFPs) and the drift scale ($\lambda _{A} = 3K_{A}/v$) are independent of $A/Z$. This emphasizes the fact that in modulation studies this is the case for protons and all GCR nuclei, meaning that there are no fundamental differences between their modulation for a given rigidity, time and place in the heliosphere.

Fig. 4

Left panel: Rigidity dependence of $K_{A}$, as given by Eq. (10), at 1 AU (Earth) between 2006 and 2009 for GCR species with different $A/Z$. Right panel: Corresponding $K_{A}/\beta$ ratio as a function of rigidity

The MFP’s and $\lambda _{A}$ at Earth for a given rigidity only change with time as shown in Fig. 5. Here, the MFPs and $\lambda _{A}$ as a function of rigidity at Earth, as used in the model, are shown for seven half-year periods between 2006 and 2009: 06/11/14-06/12/12 (2006e), 07/05/24-07/06/21 (2007m), 07/12/01-07/12/29 (2007e), 08/06/09-08/07/06 (2008m), 08/11/20-08/12/17 (2008e), 09/05/30-09/06/26 (2009m), 09/08/20-09/09/16 (2009e). The parallel MFPs $\lambda _{\parallel}$ are shown as solid lines; the perpendicular MPFs in the radial ($\lambda _{\bot r}$) and polar ($\lambda _{\bot \theta }$) directions as dashed and dashed-dotted lines respectively; and $\lambda _{A}$ is shown as dotted lines. These MFPs and $\lambda _{A}$ are required to reproduce the proton and helium spectra measured by PAMELA from 2006e to 2009e as will be shown below. Therefore, for the modeling done here, a different set of MFPs and $\lambda _{A}$ to that shown in Fig. 5 may not reproduce optimally compatible results with experimental data.

Fig. 5

The three mean free paths (MFPs), as used in the model, shown as a function of rigidity at Earth; parallel MFPs ($\lambda _{\parallel}$) as solid lines; perpendicular MFPs in the radial ($\lambda _{\bot r}$) and polar ($\lambda _{\bot \theta }$) directions as dashed and dashed-dotted lines, respectively, and the drift scale ($\lambda _{A}$) as dotted lines. This is done between 2006 and 2009 for one Carrington rotation period (∼27 days) each at the end of seven half-year periods indicated by different colours: (06/11/14-06/12/12 (2006e), 07/05/24-07/06/21 (2007m), 07/12/01-07/12/29 (2007e), 08/06/09-08/07/06 (2008m), 08/11/20-08/12/17 (2008e), 09/05/30-09/06/26 (2009m), 09/08/20-09/09/16 (2009e))

2.2 Very local interstellar spectra

The VLIS’s of GCRs are of central importance in the general understanding of the heliospheric modulation because they always provide the input spectra in numerical models to be modulated from a given HP position, into the heliosphere, up to the Earth. In this work the assumed proton VLIS is given in detail by Bisschoff et al. (2019), whereas the total helium (He) VLIS is derived by adding the GALPROP adjusted VLIS’s of He-3 and He-4, with the requirement that sum of the two gives reasonable compatibility to V1 (Stone et al. 2013; Cummings et al. 2016) and PAMELA (Munini et al. 2019; Marcelli et al. 2020) observations at lower and higher rigidities, respectively.

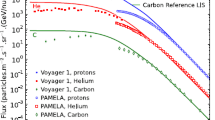
Figure 6 depicts three VLIS’s, for He-3 and He-4 computed with GALPROP as described by Bisschoff et al. (2019), and the corresponding VLIS derived for total He in comparison with V1 observations beyond the HP at low rigidities (Stone et al. 2013; Cummings et al. 2016) and with PAMELA observations at high rigidities for He at the Earth (Marcelli et al. 2020). Evidently, the VLIS for He closely matches the V1 and PAMELA observations. With separate VLIS’s for He-3 and He-4, the three modulated ratios $p$/He-3, $p$/He-4 and $p$/He can be done with improved confidence and accuracy. This is done and discussed in Sect. 3.3.

Fig. 6

The computed VLIS for He-3 (dotted purple line), He-4 (dotted green line) and total He (solid red line) compared to V1 observations at a radial distance of ∼122 AU; open red circles from Stone et al. (2013); filled red circles from Cummings et al. (2016) and PAMELA observations at 1 AU during 2009e; filled blue circles from Marcelli et al. (2020). The VLIS for total He is obtained by adding together the GALPROP computed VLIS’s for He-3 and He-4

3 Modeling results and discussion

3.1 Spectra of protons and helium nuclei observed by PAMELA between 2006 and 2009

The panel on the left of Fig. 7 shows the seven proton spectra in terms of rigidity measured by PAMELA. These spectra cover a period of one Carrington rotation (∼27 days) each at the end of a half year period during the 2006 to 2009 solar minimum period (coloured coded as 2006e, 2007m, 2007e, 2008m, 2008e, 2009m and 2009e); shown in the right panel is the corresponding intensity ratios relative to 2006e, indicating how the spectra became gradually softer towards solar minimum modulation late in 2009. The spectra presented here have a rigidity range from ∼0.4 GV to ∼47.0 GV, all observed during the $A < 0$ HMF polarity cycle as published by Adriani et al. (2013).

Fig. 7

Galactic proton spectra (left panel) observed by the PAMELA experiment, reported here as a function of rigidity for seven periods indicated by 2006e, 2007m, 2007e, 2008m, 2008e, 2009 m and 2009e, respectively. Right panel shows the corresponding intensity ratios relative to 2006e. These spectra were observed at Earth in the $A < 0$ polarity cycle during the solar minimum of 2006 to 2009 (from Adriani et al. 2013)

Figure 8 shows seven corresponding PAMELA Helium (He) spectra (left panel), measured at similar periods of time as the proton spectra in Fig. 7, and the corresponding intensity ratios relative to 2006e (right panel) as a function of rigidity. The rigidity range for He is from ∼0.92 GV to ∼43.0 GV, indicating the availability of the He spectra for the rigidity range as reported for protons. These He spectra, as the combined levels of He-4 and He-3, were recently published by Marcelli et al. (2020).

Fig. 8

Galactic Helium (He) spectra (left panel) as a function of rigidity observed by the PAMELA experiment for seven periods, from 2006e to 2009e, as indicated. Right panel shows the corresponding intensity ratios relative to 2006e. These spectra, from Marcelli et al. (2020), were observed at similar times as the proton spectra in Fig. 7

When comparing Figs. 7 and 8, it is evident that these modulated proton and helium spectra exhibit the same qualitative modulation features as expected from a modulation theory point of view. The observed characteristics are the negative spectral slope values at high rigidities and progressive less modulation as a function of increasing rigidity, a peak (maximum value) in intensity, with positive slopes below this turn-around rigidity. At lower rigidities the slopes of these spectra settle into a steady value, known as the ‘adiabatic slope’ or ‘adiabatic limit’. The spectral shapes at varying rigidities depend on the underlying heliospheric modulation conditions e.g. the proton spectral fall in 2009e begins at a lower rigidity than in 2006e. Also, as modulation conditions changed from 2006e to 2009e, the rigidity dependence of the spectral fall is more pronounced in proton observations than for He. Quantitatively, the right panel of Fig. 7 indicates that the changing heliospheric modulation conditions between 2006e and 2009e caused the observed proton intensities in 2009e to be ∼2.5 higher than in 2006e at ∼0.4 GV. Whereas for He, shown in the right panel of Fig. 8, the observed relative intensity maximum occurs at ∼1.0 GV and is ∼2.1 higher in 2009e than in 2006e.

Combined with precise VLIS for protons and helium nuclei, these observations provide the opportunity to study in greater detail than before how differently GCR species with a dissimilar mass-to-charge ratio ($A/Z$) are modulated down to a few GV at the Earth in a quiet heliosphere. It is an objective of this work to establish, when using the 3D modulation model described in Sect. 2, if both the PAMELA proton and total He spectra could be reproduced using the same consistent modeling approach, and additionally to distinguish explicitly between He-4 and He-3 modulation applicable from 2006e to 2009e period. This approach and computed results can then be used to compare the simulated proton to He ratio ($p$/He) with how the PAMELA observed ratio changed between 2006e and 2009e, and additionally give these ratios for the lower rigidity range where no observations are available.

3.2 Computed spectra of protons and helium nuclei from 2006 to 2009

In an attempt to improve our understanding of the modulation of the two GCR helium nuclei, the model is first applied to the modulation of GCR protons at the Earth with the aim of reproducing carefully the selected PAMELA proton spectra between 2006 and 2009. We follow the approach as was described by Potgieter et al. (2014); see also Potgieter and Vos (2017), now using an updated set of modulation parameters in the model, following the same approach of Aslam et al. (2019a). This validates the model and gives a way for a meaningful comparison with the corresponding modeling of He spectra, using the exact same set of modulation parameters, diffusion coefficients and drift coefficient, with their $A/Z$-value and VLIS the only differences remaining. Therefore, to reproduce the PAMELA proton spectra from 2006e to 2009e, the TPE was solved for each period of the measured spectra by using the calculated average values of the HCS tilt and the HMF magnitude at the Earth shown in Fig. 1, together with appropriate adjustments to the diffusion and drift coefficients.

Figure 9 depicts these computed spectra overlaid on the corresponding observed proton spectra taken from Fig. 7, shown at the Earth (1 AU in the equatorial plane with $\theta = 90^{\circ}$) with respect to the proton VLIS specified at the HP at 122 AU during this $A < 0$ magnetic polarity cycle. The effect of these varying heliospheric modulation conditions between 2006 and 2009 on GCR proton spectra were discussed in detail by Potgieter and Vos (2017). The essence of Fig. 9 is to show that the PAMELA proton spectra are well reproduced by our model across all rigidities. The next step is to apply the model to He modulation using the same set of modulation parameters, diffusion and drift coefficients. First, this is done separately for He-4 and He-3. For comparison with PAMELA observations these computed spectra are added up to describe what is called the total He spectra for the mentioned period. This approach requires that the VLIS’s for both isotopes must be known beforehand as described in Sect. 2.2 and specified as initial conditions in the model at 122 AU.

Fig. 9

Left panel shows the VLIS for GCR protons (black line) specified at the HP (122 AU) together with the modulated differential intensity computed (coloured solid lines) as a function of rigidity at the Earth for the solar minimum period of 2006e to 2009e. Right panel shows the corresponding computed intensity ratios as solid lines relative to 2006e. These computed spectra are compared to PAMELA proton observations from Fig. 7 indicated by coloured open circles

The VLIS’s for He-4 and He-3 are shown in the left panel of Fig. 10, together with the computed, modulated spectra for He-4 and He-3 as a function of rigidity at the Earth between 2006e and 2009e; the time periods are according to what was shown in Fig. 8. The differences between the VLIS’s and modulated spectra for He-4 and He-3 are displayed clearly in Fig. 10. Notice that apart from the large difference in intensity levels, the slopes of the VLIS’s at low rigidities for He-3 and He-4 are significantly different, also having spectral peaks at different rigidities. These aspects greatly influence the total amount of He modulation between the outer boundary and the Earth at a given rigidity and also the shape of the modulated spectra at Earth, particularly, how adiabatic energy losses shape these spectra at the Earth below a few hundred MV determined by the VLIS at a much higher rigidity; in this context, see e.g. Moraal and Potgieter (1982).

Fig. 10

Left panel: Modulated He-4 (⁴He₂) (solid lines) and He-3 (³He₂) (dashed lines) spectra computed as a function of rigidity shown at the Earth from 2006e to 2009e., together with their respective VLIS’s (dark grey lines) specified at 122 AU. Right panel: Corresponding intensity ratios are shown for both He-4 (solid lines) and He-3 (dashed lines) relative to 2006e as was done for protons in Fig. 9

The right panel of Fig. 10 highlights these differences and shows how the computed intensities increased for both isotopes relative to 2006e as function of rigidity. Noteworthy is that for the same set of modulation parameters and diffusion coefficients, the He-4 computed intensities increased relatively more than He-3 below ∼3.0 GV as solar modulation changed from 2006e to 2009e. Above this rigidity, the differences in relative increases are small to become negligible with increasing rigidity. Evidently, the He-3 did not undergo similar spectral changes to that of He-4 from 2006e to 2009e at lower rigidities. These differences between He-4 and He-3 are the consequence of how the combined interplaying modulation mechanisms in the heliosphere affect the modulated spectra based on their $A/Z$ and specifically on their VLIS’s.

In what follows, the computed modulation of GCR protons (p) is compared with total GCR Helium (He), obtained by adding up the modulated spectra and VLIS’s for He-3 and He-4 as shown in Fig. 10. In the left panel of Fig. 11 the computed spectra for protons and He are shown at the Earth over an extended rigidity range, from 50 GV down to 0.14 GV, in relation to their VLIS’s, respectively. This figure depicts how both proton and total He spectra at the Earth decreased significantly with decreasing rigidity in relation to their VLIS’s. The right panel of Fig. 11 gives the modulated intensity ratios of protons (solid lines) and He nuclei (dashed lines) relative to their respective 2006e spectra as a function of rigidity, and how adiabatic energy losses shape the spectral slopes of the modulated spectra to have spectral indices not varying much for protons and total He at low rigidities. Quantitatively, the largest relative increase for both protons and He occurs at lower rigidities but with different values based on their respective VLIS’s. As an example, at a rigidity of 0.14 GV, He increased by a factor of ∼2.1 from 2006e to 2009e, while protons increased by ∼2.5 at the same rigidity. Indeed the computed proton intensities continue to increase noticeably more than He below ∼1.0 GV, illustrating that adiabatic energy losses become evident at different rigidities for protons and total He, as indicated by when the spectral indices of the modulated spectra at these low rigidities remain essentially unchanged with decreasing rigidity. Note how in the right panel the ratios below ∼1 GV become gradually and progressively less rigidity dependent with decreasing rigidity and that this begins at a higher rigidity for He than for protons, and for He-3 than for He-4 (Fig. 10). Evidently, there are noticeable differences in the amount of modulation for protons and total He from 2006e to 2009e at lower rigidities. Therefore, the $p$/He ratio as a function of time is expected to exhibit changes below ∼1.0 GV in response to changing solar activity. This time dependence is highlighted further in Sect. 3.3.

Fig. 11

Left panel: Modulated proton (p) spectra (solid lines) and He spectra (dashed lines) computed as a function of rigidity, shown at the Earth, together with their respective VLIS’s represented by dark grey lines, from 2006e to 2009e. Right panel: Corresponding intensity ratios are shown for protons (solid lines) and helium (dashed lines) relative to 2006e. To obtain the modulated He spectra and the VLIS’s, the modulated spectra and LIS’s for He-3 and He-4 were respectively added together

Figure 12 shows the observed He spectra from Fig. 8 overlaid by the corresponding computed spectra at the Earth with respect to the total He VLIS. The effect of continuously but slowly varying heliospheric modulation conditions on He can be noted below 20–30 GV in this figure. These modulated He spectra exhibit a characteristic peak in each spectrum just below 2 GV in all seven half-year periods, but the rigidity where the peaks occur gradually shifts to lower values with decreasing modulation, as previously discussed. Evidently, the PAMELA He spectra from 2006e to 2009e are reproduced efficiently by the model using the same diffusion coefficients and drift coefficient as for protons. These computed spectra at $P < {\sim}0.92$ GV, where observational data is unavailable, serve as a prediction of what occurs at these low rigidities for modulation conditions such as between 2006e and 2009e. This is further highlighted by the computed intensity ratios of each time period with respect to the 2006e spectrum, along with the PAMELA He spectra ratio as shown in the right panel of Fig. 12. The modeling ratio increases significantly with decreasing rigidity below ∼20 GV, consistent to the observed ratio. As expected, the ratio is highest for 2009e similar to that for protons. Note how the computed ratios gradually flatten off to reach steady values at the lower rigidities, indicating that at even lower rigidities the modulation difference between 2006 and 2009 levels of solar activity will remain unchanged for helium.

Fig. 12

Left panel: Computed differential intensity for He (solid lines) is shown as a function of rigidity at the Earth between 2006e and 2009e as used before. Right panel: Corresponding intensity ratios relative to 2006e as a function of rigidity. Corresponding PAMELA He observations from Fig. 8 are shown as open circles in both panels

3.3 Proton to helium ratios

To investigate and uncover effects on $p$/He caused by the difference in their VLIS’s and those caused by $A/Z$, Fig. 13 shows four selected half-year periods of the modulated spectra (obtained with proton and He-4 VLIS’s) as a function of rigidity, at the Earth from 2006e (top left panel) to 2009e (bottom right panel), with respect to their corresponding VLIS’s at 122 AU. For illustrative purposes (as a numerical modeling exercise), three sets of solutions are shown using proton and He-4 VLIS’s: first, modulated spectra assuming $A/Z = 1.0$; second with $A/Z = 1.5$ and then with $A/Z = 2.0$. For example, the solid green lines are the modulated spectra computed as He-4 ($A/Z=2$) but based on a VLIS applicable to protons, and so on. In each panel, the lines of the same colour represent modulation differences between two species with the same $A/Z$ but with different VLIS’s, whereas that between solid lines (or dashed lines) is the difference due to $A/Z$ alone. Allowing this means that the diffusion and drift coefficients are the same for both GCR species as a function of rigidity. Therefore, Fig. 13 demonstrates the simulated effects on modulated spectra caused by differences in $A/Z$ as compared to those due to VLIS’s. Quantitatively, the effects due to differences in their VLIS’s are clearly larger. A notable spectral feature of interest due to $A/Z$ is that the rigidity where the peak in maximum intensity occurs gradually shifts to higher values with increasing $A/Z$. This figure illustrates the general features and characteristics of the expected modulated spectra at the Earth of species with different VLIS’s and $A/Z$.

Fig. 13

Illustration of modulated spectra for two GCR species at the Earth because of different VLIS’s at 122 AU and $A/Z$-values. Modulated spectra (solid lines and dashed lines are obtained with proton and He-4 (⁴He₂) VLIS’s respectively) computed as a function of rigidity at the Earth for 2006e (top left panel) to 2009e (bottom right panel), with respect to their corresponding VLIS (black solid lines for proton and black dashed lines for He-4). Three sets of solutions are shown in all panels: First, spectra with $A/Z = 1.0$ (red lines); second with $A/Z = 1.5$ (purple lines) and then with $A/Z = 2.0$ (green lines). For example, the solid green lines are the modulated spectra for He-4 but based on a proton VLIS (solid black line) and so on

When considering the effects caused by differences in VLIS’s or by $A/Z$-values on the $p$/He ratio at the Earth, it becomes relevant to also illustrate at what rigidity do these effects actually begin and their dependence on the assumed modulation conditions. Figure 14, derived from the results in Fig. 13, attempts to give an answer; at least the maximum effects from a modeling standing point. The left panel of Fig. 14 shows the corresponding intensity ratio as a function of rigidity, obtained for the three $A/Z$ scenarios ($A/Z = 1.0$ red lines; $A/Z = 1.5$ purple lines; $A/Z = 2.0$ green lines). This therefore depicts the maximum effects on the intensity ratio caused by differences in their VLIS’s alone, as modulation decreases between 2006 and 2009. Note that the intensity ratio approaches a value of ∼5.5 at $P > {\sim} 4$ GV, essentially independent of the assumed modulation conditions. Below this rigidity the sensitivity of the ratio to the assumed modulation conditions increases with decreasing rigidity. Shown in the right panel of Fig. 14 is the modulated intensity ratio obtained now by forcing the VLIS of the two species with different $A/Z$ to be the same as indicated in the legend. This panel shows the maximum effects caused by changing $A/Z$ alone between modulation conditions for 2006 and 2009. Evidently, the effects due to $A/Z$ on the ratio of intensities are not present at $P > {\sim} 4$ GV. Furthermore, the changing modulation condition from 2006 to 2009 has no effect on this ratio at these higher rigidities. However, when assuming the VLIS applicable to protons for both species, the intensity ratio decreases from 2006 to 2009 between 0.3 GV and ∼4 GV while at the same time increasing below 0.3 GV. It suffices to say that with $P > {\sim}4$ GV the $p$/He ratio at Earth is determined essentially by the shapes of their VLIS’s alone; in other words, PAMELA measurements of $p$/He at these rigidities reveal the shapes of their respective VLIS’s. Overall, Fig. 14 illustrates that the effects on $p$/He due to differences in their VLIS’s are dominant at all rigidities but those due to $A/Z$ are becoming increasingly noteworthy the lower the rigidity.

Fig. 14

Illustration of computed intensity ratios at the Earth due to different VLIS’s at 122 AU and $A/Z$-values based on the spectra shown in Fig. 13. Left panel shows ratio of intensities, obtained with a proton VLIS to that with a He-4 VLIS, as a function of rigidity between 2006e (solid lines) and 2009e (dashed lines). Three sets of ratios are shown: $A/Z = 1.0$ (red lines); second with $A/Z = 1.5$ (purple lines) and then with $A/Z = 2.0$ (green lines). In the right panel three sets of computed intensity ratios obtained with the same proton VLIS, similar to solid lines in Fig. 13, are plotted as a function of rigidity; red lines for spectra obtained with $A/Z = 1.0 / A/Z = 1.0$; purple lines with $A/Z = 1.0 / A/Z = 1.5$; green lines with $A/Z = 1.0 / A/Z = 2.0$. Again solid lines represent modulation conditions in 2006e and dashed lines in 2009e

Next, the numerical model is applied to obtain and illustrate the real $p$/He from 2006e to 2009e, now using the appropriate $A/Z$ and VLIS’s. First, in the left panel of Fig. 15, the computed $p$/He-4 and $p$/He-3 are shown respectively as a function of rigidity, ranging from 0.14 GV up to 25 GV. The right panel shows the corresponding $p$/He. In general, the prominent feature here is that $p$/He displays what may be seen as three regimes, reflecting a complex interplay of modulation processes throughout the heliosphere. The ratio of modulated spectra closely follows the corresponding VLIS ratio at rigidities $P > {\sim}5$ GV (relatively little modulation), then begins to deviate progressively from these values with decreasing rigidity (significant increased modulation), and eventually flattens off when both proton and helium spectra go into the adiabatic energy regime. Overall, from 2006e to 2009e, $p$/He increases noticeable for $P < \sim$ 0.6 GV, whereas above this rigidity these changes become gradually smaller to become negligible eventually from a modulation point of view. Figure 15 indicates that as modulation levels decrease from 2006e to 2009e, the contribution of adiabatic energy losses dissipates relatively faster for protons than for He at the same rigidity mainly due to the different slopes of their VLIS’s as mentioned before. The subsequent effect is that $p$/He increases below ∼0.6 GV despite that both the diffusion coefficients and drift coefficient change in the exact same way for protons and He nuclei during this period. The time dependence in $p$/He at lower rigidities is caused by a complex interplay between diffusion, drifts and adiabatic energy losses (see also Aslam et al. 2019a, 2019b, 2019c).

Fig. 15

Left panel: Computed $p$/He-4 (⁴He₂) (solid lines) and $p$/He-3 (³He₂) (dashed lines) as a function of rigidity at Earth from 2006e to 2009e. In the right panel the corresponding $p$/He is shown. In both panels the ratios for the relevant VLIS’s are given by the dark grey dashed and solid lines. These results are based on the appropriate $A/Z$ and VLIS’s for GCR protons and the two He isotopes

Returning to the left panel of Fig. 15, by comparing $p$/He-4 and $p$/He-3, it follows that whereas $p$/He-3 reaches a local minimum around ∼3 GV, such a minimum is not evident for $p$/He-4. The upward trend in the $p$/He-3 ratio at $P > {\sim}3$ GV indicates that proton intensities increased relatively more than He-3 intensities, while at the same time decreasing relatively more than He-4 intensities. This feature is independent of the assumed modulation conditions in the $A < 0$ magnetic polarity cycle. Clearly, $p$/He-3 displays a different rigidity dependence compared to $p$/He-4 because of the differences in their respective VLIS’s, not because of any fundamental difference in the solar modulation of these helium nuclei and protons because at high enough rigidity the three major diffusion coefficients and the drift coefficient are the same in terms of rigidity for these GCRs as illustrated in Figs. 3 and 4.

Separating the computed ratios of $p$/He-4 and $p$/He-3 allows for an investigation of how the overall $p$/He ratio changed from 2006e to 2009e at lower rigidities where observations are unavailable. Recently, comprehensive He (and other GCR nuclei) modeling was done by Shen et al. (2019) but with no separation of He-4 and He-3 done in their study; the modeling effects of He-4 were simply referred as helium. From the modeling presented in Fig. 15, it is clear that separating the effects of He-4 and He-3 is important if not crucial for understanding how exactly $p$/He changes with rigidity, an aspect that may be overlooked when considering only spectra where effects of He-3 may not be directly noticeable.

In the following, we focus on $p$/He, using total He intensities for each period under investigation. Figure 16 shows the computed $p$/He and those for PAMELA as a function of rigidity at six different times, between 2006e to 2009m. Also shown in each panel is their VLIS ratio. The value and shape of $p$/He for $P > {\sim} 4.0$ GV are reproduced quite well with the modulation model, but less so for rigidities between ∼1.0 GV and ∼4.0 GV for all the selected time periods. See also the discussions about the modeling approach given by Marcelli et al. (2020). It is interesting to note that this particular rigidity range in Fig. 16 correlates with the computed local minimum in the $p$/He-3 shown in Fig. 15. Indeed, a simple but ad hoc adjustment of the total He VLIS, both He-4 and He-3 VLIS’s, between 0.9 GV and 5 GV rigidity range (not shown) can reproduce the observed $p$/He ratio reasonably well. Making such a remark is possible only when doing numerical modeling because the modulation effects of He-3 can be separated systematically and effectively from that of He-4. However, it should also be noted that since drifts are significantly reduced below ∼1.0 GV to assure that the magnitude and rigidity dependence of the Ulysses observed latitudinal CR gradients in the heliosphere are reproduced as mentioned before (see also Gieseler and Heber 2016; Vos and Potgieter 2016), the behaviour of $p$/He between ∼1.0 GV and ∼4.0 GV is indicative of the competition between the drift and diffusion processes combined with the shapes of their VLIS’s and $A/Z$ values. Adjusting diffusion or drifts may also improve the compatibility in this rigidity range but such specific adjustments were not required at all when comparing the same model with PAMELA proton observations for these periods.

Fig. 16

The $p$/He ratios as a function of rigidity for six time periods between 2006e to 2009m. Computed and observed ratios (with uncertainties depicted by error-bars and shaded bands) are represented by the coloured lines and symbols, respectively. The corresponding $p$/He VLIS ratio is given by dark grey lines in each panel

The observed and computed $p$/He are shown together in Fig. 17, now as a function of time for six different rigidity values. Overall, there is reasonable compatibility between the computed and observed ratios, except for the noticeable decrease in PAMELA observations after 2007 around 0.92 GV, which is the lowest matching rigidity for PAMELA protons and helium nuclei. At this rigidity the ratio decreases from $p$/He ≈ 22 at the end of 2007 to $p$/He ≈ 20 in the second-half of 2009. However, for $P > 1.06$ GV the decrease in $p$/He ratio dissipates indicating that it is more prominent at lower rigidities where solar modulation is significant. However, these short-term, time-dependent effects are not included in the model, consequently, the computed ratios are unable to follow these trends in the PAMELA ratios. For $P > 1.06$ GV, the computed ratios are compatible to the time profiles of the PAMELA $p$/He but is overestimated between 1.22–1.40 GV. As previously mentioned, this aspect can be improved with a simple but ad hoc adjustment of the total He VLIS.

Fig. 17

Proton to helium ratios at various rigidities, between 920 MV and 8.45 GV, as a function of time. Observed ratios from PAMELA, reported by Marcelli et al. (2020), are given by the solid lines and filled circles; the computed ratios from the model are given by the dashed lines and open circles for the time periods as indicated

The computed $p$/He as a function of time for rigidities now ranging from 0.14 GV to 0.92 GV, are shown in Fig. 18. This figure is complimentary to Fig. 17 and shows predictions for $p$/He where PAMELA observations are unavailable. The top panel shows how $p$/He between 0.14 GV and 0.6 GV increases noticeably from 2006e to 2009e, while staying almost constant as a function of time for 0.7 GV and 0.92 GV. The bottom panel shows the same ratios relative to 2006e to highlight these changes applicable from 2006 to 2009. It follows that $p$/He increased by a factor ∼1.2 at 0.14 GV but this trend dissipates with increasing rigidity, so that at 0.92 GV, the ratio from 2008m to 2009e decreases somewhat, indicating a slow but systematic departure from where in terms of rigidity the adiabatic energy loss-diffusion dominated interplay makes way for a drift-diffusion dominated interplay in the model. In this context, see Figs. 6 and 7 by Potgieter and Vos (2017).

Fig. 18

Top panel: Computed $p$/He from the modulation model as a function of time at six selected rigidity values, between 0.14 GV and 0.92 GV, according to different colours as indicated. Bottom panel: Similar to the top panel but now normalized with respect to $p$/He for 2006e to highlight these changes applicable from 2006 to 2009

4 Summary, conclusions and outlook

The availability of simultaneous measurements of GCR protons (∼0.4 GV to ∼47.0 GV) and helium (∼0.92 GV to ∼43.0 GV) by PAMELA during the solar minimum period from 2006 to 2009, as shown in Figs. 7 and 8, have motivated the detailed modeling in this work. The essentials of the numerical model together with the elements of the diffusion and drift tensors have been published by Potgieter and Vos (2017) and recently by Bisschoff et al. (2019) and Aslam et al. (2019a). Also, this model has been successful in reproducing charge-sign dependent modulation observed by PAMELA from 2006 to 2009 over a wide rigidity range (e.g., Di Felice et al. 2017; Aslam et al. 2019b, 2019c). In this work the 3D model is applied to the modulation of the two helium nuclei with its particular isotopic challenges. The modeling of He-3 and He-4 is done separately and then added together to obtain the modulation for total helium (He). This requires that the VLIS’s of both helium isotopes, shown in Fig. 6, must be known beforehand and is obtained by applying GALPROP models as described and acknowledged by Bisschoff et al. (2019).

Figures 9 and 12 show that the model reproduces PAMELA measurements of both protons and helium nuclei quite well using the exact same set of modulation parameters, three diffusion coefficients and the drift scale. This is quite important to understand how differently GCR species with a dissimilar $A/Z$ are modulated down to a few hundred MV. To highlight this point further, the numerical modeling is extended below 0.92 GV, where PAMELA observations for He are absent. This provides predictions of $p$/He down to 0.14 GV, where the particular effects described in this work become quite significant.

We find from the modeling that He-3 intensities do not undergo identical spectral changes to that of He-4 from 2006 to 2009 for $P < {\sim} 4.0$ GV. This is mainly due to differences in their VLIS’s. As a result $p$/He-3 display a different trend in terms of rigidity compared to $p$/He-4. Considering $p$/He, it is found that it decreases modestly from a magnitude of ∼5.5 above ∼4.0 GV, essentially independent of the assumed modulation conditions. Whereas below this rigidity, the $p$/He ratio increases with decreasing rigidity and significant variations are predicted starting from ∼0.6 GV down to lower rigidities, depending on the assumed solar modulation conditions. Moreover, the value and shape of the observed $p$/He is reproduced quite well by the model above ∼4.0 GV, but less effective between ∼1.0 GV and ∼4.0 GV for the selected time periods. Another way to improve compatibility between the computed $p$/He and observations, though not compelling and hence not shown, is to adjust the total He VLIS in an ad hoc manner at rigidities between 0.9 GV and 5 GV. This indicates that a thorough modeling study of He-3 may be worthwhile to do in future, even including a deuteron (H-2) study, while assuring that inconsistencies are avoided.

The differences between proton and helium modulation effects are found to be the consequence of how the combined interplaying modulation mechanisms in the heliosphere affect the modulated spectra based on their $A/Z$ and in particular on their respective VLIS’s. There is no reason to believe that there are any fundamental differences between these GCRs when modulated inside the heliosphere.

The next phase of our modeling will be devoted to repeating the essence of this study for the period of increasing solar activity after 2009 until the end of the PAMELA mission (Martucci et al. 2018) and with the addition of AMS-02 observations since May 2011 (Aguilar et al. 2018). The latter observations indicate an interesting time-dependence in the $p$/He ratio after 2014 (Corti et al. 2019a, 2019b; Tomassetti et al. 2019) which requires a focused and more advanced numerical study because simulating GCR modulation during times of maximum solar activity, including a HMF polarity reversal, is challenging (see Aslam et al. 2019b, 2019c). Refined computations, especially at high rigidities with $P > 10$ GV (see e.g., Usoskin et al. 2017; Koldobskiy et al. 2019), where modulation effects are relatively small and easily overlooked in numerical modeling, are also necessary.