Metallicity calibration and photometric parallax estimation: I. UBV photometry

Abstract

We present metallicity and photometric parallax calibrations for the F and G type dwarfs with photometric, astrometric and spectroscopic data. The sample consists of 168 dwarf stars covering the colour, iron abundance and absolute magnitude intervals $0.30<(B-V)_{0}<0.68~\mbox{mag}$, $-2.0<[\mathrm{Fe}/\mathrm{H}]<0.4~\mbox{dex}$ and $3.4< M_{V}<6.0~\mbox{mag}$, respectively. The means and standard deviations of the metallicity and absolute magnitude residuals are small, i.e. $\langle\Delta[\mathrm{Fe}/\mathrm{H}]_{res}\rangle=0$ and $\sigma=0.134~\mbox{dex}$, and $\langle\Delta (M_{V})_{res}\rangle=0$ and $\sigma=0.174~\mbox{mag}$, respectively, which indicate accurate metallicity and photometric parallax estimations.

1 Introduction

Stellar metallicity and kinematics are two important means to understand the formation and evolution of our Galaxy. Metallicity of a star can be determined spectroscopically or photometrically. One needs more accurate analyses for the first procedure which can be carried out only for nearby stars, while the second one, the photometric procedure, can be applied to stars at large distances as well. The second procedure has a long history. We are indebted to Roman (1955) who discovered the correlation between the weakness of the spectral lines and the ultra-violet (UV) excess, $\delta(U-B)$, of the stars.

It has been a custom to use the $(U-B)\times(B-V)$ two-colour diagram of the Hyades cluster to estimate the $\delta(U-B)$ colour excesses, i.e. $\delta(U-B)$ of a star is the difference between the UV colours of the given star and the Hyades’ star with the same $B-V$ colour. Schwarzschild et al. (1955), Sandage and Eggen (1959) and Wallerstein (1962) interpreted the UV excess with the “blanketing model”, i.e. the UV excesses of the stars, with the same metal abundance but different $B-V$ colours are different. This is important for the red stars where the blanketing line is parallel to the intrinsic Hyades line and hence $\delta(U-B)$ is guillotined. Sandage (1969) used a procedure to normalize the UV excesses, as explained in the following. He separated 112 high proper motion stars into 16 sub-samples with mean colours $B-V=0.35, 0.40, 0.45, \ldots, 1.10$, and compared the UV excess for each colour, $\delta(U-B)$, with the one for $(B-V)_{0}=0.6$, $\delta_{0.6}(U-B)$, which is the maximum UV excess for a given star. Then, he adopted the ratio $\delta(U-B)_{0.6}/\delta(U-B)$ as a normalized factor for the UV excess for the corresponding $B-V$ colour.

Carney (1979) normalized the UV excesses of 101 dwarfs using the procedure of Sandage (1969) and calibrated them to the iron abundance $[\mathrm{Fe}/\mathrm{H}]$. Karaali et al. (2003) improved this calibration using a different procedure and 88 dwarf stars. These calibrations provide iron abundances in the $\mathit{UBV}$ photometry. Other studies offered calibration in different photometries, including $\mathit{UBV}$, (i.e. Walraven and Walraven 1960; Strömgren 1966; Cameron 1985; Laird et al. 1988; Buser and Fenkart 1990; Trefzger et al. 1995). Two recent metallicity calibrations which provide iron abundances with $\mathit{UBV}$ photometry are those of Karataş and Schuster (2006) and Karaali et al. (2011).

The distance of a star is an important parameter in investigation of the kinematic structure of our Galaxy which can be determined via trigonometric or photometric parallaxes. Trigonometric parallax procedure can be applied only to nearby stars. Hipparcos (ESA 1997; van Leeuwen 2007) is the main source for this parallax. For stars at large distances, only photometric parallax is available, which is the combination of the apparent and absolute magnitude of a star in question. Absolute magnitude estimation is another problem for the researchers. The widely used procedure for absolute magnitude estimation is based on the offset from a standard main-sequence, where Hyades is generally used for this purpose (Laird et al. 1988; Nissen and Schuster 1991; Karaali et al. 2003; Karataş and Schuster 2006).

The colour-absolute magnitude of a specific cluster can also be used for absolute magnitude estimation of stars in a given population, such as thin and thick discs, and halo. The cluster is chosen such that its metallicity is compatible with the mean metallicity of the population in question. Details for this procedure can be found in Phleps et al. (2000), Chen et al. (2001), and Siegel et al. (2002).

In this study, we present two calibrations; one for the iron abundance $[\mathrm{Fe}/\mathrm{H}]$, and another one for the absolute magnitude offset $\Delta M_{V}$, in terms of reduced UV excess, $\delta_{0.6}(U-B)$. We used the reduced Hipparcos astrometric data (van Leeuwen 2007) for the first time and improved both the metallicity and absolute magnitude calibrations. We organized the paper as follows. The data are presented in Sect. 2. The procedure is given in Sect. 3, and Sect. 4 is devoted to Summary and Discussion.

2 Data

The data used in our study is a combination of the star samples given in four spectroscopic studies, i.e. Bensby et al. (2014), Nissen and Schuster (2010), Reddy et al. (2006), and Venn et al. (2004). We separated the F-G dwarf stars in these studies with the temperature and surface gravity constraints of Cox (2000), i.e. $5310< T_{eff}(K)<7300$, and $\log g>4$ (cgs) and reduced the multiple observations to a single one. The number of stars taken from the mentioned studies in the order given above which supply the constraints of Cox (2000) are 263, 83, 51, and 32, respectively. After excluding the binary and variable stars from the sample, as well as the multiple observations, the total star sample reduced to 168. The iron abundances of these stars were also taken from the mentioned four spectroscopic studies. We used the reduced Hipparcos parallaxes (van Leeuwen 2007) and estimated the distances of the sample stars using the following equation:

$$ d~(\mbox{pc})=1000/\pi~(\mbox{mas}). $$

(1)

The $V$ apparent magnitudes and, $U-B$ and $B-V$ colours of the sample stars are provided from the catalogue of Mermilliod (1997) and they are de-reddened by the procedure explained in the following. We adopted the total absorption for the model, $A_{\infty}$, (Schlafly and Finkbeiner 2011) and estimated the total absorption for the distance of the star, $A_{d}$, by the following equation of Bahcall and Soneira (1980):

$$ A_{d}(b)=A_{\infty}(b) \biggl[1-\exp \biggl(\frac{-|d~\sin(b)|}{H} \biggr) \biggr], $$

(2)

where $b$ and $d$ are the Galactic latitude and distance of the star, respectively, and $H$ is the scale-height of the dust ($H=125~\mbox{pc}$; Marshall et al. 2006). Then, the colour excess of the star, $E_{d}(B-V)$, could be estimated by the following equation of Cardelli et al. (1989) and was used in the evaluation of the colour excess $E_{d}(U-B)$ given by Garcia et al. (1988):

$$\begin{aligned} &E_{d}(B-V)=A_{d}(b)/3.1, \end{aligned}$$

(3)

$$\begin{aligned} &E_{d}(U-B)=0.72\times E_{d}(B-V) \\ &\phantom{E_{d}(U-B)=\,}+0.05\times E_{d}(B-V)^{2}. \end{aligned}$$

(4)

Finally, the de-reddened $V_{0}$ magnitude and colour indices are:

$$\begin{aligned} &V_{0}= V-3.1\times E_{d}(B-V), \\ &(B-V)_{0}=(B-V)-E_{d}(B-V), \\ &(U-B)_{0}=(U-B)-E_{d}(U-B). \end{aligned}$$

(5)

Thus, we estimated the absolute magnitudes of the stars using the necessary parameters in the well known Pogson equation, i.e.

$$ V_{0}-M_{V}=5\times \log d-5. $$

(6)

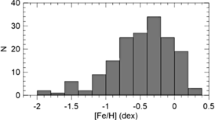
Data for the 168 sample stars are given in Table 1. They cover the colour range $0.30<(B-V)_{0}<0.68~\mbox{mag}$. The distributions of the iron abundance, relative parallax errors and the absolute magnitudes are given in Figs. 1, 2 and 3. The mode value of the metallicity histogram in Fig. 1 corresponds to $-0.3~\mbox{dex}$, while the iron abundances cover the range $-2<[\mathrm{Fe}/\mathrm{H}]<+0.4~\mbox{dex}$. However, the number of stars with $[\mathrm{Fe}/\mathrm{H}]<-1.2$ and $[\mathrm{Fe}/\mathrm{H}]>0.2~\mbox{dex}$ are only 14. The number of stars with relative parallax error $\sigma_{\pi}/\pi\leq 0.1$ is 141, which comprise about 84% of the complete sample. The mode value of absolute magnitudes of the sample stars is calculated to be $M_{V}=4.5~\mbox{mag}$. The absolute magnitudes in Fig. 3 range from 3.4 to 6.0 mag. The data for the two-colour diagram, $(U-B)_{0}\times(B-V)_{0}$, and $M_{V}\times(B-V)_{0}$ colour-absolute magnitude diagram for the Hyades cluster were taken from Sandage (1969) and Karaali et al. (2003), respectively, and then they were fitted to fifth degree polynomial equations as follows:

$$\begin{aligned} (U-B)_{0} =&2.791(0.702)-20.567(5.558)\times(B-V)_{0} \\ &{}+58.355(16.920)\times(B-V)_{0}^{2} \\ &{}-81.837(24.836)\times(B-V)_{0}^{3} \\ &{}+59.22(17.631)\times(B-V)_{0}^{4} \\ &{}-17.115(4.857)\times(B-V)_{0}^{5}. \end{aligned}$$

(7)

and

$$\begin{aligned} M_{V} =&5.661(3.185)-36.582(22.392)\times(B-V)_{0} \\ &{}+133.228(58.043)\times(B-V)_{0}^{2} \\ &{}-188.632(72.402)\times(B-V)_{0}^{3} \\ &{}+122.703(43.577)\times(B-V)_{0}^{4} \\ &{}-29.961(10.156)\times(B-V)_{0}^{5}. \end{aligned}$$

(8)

The numbers in parenthesis indicate the error values of the related coefficients. The correlation coefficient and standard deviation of Eq. (7) and Eq. (8) are $R^{2}=0.999$ and $\sigma=0.007~\mbox{mag}$ and $R^{2}=0.989$ and $\sigma=0.164~\mbox{mag}$, respectively.

Fig. 1

Metallicity distribution of the sample stars

Fig. 2

Distribution of the relative parallax errors for the sample stars

Fig. 3

Absolute magnitude distribution for the sample stars

Table 1 Data for the sample stars used in our study. The columns give: ID, Equatorial coordinates, Hipparcos number, $V$ apparent magnitude, $U-B$ and $B-V$ colours, colour excess reduced to the distance of the star ($E_{d}(B-V)$), parallax and its error ($\pi$), effective temperature ($T_{eff}$), surface gravity ($\log~g$), iron abundance ($[\mathrm{Fe}/\mathrm{H}]$), and reference

3 Procedure

3.1 Metallicity calibration

We used the same procedure in Karaali et al. (2005) and Karataş and Schuster (2006) for the metallicity calibration. However, our data are different than the cited studies. As stated in Sect. 2, our metallicities (the iron abundances) are provided from recent studies (Bensby et al. 2014; Nissen and Schuster 2010; Reddy et al. 2006; Venn et al. 2004). Hence, we expect more accurate iron abundances. The same case holds for the absolute magnitudes and distances which are estimated via the re-reduced Hipparcos parallaxes (van Leeuwen 2007) and hence they are more accurate than the ones published formerly (ESA 1997). We fitted the guillotine factors of Sandage (1969) in sixteen $B-V$ colours to a sixth degree polynomial as in the following which could be used to evaluate a guillotine factor (normalized factor) for each $B-V$ colour:

$$\begin{aligned} f =&\delta(U-B)_{0.6}/\delta(U-B)=8.175-83.963\times(B-V)_{0} \\ &{}+409.970\times(B-V)_{0}^{2}-1018.242 \times(B-V)_{0}^{3} \\ &{}+1341.239\times(B-V)_{0}^{4}-889.844 \times(B-V)_{0}^{5} \\ &{}+234.468\times(B-V)_{0}^{6}. \end{aligned}$$

(9)

Data used for the metallicity calibration are given in Table 2. We fitted the iron abundances (Table 1) in terms of normalized UV excesses to a third degree polynomial as follows and presented in Fig. 4:

$$\begin{aligned} {[\mathrm{Fe}/\mathrm{H}]} =&0.105(0.010)-5.428(0.521)\times \delta_{0.6} \\ &{}+7.340(5.895)\times \delta_{0.6}^{2} \\ &{}-50.081(16.359)\times \delta_{0.6}^{3}, \end{aligned}$$

(10)

where $\delta_{0.6}$ indicates $\delta_{0.6}(U-B)$. The correlation coefficient and standard deviation of Eq. (10) are $R^{2}=0.949$ and $\sigma=0.134~\mbox{dex}$, respectively.

Fig. 4

Metallicity calibration. The solid line corresponds to the relation in Eq. (10). The dashed lines denote $\pm 1\sigma$ prediction levels

Table 2 Data used in the calibrations. The columns give: ID, Hipparcos number, de-reddened apparent magnitude $V_{0}$ and $(B-V)_{0}$, $(U-B)_{0}$ colours, $(U-B)_{Hya}$ colour for the Hyades cluster, UV excess $\delta(U-B)$, normalized factor $f$, normalized UV excess $\delta_{0.6}$, original absolute magnitude $(M_{V})_{org}$, absolute magnitude for the Hyades cluster $(M_{V})_{Hya}$, absolute magnitude offset $\Delta M_{V}$, estimated absolute magnitude $(M_{V})_{est}$, and absolute magnitude residuals $(M_{V})_{res}$

We estimated the iron abundances of the sample stars, $[\mathrm{Fe}/\mathrm{H}]_{est}$, using Eq. (10) and compared them with the original ones (Fig. 5). There is a linear relation between two sets of iron abundances. The mean and the standard deviation of the residuals (Table 2, Fig. 5) are small, $\langle\Delta[\mathrm{Fe}/\mathrm{H}]\rangle=0$ and $\sigma=0.134~\mbox{dex}$, confirming the accuracy of our procedure.

Fig. 5

Comparison of the original ($[\mathrm{Fe}/\mathrm{H}]_{org}$) and estimated ($[\mathrm{Fe}/\mathrm{H}]_{est}$) metallicities (a) and distribution of the metallicity residuals ($\Delta [\mathrm{Fe}/\mathrm{H}]_{res}$) respect to the original metallicities (b) for the sample stars. The dashed lines denote $\pm 1\sigma$ prediction levels

3.2 Absolute magnitude calibration

We preferred the widely used procedure mentioned in the introduction for the absolute magnitude calibration which is based on the offset from a standard main sequence. The absolute magnitude-colour diagram for the sample stars is given in Fig. 6 confronted to the main sequence of Hyades cluster. The iron abundances of the sample stars are also indicated with different symbols in this diagram, where a trend in the metallicity can be noticed in the direction of the absolute magnitude.

Fig. 6

Colour-absolute magnitude diagram for the sample stars. The curve denotes the intrinsic Hyades sequence. Symbols correspond to different metallicities as indicated in the panel

We estimated the differences between the absolute magnitudes of the sample stars and the Hyades’ stars of equal $(B-V)_{0}$ colour, $\Delta M_{V}=M_{V}-(M_{V})_{Hya}$, and then plotted them against normalized UV excesses, $\delta_{0.6}(U-B)$, (Table 2 and Fig. 7) which yields the following third degree polynomial:

$$\begin{aligned} \Delta M_{V} =&-0.174(0.036)+5.278(1.141)\times \delta_{0.6} \\ &{}-5.292(1.007)\times \delta_{0.6}^{2} \\ &{}+28.477(5.237)\times \delta_{0.6}^{3}. \end{aligned}$$

(11)

The correlation coefficient and standard deviation of Eq. (11) are $R^{2}=0.824$ and $\sigma=0.174~\mbox{mag}$, respectively.

Fig. 7

Absolute magnitude offset versus normalized UV excess for the sample stars. The solid line corresponds to the relation in Eq. (11). The dashed lines denote $\pm 1\sigma$ prediction levels

We estimated the absolute magnitudes of the sample stars, $(M_{V})_{est}$, by replacing their normalized UV excesses into Eq. (11), and compared them with the original ones, $(M_{V})_{org}$, to test the accuracy of the procedure. The comparison is shown in Fig. 8, and the residuals are listed in Table 2. As in the case of iron abundances, there is a linear relation between the two sets of absolute magnitudes, and the mean and the standard deviation of the residuals are small, $\langle\Delta M_{V}\rangle=0$ and $\sigma=0.174~\mbox{mag}$, confirming the accuracy of the procedure used in our study.

Fig. 8

Comparison of the original $(M_{V})_{org}$ and estimated $(M_{V})_{est}$ absolute magnitudes (a), and distribution of the absolute magnitude residuals $(\Delta M_{V})_{res}$ respect to the original absolute magnitudes (b), for the sample stars. The dashed lines denote $\pm 1\sigma$ prediction levels

3.3 Comparison with other analyses in the literature

The metallicity calibration is carried out with the same procedure descried in Carney (1979), Karaali et al. (2003), Karaali et al. (2011), and Karataş and Schuster (2006). However, there are some differences between these calibrations due to different data.

The metallicity calibrations in the literature and in this study are plotted in Fig. 9 with different symbols, i.e. (+): Carney (1979), (•): Karaali et al. (2003), ($\Box$): Karataş and Schuster (2006), (△): Karaali et al. (2011), and (⋆): this study. Our calibration provides richer metallicities, $0.0<\Delta [\mathrm{Fe}/\mathrm{H}]<0.1~\mbox{dex}$, for the metal-poor stars with $[\mathrm{Fe}/\mathrm{H}]<-0.6~\mbox{dex}$ respect to the cited calibrations except the ones in Carney (1979) which give poorer metallicities compared to all calibrations mentioned in this study. Metal-rich part of the our calibration is compatible with the one in Karataş and Schuster (2006) in the interval $0.2<[\mathrm{Fe}/\mathrm{H}]<0.4~\mbox{dex}$, and for the intermediate metallicities, $-0.6<[\mathrm{Fe}/\mathrm{H}]<0.2~\mbox{dex}$, our calibration curve occupies a central position with respect to the other ones.

Fig. 9

Comparison of the metallicity calibrations for different studies as indicated in the panel

We applied the four cited metallicity calibrations to the sample stars used in our study for a further comparison of our results with the ones in cited studies. We replaced their normalized UV excesses, $\delta_{0.6}$, in the corresponding metallicity calibrations in Carney (1979), Karaali et al. (2003, 2011) and Karataş and Schuster (2006), and estimated the iron abundance, $[\mathrm{Fe}/\mathrm{H}]_{est}$, of each star. Then, we evaluated the residual metallicities, $\Delta[\mathrm{Fe}/\mathrm{H}]_{res}=[\mathrm{Fe}/\mathrm{H}]_{org}-[\mathrm{Fe}/\mathrm{H}]_{est}$, and plotted them in terms of $[\mathrm{Fe}/\mathrm{H}]_{org}$ in Fig. 10 for each study, where $[\mathrm{Fe}/\mathrm{H}]_{org}$ denotes the original iron abundances. The means and the corresponding standard deviations of the residuals are $\langle\Delta[\mathrm{Fe}/\mathrm{H}]\rangle=0$, −0.03, 0.05, and 0.05 dex; and $\sigma=0.161$, 0.144, 0.145, and 0.145 dex for the studies in the order given above. The mean of the residuals and their standard deviation, $\langle\Delta [\mathrm{Fe}/\mathrm{H}]\rangle=0$ and $\sigma=0.134~\mbox{dex}$, in our study are equal or smaller than the ones for the cited studies which indicate that the new data used in our study improved the metallicity calibration.

Fig. 10

Distribution of the metallicity residuals $(\Delta [\mathrm{Fe}/\mathrm{H}])_{res}$ respect to the original metallicities for four studies as indicated in the panels

A similar comparison is carried out for the absolute magnitudes. We applied the absolute magnitude calibrations, i.e. $\Delta M_{V}$ offsets versus normalized UV excesses $\delta_{0.6}$, in Laird et al. (1988), Karaali et al. (2003), and Karataş and Schuster (2006) to the sample stars in our study and estimated their absolute magnitudes $(M_{V})_{est}$. Then, we evaluated the residuals $(\Delta M_{V})_{res}=(M_{V})_{est}-(M_{V})_{org}$ and plotted them in terms of $(M_{V})_{org}$ in Fig. 11, where $(M_{V})_{org}$ denotes the original absolute magnitudes. The mean of the residuals and the corresponding standard deviations are $\Delta (M_{V})_{res}= -0.218, -0.086, \mbox{and } -0.015~\mbox{mag}$; and $\sigma=0.272$, 0.192, and 0.202 mag, for the cited studies in the order given above. The mean of the absolute magnitude residuals (0 mag) and their standard deviation (0.174 mag) in our study are (absolutely) much smaller than the corresponding ones in the cited studies which is a result of the improved data used in our study.

Fig. 11

Distribution of the absolute magnitude residuals $(\Delta M_{V})_{res}$ respect to the original absolute magnitudes three studies as indicated in the panels

4 Summary

We used a sample of F-G dwarfs taken from different sources and calibrated their iron abundances and absolute magnitudes in terms of UV excesses. We used the re-reduced Hipparcos parallaxes (van Leeuwen 2007) for the first time and obtained accurate distances and absolute magnitudes. Our sample consists of 168 dwarf stars covering the colour, iron abundance and absolute magnitude intervals $0.30<(B-V)_{0}<0.68~\mbox{mag}$, $-2.0<[\mathrm{Fe}/\mathrm{H}]<0.4~\mbox{dex}$ and $3.4< M_{V}<6.0~\mbox{mag}$, respectively. The means and standard deviations of the metallicity and absolute magnitude residuals are small, i.e. $\langle\Delta[\mathrm{Fe}/\mathrm{H}]_{res}\rangle=0$ and $\sigma=0.134~\mbox{dex}$, and $\langle\Delta (M_{V})_{res}\rangle=0$ and $\sigma=0.174~\mbox{mag}$, respectively, which indicate accurate metallicity and photometric parallax estimations.

$\mathit{UBV}$ is the oldest standard photometry in astronomy. Hence, many calibrations are carried out with this system. Although many other photometric systems such as Sloan Digital Sky Survey (SDSS; York et al. 2000), Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006) and Wide field Infrared Survey Explorer (WISE; Wright et al. 2010) are defined on different spectral bands for different purposes, the $\mathit{UBV}$ is still widely used due to its advantage, i.e. apparently bright stars for which reliable trigonometric parallaxes and hence distances can be provided in this system. This is the main reason that we preferred the $\mathit{UBV}$ photometry in this study. However, we plan to extend this calibrations to other photometric systems which are widely used for other purposes. Our favorite photometric system is the SDSS which provide useful investigations in the Galactic structure. We can use the transformation equations in the literature and transform our calibrations to the SDSS data. Then, we can apply them to a larger sample of stars observed with SDSS photometry. This will be the subject of a second study.