Updated rotating mass dipole with oblateness of one primary (II): out-of-plane equilibria and their stability

Abstract

Out-of-plane equilibrium points of the updated rotating mass dipole are investigated in this paper. The updated dipole system is consistent with a point mass connecting a spheroid with a massless rod in a constant distance. The oblateness of the spheroid allows the existence of out-of-plane equilibrium points. These equilibria are determined numerically based on the three dimensional dynamic equations. The influence of the system parameters on the position of these equilibria associated with the topological structure is analyzed in a parametric way. The stability of these equilibria is explored with linearized dynamic equations. Two particular cases with a prolate or an oblate spheroid of the first primary are presented to examine its influence on the distribution of the out-of-plane equilibrium points around the second primary.

1 Introduction

The well-known circular restricted three body problem (CRTBP) was first proposed by Euler and Lagrange in 1772 by introducing the synodic coordinate system, which led to the Jacob’s integral (Szebehely 1967). Such a problem has attracted the attentions of mathematicians and celestial mechanicians for centuries, and still has an impact on recent work in space dynamics, including but not limited to the existence of the Trojan asteroids (Murray and Dermott 1999), the basic dynamics of the Sun-Earth (or Earth-Moon) system and the artificial equilibria (McInnes et al. 1994). The CRTBP possesses two bodies moving in circular, coplanar orbits around their center of mass where the massless third body can not affect the two massive bodies (also called ‘two primaries’). It provides a good approximation for certain systems by treating the two major planets as point masses.

The inherent assumptions of the CRTBP with point masses and circular motions undoubtedly simplify the complexity of the three body problem, but it can be only used as the first-step approximation since many significant effects of realistic dynamic systems are not taken into account. For example, the observed orbits of celestial bodies in the solar system are non-coplanar and non-circular. Particularly, the gravitational effect of the fourth body sometimes is required to be considered, such as the theory of the weak stability boundary. The weak stability boundary lunar transfer trajectory was proposed by Belbruno and Miller (1993) and has been successfully applied in the Japanese Hiten probe (Kawaguchi et al. 1995). Consequently, the improvement of the CRTBP is somewhat necessary to enrich its applications to more complicated systems.

Up to date, there have been a number of modified models based on the CRTBP. One of them is the elliptical restricted three body problem, referred to as ERTBP, with the assumption that the two primaries revolve around the system center of mass in their gravitational potential (Baoyin and McInnes 2006). A non-uniformly rotational pulsating-coordinate system is usually used in the ERTBP resulting in the time-varying Hamiltonian of the system (Szebehely 1967). Furthermore, the radiation of the primaries can be also added into the CRTBP or ERTBP (Singh and Umar 2012), which was investigated as the photo-gravitational restricted three body problem (Chernikov 1970). Another notable improvement of the CRTBP is the assumption of spherical primaries instead of the point masses. Then the oblateness of each primary can be counted on the motion of the third body (Sharma 1987). Besides the above intensive studies on the CRTBP, its generalized form of the rotating mass dipole has also been presented by Chermnykh (1987). In this classical rotating mass dipole system (CRMDP), the mutual gravitational force between the two primaries can be less or greater than the centrifugal force by introducing a massless rod in a constant distance connecting the two primaries.

Equilibrium points and their associated manifolds are usually the starting point to investigate the concerned dynamical system. Besides the equilibrium points in the equatorial plane specified in the Part I (Zeng et al. 2015a, 2015b), out-of-plane equilibria may exist for the updated rotating mass dipole (URMDP) where one primary is a spheroid with oblateness. The existence of the out-of-plane equilibria may be first pointed out by Radzievskii (1950) in the photo-gravitational restricted three body problem. Such equilibria were also obtained by Douskos and Markellos (2006) in the CRTBP by taking the oblateness of the second primary into account. Their results were then extended by Singh and Umar (2012) to the ERTBP with radiating and oblateness. Particularly, if the mass of the second primary is approaching zero with a limiting process, the out-of-plane equilibria should be located on the axis $oz$ which is aligned with the angular momentum of the system (Perdiou et al. 2005; Douskos et al. 2012). However, among the discussions on these modifications of the CRTBP, the out-of-plane equilibria regarding the URMDP were rarely presented.

The aim of this paper is to numerically investigate the out-of-plane equilibria of the URMDP along with their stabilities. Consequently, the focus of this paper is the basic dynamical properties of the URMDP rather than the astronomical applications, such as the tidal locked binary systems (Shang et al. 2014) or nearly axisymmetrical elongated celestial bodies (Zeng et al. 2015a, 2015b). In Sect. 2 the dynamic model regarding the existence of out-of-plane equilibrium points are presented along with numerical determinations. Section 3 discusses the dependence of these equilibria on the system parameters, including the force ratio, the mass ratio and the oblateness of the second primary. The linearized stability of these equilibria is examined in Sect. 4. Extended cases by considering the first primary as a prolate or oblate spheroid combining with an oblate second primary are introduced to investigate the out-of-plane equilibria in such a particular system.

2 Out-of-plane equilibrium points of the updated dipole system

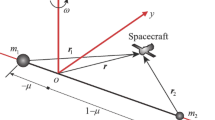
The updated rotating mass dipole system is illustrated in Fig. 1 with a sketch map where the second primary $m_{2}$ is an oblate spheroid. The more massive primary can be treated as a point mass $m_{1}$ or a spheroid with negligible physical size. The massless rod with a constant distance connecting the two primaries revolves in the plane $oxy$ which is the same as the equatorial plane of the primary. Based on Part I (Zeng et al. 2015a, 2015b), the equations of motion of the test particle in the gravitational field of the URMDP can be specified as

$$\begin{aligned} &\begin{aligned}[b] \ddot{x} - 2\omega \dot{y} &= \omega^{2} \biggl\{ x - \kappa \biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{3}} \\ &\quad + \frac{\mu ( x + \mu - 1 )}{r_{2}^{3}} \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} - \frac{15A_{2}z^{2}}{2r_{2}^{4}} \biggr) \biggr] \biggr\} \end{aligned} \end{aligned}$$

(1)

$$\begin{aligned} &\begin{aligned}[b] \ddot{y} + 2\omega \dot{x} &= \omega^{2}y \biggl\{ 1 - \kappa \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{3}} \\ &\quad + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} - \frac{15A_{2}z^{2}}{2r_{2}^{4}} \biggr) \biggr] \biggr\} \end{aligned} \end{aligned}$$

(2)

$$\begin{aligned} &\ddot{z} = \kappa \omega^{2}z \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{3}} + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{9A_{2}}{2r_{2}^{2}} - \frac{15A_{2}z^{2}}{2r_{2}^{4}} \biggr) \biggr] \end{aligned}$$

(3)

where $[x, y, z]^{\mathrm{T}}$ are the three components of the position vector $\boldsymbol{r}$ in the body-fixed rotating frame $oxyz$, $\omega = \boldsymbol{\omega} \cdot {\boldsymbol{z}}$ is the magnitude of the angular velocity and $\mu$ is the mass ratio defined as $\mu = m_{2} / (m_{1} + m_{2})$. The parameter $A_{2}$ is the oblateness of the second primary which can be taken negative values corresponding to a prolate spheroid. Here, $r_{1}$ and $r_{2}$ are the distance between the particle and the two primaries

$$ \left \{ \textstyle\begin{array}{l} r_{1} = \sqrt{ ( x + \mu )^{2} + y^{2} + z^{2}} \\ r_{2} = \sqrt{ ( x + \mu - 1 )^{2} + y^{2} + z^{2}} \end{array}\displaystyle \right . $$

(4)

Another key parameter is the force ratio $\kappa$ which is defined as the ratio between the gravitational force and the centrifugal force with respect to the two primaries. The dynamical Eqs. (1) to (3) admits the Jacobi integral

$$\begin{aligned} C &= \frac{\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2}}{2} - \frac{\omega^{2}}{2} \bigl( x^{2} + y^{2} \bigr) \\ &\quad - \kappa \omega^{2} \biggl\{ \frac{1 - \mu}{r_{1}} + \frac{\mu}{r_{2}} \biggl[ 1 + \frac{A_{2}}{2r_{2}^{2}} \biggl( 1 - \frac{3z^{2}}{r_{2}^{2}} \biggr) \biggr] \biggr\} \end{aligned}$$

(5)

When all velocity components are zero, the above equation gives the zero-velocity surface of the possible motion.

Fig. 1

Schematic map of the updated rotating mass dipole with oblateness of the second primary

The equilibrium points out of the plane $oxy$ can be found by setting all velocity and acceleration terms to be zero and solving the right sides of Eqs. (1)–(3). Obviously, $y = 0$ satisfies Eq. (2) resulting in that the out-of-plane equilibrium points are in the plane $oxz$. Finally, the corresponding equations for these equilibria with $z \neq 0$ are

$$\begin{aligned} &x - \kappa \biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{3}} + \frac{\mu ( x + \mu - 1 )}{r_{2}^{3}} \\ &\quad \times \biggl( 1 + \frac{3A_{2}}{2r_{2}^{2}} - \frac{15A_{2}z^{2}}{2r_{2}^{4}} \biggr) \biggr] = 0 \end{aligned}$$

(6)

$$\begin{aligned} &\frac{ ( 1 - \mu )}{r_{1}^{3}} + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{9A_{2}}{2r_{2}^{2}} - \frac{15A_{2}z^{2}}{2r_{2}^{4}} \biggr) = 0 \end{aligned}$$

(7)

where the two radii can be deduced to

$$ \left \{ \textstyle\begin{array}{l} r_{1} = \sqrt{ ( x + \mu )^{2} + z^{2}} \\ r_{2} = \sqrt{ ( x + \mu - 1 )^{2} + z^{2}} \end{array}\displaystyle \right . $$

(8)

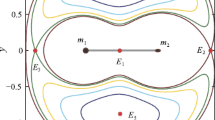
The locations of out-of-plane equilibria are hard to be obtained with analytical expressions. Therefore, approximated solutions in the form of power series to third order were given in previous publications (Perdiou et al. 2005; (Douskos and Markellos 2006)). Here, only the numerical results are presented to determine the coordinates of these equilibrium points. Figure 2 illustrates the equilibria in the plane $oxz$ along with associated zero-velocity curves. The mass ratio and force ratio are 0.5 and 1.0 of the URMDP, respectively. The oblateness of the second primary is 0.01 corresponding to an oblate primary. The three collinear equilibrium points are also given in the figure. Two new equilibria which are nearly right above and below the oblate primary, named $E_{z1}$ and $E_{z2}$, are symmetrical with respect to the axis $ox$. They are solved by using the default solver of MATLAB’s fsolve. Note that the use of $x_{0} = 1 - \mu$ and $z_{0} =\sqrt{3A_{2}}$ as initial values is effective to numerically determine the positions of the equilibria $E_{zi}$ ($i =1, 2$) which is similar to that given by Douskos and Markellos (2006). The coordinates of $E_{z1}$ is $[0.4998,\ 0,\ 0.1728]^{\mathrm{T}}$ whereas $E_{z2}$ is $[0.4998,\ 0,\ -0.1728]^{\mathrm{T}}$. It should be pointed out that there is no out-of-plane equilibrium point with non-positive $A_{2}$, indicating that such equilibria only exist with an oblate primary of the URMDP.

Fig. 2

Zero-velocity curves and equilibria of the URMDP in the plane $oxz$ with $\kappa = 1$ and $\mu = 0.5$ and $A_{2} = 0.01$

3 Parametric study

The influence of concerned parameters on the positions of out-of-plane equilibria will be studied in this section, including the force ratio, the mass ratio and the oblateness. The investigated region for the force ratio is taken to be [0.1, 30] which already covers a big range from the very fast-spinning case to the state of slow-spinning. The mass ratio is set to be [0.01, 0.5] since $m_{1} \geq m_{2}$. Such a region should be enough to show the influence of the parameter on the equilibria. The region of the oblateness $A_{2}$ is [0, 0.05] where the upper boundary is the same as that given in Part I (Zeng et al. 2015a, 2015b).

3.1 Influence of [$\kappa$, $\mu$] on the equilibria

To investigate the influence of the force ratio and mass ratio on the position of the equilibria, the oblateness of the second primary is arbitrarily set to be 0.02. The admissible region of the force ratio is [0.1, 30] whereas the mass ratio takes some discrete values in 0.1, 0.2, 0.3, 0.4 and 0.5. Figure 3 shows the position variation of the equilibria along with the variation of these two parameters. Only the sketch map of the second primary is given for each case of different mass ratio. The more massive primary and the massless rod are omitted from the figure.

Fig. 3

Variation of the out-of-plane equilibrium points of the URMDP with $A_{2} = 0.02$ by varying $\kappa$ and $\mu$

Taking the case of $\mu = 0.1$ as an example, with the increase of $\kappa$ the equilibrium point $E_{z1}$ moves away from the second primary and then goes back along the clockwise direction. The variational trend of $E_{z2}$ is similar to that of $E_{z1}$ with axisymmetrical transformation. Particularly, the position of these two equilibria varies in a relatively small range with $\kappa \geq 1$ compared to that with $\kappa < 1$. It indicates that fast-spinning asteroids have greater impact on the out-of-plane equilibrium point than the slow-spinning ones. The variational trend of the equilibria position with other fixed values of the mass ratio is similar to the scenario with $\mu = 0.1$.

When the value of $\kappa$ is fixed, the location of the equilibrium point $E_{z1}$ is presented in Table 1 with respect to different values of $\mu$. Here, the value of $\kappa$ is unity which is suitable to be applied to the tidal locked celestial bodies (Scheeres 2012) where the oblateness is still 0.02. With the increase of $\mu$, the $z$-coordinate of $E_{z1}$ increases to make the equilibrium point away from the oblate primary. At the same time, its $x$-coordinate shifts close to the line of $x_{0} = 1 - \mu$. Such a variational trend can be also seen from Fig. 3 where the equilibrium points have been marked with circles corresponding to the cases with $\kappa = 1$ and $A_{2} = 0.02$. Note that the existence and locations of these equilibria depend on the parameters of $\kappa$, $\mu$ and $A_{2}$. Thus, there may be not real-number roots of Eqs. (6) and (7). Such cases are out of scope of this study and will not be discussed any more.

Table 1 The position of out-of-equilibrium point $E_{z1}$ with $\kappa = 1$ and $A_{2} = 0.02$

3.2 Effect of $A_{2}$ on the equilibria

In this section the influence of $A_{2}$ on the equilibrium points will be analyzed numerically. Without loss of generality, the force ratio $\kappa$ is set to be unity and the two primaries of the URMDP are with equal mass indicating $\mu = 0.5$. Table 2 shows the variational trend of the position of the equilibrium point $E_{z1}$ along with the variation of $A_{2}$. With the increase of the oblateness from 0.005 to 0.05, the $x$-coordinate of the point shifts away from the line of $x_{0} = 1 - \mu$ to the left side. At the meanwhile, its $z$-coordinate also moves away from the oblate primary. Therefore, the increase of oblateness makes the out-of-plane equilibria away from the oblate primary.

Table 2 The position of out-of-equilibrium point $E_{z1}$ with $\kappa = 1$ and $\mu = 0.5$

Figure 4 illustrates the equilibrium points and corresponding zero-velocity curves in the plane $oxz$ with $A_{2} = 0.01, 0.02, 0.03, 0.04\ \mbox{and}\ 0.05$. It can be seen that there are some fixed points locating on the zero-velocity curves. With the increase of the oblateness, the zero-velocity curves right above the second primary with the same value of $C$ go approaching the oblate primary. When the value of $A_{2}$ is 0.04, the two separated regions of possible motion are connected into a unified one. It means that the value of $A_{2}$ has a significant impact on the topological structure around the URMDP in the plane $oxz$. Detailed discussions can be made in terms of the variation of such topological structure in further studies.

Fig. 4

Variation of the out-of-plane equilibrium points of the URMDP with $\kappa = 1$ and $\mu = 0.5$

4 Stability of the equilibrium points

The same method ever used in Part I (Zeng et al. 2015a, 2015b) is adopted to investigate the stability of the out-of-plane equilibrium points. Let the coordinates $[x_{E},\ y_{E},\ z_{E}]^{\mathrm{T}}$ be the position of the equilibrium point $E_{z}$ in the plane $oxz$. Assume an initial perturbing vector $[ \xi, \eta, \zeta]^{\mathrm{T}}$ added to the nominal position as

$$ \left \{ \textstyle\begin{array}{l} \xi = x - x_{E} \\ \eta = y - y_{E} \\ \zeta = z - z_{E} \end{array}\displaystyle \right . $$

(9)

Then, the linearized dynamic equations can be derived by substituting Eq. (9) into Eqs. (1) to (3) as

$$ \left \{ \textstyle\begin{array}{l} \ddot{\xi} - 2\omega \dot{\eta} + W_{xx}\xi + W_{xy}\eta + W_{xz}\zeta = 0 \\ \ddot{\eta} + 2\omega \dot{\xi} + W_{xy}\xi + W_{yy}\eta + W_{yz}\zeta = 0 \\ \ddot{\zeta} + W_{xz}\xi + W_{yz}\eta + W_{zz}\zeta = 0 \end{array}\displaystyle \right . $$

(10)

where the effective potential $W$ has been given in Part I as

$$\begin{aligned} W &= - \frac{\omega^{2}}{2} \bigl( x^{2} + y^{2} \bigr) - \kappa \omega^{2} \biggl\{ \frac{1 - \mu}{r_{1}} \\ &\quad + \frac{\mu}{r_{2}} \biggl[ 1 + \frac{A_{2}}{2r_{2}^{2}} \biggl( 1 - \frac{3z^{2}}{r_{2}^{2}} \biggr) \biggr] \biggr\} \end{aligned}$$

(11)

The well-known Hessian matrix can be defined as

$$ \nabla^{2}W = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} W_{xx} & W_{xy} & W_{xz} \\ W_{yx} & W_{yy} & W_{yz} \\ W_{zx} & W_{zy} & W_{zz} \end{array}\displaystyle \right ] $$

(12)

whose elements are

$$\begin{aligned} &\begin{aligned}[b]W_{xx} &= \frac{\partial^{2}W}{\partial x^{2}} \\ & = - \omega^{2} + \kappa \omega^{2}\biggl[ \frac{1 - \mu}{r_{1}^{3}} - \frac{3 ( 1 - \mu ) ( x + \mu )^{2}}{r_{1}^{5}} \\ &\quad + \frac{\mu}{r_{2}^{3}} - \frac{3\mu ( x + \mu - 1 )^{2}}{r_{2}^{5}} + \frac{3\mu A_{2}}{2r_{2}^{5}} -\cdots \\ &\quad -\frac{15\mu A_{2} ( x + \mu - 1 )^{2}}{2r_{2}^{7}} - \frac{15\mu A_{2}z^{2}}{2r_{2}^{7}}\\ &\quad + \frac{105\mu A_{2}z^{2} ( x + \mu - 1 )^{2}}{2r_{2}^{9}} \biggr]\end{aligned} \end{aligned}$$

(13)

$$\begin{aligned} &\begin{aligned}[b]W_{yy} &= \frac{\partial^{2}W}{\partial y^{2}} \\ &= - \omega^{2} + \kappa \omega^{2}\biggl[ \frac{1 - \mu}{r_{1}^{3}} - \frac{3 ( 1 - \mu )y^{2}}{r_{1}^{5}} + \frac{\mu}{r_{2}^{3}}\\ &\quad - \frac{3\mu y^{2}}{r_{2}^{5}} + \frac{3\mu A_{2}}{2r_{2}^{5}} -\cdots \\ &\quad -\frac{15\mu A_{2}y^{2}}{2r_{2}^{7}} - \frac{15\mu A_{2}z^{2}}{2r_{2}^{7}} + \frac{105\mu A_{2}z^{2}y^{2}}{2r_{2}^{9}} \biggr]\end{aligned} \end{aligned}$$

(14)

$$\begin{aligned} &\begin{aligned}[b]W_{zz} &= \frac{\partial^{2}W}{\partial z^{2}} \\ & = \kappa \omega^{2} \biggl[ \frac{1 - \mu}{r_{1}^{3}} - \frac{3 ( 1 - \mu )z^{2}}{r_{1}^{5}} + \frac{\mu}{r_{2}^{3}} - \frac{3\mu z^{2}}{r_{2}^{5}} \\ &\quad + \frac{9\mu A_{2}}{2r_{2}^{5}} - \frac{45\mu A_{2}z^{2}}{r_{2}^{7}} + \frac{105\mu A_{2}z^{4}}{2r_{2}^{9}} \biggr] \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned} &\begin{aligned}[b] W_{xy} &= W_{yx} \\ & = \frac{\partial^{2}W}{\partial x\partial y} \\ & = - 3\kappa \omega^{2}y\biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{5}} + \frac{\mu ( x + \mu - 1 )}{r_{2}^{5}} +\cdots \\ &\quad +\frac{5\mu A_{2} ( x + \mu - 1 )}{2r_{2}^{7}} - \frac{35\mu A_{2} ( x + \mu - 1 )z^{2}}{2r_{2}^{9}} \biggr]\end{aligned} \end{aligned}$$

(16)

$$\begin{aligned} &\begin{aligned}[b] W_{xz} &= W_{zx} \\ & = \frac{\partial^{2}W}{\partial x\partial z}\\ & = - 3\kappa \omega^{2}z\biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{5}} + \frac{\mu ( x + \mu - 1 )}{r_{2}^{5}} +\cdots \\ &\quad +\frac{15\mu A_{2} ( x + \mu - 1 )}{2r_{2}^{7}} - \frac{35\mu A_{2} ( x + \mu - 1 )z^{2}}{2r_{2}^{9}} \biggr]\end{aligned} \end{aligned}$$

(17)

$$\begin{aligned} &\begin{aligned}[b] W_{yz} &= W_{zy} \\ & = \frac{\partial^{2}W}{\partial y\partial z} \\ & = - 3\kappa \omega^{2}z \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{5}} + \frac{\mu}{ r_{2}^{5}} + \frac{15\mu A_{2}}{2r_{2}^{7}} - \frac{35\mu A_{2}z^{2}}{2r_{2}^{9}} \biggr] \end{aligned} \end{aligned}$$

(18)

By using the state variable vector $\boldsymbol{\chi} = [ \xi, \eta, \zeta,\dot{\xi},\dot{\eta},\dot{\zeta} ]^{\mathrm{T}}$, the second-order nonlinear differential equation (10) can be transformed into $\dot{\boldsymbol{\chi}} = \varPhi \boldsymbol{\chi}$ where the state transition matrix $\varPhi$ is (Szebehely 1967)

$$ \varPhi = \left [ \textstyle\begin{array}{c@{\quad }c} \mathbf{0}_{3 \times 3} & \mathbf{I}_{3 \times 3} \\ - \nabla^{2}W & - \varOmega \end{array}\displaystyle \right ]_{6 \times 6} $$

(19)

where $\mathbf{0}_{3\times3}$ and $\mathbf{I}_{3\times3}$ are the third-order zero matrix and identity matrix, respectively. The term $\nabla^{2}W$ is the Hessian matrix in Eq. (12) and the other matrix is defined as

$$ \varOmega = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} 0 & - 2\omega & 0 \\ 2\omega & 0 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ] $$

(20)

The stability of the equilibrium point can be determined based on the eigenvalues of the corresponding state transition matrix $\varPhi$. The equilibrium point is linearly stable if and only if the eigenvalues of $\varPhi$ are all non-positive. Otherwise, the equilibrium point is unstable. Additionally, the characteristic equation of Eq. (10) is

$$ \left\vert \textstyle\begin{array}{c@{\quad }c@{\quad }c} \lambda^{2} + W_{xx} & - 2\omega \lambda + W_{xy} & W_{xz} \\ 2\omega \lambda + W_{yx} & \lambda^{2} + W_{yy} & W_{yz} \\ W_{zx} & W_{zy} & \lambda^{2} + W_{zz} \end{array}\displaystyle \right\vert = 0 $$

(21)

where $\lambda$ denotes the eigenvalues of Eq. (10). Equation (21) can be expanded to a sixth-order nonlinear equation as

$$\begin{aligned} &\lambda^{6} + ( W_{xx} + W_{yy} + W_{zz} + 4\omega^{2} )\lambda^{4} +\cdots \\ &\qquad + ( W_{xx}W_{yy} + W_{yy}W_{zz} + W_{zz}W_{xx} - W_{xy}^{2} - W_{yz}^{2} \\ &\qquad - W_{xz}^{2} + 4\omega^{2}W_{zz} )\lambda^{2} +\cdots \\ &\qquad + ( W_{xx}W_{yy}W_{zz} + 2W_{xy}W_{xz}W_{yz} - W_{xx}W_{yz}^{2} \\ &\qquad - W_{yy}W_{xz}^{2} - W_{zz}W_{xy}^{2} ) \\ &\quad = 0 \end{aligned}$$

(22)

Here, Eq. (22) is equivalent to Eq. (19) which holds the same eigenvalues. Consequently, the stability of the linearized system in Eq. (10) can be identified by using either Eq. (19) or Eq. (22) which can be also as verification for each other. For this specific problem, Eq. (16) is zero for the out-of-plane equilibria which can slightly reduce the calculation effort.

Tables 3 and 4 summarize the eigenvalues of the equilibrium point $E_{z1}$ of the URMDP with different system parameters. These eigenvalues are the same for the other axisymmetrical equilibrium point $E_{z2}$. Here we use $E_{z}$ to denote the two out-of-plane equilibria around the second primary. The sample results given here are obtained with $\mu \in [0.1, 0.5]$ and $A_{2} \in [0.01, 0.05]$. Only two values of $\kappa = 0.1$ and $\kappa = 1$ are listed which can be as a representative for other cases. For instance, the eigenvalues for the case of $\kappa = 9$ are in the same type with the case of $\kappa = 1$ according to our simulations.

Table 3 Eigenvalues of the equilibrium point $E_{z1}$ of the URMDP with $\kappa = 0.1$

Table 4 Eigenvalues of the equilibrium point $E_{z1}$ of the URMDP with $\kappa = 1$

Generally speaking, the equilibria $E_{z}$ is unstable since there is always a positive real number in the three pair of roots. Even though unstable, there are still some different cases along with the variation of the parameters. First, for the fixed values of $\kappa$ and $\mu$, the divergence speed of the unstable mode decreases with the increase of the oblateness due to the decrease of $| \lambda |$. For a fixed $A_{2}$ and $\kappa > 0.3$, the divergence speed of the unstable model increases along with the increase of the mass ratio. However, the variational trends for $\kappa < 0.3$ are a little complicated which can be seen from the first column of Table 3. Particularly, there are changes of the topological structure due to the variation of the parameters. For most cases in Table 3, there are two pairs of imaginary and a pair of real number. It corresponds to a four-dimensional stable manifold and a two-dimensional unstable manifold. But there are four groups of eigenvalues which are consisted with two pairs of real numbers and a pair of imaginary, which corresponds to a two-dimensional stable manifold and a four-dimensional unstable manifold. The change of its topological structure has a great influence on the particles around these equilibrium points.

5 Extended case of the out-of-plane equilibria

After the above discussions, an extension of the dynamic model in a particular case is presented to deal with both oblate primaries of equal oblateness. It means $A_{1} = A_{2} = A$ which are positive numbers for oblate primaries. Based on Part I (Zeng et al. 2015a, 2015b), the effective potential of this rotating dipole system is

$$\begin{aligned} V &= - \frac{\omega^{2}}{2} \bigl( x^{2} + y^{2} \bigr) - \kappa \omega^{2} \biggl\{ \frac{1 - \mu}{r_{1}} \biggl[ 1 + \frac{A}{2r_{1}^{2}} \biggl( 1 - \frac{3z^{2}}{r_{1}^{2}} \biggr) \biggr] \\ &\quad + \frac{\mu}{r_{2}} \biggl[ 1 + \frac{A}{2r_{2}^{2}} \biggl( 1 - \frac{3z^{2}}{r_{2}^{2}} \biggr) \biggr] \biggr\} \end{aligned}$$

(23)

and the angular velocity of the dipole system is degenerated to

$$ \omega = \sqrt{1 + 3A} $$

(24)

By setting all velocity and acceleration components to be zero, the out-of-plane equilibria can be obtained under such conditions by solving

$$ V_{j} = \frac{\partial V}{\partial j} = 0, \quad j = x,y,z $$

(25)

which can be expanded as

$$\begin{aligned} &\begin{aligned}[b]V_{x} &= - \omega^{2}x + \kappa \omega^{2} \biggl[ \frac{ ( 1 - \mu ) ( x + \mu )}{r_{1}^{3}} \\ &\quad \times \biggl( 1 + \frac{3A}{2r_{1}^{2}} - \frac{15Az^{2}}{2r_{1}^{4}} \biggr) + \frac{\mu ( x + \mu - 1 )}{r_{2}^{3}} \\ &\quad \times\biggl( 1 + \frac{3A}{2r_{2}^{2}} - \frac{15Az^{2}}{2r_{2}^{4}} \biggr) \biggr] \end{aligned} \end{aligned}$$

(26)

$$\begin{aligned} &\begin{aligned}[b]V_{y} &= - \omega^{2}y \biggl\{ 1 - \kappa \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{3}} \biggl( 1 + \frac{3A}{2r_{1}^{2}} - \frac{15Az^{2}}{2r_{1}^{4}} \biggr)\\ &\quad + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{3A}{2r_{2}^{2}} - \frac{15Az^{2}}{2r_{2}^{4}} \biggr) \biggr] \biggr\} \end{aligned} \end{aligned}$$

(27)

$$\begin{aligned} &\begin{aligned}[b]V_{z} &= \kappa \omega^{2}z \biggl[ \frac{ ( 1 - \mu )}{r_{1}^{3}} \biggl( 1 + \frac{9A}{2r_{1}^{2}} - \frac{15Az^{2}}{2r_{1}^{4}} \biggr)\\ &\quad + \frac{\mu}{r_{2}^{3}} \biggl( 1 + \frac{9A}{2r_{2}^{2}} - \frac{15Az^{2}}{2r_{2}^{4}} \biggr) \biggr]\end{aligned} \end{aligned}$$

(28)

where Eq. (27) is always zero with $y = 0$ indicating that the out-of-plane equilibrium points are in the plane $oxz$. Consequently, the terms $r_{1}$ and $r_{2}$ in Eq. (26) and Eq. (28) satisfy Eq. (8).

Table 5 summarizes the locations of the out-of-plane equilibria with positive $z$-coordinates under the conditions of $\kappa = 1$ and $\mu = 0.5$. The equilibria above and below $m_{1}$ are referred to as $E_{z3}$ and $E_{z4}$ to distinguish them with those around $m_{2}$. With equal oblateness of the two primaries, the gravitational potential (or effective potential) is axisymmetrical with respect to the three axis of the body-fixed frame. Therefore, $E_{z1}$ is symmetrical with $E_{z2}$ with respect to the axis $ox$ where $E_{z3}$ and $E_{z4}$ are the same. Moreover, $E_{z1}$ is symmetrical with $E_{z3}$ with respect to the axis $oz$ where $E_{z2}$ and $E_{z4}$ are also symmetrical points. Such a relationship can be also seen from Table 5. Focusing on the position of $E_{z1}$ by combining Table 2 and Table 5, the influence of the oblateness of the more massive primary can be drawn. The $x$-coordinate changes from 0.4922 $(A_{2} = 0.05)$ to the current 0.4933 $(A = 0.05)$ showing that $E_{z1}$ moves close to the line of $x_{0} = 1 - \mu$. Its $z$-coordinate changes from 0.3785 to the current 0.3774 where $E_{z1}$ go approaching $m_{2}$ along $oz$ direction.

Table 5 The position of out-of-equilibrium point $E_{z}$ with $\kappa = 1$ and $\mu = 0.5$

Another case is that the prolate primary $m_{1}$ connected with an oblate primary $m_{2}$ with $-A_{1} = A_{2} = A$ corresponding to a slight modification of Eq. (23) and the angular velocity $\omega = 1$. The out-of-plane equilibria around $m_{1}$ will vanish whereas $E_{z1}$ and $E_{z2}$ still exist. The coordinates of $E_{z1}$ are listed in Table 6 with $\kappa = 1$, $\mu = 0.5$ and different values of $A$. Taking the scenario of $A = 0.05$ as an example, the equilibrium point $E_{z1}$ moves to the upper-left side relative to the oblate primary. If both primaries are prolate spheroids, the out-of-plane equilibrium points do not exist any more. There should be some interesting features regarding two prolate spheroids. Since the focus of this paper is out-of-plane equilibrium point such an investigation will be left for further studies if needed.

Table 6 The position of out-of-equilibrium point $E_{z1}$ with $\kappa = 1$ and $\mu = 0.5$

The out-of-equilibrium points associated with corresponding zero-velocity curves are illustrated in Fig. 5 with $\kappa = 1$ and $\mu = 0.5$ of the update rotating mass dipole. To see clearly the topological structure of zero-velocity curves, the oblateness of the second primary is set to be 0.05. In Fig. 5a, the structure is symmetrical with respect to both axis $ox$ and axis $oz$ where the first primary is of same oblateness as the second one. Three collinear equilibrium points are on the axis $ox$ which are not shown but can be found based on the zero-velocity curves. Figure 5b presents the case that the first primary is a prolate spheroid with $A = -0.05$. The variation of the topological structure occurs with vanishment of $E_{z3}$ ($E_{z4}$) around $m_{1}$. Conversely, two new collinear equilibrium points besides the three classical points emerge by the side of $m_{1}$.

Fig. 5

Zero-velocity curves and equilibria of the rotating dipole system with two equal oblate primary in the plane $oxz$ with $\kappa = 1$ and $\mu = 0.5$

As a preliminary study, the discussions about the extend cases will be ended by only examining the existence of these out-of-plane equilibrium points in terms of the rotating mass dipole with oblateness. The stability of these equilibria can be examined by using the framework presented in Sect. 4. It should be expected that these points are unstable. The application of these points in a realistic celestial system (such as the Saturn-Tethys system) has never been analyzed which could be proposed in the future.

As a preferable candidate to simply approximate the nearly axisymmetrical natural elongated bodies, the rotating mass dipole is necessary to be examined in terms of its dynamical features as a first step. The oblateness of one primary, specifically an oblate spheroid, provides a new observation of its topological structure resulting in a pair of new equilibrium points emerge in the plane $oxz$. The slight modification of the vicinal topological structures due to the oblateness may give a more accurate approximation of the potential of irregular shaped elongated bodies. In fact, it is very difficult to find long-term (nearly) periodic orbits around irregular shaped minor celestial bodies. Up to date, some numerical shooting methods (Yu and Baoyin 2012) or generating from stable manifolds around equilibrium points (Scheeres 2012) have been proposed to search for such periodic orbits applying to the asteroid 216 Kleopatra and 433 Eros. Based on the current work, some analytical results obtained by using the dipole system may be adopted as initial guesses to generate required orbits around elongated bodies.

6 Conclusions

An updated rotating mass dipole with an oblate second primary has been discussed in terms of its three dimensional dynamical properties. The oblateness allows the existence of out-of-plane equilibrium points in the vicinity of the oblate primary. There are two equilibrium points nearly above and below the oblate primary in the plane $oxz$. They are symmetrical with respect to the axis $ox$ which is aligned with the massless rod connecting the two primaries. The oblateness of the second primary has a great influence on the position of the out-of-plane equilibrium points. When the force ratio and mass ratio of the rotating mass dipole are fixed, the equilibria shift away to the upper-left direction from the oblate primary with the increase of the oblateness.

According to the linearized equations, these out-of-plane equilibria are unstable since there is always a positive eigenvalues of the characteristic equation. The topological structure varies along with the variation of the system parameters, including the force ratio, the mass ratio and the oblateness. It is changed from a four-dimensional stable manifold to a two-dimensional stable manifold with the increase of the force ratio. The influence of the oblateness of the first primary is also taken into account regarding the equilibria around the second primary. Two particular cases are considered, i.e., the first primary with equal or opposite oblateness of the second primary. The topological structure around the rotating mass dipole has significant changes due to the oblateness of the first primary. The equilibrium points around the second primary go approaching it when the first primary is a prolate spheroid. Conversely, these equilibria move away from the second primary due to the oblate first primary.