1 Introduction

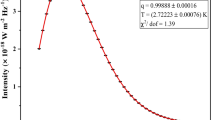
The extragalactic infrared background radiation (EIB) spectrum gives us information on the cosmic history of the energy released from stellar objects, protogalaxies, and galaxies. This background radiation was discovered by analyzing the COBE FIRAS and DIRBE data (Fixsen et al. 1998; Puget et al. 1996; Hauser et al. 1998). As noted by Dole et al. (2006), this detected background radiation represents about half of the extragalactic background light (EBL), because it covers wavelength range from 1 μm to 1000 μm, i.e. the infrared region. The far infrared wavelength interval from 125 μm to 2000 μm was used in the COBE FIRAS experiments and their data contain foreground emission from the interplanetary, Galactic interstellar dust and extragalactic background emission (Fixsen et al. 1998). To separate the different components of the emission was used three different methods. As a result, the analytical expression for average spectrum in the v=125–2000 μm wavelength interval at temperature T=18.5±1.2 K has been proposed to describe the extragalactic Far InfraRed Background (FIRB) spectrum (Fixsen et al. 1998). It is essential to note that this spectrum differs from the monopole spectrum (Fixsen et al. 1994) by the spectral emissivity coefficient.

The extragalactic far infrared background spectrum was detected in the finite wavenumber range from 125 μm to 2000 μm. Thus, for the construction of thermodynamics of the extragalactic far infrared background (FIRB) radiation, as well as the radiative properties, we have to use this specific range of wavenumbers.

In Fisenko and Lemberg (2014), the exact expressions for the temperature dependences of the thermodynamic and radiative properties of the Cosmic Microwave Background radiation for the monopole and dipole spectra were obtained. However, the extragalactic spectrum differs from the blackbody spectrum because of the spectral emissivity factor \(\varepsilon(\tilde{v},T)\) and, thus, difficult to construct the exact expressions. In this case, we will be using numerical methods for calculating the thermodynamic and radiative properties of the FIRB radiation.

In previous studies (Fisenko and Ivashov, 2009; Fisenko and Lemberg, 2012, 2013), the thermodynamic functions of the thermal radiation of real bodies in the finite frequency range at high temperatures were obtained by using numerical methods. The calculated values for the radiative and thermodynamic functions were in good agreement with experimental data.

In the present work, the radiative and thermodynamic properties of the extragalactic far infrared background radiation, such as the total emissivity, total radiation power per unit area, total energy density, number density of photons, Helmholtz free energy density, entropy density, heat capacity at constant volume, and pressure received in the (0.15–2.4) THz frequency interval at the mean temperature T=18.5 K are calculated. Using formulas v=v 0(1+z) and T=T 0(1+z), the radiative and thermodynamic functions were calculated at redshift z=1.5.

2 Extragalactic spectrum

According to Fixsen et al. (1998), the average spectrum of the extragalactic Far InfraRed Background (FIRB) radiation in the \(5~\mathrm{cm}^{ - 1} \le\tilde{v} \le80~\mathrm{cm}^{ - 1}\) range of wavenumbers is presented as:

$$ I_{\tilde{v}}(T) = \varepsilon(\tilde{v},T)B_{\tilde{v}}(T), $$
(1)

where

$$ \varepsilon(\tilde{v},T) = \varepsilon_{0} \biggl( \frac{\tilde{v}}{\tilde{v}_{0}} \biggr)^{0.64 \pm0.12} $$
(2)

is the spectral emissivity. Here ε 0=(1.3±0.4)×10−5, \(\tilde{v}_{0} = 100~\mbox{cm}^{-1}\) and T=18.5±1.2 K. \(B_{\tilde{v}}(T)\) is the Planck function in the wavenumber domain.

Using a procedure proposed in Fisenko and Lemberg (2014) for presenting the Planck function \(B_{\tilde{v}}(T)\) in the frequency domain, we obtain the expression for the spectral energy density \(I^{\mathrm{P}}(v,T) = \frac{4\pi}{c}B_{v}(T)\) in the form

$$ I^{\mathrm{P}}(v,T) = \frac{8\pi h}{c^{3}}\frac{v^{3}}{e^{\frac{hv}{k_{\mathrm{B}}T}} - 1}. $$
(3)

According to Eq. (3), the Eq. (1), in the frequency domain v has the structure:

$$ I^{\prime}_{v}(T) = \varepsilon(v,T)I^{\mathrm{P}}(v,T), $$
(4)

where

$$ \varepsilon(v,T) = \varepsilon_{0} \biggl( \frac{v}{v_{0}} \biggr)^{0.64 \pm0.12}. $$
(5)

Here ε 0=(1.3±0.4)×10−5 and v 0=3 THz.

Then, in accordance with Eq. (4), the total energy density of the extragalactic FIRB radiation is presented in the form

$$ I_{0}(v_{1},v_{2},T) = \int _{\nu_{1}}^{\nu_{2}} I'_{v}(T) \mathrm{d}\nu= \int_{\nu_{1}}^{\nu_{2}} \varepsilon(v,T)I^{\mathrm{P}}(v,T) \mathrm {d}\nu. $$
(6)

The Stefan-Boltzmann law or the total radiation power per unit area is defined as

$$ I'_{0}(v_{1},v_{2},T) = \frac{4\pi}{c}I_{0}(v_{1},v_{2},T). $$
(7)

The total emissivity in the finite range of frequencies ν 1≤ν≤ν 2 has the following structure:

$$ \varepsilon(T) = \frac{I_{0}(v_{1},v_{2},T)}{\int_{\nu_{1}}^{\nu_{2}} I^{\mathrm{P}}(v,T)\mathrm{d}\nu}. $$
(8)

In Eq. (8), the total energy density of the blackbody radiation \(\int_{\nu_{1}}^{\nu_{2}} I^{\mathrm{P}}(v,T)\mathrm{d}\nu\), according to Fisenko and Lemberg (2014), has the form

$$ \int_{\nu_{1}}^{\nu_{2}} I^{\mathrm{P}}(v,T)\mathrm{d}\nu= \frac{48\pi (k_{\mathrm{B}}T)^{4}}{c^{3}h^{3}}\bigl[P_{3}(x_{1}) - P_{3}(x_{2}) \bigr], $$
(9)

where \(x = \frac{hv}{k_{\mathrm{B}}T}\). P 3(x) is defined as

$$ P_{3} ( x ) = \sum_{s = 0}^{3} \frac{(x)^{s}}{s!} \mathrm{Li}_{4 - s}\bigl(e^{ - x}\bigr). $$
(10)

Here

$$ \mathrm{Li}_{4 - s}\bigl(e^{ - x}\bigr) = \sum _{k = 1}^{\infty} \frac{e^{ - kx}}{k^{4 - s}} $$
(11)

is the polylogarithm function (Abramowitz and Stegun 1972).

Using Eq. (9) gives us the following expression for Eq. (8)

$$ \varepsilon(T) = \frac{c^{3}h^{3}}{48\pi (k_{\mathrm{B}}T)^{4}}\frac{I_{0}(v_{1},v_{2},T)}{[P_{3}(x_{1}) - P_{3}(x_{2})]}. $$
(12)

The thermodynamic functions of FIRB radiation are determined as follows:

  1. (1)

    Helmholtz free energy density \(f = \frac{F}{V}\) (Landau and Lifshitz 1980)

    $$\begin{aligned} f(v_{1},v_{2},T) =& \frac{8\pi k_{\mathrm{B}}}{c^{3}}T\int _{v_{1}}^{v_{2}} v^{2}\varepsilon(v,T) \\ &{}\times\ln( \bigl(1 - e^{ - \frac{hv}{k_{\mathrm{B}}T}}\bigr)dv \end{aligned}$$
    (13)
  2. (2)

    Entropy density \(s = \frac{S}{V}\):

    $$ s = - \frac{\partial f(v_{1},v_{2},T)}{\partial T} $$
    (14)
  3. (3)

    Heat capacity of at constant volume per unit volume \(c_{V} = \frac{C_{V}}{V}\):

    $$ c_{V} = \biggl( \frac{\partial I_{0}(v_{1},v_{2},T)}{\partial ( T )} \biggr)_{V} $$
    (15)
  4. (4)

    Pressure of photons P:

    $$ P = - f(v_{1},v_{2},T) $$
    (16)
  5. (5)

    The number density of photons \(n = \frac{N}{V}\):

    $$ n = \frac{8\pi}{c^{3}}\int_{v_{1}}^{v_{2}} \frac{\varepsilon(v,T) v^{2}}{e^{x} - 1}dv $$
    (17)

Here it is important to note that any thermodynamic functions of the extragalactic FIRB radiation can be determined using Eq. (6) and Eqs. (13)–(17). For example, the enthalpy density is defined as f=I 0(v 1,v 2,T)+P.

To calculate the values of the total energy density Eq. (6), the number density of photons Eq. (17) and Helmholtz free energy density Eq. (13) the Simpson rule was applied (Abramowitz and Stegun 1972). Knowledge of the total energy density and Helmholtz free energy density allows us to calculate the total emissivity, pressure in the finite range of frequencies from 0.15 THz to 2.4 THz at the mean temperature T=18.5 K. The results are presented in Table 1.

Table 1 Calculated values of the radiative and thermodynamic state functions at redshift z=0 for the average spectrum of the extragalactic far infrared background radiation. v 1=0.15 THz, v 2=2.4 THz, and T=18.5 K
Full size table

The values of the entropy density and heat capacity at constant volume were calculated using the method of numerical differentiation (Abramowitz and Stegun 1972). The calculated values of these thermodynamic functions are presented in Table 1.

Let us calculate the total intensity \(\tilde{I}(v_{1},v_{2},T)\) received in the finite frequency range (0.15–2.4) THz. According to Fixsen et al. (1998), a value of \(\tilde{I}(v_{1},v_{2},T)\) is equal to 14 nW m−2 sr−1. Using the relationship between the total intensity \(\tilde{I}(v_{1},v_{2},T)\) and the total energy density I 0(v 1,v 2,T)

$$ \tilde{I}(v_{1},v_{2},T) = \frac{c}{4\pi} I_{0}(v_{1},v_{2},T), $$
(18)

in accordance with Table 1, we obtain \(\tilde{I}(v_{1},v_{2},T) = 13.6~\mbox{nW}\,\mbox{m}^{-2}\,\mbox{sr}^{-1}\). This value is about 19.4 % of the total expected flux (70 nW m−2 sr−1) associated with the production of metals throughout the history on the universe (Dwek et al. 1998). As seen, the calculated value is in good agreement with the experimental data obtained in Fixsen et al. (1998).

Here it is important to note that the calculated values of the thermodynamic and radiative functions represent the state of the universe at the present time, which corresponds to the redshift z=0.

In Pei et al. (1999), it was noted that 85 % of the integrated galaxy light arises from galaxies at z<1.5. This value of redshift corresponds to the peak in the history of star-formation and rapid growth of the stellar mass in galaxies. Therefore, we calculate the radiative and thermodynamic properties of the extragalactic FIRB radiation at redshift z=1.5.

It is well known that in an expanding universe the temperature T and the frequency v depends on the redshift z (Sunyaev and Zel’dovich 1980), in accordance with the formulas v=v 0(1+z) and T=T 0(1+z). In this case, for numerical calculation of the radiative and thermodynamic functions of the extragalactic FIRB radiation, we should the mean temperature T=18.5 K replace by T=46.25 K and the finite frequency interval 0.15 THz–2.4 THz should be replaced by 0.375 THz–6 THz. In Table 2, the calculated values of the radiative and thermodynamic functions of the extragalactic far infrared background radiation at redshift z=1.5 are presented. According to Table 2, the total intensity \(\tilde{I}(v_{1},v_{2},T)\) received in the finite frequency range (0.375–6) THz is equal to 503.3 nW m−2 sr−1.

Table 2 Calculated values of the radiative and thermodynamic state functions at redshift z=1.5 for the average spectrum of the extragalactic far infrared background radiation. v 1=0.375 THz, v 2=6 THz, and T=46.25 K
Full size table

3 Conclusions

In this paper, the radiative and thermodynamic properties of extragalactic far infrared background radiation in the finite range of frequencies 0.15 THz≤v≤2.4 THz at the mean temperature T=18.5 K are calculated. The calculated value of the total intensity \(\tilde{I}(T) = 13.6~\mbox{nW}\,\mbox{m}^{-2}\,\mbox{sr}^{-1}\) received in the finite frequency interval from 0.15 THz to 2.4 THz is in good agreement with the experimental data (Fixsen et al. 1998). As noted in Dwek et al. (1998) that the total intensity expected from the energy released by stellar nucleosynthesis over cosmic history is 70 nW m−2 sr−1. As can be seen, that \(\tilde{I}(T) = 13.6~\mbox{nW}\,\mbox{m}^{-2}\,\mbox{sr}^{-1}\) is about 19.4 % of this total intensity.

The radiative and thermodynamic functions of the extragalactic far infrared background radiation at redshift z=1.5 are calculated.

In conclusion we note that, as in the case of the monopole and dipole spectra (Fisenko and Lemberg 2014) is desirably to obtain exact expressions for the temperature dependences of the radiative and thermodynamic functions of the extragalactic far infrared background radiation. This topic will be point of discussion in subsequent publication.