1 Introduction

The influence of the Prandtl number on wall-to-fluid thermal exchange mechanisms in single-phase flows is widely described in the literature, namely the augmentation of the Prandtl number causes the increasement of the thermal transfer rate. For two-phase flows, wall-to-fluid thermal transfer mechanisms is yet few understood due to the number of variables affecting the flow dynamics, such as bubble’s shape, turbulence, number of bubbles, quantity of dispersed phase fraction in the domain, bouyancy effects, and several other factors which could contribute to the modification of the thermal transfer rate of a two-phase flow problem. Investigations using a simple configuration and isolating other factors affecting the thermal transfer mechanisms may be important to quantify the relevance of a particular factor pertinent to the wall-to-fluid thermal transfer. Benchmarks using CFD in well-known geometries and considering simplified assumptions of physical conditions may provide key information for complex problems. Therefore, the present paper reports an extensive quantitative and qualitative study of the influence of the overall Prandtl number and the bubble size on the wall-to-fluid thermal transfer rate in two-phase flows in the classical problem of a differentially heated cavity.

The thermodynamic effects of the addition of bubbles to a single-phase flow have been widely described in several experimental and numerical studies in the literature. According to Deen and Kuipers [1], it is generally agreed that the introduction of a gas into a liquid enhances the turbulence in the medium and thus increases the thermal transfer rate to immersed surfaces. Deen and Kuipers [1] additionally defend the thesis that higher gas velocities enhance even more the thermal transfer rate. Deckwer [2] suggested that the presence of bubbles can increase the thermal transfer rate in a gas–liquid bubble column by more than one order of magnitude. Oresta et al. [3] studied the thermal transfer mechanisms in the case of Rayleigh–Bénard convection in a liquid with vapor bubbles. They concluded that the presence of bubbles had a profound effect on the structure of the flow and on the calculated Nusselt number. Deen and Kuipers [1] found that the passage of a bubble in a vertical channel increased the local thermal transfer from a hot wall. Tamari and Nishikawa [4] reported that the presence of bubbles increased the convection due to the addition of a bouyancy force. Dabiri and Tryggvason [5] studied turbulent bubbly flow and reported that the presence of bubbles increased the mixing and reduced the temperature difference between the hot wall and the bulk of the flow. They found that the Nusselt number increased by 60% when bubbles were included in the domain (considering 3% of volume fraction). According to Dabiri and Tryggvason [5], the presence of moving bubbles generally increases the local thermal transfer. Bukhari et al. [6] studied natural convection for a two-phase flow and concluded that thermodynamic patterns, such as the thermal exchange at the interface, may be directly affected by some hydraulic patterns, such as the velocity field. They concluded that the turbulent structures in the air and water phases played an important role in enhancing the thermal and mass transfer rates. Chandra and Chhabra [7] presented a quantitative analysis of the influence of the Prandtl and the Grashof numbers on single-phase flows, demonstrating the importance of the Prandtl number in regulating the thermal transfer rate for immersed surfaces in single-phase flows.

Although the literature has obtained, in general, higher wall-to-fluid thermal transfer coefficients in two-phase flows compared to single-phase flows, quantitative analysis or conclusions elucidating the causes of the numerical or experimental results previously obtained are scarce. In addition, some studies have presented opposite results, such as Qiu et al. [8], who found a reduction in the thermal transfer rate on including bubbles in the flow.

It is thus imperative to examine the thermal transfer characteristics using dimensionless parameters in order to establish general conclusions and to improve the understanding of the mechanisms underlying thermal transfer. In the present work, computational simulations of single-phase and two-phase flows are presented in order to evaluate the relation between the Prandtl number and the thermal transfer rate in a cubic cavity. The influence of the bubble size is also evaluated in the present paper. Since information about the thermal transfer rate in single-phase and two-phase flows is crucial to several industrial processes as well as to various equipment employed in engineering applications, the present paper may guide and improve the efficiency of the thermal transfer operations. Finally, the present paper presents new insights into the thermal transfer mechanisms, opening new research opportunities related to non-isothermal two-phase flows.

2 Physical Model

The physical model used in the present paper consists of a three-dimensional cavity where the flow is subjected to thermal effects. A cavity is used as physical model due to its simple geometry [9] and presence in several industrial applications [10].

The analysis conducted in the present paper was performed while imposing constant values for the Grashof number and different values of the Prandtl number and bubble radius. The Grashof number represents the ratio of buoyancy to viscous force on a fluid and is defined according to the following equation [11]:

$$ Gr= \frac{g \beta (T_{s}-T_{\infty}) L^{3}}{\nu^{2}} $$
(1)

where g is the acceleration due to gravity, β is the volumetric expansion coefficient, Ts is the temperature at the reference surface, T∞ is the temperature far away from the surface of reference, L is the characteristic length, and ν is the kinematic viscosity. The Prandtl number defines the ratio of momentum diffusivity to thermal diffusivity and is given by the following expression [11]:

$$ Pr= \frac{\mu Cp }{k} $$
(2)

where Cp is the specific heat, μ is the dynamic viscosity, and k is the thermal conductivity.

In the analysis of the simulations, the overall Prandtl number (Prove) of the flow was calculated, defined by the following expression:

$$ Pr_{ove}= \varphi Pr_{dis} + (1-\varphi) Pr_{con} $$
(3)

where φ is the volume fraction of the dispersed phase in the domain, Prdis is the Prandtl number for the dispersed phase, and Prcon is the Prandtl number for the continuous phase.

The simulations were performed employing the Oberbeck–Boussinesq approximation (OB) in a cubic cavity with a characteristic length L. The characteristic length L was equal to 1.0 m in all the simulations. Bouyancy and gravity forces were neglected.

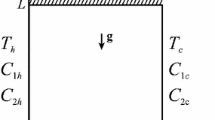
The domain boundaries were named using geographic orientation, namely north, south, east, west, bottom, and top faces. A schematic image of the configuration of the cavity used in the present work and the names of the domain boundaries are presented in Fig. 1.

Fig. 1
figure 1

Physical model with the names of the domain boundaries

Full size image

Null velocity and null pressure gradient were imposed at all the domain faces. The acceleration of gravity was assumed to be 9.81 m/s2. The east and west wall were given an imposed high (Th) and low (Tl) temperature, respectively; and the other walls were considered adiabatic. The initial conditions for all the simulations were: null velocity, null pressure, and temperature of Tl in all the domain.

The prediction of the thermal exchange rate between the flow and the east wall (kept at a fixed temperature Th) was conducted over the entire time of the simulations. The thermal transfer rate was calculated using the spatial mean Nusselt number at the east wall. The Nusselt number (Nu) represents the ratio between the conductive and convective thermal transfer processes; therefore, when Nu < 1, conduction is predominant, and when Nu > 1, the advection effects are more predominant than conduction [12]. The Nusselt number may be defined by the following expression [1]:

$$ Nu= \frac{L}{{\Delta} T} \frac{\delta T}{\delta x}|_{x = 0} $$
(4)

where T is the temperature and ΔT is the temperature difference between the east and west walls.

All the analysis conducted in the present paper employed the calculation of the spatial mean Nusselt number (\(\bar {Nu}\)) at the east wall. The spatial mean Nusselt number was defined by the following expression:

$$ \bar{Nu}=\frac{ {{\sum}_{1}^{n}} Nu }{n} $$
(5)

where n is the number of computational cells at the east wall.

In two-phase flows, the bubble is constantly subjected to relatively high velocities due to the dynamics of the flow, causing the bubble to move and its shape to deform over time. In order to preserve the spherical shape of the bubbles, all the two-phase flow simulations were performed while imposing a constant and relatively high surface tension coefficient, which was defined as 30.0 N/m. This was imposed since Dabiri and Tryggvason [5] reports the influence of the bubble shape on the thermal transfer dynamic; therefore, the shape of the bubble was not studied in the present paper. Since \(\frac {Gr}{Re^{2}}>>1\), forced convection may be neglected.

3 Mathematical Model

The continuity, momentum, and energy equations were solved employing the following expressions:

$$ \mathbf{\nabla} .\mathbf{v}= 0, $$
(6)

where v is the fluid velocity.

$$ \rho_{0} \frac{D\mathbf{v}}{Dt}= -\mathbf{\nabla} p + (\rho-\rho_{0}) \mathbf{g} + \mu \nabla^{2} \mathbf{v}+ \overrightarrow{f}_{st} (\mathbf{x},t), $$
(7)

where t is the time, p is the pressure, ρ0 is the specific mass of reference, and \(\overrightarrow {f}_{st}\) is the source term used to model the effects of the force of surface tension.

$$ \rho_{0} Cp \frac{DT}{Dt}= \mathbf{\nabla} . (k \mathbf{\nabla} T ). $$
(8)

where α is the thermal diffusivity. The Oberbeck–Boussinesq approximation was employed in order to model the effects of a variable specific mass. The following thermodynamic relation was employed in the momentum equation to compute these effects: a temperature function [11]

$$ (\rho - \rho_{0})\mathbf{g} = -\rho_{0}\beta(T-T_{0})\mathbf{g} $$
(9)

where T0 is the temperature of reference.

Finally, the effects of surface tension were included in the formulation using the model of Brackbill et al. [13]. This model specifies the force of surface tension per unit of volume as

$$ \overrightarrow{f}_{st} (\mathbf{x},t) = \frac{\rho \sigma \kappa \nabla \phi}{\frac{1}{2}(\rho_{liq}+\rho_{vap})}, $$
(10)

where σ is the surface tension coefficient and kappa is the curvature.

4 Numerical Model

The partial differential equations were solved with a standard finite volume method on a staggered rectangular three-dimensional grid. The velocity–pressure coupling was accomplished using a two-step projection method [14] with an explicit treatment for advection terms and an implicit treatment for pressure and diffusion terms. The Barton scheme [15] was used for the spatial discretization of the advective terms. The energy equation was solved implicitly using a multigrid-multilevel solver. The transient equations were solved using the MFSim program, which has been developed over the last ten years in cooperation with a large research group and with the scientific support of Petrobras, a semi-public Brazilian multinational corporation in the petroleum industry, headquartered in Rio de Janeiro, Brazil. The turbulence modeling was performed using Large Eddy Simulation (LES) and the turbulence closure was done via the dynamic model of Germano et al. [16] and Lilly [17].

The duration of the simulations was defined according to the stabilization of the calculation of the spatial mean Nussel number at the east wall. All simulations were performed in a parallel environment in the fluid mechanics laboratory cluster at the Federal University of Uberlândia, Brazil. The code uses single and multi-block structured meshes and a variable time step. The magnitude of the allowable time step for stable calculations is determined from the convective and viscous terms. The constraint is defined according to the CFL (Courant–Friedrichs–Lewis condition) and the mesh size [18]. The tolerance of the numerical model in providing a solution to the continuity, momentum, and energy equations was 10− 6. In order to ensure the incompressibility condition, the velocity divergence in each computational cell was evaluated and was not higher than 10− 11 s− 1 during all the performed simulations.

A volume of fluid (VOF) method [19] was applied to determine the location of the interface and the transport. VOF employs a color function φ(x, t) to indicate the fractional amount of fluid present at a certain position x and at time t. The color function φ is calculated using the following equation [20]:

$$ \frac{\partial \varphi}{\partial t}+ [\mathbf{v}_{normal}.\nabla \varphi]= 0. $$
(11)

The flow fluid properties were calculated based on the volume fraction of the continuos and dispersed phases, as Deen et al. [1]:

$$ \rho =\varphi \rho_{dis} + (1- \varphi) \rho_{con} $$
(12)
$$ \mu =\varphi \mu_{dis} + (1- \varphi) \mu_{con} $$
(13)
$$ k =\varphi k_{dis} + (1- \varphi) k_{con} $$
(14)
$$ cp =\varphi cp_{dis} + (1- \varphi) cp_{con} $$
(15)

The VOF method applied in the MFSim code employed the PLIC algorithm [20] and the curvature was computed using the Least Squares method [21]. The two-phase flow model was previously validated in Franco et al. [22]. In addition, spurious currents were evaluated in the latter work and it presented none relevance for even complex computational simulations of multiple ascending bubbles. For more details, the readers are invited to see the work of Franco et al. [22].

5 Validation of the Numerical Model

Two validation cases are presented in this section, namely modelling natural convection in single-phase flows (case 1) and modelling natural convection in two-phase flows (case 2).

5.1 Validation case 1: simulations of natural convection in single-phase flows

Natural convection simulations in a cubic cavity assuming a Rayleigh number of 1.89 × 105 were performed using OB for validation purposes. Temperature profiles were plotted and then compared with the experimental results of Krane and Jessee [23] and the numerical results of Padilla et al. [24].

A uniform temperature field was imposed on the east (Thigh) and west (Tlow) walls. The south and north walls were considered adiabatic, and a linear temperature field, given by the expression \(T(x,y,0) = T(x,y,L) = T_{high}-(T_{high}-T_{low}) \frac {x}{L}\), was imposed on the bottom and top walls.

Two dimensionless temperature lines from inside the domain were extracted from the numerical results, namely, T∗(x, L/2,L/2) and T∗(L/2,y, L/2). The expression for the dimensionless temperature is given by

$$ T^{*} (dimensionless) = \frac{T}{T_{east}-T_{west}}, $$
(16)

where Teast represents the temperature at the east wall and Twest represents the temperature at the west wall.

Figure 2a presents the dimensionless temperature along the line T∗(x, L/2,L/2) for OB. Likewise, Fig. 2b presents the dimensionless temperature along the line T∗(L/2,y, L/2) for OB.

Fig. 2
figure 2

Dimesionless temperature along the lines T∗(x, L/2,L/2) and T∗(L/2,y, L/2), for Ra = 1.89 × 105 with OB

Full size image

The simulations using OB demonstrated good agreement with the experimental data of Krane and Jessee [23] and with the numerical data of Padilla et al. [24], as observed in Fig. 2. The numerical results from the present paper are slightly closer to those reported in the numerical work of Padilla et al. [24] than those from the experimental work of Krane and Jessee [23].

The average relative difference (ε) between the experimental data and the computed values from the present work are shown in Table 1. According to the results seen in Table 1, OB provides numerical results with low deviation from the experimental data of Krane and Jessee [23]. The maximum difference between the experimental data and OB was 7.3% for the most fine grid.

Table 1 Average relative difference (ε) between OB and the experimental data of Krane and Jessee [23]
Full size table

In order to present a grid quality analysis, the dimensionless temperatures obtained for the three different meshes were compared. The temperature from the line T∗(x, L/2,L/2) was chosen for the comparison between the different meshes. Table 2 shows the data for x/L = 0.2, x/L = 0.5 and x/L = 0.8 using OB. The relative difference between two sucessive grid configurations (ψ) is also presented in Table 2.

Table 2 Dimensionless temperature for OB for x/L = 0.2, x/L = 0.5 and x/L = 0.8 from the line T∗(x, L/2,L/2)
Full size table

Since the temperature field was solved using a second-order scheme, it is expected that the error found for a grid with size ζ is one-fourth that obtanied for a grid with size 2 ζ. When the relative difference between the error obtained for two grids is significantly low and its values are close to the reference, it is assumed that this is a good quality grid. As seen in Table 2, the grid configuration of 32 × 32 × 32 is of great quality since its values are very close to the experimental data from the literature (seen in Table 2), as well as the fact that the relative difference between the error with the coarser grid is not significant compared to the 32 × 32 × 32 grid. Therefore, based on the numerical results obtained in the simulations presented in this section, it can be concluded that both formulations are in accordance with the literature, assuring us of the accuracy of the numerical methods employed.

5.2 Validation case 2: simulations of natural convection in two-phase flows

Natural convection in two-phase flow was simulated and validated by the calculation of the spatial mean Nusselt number at the east wall. Qiu et al. [8] presented this numerical experiment of natural convection with two-phase flow using Oberbeck-Boussinesq approximation (since the specific mass was the same for the two fluids, and the other fluid properties were different).

Null velocities and null pressure gradient were imposed to all the domain faces. The east and west walls have, respectively, a uniform high (Th) and low temperature (Tl). The south, north, bottom and top walls are adiabatic. The fluid is at rest in initial conditions and the temperature field is uniform and igual to Tl.

The Prandtl number was set as 0.71 and Rayleigh number was 103 for the dispersed phase and 104 for continuos phase. The dispersed phase consisted of a bubble in the center of the cavity. Two values of initial bubble radius were tested, namely: 0.15L and 0.31L. The wall-to-fluid thermal transfer rate was examined by means of the spatial mean Nusselt number calculation. A computational grid with one and two levels of refinement were tested and the base level presented 32 × 32 × 32 cells.

The Fig. 3 shows the isotherms in the cases of a bubble initial radius of 0.15L and 0.31L, respectively.

Fig. 3
figure 3

Isotherms at central xz-plane for r = 0.15L (a) and r = 0.31L (b). Interface is represented by a contour line

Full size image

The presence of the bubble changed significantly the thermal transfer pattern inside the cavity as shown in the Fig. 3. As seen in the Fig. 3, the isotherms tend to be more vertical inside the bubble, as found by Qiu et al. [8]. The Fig. 4 shows the clockwise movement described by the bubble inside the cavity due to thermal bouyancy effects, as previously reported by Qiu et al. [8].

Fig. 4
figure 4

Velocity field at the central xz-plane considering r = 0.15L (a) and r = 0.31L (b). The interface is represented by a contour line

Full size image

A 3D visualization of the interface contour is shown in the Fig. 5.

Fig. 5
figure 5

Temperature and isotherms visualization for r = 0.15L (a) and r = 0.31L (b). The interface is represented by a contour line

Full size image

The spatial mean Nusselt number presented good agreement with Qiu et al. [8] for the two different initial radius tested. The Table 3 shows the spatial mean Nusselt number found in the present paper and the ones found from the literature.

Table 3 Spatial mean Nusselt number at the east wall for two values of bubble’s initial radius
Full size table

The introduction of a bubble with a larger radius caused the reduction of the spatial mean Nussselt number at the heated wall, similarly to the results found by Qiu et al. [8]. The influence of the Grashof number in the local thermal transfer was significantly visible in the previous table, since the overall Grashof number was lowered by the introduction of a dispersed phase, as previously stated by the literature for single-phase-flows [9].

The computational simulations of the present work were performed using a mesh with one refinement level and a base level with 32 × 32 × 32 cells. since the grid configuration using one refinement level presented results with good agreement and mesh convergence was achieved with the most refined level.

6 Influence of the Prandtl Number on Single-Phase Flows

The literature already accepts the general hypothesis of the thermal transfer rate augmentation due to the increasement of the Prandtl number on single-phase flows. Therefore, the results shown here only confirm and illustrate the influence of the Prandtl number on the temperature field in single-phase flows.

Simulations were conducted using a Grashof number of 1.4 × 103 and two values of the Prandtl number were tested: Pr = 0.71 and Pr = 7.10. Figure 6 shows the isotherms and the temperature field for the simulations with Grashof number 1.4 × 103 and Prandtl numbers Pr = 0.71 and Pr = 7.10.

Fig. 6
figure 6

Isotherms and temperature field for Gr = 1.4 × 103 and Pr = 0.71 (a) as well as for Pr = 7.1 (b)

Full size image

According to the Fig. 6, the Prandtl number affected the temperature field since the pattern of the isotherms was completely different between the Fig. 6a and b. The pattern of the isotherms changed a great deal as the Prandtl number changed from 0.71 to 7.1 since the isovalues of temperature became more horizontal compared to the bottom and top walls. The temperature field presents a strong stratification profile at the cavity center due to advection effects for the case of Pr= 7.1 and the case with Pr= 0.71 shows no stratification because of the low advection magnitude since Nu < 1.

The spatial mean Nusselt number was computed at the east wall and the highest thermal transfer rate was associated to the simulations with the highest value of the Prandtl number, as shown is Table 4.

Table 4 Summary of the thermal transfer rate results in the single-phase flow cases
Full size table

According to the results found here, the Prandtl number affected the wall-to-fluid thermal transfer rate as well as the pattern of the isotherms. Next, the influence of the Prandtl number on two-phase flows is evaluated.

7 Two-Phase Flow Simulations Where the Prandtl Number of the Dispersed Phase is Higher than the Prandtl Number of the Continuous Phase

In this section, two-phase flows are investigated in the situation where the Prandtl number of the dispersed phase is higher than the Prandtl number of the continuous phase. The results of three different analyses are presented in this section, namely:

  • Prdis > Prcon and the effects of varying the overall Prandtl number variation;

  • Prdis > Prcon and the effects of varying the bubble size;

  • Prdis > Prcon and the effects of varying both the bubble size and overall Prandtl number variation.

In Section 7.1, the results of two-phase flow simulations are presented, in which there was an initial bubble radius of 0.31L and the overall Prandtl numbers analyzed were 1.06 and 1.51. In Section 7.2, the results of two-phase flow simulations are presented, in which the overall Prandtl number was 1.06 and two bubble radii were tested: r = 0.31L and r = 0.40L. Lastly, in Section 7.3, the results of two-phase flow simulations will be presented, in which the overall Prandtl numbers were 1.51 and 2.30 and the bubble radii were r = 0.31L and r = 0.39L.

7.1 Simulations with P r dis > P r con and the effects of variations in the overall Prandtl number

In this subsection, there will be presented the results of two-phase flow simulations with a dispersed phase with a bubble radius of 0.31L. The Grashof number was taken equal 1.4 × 103 and the continuous phase had a Prandtl number of 0.71.

First, the Prandtl number for the dispersed phase was five times higher than in the continuous phase (Prdis = 3.55 and Prcon = 0.71, leading to an overall Prandtl number of 1.06). Then, a simulation was performed considering a dispersed phase with Prandtl number ten times higher than the continuous phase (Prdis = 7.10 and Prcon = 0.71, leading to an overall Prandtl number of 1.51).

Figure 7 shows the isotherms and temperature field in the two-phase flow cases with Gr=1.4 × 103 and Prove = 1.06 a and Prove = 1.51 b.

Fig. 7
figure 7

Isotherms and temperature field at the central xz-plane with Gr=1.4 × 103, Prove = 1.06 (a) and Prove = 1.51 (a). The isotherms are represented with 20 thin isovalue contours. The thick contour represents the position of the interface. The temperature field is presented in grayscale

Full size image

According to Fig. 7, the configuration of the isotherms was deeply modified inside the dispersed phase. The isotherms in Fig. 7 were not primarily vertical, since the isotherms were more horizontal inside the dispersed phase.

Figure 8 shows the evolution over time of the spatial mean Nusselt number for the single-phase case (Pr = 0.71), the two-phase flow case with Prove = 1.06, and the two-phase case with Prove = 1.51.

Fig. 8
figure 8

Temporal evolution of the spatial mean Nusselt number for the single-phase case (Pr = 0.71) and two-phase flow cases with Prove = 1.06 and Prove = 1.51

Full size image

Figure 8 shows the severe influence of the overall Prandtl number on the spatial mean thermal transfer rate. As the overall Prandtl number increases, the spatial mean Nusselt number increases. In comparison to the single-phase case, the two-phase cases demonstrate a significant increase in the mean thermal transfer rate due to the variation of the overall Prandtl number.

Table 5 summarizes the data related to the simulations presented in this subsection.

Table 5 Summary of the thermal transfer rate results for the effect of varying the overall Prandtl number
Full size table

According to Table 5, the spatial mean Nusselt number increased as the overall Prandtl number was increased. The minimum values of the thermal transfer rate (\(\bar {Nu}_{min}\) seen in Table 5) are associated to the moment when the dispersed phase was the farthest from the east wall. In addition, the maximum values of the thermal transfer rate (\(\bar {Nu}_{max}\) seen in Table 5) were related to the moment when the dispersed phase was the nearest to the east wall. Therefore, the proximity of the dispersed phase to the east wall was a important factor affecting the Nusselt number when Prdis > Prcon.

7.2 Simulations with P r dis > P r con and the effects of variations in the bubble size

In this subsection, the results of two-phase flow simulations with a dispersed phase with a bubble radius of 0.31L and 0.40L will be presented. The Grashof number was taken equal to 1.4 × 103 and the continuous phase had a Prandtl number of 0.71. The overall Prandtl number was 1.06 for both simulations (r = 0.31L and r = 0.40L).

Figure 9 shows the temporal evolution of the spatial mean Nusselt number for the single-phase case (Pr = 0.71), the two-phase flow with r = 0.31L (Prove = 1.06), and the two-phase flow with r = 0.39L (Prove = 1.06).

Fig. 9
figure 9

Evolution of the spatial mean Nusselt number for the single-phase case (Pr = 0.71), two-phase flow with r = 0.31L (Prove = 1.06), and two-phase flow with r = 0.40L (Prove = 1.06)

Full size image

According to Fig. 9, the spatial mean Nusselt number varied in time for both cases (r = 0.31L and r = 0.40L). The variations of the spatial mean Nusselt number were more prominent in the case for the bubble radius of 0.31L compared to the case with r = 0.40L.

Table 6 summarizes the data related to the simulations treated in this subsection.

Table 6 Summary of the effects on the thermal transfer rate of bubble size variation with the Grashof number equal to 1.4 × 103 and overall Prandtl number was 1.06
Full size table

According to Table 6, the bubble radius directly affected the thermal transfer rate in time. The smaller bubble radius was associated to a higher maximum and mean value of thermal transfer rate compared to the case with larger bubble radius. According to visual observations over the simulation time, the proximity between the wall and the bubbles was higher for the case with r = 0.31L in comparison to r = 0.40L. Therefore, the size of the bubble radius had consequences for the bubble movement inside the cavity and probably the distance effect may have promoted the difference in the Nusselt number calculations.

7.3 Simulations with P r dis > P r con and the effects of simultaneous variation of the bubble size and overall Prandtl number

This subsection presents the results of two-phase flows simulations with a dispersed phase with a bubble radius of 0.31L and 0.39L and overall Prandtl numbers of 1.51 and 2.30, respectively. Here, the effects of the bubble radius size were taken into account as well as the influence of varying the overall Prandtl number.

Simulations of natural convection were performed assuming Gr = 1.4 × 103 and Pr = 7.1 for the dispersed phase and Pr = 0.71 for the continuous phase. The simulations were performed for two different initial bubble radii, namely r = 0.31L and r = 0.39L. The overall Prandtl number was 0.71 for the single-phase flow, 1.51 for the two-phase flow with dispersed phase with radius of 0.31L, and 2.30 for the simulation of a two-phase flow with an spherical dispersed phase with radius of 0.39L.

Figure 10 shows the isotherms for the two-phase cases with overall Prandtl numbers of 1.51 and 2.30.

Fig. 10
figure 10

Isotherms at the central xz-plane for Gr=1.4 × 103 and overall Prandtl numbers of 1.51 and 2.30. The isotherms are represented by 20 thin isovalue contours. The thick contour represents the position of the interface. The temperature field is presented in grayscale

Full size image

Figure 10 illustrates the consequences of varying the overall Prandtl number on the temperature field since the isotherms were modified compared to the single-phase case. As seen in Fig. 7, inside the dispersed phase, the isotherms exhibit a deeply modified aspect since the isotherms were mainly horizontal inside the dispersed phase. In addition, the larger size of the dispersed phase in Fig. 10b compared to Fig. 10a intensified the impact of the Prandtl number on the temperature field. In general, the closer the dispersed phase was from the east wall, higher was the spatial mean Nusselt number at the east wall.

Figure 11 shows the temporal evolution of the spatial mean Nusselt number for the single-phase case (Pr = 0.71), the two-phase flow with r = 0.31L (Prove = 1.51), and the two-phase flow with r = 0.39L (Prove = 2.30).

Fig. 11
figure 11

Evolution of the spatial mean Nusselt number for the single-phase case (Pr = 0.71), two-phase flow with r = 0.31L (Prove = 1.51), and two-phase flow with r = 0.39L (Prove = 2.30)

Full size image

According to Fig. 11, the spatial mean Nusselt number was intensified as the overall Prandtl number increased. Since the enlargement of the bubble radius increases the overall Prandtl number indirectly, it was expected that the simulation with the larger bubble would yield a larger thermal transfer rate compared to the simulation with the smaller radius. According to Fig. 11, the mean Nusselt number for the two-phase flows cases were severely altered from about − 10.0% to almost + 60.0% compared to the single-phase case. The thermal transfer rate was more enhanced in the simulation with the radius 0.39L compared to the simulation performed with the radius 0.31L.

Table 7 summarizes the data related to the simulations treated in this subsection.

Table 7 Summary of the thermal transfer rate results to compute the effects of varying the overall Prandtl number and bubble radius
Full size table

Table 7 presents a quantitative confirmation of the influence of the Prandtl number on the thermal transfer rate according to the calculated spatial mean Nusselt number. The spatial mean Nusselt number increased almost 30% and 15% by the addition of the dispersed phase with an initial radius of 0.39L and 0.31L, respectively. Therefore, Table 7 confirms that the thermal transfer rate was enhanced as the overall Prandtl number of the flow mixture increased.

The influence of the overall Prandtl number may explain the reason why the literature has been reporting an increase of the thermal transfer rate at surfaces by the introduction of bubbles. Dabiri and Tryggvason [5] found that the bubbles’s presence raised the Nusselt number at the heated wall, especially in the case with higher Prandtl number. The present paper is in acordance with Dabiri and Tryggvason [5] since the Prandtl number had a great impact on the thermal transfer mechanisms.

In the present paper, the closer the dispersed phase was to the heated wall, the higher was the spatial mean Nusselt number compared to the single-phase flow case. Similarly, the spatial mean Nusselt number increased in the simulations in which the distance between the bubbles and the wall were lower in Dabiri and Tryggvason [5].

As found by Dabiri and Tryggvason [5], when the dispersed phase was in the vinicity of the heated wall, the void fraction stirred up the viscous layer and reduced the size of the conduction region near the wall, improving the thermal transfer rate. In addition, when the dispersed phase was far from the heated wall, its influence was not significant and no improvement in the thermal transfer rate was observed.

8 Two-Phase Flow Simulations in which the Prandtl Number for the Dispersed Phase Was Lower than the Prandtl Number for the Continuous Phase

This section will present results for two-phase flows investigated in the situation where the Prandtl number for the dispersed phase is lower than the Prandtl number for the continuous phase. Three different analyses were performed, namely:

  • Prdis < Prcon and the effects of overall Prandtl number variation were computed

  • Prdis < Prcon and the effects of bubble size variation were evaluated

  • Prdis < Prcon and the effects of simultaneous variations in the bubble size and overall Prandtl number were analyzed.

Section 8.1 presents the results of two-phase flow simulations with an initial bubble radius of 0.31L and overall Prandtl numbers 6.3 and 6.22. Section 8.2 will present the results of two-phase flow simulations with an overall Prandtl number of 6.22 and two bubble radii: 0.31L and 0.40L. Section 8.3 will present the results of two-phase flow simulations with overall Prandtl numbers of 6.3 and 5.5 considering an initial bubble radius of 0.31L and 0.39L, respectively.

8.1 Simulations with P r dis < P r con and the effects of the overall Prandtl number variation

In this subsection, the results of two-phase flow simulations with an initial bubble radius of 0.31L will be presented. The Grashof number was taken equal to 1.4 × 104 and the continuous phase had Prandtl number 7.10. First, the Prandtl number for the dispersed phase was one-tenth that of the continuous phase (Prdis = 0.71 and Prcon = 7.10 leading to an overal Prandtl number of 6.30). Then, a simulation was performed considering a dispersed phase with Prandtl number only 1% that of the continuous phase (Prdis = 0.071 and Prcon = 7.10 leading to an overal Prandtl number of 6.22).

Figure 12 shows the configuration of the isotherms in the two-phase flow cases with Gr=1.4 × 104 and Prove = 6.30 a and Prove = 6.22 b.

Fig. 12
figure 12

Isotherms at central xz-plane for Gr=1.4 × 104, Prove = 6.30 and Prove = 6.22. The isotherms are represented with 20 thin isovalue contours. The thick contour represents the position of the interface. The temperature field is presented in grayscale

Full size image

Figure 12 shows the configuration of the isotherms modified inside the dispersed phase. The isotherms inside the dispersed phase were more vertical than the isotherms seen in the figure for the single-phase case with Pr = 7.1 (Fig. 6b). The tendency of the isotherms to be more vertical was acentuated in the case with lower overall Prandtl number (Fig. 12b).

Figure 13 shows the temporal evolution of the spatial mean Nusselt number for the single-phase case (Pr = 7.1) as well as the two-phase flow cases with Prove = 6.3 and Prove = 6.22.

Fig. 13
figure 13

Evolution of the patial mean Nusselt number for the single-phase case (Pr = 7.1) and the two-phase flows cases with Prove = 6.3 and Prove = 6.22

Full size image

According to Fig. 13, the mean thermal transfer rate was reduced by the introduction of a bubble with lower Prandtl number than the continuous phase. The case with higher overall Prandtl number was associated to higher peaks of the spatial mean Nusselt number in comparison to the case with a lower overall Prandtl number.

Table 8 summarizes the results treated in the present subsection.

Table 8 Summary of the thermal transfer rate results to compute the effects of varying the overall Prandtl number
Full size table

According to Table 8, the reduction of the thermal transfer rate was accompanied by a reduction of the overall Prandtl number. Since the overall Prandtl numbers from the two-phase flow cases were very similar, the thermal transfer rates between them were not significantly different. However, between the single-phase and two-phase cases, the influence of the overall Prandtl number is evident on the calculated thermal transfer rate.

8.2 Simulations with P r dis < P r con and the effects of varying the bubble size

This subsection will present the results of two-phase flow simulations with initial bubble radii of 0.31L and 0.40L. The Grashof number was taken equal to 1.4 × 104 and the continuous phase had a Prandtl number of 7.10. The overall Prandtl number was 6.22.

Figure 14 shows the temporal evolution of the spatial mean Nusselt number for the single-phase case (Pr = 7.1) as well as that for the two-phase flow cases (Prove = 6.22) with r = 0.31L and r = 0.40L.

Fig. 14
figure 14

Evolution of the spatial mean Nusselt number for the single-phase case (Pr = 7.1) and the two-phase flows cases with Prove = 6.22 considering r = 0.31L and r = 0.40L

Full size image

According to Fig. 14, the spatial mean Nusselt number varied in time for both cases (r = 0.31L and r = 0.40L). The simulation with the bubble radius of 0.40L presented a more visible reduction of the thermal transfer rate compared to the case with a smaller bubble radius (r = 0.31L).

Table 9 shows the main results of the simulations presented in this subsection.

Table 9 Summary of the thermal transfer rate results to compute the effects of the bubble size variation with Grashof number equal to 1.4 × 104 and the overall Prandtl number was 6.22
Full size table

According to Table 9, the bubble radius influenced the thermal transfer rate. The larger bubble radius presented the lower mean, minimum and maximum thermal transfer rates in time. In the visual observations during the simulations, it was confirmed that, in general, the distance between the dispersed phase and the wall was lower, affecting the calculated value of the Nusselt number, similar to what was seen in the previous section. Therefore, the influence of the bubble radius was related to the proximity of the bubble to the wall during the bubble movement inside the domain.

8.3 Simulations with P r dis < P r con and the effects of simultaneously varying the bubble size and overall Prandtl number

This subsection will present the results of two-phase flow simulations of natural convection considering Gr = 1.4 × 104 and bubble initial radii of 0.31L and 0.39L. The dispersed phase had Prdis = 0.71 and the continuous phase Prcon = 7.1. In addition, a simulation of single-phase flow was performed considering Pr = 7.1.

The overall Prandtl number of the two-phase flow simulation using an initial bubble radius of r = 0.31L was 6.3 and the overall Prandtl number for the case with r = 0.39L was 5.5. A similar simulation was conducted by Qiu et al. [8] using different initial radius for the dispersed phase.

Figure 15 shows the isotherms for the cases with Prove = 6.3 and Prove = 5.5.

Fig. 15
figure 15

Isotherms at central xz-plane for Gr=1.4 × 104, Prove = 6.3 (a) and Prove = 5.5 (b). The isotherms are represented with 20 thin isovalue contours. The thick contour represents the interface position. The temperature field is presented in grayscale

Full size image

According to Fig. 15, the isotherms presented a different pattern inside the dispersed phase compared to the single-phase flow. The isotherms inside the dispersed phase in Fig. 15 were less horizontal than the isotherms in the single-phase case, indicating the severe impact on the temperature field of the presence of the dispersed phase. The behavior of the isotherms inside the dispersed phase presented in the present paper are in accordance with the results of Qiu et al. [8], in which the isotherms inside the dispersed phase tended to be more vertical rather than horizontal.

Figure 15b illustrates the intensified effect previously seen in Fig. 15a due to the larger radius of the dispersed phase. The effect of the size of the radius on the thermal transfer rate was also reported by Qiu et al. [8], who reported a reduction in the mean Nusselt number as the radius of the dispersed phase was increased. Therefore, the thermal transfer rate and the overall Prandtl number of flow mixture have a straightforward connection, as demonstrated in the former sections.

Figure 16 shows the evolution in time of the spatial mean Nusselt number for the single-phase case (Pr = 7.1), the two-phase case with Prove = 6.3, and the two-phase case with Prove = 5.5.

Fig. 16
figure 16

Evolution of the spatial mean Nusselt number for the single-phase case (Pr = 7.1) and two-phase flows cases with a dispersed phase with radii of 0.31L (Prove = 6.3) and 0.39L (Prove = 5.5)

Full size image

According to Fig. 16, the spatial mean Nusselt number was directly affected by varying the overall Prandtl number. The increase of the bubble radius intensified the importance of the Prandtl number for the dispersed phase, reducing even more the Nusselt number.

According to Fig. 16, the spatial mean Nusselt number at the east wall presented values from about + 2% to almost − 12% compared to the single-phase case. The results reported in Fig. 16 demonstrate the decrease in the spatial mean Nusselt number when the dispersed phase was in the vinicity of the heated wall; the thermal transfer rate increases when the dispersed phase moved far away from the heated wall. The maximum value of the Nusselt number was approximately the value from the single-phase case, since the dispersed phase has little influence on the thermal transfer rate when it is away from the heated wall.

Figure 16 presents an example of the case where the addition of a dispersed phase did not enhance the thermal transfer rate at a surface in contact with a two-phase flow. In fact, the results presented in Fig. 16 show the severe reduction of the spatial mean Nusselt number in the two-phase flow cases compared to the single-phase case. In addition, Fig. 16 illustrates the intensification of the influence of the overall Prandtl number on the thermal transfer rate in the case where the radius of the dispersed phase was larger. Therefore, the overall Prandtl number of the flow mixture and the bubble radius control the reduction of the thermal transfer rate in Fig. 16, since the tendency observed for the case with the bubble initial radius of 0.31L was more evident for the case where the initial bubble radius was 0.39L.

Table 10 presents the influence of the overall Prandtl number and the bubble radius on the thermal transfer rate using the spatial mean Nusselt number at the east wall.

Table 10 Summary of the thermal transfer rate results to compute the effects of varying the overall Prandtl number and the bubble radius
Full size table

Table 10 presents the effects of the overall Prandtl number of the flow mixture on the spatial mean Nusselt number calculated at the heated wall. As the overall Prandtl number of the flow mixture decreases, the mean Nusselt number decreases. In accordance with a similar simulation performed by Qiu et al. [8], it was found that the thermal transfer rate decreased as the bubble radius increased. The variation of the Nusselt number compared to the single-phase flow case presented in Table 10 goes against the generally accepted hypothesis that the Nusselt number increases with the introduction of bubbles in single-phase flows.

Based on the results from Dabiri and Tryggvason [5], the authors of the present paper believe in the intensification of the reduction of the Nusselt number presented in Table 10 if the distance between the walls and the dispersed phase is lower. Finally, this last section has provided several results refuting the argument generally seen in the literature that the introduction of bubbles necessarily increases the wall-to-fluid thermal transfer rate. Future research needs to be conducted in order to analyze new factors related to this topic, such as the influence of the bubble shape on the thermal transfer rates.

9 Conclusions

The research presented in this paper conducted a detailed qualitative and quantitative analysis of the influence of the bubble radius size and the overall Prandtl number on the wall-to-fluid thermal transfer rate in two-phase flow in a cubic cavity. According to the results obtained here, the overall Prandtl number and the bubble radius size contributed to changes in the Nusselt number in the classical problem of a differentially heated cavity.

The Prandtl number is found to be a crucial parameter for evaluating thermal transfer rates in two-phase flows in cavities since the overall Prandtl number of the mixture of fluids controlled the increase or decrease of the thermal transfer rate compared to the single-phase flows. In addition, the bubble radius size affected the pattern of bubble movement inside the cavity, which changed the proximity between the dispersed phase and the heated walls modyfying the local thermal transfer rate.

Finally, the presence of a dispersed phase did not in itself increase the wall-to-fluid thermal transfer as previously stated in the literature; however, the Prandtl number of the flow mixture affects the variations of the local and the mean thermal transfer rate.

The results obtained in the present paper may guide future works on more complex physical problems related to two-phase flows since it was restricted to the configuration of a cubic cavity and some physical assumptions were assumed, Finally, the authors of the present paper suggest future investigations on the effects of the Prandtl number combined with other flow characteristics, such as bouyancy, bubble shape or modelling multiples bubbles.