Wall Oscillation Induced Drag Reduction Zone in a Turbulent Boundary Layer

Abstract

Spanwise oscillation applied on the wall under a turbulent boundary layer flow is investigated using direct numerical simulation. The temporal wall-forcing produces a considerable drag reduction (DR) over the region where oscillation occurs. Three simulations with identical oscillation parameters have been performed at different Reynolds numbers with one of them replicating the experiment by Ricco and Wu (Exp. Therm. Fluid Sci. 29, 41–52, 2004). The downstream development of DR in the numerical simulation and experiment is nearly identical. The velocity profiles and the indicator function are investigated with respect to the variation in DR and Reynolds number. The DR affects the slope of the logarithmic part of the velocity profile in accordance with previous theoretical findings. Low speed streaks are visualized and the bending of longitudinal vortices related to the drag reduction phenomenon is discussed. In addition, the visualization is compared with the corresponding results from the experiments. The spatial transient of the DR before reaching its maximum value is analyzed and is found to vary linearly with the oscillation period. An analysis of the energy budget is presented and the fundamental differences compared to the streamwise homogeneous channel flow are elucidated. While the power budget improves with increasing Reynolds number, it is shown that the net power remains negative for the wall forcing parameters considered here, even under ideal conditions. On the other hand, the analysis together with channel and boundary layer flow data in the literature provides an estimation of net energy saving for boundary layer flows which depends on the streamwise extent of the oscillating zone.

1 Introduction

Turbulence is a flow phenomenon with many technological and engineering applications and the plethora of length and time scales which ranges from large planetary scales to smallest scales in the order of a micron make analyses challenging. Nevertheless, turbulence control with the objective of reducing skin friction drag has been a subject of intense research in recent times because of the implied energy and cost savings. Wall motion is one such technique which reduces the skin friction and has been investigated in the past [1] with differing degree of complicated control mechanisms. Also, in the past years, experiments and numerical studies have explored and demonstrated that a simple wall oscillation can significantly attenuate turbulence. However, even after years of research the exact mechanism for the phenomenon is still largely unknown. The aim of the present study is to provide the conceptual differences between the wall motion effects on the non-parallel boundary layer compared to the in the past often investigated streamwise homogeneous channel flow. In addition, comparison with experimental data, both statistical and instantaneous, is made.

Turbulent flow in a channel with wall oscillation was studied for the first time using direct numerical simulation (DNS) by Jung et al. [2]. Subsequently, Baron and Quadrio [3] reported the effect of the oscillations on the turbulent energy budget. DNS with oscillating walls of both channel and pipe flow were performed by Choi et al. [4] who also proposed a mechanism for drag reduction (DR). They provided a phenomenological explanation related to high speed fluid entering underneath the low-speed streaks and their effects on streamwise vortices to be the prime cause for DR. The transient behavior of the flow with first few cycles of wall oscillations were analyzed by Quadrio and Ricco [5] using DNS of channel flow. They observed that the analytical solution of second Stokes problem matched spanwise velocity profile from the simulation results. In another work by Quadrio and Ricco [6], only lower amplitudes of oscillation were shown to have net energy savings. Touber and Leschziner [7] focused on performing DNS with sub-optimal oscillation period in order to show the importance of phase-wise turbulence statistics. Yakano et al. [8] used conditional averaging to investigate the modification of quasi-streamwise vortices by wall oscillation and its relation to DR.

Various attempts to explain the DR phenomenon have been published in last ten years. Xu and Huang [9] offers an explanation of the DR via the Reynolds stress transport equations. Ricco and Quadrio [10] derived a Stokes layer based parameter, which formed a linear relation with the resulting DR. Ricco et al. [11] provided a plausible explanation of the DR from an analysis of enstrophy transport in a channel flow with the aid of DNS where they claim that enstrophy is increased due to the Stokes motion and this increase in both enstrophy and dissipation leads to drag reduction. Later, phase-wise statistics was utilized by Agostini et al. [12, 13] to modify the view of the dissipation and provided partially the explanation for the DR.

Laadhari et al. [14] confirmed that the DR technique also applied to the boundary layer flow. Subsequently, a lot of the experimental efforts have been focused on the turbulent boundary layer. Choi [15] conducted experiments to study the dynamics of the near wall structures. He described the bending of low speed streaks which was later confirmed by Ricco [16] who also reported the proportionality of the bending angle of the streaks and DR.

Spatial development of the DR was explored in the experimental work by Choi et al. [17] who reported a DR upstream of the start of oscillating portion of the wall. Also, Ricco and Wu [18] investigated the downstream development of the drag reduction but no upstream influence could be detected. In addition, the recent DNSs by Skote [19] and Yudhistira and Skote [20] of a boundary layer with similar oscillating parameters did not indicate any upstream influence.

Most of the previous DNS studies of drag reduced flows have focused on channel flow with the benefits of periodic boundary conditions which reduce the computational costs. However, less work has been done to explore the wall forcing effects on a turbulent boundary layer using numerical simulations. Note that the local drag reduction decreases downstream for a spatially growing boundary layer flow in contrast to the channel flow where drag reduction remains constant in both time and space after attaining an equilibrium value. The same numerical code used for the present investigation has previously been used for both temporal and spatial oscillations of the wall under a turbulent boundary layer [19,20,21,22,23,24]. In addition, Lardeau and Leschziner [25] reported their findings for boundary layer flows using DNS where they focused on the transition of the skin friction to a steady low-drag state and perform phase-averaged analysis of turbulent statistics. Skote [26] derived an expression which predicts the slope of the logarithmic part of the velocity profile, and it will be confirmed by the present DNS data.

The question of how the DR effects diminish with Reynolds number has been discussed both in the context of channel flow [27,28,29] and boundary layer flow [24]. In the present work, we expand the discussion by considering the total power budget.

A DNS simulation with same oscillation parameters (but lower Reynolds number) as in Ricco and Wu [18] was performed by Skote [19]. It confirmed that the resulting higher DR in DNS when compared with the experiments, is due to the lower Reynolds number in DNS. In the simulations presented here, the oscillation parameters remain identical. However, the Reynolds number is chosen to exactly match the one in the experiments [18]. Furthermore, three additional simulations at lower Reynolds numbers are presented while retaining the other parameters constant, in order to elucidate the dependency of the power saving on Reynolds number. Conclusions about the cost effectiveness drawn from previous channel (internal) flow investigation are refined in order to extend their applicability to boundary layer (external) flow. The objectives of the paper is to (the related sections are given in parenthesis):

• 1. Compare the DNS results with the experimental data [16, 18] (3.1, 3.2 3.3).

• 2. Confirm and expand on earlier reported results regarding the

  • (a) Velocity profile (3.2).

  • (b) Stokes layer (3.4).

  • (c) Streak length (3.3).

• 3. Investigate the initial transients in the drag reduced boundary layer (3.5).

• 4. Outline a method for predicting potential net energy saving in the controlled boundary layer flow (3.6).

The rest of the paper is organized as follows. In Section 2, the numerical scheme and simulation parameters are presented. The results are discussed in Section 3 which has been subdivided into five parts. In the first part Section 3.1, comparison with experiments [18] is made regarding the DR. Analysis of the velocity profile is conducted in Section 3.2 and verification of the theoretical findings by Skote [26] is made. In the third part Section 3.3, near wall structures are visualized for comparison between manipulated and reference (unmanipulated) flow. In addition, the instantaneous flow results are compared with experimental data from Ricco [16]. Analytical solutions for second Stokes problem are compared with the simulation results in Section 3.4, together with an investigation on how half-plane oscillations influence the theory. The initial spatial transients leading up to the point where the DR obtains its maximum value are investigated in Section 3.5. Feasibility with respect to net power savings are presented in Section 3.6 together with a discussion on the important differences between the analysis of the boundary layer flow as compared to streamwise homogeneous channel flow. Lastly, conclusions are mentioned in Section 4.

2 Numerical Method and Simulation Parameters

The same numerical code and grid resolution is used as in previous simulations of oscillating turbulent boundary layer performed by Yudhishtira and Skote [20] and Skote [19]. The numerical code used, SIMSON (A Pseudo-Spectral Solver for Incompressible Boundary Layer Flows) was originally developed at KTH, Stockholm [30].

2.1 Numerical scheme

A pseudo-spectral method with Fourier discretization in the streamwise and spanwise directions, and Chebyshev polynomials in the wall-normal direction has been used. The simulations are started with a laminar boundary layer at the inflow. A random volume force near the wall at the beginning of the computational domain is used to trigger the flow to transition.

At the end of the domain, a fringe region is added, to enable simulations of spatially developing flows. The flow in this region is forced from the outflow of the physical domain to the inflow. In this way the physical domain and the fringe region together satisfy periodic boundary conditions. The implementation is done by adding a volume force

$$ F_{i}=\lambda(x)(v_{i}-\widetilde{u}_{i}) $$

(1)

to the Navier-Stokes equations,

$$ \frac{\partial \widetilde{u}_{i}}{\partial t}+\widetilde{u}_{j}\frac{\partial \widetilde{u}_{i}}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial \widetilde{p}}{\partial x_{i}}+\nu\frac{\partial^{2}\widetilde{u}_{i}}{\partial {x_{j}^{2}}}+F_{i} $$

(2)

The force F_i applies to the fringe region only where λ(x) is the strength of the forcing and v_i is the laminar inflow velocity profile the solution $\widetilde {u}_{i}$ is forced to. Hence, v_i is the solution to the Blasius equation. The fringe function is required to have minimum upstream influence and is designed as

$$ \lambda(x)=\lambda_{max}f(x) $$

(3)

with

$$ f(x)= S\left( \frac{x-x_{fstart}}{{\Delta} x_{rise}}\right)-S\left( \frac{x-x_{fend}}{{\Delta} x_{fall}}+ 1\right). $$

(4)

Here λ_max is the maximum strength of the fringe, x_fstart and x_fend denotes the spatial extent of the region where the fringe is non-zero, Δx_rise and Δx_fall are the rise and fall distance of the fringe function respectively. S(η) is a continuous step function that varies from zero for η ≤ 0 to unity for η ≥ 1, and is given by,

$$\begin{array}{@{}rcl@{}} S(\eta)=\left\{\begin{array}{ll} 0, & \eta\leq0,\\ 1/(1+e^{(1/(\eta-1)+ 1/\eta)}), & 0<\eta<1,\\ 1, & \eta\geq1. \end{array}\right. \end{array} $$

(5)

The advantage of this expression is that S(η) has continuous derivatives of all orders. The function f(x) is also used in enforcing the wall oscillation boundary condition as described in Section 2.2 below.

The time integration is performed using a third-order Runge-Kutta-scheme for the non-linear terms and a second-order Crank-Nicolson method for the linear terms. A 3/2-rule is applied to remove aliasing errors from the evaluation of the non-linear terms when calculating FFTs in the wall parallel plane.

2.2 Numerical parameters

All quantities are non-dimensionalized by the free-stream velocity (U_∞) and the displacement thickness (δ^∗) at the starting position of the simulation (x = 0), where the flow is laminar. The Reynolds number is set by specifying $Re_{\delta ^{*}}=U_{\infty }\delta ^{*}/\nu$ at the laminar inlet (x = 0).

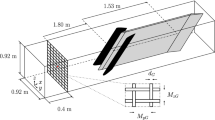
Wall oscillation is imposed at different locations to examine the influence of Re_Θ (Re_Θ = U_∞Θ/ν, Θ being the momentum thickness) on DR. Three different Re_Θ were tested at 375, 505 and 1400. These Re_Θ values refer to the Reynolds number at which the oscillation starts, and the notation $Re_{{\Theta }_{start}}$ will be used hereafter. The streamwise location at which the oscillation was introduced corresponds to x = 140 (case 1), x = 250 (case 2) and x = 939 (case 3). The third case has been setup to exactly replicate the conditions used by Ricco and Wu [18] in their water tunnel experiments. An additional simulation using an oscillation amplitude which varies downstream is denoted case 4. The simulation denoted as case 2 has been presented earlier by Skote [19]. Since cases 1, 2 and 4 are performed at a lower Re, the computational box is in these cases smaller. For case 3, a much longer box is used to accommodate the growth of Re before the oscillations commence. Note that it is not advisable to use a short computational box even if the zone of oscillations is limited. The reason being that a DNS which starts at a larger Reynolds number requires a long streamwise length to reach equilibrium [31].

Table 1 gives the different parameters chosen for the computational box and grid. The length of the computational box is given in simulation length units (${\delta }_{x = 0}^{*}$). Note that cases 1 and 2 do not include the recovery region downstream of the point where oscillations cease.

Table 1 Numerical parameters for the simulations presented

After an initial trip of the flow, the flow undergoes transition to fully turbulent flow. A section of this turbulent flow is then subjected to wall oscillations. Since the boundary layer grows downstream, the wall-normal extent of the computational box is increased by 250% for case 3 as compared with the other three simulations.

Due to the fringe region, the results from the last 150 simulation units for case 1 and case 2, and 400 units for case 3 have been discarded to ensure that there are no upstream effects. The transition region is between x = 5 and x = 100. Thus, the region of a fully developed turbulent boundary layer, free from any influence of the numerical method, is x = 100 − 480 for case 1, 2 and 4, and x = 100 − 2000 for case 3.

The implementation of the oscillating spanwise wall-velocity is identical to the one used by Skote [19]. The wall oscillation is applied in the spanwise direction in a particular streamwise region. Therefore, a profile function f(x), see Eq. 4, is utilized to define the domain where the oscillation occurs. The form of the wall velocity boundary condition is given by

$$ W|_{y = 0}=f(x)W_{m}\sin(\omega t) $$

(6)

where f(x) is the profile function discussed above, and W_m is the maximum wall velocity. The parameter ω is the angular frequency of the wall oscillation, which is related to the period through ω = 2π/T. For the purpose of defining the oscillation zone, the parameters x_fstart and x_fend are set to x_start and x_end, respectively, according to Table 2. The parameters Δx_rise and Δx_fall are set to 10 in all the simulations presented here. Furthermore, the gradual increase of the profile function prevents the spurious oscillations (Gibb’s phenomena) which might otherwise be introduced due to a discontinuous jump in the velocity around the starting point of wall forcing.

Table 2 Oscillation parameters for the simulations presented

The resolution used for the simulations are summarized in Table 1 as shown in + units. Note that unless otherwise stated, the + superscript indicates that the quantity is made non-dimensional with the friction velocity of the unmanipulated boundary layer (the reference case), denoted ${u}_{\tau }^{0}$, and the kinematic viscosity (ν). Note that ${u}_{\tau }^{0}$ varies with streamwise position and we choose to use the value at the starting position of the oscillations when calculating the resolution in wall-units.

The sampling time for the reference case was 16,800 in time units (${\delta }_{x = 0}^{*} /U_{\infty }$), and started only after a stationary flow (in the statistical sense) was reached. In the cases with wall forcing, the reference case was used as the initialized flow field and an additional 4000 time units was simulated before statistics was sampled during another 12,000 time units, corresponding to 180 periods of oscillation.

In all the simulations presented here, the angular frequency (ω) of the wall oscillation and the maximum wall velocity (W_m) is set such that they in wall units corresponds to T⁺ = 67 and ${W}_{m}^{+}= 11.3$ based on ${u}_{\tau }^{0}$ taken from the start of the oscillation. The values of the oscillation parameters and the $Re_{\delta ^{*}}$ at the laminar inlet (x = 0) are given in Table 2. Note that the value of ${W}_{m}^{+}$ and T⁺ changes with streamwise position because local u_τ varies whereas W_m and T are kept fixed.

3 Results

The results from the reference cases are compared with the data from Schlatter and Örlü [31] who performed extensive DNS of flow over flat plate and compared with several experiments, and can now be considered as the standard database for comparison of turbulent statistics. Figure 1 shows a comparison for the skin friction coefficient at different Re_Θ for the data from Ref. [31] (in circles) with our current DNS results. The broken black line is the result from cases 1 and 2, while the solid black line represents case 3. The results show good agreement with Schlatter and Örlü [31] and hence for comparison of drag reduction, where C_f which is a significant quantity, can be assumed to be matching well with other databases. Furthermore, the empirical expressions from Smits et al. [32] (the green line) and Nagib et al. [33] (the blue line) are given in the figure. Note that our cases 1 and 2 agrees well with the low Reynolds number profile [32] while our case 3 matches the high Reynolds number profile [33]. The reason for the deviating skin friction coefficients for cases 1 and 2 compared to case 3 is the higher Reynolds number at the inlet (see Table 2). The C_f from case 3 (the dotted red line) is added in the figure to illustrate the dramatic influence the wall oscillation has on the skin friction.

Fig. 1

Color online. Skin friction coefficient C_f from present DNS (reference cases in black): (−) case 3, (−−) cases 1 and 2; circles represent C_f from Ref. [31]; green (light grey) line is the low Reynolds number empirical profile [32], while the blue line (dark grey) is the high Reynolds number empirical profile [33]; dotted red line is the friction coefficient for case 3 with wall oscillation

3.1 Comparison of DR with experiments

This section discusses the comparison of results with experiments on temporal wall oscillations performed in water tunnel [18]. The oscillation parameters used in the experiment are T⁺ = 67, ${W}_{m}^{+}= 11.3$ at Re_Θ = 1400. Temporal oscillations were imposed on the wall for a region of 10δ in the streamwise direction where δ is the boundary layer thickness at the start of the oscillation. The present simulation (case 3) has been setup to exactly match the experiments by starting the wall oscillation at the streamwise location where Re_Θ = 1400 and for a region of 10δ which corresponds to x = 939 − 1165 where the wall boundary condition is modified from the no-slip boundary condition according to Eq. 6.

The data for the first 50 oscillations is discarded so as to reach stable drag reduction values. In order to verify the convergence, statistics where compared for two time windows t₁ and t₂, each consisting of 90 oscillations. Reynolds shear stress was compared for these two time windows which is the most sensitive statistical quantity [20] with respect to the total sampling time, and was found to have reached a stationary state. The data presented here has been averaged for time interval t₁ + t₂ equivalent to 180 oscillations.

The resulting drag reduction (DR) is calculated from

$$ \text{DR}(\%)= 100\frac{{C}_{f}^{0}-C_{f}}{{C}_{f}^{0}}, $$

(7)

where ${C}_{f}^{0}$ is the skin friction of the reference case. Variation of DR(%) in the streamwise direction is shown in Fig. 2 and is compared with experimental data provided by Ricco and Wu [18]. There is a strong response to wall oscillations introduced at x/δ = 0 in the first 1δ region. The experimental data exhibit a slightly more rapid increment of DR than the simulation results, which can be attributed to the slower response in the DNS due to the profile function when implementing the wall oscillation (as shown in Eq. 6). After the initial spike in DR values, the increase is gradual from 1δ to 3δ reaching an equilibrium value range from 23%–25% which until 10δ remains slightly higher (≈ 1%) than those reported from the experiment. Thereafter, the oscillation is stopped at 10δ and the DR decays with a response that matches the experimental values quite remarkably, and suggests the high fidelity of the current simulations. Note also that the measurement data after the oscillation has ceased are more accurate since they are more straight forwardly obtained there (Pierre Ricco, private communication). In addition, the present results also match a similar experiment by Trujillo et al. [34] as shown in Fig. 2 (filled squares).

Fig. 2

DR(%) as a function of streamwise coordinate for T⁺ = 67, ${W}_{m}^{+}= 11.3$, (−) present DNS results (case 3) as compared to experimental results from (o) from Ref. [18], ($\blacksquare$) from Ref. [34]. The three broken lines are representing case 1 (⋯), case 2 (−−) and case 4 (−⋅−)

Included in Fig. 2 are the resulting DR from case 1 and 2. Note that case 1 is covering a larger streamwise portion as the zone of oscillation is wider (see Table 2). The DR is clearly reduced with increasing Reynolds number. Further discussion around this will be offered in Section 3.6 below. The additional simulation with a varying amplitude (W_m(x)) in the streamwise direction (case 4) is also included although the results from this case will also be discussed in Section 3.6. Only the cases 3 and 4 include the recovery region after the end of the oscillation zone since the wall forcing ends close to the end of the computational box for cases 1 and two (see Table 2).

Note that the DR will not reach a constant value further downstream if the actuation zone was longer, which can be deduced from a longer simulation presented in [24, 35].

The decay of the DR after the oscillating zone ends is more rapid than the corresponding transients (the relatively slow increase of DR) at the start of the oscillations. In addition, after the oscillation has been stopped, weak drag increase (DI) is observed, but the precise shape of the downstream DI is not conclusive. The DR is calculated through the ratio between skin frictions (see Eq. 7) which are highly fluctuating quantities and the variations are enhanced when the ratio is calculated. Very small perturbation of the values may be amplified when calculating the DR according to Eq. 7. The DI for the two cases (3 and 4) for which the recovery region has been included is similar although the DR is much higher for case 4 compared to case 3 (due to the lower Reynolds number for the former).

As can be seen in Fig. 3, where the skin friction in the interval x/δ = 8 to 18 is presented for case 3, the two values are not very far apart once the oscillation is stopped. Thus, in order to obtain the complete detailed picture of the DR/DI development after the oscillation stops, the simulation would need to be continued for a very long time that present resources do not permit. On the other hand, the effect of the eventual DI is small and would not affect the energy budget (see Section 3.6) in any considerable way. The skin friction is shown as a function of the local Reynolds number in the lower panel of Fig. 4, and the two C_f curves are evidently more similar than when plotted versus x. Hence, the DI observed in the upper panel can to a large extent be explained by the altered state of the boundary layer (with a different Re_Θ), and is most probably also the cause for the DI observed in [25] and [36]. This is consistent with the conclusions by Stroh et al. [37] that the remaining effect downstream of the control region can be explained by a streamwise shift of the virtual origin of the turbulent boundary layer. Nevertheless, it could be interesting to compare these spatial transients with temporal transients in the channel flow geometry which would be a result of suddenly stopping the oscillations and then follow the time evolution of the skin friction when it is being restored to its original value.

Fig. 3

C_f as a function of x/δ (upper panel) and local Re_Θ (lower panel). Solid line is the reference case and broken line is case 3

Fig. 4

Color online. Comparison of mean velocity profile at a streamwise location of x/δ = 6.4 scaled with local u_τ. (−) Results from DNS for the reference case; (−−) Results from DNS for ${W}_{m}^{+}= 11.3$, T⁺ = 67; (∘) Results from experiments [18] for ${W}_{m}^{+}= 9$, T⁺ = 83. Black curves are representing case 3 while red (grey) color indicates case 2

3.2 Velocity profile

In the presentation of results in this section, the scaling is done using the local friction velocity u_τ (utilizing the data from each of the cases) at the streamwise location from which profiles are presented. Case 3 will be compared with the experimental data as the Reynolds numbers are identical for this case. In addition, comparison with the lower Reynolds number case 2 will be made.

Mean streamwise velocity profile at x/δ = 6.4 (broken black line) is compared with the experimental data (circles) in Fig. 4. This position was chosen by Ricco and Wu [18] to avoid any transitional effects, and the same location has been chosen here for the sake of comparison (Re_Θ is equal to 658 and 1537 for the reference case 2 and 3, respectively, at x/δ = 6.4). However, the experimental results are for a different set of parameters at ${W}_{m}^{+}= 9$, T⁺ = 83 which accounts for the differences since the DR is slightly lower for those parameters than for ${W}_{m}^{+}= 11.3$, T⁺ = 67, and consequently the local u_τ is larger, hence making the profile of u⁺ from the experiments be lower than the DNS.

When comparing with the reference case (solid lines), it can be seen in Fig. 4 that the log layer shifts in the wall-normal direction which indicates the upward shift of turbulent fluctuations from the near wall region resulting in a diminished skin friction coefficient. The log layer from experiments falls on top of the present DNS results.

For case 2 (the red profiles) very similar effect of the DR can be observed as for case 3, although the effect is slightly stronger due to the larger DR for case 2. Note that the difference in the profiles from the reference case (black and red solid lines) is due to the variation in Reynolds number between case 2 and 3.

In order to investigate the effect of the DR on the velocity profile in more detail, the indicator function,

$$ \sigma=y^{+} \mathrm{d} u^{+}/\mathrm{d} y^{+}, $$

(8)

is computed and illustrated for case 2 and 3 in Fig. 5. The two solid lines (red for case 2 and black for case 3) are the indicator function for the reference case. The local minimum of σ indicates the slope of the logarithmic layer and is observed to be 1/0.40 and 1/0.43 for case 2 and 3, respectively. These values are indicated by the thin horizontal lines in the figure. Hence, a small variation with Reynolds number is detected as can be expected at these low Reynolds number flows. Note that the decreasing value of the slope for the reference flow with Reynolds number agree with previous high-Reynolds number LES [38]. The constant value of 1/0.384 which is obtained for very high Reynolds number (experimentally) is occurring in the plateau value at a slightly higher position in the boundary layer (see [33]).

Fig. 5

Color online. Indicator function (σ) for case 2 (red (grey) curves) and case 3 (black curves). Solid lines are for the reference case while the DR cases are illustrated with dashed lines. The thin solid horizontal lines are indicating the minimum of σ and correspond to 1/κ for the reference cases (at different Reynolds numbers). The thin dashed horizontal lines are the values calculated from 1/κr with κ taken from the minimum of σ from the reference case while r is calculated from the DR. The values calculated (the dashed lines) coincide with the minimum of σ for case 2 and 3

On the other hand, the minimum of σ has increased for the DR flows, see the dashed lines in Fig. 5. Skote [26] derived theoretically that the slope is changing from the original value (1/κ) to 1/κr where

$$ r=\frac{u_{\tau}}{{u}_{\tau}^{0}}=\sqrt{C_{f} / {C}_{f}^{0}}. $$

(9)

The values of 1/κr (calculated as 1/0.34 and 1/0.37, for case 2 and 3, respectively) are plotted as the thin dashed lines in Fig. 5 and are coinciding with the minimum of the indicator function. Thus, the theoretical expression derived by Skote [26] is confirmed with the present data.

The change in the slope of the log-layer is absent in channel flow (if the temporal transients have been given time to vanish), while the effects would disappear after a sufficiently long zone of wall oscillations in the boundary layer case.

More turbulence statistics in the form of comparison of Reynolds stresses between the DNS and experiments can be found in Ref. [39].

3.3 Streak visualization

The bending of low speed streaks which was first reported by Choi [15] was studied extensively by Ricco [16] for turbulent boundary layer flows using experiments. Bandyopadhyay [40] proposed a drag reduction mechanism based on the reorientation of vorticity and correlated it to Stokes second problem. Recently, Touber and Leschziner [7] presented a detailed analysis of streak modification in a channel flow and reported periodic streak reorientation in the near wall region based on the phase of the oscillation. Figure 6 shows the results from the visualization experiments [16] on a boundary layer flow in the streamwise-spanwise (x − z) plane, where the flow was visualized by hydrogen bubbles generated by hydrolysis of water obtained by means of an energized platinum wire at y⁺ = 5. Low speed streaks were recognized by identifiable single longitudinal bubble structures. As can be seen in Fig. 6a, the low speed streaks (the stretched bubble) remain stable for some distance and then burst. Figure 6b shows that these streaks are still present once the oscillation is applied. Furthermore, the streaks are tilting cyclically in the region where oscillation takes place. A similar visualization was done based on the present DNS results (case 3) and are shown in Fig. 6c, d, e, f. The quantity shown is the streamwise velocity fluctuations in a plane located at approximately y⁺ = 10. For the unoscillating section of the flow, the low speed streaks are clearly visible as seen in Fig. 6c and maintain the typical spanwise spacing of 100 wall units.

Fig. 6

For all the above figures, flow is from left to right a Low speed streak visualization for unoscillated flat plate by Ricco [16], b Inclination of low speed streak on applying wall oscillation [16], c Low speed streaks (darker regions) from present DNS results for the unoscillated flat plate, d Wall oscillation which begins from the solid line shows the bending of low speed streaks, e Within the zone of oscillation the streaks remain inclined throughout, f Solid line denotes the end of wall oscillation after which the streaks again align themselves to the streamwise direction. Figures a and b reprinted from Modification of near-wall turbulence due to spanwise wall oscillations, Pierre Ricco, Journal of Turbulence, 1 July 2004, by permission of Taylor & Francis Ltd, http://www.tandf.co.uk/journals

After the oscillation for the wall is introduced, the streaky structures can be identified as shown in Fig. 6d and their characteristic bending within the region of oscillation is illustrated in Fig. 6e. The inclination of the streaks is similar throughout the zone of oscillation (for a particular time instance). Once the oscillation is stopped (Fig. 6f), the streak orientation reverts to being streamwise. It is worthwhile to note that the flow shows a fast response by streak reorientation both at the beginning and the end of the oscillating segment.

The angle of inclination of streaks (ϕ) is a consequence of the two competing external velocities acting on the boundary layer. While the freestream tries to convect the low speed streaks in the streamwise direction, there is at the same time a spanwise component of velocity due to the wall oscillation. A vector addition of the two velocity components leads to the bending of streaks. By utilizing the Stokes solution for the second problem, the maximum deflection angle of streak with respect to streamwise direction can be calculated [16] as,

$$ \phi = \tan^{-1}\left( \frac{{W}_{m}^{+}\exp \left( -y^{+}\sqrt{\pi/T^{+}}\right)}{U_{\infty}^{+}}\right) $$

(10)

Ricco [16] mentioned that DR is proportional to ϕ. For DR ∼ 25%, he reported a ϕ = 27^∘ while for the present DNS data we obtain ϕ = 25^∘. In addition, from Fig. 6c and e, one can observe that the relative spacing between the streaks has increased. This increased spacing was also observed by Ricco [16] for DR values higher than 25%. Furthermore, from these figures one may observe the reduced lengths of the streaks. From the DNS we estimate that the streak length is around 240 while Ricco [16] reported a higher value of 340 for the case with a DR of 25%. However, that experiment was conducted with T⁺ = 167, while another experiment using T⁺ = 67.5 (with a DR of 38%) yielded a streak length of 240, which is similar to the present DNS result at T⁺ = 67. Hence, we speculate that the length may be proportional to the oscillating period and not to the amount of DR.

3.4 Instantaneous spanwise velocity profile

Laminar flow produced by an oscillating wall allows an analytical solution [41] (Stokes second problem) which yields the boundary layer profile:

$$ W(y,t)=W_{m} \exp(-\eta)\sin(\omega t - \eta) $$

(11)

where $\eta =y \sqrt {\omega /2\nu }$.

The profile Eq. 11 is not an exact expression of W in this case, since the spatially developing boundary layer has been approximated with a parallel flow (hence, the normal velocity is zero and W is independent of x in the spanwise momentum equation). Furthermore, the Stokes solution does not take into account the spatial transient of the velocity profile after the introduction of wall oscillation, or in other words, the classical Stokes solution is independent of the streamwise location. An analytical solution for the spatially developing flow with half-plane motion has been derived by Zeng and Weinbaum [42]. This solution is valid for a case where one part of the plate is stationary and the other oscillating, and is hence a good representation of the present simulation set-up. Consequently, the profiles are given as a function of the streamwise coordinate, capturing the spatial transients involved. However, this transient is limited to a very small region of less than one grid point spacing. Hence, when comparing simulation data and theory, the spatial transient may be neglected. In addition, note that the exact laminar solution would need to take the non-parallel effect into account, which was done by Hicks and Ricco[43] who studied the oscillating wall beneath the Blasius boundary layer. Hence, the exact solution in the present case would be a combination of the solutions provided by Zeng & Weinbaum and Hicks & Ricco.

Comparison of DNS profiles from case 3 match reasonably well with the classical Stokes solution as shown in Fig. 7. The instantaneous DNS profiles have been taken after a sufficiently long time (after ∼ 180 oscillation cycles) at four different instants when the wall velocity is at its maximum, minimum and zero value. The profiles are shown for streamwise location where there are no spatial gradients present (x = 1100). Note that the profiles have been averaged only in the spanwise direction. The close agreement between DNS data and the profile Eq. 11 confirms previous findings in [19]. For channel [4, 5] and pipe [44, 45] flows, similar agreement between the laminar Stokes layer and instantaneous velocity profiles has been observed.

Fig. 7

(—) Stokes solution Eq. 11 and (−⋅−) DNS results for case 3. The four set of curves are at time instants with maximum, minimum and zero wall velocity

3.5 The initial transients

The temporal and spatial transients before the flow is fully adjusted to the imposed wall oscillation were investigated by Skote [19] who found a strong correlation between the two. In this section the initial transient before the maximum of DR (DR_max) has been reached is investigated. The coloured symbols in Fig. 8 are from data sets with similar oscillation parameters but different Reynolds numbers. The circles represent the present data from the present case 1 (green), case 2 (blue) and case 3 (red). The fourth symbol (diamond) in cyan is data for a case with ${W}_{m}^{+}= 10.7$ and T⁺ = 76.4 from Ref. [24]. An approximate logarithmic dependence on the Reynolds number can be observed. Here we measure the distance between the start of oscillations to the position of DR_max as the difference in Re_Θ of the uncontrolled boundary layer at the two positions, denoted ΔRe_Θ.

Fig. 8

Color online. The distance between start of oscillations to the position of DR_max. Circles (○) in green (light grey) for case 1, blue (dark grey) for case 2, and red (grey) for case 3. The cyan coloured $\lozenge$ is data from [24]. The black symbols are data from cases with T⁺ = 132 with W⁺ = 17 ($\square$) from [20], W⁺ = 12 (×) from [19] and W⁺ = 6 (▽) from [19]

However, when previous data from identical Re_Θ = 505 and T⁺ = 132, but with very different values of ${W}_{m}^{+}$ and hence DR, are included (black symbols in Fig. 8), similar ΔRe_Θ are obtained, indicating that the amount of DR does not influence the transient length. The DR for the case represented by the black $\square$, × and ▽ is 37.0%, 29% and 19%, respectively. However, the result from the present data set at T⁺ = 67 (case 2) exhibits a much shorter ΔRe_Θ as compared with the others at T⁺ = 132, at identical Re_Θ = 505. In order to show that it is indeed the oscillation period that determines the transient (at identical Reynolds number), two more simulation were performed at Re_Θ = 505 with T⁺ = 30 and T⁺ = 176. In Fig. 9 all the cases at this Reynolds number are shown. The original simulation (case 2) is the blue circle while the additional ones at T⁺ = 30 and T⁺ = 176 are shown in green and red colour, respectively. The black symbols are the previous data at T⁺ = 132. Instead of ΔRe_Θ, the distance in plus units, denoted Δx⁺, is used. A linear expression reading,

$$ {\Delta} x^{+}= 1877 + 8.05 T^{+} $$

(12)

or, equivalently,

$$ {\Delta} Re_{{\Theta}}= 92 + 0.423 T $$

(13)

can be made fit the data.

Fig. 9

Color online. The distance between start of oscillations to the position of DR_max. Circles (○) in blue is the present case 2, while green represents T⁺ = 30, and red T⁺ = 176. The black symbols are the same as in Fig. 8

Thus, neither the magnitude of the forcing nor the resulting DR influence the distance from the starting point to the location of DR_max. Instead, this distance ΔRe_Θ is predicted by the period of the forcing only.

3.6 Energy budget

To compute the net energy savings, we need to take into account both the energy required for wall oscillation and compare to the savings due to DR. The derivation of these terms was given for channel flow by Quadrio and Ricco [6] which was extended to the boundary layer case by Skote [19]. Note that the exercise of going through the energy budget is not to explore the present DNS cases and hope to achieve a net energy saving, but rather to develop a methodology whereby more readily obtained channel data can be used to draw conclusions about the possible energy saving in the boundary layer flow, especially for lower forcing amplitudes.

In order to compute the saved power P_sav(%), DR (as percentage of ratio of skin-friction coefficients from reference and oscillated cases based on Eq. 7) is integrated for a region with approximately constant value of DR. The total saved power can be written as,

$$ P_{sav}(\%)=\frac{1}{L}{\int}_{\!\!\!\!x_{i}}^{x_{f}}DR(\%)\mathrm{d}x $$

(14)

where x_i denotes the position at which the initial transients disappear (which is slightly downstream of where the maximum DR occurs), x_f denotes a point slightly upstream of the endpoint for the oscillation, and $L=x_{f}-x_{i}$. The positions x_i and x_f for the three cases are shown in Table 3. In the table, the saved power P_sav(%) from expression Eq. 14 is given, and the reduction is very mild between cases 1 and 2, while case 3 exhibits a considerable lower value. In order to understand this, the local power saving given by

$$ {P}_{sav}^{loc}(\%)= 100\left( 1-\frac{C_{f}}{{C}_{f}^{0}}\right) = DR(\%) $$

(15)

is plotted in Fig. 10. The circles denote the total saved power P_sav(%) while the lines represent the local saved power according to expression Eq. 15. Thus, the reason for the similar P_sav(%) in cases 1 and 2, despite different $Re_{{\Theta }_{start}}$, is the longer zone of oscillation in the low Reynolds number case 1. The DR (and hence ${P}_{sav}^{loc}(\%)$) is decreasing rapidly downstream and lowers the total power saved P_sav(%). In Fig. 10, the DR is plotted only for the range x_i to x_f which correspond to the Reynolds numbers ${Re_{\Theta }}_{i}$ and ${Re_{\Theta }}_{f}$, given in Table 3.

Table 3 Power budget for cases 1–3

Fig. 10

Color online. The local power saving ${P}_{sav}^{loc}(\%)$ in green (light grey) for case 1, blue (dark grey) for case 2, red (grey) for case 3. The straight line in cyan represents ${Re}_{{\Theta }}^{-0.153}$. The circles (○) represent P_sav(%) from Eq. 14. The cross (×) is channel flow data from Ref. [6]

In addition, the maximum DR (DR_max) as a function of Re_Θ was concluded to follow the expression

$$ DR_{max} = A/Re_{{\Theta}} + B $$

(16)

where A = 2884 and B = 23.44, in Ref. [24]. However, an equally good expression can be found by letting

$$ DR_{max} = C {Re}_{{\Theta}}^{\gamma} $$

(17)

with C = 79.5 and γ = − 0.153, which is represented by the solid straight line (cyan) in Fig. 10. Here, Re_Θ is the local Reynolds number at the position where the maximum DR occurs (i.e. after the initial spatial transients). The expression Eq. 17 is in line with the channel flow (for which DR_max uniquely specifies the DR) investigations by Ricco and Quadrio [10], Touber and Leschziner [7] and Hurst et al. [29].

Compared with the DR_max trend (cyan in Fig. 10), the local DR is rapidly decreasing downstream, hence making the value of DR_max a poor indicator of the possible energy saving. On the other hand, the development of DR_max, which is similar to the channel flow although the DR is slightly larger in that case, can be used as an upper bound for the possible energy saving. Also included in Fig. 10 is the channel flow data (DR = 31.2) from Quadrio and Ricco [6] with identical oscillation parameters at Reynolds number Re_τ = 200. Converting the Reynolds number according to the relation provided by Eitel-Amor et al. [38],

$$ Re_{\tau} = 0.596 {Re}_{{\Theta}}^{0.923} $$

(18)

yields a corresponding Re_Θ = 545. Hence, the DR is larger for the channel flow, which confirms the conclusion drawn by Lardeau and Leschziner [25], while the DR of the boundary layer is further affected negatively by the spatial development downstream. In addition, the degradation of the local DR is more severe for case 3 for which $Re_{{\Theta }_{start}}$ is larger. Observing that the DR profiles are linear in Fig. 10 we can calculate the exponent α in $DR \sim {Re}_{{\Theta }}^{\alpha }$ to be − 0.512, − 0.584 and − 1.72 for case 1, 2 and 3, respectively. The rapid decrease of ${P}_{sav}^{loc}(\%)$ in Fig. 10 may be due to long persistent spatial transients despite that the initial transients (see Fig. 2) are excluded. On the other hand, the spatial transients can be persistent and cover a larger extent in the streamwise extension as was demonstrated in Ref. [24, 35]. A complete study of this requires very long computational boxes and is outside the scope of the present investigation. In addition, for practical applications the zone of oscillation may not be long since shorter segments may be easier to implement, hence making the spatial transients as illustrated in Fig. 10 very important for the energy saving assessment.

Similarly, the wall oscillation requires power input which can also be defined in terms of the friction power of the reference flow [19] and can be written as:

$$ P_{req}(\%)= 100\frac{{W}_{m}^{2}}{2} \sqrt{\nu \omega / 2}\left/ \frac{U_{\infty}}{L} {\int}_{\!\!\!\!x_{i}}^{x_{f}} \left( {u}_{\tau}^{0}\right)^{2} \mathrm{d}x. \right. $$

(19)

The values calculated are given in Table 3 with the cost decreasing as the Re is increasing. However, the local required power, given as,

$$ {P}_{req}^{loc}(\%)= 100\frac{{W}_{m}^{2}}{2} \sqrt{\nu \omega / 2}\left/ \frac{{U}_{\infty}^{3}}{2} {C}_{f}^{0}, \right. $$

(20)

and plotted in Fig. 11, is increasing with Re. By noting that ${C}_{f}^{0} \sim {Re}_{{\Theta }}^{-0.25}$ from e.g. the empirical expression by Smits et al. [32],

$$ {C}^{0}_{f}= 0.024 {Re}_{{\Theta}}^{-1/4}, $$

(21)

it can be concluded that ${P}_{req}^{loc} \sim {Re}_{{\Theta }}^{0.25}$. The local required power according to Eq. 20 is plotted for x_i to x_f as the solid lines in Fig. 11 with the same color coding as in Fig. 10. The ${P}_{req}^{loc}$ is increasing with the local Re_Θ. The total required power according to Eq. 19 is indicated by the circles placed in the middle of the interval (x_i to x_f). The values (also given in Table 3) are decreasing with $Re_{{\Theta }_{start}}$. Note that the values of P_req(%) depends on both the initial transient (determining x_i) and the length of the zone of oscillation (determining x_f).

Fig. 11

Color online. The local power required (${P}_{req}^{loc}$) in the same color coding as in Fig. 10. Solid lines represent the true required power from expression (20). Broken lines illustrate the corresponding expression (22) for streamwise homogeneous channel flow. The straight line in cyan represents ${Re}_{{\Theta }}^{-0.125}$. The horizontal line (magenta) is DNS data for a case with varying W_m (case 4) compared with expression (26) indicated by the circle

The net saved power is then defined as P_net = P_sav − P_req and is given in Table 3. If P_net is negative it indicates that the input power required to oscillate the wall is greater than the saved power due to streamwise DR.

One important observation from these results is that the net energy saving is increasing with Re_Θ while keeping the amplitude of oscillation ${W}_{m}^{+}$ and T⁺ constant. Note that this trend, however, does not necessarily mean that positive net energy saving is possible at higher Re_Θ as will be explained in the following.

We already have an estimate of the upper bound for the energy saving in the form of expression Eq. 17 which is related to the corresponding channel flow expression. In order to get an upper bound of the net energy saving, a similar lower bound for the required energy is needed. Again, we can obtain this by using the corresponding channel flow expression.

First, we convert the expression Eq. 20 to:

$$ {P}_{req}^{cha}(\%)= 100\frac{({W}_{m}^{+})^{2}}{2} \sqrt{\frac{\pi}{2T^{+}}} \sqrt{{C}_{f}^{0}}, $$

(22)

by letting u_τ be constant, which is only valid for a streamwise homogeneous flow such as a channel geometry [10, 46]. Expression (22) yields that ${P}_{req}^{cha} \sim {Re}_{{\Theta }}^{-0.125}$ when utilizing Eq. 21, which is illustrated by the solid line (cyan) in Fig. 11. Formula (22) would be valid for the boundary layer case if ${W}_{m}^{+}$ and T⁺ were constant over the oscillating zone. Note that we can compare with channel flow by utilizing Eq. 18 which yields ${P}_{req}^{cha} \sim {Re}_{\tau }^{-0.135}$. The value of the exponent − 0.135 is very close to the value − 0.136 obtained by Ricco and Quadrio [10].

The values ${W}_{m}^{+}= 11.3$ and T⁺ = 67 in expression Eq. 22 result in the broken lines in Fig. 11, and follows the line given by ${P}_{req}^{cha} \sim {Re}_{{\Theta }}^{-0.125}$ closely. This is merely a reflection of that the Eq. 21 is a good representation of the skin friction. Hence, for a channel flow the local and total required power follow the same trend (${Re}_{{\Theta }}^{-0.125}$ or ${Re}_{\tau }^{-0.135}$). However, the values of ${W}_{m}^{+}$ and T⁺ are not constant in the boundary layer and the total required power is given by expression Eq. 19 while the local required power follows ${Re}_{{\Theta }}^{0.25}$ as shown above. Expression Eq. 22 constitutes the theoretical minimum value of the required power for the oscillating wall in the boundary layer flow. However, the power spent is much larger as can be observed when comparing the solid and dashed curves in Fig. 10, due to the non-constant ${W}_{m}^{+}$ and T⁺. That the solid and broken lines start at different values is due to that the initial transients are being excluded (i.e. x_i is being used, not x_start) for consistency with the energy saving analysis.

Comparing with the channel flow data from from Quadrio and Ricco [6], who reported P_req = 87.5 with identical oscillation parameters and Re_Θ = 545, we note that the required power is less severe for the boundary layer. However, the required power is completely determined by ${C}_{f}^{0}$ (when considering identical oscillation parameters, see Eq. 22), hence the difference in P_req is attributed to a larger skin friction (at identical Reynolds numbers) for the channel flow compared to the boundary layer flow. In fact, inserting the value of ${C}_{f}^{0}= 7.93 \cdot 10^{-3}$ (taken from Ref. [6] in Eq. 22 yields P_req = 87.1, close to the reported 87.5. By utilizing the empirical relation from Pope [47],

$$ {C}_{f}^{0} \text{(channel)}= 0.0336 {Re}_{\tau}^{-0.273}, $$

(23)

together with the formulas Eqs. 18 and 21, we can write:

$$ \frac{{C}_{f}^{0} \text{(channel)}}{{C}_{f}^{0} \text{(b.l.)}}= 1.61 {Re}_{{\Theta}}^{-0.002} \approx 1.61. $$

(24)

Hence, the required power is $\sqrt {1.61}$ larger for the channel compared to boundary layer flow at identical Reynolds numbers.

In order to provide an estimate of the maximum possible (upper bound) net energy saving, we make the assumption that both the initial and the more persistent spatial transients can be prevented when considering the power saving. At the same time we observe that the minimum required power follow the streamwise homogeneous flow expression Eq. 22.

Hence, under ideal conditions, the net power saving is:

$$ {P}_{net}^{opt}(\%)=C {Re}_{{\Theta}}^{-0.153} - D {Re}_{{\Theta}}^{-0.125}, $$

(25)

where C = 79.5 is from Eq. 17 and D = 151.4 can be calculated from Eqs. 21 and 22. The expression Eq. 25 is plotted in Fig. 12 as the solid line and it slowly increases with Reynolds number. However, for the boundary layer cases considered here, the required power is much larger (due to constant W_m with varying ${W}_{m}^{+}$), while the power saving is less (due to persistent spatial transients) than for the ideal conditions, and are plotted in Fig. 12 as crosses. Since we are considering the flow as streamwise homogeneous and without spatial transients, ${P}_{net}^{opt}(\%)$ is presented versus $Re_{{\Theta }_{start}}$. For consistency we also plot (but choosing $-{P}_{net}^{opt}(\%)$ instead) in log-scale, see the inset in Fig. 12. Note that it is easy to draw the erroneous conclusion that Eq. 25 predicts decreasing net power saving (since the first term has a larger negative exponent than the second term). However, the decreasing behavior of Eq. 25 is confined to very small values of $Re_{{\Theta }} \sim \mathcal {O} (10^{-6})$. Hence, although the values of P_net increase with Reynolds number, the values will not become positive as shown by the theoretical estimate of the maximum possible yield Eq. 25.

Fig. 12

The net power saving for case 1, 2 and 3 (crosses) compared to the net power saving as given by Eq. 25 as the solid line

Furthermore, if ${W}_{m}^{+}$ is a constant, the expression Eq. 20 yields a constant:

$$ {P}_{req}^{loc}(\%)= 100\frac{({W}_{m}^{+})^{2}}{U_{\infty}} \sqrt{\nu \omega / 8}. $$

(26)

In order to verify this, the additional DNS (case 4) was performed with the same numerical parameter as case 1 (except that x_end was set to 390), with a varying oscillation amplitude such that ${W}_{m}^{+}= 11.3$ remains constant for all x. The DNS data evaluated with Eq. 20 is given by the horizontal line (magenta) in Fig. 11, while the value offered by Eq. 26 is indicated by the circle (positioned arbitrarily in the middle of the interval in x). Hence the DNS data confirm our findings. Note that only ${W}_{m}^{+}$ is kept constant in order to get a constant ${P}_{req}^{loc}$. If also T is adjusted downstream such that T⁺ is constant the resulting ${P}_{req}^{loc}$ would be parallel to the channel flow expression Eq. 22, i.e. the cyan line in Fig. 11. In Fig. 2 the DR for this case is shown to be lower than for case 1 which is explained by the decreasing W_m downstream. Hence, the penalty for keeping ${P}_{req}^{loc}$ constant is a lower ${P}_{sav}^{loc}$.

From a practical point of view, W_m will remain constant in an implementation and it is hence important to take into account that the total power spent will depend on the locally increasing ($\sim {Re}_{{\Theta }}^{0.25}$) power (and thus the extent of the oscillating zone) when estimating the net power budget.

We conclude this section by noting that although the net energy budget remains negative for the present oscillation parameters, the net power saving can be positive for smaller oscillation amplitudes. In Fig. 13 the DR from channel flow DNS [6] is plotted as a function of the forcing amplitude, together with the older boundary layer cases [19, 20] and the present case 2, all performed at roughly the same Reynolds number (Re_Θ = 545 and 505 for the channel and boundary layer, respectively). Note that the maximum DR is shown for the boundary layer cases and that DR_max can be interpreted as ${P}_{sav}^{loc}(Re_{{\Theta }}=Re_{{\Theta }_{start}}+{\Delta } Re_{{\Theta }})$. The channel flow data can be utilized to predict DR_max for the boundary layer although the values for the channel are consistently slightly higher as noted above. Furthermore, the influence of the oscillation period is not very prominent for these cases as the two channel flow data sets are from DNS with both T⁺ = 100 and T⁺ = 125, while the boundary layer data are from DNS with T⁺ = 67 (the present case 2) and T⁺ = 132 (the black symbols in Fig. 13).

Fig. 13

Color online. The DR from channel flow DNS [6] for T⁺ = 100 (green $\lozenge$) and T⁺ = 125 (red △). The blue (○) represents the present boundary layer case 2 at T⁺ = 67. The black symbols are data from boundary layer cases with T⁺ = 132 with W⁺ = 17 ($\square$) from [20], $W^{+}= 12$ (×) from [19] and W⁺ = 6 (▽) from [19]. The solid line is ${P}_{req}^{loc}$ at $Re_{{\Theta }}=Re_{{\Theta }_{start}}+{\Delta } Re_{{\Theta }}$. The inset shows total net power for the boundary layer case at W⁺ = 6 as a function of ${Re_{\Theta }}_{e}$

In addition, the local required power for the boundary layer at $Re_{{\Theta }}=Re_{{\Theta }_{start}}+{\Delta } Re_{{\Theta }}$ is plotted as the solid line. As evident from Fig. 13, a positive net energy budget can be obtained for ${W}_{m}^{+}<8$ with an optimum around ${W}_{m}^{+}= 5$ or 6. According to the analysis above,

$$ {P}_{net}^{loc}={P}_{sav}^{loc}-{P}_{req}^{loc}=\mathcal{P}_{s} {Re}_{{\Theta}}^{\alpha}-\mathcal{P}_{r} Re^{0.25}_{{\Theta}} $$

(27)

where $\mathcal {P}_{s}$ and $\mathcal {P}_{r}$ are constants calculated from the relations above. Utilizing the data from [19] the exponent α can be obtained as − 0.98. In the inset of Fig. 13 the total net power is shown which is obtained by integrating ${P}_{net}^{loc}$ between Re_Θs and Re_Θe where ${Re_{\Theta }}_{s}=Re_{{\Theta }_{start}}+{\Delta } Re_{{\Theta }}$ and Re_Θe is the endpoint of the oscillating zone. The total gain becomes zero when Re_Θe ≈ 900. The simulation in [19] was performed with Re_Θe = 724 giving a net power saving of 2.8%.

Hence, although positive net energy saving can be obtained in channel flow, the energy saving for the boundary layer case will suffer from rapidly degrading performance with larger zone length. However, this drawback may be alleviated by using shorter segments of oscillating zones, as was done in [21].

4 Conclusions

Direct numerical simulations have been performed to study the effect of wall oscillation on the turbulent boundary layer at different Re for same wall velocity and frequency (in wall units). The resulting DR and its variation in the streamwise direction is in excellent agreement with findings from experiments conducted by Ricco and Wu [18]. Mean velocity profiles exhibit the shifting of log layer away from the wall and the slope is altered by the DR in agreement with the theoretical findings by Skote [26].

Streaks are visualized and their bending as a result of the oscillating wall is demonstrated and compared with the visualizations by bubbles in the experiment by Ricco [16]. In addition, other characteristics such as increased streak spacing is observed when oscillations are applied. While the streak tilting angle is directly proportional to the amount of drag reduction, we speculate that the length of the streak is related to the period of the wall forcing. The instantaneous spanwise velocity profiles are compared with the analytical profiles and it is concluded that the non-homogeneity in the streamwise direction due to the finite size of the oscillatory zone has very little influence on the profiles.

When investigating the initial spatial transients before the DR reaches its maximum, a linear variation with the oscillation period was detected.

The local power saving is decreasing rapidly downstream due to the sharp decline in the local drag reduction (because of persistent spatial transients). At the same time, the local required power for the forcing increases rapidly due to that the oscillation amplitude is kept constant downstream. These two effects combined renders the net power saving less favorable than an ideal case with no spatial transients and homogeneous streamwise flow. Although the net power saving is increasing with Reynolds number, a comparison with the ideal case clarifies that a positive saving will not be materialized with the oscillation parameters considered here. By revisiting a simulation with smaller oscillation amplitude for which a positive net energy saving was obtained, the influence of the length of the oscillation zone was shown to have a negative impact on the performance. Hence, shorter segments at an optimal spacing will be preferable in a practical implementation.