1 Introduction

The human phonation is highly interesting phenomenon under ongoing research, see e.g. [1]. Despite substantial advances in latest years the human phonation process has not been fully understood yet. A better understanding can help e.g. to improve treatment of people with voice disorders or to design suitable vocal exercises for singers and other voice professionals. The economic losses connected with the voice malfunction only in USA are estimated up to $160 billions per year, see [2].

There are a lot of works studying the process of human phonation. It is important to understand the basic principles of voice production for the medical reasons. Due to the practical inaccessibility of the vocal folds recently the mathematical modeling and numerical simulations have become to be an important tool used in the research, see e.g. [3].

The voiced sound is created in the glottis - the narrow airway between the two vibrating vocal folds, whose vibration is induced by the flowing air. The human phonation is a multi-physical complex problem, which consists of three different physical fields — the deformation of the vocal folds (elastic body), the complex fluid flow and the acoustics together with mutual couplings. This problem is usually called the fluid-structure-acoustic interaction (FSAI) see e.g. [4].

Particularly the FSAI includes the interaction of the flowing fluid with the elastic structure and consequently the changes of the fluid domain have to be treated, see e.g. [5]. The air flow through the vocal tract is characterized by small Mach numbers and therefore it can be modeled as incompressible fluid. Nevertheless, the involved velocities are still high enough to obtain quite complex possibly turbulent flow structures particularly nearby the glottis. This results in high computational demand namely for 3D numerical approximations, see e.g. [6].

That is why in many cases the flow model is either simplified or the coupling of the flow problem to the motion of the vocal fold is omitted. This means for instance that the flowing fluid/air is considered in a rigid geometry as in [6] or on the computational domain surrounding harmonically vibrating vocal folds, see e.g. [7] or more recently [8], where 3D simulations were performed and the acoustic signal was analyzed.

The numerical solution of the 2D Navier-Stokes equations coupled with the structure motion has been used e.g. in [9], where the finite volume approximations were coupled with a two-mass dynamic model of the vocal fold. Similar approach was also used later in [10]. The full fluid-structure interaction problem was approximated by the coupled FE models of the vocal folds and airflow e.g. in [11] or [12]. This approach is still used in many studies, e.g. [5] or [13], but it is still difficult and computationally highly demanding. The analysis of the created acoustic signal is however often missing.

The full FSAI problem was addressed e.g. in [14], where the sound propagation was simulated with the aid of an acoustic analogy. The Lighthill analogy was applied using results of the fluid-structure interaction (FSI) simulation, but the acoustic domain did not include any vocal tract downstream of the glottis. In [8] the aeroacoustic 3D problem with a vocal tract was successfully solved utilizing the Lighthill analogy and the analogy given by acoustic perturbation equations introduced in [15], but the fluid flow simulations were performed on the computational domain considering only a prescribed movement of vocal folds (VF) walls.

In this paper the 2D simulation of a FSAI problem is considered and the analogy, based on the Perturbed Convective Wave Equation (PCWE) [16], is applied. The FSI problem is solved and the computed acoustic sources are employed to describe the sound propagation through the vocal tract corresponding to the pronunciation of the vowel [u:]. The strong coupling between the fluid and the structure is considered and realized by transmission conditions on the common interface. The effects of the time varying fluid domain are incorporated with the Arbitrary Lagrangian-Eulerian (ALE) method. Since the intensity of the resulting acoustic field is assumed to be small, the feedback from acoustics to fluid flow as well as from acoustics to the structure motion is neglected similarly as in [14]. In order to determine the created sound the PCWE analogy is used and compared to the Lighthill acoustic analogy. The perfectly matched layer (PML) technique is applied to absorb the reflection of the outgoing waves at the artificial boundaries, see [17]. All the three physical sub-problems are discretized in space by the finite element method (FEM), particularly for the fluid flow approximation the Streamline-Upwind/Petrov-Galerkin stabilized finite element method is used, see [18].

The paper is organized as follows. In Section 2 the mathematical description of FSAI problem is given together with all governing equations and introduction of Lighthill and PCWE analogy. Section 3 includes the implementation of the numerical schemes based on the FEM method. The numerical results of flow induced vibration and sound generation as well as propagation are presented and discussed in Section 4.

2 Mathematical Description

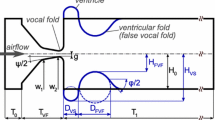
In order to mathematically describe the human phonation problem a two-dimensional FSAI problem is considered. The FSI computational domain, schematically shown in Fig. 1, is a subset of a substantially larger acoustic domain Ωa of sound propagation, see Fig. 2. The FSI domain consists of computational fluid domain \({{\Omega }^{f}_{t}}\) and the deformed elastic structure \({{\Omega }^{s}_{t}}\) (the vocal fold). The deformation of the elastic structure is solved on the reference state \({\Omega }^{s}_{\text {ref}}\) and described in the Lagrangian coordinates, i.e. the computational domain \({\Omega }^{s} := {\Omega }^{s}_{\text {ref}}\) does not depend on time.

Fig. 1
figure 1

Scheme of vocal folds model and fluid domain with boundaries marked before (left) and after (right) a deformation

Full size image
Fig. 2
figure 2

Scheme of acoustic domain. The propagation domain consists of the sound source region, the vocal tract and the far field. Propagation region is enclosed by the PML regions

Full size image

Similarly, the domain \({\Omega }^{f}_{\text {ref}}\) denotes the reference fluid domain, i.e. the domain occupied by fluid at the time instant t = 0 with the common interface \({\Gamma }_{\mathrm {W_{\text {ref}}}} = {\Gamma }_{\mathrm {W_{0}}}\) between the fluid and the structure domain. But the reference domain \({\Omega }^{f}_{\text {ref}}\) is transformed to the deformed domain \({{\Omega }^{f}_{t}}\) with the interface \({\Gamma }_{\mathrm {W_{\mathrm {t}}}}\) using the ALE method at any time instant t.

2.1 Elastic body – linear elasticity

The motion of the elastic body Ωs described by the deformation u(X, t) = (u1, u2) is governed by equations

$$ \rho^{s} \, \frac{\partial^2 u_{i}}{\partial t^{2}} - \frac {\partial \tau_{ij}^{s}(\mathbf{u})}{\partial X_{j}} = {f_{i}}^{s} \quad \text{in} \ {\Omega}^{s} \times (0,\mathrm{T}), $$
(1)

where ρs denotes the structure density, the tensor \(\tau _{ij}^{s}\) is the Cauchy stress tensor, the vector \(\mathbf {f}^{s}=({f_{1}^{s}}, {f_{2}^{s}})\) is the volume density of an acting force and X = (X1, X2) are the reference coordinates. Using the assumption of the linear relation between the deformation and the stress tensor given by the generalized Hook law and assuming the isotropic material leads to

$$ \tau_{ij}^{s} = \lambda^{s} (\text{div} \ \mathbf{u})\, \delta_{ij} + 2 \mu^{s} e_{ij}^{s}, $$
(2)

where λs, μs are Lamé coefficients depending on the Young modulus of elasticity Es and the Poisson ratio σs, see e.g. [19]. The tensor \(\mathbb {I} = (\delta _{ij})\) is the Kronecker’s delta and the tensor \(\mathbf {e}^{s} = (e_{ij}^{s})\) is the strain tensor. Using small displacements assumption the strain tensor components read

$$ e_{ij}^{s} = \frac{1}{2}\left( \frac{\partial u_{i}}{\partial X_{j}} + \frac{\partial u_{j}}{\partial X_{i}} \right). $$
(3)

The formulation of elastic problem (4) is completed by the following initial and boundary conditions

$$\begin{array}{@{}rcl@{}} &&\text{a)} \quad \mathbf{u}(X, 0) = \mathbf{u}_{0}(X),\ \frac{\partial \mathbf{u}}{\partial t}(X, 0) = \mathbf{u}_{1}(X) \qquad \text{for} \ X \in \ {\Omega}^{s}, \\ &&\text{b)} \quad \mathbf{u}(X, t) = \mathbf{u}_{\text{Dir}}(X, t) \qquad \quad\,\,\,\, \quad \text{for} \ X \in {\Gamma}_{\text{Dir}}^{s}, \ t \in (0,\mathrm{T}), \\ &&\text{c)} \quad \tau_{ij}^{s}(X, t) \, {n_{j}^{s}}(X) = {q_{i}^{s}}(X, t), \ \ \quad \text{for} \ X \in {\Gamma}_{\mathrm{W_{t}}}^{s}, \ t \in (0,\mathrm{T}), \end{array} $$
(4)

where the \({\Gamma }_{\mathrm {W_{ref}}}, {\Gamma }_{\text {Dir}}^{s}\) are mutually disjoint parts of the boundary \(\partial {\Omega }^{s} = {\Gamma }_{\mathrm {W_{ref}}} \cup {\Gamma }_{\text {Dir}}^{s}\) (see Fig. 1) and \({n_{j}^{s}}(X)\) are the components of the unit outer normal to \({\Gamma }_{\mathrm {W_{ref}}}\).

2.2 ALE method

The key element of ALE method is the use of a diffeomorphism At which maps the reference (undistorted) domain \({\Omega }^{f}_{\text {ref}}\) on to the domain \({{\Omega }^{f}_{t}}\) at any instant time t ∈ (0,T). Assuming that \(\frac {\partial A_{t}}{\partial t} \in C({{\Omega }}^{f}_{\text {ref}})\) the ALE domain velocity wD is defined by

$$ \mathbf{w}_{D}(A_{t}(X),t) = \frac{\partial }{\partial t} {A}_{t}(X), \quad t \in (0,\mathrm{T}), \ X \in {\Omega}^{f}_{\text{ref}}. $$
(5)

The ALE derivative is introduced as the time derivative with respect to a fixed point X in the reference domain \({\Omega }^{f}_{ref}\). It satisfies the following relation

$$ \frac{D^{A}}{Dt} f(x, t) = \frac{\partial f}{\partial t}(x, t) + \mathbf{w}_{D}(x, t) \cdot \nabla f(x,t). $$
(6)

The more details and practical construction of ALE mapping is described e.g. in [5] or [20].

2.3 Fluid flow

The viscous incompressible fluid in \({{\Omega }^{f}_{t}}\) is modeled by the Navier-Stokes equations in the ALE form

$$ \frac{D^{A} \mathbf{v}}{Dt} + ((\mathbf{v} - \mathbf{w}_{D}) \cdot \nabla) \mathbf{v} - \nu^{f} {\Delta} \mathbf{v} + \nabla p = \mathbf{0}, \quad \text{div} \ \mathbf{v} = 0 \quad \text{in} {{\Omega}^{f}_{t}}, $$
(7)

where v(x, t) denotes the fluid velocity, p is the kinematic pressure and νf is the kinematic fluid viscosity, see [5].

Equation 7 are equipped with the initial condition at t = 0 and boundary conditions at any t ∈ (0,T)

$$\begin{array}{@{}rcl@{}} &&\text{a)} \qquad\qquad\qquad \mathbf{v}(x, 0) = \mathbf{v}_{0}(x) \qquad\qquad\qquad \text{ for } x \in {\Omega}^{f}_{\text{ref}},\\ &&\text{b)} \qquad\qquad\qquad \mathbf{v}(x, t) = \mathbf{w}_{D}(x, t) \qquad\qquad\,\,\,\, \text{ for } x \in {\Gamma}_{\text{Dir}}^{f} \cup {\Gamma}_{\mathrm{W_{t}}},\\ &&\text{c)} \ p(x, t) \mathbf{n}^{f} - \nu^{f} \, \frac{\partial \mathbf{v}}{\partial \mathbf{n}^{f}}(x, t) = -\frac{1}{2} \mathbf{v}(\mathbf{v} \cdot \mathbf{n}^{f})^{-} + p_{\text{ref}} \mathbf{n}^{f} \text{for} x \in {\Gamma}_{\text{In}}^{f} \cup {\Gamma}_{\text{Out}}^{f}, \end{array} $$
(8)

where nf is unit outer normal to boundary \(\partial {{\Omega }_{t}^{f}}\) and pref is a reference pressure. This pressure value is a constant along the chosen boundary, but it can has different values: \(p_{\text {ref}}^{in}\) at the inlet \({\Gamma }_{\text {In}}^{f}\) and \(p_{\text {ref}}^{out}\) at the outlet \({\Gamma }_{\text {Out}}^{f}\). The condition (8 c) is a modification of the well-known do-nothing boundary condition, see e.g. [21].

2.4 Aeroacoustics

The acoustic domain Ωa, where the acoustic problem is solved, is shown in Fig. 2 (for detailed dimensions see Fig. 3). It is decomposed into three parts \({\Omega }^{a}_{\text {src}}, {\Omega }^{a}_{\text {air}}\) and \({\Omega }^{a}_{\text {pml}}\), where \(\overline {{\Omega }^{a}} = \overline {{\Omega }^{a}_{\text {src}}} \cup \overline {{\Omega }^{a}_{\text {air}}} \cup \overline {{\Omega }^{a}_{\text {pml}}}\). The domain \({\Omega }^{a}_{\text {src}}\), where the acoustic sources are evaluated from the computed flow field, is the same as reference fluid domain, i.e. \({\Omega }^{a}_{\text {src}} = {\Omega }^{f}_{\text {ref}}\). (The deformation of the acoustic domain \({\Omega }^{a}_{\text {src}}\) in time is not considered.) The domain \({\Omega }^{a}_{\text {air}}\) represents a part of the vocal tract behind the glottis up to mouth including in addition a far field region, i.e. the outer space.

Fig. 3
figure 3

The mesh of the acoustic domain with dimensions, LProl denotes length of prolongation. The microphone is located at [0.25m, 0m]

Full size image

Both aforementioned domains are enclosed by PML domain \({\Omega }^{a}_{\text {pml}}\) in order to absorb the outgoing sound waves at the free boundaries of the acoustic domain, i.e. at the inlet and at boundaries of the far field region, for details see [17]. PML is a technique capable to correctly simulate open-boundary problem in bounded domains. It consists of a few layers of elements, where the sound waves are damped. The most important property is that there is no reflection at the interface between propagation region and PML. For the formulation and numerical implementation we refer to [17].

The acoustic problem is solved either with the Lighthill acoustic analogy or by PCWE analogy. The Lighthill acoustic analogy is more general and can be applied for wider range of Mach numbers or in case of thermal transport. On the other hand the PCWE analogy based on quantities splitting provides directly acoustic pressure.

2.4.1 Lighthill analogy

Let us assume a small region with flow described by velocity v and fluctuating pressure p′ = p − p0 and density \(\rho ^{\prime } = \left (\rho ^{f} - {\rho ^{f}_{0}}\right )\) inside a large fluid volume at rest with density \({\rho ^{f}_{0}}\) and pressure p0. The fluid obeys momentum conservation in the form

$$ \frac{\partial \rho^{f} v_{i}}{\partial t} + \frac{\partial \pi_{ij}^{0}}{\partial x_{j}} = -\frac{\partial (\pi_{ij} - \pi_{ij}^{0})}{\partial x_{j}}, $$
(9)

where \(\pi _{ij} = \rho ^{f} v_{i} v_{j} + (p - p_{0}) \delta _{ij} - \tau ^{f}_{ij}\) is the momentum flux tensor and \(\tau ^{f}_{ij}\) is the fluid viscous stress tensor. The tensor \(\pi _{ij}^{0} = (p - p_{0}) \delta _{ij} = {c_{0}^{2}}(\rho ^{f} - {\rho ^{f}_{0}}) \delta _{ij}\) denotes the momentum flux at the rest state (without any flow), where c0 denotes the speed of sound. The hypothetical stationary acoustic medium exposed to the same stress as it is in flow regime leads to the same sound propagation described by the density fluctuation. This stress is described by the Lighthill tensor T = (Tij)

$$ T_{ij} = \pi_{ij} - \pi_{ij}^{0} = \rho^{f} v_{i} v_{j} + ((p - p_{0}) - {c_{0}^{2}}(\rho^{f} - {\rho^{f}_{0}})) \delta_{ij} - \tau^{f}_{ij}. $$
(10)

The combination of Eq. 9 and the mass conservation law leads to the form of inhomogeneous wave equation

$$ \frac{1}{{c^{2}_{0}}} \frac{\partial^2 p^{\prime}}{\partial t^2} - \frac{\partial^2 p^{\prime}}{\partial x_i \partial x_i} = \frac{\partial^{2} T_{ij}}{\partial x_{i} \partial x_{j}}, $$
(11)

for the unknown pressure fluctuation p′ = p − p0. This was first derived by Lighthill in 1952, see [22]. The pressure fluctuation p′ is equal to the acoustic pressure pa only outside flow domain because inside the source region must be regarded as a superposition of acoustic and hydrodynamic pressure.

In what follows, the Lighthill tensor is approximated by

$$ T_{ij} \approx {\rho^{f}_{0}} v_{i} v_{j}, $$
(12)

where the viscous stress \(\tau ^{f}_{ij}\) and the stresses connected with heat conduction \((p^{\prime } - {c_{0}^{2}} \rho ^{\prime }) \delta _{ij}\) were neglected, see [22].

The wave Eq. 11 is equipped with the zero initial condition and the boundary of acoustic domain ∂Ωa with the outer unit normal na is considered as sound hard

$$ \frac{\partial p^{\prime}}{\partial \mathbf{n}^{a}}(x, t) = 0 \qquad \text{for} \ x \in \ \partial {\Omega}^{a}, \ t \in (0,\mathrm{T}), $$
(13)

which means that sound waves are there reflected back to the acoustic domain Ωa.

2.4.2 Perturbed convective wave equation (PCWE)

The PCWE analogy is based on splitting of physical quantities into mean \(\overline {\mathbf {v}}, \overline {p}\) and fluctuating parts v′, p′ (for precise derivation and discussion see [23]). The fluctuating variables are then further divided into non-acoustic (incompressible) components and acoustic parts

$$ \mathbf{v} = \overline{\mathbf{v}} + \mathbf{v}^{\prime}(t) = \overline{\mathbf{v}} + \mathbf{v}^{ic}(t) + \mathbf{v}^{a}(t), \quad p = \overline{p} + p^{\prime}(t) = \overline{p} + p^{ic}(t) + p^{a}(t). $$
(14)

Inserting expressions (14) into Navier-Stokes system of equations, neglecting the nonlinear terms and using the assumption of irrotational acoustic field (∇×va = 0), isentropic flow (\(p^{\prime } - {c_{0}^{2}} \rho ^{\prime } = const.\)) and incompressibility (∇⋅vic = 0) results into

$$\begin{array}{@{}rcl@{}} \frac{\partial p^{a}}{\partial t} + \overline{\mathbf{v}} \cdot \nabla p^{a} + {\rho^{f}_{0}} {c_{0}^{2}} \nabla \cdot \mathbf{v}^{a} & =& - \frac{D p^{ic}}{Dt}, \end{array} $$
(15a)
$$\begin{array}{@{}rcl@{}} \qquad \frac{\partial \mathbf{v}^{a}}{\partial t} + \nabla (\overline{\mathbf{v}} \cdot \mathbf{v}^{a}) + \frac{1}{{\rho^{f}_{0}}} \nabla p^{a} & =& \mathbf{0}, \end{array} $$
(15b)

where the substantial derivative \(\frac {D}{Dt} = \frac {\partial }{\partial t} + \overline {\mathbf {v}} \cdot \nabla \). Equation 15 are then rewritten into a single scalar equation with the use of an acoustic potential ψa related to the acoustic particle velocity (va = −∇ψa). Thus the expression for \(p^{a} = {\rho ^{f}_{0}} \frac {D \psi ^{a}}{Dt}\) is obtained from Eq. 15b and then from Eq. 15a we obtain

$$ \frac{1}{{c^{2}_{0}}} \frac{\partial^{2} \psi^{a}}{\partial t^{2}} - {\Delta} \psi^{a} = -\frac{1}{{\rho^{f}_{0}} {c_{0}^{2}}} \frac{D p^{ic}}{Dt}. $$
(16)

In Eq. 16pic is the pressure obtained from the solution of incompressible fluid flow problem (7). The acoustic pressure pa can be afterwards evaluated as \(p^{a} = {\rho ^{f}_{0}} \frac {\partial \psi ^{a}}{\partial t} + {\rho ^{f}_{0}} \overline {\mathbf {v}} \cdot \nabla \psi ^{a}\).

For the considered low Mach number flows the mean velocity is neglected (\(\overline {\mathbf {v}} = 0\)) on the left hand side of Eq. 16 in order to simplify the solution. It means that the supposedly small convection effects are completely disregarded. On the other hand in order to incorporate sound sources arising in glottis connected with steady pressure gradient we keep the full version of the right hand side. So the simplified PCWE equation (16) reads

$$ \frac{1}{{c^{2}_{0}}} \frac{\partial^2 \psi^{a}}{\partial t^2} - {\Delta} \psi^{a} = -\frac{1}{{\rho_{0}^{f}} {c_{0}^{2}}} \frac{D p^{ic}}{Dt}. $$
(17)

The Eq. 17 is equipped with the zero initial condition and the boundary of acoustic domain ∂Ωa is considered as sound hard, practically realized by setting \(\frac {\partial \psi ^{a}}{\partial \mathbf {n}^{a}} = 0\).

2.5 Coupling conditions

The FSI problem is a coupled problem, i.e. the location of common interface \({\Gamma }_{W_{t}}\) at any time t depends also on solution of the FSI problem. Its location corresponds to the establishing force equilibrium between the aerodynamic and the elastic forces and it can be implicitly described as

$$ {\Gamma}_{\mathrm{W_{t}}} = \left\{ x \in \mathbb{R}^{2}|\, x = X + \mathbf{u}(X,t),\, X \in {\Gamma}_{\mathrm{W_{ref}}} \right\}. $$
(18)

For the elastic problem the Neumann boundary condition (4 c) is prescribed with \({q_{i}^{s}}\) given by the aerodynamic forces as

$$ {q^{s}_{i}}(X, t) = - \sum\limits_{j = 1}^{2} \sigma_{ij}^{f}(x)\,{n_{j}^{f}}(x), \quad x = X + \mathbf{u}(X,t), \ X \in {\Gamma}_{\mathrm{W_{ref}}}, $$
(19)

where \(\sigma _{ij}^{f} = -{\rho ^{f}_{0}} p \delta _{ij} + {\rho ^{f}_{0}} \nu ^{f} \left (\frac {\partial v_{i}}{\partial x_{j}}+\frac {\partial v_{j}}{\partial x_{i}}\right )\) for i, j ∈{1,2} are components of the fluid stress tensor. The fluid flow problem is completed with the Dirichlet boundary condition postulated by Eq. 8 b. It enforces the continuity between fluid motion and elastic body deformation across the boundary \({\Gamma }_{\mathrm {W_{t}}}\).

Since the backward effect of the acoustic field to the flow field is not considered, the forward coupling has the form of flow field postprocessing, where for each time step the acoustic sources in \({\Omega }^{a}_{\text {src}}\) according to Eq. 12 are evaluated and then inserted into Eq. 11 or the right hand side of Eq. 17 is evaluated and then Eq. 17 is solved.

3 Numerical Scheme

The same sequence of steps is applied in derivation of numerical algorithm for all three subproblems. Firstly, all partial differential Eqs. 1, 7 and 11 or 17 are reformulated in a weak sense in space for the purpose of application of the FEM. Then this semi-discrete system is discretized in time by the finite difference scheme with the equidistant time step \({\Delta } t = \frac {T}{N}, N >> 1\).

3.1 Elastic body

To achieve weak formulation, Eq. 1 is multiplied by a test function ψ and integrated over the whole domain Ωs. The application of the Green theorem and Hooke law (2) leads to the form

$$ \left( \rho^{s} \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}, {\psi} \right)_{{\Omega}^{s}} + \left( \lambda^{s} (\text{div} \ \mathbf{u})\, \mathbb{I} + 2 \mu^{s} \mathbf{e^{s}}(\mathbf{u}), \mathbf{e^{s}}({\psi}) \right)_{{\Omega}^{s}}= \left( \mathbf{f}^{s}, {\psi} \right)_{{\Omega}^{s}} + \left( \mathbf{q}^{s}, {\psi} \right)_{{\Gamma}_{\text{Neu}}^{s}}, $$
(20)

which needs to be satisfied for all ψ ∈V. The notation \((\cdot , \cdot )_{\mathcal {D}}\) means the scalar product in the Lebesque spaces \(L^{2}(\mathcal {D})\) or \(\mathbf {L}^{2}(\mathcal {D})\). The space V = V × V, where \(V = \{\phi \in W^{1,2}({\Omega }^{s}) | \phi = 0 \text { on} {\Gamma }_{\text {Dir}}^{s} \}\), and W1,2(Ω) is the Sobolev space, see [24]. The solution u is approximated by uh in a finite element space. Then the numerical solution uh can be expressed as a linear combination of basis functions \({\psi }_{1}, \ldots , {\psi }_{N_{h}}\), i.e. the approximate solution reads \(\mathbf {u}_{h}(x, t) = {\sum }_{j = 1}^{N_{h}} \alpha _{j}(t) {\psi }_{j}(x)\). Using this and setting ψ = ψi in Eq. 1 yields the system of ordinary differential equations of second order for the unknown coeffients αj(t)

$$ \mathbb{M}^{T} \ddot{\alpha} + \mathbb{C}^{T} \dot{\alpha} + \mathbb{K}^{T} {\alpha} = \mathbf{b}(t), $$
(21)

where the matrix \(\mathbb {C} = \epsilon _{1} \mathbb {M} + \epsilon _{2} \mathbb {K}\) was added as the proportional damping with parameters 𝜖1, 𝜖2 chosen such, that the whole elastic system is weakly damped. The vector b(t) has components \(b_{i}(t) = (\mathbf {f}^{s}, {\psi }_{i})_{{\Omega }^{s}} + (\mathbf {q}^{s}, {\psi }_{i})_{{\Gamma }_{\text {Neu}}^{s}}\) and the elements of matrices \(\mathbb {M} = (m_{ij}), \mathbb {K} = (k_{ij})\) are given by

$$ {m}_{ij} = (\rho^{s} {\psi}_{j}, {\psi}_{i})_{{\Omega}^{s}}, \quad {k}_{ij} = (\lambda^{s} (\text{div} \ {\psi}_{j})\, \mathbb{I} + 2 \mu^{s} \mathbf{e}^{s}({\psi}_{j}), \mathbf{e}^{s}({\psi}_{i}))_{{\Omega}^{s}}. $$
(22)

System (21) is numerically discretized in time by the Newmark method, see for example [25] or [5].

3.2 Fluid flow

Now, Eq. 7 is at first discretized in time by the BDF2 scheme. The ALE derivative is approximated by

$$ \frac{D^{A} \mathbf{v}}{Dt}(t_{n + 1}) \approx \frac{3{\mathbf{v}}^{n + 1} - 4\overline{\mathbf{v}}^{n} + \overline{\mathbf{v}}^{n-1}}{2 {\Delta} t}, $$
(23)

where for a fixed time instant tn+ 1 we denote \(\overline {\mathbf {v}}^{i}(x) = \mathbf {v}^{i}(\tilde {x})\) for \(\tilde {x} = A_{t_{i}}(A^{-1}_{t_{n + 1}}(x))\), i ∈{n − 1, n} and \(x \in {\Omega }^{f}_{n + 1}\). For the sake of simplicity in next sections we omit the time index n+ 1 and set \({\Omega }^{f} := {\Omega }^{f}_{t_{n + 1}}\). Then the weak spatial formulation of Eq. 7 in time tn+ 1 leads to the problem of searching for a function pair V = (v, p) such, that

$$ a(V, {\Phi}) = f({\Phi}), $$
(24)

is satisfied for any test function Φ = (φ, q) from space X × M. The space X = X × X is introduced \(X = \left \{f \in W^{1,2}({\Omega }^{f})| \, f = 0 \text { on } {\Gamma }_{\text {Dir}}^{f} \cup {\Gamma }_{\text {In}}^{f} \cup {\Gamma }_{\mathrm {W_{t_{n + 1}}}}^{f} \right \} \subset W^{1,2}\left ({\Omega }^{f}\right )\) and M = L2(Ωf).

The form a(⋅,⋅) is given by

$$\begin{array}{@{}rcl@{}} &&a(V, {\Phi}) = \left( \frac{3\mathbf{v}}{2{\Delta} t}, {\varphi} \right)_{{\Omega}^{f}} + \frac{1}{2}(((\mathbf{v} - 2\mathbf{w}_{D}^{n + 1}) \cdot \nabla) \mathbf{v}, {\varphi})_{{\Omega}^{f}} - \frac{1}{2} ((\mathbf{v} \cdot \nabla) {\varphi}, \mathbf{v})_{{\Omega}^{f}} + \\ && \quad + \frac{1}{2} ((\mathbf{v} \cdot \mathbf{n})^{+} \mathbf{v}, {\varphi})_{{\Gamma}_{\text{Out}}^{f}} + \nu^{f} (\nabla \mathbf{v}, \nabla {\varphi})_{{\Omega}^{f}} - (p, \text{div}\, {\varphi})_{{\Omega}^{f}} + (q, \text{div}\, \mathbf{v})_{{\Omega}^{f}} \end{array} $$
(25)

and functional \(f({\Phi }) = \left (\frac {4\overline {\mathbf {v}}^{n} - \overline {\mathbf {v}}^{n-1}}{2{\Delta } t}, {\varphi } \right )_{{\Omega }^{f}}\). The nonlinear system of Eq. 24 is solved by fixed point iteration.

In order to prevent numerical instabilities associated with high Reynolds numbers, the streamline-upwind/Petrov-Galerkin (SUPG) and the pressure-stabilization/Petrov-Galerkin (PSPG) together with ’div-div’ stabilization are applied. These methods keep algorithm stable, consistent and still accurate, see e.g. [18], [5]. The stabilization introduces additional terms to weak formulation (24). The stabilized problem solved on a regular triangulation \(\mathcal {T}_{h}\) reads: find V = (v, p) such that

$$\begin{array}{@{}rcl@{}} a(V, {\Phi}) &+& \sum\limits_{K \in \mathcal{T}_{h}} \delta_{K} \left( \frac{3\mathbf{v}^{}}{2 {\Delta} t} + ((\overline{\mathbf{v}}^{n} - \mathbf{w}_{D}) \cdot \nabla) \mathbf{v} + \nabla p - \nu {\Delta} \mathbf{v},\, \zeta({\Phi}) \right)_{K} +\\ &+& \sum\limits_{K \in \mathcal{T}_{h}} \tau_{K} \left( \text{div}\, \mathbf{v}, \text{div}\, {\varphi} \right)_{K} = f({\Phi}) + \sum\limits_{K \in \mathcal{T}_{h}} \delta_{K} \left( \frac{4 \overline{\mathbf{v}}^{n} - \overline{\mathbf{v}}^{n-1}}{2 {\Delta} t},\, {\zeta}({\Phi}) \right)_{K}, \end{array} $$
(26)

for all Φ = (φ, q) ∈X × M, where short notation \({\zeta }({\Phi }) := ((\overline {\mathbf {v}}^{n} - \mathbf {w}_{D}) \cdot \nabla ) {\varphi } + \nabla q\) was used. The parameters τK and δK are locally defined using the local element length hK and local Reynold number ReK, see [5]. For practical computation the P1-bubble/P1 elements were chosen. This element according to [26] satisfies the well-known Babuška-Brezzi condition.

3.3 Coupling algorithm for FSI problem

The advantage of hybrid approach is that FSI problem can be solved independently and the acoustic sources are then calculated anytime later from the stored values of fluid pressure and velocities. The algorithm solving FSI problem is implemented in the form of strong coupling:

We start with the initial values \(\mathbf {v}^{0}, p^{0}, \mathbf {u}_{0}, \mathbf {q}^{s}_{0}, A_{t_{0}}\) and \({\Omega }^{f}_{t_{0}}\). Then for n = 0,1,… we proceed the computation in the following steps, where index l denotes inner iteration on relevant time level:

  1. 0.

    Set l = 0 and \(\mathbf {q}^{s}_{n + 1,0} = \mathbf {q}^{s}_{n}\).

  2. 1.

    Solve (21) with \(\mathbf {q}^{s}_{n + 1,l}\) in order to obtain the approximation of the solution un+ 1, l at time tn+ 1.

  3. 2.

    Construct the ALE mapping \(A_{t_{n + 1,l}}\) based on the found deformation un+ 1, l and determine \({\Omega }^{f}_{t_{n + 1,l}}\). Afterwards calculate the domain velocity deformation as \(\mathbf {w}_{D}^{n + 1,l}(x) = \frac {3A_{t_{n + 1,l}}(X) - 4A_{t_{n}}(X) + A_{t_{n-1}}(X)}{2 {\Delta } t}, \)where \(x = A_{t_{n + 1,l}}(X)\).

  4. 3.

    Solve the system (26) to acquire vn+ 1, l, pn+ 1, l defined on \({\Omega }^{f}_{t_{n + 1,l}}\).

  5. 4.

    Determine the aerodynamic forces \({\mathbf {q}}^{s}_{n + 1,l + 1}\) on the interface given by (19) from known values vn+ 1, l, pn+ 1, l.

  6. 5.

    Check if the condition \(|{\mathbf {q}}^{s}_{n + 1,l + 1} - \mathbf {q}^{s}_{n + 1,l}| < \epsilon \) is satisfied for a suitably chosen constant 𝜖. Then

    • If yes, denote all quantities fn+ 1 := fn+ 1, l, increase the time indexes n := n + 1, l := 0 and continue with step 1 on the new time level.

    • If no, increase only the iteration index l := l + 1 and continue with step 1.

3.4 Acoustics

In the case of Lighthill analogy Eq. 11 is multiplied by test function η and integrated over the whole acoustic domain Ωa, which leads to

$$ \left( \frac{1}{{c_{0}^{2}}} \frac{\partial^2 p^{\prime}}{\partial t^2}, \eta \right)_{{\Omega}^{a}} - \left( {\Delta} {p^{\prime}}, \eta \right)_{{\Omega}^{a}} = \left( \text{div}\, (\text{div}\, \mathbf{T}), \eta \right)_{{\Omega}^{a}}. $$
(27)

The application of the Green theorem together with boundary condition (13) gives us

$$ \left( \frac{1}{{c_{0}^{2}}} \frac{\partial^2 p^{\prime}}{\partial t^2}, \eta \right)_{{\Omega}^{a}} + \left( \nabla {p^{\prime}}, \nabla \eta \right)_{{\Omega}^{a}} = -\left( (\text{div}\, \mathbf{T}), \nabla \eta \right)_{{\Omega}^{a}}, $$
(28)

Finally, the restriction of test functions to finite element space and seeking solution \(p^{\prime }_{h}(t, x) = {\sum }_{j = 1}^{N_{h2}} \gamma _{j}(t) \eta _{j}(x) \in V_{h} \subset W^{1,2}({\Omega }^{a})\) yields

$$ \mathbb{M}^{a} \ddot{\gamma} + \mathbb{K}^{a} {\gamma} = \mathbf{b}(t), $$
(29)

where elements of matrices \(\mathbb {M}^{a} = (m_{ij}^{a}), \mathbb {K}^{a} = (k_{ij}^{a})\) are given as

$$ {m}^{a}_{ij} = \left( \frac{1}{{c_{0}^{2}}} {\eta_{i}}, \eta_{j} \right)_{{\Omega}^{a}}, \quad {k}^{a}_{ij} = \left( \frac{\partial \eta_{i}}{\partial x_{m}}, \frac{\partial \eta_{j}}{\partial x_{m}} \right)_{{\Omega}^{a}}, $$
(30)

and components of vector b(t) here in Lighthill case denoted as \(\mathbf {b}^{LH}(t) = ({b}^{LH}_{i})\) are

$$ {b}^{LH}_{i} = -\left( \frac{\partial T_{jm}}{\partial x_{m}}, \frac{\partial \eta_{i}}{\partial x_{j}} \right)_{{\Omega}^{a}}. $$
(31)

For PCWE analogy (17) the same procedure is applied leading to the same form as Eq. 29, with a different right hand side term \(\mathbf {b}(t) := \mathbf {b}^{PCWE}(t) = ({b}^{PCWE}_{i})\) computed according to

$$ {b}^{PCWE}_{i} = -\left( \frac{1}{{\rho_{0}^{f}} {c_{0}^{2}}} \left( \frac{\partial p^{ic}}{\partial t} + \overline{\mathbf{v}} \cdot \nabla p^{ic} \right), \eta_{i} \right)_{{\Omega}^{a}}. $$
(32)

System (29) is numerically discretized in time by the Newmark method.

4 Numerical Results

In this section the numerical results of FSI problem are presented and then the analysis of acoustic sources and sound propagation simulation is shown. For the FSI as well as for the transient acoustic simulation the time step was chosen as 2.5 ⋅ 10− 5 s.

4.1 FSI problem

Figure 4 shows the vocal fold (VF) model shape based on the article [27] with initial gap between VFs 2.0 mm. The vocal folds are divided into four parts with different material parameters. The Young modulus was chosen in the following way: epithelium – Es = 50 kPa, ligament – Es = 25 kPa, lamina propria – Es = 20 kPa and muscle – Es = 30 kPa, see Fig. 4. For all parts the same Poisson ratio σ = 0.45 was selected. The damping parameters were considered as 𝜖1 = 5 s− 1, 𝜖2 = 2.0 ⋅ 10− 5 s. The structure density ρs was set to ρs = 1000 kg/m3, the fluid density to ρf = 1.185 kg/m3 and the kinematic viscosity of the fluid to νf = 1.47 ⋅ 10− 5 m/s2.

Fig. 4
figure 4

Left: The computational mesh in the structure domain with marked different layers of materials and with dimensions shown in mm. The point A with coordinates [11.57mm,− 1.50mm] is shown. Right: The detail of the fluid and acoustic meshes inside the glottis region. The CFD mesh is shown in red color and the acoustic mesh is plotted with black color

Full size image

The FSI problem was solved with the prescribed kinematic pressure difference between the inlet and the outlet \({\Delta } p = \rho ^{f} (p_{\text {ref}}^{in} - p_{\text {ref}}^{out}) = 1600\, \text {Pa}\). The VFs were released for the interaction after 0.01 s of the computation, when the flow field was already fully developed. Figure 5 illustrates a typical behavior of the flow induced vibration of a selected point A from the top surface of VF. After a short time stable oscillations appear. The spectrum of the VF displacement computed by the Fourier transform shows the excitation of first two eigenmodes of VF at frequencies f1 = 112 and f2 = 228 Hz. This is in good correspondence with the results reported in [27].

Fig. 5
figure 5

Left: The time evolution of displacement of chosen point A in y-direction. Right: The normalized Fourier transform of the time signal

Full size image

4.2 Aeroacoustics

The calculated sound sources for both acoustic analogies are analyzed and then used for the transient simulation of sound propagation through vocal tract.

4.2.1 Sound sources

The computed sound sources in the form of approximative Lighthill tensor (31) or PCWE source (32) were analyzed by Fourier transform on the original CFD grid. The results show that the location of main sound sources for frequency 232 Hz is inside the glottis. The higher frequency sources like e.g. at 2486 Hz are mainly located in the channel behind the glottis, see Fig. 6. The sound sources obtained by the Lighthill analogy and by PCWE are similar.

Fig. 6
figure 6

The computed sound source densities (The acoustic source values are divided by average triangle area at every point of triangulation.) at 232 Hz (upper panel) and 2486 Hz(lower panel), normalized by their maximal values. Left are results for PCWE analogy, right for Lighthill analogy, respectively

Full size image

The structure of sound sources at 232 Hz matches the sound source of dipole character described in [23], see details of sound sources at the glottis area in Fig. 6. In Lighthill case the sound sources are located predominantly in the vicinity of VF interface corresponding with high velocity gradients here, whereas PCWE sources are connected with time and spatial pressure derivative, which is less compact compared to the velocity field.

The acoustic sources at 2486 Hz behind glottis associated with the free jet pouring out of an opening (glottis) can be considered as quadrupole, see Fig. 6. In Lighthill case the acoustic sources are primarily located in the shear layer of the jet, whereas in the case of PCWE the sound source structure is similar but with considerably higher magnitude. It agrees well with the results of [23].

4.2.2 Sound propagation in the vocal tract model

Since the acoustic problem does not need such a fine mesh as in case of the FSI problem, the sound sources were projected onto the coarser acoustic mesh after their evaluation on the original CFD mesh, see Fig. 4 right. The implemented projection procedure conserves the overall acoustic energy, see [28].

The computed sound sources are then used as input for transient solution of wave Eq. 29, which is solved on acoustic mesh including model of vocal tract for vowel [u:], see Fig. 3. The cross-sections of vocal tract model are based on the MRI data from [29], but the prolongated version of the vocal tract model was used in our computation in order to connect CFD domain more smoothly to model of vocal tract. Additional prolongation arises from fact, that original measurement of published cross-sections starts directly behind glottis and not behind end of CFD domain.

The Fourier transform of the acoustic pressure monitored at the microphone position (see Fig. 3) is shown in Fig. 7. The obtained frequencies of the peaks exhibit a very rough correspondence with the frequencies of first three formants measured for the vowel [u:] in [29]. The most dominant frequencies obtained by the Lighthill analogy have values 405, 1092 and 2486 Hz. The first frequency captures well the first formant, while the others have much smaller amplitude and they are shifted up by approximately 10% than the expected values.

Fig. 7
figure 7

The normalized Fourier transform of acoustic pressure obtained by Lighthill and PCWE analogy and measured at microphone position computed from 0.9 s signal length. The dominant frequencies of simulation are highlighted with arrows and values. The black vertical lines mark the formant frequencies 389 Hz,987 Hz and 2299 Hz taken from article [29]

Full size image

The dominant frequencies of PCWE analogy are 547, 1090 and 2499 Hz. The first formant is not recognized well, the second and third formant frequencies correspond with values reported in previous case. The frequency shift is probably caused by the additional volume introduced by the prolongation of the vocal tract.

5 Conclusion

The general mathematical problem of the fluid-structure-acoustic interaction was described on the example of phonation. The hybrid partitioned approach was used and the Lighthill and perturbed convective wave equation analogy were applied for the determination of the acoustic sources and computation of their propagation in the vocal tract model. The all considered physical problems were numerically solved by the finite element method. The fluid solver was stabilized by SUPG, PSPG and ’div-div’ method.

The flow induced vibrations of the vocal folds model were computed by the in-house developed program. Stabilized vibrations of vocal folds appeared with the dominant frequencies equal to the first two eigenmodes. The sound sources were computed and projected onto the coarser acoustic grid. Their analysis showed correctly the dipole character of the sound sources located at the glottis and the quadrupoles connected with the free stream type of flow behind the glottis.

The results of sound propagation were obtained by Coupled Field Simulation (CFS++) solver from the evaluated acoustic sources. The perfectly matched layer was used to absorb outgoing waves without reflection at the boundaries of acoustic domain. In the end the dominant acoustic frequencies over 1 kHz obtained by the Perturbed Convective Wave Equation analogy agreed quite well with reported formants of vowel [u:], whereas Lighthill analogy captured the first formant better.