Sea-horse optimizer: a novel nature-inspired meta-heuristic for global optimization problems

Abstract

This paper proposes a novel swarm intelligence-based metaheuristic called as sea-horse optimizer (SHO), which is inspired by the movement, predation and breeding behaviors of sea horses in nature. In the first two stages, SHO mimics different movements patterns and the probabilistic predation mechanism of sea horses, respectively. In detail, the movement modes of a sea horse are divided into floating spirally affected by the action of marine vortices or drifting along the current waves. For the predation strategy, it simulates the success or failure of the sea horse for capturing preys with a certain probability. Furthermore, due to the unique characteristic of the male pregnancy, in the third stage, the proposed algorithm is designed to breed offspring while maintaining the positive information of the male parent, which is conducive to increase the population diversity. These three intelligent behaviors are mathematically expressed and constructed to balance the local exploitation and global exploration of SHO. The performance of SHO is evaluated on 23 well-known functions and CEC2014 benchmark functions compared with six state-of-the-art metaheuristic algorithms. Finally, five real-world engineering problems are utilized to test the effectiveness of SHO. The experimental results demonstrate that SHO is a high-performance optimizer and positive adaptability to deal with constraint problems. SHO source code is available from: https://www.mathworks.com/matlabcentral/fileexchange/115945-sea-horse-optimizer

1 Introduction

An optimization problem refers to seek the best solution and achieve the optimal value of its objective function under a series of constraints. Before the era of heuristic optimization, the canonical optimization algorithms, such as the gradient descent method and the Newton-like method, were the most common methods for solving some mathematical and applied problems. However, these methods tend to trap into local optimum when handling the large-scale, high-dimensional and nonlinear complex problems, or even have difficult to solve them under more complex multi-coupling constraints [1]. Fortunately, a variety of metaheuristic algorithms (MAs) have been created to tackle these challenging issues. In general, MAs are a community of nature-inspired methods with certain stochastic operators [2]. Obviously, randomness is the essential characteristic of MAs [3], which means that the obtained solutions in each iteration are different with probabilities and may be scattered anywhere in the search space. Compared with the traditional optimization techniques, it is not completely guarantee that every iterative feasible solution becomes better, but has a greater capacity to escape local extremum, which is beneficial to explore and obtain the global optimal solution by multi-agent parallel iterations. Besides, MAs do not depend on the gradient information of functions and no strict requirements for their differentiability and convexity. Moreover, MAs are also not sensitive to initial positions of individuals. As a result, benefit from simple heuristic mechanisms and implementation procedures, MAs have become a class of effective substitutions for the canonical optimization methods to solve large-scale, high-dimensional, and multi-objective complex problems. In recent years, MAs have been successfully applied in feature selection [4], berth allocation [5], multi-objective optimization [6], and many other fields.

As shown in the first part of Fig. 1, the traditional metaheuristics use only one search agent for searching in each iteration. For example, Simulated Annealing (SA) [7] is inspired by the solid annealing principle. Based on the greedy strategy, it adds stochastic factors to get a new better solution than the current one with iterations. Tabu Search (TS) [8] uses the short-term memory to record and select the optimization process to guide the next search direction. However, these methods are accessible to get local optimums rather than the global optimum, because only single point is employed for searching and mining solutions.

Fig. 1

Classification of metaheuristic algorithms

Different from the first-part heuristic methods, most of current metaheuristics are employing multi- agents in the population to perform parallel iterative searching. Considering the difference of heuristic mechanisms, they can be roughly divided into other four categories, as shown in Fig. 1. The first category belongs to evolutionary algorithms (EAs), which is inspired by evolutionary behaviors in nature [9], such as genetic or mutation. EAs simulate the collective learning in a group with multiple individuals, and each represents a feasible solution in the search space. In order to improve fitness values and develop towards the global optimum, EAs are initiated by randomly generating a population and further iteratively evolved by certain evolutionary operators including selection, mutation, or recombination. In each iteration, due to the randomness of evolutionary operators [10], this kind of metaheuristics have the strong local extremum avoidance ability in most cases. And the more popular are Genetic Algorithm (GA) [11] imitating Darwin’s natural selection theory and the principles of genetics. In addition, EAs also consist of Differential Evolution (DE) [12], Genetic Programming (GP) [13], and Evolutionary Strategies (ES) [14]. For the second category, the swarm-based intelligence algorithms (SIs) [15] are inspired by intelligent behaviors of biological communities in nature. SIs mainly simulate social behaviors and information exchanges from plants, animals or other living creatures. The outstanding feature of SIs utilizes the swarm intelligence to search cooperatively, which results in finding the optimal solution in the search space. Frequently, the hunting, predation and reproduction are common and familiar social behaviors in animals. Based on these behaviors, many metaheuristics have been proposed continuously, including Particle Swarm Optimization (PSO) [16]，Grey Wolf Optimizer (GWO) [17], Ant Lion Optimizer (ALO) [18], Dragonfly Algorithm (DA) [19], Crow Search Algorithm (CSA) [20], Squirrel Search Algorithm (SSA) [21], Seagull Optimization Algorithm (SOA) [22], Harris Hawks Optimization (HHO) [23], Chimp Optimization Algorithm (ChOA) [24], Tunicate Swarm Algorithm (TSA) [25], Marine Predators Algorithm (MPA) [26], Slime Mould Algorithm (SMA) [27] and Golden Eagle Optimizer (GEO) [28]. Moreover, some plant-inspired SIs in this category are also presented, such as Flower Pollination Algorithm (FPA) [29] from the pollination mechanism of flowering plants, and Sun Flower Optimization (SFO) [30] motivated by the light orientation rule of plants. Besides, certain Human-based SIs have been raised in recent years, for instance, Behavior-based Optimization Algorithm (HBBO) [31], Forensic-based Investigation algorithm (FBI) [32], Political Optimizer (PO) [33], Group Teaching Optimization Algorithm (GTOA) [34]. The third category is Physics-based metaheuristics, which contains Multi-verse Optimizer (MVO) [35], Artificial Electric Field Algorithm (AEFA) [36], Henry Gas Solubility Optimization (HGSO) [37], Archimedes Optimization Algorithm (AOA) [38] and Equilibrium Optimizer (EO) [39].

In addition, many researchers have recently proposed MAs based on certain mathematical rules, that is, they take the mathematical rules or formulas as heuristics. MAs are easier to make a more logical explanation for their optimization process and have strong adaptation to address some complex optimizing problems. And more and more MAs based on certain specific mathematical laws are proposed, such as Sine Cosine Algorithm (SCA) [40] drawing lessons from the sine and cosine formulas, self-organizing map (EA-SOM) [41], Gradient-based Optimizer (GBO) [42] and RUNge Kutta optimizer (RUN) [43].

Although existing metaheuristic algorithms can be utilized for solving many challenging problems, their flexibility does not mean that they are cost-free. Wolpert and Macready [44] introduced the No Free Lunch (NFL) theorem, whose conclusion is that the performance of optimization algorithms is equivalent for the mutual compensation of all possible functions. In other words, the superiority of an optimization algorithm on a particular set of problems does not necessarily ensure the same properties on other problems. This is the basis for the development of optimization theory. Up to now, how to strike a proper balance between exploration and exploitation for MAs is still a vital problem to be solved. Hence, in this paper, a new swarm-based intelligence optimization algorithm is proposed: Sea-horse Optimizer (SHO). SHO mimics the moving, predating and breeding behaviors of sea horses in nature. The main contributions of this paper can be shown as bellows:

• Different movement modes, the probabilistic predation mechanism and the unique breeding characteristic of sea horses are constructed and expressed mathematically in detail.

• The effectiveness of the proposed algorithm is evaluated on 23 well-known functions and CEC2014 benchmark functions.

• Statistical analysis, convergence analysis, Wilcoxon test, and Friedman test are used to evaluate optimization performance of SHO, and the experimental results are compared with six state-of-the-art metaheuristic algorithms.

• The constraint programming of SHO is studied for dealing with six common engineering design problems.

The remainder of this paper organizes as follows. Section 2 introduces the motivation and mathematical modeling of the proposed algorithm in detail. Section 3 analyzes the experimental results of SHO compared with six metaheuristics on 53 benchmark functions. In Section 4, SHO is applied in engineering design problems. Finally, Section 5 concludes our works and prospects for future studies.

2 Sea-horse optimizer (SHO)

This section presents a detailed introduction of the SHO algorithm. Firstly, this paper provides the life of sea horses and specifies the motivation of the proposed SHO algorithm. Then, the mathematical modellings are constructed. Finally, the complexity of the algorithm is analyzed and discussed.

2.1 Sea horse

The sea horse (Fig. 2), scientifically known as hippocampus, is a general term for several kinds of small fish in warm waters. Sea horses are widely distributed in the tropical, subtropical, and temperate shallow waters [45]. There are about 80 species of sea horses, including some unnamed species [46].

Fig. 2

The behaviors of the sea horse

Sea horse gets its name because its head resembles a horse’s head. The length of a sea horse varies from 2 cm to 30 cm. For example, the adult size of pygmy sea horse is only about 2 cm, while the adult hippocampus abdominalis can be up to 30 cm in length [47]. The snout of a sea horse likes a tubular. Its length affects the rotation of the head and is deemed to be closely related to feeding [48]. Roos et al. [49] investigated that the sea horse has relatively strong predation ability in the larval stage. Sea horses mainly prey on zooplankton and small crustaceans, such as small bran shrimp [50]. When feeding, the tubular kiss extends to the food, puffing out the cheeks and opening the mouth to suck the food. The head of a sea horse generally protrudes from the top, forming a crown. The gills department is uplifted, and the opercular usually has a radial crest. There is only one dorsal fin between trunk and tail for propulsion, and no ventral or caudal fins. Its entire body is completely surrounded by membranous bone plates. Sea horses generally live in clean, low-tide waters that are rich in algal and coral. To rest and escape prey, sea horses change their color with matching that of surroundings.

The tail of a sea horse has a structure and function that no other fish has. Studies [51] have shown that this tail’ cross-sectional area is square, with each layer of bones consisted of four tightly wound L-shaped bones, which is to protect the middle spines and improve the grasping capacity of the tail for wrapping around the attached objects to rest or carry the body weight upside down. Besides, the sea horse has a special swimming posture. After releasing the algae attached to its tail, a sea horse stands with its head upright in the water and relies entirely on its dorsal and pectoral fins for movement.

Sea horses are the one and only animal on earth that males give birth to offspring, as shown in Fig. 2b. The male sea horse has a brood pouch in front or on the side of its abdomen. During mating, the female sea horse releases ova into the brood pouch, and the male is responsible for fertilizing those ova. Meanwhile, the male sea horses keep the fertilized ova in the brood pouch until they are fully formed and then release them into the seawater.

2.2 Inspiration

Predation, movement and breeding behaviors are particularly critical for the life of the sea horse, which are described below.

• In terms of movement behavior, the sea horse sometimes curls the tail around a stem (or leaf) of algae. Since the stems present spiral floating changes around the roots of algae under the action of marine vortices, the sea horse carries out spiral movement at this time. At other times, Brownian motion occurs when the sea horse hangs upside down from drifting algae or other objects and moves randomly with the waves.

• For predation behavior, sea horses make use of the head’s particular shape to sneak up on the prey, and then capture it with up to a 90% chance of success.

• For breeding behavior, the male and female sea horses randomly mate to produce new offspring, which contributes to inheriting certain excellent information from their fathers and mothers.

In summary, these three behaviors enable sea horses to adapt to environment and survive better. The proposed SHO algorithm is mainly inspired by the above-mentioned three behaviors. Therefore, these behaviors are our motivation to develop this novel optimizer through mathematical modellings.

2.3 Sea-horse optimizer

The proposed SHO algorithm consists of three crucial components, i.e., movement, predation and breeding. To balance the exploration and exploitation of SHO, the local and global search strategies are designed for the social behaviors of movement and predation, respectively. And the breeding behavior is performed with the completion of the first two behaviors. Their mathematical modellings would be expressed and discussed as follows in detail.

2.3.1 Initialization

Similar to other existing metaheuristics, SHO also starts from the population initialization. Suppose each sea horse represents a candidate solution in the search space of problems, the whole population of sea horses (termed by Seahorses ) can be expressed as:

$$ Seahorses=\left[\begin{array}{ccc}{x}_1^1& \cdots & {x}_1^{Dim}\\ {}\vdots & \ddots & \vdots \\ {}{x}_{pop}^1& \cdots & {x}_{pop}^{Dim}\end{array}\right] $$

(1)

where Dim denotes the dimension of the variable and pop is the population size.

Each solution is randomly generated between the lower bound and upper bound of a specify problem, denoted by LB and UB, respectively. The expression of the i^th individual X_i in search space [LB, UB] is

$$ {\displaystyle \begin{array}{l}{X}_i=\left[{x}_i^1,\dots, {x}_i^{Dim}\right]\\ {}{x}_i^j=\mathit{\operatorname{rand}}\times \left({UB}^j-{LB}^j\right)+{LB}^j\end{array}} $$

(2)

where rand denotes the random value in [0, 1]. ${x}_i^j$ denotes the j^th dimension in the i^th individual. i is a positive integer ranging from 1 to pop and j is a positive integer in the range [1, Dim]. LB^j and UB^j imply the lower bound and the upper bound of the j^th variable of the optimized problem.

Taking the minimum optimization problem as an example, the individual with the minimum fitness is regarded as the elite individual, denoted by X_elite. X_elite can be obtained by Eq. (3).

$$ {X}_{\boldsymbol{elite}}= argmin\left(f\left({X}_i\right)\right) $$

(3)

where f(⋅) represents the objective function value of a given problem.

2.3.2 The movement behavior of sea horses

For the first behavior, the different movement patterns of sea horses approximately follow the normal distribution randn(0, 1). In order to trade off the exploration and exploitation performance, we take r₁ = 0 as the cut-off point, half for the local mining and the other half for the global search. So movements can be divided into the following two cases.

Case 1

The spiral motion of the sea horse with the vortex in the sea. It mainly realizes the local exploitation of SHO, when the normal random value r₁ is located at the right side of the cut-off point. Sea horses are moving towards the elite X_elite by following the spiral motion. Especially, the Lévy flight [52] is employed to simulate the movement step size of sea horses, which is conducive to the sea horse with the high probability crossing to other positions in early iterations and avoiding the excessive local exploitation of SHO. At the same time, this spiral moving mode of the sea horse changes constantly the rotation angle for expanding the neighborhoods of current local solutions. In this case, it can be expressed mathematically to generate the new position of a sea horse as follows:

$$ {X}_{new}^1\left(t+1\right)={X}_i(t)+ Levy\left(\lambda \right)\left(\left({X}_{elite}(t)-{X}_i(t)\right)\times x\times y\times z+{X}_{elite}(t)\right) $$

(4)

where x = ρ ×  cos (θ), y = ρ ×  sin (θ) and z = ρ × θ denote three-dimensional components of coordinates (x, y, z) under the spiral movement, respectively, which are helpful to update the positions of search agents. ρ = u × e^θv represents the length of the stems defined by the logarithmic spiral constants u and v (Set to u = 0.05 and v = 0.05). θ is the random value between [0, 2π]. Levy(z) is the Lévy flight distribution function and is calculated by Eq. (5) [52].

$$ \boldsymbol{Levy}(z)=s\times \frac{w\times \sigma }{{\left|k\right|}^{\frac{1}{\lambda }}} $$

(5)

In Eq. (5), λ is the random number between [0, 2] (Set to λ = 1.5 in this paper). s is a fixed constant of 0.01. w and k are random numbers between [0, 1]. σ is calculated by using Eq. (6).

$$ \sigma =\left(\frac{\varGamma \left(1+\lambda \right)\times \sin \left(\frac{\pi \lambda}{2}\right)}{\varGamma \left(\frac{1+\lambda }{2}\right)\times \lambda \times {2}^{\left(\frac{\lambda -1}{2}\right)}}\right) $$

(6)

Case 2

The Brownian motion of the sea horse with the sea waves. Under the action of drifting, the exploration of SHO is carried out, when r₁ is located at the left side of the cut-off point. In this case, the search operation is important for the local extremum avoidance of SHO. Brownian motion is applied to mimic another moving length of the sea horse for ensuring its better exploration in the search space. Its mathematical expression for this case is

$$ {X}_{new}^1\left(t+1\right)={X}_i(t)+\mathit{\operatorname{rand}}\ast l\ast {\beta}_t\ast \left({X}_i(t)-{\beta}_t\ast {X}_{elite}\right) $$

(7)

where l is the constant coefficient (Set to l = 0.05 in this paper). β_t is the random walk coefficient of Brownian motion, which is a random value obeying the standard normal distribution in essence. And it can be given by using Eq. (8) [53].

$$ {\beta}_t=\frac{1}{\sqrt{2\pi }}\mathit{\exp}\left(-\frac{x^2}{2}\right) $$

(8)

Totally, these two cases can be formulated to obtain the new position of the sea horse at iteration t as follows.

$$ {\displaystyle \begin{array}{l}{X}_{new}^1\left(t+1\right)=\\ {}\Big\{\begin{array}{ll}{X}_i(t)+ Levy\left(\lambda \right)\left(\left({X}_{elite}(t)-{X}_i(t)\right)\times x\times y\times z+{X}_{elite}(t)\right)& {r}_1>0\\ {}{X}_i(t)+\mathit{\operatorname{rand}}\ast l\ast {\beta}_t\ast \left({X}_i(t)-{\beta}_t\ast {X}_{elite}\right)& {r}_1\le 0\end{array}\end{array}} $$

(9)

where r₁ = randn() is a normal random number.

Figure 3 illustrates the position updating diagram of the sea horse by following two kinds of different movement modes, i.e., the spiral or Brownian motion, and both are reflected the moving randomness of the sea horse based on the uncertain environment in the sea.

Fig. 3

Different motion patterns of the sea horse in sea

2.3.3 The predation behavior of sea horses

There are two outcomes for the sea horse to prey on zooplankton and small crustaceans: success and failure. Considering that the probability of the sea horse succeed in capturing food is over 90%, the random number r₂ of SHO is designed to distinguish these two results and set to a critical value with 0.1. Since the elite, to a certain, indicates the approximate position of the prey, the predation success emphasizes the exploitation ability of SHO. If r₂ > 0.1, it means that the predation of the sea horse is successful, that is, the sea horse sneaks up on the prey (elite), moves faster than the prey and finally captures it. Otherwise, when the predation fails, the response speed of both is opposite to that before, which implies the sea horse trends to explore the search space. The mathematical expression of this predation behavior is:

$$ {\displaystyle \begin{array}{l}{X}_{new}^2\left(t+1\right)=\\ {}\Big\{\begin{array}{cc}\alpha \ast \left({X}_{elite}-\mathit{\operatorname{rand}}\ast {X}_{new}^1(t)\right)+\left(1-\alpha \right)\ast {X}_{elite}& if\kern0.20em {r}_2>0.1\\ {}\left(1-\alpha \right)\ast \left({X}_{new}^1(t)-\mathit{\operatorname{rand}}\ast {X}_{elite}\right)+\alpha \ast {X}_{new}^1(t)& if\kern0.1em {r}_2\le 0.1\end{array}\end{array}} $$

(10)

where ${X}_{new}^1(t)$ denotes the new position of the sea horse after movement at the iteration t. r₂ is the random number between [0, 1]. α decreases linearly with iterations to adjust the moving step size of the sea horse for hunting prey, and calculates by Eq. (11).

$$ \alpha ={\left(1-\frac{t}{T}\right)}^{\frac{2t}{T}} $$

(11)

where T denotes the maximum number of iterations.

Figure 4 displays the two possible outcomes of the predation behavior of the sea horse. As shown in Fig. 4, the blue star position indicates the updated position of the sea horse, and the approximate position of the prey is marked with the red dot. It can be seen from Fig. 4a that when the sea horse preys successfully, the sea horse moves to the elite position. Under the control of parameter α, it will gradually converge to the global optimal individual with the iterations increasing. In Fig. 4b, the global search is performed because the prey cannot be captured. The parameter 1 − α is applied to the vector between the current individual and the elite, and α is acted on the current updated individual. This is designed to allow sea horses to globally search in the early iterations and avoid over-exploiting in the later iterations.

Fig. 4

Predation process of the sea horse

2.3.4 The breeding behavior of sea horses

The population is categorized into male and female groups according to their fitness values. It is worthwhile emphasizing that, since male sea horses are responsible for breeding, the SHO algorithm takes half of the individuals with best fitness values as fathers and the other half as mothers. This division will facilitate the inheritance of good characteristics between fathers and mothers for producing the next generation, and avoid the over-localization of new solutions. The concise mathematical expression for the role assignment of sea horses is

$$ {\displaystyle \begin{array}{l} fathers={X}_{sort}^2\left(1: pop/2\right)\\ {} mothers={X}_{sort}^2\left( pop/2+1: pop\right)\end{array}} $$

(12)

where ${X}_{\boldsymbol{sort}}^2$ denotes all ${X}_{new}^2$ in ascending order of fitness values. fathers and mothers indicate from the male and female populations, respectively.

Males and females are randomly mated to produce new offspring. To make the proposed SHO algorithm execute easily, it is assumed that each pair of sea horses only breeds a child. The expression of the i^th offspring is as follows.

$$ {X}_i^{\boldsymbol{offspring}}={r}_3{X}_i^{\boldsymbol{father}}+\left(1-{r}_3\right){X}_i^{\boldsymbol{mother}} $$

(13)

where r₃ is the random number between [0, 1]. i is a positive integer in the range of [1, pop/2]. ${X}_i^{\boldsymbol{father}}$ and ${X}_i^{\boldsymbol{mother}}$ represent randomly selected individuals from the male and female populations, respectively.

The breeding process of sea horses is shown in Fig. 5. As seen from Fig. 5a, each individual is sorted in ascending order according to their fitness values. Figure 5b shows approximatively the position of a new generated offspring. It is randomly created in the line between parents, which effectively transmits genetic information between two subpopulations.

Fig. 5

Breeding process of sea horses

2.3.5 The implementation process of SHO

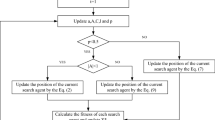
The pseudo-code of the proposed SHO algorithm is shown in Algorithm 1. The implementation process of SHO starts the population initialization by creating a set of random solutions. After the sea horse population is updated by Eqs. (9) and Eq. (10), Eq. (11) is employed to breed the offspring. A new population is composed of the offspring and the previous updated sea horses. However, the size of this new population is 1.5Pop. To prevent the population from expanding without limit, each individual in the new population is estimated. Individuals are sorted in ascending order from top to bottom according to fitness values, and the first pop sea horses are iteratively selected as the new population for the next evolutionary process.

2.4 Computational complexity

The complexity is an important indicator to theoretically measure the optimization performance of algorithms. The time and space complexity of the proposed algorithm are discussed below.

The time complexity analysis is as follows.

• (i) It takes O(n × Dim) time to initialize the population of sea horses, where n denotes the population size and Dim represents the dimension of variables. O(n) is required to calculate the fitness value of each sea horse.

• (ii) During iterations, calculating the fitness value of each sea horse is O(Maxiteration × n) time, where Maxiteration is the maximum number of iterations.

• (iii) In SHO, defined the movement behavior, predation behavior and breeding behavior of sea horses need O(Maxiteration × n × Dim) time.

Hence, the total computational time complexity of the proposed SHO algorithm is O(Maxiteration × n × Dim).

For the space complexity, the maximum space is considered to be occupied during the generation of the offspring in the iterations. Therefore, the space complexity of SHO is O(n × Dim).

3 Experimental results and discussion

This section is the simulation experiment of SHO. To validate SHO’s performance of local exploitation, local extremum avoidance and global exploration, the statistical analysis and convergence analysis were performed on 23 well-known functions and CEC2014 benchmark functions. Then, the high dimensional optimization performance of SHO was also verified. Finally, statistical tests were carried out on these test functions. Six state-of-the-art metaheuristics, namely GA [11], DA [19], SCA [40], ChOA [24], TSA [25] and SFO [30], were compared with our proposed SHO algorithm. Table 1 shows the parameter settings of all metaheuristics. All experiments have been accomplished on MatlabR2018a version with the operating system of Windows 10(64-bit) and Intel(R) Core(TM) I7-9750H CPU (@ 2.60 GHz).

Table 1 Parameter settings of all algorithms

3.1 Benchmark functions

23 well-known functions can be grouped into three categories, namely unimodal, multimodal and fixed-dimension multimodal functions. In detail, the unimodal functions F1 − F7 (in Table 2) have one and only one global optimal value, which are used to estimate the convergence accuracy and convergence speed. Multimodal functionsF8 − F13 (in Table 3) with multiple local optimums are appropriate for testing the local extreme avoidance and the global exploration performance. The global exploration ability in low-dimensional conditions can be tested by fixed-dimension multimodal functions F14 − F23 (in Table 4). Moreover, the proposed SHO algorithm is further evaluated in the modern universal test suite CEC2014 benchmark functions, as reported in Table 5. CEC2014 suite is the general test standard of modern algorithms, which has strong test suitability for all kinds of metaheuristic algorithms. Because of the dynamic and complexity of these benchmark functions, they are more convincing to validate the optimization performance of the proposed SHO. In order to keep the competition fairness and objectivity of each metaheuristic, all algorithms have been independently run for 30 times in each experiment. Mean (Mean) and Standard deviation (Std) results of 30 experiments were employed as statistical indicators to measure their optimization performance.

Table 2 Unimodal functions

Table 3 Multimodal functions

Table 4 Fixed-dimension Multimodal functions

Table 5 Summaries of CEC-2014 benchmark functions [54]

3.2 Qualitative analysis

This experiment was performed on the first two dimensions of variables in 23 well-known functions, mainly aiming to observe the behavioral optimization ability of SHO. The population size and the maximum number of iterations were set to 30 and 500, respectively. Figure 6 depicts the qualitative measurements of SHO for tackling partial unimodal and multimodal functions. The first column describes the topological structures of test functions in a two-dimensional view of the first two variables. The last 4 columns are the test indictors, respectively the search history, the trajectory of 1st sea horse in the first dimension, the average fitness of all sea horses and convergence curve.

Fig. 6

Quantitative analysis results included topological structure, search history, the trajectory of 1st sea horse, average fitness of all sea horses and convergence curve

The search history can reflect the position distribution of all sea horses during the iterative process, where the red rot represents the global optimal solution obtained by SHO. It can be evidently detected from the second column of Fig. 6 that numerous search agents cluster surrounding global optimum in unimodal functions. Yet for multimodal functions, many search agents scatter mostly near multiple local optima in the whole search space. For unimodal functions, it is beneficial to the local re-exploitation of the proposed SHO algorithm to seek a higher accuracy. In terms of multimodal functions, the decentralized form reveals sea horses’ exploration throughout the whole region and the tradeoff situation among several local optimal values.

The first dimensional trajectory of 1st sea horse is devoted to reflect the primary exploratory behavior of the search agent. As shown in the third column of Fig. 6, the curve fluctuates significantly in the initial stage of iterations, while the amplitude of vibration tends to be slow felt in late iterations. The curve changes guarantee that SHO turns from global exploration to local exploitation iterative process by degrees. In unimodal functions, the duration of the oscillation state is short, which indicates that SHO converges quickly. However, the difference is that the oscillation state in multimodal functions usually lasts for long times, even exceeding 60%–70% of the iterative process, which reflects the global exploration capacity of SHO.

The average fitness value represents the average target value of all sea horses in each iteration. It is mainly used to reflect the general tendency of population evolution. In the fourth column of Fig. 6, it can be found intuitively that the entire population progresses from the initial stage to the last. With the constant updating of sea horses, the average fitness values lean to decline. For unimodal functions, the curve drops rapidly merely at the beginning of iteration. After the rapid descent, the tangent slope of the curve fluctuation verges on stable. This embodies that SHO converges to near the optimal value in early iterations and then strengthens the exploitation accuracy. In contrast, multimodal functions have steeper curve rates. The amplitude of the curve decreases with the increase of the number of iterations, which implies the global exploration in the early stage and local exploitation in the later stage of SHO.

The convergence curve represents the behavior of the optimal solution obtained by the sea horse so far. In unimodal functions, the curves drop rapidly after refining solutions. The curves of most multimodal functions descend step by step. This is due to jumping out close a local optimal solution and gradually searching to the global optimal solution. Meanwhile, the switching time between global exploration and local exploitation can also be seen from curves.

3.3 Exploitation analysis

Table 6 shows the statistical results of SHO and other methods evolving 15,000 (30 × 500) times on unimodal functions. According to Table 6 analysis, SHO achieves best results in 12/14 indicators. For Mean indexes, SHO can outperform other algorithms on seven unimodal functions. The average optimization performance of GA, DA and SFO perform poorly on functions F1, F2, F3, F5, and F6. For functions F1, F2, and F3, SHO has a greater competitive advantage in optimization accuracy than TSA, which ranked 2. For Std indexes, SHO is optimal on other functions except functions F5 and F6. Std indicators for functions F5 and F6, in spite of ChOA is the best followed by SHO, the accuracy is the same order of magnitude as ChOA and the difference is not remarkable. Unimodal test results demonstrate that SHO has the advantages of higher local exploitation capacity, high convergence accuracy, and strong algorithm stability and robustness. Meanwhile, these testing results indicate that the long step search of the spiral motion influenced by vortex and the search to the elite in the predation stage can ensure the exploitation of the searching agents for the global optimal.

Table 6 Statistical results of unimodal functions

3.4 Exploration analysis

Table 7 provides the statistical results of 15,000 (30 × 500) evolutions of each algorithm on multimodal functions. Multimodal functions have several local optimal values, which are applied to test the global optimization ability of the algorithm. Table 7 reveals that SHO performs best in 5/6 of multimodal functions for Mean indicators. For functions F9 and F10, SHO can obtain the global optimal value, while other algorithms can only search for lower precision (i.e., GA and DA). Likewise, SHO has more outstanding exploration capacity than other algorithms on functions F10, F12and F13. It shows that Brownian motion under the action of drifting plays an important role in these functions. To some extent, SHO can jump out of local extreme values and develop to the global optimal. For function F8, GA ranked first in average optimization performance, and TSA ranked second. For functions F9, F10, F11, and F12, the standard deviation results of SHO are better than other algorithms, especially the standard deviation results of SHO on functions F9 and F11 can reach 0. In addition, the Std results of ChOA are optimal on functions F8 and F13.

Table 7 Statistical results of multimodal functions

Table 8 shows the statistical results of all algorithm evolutions for 15,000 (30 × 500) times on fixed-dimension multimodal functions. It can be seen from Table 8 that SHO has superior Mean indicators on functions F15, F16, F17, and F18. For function F14, ChOA has the best Mean and Std indicators and DA achieves suboptimal optimization results. SHO obtains the best average fitness and minimal Std indicator on function F15. Although SCA, DA, SFO, CHOA and SHO can find global optimal value on function F16, SHO has better standard deviation result, which proves that SHO is still competitive. For functions F17 and F18, DA, SFO and SHO can obtain the global optimal value, as well as the corresponding Std indicators are SFO and SHO minimum respectively. However, SHO’s optimization performance on functions F19 to F23 are relatively general, but SHO is still better than some comparison algorithms such as GA, SCA and CHOA. For function F19, DA’s Mean and Std results are the best and SFO gets the second-best results. TSA has the best Mean indicator on function F20. DA is superior to other algorithms on function F21. For functions F22 and F23, DA and SFO respectively achieve best Mean indicators.

Table 8 Statistical results of fixed-dimension multimodal functions

The results of multimodal functions show that SHO has good global optimization performance and can effectively avoid local extremums. Competing with the new or state-of-the-art metaheuristic methods, SHO still has high convergence accuracy and strong robustness. The results reflect the global exploration by Brownian motion and the population diversity of generated offspring.

3.5 Convergence analysis

Convergence analysis can clearly comprehend local exploitation and global exploration process of the algorithm. Figure 7 shows the convergence curves of GA, DA, SCA, SFO, TSA, ChOA and SHO for partial test functions. As can be seen from the Fig. 7, SHO has the better parallel optimization capacity. The differences of local exploiting performance between different algorithms are presented on functions F3, F5 and F7, and SHO’s optimization ability is the best in these functions. For the reason that SHO is impacted by the adaptive parameter α and the way of the spiral motion, which make SHO converge toward the optimal solution faster than other comparison algorithms, and subsequently re-exploit the optimization precision. However, other algorithms are defective in obtaining higher convergence accuracy under the same population size and iteration numbers. The convergence curves of multimodal functions show the global optimization potential of different algorithms. For function F10, SHO has the most obvious exploration performance. It firstly jumps out of the local optimal value and concentrates accurately near global optimums, while other algorithms converge slowly. It should be noted that on function F11, SHO achieves the global optimal value 0 during iterations. Since the figure shows an average fitness value in logarithmic terms, the curve breaks during iterations. For function F12, apart from the rapid convergence in early iterations, SHO can still be re-exploited in late iterations. For function F15, SHO shows outstanding optimization accuracy. Even if other algorithms, such as DA and SFO, can find the global optimal value, SHO has the fastest convergence speed on functions F16 and F18. Convergence curves of SHO on multimodal functions show that, sea horses tend to seek optimal solution in the whole search space through Brownian motion of floating action and offspring renewal in early iterations, while sea horses exploit precisely through spiral motion and the successful predation stage in later iterations. Therefore, convergence analysis proves that the proposed SHO is effective.

Fig. 7

Convergence analysis of SHO and comparison algorithms

3.6 Performance analysis of SHO on CEC2014 benchmark functions

To further verify SHO’s local extremum avoidance, the challenging CEC2014 benchmark functions are used to test compared with six well-known algorithms. The maximum number of iterations for all algorithms is set to 1000. CEC2014 benchmark functions are composed of basic functions via translation, rotation, or combination. They are more difficult to search for optimization in that their functions are fairly dynamic and complex with many local optimal values. Table 9 shows the test results of SHO and six comparison algorithms. It can be seen that SHO obtains better average fitness values on 21/30 functions. In terms of unimodal functions, SHO achieves the best Mean and Std results compared other algorithms on functions CEC − 1 and CEC − 3, while the Mean and Std results of DA are the best on functions CEC − 2 and CEC − 4. GA and SFO are inferior to that of other algorithms on unimodal functions. For multimodal functions CEC − 5, CEC − 6, CEC − 8, CEC − 10, CEC − 11, CEC − 12, and CEC − 15, SHO outperforms other algorithms with stronger exploration performance. Moreover, SHO has the minimum Std result on function CEC − 12. SHO also shows stronger optimization performance on most of hybrid functions. For example, SHO achieves the best Mean results on functions CEC − 17, CEC − 20, CEC − 21 and CEC − 22, and has the best Std result on function CEC − 20. Except functions CEC − 26 and CEC − 28, SHO’s Mean results can obtain the best on the other composition functions, and its Std values are the minimum on functions CEC − 24 and CEC − 25. The test results on CEC2014 benchmark functions further show that SHO is more competitive than other algorithms.

Table 9 Results of the comparative methods on CEC2014 benchmark functions

Figure 8 shows the boxplots for seven algorithms on CEC2014 benchmark functions. If ‘+’ has appeared outside the upper limit, it meant that the algorithm has a poor search accuracy in 30 runs. Otherwise, if ‘+’ was outside the lower limit, it indicated that the algorithm can be fully explored and exploited to search for the superior precision value. It can be seen from the Fig. 8 analysis that SHO displays ‘+’ out of the upper edge for a total of 3 times (functions CEC − 6, CEC − 10 and CEC − 20), which has the least number of occurrences compared with other algorithms. The medians of SHO are lower than that of the other six algorithms. Additionally, SHO has the smallest differences between upper and lower limits of functions CEC − 20 and CEC − 25. The boxplots verifies that SHO has strong robustness and stability. As described above, SHO algorithm shows superior optimization performance on CEC2014 benchmark functions.

Fig. 8

Box plot of the proposed SHO and six comparison algorithms on CEC2014 benchmark functions

3.7 Scalability analysis of SHO

This subsection evaluates the adaptability of SHO in high dimensional problems. In order to make compares more concise and effective, two groups of experiments were conducted by selecting representative test functions. The first set of functions came from F1, F2, F3, F12 and F13 of 23 well-known functions. They can test the local exploitation accuracy and global optimization ability of the algorithm, representing the traditional unimodal test functions. For the first group, dimensions were set to 10, 30, 50, 100, and 500. The second experiment was designed for high-dimensional optimization performance on CEC2014 benchmark functions. In the second set, simple multimodal functions CEC − 5, hybrid function CEC − 22, composition functions CEC − 24, CEC − 25 and CEC − 27 were selected. Because of the complexity of composition functions, they are more difficult to search for optimization in high dimensions. Using these functions evaluate the performance of the algorithm to deal with high-dimensional problems more closely to the difficulty of practical application problems, which make the scalability analysis more sufficient. Since the CEC2014 benchmark functions ran with variable dimensions only 10, 30, 50 and 100, these four dimensions were tested separately. SHO is compared with the above six comparison algorithms. Each algorithm was operated independently for 30 times, and the average fitness value is taken as the statistical indicator. The population size and maximum iteration times of group 1 and group 2 were set to 30 × 500 and 30 × 1000, respectively.

Figure 9 shows the change trends of log-average fitness values for seven algorithms in different dimensions. As can see from Fig. 9 that y values of all algorithms are in positive proportion to the increase of x values. This suggests that higher dimensions lead to problems solving more difficult. In the first set experiment, SHO is able to maintain the optimal average fitness value in the high-dimensional case for six functions, compared with other algorithms. The SHO algorithm is obviously superior to other comparison algorithms in all dimensions on functions F1, F3, and F4. On function F2, the change amplitude of y value is basically the same when the seven algorithms transition from 10 dimension to 100 dimension. However, from 100 to 500 dimensions, GA and SFO algorithms change more, while other algorithms are more stable. The slope of SHO curve changes more stable than other algorithms, especially on functions F10 and F12 when the dimension transitions from 100 to 500. The first set of experimental results confirm the dimensional insensitivity of SHO. Simultaneously, SHO can accurately track the difficulty of problems caused by the increase of dimensions, and search for better accuracy. In the second set of the experiment, SHO remains optimal in each dimension of functions CEC − 5, CEC − 12 and CEC − 27. For function CEC − 22, the variation degree of SHO, DA and SCA have things in common. Even though DA is better than SHO when the dimension is 50, SHO is still optimal in the dimension 100. On function CEC − 24, SHO and ChOA have similar searching accuracy in each dimension. For function CEC − 25, seven algorithms do not change significantly when the dimension rises from 10 to 30, however, as the dimension is larger, SHO can still outperform other algorithms while keeping the original parallel optimization accuracy. High-dimensional test results show that SHO is a reliable algorithm that maintains an effective best-finding situation and adaptability in handling more complex high-dimensional problems.

Fig. 9

Scalability analysis of different algorithms

3.8 Statistical analysis

In order to avoid accidental test results, statistical tests are performed by using the Wilcoxon rank-sum test statistical method [55] applying a significance level of 5%. Further this method is used to evaluate the effectiveness and superiority of SHO. SHO was used as the control algorithm, and pairwise comparison was made with the other six algorithms. If the p value generated by the two algorithms is less than 5%, it indicates that there is a significant difference between the two algorithms in statistical significance. Otherwise, the difference between the two algorithms is not obvious. Two groups of tests were conducted. The first group performed mann-Whitney U test of SHO on the first 13 well-known functions. The second group was a more powerful mann-Whitney U test on CEC2014 benchmark functions.

Tables 10 and 11 are the summary of test results, where ‘+’ represents significant difference and ‘-’ represents poor significant difference. In Table 10, SHO conducts 78 (13 × 6) groups of experiments, among which 74 groups of data shows significant differences. 157 of 180 (30 × 6) comparisons are ‘+’ in Table 11. The results of the two groups verify that the optimization performance of the SHO algorithm is better than the other six comparison algorithms in the statistical sense.

Table 10 Wilcoxon rank-sum test results for SHO against other algorithms on 13 well-known functions

Table 11 Wilcoxon rank-sum test results for SHO against other algorithms on CEC2014 benchmark functions

In addition, Friedman rank test [56] is a nonparametric method that uses rank to implement significant differences for multiple population distributions. Friedman rank tests of seven algorithms were performed on the most challenging CEC2014 benchmark functions to compare their comprehensive average performance. Table 12 shows Friedman test results of seven algorithms. As is shown in Table 12, SHO ranked the first and is significantly better than the other six comparison algorithms. Thus, Friedman rank tests demonstrate that the proposed SHO is effective and stable.

Table 12 Friedman rank test results for SHO and other algorithms on CEC2014 benchmark functions

4 SHO for engineering design problems

In this section, the proposed SHO is applied to solve five real-world optimization problems, namely tension/compression spring design problem, reducer design problem, pressure vessel design problem, cantilever beam design problem, and welded beam design problem. Meanwhile, SHO is compared with some famous metaheuristic algorithms to evaluate its constraint programmability. Since real-world optimization problems have been constrained by inequalities or equalities, a simple method to deal with constraints was adopted that was the static penalty function. In this method, the solution is punished for violating the constraints, thus a constrained problem is converted into an unconstrained problem. For each real-world optimization problem, SHO was independently run for 30 times, as well as the statistical indicators consisted of maximum value (Worst), minimum value (Best), mean value (Mean) and standard deviation (Std) of 30 runs. The population size and the maximum number of iterations were set to 30 and 500.

4.1 Tension/compression spring design problem

In this case, it can define goals as minimizing the weight of the spring. Its specific design is shown in Fig. 10. There are three decision variables in this problem, which are wire diameter (d), mean coil diameter (D) and the number of active coils (N). The mathematical model is as follows.

$$ {\displaystyle \begin{array}{c}\overrightarrow{x}=\left[{x}_1,{x}_2,{x}_3\right]=\left[d,D,N\right]\\ {}\min \kern0.30em Z\left(\overrightarrow{x}\right)=\left({x}_3+2\right){x}_2{x_1}^2\end{array}} $$

Fig. 10

Tension/compression spring design problem

$$ {\displaystyle \begin{array}{c}s.t.\kern0.5em {g}_1\left(\overrightarrow{x}\right)=1-\frac{x_2^3{x}_3}{71785{x}_1^4}\le 0\\ {}\kern0.5em {g}_2\left(\overrightarrow{x}\right)=\frac{4{x}_2^2-{x}_1{x}_2}{12566\left({x}_2{x}_1^3-{x}_1^4\right)}+\frac{1}{5108{x}_1^2}\le 0\\ {}\begin{array}{cc}& {g}_3\left(\overrightarrow{x}\right)=1-\frac{140.45{x}_1}{x_2^2{x}_3}\le 0\end{array}\\ {}\begin{array}{cc}& {g}_4\left(\overrightarrow{x}\right)=\frac{x_1+{x}_2}{1.5}-1\le 0\end{array}\end{array}} $$

(14)

In this case, the limits of decision variables are 0.05 ≤ x₁ ≤ 2.00,0.25 ≤ x₂ ≤ 1.30 and 2.00 ≤ x₃ ≤ 15 .00. Presently, metaheuristic algorithms that have been successfully applied this problem including GA [57], CA [58], CPSO [59], WOA [38], GEO [28], SCA [60], HS [60], GWO [42], and AOA [38]. The proposed SHO algorithm is compared with these algorithms, and the optimal results obtained by each algorithm are shown in Table 13. As can be seen from Table 13, SHO can reach the minimum optimal value compared with ten algorithms. Table 14 shows the statistical results of all algorithms. Apparently, on the premise of less evolutions, SHO still has lower Mean and Std indicators than other algorithms. The results of the two tables prove that SHO has good applicability in this problem.

Table 13 Optimal results of different algorithms for tension/compression spring design problem

Table 14 Statistical results of different algorithms for tension/compression spring design problem

4.2 Reducer design problem

Reducer design problem is to design a simple gear box between the engine and propeller of the aircraft, so as to facilitate the normal operation of the propeller and engine. The specific schematic diagram of reducer design problem is shown in Fig. 11. The objective of this problem finds the combination that minimizes the total number of reducers, which involves constraints such as bending stress of the gear teeth, surface stress, transverse deflections of the shafts and stresses in the shafts. There are seven decision variables to control this problem, namely, face width (x₁), the module of teeth (x₂), number of teeth in the pinion (x₃), length of the first shaft between bearings (x₄), length of the second shaft between bearings (x₅), diameter of first (x₆) and diameter of the second shafts (x₇). The mathematical expression is as follows.

$$ {\displaystyle \begin{array}{c}\min \kern0.3em Z=0.7854{x}_1{x}_2^2\left(3.3333{x}_3^2+14.9334{x}_3-43.0934\right)-\\ {}1.508{x}_1\left({x}_6^2+{x}_7^2\right)+7.4777\left({x}_6^3+{x}_7^3\right)+0.7854\left({x}_4{x}_6^2+{x}_5{x}_7^2\right)\end{array}} $$

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}s.t.{g}_1(x)=\frac{27}{\left({x}_1{x}_2^2{x}_3\right)}-1\le 0\\ {}{g}_2(x)=\frac{397.5}{\left({x}_1{x}_2^2{x}_3^2\right)}-1\le 0\end{array}\\ {}{g}_3(x)=\frac{1.93{x}_4^3}{\left({x}_2{x}_3{x}_6^4\right)}-1\le 0\end{array}\\ {}{g}_4(x)=\frac{1.93{x}_5^3}{\left({x}_2{x}_3{x}_7^4\right)}-1\le 0\\ {}{g}_5(x)=\frac{1}{\left(110{x}_6^3\right)}\times \sqrt{{\left(\frac{745{x}_4}{x_2{x}_3}\right)}^2+16.9\times {10}^6}-1\le 0\end{array}\\ {}{g}_6(x)=\frac{1}{\left(85{x}_7^3\right)}\times \sqrt{{\left(\frac{745{x}_5}{x_2{x}_3}\right)}^2+157.5\times {10}^6}-1\le 0\\ {}{g}_7(x)=\frac{x_2{x}_3}{40}-1\le 0\end{array}\\ {}{g}_8(x)=5\frac{x_2}{x_1}-1\le 0\\ {}{g}_9(x)=\frac{x_1}{12{x}_2}-1\le 0\end{array}\\ {}{g}_{10}(x)=\frac{1.5{x}_6+1.9}{x_4}-1\le 0\\ {}{g}_{11}(x)=\frac{1.1{x}_7+1.9}{x_5}-1\le 0\end{array}} $$

(15)

Fig. 11

Speed reducer design problem

Range of decision variables: ${\displaystyle \begin{array}{c}2.6\le {x}_1\le \mathrm{3.6,0.7}\le {x}_2\le \mathrm{0.8,17}\le {x}_3\le 28\\ {}7.3\le {x}_4\le \mathrm{8.3,7.3}\le {x}_5\le \mathrm{8.3,2.9}\le {x}_6\le \mathrm{3.9,5.0}\le {x}_7\le 5.5\end{array}}$

The proposed algorithm is compared with SC [61], GA [38], HS [60], SCA [60], GWO [42], WOA [42], HGSO [37] and AOA [38] previously applied, and the optimal results are shown in Table 15. According to Table 15 analysis, SHO is able to obtain the best solution compared with eight algorithms, which is obviously better than GA, SCA, and HS. Table 16 shows the statistical results of all algorithms. SHO can obtain the optimal value for Mean indicator under the precondition of fewer evolution times, but the shortcoming is that Std indicator has not reached the expected result.

Table 15 Optimal results of different algorithms for speed reducer design problem

Table 16 Statistical results of different algorithms for speed reducer design

4.3 Pressure vessel design

The primary objective of pressure vessel design minimizes the total cost of material forming and welding for cylindrical vessels. Figure 12 shows the design of pressure vessel design and the representation of parameters at the corresponding locations. This problem contains four decision variables, namely shell thickness (T_s), head thickness (T_h), entry radius (R), and length of cylindrical section without considering the head (L). The mathematical expression is described as follows.

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\begin{array}{c}\overrightarrow{x}=\left[{x}_1,{x}_2,{x}_3,{x}_4\right]=\left[{T}_s,{T}_h,R,L\right]\\ {}\begin{array}{c} minz\left(\overrightarrow{x}\right)=0.6224{x}_1{x}_3{x}_4+1.7781{x}_2{x}_3^2+\\ {}3.1661{x}_1^2{x}_4+19.84{x}_1^2{x}_3\end{array}\\ {}s.t.{g}_1\left(\overrightarrow{x}\right)=-{x}_1+0.0193{x}_3\le 0\end{array}\\ {}{g}_2\left(\overrightarrow{x}\right)=-{x}_2+0.00954{x}_3\le 0\\ {}{g}_3\left(\overrightarrow{x}\right)=-\pi {x}_3^2{x}_4-\frac{4}{3}\pi {x}_3^3+1296000\le 0\end{array}\\ {}{g}_4\left(\overrightarrow{x}\right)={x}_4-240\le 0\\ {}0\le {x}_1\le 990\le {x}_2\le 9910\le {x}_3\le 20010\le {x}_4\le 200\end{array}} $$

(16)

Fig. 12

Pressure vessel design

Table 17 displays the optimal results of SHO and comparison algorithms such as CPSO [59], SMA [27], GWO [60], WOA [38], HHO [23], AEO [62], SCA [60], MPA [26], EO [39], AOA [38], and AO [63] for solving this problem. It can be detected from the Table 17 that the proposed SHO algorithm is superior to elven algorithms. It is noted that the comparison results are more obvious for MFO, WOA, and CPSO. In addition, it is comparable to new algorithms MPA, AOA, and AO. Table 18 shows the statistical results of these algorithms. SHO achieves the best Mean indicator. This result indicates that SHO can replace some traditional algorithms to solve this problem well after improving the number of evolutions.

Table 17 Optimal results of different algorithms for pressure vessel design

Table 18 Statistical results of different algorithms for pressure vessel design

4.4 Cantilever beam design problem

The purpose of this problem is to discover the optimal weight of the cantilever arm with setting an upper limit on the vertical displacement of the free end. Figure 13 exhibits a concrete illustration of a cantilever beam. The cantilever beam consists of five elements, each of which is a hollow section with a constant thickness. There are five decision variables and one constraint in the case. The mathematical expression is as follows.

$$ {\displaystyle \begin{array}{c}\min Z(x)=0.0624\times \left({x}_1+{x}_2+{x}_3+{x}_4+{x}_5\right)\\ {}\begin{array}{cc}s.t.& g(x)=\frac{61}{x_1^3}+\frac{37}{x_2^3}+\frac{19}{x_3^3}+\frac{7}{x_4^3}+\frac{1}{x_5^3}-1\le 0\\ {}& 0.01\le {x}_1,{x}_2,{x}_3,{x}_4,{x}_5\le 100\end{array}\end{array}} $$

(17)

Fig. 13

Cantilever beam design problem

Table 19 lists the optimal results of SHO, MA [64], GCA_I [64], GCA_II [64], and MFO [65]. SHO outperforms four comparison algorithms. Table 20 shows the statistical results of these algorithms.

Table 19 Optimal results of different algorithms for cantilever beam design problem

Table 20 Statistical results of different algorithms for cantilever beam design problem

4.5 Welded beam design

The design cost of welding beam is minimized under the constraint of weld shear stress (τ), bending stress (σ) in the beam, buckling load (P_c) on the rod and deflection of the beam end (δ). There are four variables that determine this problem, namely welding thickness (h), length of bar attachment (l), bar height (t) and bar thickness (b) (Fig. 14).

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\overrightarrow{x}=\left[{x}_1,{x}_2,{x}_3,{x}_4\right]=\left[h,l,t,b\right]\\ {} minZ\left(\overrightarrow{x}\right)=1.10471{x}_1^2{x}_2+0.04811{x}_3{x}_4\left(14.0+{x}_2\right)\end{array}\\ {}s.t.{g}_1\left(\overrightarrow{x}\right)=\tau \left(\overrightarrow{x}\right)-13600\le 0\\ {}{g}_2\left(\overrightarrow{x}\right)=\sigma \left(\overrightarrow{x}\right)-30000\le 0\end{array}\\ {}{g}_3\left(\overrightarrow{x}\right)=\delta \left(\overrightarrow{x}\right)-0.25\le 0\\ {}{g}_4\left(\overrightarrow{x}\right)={x}_1-{x}_4\le 0\end{array}\\ {}{g}_5\left(\overrightarrow{x}\right)=P-{P}_c\left(\overrightarrow{x}\right)\le 0\\ {}{g}_6\left(\overrightarrow{x}\right)=0.125-{x}_1\le 0\end{array}} $$

(18)

Fig. 14

Welded beam design problem

${g}_7\left(\overrightarrow{x}\right)=1.10471{x}_1^2+0.04811{x}_3{x}_4\left(14.0+{x}_2\right)-5.0\le 0$ 0.1 ≤ x₁ ≤ 20.1 ≤ x₂ ≤ 100.1 ≤ x₃ ≤ 100.1 ≤ x₄ ≤ 2

where $\tau \left(\overrightarrow{x}\right)=\sqrt{{\left({\tau}^{\prime}\right)}^2+2{\tau}^{\prime }{\tau}^{\prime \prime}\frac{x_2}{2R}+{\left({\tau}^{\prime \prime}\right)}^2},{\tau}^{\prime }=\frac{6000}{\sqrt{2}{x}_1{x}_2}$,

$$ {\displaystyle \begin{array}{c}\begin{array}{c}{\tau}^{\prime \prime }=\frac{MR}{J},M=6000\left(14+\frac{x_2}{2}\right),R=\sqrt{\frac{x_2^2}{4}+{\left(\frac{x_1+{x}_3}{2}\right)}^2}\\ {}J=2\left\{\sqrt{2}{x}_1{x}_2\left[\frac{x_2^x}{4}+{\left(\frac{x_1+{x}_3}{2}\right)}^2\right]\right\},\sigma \left(\overrightarrow{x}\right)=\frac{504000}{x_4{x}_3^2}\end{array}\\ {}\delta \left(\overrightarrow{x}\right)=\frac{65856000}{\left(30\times {10}^6\right){x}_3^2{x}_4}\\ {}{P}_c\left(\overrightarrow{x}\right)=\frac{4.013\left(30\times {10}^6\right)\sqrt{\frac{x_3^2{x}_4^6}{36}}}{196}\left(1-\frac{x_3}{28}\sqrt{\frac{30\times {10}^6}{4\left(12\times {10}^6\right)}}\right)\end{array}} $$

Table 21 shows the optimal solutions of SHO, HHO [23], CPSO [59], GWO [60], SCA [60], WOA [38], GEO [28] and MVO [60] algorithms for tackling this problem. Among the eight algorithms, SHO has the better design cost, which confirms that SHO has higher optimization ability. The statistical results of these algorithms are given in Table 22. It can be seen that SHO has better Mean and Std indicators. Hence, these results prove that SHO can achieve ideal results with other algorithms at a lower computational cost.

Table 21 Optimal results of different algorithms for welded beam design

Table 22 Statistical results of different algorithms for welded beam design problem

5 Conclusion

In this paper, a novel sea horse optimizer (SHO) was presented based on natural heuristics. The proposed SHO algorithm simulates three kinds of intelligent behaviors of sea horses, which are feeding, male reproduction, and movement. Firstly, SHO employs the logarithmic helical equation and Levy flight to mathematically express and construct for the spiral floating. The aim is to make sea horses move randomly with large span step size and improve the local exploitation of SHO. Meanwhile, Brownian motion is used to explore the search space more comprehensively. Then, the speed between the sea horse and the prey are set according to the probability to express whether the predation success or failure. In order to regulate constantly the search neighborhoods of the proposed SHO algorithm, adaptive parameter is introduced into the predation behavior. Finally, based on the new generated population by following the first two behaviors, offspring are bred, which inherit the good genetic characteristics from their fathers and increase the diversity of individuals in population.

Qualitative experiments analyzed the influence of different behaviors of sea horses on different stages of the proposed SHO algorithm from the search history, the trajectory of 1st sea horse, average fitness of all sea horses and convergence curve. 23 well-known functions were selected to verify the local exploitation accuracy and global exploration ability of algorithms. Meanwhile, CEC2014 benchmark functions were used to test the local extreme value avoidance of the algorithm and the effectiveness of SHO in the high-dimensional case of the two sets of test functions.

Experimental results show that SHO is significantly superior to six state-of-the-art comparison algorithms on seven unimodal functions and most of the multimodal functions. For CEC2014 benchmark functions, SHO also has stronger local extremum avoidance than the other six algorithms. Simultaneously, SHO has fast convergence speed and good local extremum avoidance proved by convergence analysis. It can still keep high convergence accuracy in higher dimensions. The results of Wilcoxon rank sum test and Friedman rank test prove the superiority of SHO on most test functions. Finally, the application of SHO in several practical engineering problems verify that SHO has high optimization ability and low computational cost, which can replace some traditional metaheuristics or certain new proposed algorithms in recent years.

In the future, SHO can be applied in a wider range of fields, such as the hyper-parameter optimization of extreme learning machines and the intelligent solving of complex optimization problems. In addition, multi-objective and binary versions of SHO can be further developed to address multi-objective and discrete optimization problems.