1 Introduction

One of the latest proposed Multi-Criteria Decision-Making (MCDM) methods is the Best-Worst Method (BWM); it is commonly used to compute attribute weights [44]. The method demonstrates several benefits: high consistency in results, fewer violations, reduced pairwise comparisons, and its total deviation, flexibility, and simplicity makes this method perform better than other MCDM methods. Further, because of constraints on knowledge, time, and experience, the BWM method has lent itself to significant research [3, 14, 36, 37]. There are different concepts and theories, such as the fuzzy set theory [56] and Z-number [57] to tackle this issue in various fields. For instance, fuzzy set theory has been applied in supplier evaluation [12], risk assessment [21, 54], and analysis of large-scale group decision-making [52]. In this regard, some researchers extended the conventional BWM method based on using these uncertainty concepts and applied it in different fields [20, 23, 25, 27, 33, 34, 38, 45]. Furthermore, non-interference certainty and reliability lead to extend this method to the fuzzy environment (FBWM) [24] and Z-number (ZBWM) concepts [1].

Generally, the information for planning and decision-making is mainly captured with uncertainty. Therefore, human rationality alone cannot fulfill the demands and objectives of the organizations. That is to say, the existence of uncertainty in determining the exact weights in weighting methods based on experts’ objectives can lead to an increase in the levels of ambiguity [28]. To address this shortcoming, Ghoushchi and Khazaeili [19] proposed the Importance-Necessity concept, namely G-numbers, to decrease ambiguity in the decision-making process. G-numbers include two fuzzy variables and indicates in the form of G = (I, N). The primary aim of this method is to reduce the uncertainty of information based on I (Importance) and N (Necessity) components. I and N are linguistic variables; for instance, the task of allocating a budget for a project might be rated as (high) or (very high).

Since decision-makers play an important role in assigning a weight to criteria and scoring the alternatives in the BWM method as in other MCDM techniques, it is crucial to reduce the ambiguity in its process. In other words, in other words, a question may be raised about how certain decisions are made regarding their Importance and Necessity in assigning crisp values [5, 6, 10, 11]. In this regard, this study aims to address this important question about human multi-criteria decisions by proposing an extended version of BWM based on G-numbers (GBWM). The concept of importance is one of the significant indicators in the decision-making process. The importance of an activity, criteria, or measurement indicates its value in the prevailing condition. Although, sometimes, there is no necessity of doing an activity that seems to be important. In other words, there are several important issues in a different process, but only some of them are necessary for consideration. Uncertainty and ambiguity can be reduced by combining Importance and Necessity [19]. The integration of G-numbers with the BWM can simultaneously consider the uncertainty and ambiguity in its decision-making process in comparison with other existent methods. In fact, timely implementation of a sensitive activity or considering special criteria can inform decision-makers about circumstances and they can take appropriate action in a suitable time. The output of the GBWM method is to rank the identified criteria and determine their weight. This method can be used alone to identify important criteria, or it can be combined with an outranking method like TOPSIS, MOORA, or other similar ones to prioritize alternatives. Such methods require the obtained weights from the implementation of weighting techniques to form a weighted normalized decision matrix and to make a favorable and satisfactory decision based on several criteria [42]. According to the advantages of the GBWM method, such as simultaneous consideration of Importance and Necessity in the form of linguistic variables, it can be strongly useful for decision support systems in dealing with complex problems.

This study is organized as follows: In Section 2, a background of G-number theory and a literature review of the BWM method have been presented. The GBWM steps and transformation rules have been explained in Section 3. In Section 4, GBWM has been utilized to address the problem in two cases, including a high-cost performance car selection problem (case one) and cancer prevention (case two). Moreover, sensitivity analysis has been performed for case two to analyze the rank of criteria in a different situation. Finally, the conclusion has been presented in Section 5.

2 Background

In this section, the literature review of the BWM method has been briefly described. Afterward, the background of the G-number method is presented.

2.1 BWM method

In recent years, BWM has become a popular method to solve MCDM problems due to its advantages [36, 37]. In this method, decision-makers identify the best and worst criteria in a specific case. Then, the weight of criteria and alternatives are obtained based on a pairwise comparison. The number of pairwise comparisons in the BWM method is less than in similar methods, like the analytic hierarchy process (AHP). The ultimate scores are derived using the weights of the different sets of criteria and alternatives [33, 34, 44, 45].

BWM’s presentation has been utilized in several different fields as an appropriate method in weighting criteria and alternatives [44]. For instance, this method has been applied within the oil and gas industry to find out the importance of external forces in the operating environment that could affect sustainable supply chain management strategies [47]. de-Magistris et al. [13] identified the most valued European food label using the BWM method. Ghimire et al. [18] compared the consumers’ preference shares of turf-grass attributes. Ahmadi et al. [2] investigated about social sustainability dimension of supply chains in manufacturing companies using the BWM method. In another study, Van de Kaa et al. [50] assigned a weight to the factors that play an important factor in the selection of biomass thermochemical conversion technology in the Netherlands. You et al. [53] evaluated the operational performance of a power grid enterprise in China concerning sustainability factors. Van de Kaa et al. [51] studied the influential factors in the battle between battery and fuel cell that powered electric vehicles regarding investment decisions. Stević et al. [48] surveyed the internal transport logistics of a paper manufacturing company with the aim of the rational selection of wagons. Nawaz et al. [39] proposed a cloud broker architecture for cloud service selection. Rezaei et al. [46] assessed the crucial criteria that play a role in the quality assessment of airline baggage handling systems. Asadabadi et al. [5] presented an algorithm to extract the hidden fuzzy terms and specification process in a project.

To reduce skepticism and to obtain more realistic final results, several theories were proposed by researchers. To ascertain the validated results, proposed theories have been combined with MCDM methods. Zadeh [55] introduced the fuzzy set theory to solve practical problems under an uncertain environment. That method has been used in many applications such as safety and reliability engineering [29], the chemistry industry [8], automotive industry [43], decision making [59], and so forth. Fuzzy set theory is a useful tool to describe situations in which the data are imprecise or vague; therefore, BWM was extended to fuzzy BWM to support the lack of information and human intuitive decision-makings [24]. The good performance of the extended BWM method in different fields has been demonstrated in various studies. For instance, Amoozad Mahdiraji et al. [4] investigated prioritizing the key factors of sustainable architecture in a fuzzy environment. Guo and Zhao [24] indicated the efficiency of the fuzzy set theory in dealing with human decisions in comparison with the classical BWM method. Tian et al. [49] enhanced the performance of the classic FMEA by extending classic BWM and VIKOR methods based on the fuzzy method. Tian et al. [49] evaluated the performance of the smart bike-sharing program under uncertain conditions. In the following, the Z-number extension of BWM was introduced by Aboutorab et al. [1]. This theory is utilized in the supply management field to evaluate the capabilities of the supplier and his/her willingness to collaborate. In conclusion, both fuzzy and Z-number theories take only certainty and reliability into account and fail to consider the Importance and Necessity of each criterion and alternatives. Therefore, in this study, G-number and BWM have been combined to reduce the ambiguity in the decision-making process, especially in comparison with other similar methods, including conventional BWM and Fuzzy BWM methods.

2.2 G-number theory

The Urgent/Important principle or matrix was firstly proposed by Eisenhower [16], for deciding and prioritizing tasks by urgency and importance. In other words, it’s vital to sort out less urgent and less important tasks which should be either delegated or not done at all [7, 16]. The main aim of the Eisenhower concept is based on efficiently performing the tasks. Task prioritizing without attention to their level of necessity or urgency may reduce the management effectiveness and/or efficiency. When a task needs a real-time reaction, it is an urgent task. Our strategies, values, and goals are affected by important tasks. These tasks are not necessarily urgent.

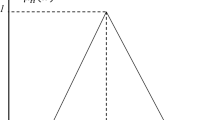
Accordingly, Eisenhower’s suggested matrix includes four quadrants (Fig. 1) [31]:

  • Quadrant 1: Important and urgent (leads to doing): tasks that need to be addressed immediately. Our long-term strategy depends on these kinds of tasks; these items require immediate attention, i.e., important issues, deadlines.

  • Quadrant 2: Important, but not urgent (leads to schedule): tasks or activities that their due date is not vital but accelerate achieving personal goals. These tasks are typically about future planning, strengthening relationships, and self-improvement.

  • Quadrant 3: Urgent, but not important (leads to delegate): activities that need real-time attention or urgency but do not play an important role in fulfilling personal missions. Most of these tasks are supportive tasks to help other people.

  • Quadrant 4: Neither important nor urgent (leads to eliminate): tasks that are neither pressing nor important and cannot help in achieving goals or performing missions. These tasks are mostly distractive activities.

Fig. 1
figure 1

Eisenhower matrix [16]

Full size image

Eisenhower classified the tasks of each category based on their importance and urgency and suggested to implement them as the desired management strategy.

Importance-based planning may realize the high-level goals of the organization, while urgent-based planning may reduce the risks of activities that must be done in real-time. Therefore, it seems organizations may consider both mentioned planning methods together to gain their goals efficiently and profitably.

Necessity is the comprehensive form of urgency, which has not gained enough attention from researchers; they mainly consider the Importance concept in MCDM issues [58]. Necessity may resolve ambiguity and represent real-world decision-making in a better and more precise way. This concept is called G-numbers.

The ordered triple is referred to as G-valuation. X is unspecified, I is the Importance and N is the Necessity component; I and N can get the value of X. For instance, an increase in the budget of education (Medium, High) is a group of G-valuations and called a G-information. The concepts of many decision-making issues can be expressed as G-information [19].

In the present study, linguistic variables like Triangular Fuzzy Numbers (TFN) for Importance and Necessity concepts are used. Furthermore, a new approach has been proposed, which enhances the capability of ambiguity reduction in the decision-making process.

2.2.1 G-number appropriateness for BWM

In this study, a method is proposed based on G-number theory and BWM. The clarification of the decision-maker’s knowledge and reduction of ambiguity is the prime reason for this integration. Moreover, considering the Importance and Necessity for each criterion based on a specific situation is the superiority of this method, compared to fuzzy BWM and Z-BWM methods. The integration of the two concepts can be useful in solving complex decision-making problems.

2.2.2 The relevant concepts

The fundamental concepts of this research, along with definitions of G-numbers and the associated arithmetic operations, are discussed comprehensively in this section.

Definition 1

A fuzzy number \( \tilde{A}=\left(a,b,c\right) \) is a TFN where a, b, and c represent the lower, modal, and upper values respectively [17]. The membership function of the TFN is defined by \( {\mu}_{\tilde{A}}(x)=X\to \left[0,1\right] \):

$$ {\mu}_{\overset{\sim }{A}}(x)=\Big\{{\displaystyle \begin{array}{c}\frac{x-a}{b-a}\kern2.28em a\le x\le b\\ {}a\kern3.479999em x=1\\ {}\frac{c-x}{c-b}\kern2.28em b\le x\le c\end{array}} $$
(1)

Definition 2

A TFN like (a, b, c) is non-negative if a ≥ 0 [7].

Definition 3

The graded mean integration representation (GMIR) is used to change a fuzzy number to a real crisp value [61]. In GMIR, crisp (\( \tilde{R} \)) of a TFN \( \tilde{R} \)indicates the ranking of the triangular fuzzy number [60]. Where \( \tilde{R}=\left(a,b,c\right) \), the GMIR \( Crisp\left(\tilde{R}\right) \) of TFN \( \tilde{R} \) can be calculated as follows:

$$ Crisp\left(\tilde{R}\right)=\frac{a+4b+c}{6} $$
(2)

Definition 4

The G-number is identified as \( G=\left(\tilde{I},\tilde{N}\right) \), where \( \tilde{I}=\left({a}_I,{b}_I,{c}_I\right) \) indicates the importance component and \( \tilde{N}=\left({a}_N,{b}_N,{c}_N\right) \) shows the necessity component on the real-valued uncertain variables. In general, I and N are described as linguistic variables. For instance, linguistic variables associated with an appointment and investment in the stock market are (high, very high) and (high, medium), respectively. An ordered pair relates to computations with G-numbers, which are TFNs [19].

Definition 5

A G-numbers set [(aI, bI, cI), (aN, bN, cN)] is non-negative if aI ≥ 0, aN ≥ 0 [19].

Definition 6

Let \( {G}_1=\left[\left({a}_I^1,{b}_I^1,{c}_I^1\right),\left({a}_N^1,{b}_N^1,{c}_N^1\right)\right] \) and \( {G}_2=\left[\left({a}_I^2,{b}_I^2,{c}_I^2\right),\left({a}_N^2,{b}_N^2,{c}_N^2\right)\right] \) be non-negative G-number andλbe a non-negative real variable. The arithmetic operations are defined as follows [19]:

$$ {\displaystyle \begin{array}{c}i\Big)\kern0.48em {G}_1\oplus {G}_2=\left[\left({a}_I^1+{a}_I^2,{b}_I^1+{b}_I^2,{c}_I^1+{c}_I^2\right),\left({a}_N^1+{a}_N^2,{b}_N^1+{b}_N^2,{c}_N^1+{c}_N^2\right)\right]\\ {} ii\Big)\kern0.36em {G}_1\ominus {G}_2=\left[\left({a}_I^1-{c}_I^2,{b}_I^1-{b}_I^2,{c}_I^1-{a}_I^2\right),\left({a}_N^1-{c}_N^2,{b}_N^1-{b}_N^2,{c}_N^1-{a}_N^2\right)\right]\\ {} ii i\Big)\kern0.24em {G}_1\otimes {G}_2=\left[\left({a}_I^1{a}_I^2,{b}_I^1{b}_I^2,{c}_I^1{c}_I^2\right),\left({a}_N^1{a}_N^2,{b}_N^1{b}_N^2,{c}_N^1{c}_N^2\right)\right]\\ {} iv\Big)\kern0.24em {G}_1\oslash {G}_2=\left[\left({a}_I^1/{c}_I^2,{b}_I^1/{b}_I^2,{c}_I^1/{a}_I^2\right),\left({a}_N^1/{c}_N^2,{b}_N^1/{b}_N^2,{c}_N^1/{a}_N^2\right)\right]\\ {}v\Big)\kern1.44em \lambda {G}_1=\left[\left(\lambda {a}_I^1,\lambda {b}_I^1,\lambda {c}_I^1\right),\left(\lambda {a}_N^1,\lambda {b}_N^1,\lambda {c}_N^1\right)\right]\end{array}} $$
(3)

Definition 7

If \( G=\left(\tilde{I},\tilde{N}\right) \) is a G-number. The G-number linguistic variable transformation rules are defined as follows [19]:

$$ G=\alpha \tilde{I}\oplus \beta \tilde{N};\kern0.6em \alpha +\beta =1;\kern0.36em \alpha, \beta \ge 0 $$
(4)

In this equation, α and β are the non-negative weights of the Importance and the Necessity components. It means that whenever α is increased, the value of β needs to be decreased.

2.2.3 Transformation rules for G-numbers linguistic variables

This section illustrates how a G-number can convert to a fuzzy number. In \( G=\left(\tilde{I},\tilde{N}\right) \), \( \tilde{I} \) indicates the Importance and \( \tilde{N} \)is the Necessity component. The G-number is transformed into TFN using Eq. (4). The values of α and β for each criterion or alternative are determined by the experts based on self-identification or they can be defined by an optimization algorithm to decrease the cost function (in contrast to our aim) [10, 11]. As β = 1 − α, Eq. (4) can be transformed into Eq. (5):

$$ G=\alpha \overset{\sim }{I}\oplus \left(1-\alpha \right)\overset{\sim }{N};\kern0.75em 0\le \alpha \le 1 $$
(5)

Using a combination of Importance (Table 1) and Necessity (Table 2), the transformation rules of linguistic variables are obtained and transformed into the TFNs. The fuzzy pairwise comparisons among criteria are based on the linguistic variables listed in Tables (1) and (2), respectively.. Afterward, the linguistic evaluations of decision-makers need to be transformed to TFNs [24, 35].

Table 1 Linguistic variables for Importance component
Full size table
Table 2 Linguistic variables for Necessity component
Full size table

As a numerical example, suppose that the linguistic variable that is chosen by the expert or the optimization algorithm for the Importance component of G-number is ‘Absolutely important’ (AI), where (\( \tilde{I}= AI \)). In the following, the Necessity component is selected ‘High Necessity’ (HN) \( \tilde{N}= HN \), based on Table 1. Moreover, the non-negative weight of the importance is α. The value is expressed as follows:

$$ G=\alpha \left(7/2,4,9/2\right)\oplus \beta \left(5/2,3,7/2\right)\kern0.48em ;\alpha +\beta =1\kern0.48em ,0\le \alpha, \beta \le 1 $$
(6)

If β = 1 − α, Eq. (5) is transformed into Eq. (7):

$$ G=\alpha \left(7/2,4,9/2\right)\oplus \left(5/2\left(1-\alpha \right),3\left(1-\alpha \right),7/2\left(1-\alpha \right)\right) $$
(7)

Then, the G-number is converted to the TFN as follows:

$$ G=\left(2.5+\alpha, 3+\alpha, 3.5+\alpha \right) $$
(8)

Repetitively applying this procedure will turn the elements of Tables 1 and 2 into the elements shown in Table 3.

Table 3 Importance-Necessity for α
Full size table

3 Proposed approach

In this section, this study seeks to reduce the ambiguity in attributing weights to the criteria by incorporating the conventional BWM method and Importance-Necessity concept (G-number) and by introducing the GBWM method. It should be noted that the same steps of Fuzzy BWM [24] have been followed to produce the rules of the G-numbers’ linguistic variables transformation (see Table 3).

3.1 GBWM steps

The implementation of the proposed GBWM method can be summarized in the following six steps:

  • Step 1: Determining a set of decision criteria

A set of decision criteria is built by decision-makers. For instance, {C1, C2, …, Cn}.

  • Step 2: Identifying the best and worst criteria

The decision-makers should determine, from their own perspective, the desirable and undesirable criteria among the set of criteria identified in Step 1. The best or desirable criterion is indicated by CB, and the worst or undesirable criterion is represented by CW.

  • Step 3: Conducting G-number pairwise comparisons between the best criteria and the other criteria.

This step aims to determine the Best-to-Others vector, and then decision-makers identify the Importance and Necessity of a best or important criterion to the others through Table 3.

$$ \left({\tilde{A}}_B^I,{\tilde{A}}_B^N\right)=\left\{\left({\tilde{a}}_{B1}^I,{\tilde{a}}_{B1}^N\right),\Big({\tilde{a}}_{B2}^I,{\tilde{a}}_{B2}^N\Big),\dots, \Big({\tilde{a}}_{Bn}^I,{\tilde{a}}_{Bn}^N\Big)\right\} $$
(9)

where aBn is the preference of B criterion to the j − th criterion and \( \left({\overset{\sim }{a}}_{BB}^I,{\overset{\sim }{a}}_{BB}^N\right)=\left(1,1,1\right) \).

  • Step 4: Conducting G-number pairwise comparison between other criteria and the worst criterion.

In this step, decision-makers determine the Importance and Necessity of other criteria to the worst criterion by using Table 3. The Others-to-Worst vector is represented in Eq. (10):

$$ \left({\tilde{A}}_W^I,{\tilde{A}}_W^N\right)=\left\{\left({\tilde{a}}_{1W}^I,{\tilde{a}}_{1W}^N\right),\Big({\tilde{a}}_{2W}^I,{\tilde{a}}_{2W}^N\Big),\dots, \Big({\tilde{a}}_{nW}^I,{\tilde{a}}_{nW}^N\Big)\right\} $$
(10)

Where in anW, the preference of j − thcriterion over the Wis identified and \( \left({\tilde{a}}_{WW}^I,{\tilde{a}}_{WW}^N\right)=\left(1,1,1\right) \).

  • Step 5: Transforming the Best-to-Others and Others-to-Worst vectors to TFNs based on Table 3, Eqs. (9) and (10) convert to the following equations:

$$ {G}_B=\left({\tilde{g}}_{B1},{\tilde{g}}_{B2},\dots, {\tilde{g}}_{Bn}\right);\kern0.72em {\tilde{g}}_{Bj}=\alpha {a}_{Bj}^I\oplus \left(1-\alpha \right){a}_{Bj}^W $$
(11)
$$ {G}_W=\left({\tilde{g}}_{1W},{\tilde{g}}_{2W},\dots, {\tilde{g}}_{nW}\right);\kern0.6em {\tilde{g}}_{jW}=\alpha {a}_{jW}^I\oplus \left(1-\alpha \right){a}_{jW}^W $$
(12)

Where j = 1, …, n and 0 ≤ α ≤ 1.

  • Step 6: Calculating the optimal weight \( \left({\tilde{w}}_1^{\ast },{\tilde{w}}_2^{\ast },\dots, {\tilde{w}}_n^{\ast}\right) \): The optimal weight for criteria should meet the requirement of \( {\tilde{w}}_B/{\tilde{w}}_j={\tilde{g}}_{Bj} \) and \( {\tilde{w}}_j/{\tilde{w}}_W={\tilde{g}}_{jW} \). To satisfy the condition for all j, the maximum absolute gaps in \( \left|\left({\tilde{w}}_B/{\tilde{w}}_j\right)-{\tilde{g}}_{Bj}\right| \) and \( \left|\left({\tilde{w}}_j/{\tilde{w}}_W\right)-{\tilde{g}}_{jW}\right| \)are minimized. Moreover, considering the non-negativity characteristic and sum condition of weights, Eq. (13) can be formulated as follows:

$$ {\displaystyle \begin{array}{c}\mathit{\min}\kern0.24em \mathit{\max}\left\{|\frac{{\tilde{w}}_B}{{\tilde{w}}_j}-{\tilde{g}}_{Bj}|,|\frac{{\tilde{w}}_j}{{\tilde{w}}_W}-{\tilde{g}}_{jW}|\right\}\\ {}s.t.\Big\{\begin{array}{c}\sum \limits_{j=1}^nR\left(\tilde{w}_{j}\right)=1\\ {}{a}_j^w\le {b}_j^w\le {c}_j^w\\ {}{a}_j^w\ge 0,\kern0.48em for\kern0.36em j=1,\dots, n\end{array}\end{array}} $$
(13)

Where \( {\tilde{w}}_B=\left({a}_B^w,{b}_B^w,{c}_B^w\right),\tilde{w}_{j}=\left({a}_j^w,{b}_j^w,{c}_j^w\right),{\tilde{w}}_W=\left({a}_W^w,{b}_W^w,{c}_W^w\right),{\tilde{a}}_{Bj}=\left({a}_{Bj},{b}_{Bj},{c}_{Bj}\right),{\tilde{a}}_{jW}=\left({a}_{jW},{b}_{jW},{c}_{jW}\right). \) In the following, the above problem is transforms to Eq. (14). (14).

$$ {\displaystyle \begin{array}{c}\mathit{\min}\kern0.24em \tilde{\xi}\\ {}s.t\Big\{\begin{array}{c}\mid \frac{{\tilde{w}}_B}{{\tilde{w}}_j}-{\tilde{g}}_{Bj}\mid \le \tilde{\xi}, for\; all\;j\\ {}\mid \frac{{\tilde{w}}_j}{{\tilde{w}}_W}-{\tilde{g}}_{jW}\mid \le \tilde{\xi}\kern0.24em for\; all\;j\\ {}\sum \limits_{j=1}^nR\left({\tilde{w}}_j\right)=1\\ {}{a}_j^w\le {b}_j^w\le {c}_j^w;\kern0.6em {a}_j^w\ge 0,\kern0.48em for\kern0.36em j=1,\dots, n\end{array}\end{array}} $$
(14)

Where \( \tilde{\xi}=\left({a}^{\xi },{b}^{\xi },{c}^{\xi}\right) \). Considering aξ ≤ bξ ≤ cξ, we assume ξ∗ = (k∗, k∗, k∗), k∗ ≤ aξ, then Eq. (15) can be formulated as follows:

$$ {\displaystyle \begin{array}{c}\mathit{\min}\;{\xi}^{\ast}\\ {}s.t.\Big\{\begin{array}{c}\frac{\left({a}_B^w,{b}_B^w,{c}_B^w\right)}{\left({a}_j^w,{b}_j^w,{c}_j^w\right)}-\left({a}_{Bj},{b}_{Bj},{c}_{Bj}\right)\mid \le \left({k}^{\ast },{k}^{\ast },{k}^{\ast}\right)\\ {}\frac{\left({a}_j^w,{b}_j^w,{c}_j^w\right)}{\left({a}_W^w,{b}_W^w,{c}_W^w\right)}-\left({a}_{jW},{b}_{jW},{c}_{jW}\right)\mid \le \left({k}^{\ast },{k}^{\ast },{k}^{\ast}\right)\\ {}\sum \limits_{j=1}^nR\left(\tilde{w}_{j}\right)=1\\ {}{a}_j^w\le {b}_j^w\le {c}_j^w,\kern0.36em {a}_j^w\ge 0,\kern0.48em j=1,2,\dots, n\end{array}\end{array}} $$
(15)

By solving the above model, optimal fuzzy weights \( \left({w}_1^{\ast },{w}_2^{\ast },\dots, {w}_n^{\ast}\right) \) are obtained. According to Rezaei’s [44] study, the superiority of the BWM method is a reduction of pairwise comparisons, which causes a lower level of inconsistency. The extension of the BWM method using G-number theory adds several powerful features to this method. Specifically, minimizing ambiguity by the addition of the Importance-Necessity concept, translating human knowledge, having fewer pairwise comparisons, handling the uncertainty of linguistic variables, implementing big-data, and considering different scenarios all respect the different values of α and β. The main weakness of this method is the subjectivity issue of the fuzzy part in translating the concept [1, 24, 44].

3.2 Consistency ratio for GBWM

A Consistency Ratio (CR) is an indicator to address the inconsistency level of pairwise comparisons. This section explains the computation of CR for GBWM. If the comparison is consistent\( \left({\tilde{a}}_{Bj}^I,{\tilde{a}}_{Bj}^N\right)\otimes \left({\tilde{a}}_{jW}^I,{\tilde{a}}_{jW}^N\right)=\left({\tilde{a}}_{BW}^I,{\tilde{a}}_{BW}^N\right) \). The \( \left({\tilde{a}}_{Bj}^I,{\tilde{a}}_{Bj}^N\right) \) indicates the preference of the best criterion to the criterion j. The \( \left({\tilde{a}}_{jW}^I,{\tilde{a}}_{jW}^N\right) \)presents the preference of jcriterion over the worst one and \( \left({\tilde{a}}_{BW}^I,{\tilde{a}}_{BW}^N\right) \) shows the preference of the best criterion over the worst one.

The G-number \( \left({\tilde{a}}_{Bj}^I,{\tilde{a}}_{Bj}^N\right)\times \left({\tilde{a}}_{jW}^I,{\tilde{a}}_{jW}^N\right)=\left({\tilde{a}}_{BW}^I,{\tilde{a}}_{BW}^N\right) \) which converts to TFN based on Eqs. (11), (12) and (16) establishes the result of this conversion.

$$ {\tilde{g}}_{Bj}\times {\tilde{g}}_{jW}={\tilde{g}}_{BW} $$
(16)

When \( {\tilde{g}}_{Bj}\otimes {\tilde{g}}_{jW}\ne {\tilde{g}}_{BW} \), it means that \( {\tilde{g}}_{Bj}\otimes {\tilde{g}}_{jW} \) may be greater or smaller than \( {\tilde{g}}_{BW} \) and the fuzzy pairwise comparisons will be inconsistent. If both \( {\tilde{g}}_{Bj} \) and \( {\tilde{g}}_{jW} \)are equal to \( {\tilde{g}}_{BW} \), the amount of inequality will be the greatest and result in \( \tilde{\xi} \). Considering the occurrence of the greatest inequality, according to the equality relation \( \left({\tilde{w}}_B/{\tilde{w}}_j\right)\otimes \left({\tilde{w}}_j/{\tilde{w}}_W\right)=\left({\tilde{w}}_B/{\tilde{w}}_W\right) \), the following equation can be obtained.

$$ \left({\tilde{g}}_{Bj}-\tilde{\xi}\right)\otimes \left({\tilde{g}}_{jW}-\tilde{\xi}\right)=\left({\tilde{g}}_{BW}+\tilde{\xi}\right) $$
(17)

For the maximum fuzzy inconsistency \( {\tilde{g}}_{Bj}={\tilde{g}}_{jW}={\tilde{g}}_{BW} \), Eq. (17) transforms to the next equation as follows:

$$ \left({\tilde{g}}_{BW}-\tilde{\xi}\right)\otimes \left({\tilde{g}}_{BW}-\tilde{\xi}\right)=\left({\tilde{g}}_{BW}+\tilde{\xi}\right) $$
(18)

Eq. (18) can be formulated as follows:

$$ {\tilde{\xi}}^2-\left(1+2{\tilde{g}}_{BW}\right)\tilde{\xi}+\left({{\tilde{g}}_{BW}}^2-{\tilde{g}}_{BW}\right)=0 $$
(19)

Based on Table 3, (3.5,4,4.5) is the maximum value of \( {\tilde{g}}_{BW} \) and is attributed to the linguistic term of “Absolutely Important” (AI) with Necessity linguistic term of “Absolute Necessity” (AN) given by the decision-makers. For \( {\tilde{g}}_{BW}=\left({a}_{BW},{b}_{BW},{c}_{BW}\right) \), the maximum value is (3.5,4,4.5), which indicates aBW = 3.50, bBW = 4 and cBW = 4.5. It illustrates that the maximum value cannot exceed 4.5; the maximum possible \( \tilde{\xi} \) is obtained by using the upper boundary cBW.

The \( \overset{\sim }{\xi } \) can be represented by a crisp value ξ. In other cases, like \( {\overset{\sim }{g}}_{BW}=\left(1,1,1\right),{\overset{\sim }{g}}_{BW}=\left(1-0.33\alpha, 1,1+0.5\alpha \right),{\overset{\sim }{g}}_{BW}=\left(3.5-2\alpha, 4-2\alpha, 4.5-2\alpha \right) \) a similar process can be performed.. Thus, it can transform Eqs. (18) to (19) as:

$$ {\xi}^2-\left(1+2{g}_{BW}\right)\xi +\left({g_{BW}}^2-{g}_{BW}\right)=0 $$
(20)

Where \( {\overset{\sim }{g}}_{BW}=1,1+0.5\alpha, 4.5-2\alpha, 4.5 \), and so on.

By solving Eq. (20), for different \( {\tilde{g}}_{BW} \), the possible peak value of ξ is used as the consistency index (CI) for GBWM (Table 4). Then the CR value can be obtained through \( {\tilde{\xi}}^{\ast } \)as follows:

$$ CR=\frac{{\tilde{\xi}}^{\ast }}{CI} $$
(21)
Table 4 Consistency Index for GBWM
Full size table

The bigger value of \( {\tilde{\xi}}^{\ast } \)can result in higher CR, and the comparisons are less reliable. This ratio is acceptable when CR < 0.1 [44].

4 Analysis of the results

In this section, the GBWM method has been applied to two case studies to demonstrate its applicability in various fields such as management and healthcare and to validate its outputs.

4.1 Case one

In this section, the GBWM method is employed to address a problem in high cost-performance car selection, discussed by Guo and Zhao [24]. A buyer must decide by evaluating alternatives based on criteria [41]. Table 5 indicates the main criteria that play an important role in the high-cost performance car selection problem.

Table 5 The considered main criteria for high-cost performance service
Full size table

Among the five identified criteria for willingness, C2 is regarded as the best criterion and C5 is selected as the worst one. Table 6 shows the linguistic variable that decision-makers assigned for G-number preference of Best-to-Others criteria.

Table 6 Best-to-Others vector
Full size table

According to Table 6, the Best-to-Others vector based on G-numbers for the capabilities criteria is presented as follows:

$$ \left({G}_B^{c_2}\right)=\left\{\left( WI, AN\right),\left( EI, EN\right),\left( FI, WN\right),\left( WI, HN\right),(AIAN)\right\} $$

Based on Table 3, the linguistic variables can be converted to TFN as follows:

$$ \left({G}_B^{c_2}\right)=\left\{\left(3.5-2.83\alpha, 4-3\alpha, 4.5-3\alpha \right),\left(1,1,1\right),\left(0.67+0.83\alpha, 1+\alpha, 1.5+\alpha \right),\left(2.5-1.83\alpha, 3-2\alpha, 3.5-2\alpha \right),\left(3.50,4,4.50\right)\right\} $$

Table 7 indicates the linguistic variable that decision-makers assigned for G-number preference of Others-to-Worst criteria.

Table 7 Others-to-Worst vector
Full size table

Based on Table 7, the Others-to-Worst vector based on G-numbers is as follows.

$$ \left({G}_W^{c_5}\right)=\left\{\left( FI, HN\right),\left( AI, AN\right),\left( FI, FN\right),\left( WI, FN\right),\left( EI, EN\right)\right\} $$

Based on Table 3, the linguistic variables can be converted as follows:

$$ \left({G}_W^{c_5}\right)=\left\{\left(2.5-\alpha, 3-\alpha, 3.5-\alpha \right),\Big(3.50,4,4.50\Big),\Big(1.50,2,2.50\Big),\Big(1.5-0.83\alpha, 2-\alpha, 2.5-\alpha \Big),\Big(1,1,1\Big)\right\} $$

In the GBWM method, the Importance (α) and Necessity (β) for each specific case should be determined by the decision-makers. Therefore, in this case, α and β have been identified equally to 0.5; it means that based on experts’ recognition, the non-negative weights of Importance and Necessity have the same value in high-cost performance car selection.

The fuzzy Best-to-Others and Others-to-Worst vector for the criteria are as below:

$$ {\displaystyle \begin{array}{l}{G}_B^{c_2}=\left[\left(2.09,2.5,3\right),\left(1,1,1\right),\left(1.09,1.5,2.5\right),\left(1.59,2,2.5\right),\left(3.5,4,4.5\right)\right]\\ {}{G}_w^{c_5}=\left[\left(2,2.5,3\right),\left(3.5,4,4.5\right),\left(1.5,2,2.5\right),\left(1.09,1.5,2\right),\left(1,1,1\right)\right]\end{array}} $$

The mathematical programming model presented in Eq. (22) can be updated as follows:

$$ {\displaystyle \begin{array}{c}\mathit{\min}\;{\xi}^{\ast}\\ {}s.t.\Big\{\begin{array}{c}-{c}_1\ast \xi \le {a}_2-2.09\ast {c}_1\le {c}_1\ast \xi \\ {}-{b}_1\ast \xi \le {b}_2-2.5\ast {b}_1\le {b}_1\ast \xi \\ {}-{a}_1\ast \xi \le {c}_2-3\ast {a}_1\le {a}_1\ast \xi \\ {}-{c}_3\ast \xi \le {a}_2-1.09\ast {c}_3\le {c}_3\ast \xi \\ {}-{b}_3\ast \xi \le {b}_2-1.5\ast {b}_3\le {b}_3\ast \xi \\ {}-{a}_3\ast \xi \le {c}_2-2\ast {a}_3\le {a}_3\ast \xi \\ {}-{c}_4\ast \xi \le {a}_2-1.59\ast {c}_4\le {c}_4\ast \xi \\ {}-{b}_4\ast \xi \le {b}_2-2\ast {b}_4\le {b}_4\ast \xi \\ {}-{a}_4\ast \xi \le {c}_2-2.5\ast {a}_4\le {a}_4\ast \xi \\ {}-{c}_5\ast \xi \le {a}_2-3.5\ast {c}_5\le {c}_5\ast \xi \\ {}-{b}_5\ast \xi \le {b}_2-4\ast {b}_5\le {b}_5\ast \xi \\ {}-{a}_5\ast \xi \le {c}_2-4.5\ast {a}_5\le {a}_5\ast \xi \\ {}-{c}_5\ast \xi \le {a}_1-2\ast {c}_5\le {c}_5\ast \xi \\ {}-{b}_5\ast \xi \le {b}_1-2.5\ast {b}_5\le {b}_5\ast \xi \\ {}-{a}_5\ast \xi \le {c}_1-3\ast {a}_5\le {a}_5\ast \xi \\ {}-{c}_5\ast \xi \le {a}_3-1.5\ast {c}_5\le {c}_5\ast \xi \\ {}-{b}_5\ast \xi \le {b}_3-2\ast {b}_5\le {b}_5\ast \xi\;\\ {}-{a}_5\ast \xi \le {c}_3-2.5\ast {a}_5\le {a}_5\ast \xi \\ {}-{c}_5\ast \xi \le {a}_4-1.09\ast {c}_5\le {c}_5\ast \xi \\ {}-{b}_5\ast \xi \le {b}_4-1.50\ast {b}_5\le {b}_5\ast \xi\;\\ {}-{a}_5\ast \xi \le {c}_4-2\ast {a}_5\le {a}_5\ast \xi \\ {}{\mathrm{a}}_1+4\ast {\mathrm{b}}_1+{\mathrm{c}}_1+{\mathrm{a}}_2+4\ast {\mathrm{b}}_2+{\mathrm{c}}_2+{\mathrm{a}}_3\\ {}+4\ast {\mathrm{b}}_3+{\mathrm{c}}_3+{\mathrm{a}}_4+4\ast {\mathrm{b}}_4+{\mathrm{c}}_4+{\mathrm{a}}_5+4\ast {\mathrm{b}}_5+{\mathrm{c}}_5=6\\ {}{a}_1\le {b}_1\le {c}_1;{a}_2\le {b}_2\le {c}_2\\ {}{a}_3\le {b}_3\le {c}_3;{a}_4\le {b}_4\le {c}_4\\ {}{a}_5\le {b}_5\le {c}_5\\ {}{a}_1,{a}_2,{a}_3,{a}_4,{a}_5\ge 0\\ {}\xi \ge 0\end{array}\end{array}} $$
(22)

By solving Model (22), the fuzzy optimal weights of the five determining criteria are calculated as follows.

$$ {\displaystyle \begin{array}{c}{w}_{c_1}^{\ast }=\left(\mathrm{0.146,0.181,0.200}\right),\kern0.36em {w}_{c_2}^{\ast }=\left(\mathrm{0.336,0.379,379}\right)\\ {}{w}_{c_3}^{\ast }=\left(\mathrm{0.157,0.209,0.224}\right),\kern0.36em {w}_{c_4}^{\ast }=\left(\mathrm{0.130,0.165,0.177}\right)\\ {}{w}_{c_5}^{\ast }=\left(\mathrm{0.077,0.087,0.092}\right),\kern0.48em {{\overset{\sim }{\xi}}_c}^{\ast }=\left(\mathrm{0.408,0.408,0.408}\right)\end{array}} $$

In the following, the GMIR can be calculated as below.

$$ {w}_1^{c\ast }=0.177,{w}_2^{c\ast }=0.368,{w}_3^{c\ast }=0.200,{w}_4^{c\ast }=0.159,{w}_5^{c\ast }=0.086,{\tilde{\xi}}^{c\ast }=0.408 $$

Therefore, the weights of five criteria ‘Quality’ (C1), ‘Price’ (C2), ‘Comfort’ (C3), ‘Safety’ (C4), and ‘Style’ (C5) are 0.177, 0.368, 0.200, 0.159, and 0.086, respectively. Finally, the value of CR must be evaluated, given that \( {\tilde{a}}_{BW}=\left( AI, AN\right) \)and CI = 8.04 (see Table 4). Therefore, the CR value is 0.05 < 0.1 and the results are consistent.

4.2 Case two

Cancer is a leading health threat worldwide [40]. However, at least half of cancers could be prevented. Understanding the cancer incidence and the major risk factors can help facilitate better cancer prevention programs [9, 15, 30]. Gotay [22] introduced ten main risk factors in cancer prevention programs. Table 8 shows the influential risk factors in cancer prevention. In this study, the Importance and Necessity of each alternative is determined by the experts using G-number theory.

Table 8 Major risk factors for cancer prevention
Full size table

Among the ten main alternatives for cancer prevention, C3 is regarded as the best criterion and C4 selected as the least important criterion compared to the other criteria. Table 9 shows the linguistic variable that decision-makers assigned for G-number preference of Best-to-Others criteria.

Table 9 Best-to-Others vector
Full size table

Table 9 indicates that the Best-to-Others vector for the capabilities criteria are as follows:

$$ \left({G}_B^{c_3}\right)=\left\{\left( FI, EN\right),\left( HI, FN\right),\Big( EI, EN\Big),\Big( AI, AN\Big),\Big( HI, HN\Big),\Big( HI, AN\Big),\Big( EI, HN\Big),\Big( FI, HN\Big),\Big( FI, FN\Big),\Big( HI, EN\Big)\right\} $$

Based on Table 3, linguistic variables can be converted to TFN as follows:

$$ \left({G}_B^{c_3}\right)=\left\{\begin{array}{c}\left(1+0.5\alpha, 1+\alpha, 1+1.5\alpha \right)\left(1.5+\alpha, 2+\alpha, 2.5+\alpha \right)\left(1,1,1\right)\left(\mathrm{3.50,4},4.50\right)\left(\mathrm{2.50,3},3.50\right)\\ {}\left(3.5-\alpha, 4-\alpha, 4.5-\alpha \right)\left(2.5-1.5\alpha, 3-2\alpha, 3.5-2.5\alpha \right)\\ {}\left(2.5-\alpha, 3-\alpha, 3.5-\alpha \right)\left(\mathrm{1.50,2},2.50\right)\left(1+1.5\alpha, 1+2\alpha, 1+2.5\alpha \right)\end{array}\right\} $$

Table 10 indicates the linguistic variable that decision-makers assigned for G-number preference of Others-to-Worst criteria.

Table 10 Others-to-Worst vector
Full size table

Based on Table 10, the Others-to-Worst vector for the capabilities criteria can be obtained as follows, the comparison of other criteria with the worst one.

$$ \left({G}_W^{c_4}\right)=\left\{\left( FI, FN\right),\Big( WI, HN\Big),\Big( AI, AN\Big),\Big( EI, EN\Big),\Big( WI, WN\Big),\Big( WI, FN\Big),\Big( AI, WN\Big),\Big( FI, FN\Big),\Big( FI, EN\Big),\Big( AI, HN\Big)\right\} $$

According to Table 3, the linguistic variables can be converted as follows:

$$ \left({G}_W^{c_4}\right)=\left\{\begin{array}{c}\left(\mathrm{1.50,2},2.50\right)\left(2.5-1.83\alpha, 3-2\alpha, 3.5-2\alpha \right)\left(\mathrm{3.50,4},4.50\right)\left(1,1,1\right)\left(\mathrm{0.67,1},1.5\right)\\ {}\left(1.5-0.83\alpha, 2-\alpha, 2.5-\alpha \right)\left(0.67+2.83\alpha, 1+3\alpha, 1.5+3\alpha \right)\\ {}\left(\mathrm{1.50,2},2.50\right)\left(1+0.5\alpha, 1+\alpha, 1+1.5\alpha \right)\left(2.5+\alpha, 3+\alpha, 3.5+\alpha \right)\end{array}\right\} $$

Based on the G-number method, the Importance (α) and Necessity (β) in each specific case should be determined by the decision-makers; therefore, in this case, α = 0.4 and β = 0.6, where α + β = 1. By substituting α = 0.4 in the linguistic variables of \( {G}_B^{c_3} \),\( {G}_W^{c_4} \), the fuzzy Best-to-Others and Others-to-Worst numerical vectors for the criteria are obtained as follows.

$$ {\displaystyle \begin{array}{c}{G}_B^{\left({c}_3\right)}=\left\{\begin{array}{c}\left(\mathrm{1.2,1.4,1.6}\right),\left(\mathrm{1.9,2.4,2.9}\right),\left(1,1,1\right),\left(\mathrm{3.5,4},4.5\right),\left(\mathrm{2.5,3},3.5\right),\left(\mathrm{3.1,3.6,4.1}\right),\left(\mathrm{1.9,2.2,2.5}\right),\\ {}\left(\mathrm{2.1,2.6,3.1}\right),\left(\mathrm{1.5,2},2.5\right),\left(\mathrm{1.6,1.8,2}\right)\end{array}\right\}\\ {}{G}_W^{\left({c}_4\right)}=\left\{\begin{array}{c}\left(\mathrm{1.5,2},2.5\right),\left(\mathrm{1.8,2.2,2.7}\right),\left(\mathrm{3.5,4},4.5\right),\left(1,1,1\right),\left(\mathrm{0.7,1},1.5\right),\left(\mathrm{1.2,1.6,2.1}\right),\left(\mathrm{1.2,2.2,2.7}\right),\\ {}\left(\mathrm{1.5,2},2.5\right),\left(\mathrm{1.2,1.4,1.6}\right),\left(\mathrm{2.9,3.4,3.9}\right)\end{array}\right\}\end{array}} $$

In the following, a non-linear constrained optimization problem is defined as follows according to Eq. (23).

$$ {\displaystyle \begin{array}{c}\mathit{\min}\;{\xi}^{\ast}\\ {}s.t.\\ {}-{c}_1\ast \xi \le {a}_3-1.2\ast {c}_1\le {c}_1\ast \xi \kern0.36em ;-{b}_1\ast \xi \le {b}_3-1.4\ast {b}_1\le {b}_1\ast \xi \\ {}-{a}_1\ast \xi \le {c}_3-1.6\ast {a}_1\le {a}_1\ast \xi \kern0.36em ;-{c}_2\ast \xi \le {a}_3-1.9\ast {c}_2\le {c}_2\ast \xi \kern0.24em \\ {}-{b}_2\ast \xi \le {b}_3-2.4\ast {b}_2\le {b}_2\ast \xi \kern0.36em ;-{a}_2\ast \xi \le {c}_3-2.9\ast {a}_2\le {a}_2\ast \xi \\ {}-{c}_4\ast \xi \le {a}_3-3.5\ast {c}_4\le {c}_4\ast \xi \kern0.36em ;-{b}_4\ast \xi \le {b}_3-4\ast {b}_4\le {b}_4\ast \xi \\ {}-{a}_4\ast \xi \le {c}_3-4.5\ast {a}_4\le {a}_4\ast \xi \kern0.36em ;-{c}_5\ast \xi \le {a}_3-2.5\ast {c}_5\le {c}_5\ast \xi \\ {}-{b}_5\ast \xi \le {b}_3-3\ast {b}_5\le {b}_5\ast \xi \kern0.36em ;-{a}_5\ast \xi \le {c}_3-3.5\ast {a}_5\le {a}_5\ast \xi \\ {}-{c}_6\ast \xi \le {a}_3-3.1\ast {c}_6\le {c}_6\ast \xi \kern0.36em ;-{b}_6\ast \xi \le {b}_3-3.6\ast {b}_6\le {b}_6\ast \xi \\ {}-{a}_6\ast \xi \le {c}_3-4.1\ast {a}_6\le {a}_6\ast \xi \kern0.36em ;-{c}_7\ast \xi \le {a}_3-1.9\ast {c}_7\le {c}_7\ast \xi \\ {}-{b}_7\ast \xi \le {b}_3-2.2\ast {b}_7\le {b}_7\ast \xi \kern0.36em ;-{a}_7\ast \xi \le {c}_3-2.5\ast {a}_7\le {a}_7\ast \xi \\ {}-{c}_8\ast \xi \le {a}_3-2.1\ast {c}_8\le {c}_8\ast \xi \kern0.36em ;-{b}_8\ast \xi \le {b}_3-2.6\ast {b}_8\le {b}_8\ast \xi \\ {}-{a}_8\ast \xi \le {c}_3-3.1\ast {a}_8\le {a}_8\ast \xi \kern0.36em ;-{c}_9\ast \xi \le {a}_3-1.5\ast {c}_9\le {c}_9\ast \xi \\ {}-{b}_9\ast \xi \le {b}_3-2\ast {b}_9\le {b}_9\ast \xi \kern0.36em ;-{a}_9\ast \xi \le {c}_3-2.5\ast {a}_9\le {a}_9\ast \xi \\ {}-{c}_{10}\ast \xi \le {a}_3-1.6\ast {c}_{10}\le {c}_{10}\ast \xi \kern0.36em ;-{b}_{10}\ast \xi \le {b}_3-1.8\ast {b}_{10}\le {b}_{10}\ast \xi \\ {}-{a}_{10}\ast \xi \le {c}_3-2\ast {a}_{10}\le {a}_{10}\ast \xi \kern0.36em ;-{c}_4\ast \xi \le {a}_1-1.5\ast {c}_4\le {c}_4\ast \xi \\ {}-{b}_4\ast \xi \le {b}_1-2\ast {b}_4\le {b}_4\ast \xi \kern0.36em ;-{a}_4\ast \xi \le {c}_1-2.5\ast {a}_4\le {a}_4\ast \xi \\ {}-{c}_4\ast \xi \le {a}_2-1.8\ast {c}_4\le {c}_4\ast \xi \kern0.36em ;-{b}_4\ast \xi \le {b}_2-2.2\ast {b}_4\le {b}_4\ast \xi \\ {}-{a}_4\ast \xi \le {c}_2-2.7\ast {a}_4\le {a}_4\ast \xi \kern0.36em ;-{c}_4\ast \xi \le {a}_5-0.7\ast {c}_4\le {c}_4\ast \xi \\ {}-{b}_4\ast \xi \le {b}_5-1\ast {b}_4\le {b}_4\ast \xi \kern0.36em ;-{a}_4\ast \xi \le {c}_5-1.5\ast {a}_4\le {a}_4\ast \xi \\ {}-{c}_4\ast \xi \le {a}_6-1.2\ast {c}_4\le {c}_4\ast \xi \kern0.36em ;-{b}_4\ast \xi \le {b}_6-1.6\ast {b}_4\le {b}_4\ast \xi \\ {}-{a}_4\ast \xi \le {c}_6-2.1\ast {a}_4\le {a}_4\ast \xi \kern0.36em ;-{c}_4\ast \xi \le {a}_7-1.2\ast {c}_4\le {c}_4\ast \xi \\ {}-{b}_4\ast \xi \le {b}_7-2.2\ast {b}_4\le {b}_4\ast \xi \kern0.36em ;-{a}_4\ast \xi \le {c}_7-2.7\ast {a}_4\le {a}_4\ast \xi \\ {}-{c}_4\ast \xi \le {a}_8-1.5\ast {c}_4\le {c}_4\ast \xi \kern0.36em ;-{b}_4\ast \xi \le {b}_8-2\ast {b}_4\le {b}_4\ast \xi \\ {}-{a}_4\ast \xi \le {c}_8-2.5\ast {a}_4\le {a}_4\ast \xi \kern0.36em ;-{c}_4\ast \xi \le {a}_9-1.2\ast {c}_4\le {c}_4\ast \xi \\ {}-{b}_4\ast \xi \le {b}_9-1.4\ast {b}_4\le {b}_4\ast \xi \kern0.36em ;-{a}_4\ast \xi \le {c}_9-1.6\ast {a}_4\le {a}_4\ast \xi \\ {}-{c}_4\ast \xi \le {a}_{10}-2.9\ast {c}_4\le {c}_4\ast \xi \kern0.36em ;-{b}_4\ast \xi \le {b}_{10}-3.4\ast {b}_4\le {b}_4\ast \xi \\ {}-{a}_4\ast \xi \le {c}_{10}-3.9\ast {a}_4\le {a}_4\ast \xi \kern0.36em \\ {}{\mathrm{a}}_1+4\ast {\mathrm{b}}_1+{\mathrm{c}}_1+{\mathrm{a}}_2+4\ast {\mathrm{b}}_2+{\mathrm{c}}_2+{\mathrm{a}}_3+4\ast {\mathrm{b}}_3+{\mathrm{c}}_3+{\mathrm{a}}_4+4\ast {\mathrm{b}}_4+{\mathrm{c}}_4+\\ {}{\mathrm{a}}_5+4\ast {\mathrm{b}}_5+{\mathrm{c}}_5+{\mathrm{a}}_6+4\ast {\mathrm{b}}_6+{\mathrm{c}}_6+{\mathrm{a}}_7+4\ast {\mathrm{b}}_7+{\mathrm{c}}_7+{\mathrm{a}}_8+4\ast {\mathrm{b}}_8+{\mathrm{c}}_8+\\ {}{\mathrm{a}}_9+4\ast {\mathrm{b}}_9+{\mathrm{c}}_9+{\mathrm{a}}_{10}+4\ast {\mathrm{b}}_{10}+{\mathrm{c}}_{10}=6\\ {}{a}_1\le {b}_1\le {c}_1;{a}_2\le {b}_2\le {c}_2;{a}_3\le {b}_3\le {c}_3;{a}_4\le {b}_4\le {c}_4\\ {}{a}_5\le {b}_5\le {c}_5;{a}_6\le {b}_6\le {c}_6;{a}_7\le {b}_7\le {c}_7;{a}_8\le {b}_8\le {c}_8\\ {}{a}_9\le {b}_9\le {c}_9;{a}_{10}\le {b}_{10}\le {c}_{10};{a}_1,{a}_2,{a}_3,{a}_4,{a}_5,{a}_6,{a}_7,{a}_8,{a}_9,{a}_{10}\ge 0\\ {}\xi \ge 0\end{array}} $$
(23)

Now, by solving this mathematical programming model (Eq. 23) [9], the optimal fuzzy weights of four main capabilities criteria can be calculated as follows:

$$ {\displaystyle \begin{array}{c}{w}_{C1}^{\ast }=\left(\mathrm{0.105,0.105,0.116}\right),\kern0.36em {w}_{C2}^{\ast }=\left(\mathrm{0.081,0.085,0.101}\right)\\ {}{w}_{C3}^{\ast }=\left(\mathrm{0.191,0.194,0.194}\right),\kern0.36em {w}_{C4}^{\ast }=\left(\mathrm{0.046,0.050,0.054}\right)\\ {}{w}_{C5}^{\ast }=\left(\mathrm{0.062,0.075,0.075}\right),\kern0.36em {w}_{C6}^{\ast }=\left(\mathrm{0.053,0.062,0.073}\right)\\ {}{w}_{C7}^{\ast }=\left(\mathrm{0.097,0.099,0.101}\right),\kern0.36em {w}_{C8}^{\ast }=\left(\mathrm{0.074,0.092,0.092}\right)\\ {}{w}_{C9}^{\ast }=\left(\mathrm{0.091,0.094,0.096}\right),\kern0.36em {w}_{C10}^{\ast }=\left(\mathrm{0.129,0.148,0.156}\right)\\ {}{\overset{\sim }{\xi}}^{\ast }=\left(\mathrm{0.495,0.495,0.495}\right)\end{array}} $$

In the following, the crisp values of criteria are calculated using definition (2) and Eq. (2).

$$ {w}_{C1}^{\ast }=0.107,{w}_{C2}^{\ast }=0.087,{w}_{C3}^{\ast }=0.193,{w}_{C4}^{\ast }=0.050,{w}_{C5}^{\ast }=0.073,{w}_{C6}^{\ast }=0.063,{w}_{C7}^{\ast }=0.099, $$
$$ {w}_{C8}^{\ast }=0.089,{w}_{C9}^{\ast }=0.094,{w}_{C10}^{\ast }=0.146,{\overset{\sim }{\xi}}^{\ast }=0.495 $$

Therefore, the weight of ten alternatives, ‘Tobacco use’ (C1),‘Exposure to infections’ (C2), ‘Nutrition’ (C3), ‘Obesity’ (C4), ‘Alcohol’ (C5), ‘Sun exposure’ (C6),‘Radiation exposure’ (C7), ‘Chemicals and other substances’ (C8), ‘Viruses and bacteria’ (C9), ‘Family history of cancer’ (C10), are 0.107, 0.087, 0.193, 0.050, 0.073, 0.063, 0.099, 0.089, 0.094, 0.146 respectively. Finally, the value of CR must be evaluated due to the fact that \( {\tilde{a}}_{BW}=\left( AI, AN\right) \)and the CI = 8.04 (see Table 4). Therefore, the CR value is 0.06 < 0.1 and the results are consistent.

4.3 Sensitivity analysis

Sensitivity analysis is a typical measure to quantify the impact of uncertainty on overall simulation/prediction uncertainty. A variety of sensitivity analysis techniques have been developed [26, 32). In this study, the rank of criteria has been obtained based on a different value of α. According to the experts, a balance value contributed to the Importance and Necessity components. In this regard, a sensitivity analysis has been done for each case study to demonstrate the ranking and consistency rate in different scenarios.

Table 11 shows the rank of criteria in Case one and Case two by considering different values for α. Regarding Case one, a comparison between different scenarios in Table 11 indicates that the lowest level of inconsistency attributes to the \( {CR}_{0.6}=\frac{0.36}{8.04}=0.045<0.1 \); thus, Scenario 6 is the best scenario among eleven scenarios. Moreover, the \( {CR}_0=\frac{1.17}{8.04}=0.146>0.1 \) has the highest inconsistency and is known as the worst scenario that decision-making can take. Scenario 2 is the primary criteria in all ten scenarios, and Scenario 5 is the worst one. Regarding the result of CIs in eleven different scenarios, Scenario 0, Scenario 1, and Scenario 2 are undesirable because of CR > 0.1 [44]; therefore, decision-makers should reconsider these pairwise comparisons. Likewise, in Table 12, lowest level of inconsistency is attributed to Scenario 6; it is the best scenario among eleven scenarios and Scenario 10 is the worst one. Generally, for 0 ≤ α ≤ 0.6 when the value of α is closer to 0.6, the value of ξ∗ decreases and for 0.6 ≤ α ≤ 1, the value of ξ∗ increases.

Table 11 Sensitivity analysis for different values of α in two case studies
Full size table
Table 12 Ranking of the criteria in BWM, Fuzzy BWM and GBWM for Case one
Full size table
Table 13 Ranking of the criteria in BWM, Fuzzy BWM and GBWM for Case two
Full size table

Focusing on Case two, the lowest level of inconsistency attributes to the \( {CR}_{0.4}=\frac{0.495}{8.04}=0.061<0.1 \); thus, Scenario 4 is the best scenario among eleven scenarios. Moreover, the \( {CR}_{10}=\frac{1.17}{8.04}=0.14>0.1 \) has the highest inconsistency and known as the worst scenario which can be chosen by decision-makers. Considering the result of CIs in eleven different scenarios, Scenario 8, Scenario 9, and Scenario 10 are undesirable because of CR > 0.1 [44]. Generally, for 0 ≤ α ≤ 0.4 when the value of α is closer to 0.4, the value of ξ∗ decreases and for 0.4 ≤ α ≤ 1, the value of ξ∗ increases.

4.4 Comparison with similar methods

As previously stated, the decision-makers encounter ambiguity in information and data in real-world problems. In this regard, some researchers tried to introduce some concepts to address this issue in decision-making problems. Among them, Zadeh [55] introduced a fuzzy concept to reduce uncertainty and ambiguity. In the following, Guo and Zhao [24] introduced fuzzy BWM and applied it in different cases to verify this method. Nevertheless, the fuzzy BWM method cannot consider the Necessity concept, along with the Importance concept. To deal with this shortcoming, the presented G-number by Ghoushchi and Khazaeili [19] can reduce the ambiguity of information by considering both the Importance and Necessity components.

In a conceptual comparison between conventional BWM, fuzzy BWM, and GBWM (proposed method), it can be said that BWM is incapable of considering uncertainty in comparison with other methods. Furthermore, GBWM can apply the concepts of Importance and Necessity in the weighting process in different situations, while fuzzy BWM can only consider the Importance concept. In an example from Guo and Zhao [24], the value of a was identified as a moderate level of 0.5 by the expert. It is necessary to explain that the way the mathematical model works in the mentioned methods is the same, and the authors have made an unbiased comparison between these methods and preserved the nature of pairwise comparisons, which is the main input of this model. Since the fuzzy BWM only requires the value of the concept of Importance, this value is extracted from Tables (6) and (7) for each pairwise comparison (the first component of the G-number in the form of a linguistic variable). Also, these extracted elements are used in the BWM model after being converted to crisp numbers. Initially, a comparison of the ranking criteria among BWM, fuzzy BWM, and GBWM, with α = 0.5, is presented in Table 12. In all three methods, ‘Price’ (C2) is the best and ‘Style’ (C5) is the worst criterion. In the case one, it can be seen that the CR for the high-cost performance selection in all methods is less than 0.1.

Regarding Case one, based on the BWM method and including decisive numbers determined by experts in pairwise comparisons, ‘Quality’ (C1), ‘Safety’ (C4), and ‘Comfort’ (C3) are second, third, and fourth criteria, respectively. With regard to the uncertainty in pairwise comparisons, fuzzy BWM is utilized for weighting criteria. In Fuzzy BWM, ‘Quality’ (C1) is still ranked second, but the rank of ‘Safety (C4)’ is upgraded one level, and the rank of the ‘Comfort (C3)’ criterion decreases one level and ranks in third place. To reduce the ambiguity and uncertainty in a pairwise comparison, the GBWM method was proposed. In this method, the rank of ‘Safety’ (C4) is in the fourth (mirroring the fuzzy BWM method), but ‘Comfort (C3)’ moves to second place (one rank lower compared to the fuzzy BWM method), and ‘Quality (C1)’ is upgraded to third place (one rank higher compared to the fuzzy BWM method). In fact, these changes occur because the Necessity concept in the pairwise comparisons process has been implemented. For example, since the Necessity of the criterion C3 is more highly rated than the criterion C2 in pairwise comparisons between criteria from the point of view of decision-makers, criterion C3 has the second rank in Table 12, while this criterion occupies third priority in the fuzzy BWM method.

The same analysis can be made for the second case (Table 13). If we consider ‘Exposure to infections’ (C2) as an example, this criterion is ranked eighth according to the BWM method, but after uncertainly is added to the pairwise comparison process through the fuzzy BWM method, this criterion climbs to seventh place. Furthermore, by simultaneously considering the concepts of Importance and Necessity in the process of pairwise comparisons in the GBWM method, ‘Exposure to infections’ (C2) is upgraded to sixth place.

5 Conclusion

Ambiguities in the decision-making procedure initiate the application of the fuzzy concept in MCDM methods. Existent fuzzy sets cannot consider both aspects of Importance and Necessity in a criterion or in alternatives. To cover this shortcoming, this study seeks to present an extended version of the BWM method using the G-numbers theory. The G-numbers approach seeks to reduce or to eliminate ambiguity in the decision-making process through considering both the Necessity and Importance components. Therefore, the obtained results are closer to reality. In addition to implementing the GBWM method in two case studies to demonstrate its applicability, the outputs of implementation of this method in a high-cost performance selection case were compared with conventional BWM and fuzzy BWM methods to validate their outputs. In Case one, all three methods reached the same ranking for best (C2) and worst (C5) criterion. In Case two, (C3) is ranked best and (C4) is ranked worst; however, the ranks of the other criteria changed through the addition of certainty or the Importance-Necessity concepts. In all the mentioned methods, there was consistency according to the CR result. Once results that are closer to real-world scenarios are reached, decision-makers can proceed more confidently with accurate measurements. Nevertheless, since experts play a direct role in doing pairwise comparisons, their opinions can lead to results consistent with their mindsets. If several experts participate in the pairwise comparisons process, the GBWM method is implemented per expert. Then, the average of obtained weights of model implementation for all experts is considered as the final solution. This, in turn, reduces the deviation from reality. When many experts or people with irrelevant backgrounds participate in the field of the studied problem, the results obtained can lead to unreliable outputs. In addition, not considering the causal relationships between some criteria can reduce the accuracy of the model’s output. For future studies, researchers can implement the proposed method in other case studies with the aim of verifying its capability and applicability in various fields. Besides, the G-numbers theory can be synchronized with other MCDM methods and group decision-making to reduce the ambiguity of information in the process of ranking various alternatives.