An efficient image retrieval method using adaptive weights

Abstract

In existing image retrieval systems using a multipoint query, the neighborhood of the various optimal query points is determined in the same way. The different nature of the various optimal query points was not taken into consideration. This approach confines the performance of the system. To overcome this confinement, in this paper, we propose an image retrieval method through adaptive weights (Aweight) which is possible to compute the various optimal query points, optimal weights and improved distance functions to improve accuracy. In addition, our method constructs clusters without re-clustering the whole feedback image set. The experiments were performed on a set of 10,800 images and the results demonstrate that the proposed method improves performance of system in terms of accuracy.

1 Introduction

Over the past few years, we have witnessed a rapid increase in the size of digital image collection along with the explosive growth of Internet applications. As a result, content based image retrieval system is a major tool for efficient exploitation of this enormous digital resource. In a typical CBIR system, the low-level visual features of images (color, texture, and shape) are automatically extracted and described by high dimensional feature vectors. These feature vectors form a feature database. To retrieve the desired images, a user presents the retrieval system with example images. Based on extracted features, the system will return a result set containing the most similar images to the original query image. Although many algorithms have been proposed to improve the accuracy of image retrieval systems based on low-level features, these algorithms fail when describing high-level semantic concepts [1]. Consequently, the accuracy of CBIR is still far from users’ need.

To approach high-level semantic concepts [2, 3], later works focused on the relevance feedback algorithms in content-based image retrieval. In relevance feedback based CBIR systems, the user selects returned images as positive or negative samples, these samples are inserted into the system as a new query for the sequent iteration of the retrieval process. As a consequence, relevance feedback is a way to scale the accuracy of CBIR systems [4].

Relevant feedback performs the computation of a new query point (or points) in the visual space and changes the coefficients of the distance function. The pioneering works in this area [5,6,7,8,9,10,11], represent a new query as a single point, based on the user’s relevance judgment to perform the adjustment of the weights of feature components to define an optimal query point and the coefficients of the distance function. These techniques are based on the assumption that images in the database that are close to the query image in the visual space are semantically related. However, the similarity between the images perceived by humans is different from the distance between them in the feature space, the relevant images are scattered in different areas of the feature space. In subsequent studies [12,13,14,15] represent new query by multiple points, which are either positive feedback samples or the centroids of clusters [16]. Consequently, we focus on a multipoint query in this paper.

In above image retrieval systems using multipoint query have limitations: First, it does not fully exploit the user’s feedback (the relevance level of each image) in determining the optimal query points. It treats different regions that contain the optimal query points equally, which is not appropriate since the different regions have distinct properties. Second, it assigns the same weight to all neighboring points of the optimal query. Third, in each round of feedback iteration, methods construct clusters with re-clustering the whole feedback images set. These three major shortcomings of above techniques that cause low accuracy and high computational complexity. Can we improve the accuracy of a content based image retrieval system by exploiting the local nature of various optimal query points (that is, automatically determine the optimal query points and corresponding adaptive weights based on feedback samples)? This article will address this question. Our method starts with the observation that “each region that contains an optimal query point has its own local characteristics, that is, each ellipsoid shape that contains an optimal query point has a different direction”. According to this observation, it is easy to recognize that the more regions the weights cover, the higher the potential for performance improvement.

In this paper, we propose an image retrieval method through adaptive weights. Instead of using a weight vector for a variety of regions that contains the various optimal query points, our method automatically computes the optimal query points and corresponding optimal weight vectors according to regions that contain the optimal query points based on user’s feedback. In our method, relations among neighboring points and optimal query points are taken into consideration through the feedback clusters. Also, the existing methods that have created the list of results by taking the neighboring points of the query optimally with the same weight, so the resulting list includes many unrelated points. To overcome this limitation, our method utilizes the relevant feedback points in previous iteration to automatically assign different weights to each neighboring point of the optimal query point. Previous methods performed clustering all the feedback images, so the computational complexity of the methods is high. To overcome this disadvantage, our method only clusters the responses in the first iteration (from the second iteration, the method only classifies the responses into clusters).

The rest of the paper is structured as follows. In Section 2, we briefly present the recent works on image retrieval using single-point and multipoint query. Section 3 describes in detail our proposed method. Section 4 describes the experiment evaluation. Finally, we draw conclusions in Section 5.

2 Related work

Previous relevance feedback studies belong to the following two ways: reweighting and querying point movement [8]. The query point movement approach essentially attempts to improve the estimate of the ideal query point by shifting it toward positive samples and away from negative samples. Query point movement techniques include two categories: single-point movement techniques and multipoint movement techniques. If the refined query at each iteration only consists of one query point, the technique is a single-point category. Conversely, it is a multipoint movement.

Image retrieval systems using single-point movement techniques, such as [6], MARS [10], and MindReader [8], construct a single query point whose distance to the positive samples is near and its distance to the negative samples is far. This idea is based on the Rocchio’s algorithm [17] that has been successfully applied in information retrieval. However, the single-point approach does not guarantee to improve the system’s performance because semantic-related images are scatted to different regions. To overcome the above drawbacks, a multipoint approach is often used. According to this approach, a variety of methods have been proposed. Studies that use a multipoint approach included Query Expansion [14, 18] and Query Decomposition [19]. In these techniques, ideal regions that are capable of containing the most relevant results are identified through query points. In query expansion, query points are grouped into clusters and their centroids are chosen as the representation. The weighted sum of the individual distances to those representations is the distance of a point to an adjusted query point. The number of relevant points involved in the cluster determines the weights. Local clusters in query expansion are different, while the single-point query movement approach considers local clusters to be equal. When relevant images in different clusters in the feature space, multipoint queries can cover irrelevant images. In this case, using separable contours may result in more semantic relevance images. The method that is proposed by [20], issues these positive queries individually and then aggregates the results later into one synthetic list. Their method improves the performance of the CBIR system because it can find relevant images distributed in the whole feature space. However, our previous work [21] pointed out their method only exploits the advantage of the integration of multiple representations and multiple systems without leveraging the semantic information of the images to improve the retrieval accuracy. The main limitation of their method is that they only use the global nature of optimal query points. This restricts the system performance. Our previous work [21] has overcome the limitations of [20]. In addition to returning relevant images that are distributed throughout the feature space, the method also determines the semantic importance of each query and improves system’s performance significantly. Consequently, our previous method does not take into account the locality of each optimal query point, and hence performance is not expected.

3 Proposed method

In this section, we focus on describing our proposed method, called Aweight. This section contains five contents. The first content is our proposed feedback diagram. The second is that the algorithm clusters a set of response images for the initial clustering step. The third is our proposed algorithm for classifying which response images will belong to which cluster in existing clusters. The fourth is our proposed technique for computing optimal query points and adaptive weights. The final content is our proposed algorithm for multipoint query with optimal query points, optimal distance functions and improved distance functions.

3.1 The proposed relevance feedback diagram

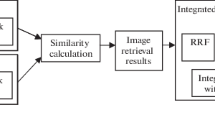
The proposed relevance feedback diagram is described in Fig. 1. In this diagram, we use a multiple representations retrieval approach [22]. Because this approach can assist in obtaining related images scattered in the visual space. The retrieval process is based on the query image that the user entered. In early stage, multiple representations based retrieval with a same Euclidean function are implemented to gather a set of visual diversity images (involves images in different clusters of feature space). After the user provides feedbacks, we achieve a visual diversity relevant set with N sample images. Then, implement the initial clustering algorithm to cluster the set of $N$ sample images into g clusters in order to obtain a training example set (the reason for building a training example set is that it does not need to be re-clustered when adding new images) and there are also g clusters in subsequent retrievals. For each cluster found (requires the user to provide the relevance level of each cluster member), based on the axis of the ellipsoid containing points in the cluster to find the optimal query point (determining the optimal query points) and the weight vector (computing the weight vectors) of the corresponding distance function. In order to get more relevant points, in this diagram, we propose an improved distance formula (computing the improved distance). The method then performs a multipoint query with g optimal query points and the g weight vectors of the corresponding distance function to obtain a “good” result set. To increase the performance of the method, it is necessary to increase the number of feedbacks from the user. However, if a new feedback occurs, the method must re-cluster all the samples which will lead to increased computational complexity of the method. Therefore, in our diagram, we propose the non-clustering technique using the training example set obtained at the first initial clustering step (incremental cluster). After each iteration, the user will check whether the results are satisfied or not. If the user is satisfied with the results, the process will end.

Fig. 1

Diagram of the proposed method

As shown in Fig. 1, the main difference between our proposed method and the existing relevant feedback image retrieval methods lies in the three main components: (a) Determining the optimal query points and Computing the weight vectors; (b) Computing the improved distance functions and (c) Incremental cluster. These components can be embedded in any relevant feedback image retrieval system, so we will describe each of these components separately.

3.2 Clustering a feedback image set

This section presents the clustering algorithm of a feedback image set using k eigenvectors to perform the initialization clustering step of the diagram on Fig. 1.

3.2.1 Represent a feedback image set by a weighted graph

To solve a clustering problem, the data representation first needs to be done [23,24,25]. This section uses a graph representation of neighboring images. Let G $=$ (V,E) be a weighted undirected graph with node set V and edge set E. The elements of V are called vertices (or nodes. Here, we represent neighboring images by a weighted undirected graph G $=$ (V,E): each image is represented as a node s_i ∈V = {s₁,s₂…,s_n}, each pair of vertices (s_i,s_j): s_i,s_j ∈V forms an edge e $\in$ E $=$ { (s_i,s_j): s_i,s_j ∈ V} and the nonnegative weight a_ij of an edge (s_i,s_j), indicating the similarity between two nodes, is a function of the similarity between nodes (images) s_i and s_j. and the non-negative weight a_ij of an edge (s_i, s_j) indicates the similarity between nodes s_i and s_j.

Affinity matrix A [26,27,28] is defined by the formula (1):

$$ a_{ij}=e^{\frac{{-\vert \vert s_{i}-s_{j}\vert \vert }^{2}}{{2\sigma }^{2}}} (\mathrm{i} \ne \mathrm{j}), \mathrm{a}_{\text{ii}}= 0 $$

(1)

where the scaling parameter $\sigma ^{\mathrm {2}}$ quickly controls a_ij falls off with the similarity between s_i and s_j. A method for choosing the scaling parameter automatically can see in [29]. The a_ij value between the two images is “high” if the two images are very similar.

3.2.2 The initial clustering algorithm

After the images are represented by a graph, the clustering can be treated as a graph partitioning problem. Among the graph partitioning methods, spectral graph partitioning ones [26, 27, 30, 31] are shown to be effective in many areas including image segmentation [26, 27], object recognition [31] and motion analysis [30]. Here, for clustered images, we use the k-way cut with k Eigenvectors method [29].

In general, the goal of a graph partitioning method is to organize the nodes into groups so that the distance between the members in the group is small, and/or the distance between the groups is high. Given a graph G $=$ (V, E) with the affine matrix A, to determine the cost of dividing nodes into two discrete sets C₁ and C₂ (C₁ ∩ C₂ = ∅ and C₁ ∪ C₂ =V) is the sum of the weights of the edges that connect the two sets. Next, we briefly describe the method based on A. Y. Ng et al. (see in detail at [29]).

First, the affinity matrix is calculated according to (1). The diagonal matrix D is the matrix whose (i, i) component are the sum of row i of A. The diagonal entries of the diagonal matrix D are defined by (2):

$$ D_{ii}={\sum}_{j = 1,\ldots,n} a_{ij} $$

(2)

The Laplacian matrix is defined as (3)

$$ L=D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\mathbf{ } $$

(3)

Find x₁,x₂,…,x_k the k largest eigenvectors of L, where x₁ = (x₁₁,x₁₂,x₁₃,…,x_1n), x₂ = (x₂₁,x₂₂,x₂₃,…,x_2n), … .x_k = (x_k1,x_k2,x_k3,…,x_kn) and form the matrix $X=[{x_{1}^{T}},{x_{2}^{T}},{\ldots } {x_{k}^{T}}]\in R^{n\times k}$.

From the matrix X, we construct the matrix Y by renormalizing each row of X for unit length

$$ Y_{ij}=\frac{\mathrm{X}_{\text{ij}}}{\left( {\sum}_{\mathrm{j}} \mathrm{X}_{\text{ij}}^{\mathrm{2}}\right) ^{\frac{1}{2}}} $$

(4)

Each point in $R^{k}$ represents a row of Y, use the K-Means algorithm to cluster them into k clusters. Finally, if row i of matrix Y was assigned to cluster j then point s_i belongs to cluster j.

Figure 2 below describes the initial clustering algorithm that uses k eigenvectors, named CISE (Clustering Images Set using Eigenvectors).

Fig. 2

CISE Algorithm

3.3 The incremental clustering

There are some clustering algorithms such as: K-mean [32], K-medoid [33],… However, whenever new images are added, these algorithms must be clustered from the beginning. Therefore, these algorithms are not suitable in the case of online requirements, for example, the case that applies to a small set of images (such as, the result of a single response) but requires clustering immediately while multiple images still need to be added and subsequent clustering does not need to proceed with previous data. The algorithm that satisfies this online case must be “incremental” or called incremental clustering.

This section presents our proposed algorithm for performing the incremental clustering step in Fig. 1, named INC (incremental clustering). INC algorithm defines the classification function through discriminant functions. In INC algorithm, based on the g clusters and training examples obtained from the CISE algorithm (see Section 3.2) to construct g discriminant functions $f_{i}(x_{k}\mathrm {)(}i\mathrm {= 1,..,}g)$. The object $x_{k}$ is assigned to the cluster i if $\forall f_{i}\left (x_{k} \right )>f_{j}\left (x_{k} \right ),j\ne i$.

Let N be the number of sample images. Let d denotes the dimension of the feature vector. Let $x_{i}=[x_{i1},{\ldots } x_{id}]$ be the feature vector of ith image, 1 ≤i ≤N. Let X denotes the matrix that contains N feature vectors $X={[x_{1},\ldots ,x_{N}]}^{T}$. $Y={[y_{1}\ldots ,y_{N}]}^{T}$ is the matrix that contains the labels of the cluster (dependent variable). We will use the symbol g to denote the number of clusters. $X^{(i)}$ is the matrix that represents the images in cluster i $X^{(i)}={[x_{1}^{(i)},\ldots ,x_{n_{i}}^{(i)}]}^{T}$ (where $n_{i}$ is the number of images for ith cluster). $\mu$ is global mean vector that is mean of the whole image set $\mu =[\bar {x}_{1},\bar {x}_{2}{\ldots } \bar {x}_{d}]$. μ⁽ⁱ⁾ is mean vector in ith cluster, $1\le \mathrm {i}\le \mathrm {g}$, $\mu ^{(i)}=[\bar {x}_{1}^{(i)},{\ldots } \bar {x}_{d}^{(i)}]$.

Let $X^{(i)^{o}}={\left (x_{1}^{(i)^{o}},x_{2}^{(i)^{o}},{\ldots } .,x_{n_{i}}^{\left (i \right )^{o}} \right )}^{T}$ be the mean corrected data of ith cluster, where $x_{j}^{(i)^{o}}$ defined by (5)

$$ x_{j}^{(i)^{o}}={(x_{j}^{(i)})}^{T}-\mu^{T},\quad1\le \mathrm{j}\le n_{i} $$

(5)

Let $c^{(i)}$ denote covariance matrix of ith cluster. It is defined by the formula (6):

$$ c^{(i)}=\frac{{(x^{(i)^{o}})}^{T}x^{(i)^{o}}}{n_{i}} $$

(6)

Let C be pooled within cluster covariance matrix. It is calculated as the following formula (7):

$$ C(rs)=\frac{1}{N}{\sum}_{i = 1}^{g} n_{i} c^{(i)}(rs) $$

(7)

Let $C^{-1}$ be the inverse matrix of C. Let P be the prior probability vector $P={[p_{1}\ldots ,p_{g}]}^{T}$ with p_i representing the prior probability of its cluster. Because we do not know the prior probability, we just assume it is equal to total image of each cluster divided by the total image, that is:

$$ p_{i}=\frac{n_{i}}{N} $$

(8)

We should assign image $x_{k}$ to cluster i that has maximum $f_{i}$. The function $f_{i}$ [34] is defined by the formula (9)

$$ f_{i}=\mu^{(i)}C^{-1}{x_{k}^{T}}-\frac{1}{2}\mu^{(i)}C^{-1}\mu^{(i)^{T}}+\ln {(p_{i})} $$

(9)

Figure 3 below is an INC (incremental clustering) algorithm that performs cluster prediction of a new image.

Fig. 3

INC algorithm

3.4 The proposed technique for determining the optimal query points and the adaptive weights

In this section, we present our proposed technique for determining the optimal query point and the adaptive weights of the distance function. The technique determines the optimal query point and the adaptive weights according to a given cluster of images. In the case of multiple clusters, this technique is performed for each cluster.

Given a cluster i, $1\le i\le g$, each image in the cluster i that is represented by $x_{j}^{(i)}={(x}_{j1},x_{j2},\ldots ,x_{jd})$, 1 ≤ j ≤ n_i. $X^{(i)}$ is the matrix that represents the images in cluster i $X^{(i)}={[x_{1}^{(i)}\ldots ,x_{n_{i}}^{(i)}]}^{T}$ (where $n_{i}$ denotes the number of images for ith cluster). Suppose the optimal query vector for cluster i is $q^{(i)}={[q_{1}^{(i)},q_{2}^{(i)},\ldots ,q_{d}^{(i)}]}^{T}\in R^{d}$. Assume a user’s evaluation information in terms of relevancy for each $x_{j}^{(i)}$, $1\le j\le n_{i}$ is $v_{j}^{(i)}$, vector $V^{(i)}={[v_{1}^{(i)},v_{2}^{(i)},{\ldots } .,v_{n_{i}}^{(i)}]}^{T}$ represents the user’s feedback of the relevance level of each image in cluster i $X^{(i)}={[x_{1}^{(i)}\ldots ,x_{n_{i}}^{(i)}]}^{T}$. Assume that the distance from $x_{j}^{(i)}$ to $q^{(i)}$ is a generalized ellipsoid distance and weight matrix $W^{(i)}=[w_{jk}^{(i)}]\in R^{dxd}$ defines a general ellipsoid distance. The problem of finding the optimal query point $q^{(i)}$ and the weight matrix $W^{(i)}$ is referred to the problem of minimizing penalties as follows:

$$\begin{array}{@{}rcl@{}} (W^{(i)},q^{(i)})&=&\underset{W^{(i)},q^{(i)}}{\arg\min}\sum\limits_{j = 1}^{n_{i}}v_{j}^{(i)}{(x_{j}^{(i)}-q^{(i)})^{T}} W^{(i)}(x_{j}^{(i)}-q^{(i)})\\ &&\text{Subject to:}~\det(W^{(i)})= 1 \end{array} $$

(10)

Where det(W⁽ⁱ⁾) is the determinant of the matrix $W^{(i)}$ (to avoid the case $W^{(i)}$ is a zero matrix).

Let $C^{(i)}=[c_{jk}^{\left (i \right )}]$ be the weighted covariance matrix of the images in the cluster i with $c_{jk}^{(i)}$ defined by (11)

$$ c_{jk}^{(i)}=\sum\limits_{l = 1}^{n_{i}} {{v_{l}}^{(i)}(x_{lk}^{(i)}-\bar{x}_{k}^{(i)})(x_{lj}^{(i)}-\bar{x}_{j}^{(i)})} $$

(11)

To solve the minimization problem, we use the method of Lagrange multipliers.

As a result, we obtain an optimal query point $q^{(i)}$ as (12):

$$ q^{(i)}=\frac{{{(X}^{(i)})}^{T}V^{(i)}}{{\sum}_{j = 1}^{n_{i}} v_{j}^{(i)} }~\text{where}~q_{j}^{(i)}=\!\frac{{\sum}_{j = 1}^{n_{i}} {v_{j}^{(i)}x_{jm}^{(i)}} }{{\sum}_{j = 1}^{n_{i}} v_{j}^{(i)} },1\le m\le d $$

(12)

and, consequently, we are also achieved a weight matrix $W^{(i)}$ as follows:

If ${{(C}^{(i)})}^{-1}$ exists, the matrix $W^{(i)}$ is

$$ W^{(i)}={{\det}(C^{(i)})}^{\frac{1}{n}}{{(C}^{(i)})}^{-1} $$

(13)

if the $C^{(i)}$ (see (11)) is singular and non-invertible, we first compute the SVD decomposition of the covariance matrix $C^{(i)}$. Since $C^{(i)}$ is a symmetric matrix, we get:

$$ C^{(i)}={\mathrm{U}^{(i)}\mathrm{D}^{(i)}{\mathrm{(U}}^{(i)})}^{T} $$

(14)

where $\mathrm {U}^{(i)}$ is a orthonormal n $\times$ n matrix and $\mathrm {D}^{(i)}=diag(\sigma _{1},\ldots ,\sigma _{s},0,\ldots ,0)$ (where s is the rank of $C^{(i)}$) is a diagonal n× n matrix. Then the matrix pseudo-inverse matrix of $C^{(i)}$ [35]. is defined as (15)

$$ (C^{(i)})^{+}={\mathrm{U}^{(i)}{(\mathrm{D}^{(i)})}^{+}(\mathrm{U}^{(i)})}^{T} $$

(15)

Where ${(\mathrm {D}^{(i)})}^{+}=diag(\frac {1}{\sigma _{1}^{(i)}},\ldots ,\frac {1}{\sigma _{s}^{(i)}},0,\ldots ,0)$. We then use instead of (13),

$$ W^{(i)}={{\alpha^{(i)}(C}^{(i)})}^{+} $$

(16)

Where $\alpha ^{(i)}={(\sigma _{1}^{(i)},\ldots ,\sigma _{s}^{(i)})}^{1/s}$.

Since the optimal query vector $q^{(i)}$ and the weight matrix $W^{\left (i \right )}$, we have the distance function as in (17):

$$ d^{\left( i \right)}(x_{j}^{(i)},q^{(i)})={(x_{j}^{(i)},q^{(i)})}^{T}W^{(i)}(x_{j}^{(i)},q^{(i)}) $$

(17)

Figure 4 below is the FQM (finding an Optimal Query Point and Weight Matrix of the Distance Function) algorithm that performs the determination of the optimal query point and the weight matrix of distance functions for cluster i.

Fig. 4

FQM algorithm

3.5 Algorithm

The FQM algorithm on Fig. 4 allows us to find the optimal query points and optimal distance functions. However, if we capture the neighboring images of this optimal query point with the corresponding optimal distance function to generate a list of returned images, the list will consist of images in the correspo- nding ellipse. Therefore, the list of returned images may include many unrelated images as shown below.

Assume that at the previous iteration, we have a cluster of 5 positive feedback samples (small circle on Fig. 5). Based on these 5 positive feedback samples, we determine the ellipse (the green dashed line) and the optimal query point (small triangle) as shown in Fig. 5.

Fig. 5

An ellipse is generated from positive feedback samples

We will use the ellipse defined on Fig. 5 to generate a list of returned results corresponding to the optimal query point and the optimal distance function. Assume that we have 21 points in this ellipse as shown in Fig. 6 with the small circle points as related points and the small cross points as unrelated points. To get the list of returned results (assuming the list contains 9 images), we will obtain 09 points (02 relevant points and 07 irrelevant points) in small ellipses (yellow dashed lines on the image in Fig. 6). Thus, the list of returned results corresponding to the optimal query point and the optimal distance function includes many unrelated images. The reason for this is because we only care about the optimal distance from any point in the ellipse to the corresponding optimal query point, i.e., the weight of the points in the ellipse is equal.

Fig. 6

Illustrate how to get a list of results including many unrelated images

To overcome the above limitations, we propose an improved distance function. The main idea is to consider each point in the ellipse to have its own weight. The weight of each point is calculated based on the number of positive feedback samples from the previous iteration in neighbor k of that point. Figure 7 illustrates the case of k equals 3, the returned points may not be in the small ellipse (the points are in the red dashed line) and thus more related points may be obtained.

Fig. 7

Illustrates how to calculate the distance from one point in the ellipse to the corresponding optimal query point

Let Cpf ($q_{opt}^{(i)})$ be the list of points in the cluster of positive feedback samples corresponding to the optimal query point i $q_{opt}^{(i)}$, i.e., the list of points in the corresponding ellipse. The ${Nearest}_{k}(p_{i})$ is the list of k points nearest to $p_{i}$. $\wedge E\mathrm {=\{}e{\vert }e{\in }{Nearest}_{k}(p_{i})e{\in Cpf(}q_{opt}^{(i)}\mathrm {)\}}$. $\wedge E\mathrm {=\{}e{\vert }e{\in }{Nearest}_{k}(p_{i})e{\in Cpf(}q_{opt}^{(i)}\mathrm {)\}}$ are the positive feedback points of the neighborhood k of $p_{i}$. Our proposed distance formula is written as follows:

$$ d_{Improved}(p_{i}q_{opt}^{\left( i \right)}\mathrm{)=}\frac{\left| E \right|}{k}{\ast }d_{FQM}(p_{i}q_{opt}^{(i)}) $$

(18)

Where: $d_{Improved}(p_{i}q_{opt}^{(i)})$ is the improvement distance from a point $p_{i}$ to the optimal query point $q_{opt}^{(i)}$. $d_{FQM}(p_{i}q_{opt}^{(i)})$ is the distance from point $p_{i}$ to point $q_{opt}^{(i)}$ according to the FQM algorithm in Fig. 4.

Figure 8 below describes an image retrieval algorithm that uses optimal query points, optimal distance functions, and improved distance functions, named Aweight.

Fig. 8

Aweight algorithm

The image retrieval algorithm using the adaptive weights in Fig. 8 is implemented as follows: First, an original query image is entered into the system by the user, the algorithm performs multiple representations retrieval by using the Euclidean distance function d with weight vector W (the default values of the weighted vectors are equal) in space S and store the initial result set in the Result(Q_initial). Subsequently, on the initial result set Result(Q_initial), the user chooses N images with corresponding relevance level $V^{(initial)}$ through the Feedback$\mathrm {(Result}\left (\mathrm {Q}_{\text {initial}} \right )\mathrm {,N,}V^{(initial)})$ function. Consequently, we have a set of N initial feedback images Relevant(Q_initial,N). On set of N feedback images Relevant(Q_initial,N), we split it into g clusters. Subsequently, g clusters are saved to X through CISE(Relevant(Q_initial,N), g, X) function to obtain the training set D$\leftarrow${ $(x_{i}y_{i})$/i $=$ 1,…,N; $y_{i}\in \{1,{\ldots } g$ } . Then, calculate the optimal query point $q^{\left (i \right )}$ and the weight matrix $W^{(i)}$ through procedure FQM(X⁽ⁱ⁾V ⁽ⁱ⁾, $q^{(i)}$, $W^{(i)}$) with the input information the value $v_{j}^{(i)}$ for each j^th image of ith cluster. Based on the optimal query point $q^{(i)}$ and g the weighted matrix $W^{(i)}$ and the distance function $d_{Improved}$, algorithm returns the k images on S through $<$g, $\{q^{(1)}$, q⁽¹⁾,...q^(g)}{W⁽¹⁾,W⁽¹⁾,…,W^(g)},d_Improved,S,k > and assigns it to Result(Q_opt). On the Result(Q_opt), the user chooses N’ feedback images with corresponding relevance levels $V^{(opt)}$ through the Feedback$\mathrm {(Result}(\mathrm {Q}_{\text {opt}})\mathrm {N}^{{\prime }}V^{(opt)})$ function to have the set Relevant(Q_opt,N’). Since the algorithm does not re-cluster all feedback images, it is necessary to predict the cluster of each x_j ∈ Relevant(Q_opt,N’) (j $=$ 1..N’) through INC(D, x_j ∈ Relevant(Q_opt,N’), i) procedure and add x_j to the cluster $X^{(i)}$ through Add(x_j, $X^{(i)})$. This process only stops when the user is satisfied with the results.

4 Experimental results

4.1 Test environment

4.1.1 The set of images

We use a subset of images from the Corel Photo Gallery to perform our experiments. This subset contains 10800 images with 80 different categories. These categories include elephants, autumn, bonsai, aviation, castle, clouds, dogs, icebergs, primate, ship, stalactites, forward fire, tigers, trains, waterfalls,… each which contains 100 or more images. The size of every image in the subset of images is either 120 $\times$ 80 or 80 $\times$ 120.

4.1.2 Low-level visual feature vectors of images

In the experiment, we use two types of low-level features of the image including color features and texture features. For color features, we employ the color histogram, color correlogram and color moment to represent the color information. We employ wavelet transform and Gabor Wavelet to represent the texture features of images. Combine these features, we have a vector of 190 components (i.e., $32 + 64+ 6 + 40+ 48 = 190$).

4.1.3 Representations for each image

In this experiment, we employ four image representations for each image including color, color negative, grayscale, and grayscale-negative (where each representation contains three color features and two texture features). To get a similarity, these features are compared pairwise and then combined linearly with equal weights. Five features of each representation form 2-d table with 10800 lines (each line of the table represents a feature vector of the image of 190 elements).

4.1.4 Ground truth

In the experiments, we use the COREL category as a ground truth (i.e., we regard all the images in the same COREL category to be relevant) to obtain the relevance feedback since the user wants to retrieve the images based on high-level concepts. The ground truth file contains 1,981,320 thousand vector features with three components: image queryID, imageID and relevance.

4.2 Simulate user feedback

To simulate user feedback on the Corel Photo Gallery, we perform an initial query to get the the initial query result set. Then, based on the ground truth of images from the Corel image database, the system will identify N relevant images in this initial query set. The relevant images from the first iteration will be grouped into g clusters and the training set is created from this g clusters. Next, g clusters are used to construct optimal query points and determine the weights for subsequent retrieval. Then, the retrieval results are combined to create a composite result list according to the disjunctive queries strategy. From the second iteration, still base on the ground truth, the new feedbacks will be added to the clusters instead of clustering from the beginning.

4.3 Evaluation

In our experiment, the parameters were chosen as follows:

The performance of the system is evaluated on COREL database including 10800 images, all images in the database were selected as the query images. We evaluate our method based on the average accuracy of 10800 query images. Each query will have 100 returned images. We chose 100 returned images for a query because users usually only view within two screens and each screen contains 50 images.

We use average accuracy and standard deviation to evaluate the performance of compared methods. Average accuracy is the percentage of relevant images in the top ranked images presented to the user and is calculated by the average of all queries. Average accuracy is the principal evaluation criterion, which evaluates the accuracy of comparative methods. Standard deviation is used to measure the variation of average accuracy.

Table 1 The average accuracy in three feedbacks of the compared methods (i.e., CRF, DSSA, WATH, SAF and AWEIGHT)

4.3.1 Evaluate the overall accuracy of our proposed method

Three feedback settings are made to compare the 2, 4 and 8 query points and one feedback strategy (see Section 4.2). Our method is compared with four other methods including CRF(Complementary Relevance Feedback) [3], DSSA (Discriminative Semantic Subspace Analysis) [12], WATH (Weighted Average of Triangular Histograms) [36] and SAF (shape annotation framework) [37]. In our experiments, we obtained an average accuracy of 10800 queries at levels 2, 4, and 8 query points. Moreover, there are three feedback loops which are used in our experiment. The experimental results are shown in Fig. 9. the horizontal axis represents the number of query points and the vertical axis representing the accuracy of the methods. The reason we use only up to 8 query points is that: First, the number of samples for three feedback iterations is often not large enough to produce more clusters. Second, we also want to show that although the number of query points is not much, our method’s accuracy is still high. Four curves indicate the accuracy of the five methods including DSSA, CRF, WATH, SAF and AWEIGHT.

Fig. 9

Compare the accuracy of the five methods

The average accuracy of 10800 queries is shown in Table 1 and by the graph in Fig. 9 below. Because the space of the article is limited, we only show the average accuracy of 80 query categories (see Table 2 in Appendix A), and the full average accuracy of 10800 queries is displayed on the website: http://117.6.134.238:368/Aweight_results.html.

Table 1 shows the average accuracy of five methods, CRF, DSSA, WATH, SAF and our AWEIGHT method at the second feedback loop with the number of query points are 2, 4 and 8. With two query points, our method has higher accuracy than the four methods CRF, DSSA, WATH, SAF are 9.37%, 1.89%, 4.68% and 5.86%, respectively. For four query points, our method has higher accuracy than the four methods CRF, DSSA, WATH, SAF are 18.008%, 6%, 11.028 and 13.398%, respectively. At eight query points, our method has higher accuracy than the four methods CRF, DSSA, WATH, SAF are 19.26%, 2.79%, 9.07% and 11.67%, respectively.

In Fig. 9, we find that as the number of points increases, the accuracy of the four methods increases. The main reason for this is because it uses a multipoint approach, which uses multiple query points to better cover the feature space. However, the AWEIGHT method outperforms the remaining four methods in all cases of 2, 4 and 8 query points. Our method is high because it takes advantage of the local information of the various query points.

Figure 10 shows the standard deviations of the compared methods. As can be seen from Fig. 10, the standard deviation of our proposed method is better than the four compared methods (i.e., CRF, DSSA, WATH and SAF) for all three cases of 2, 4, and 8 query points.

Fig. 10

Compare the standard deviation of the five methods

To test the sensitivity of our proposed method, we randomly select 1000 images on the corel database as the query images. We also asked 50 students to respond to 1000 queries (represent the subjective perception of the user). Figure 11 shows the average accuracy of our proposed method in two scenarios: the first is to use the ground truth of images from the Corel image database, called Aweight_GT (Aweight with Ground Truth). The second is to use the subjective perception of the user, called Aweight_UP (Aweight with User Perception). From Fig. 11 it can be seen that the average accuracy of our proposed method with the use of feedback from students has decreased but not much.

Fig. 11

Compare the average accuracy of Aweight_GT and that of Aweight_UP

4.3.2 Evaluate the accuracy of the proposed method under the circumstances

To illustrate the first three advantages of our proposed method, we conducted experiments to compare our proposed method with the following cases: First, Aweight does not take advantage of the locality of a region to determine optimal query points and optimal distance functions, called Aweight_WLNR (Aweight without local nature of the region). Second, Aweight does not use improved distance functions, called Aweight_WIDF (Aweight without improved distance functions). In addition, we also compared our proposed method with the FGSSH (Fast graph similarity search via hashing) [38,39,40]. Figure 12 shows the average accuracy of 10800 query images with three feedback iterations for 2, 4, and 8 query points.

Fig. 12

Compare the average accuracy of the original Aweight with Aweight_WLNR, Aweight_WIDF and FGSSH

As can be seen in Fig. 12, the proposed Aweight method consistently outperforms the Aweight_WLNR, Aweight_WIDF and FGSSH. Also, in our experiments, we found that Aweight_WLNR’s accuracy was much less than that of Aweight and that of Aweight_WIDF. This indicates that the locality of the region has a great influence on the retrieval results.

So, experimental results in Fig. 12 demonstrate the first three advantages of our proposed method of utilizing the locality of a regions to determine the optimal query points, optimal weights (or optimal distance functions) and improved distance functions.

4.3.3 Computational efficiency

Another advantage of the Aweight method is the efficiency achieved by using incremental clustering. With this clustering, the expensive clustering calculation in each feedback loop is avoided. We used queries to evaluate the computation time of our Aweight system with that of the system when no incremental clustering is used called Aweight_WRC (Aweight without Re-Cluster). We selects all 10800 images in the Corel database as query images and their average query processing time (Fig. 13) for three iterations. From Fig. 13, we can see that the query processing time of our Aweight system is much less than that of Aweight_WRC. The results indicate that the incremental clustering step in the Aweight method is very time efficient.

Fig. 13

The image retrieval time of the proposed method for two different cases

5 Conclusions

This paper presents our proposed Aweight method, an efficient image retrieval scheme for improving the performance of multiple point retrieval systems. Aweight effectively exploits user’s feedback information through the relevance levels of each feedback image to determine the optimal query points. Aweight fully exploits the locality of each optimal query point instead of using the global nature of the optimal query points as the CBIR systems did. Aweight acquires neighboring points in a way that fully depends on the local nature of each optimal query point. Therefore, Aweight creates neighboring points according to the characteristics of each optimal query. Aweight implements an incremental clustering of user feedback images: The samples in the first feedback were used as training; Samples from the second and subsequent feedbacks will be added to the cluster without having to recluster the whole sample; Increased clustering allows Aweight to take advantage of a lot of feedback and does not need to speed up computing. In this sense, Aweight is a method that can be applied in multi-user CBIR systems, multipoint systems with a convex and concave shape.

Therefore, we can conclude that the proposed Aweight method outperforms the DSSA, CRF, WATH and SAF methods.

Appendices

Appendix A

The average accuracy of the AWEIGHT method in each of the 80 categories

Table 2 The average accuracy of the AWEIGHT method in each of the 80 categories with three iterations

Appendix B

The retrieval interface with the initial query image that has ID 84025 of the category pl_flower in the Corel Photo Gallery

Fig. 14

The resulting interface implements the initial query. The result set contains 40 retrieved relevant images over 100 retrieved images

Fig. 15

The top results after one feedback iteration for the initial query. The result set contains 77 retrieved relevant images over 100 retrieved images (Images with red borders in Figs. 14, 15, 16 and 17 imply the same category art_dino with the query image)

Fig. 16

The top results after two feedback iterations for the initial query. The result set contains 86 retrieved relevant images over 100 retrieved images

Fig. 17

The top results after three feedback iterations for the initial query. The result set contains 100 retrieved relevant images over 100 retrieved images